Optimization of Shared Autonomous Vehicles Routing Problem: From the View of Parking
Abstract
1. Introduction
2. Literature Review
2.1. Shared Autonomous Vehicles
2.2. Vehicle Routing Problem with Intermediate Stops
3. Formulation
3.1. Route Constraints
3.2. Time Constraints
4. Proposed Heuristic Solution Framework
| Algorithm 1. The procedure of the VNS. | |
| Input | the set of neighborhood structures , that will be used in the shaking phase |
| Output | The optimized solution |
| 1 | Construct the initial solution |
| 2 | local search |
| 3 | |
| 4 | repeat |
| 5 | shake |
| 6 | |
| 7 | if |
| 8 | , |
| 9 | else |
| 10 | |
| 11 | end if |
| 12 | until |
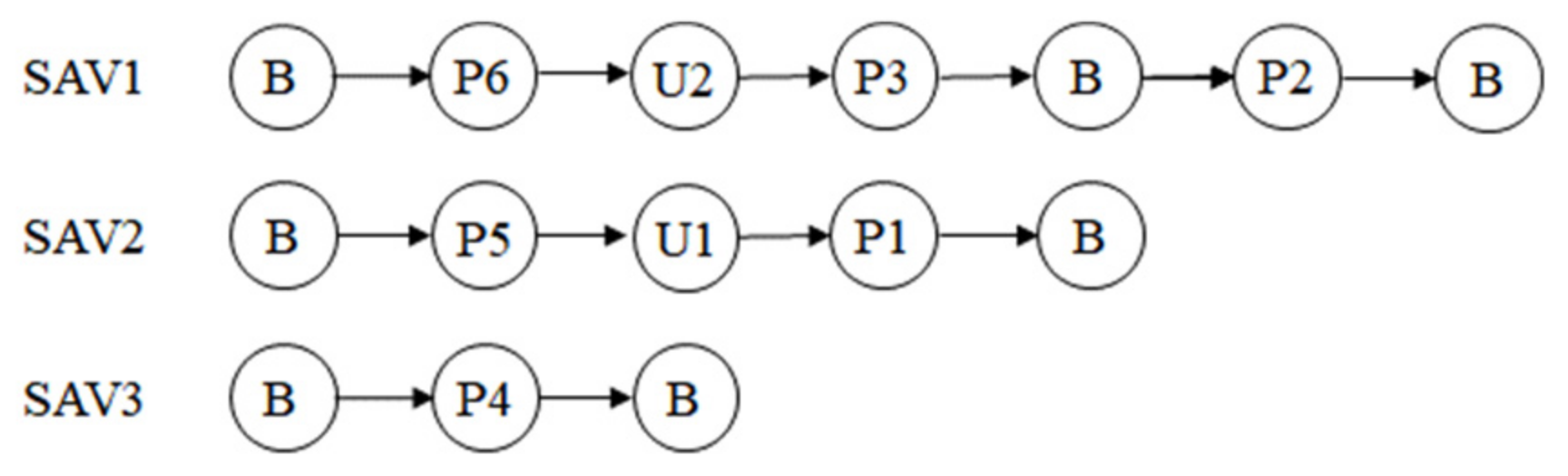
4.1. Label Sequences of Routes
4.2. Construction Algorithm
4.3. Shaking
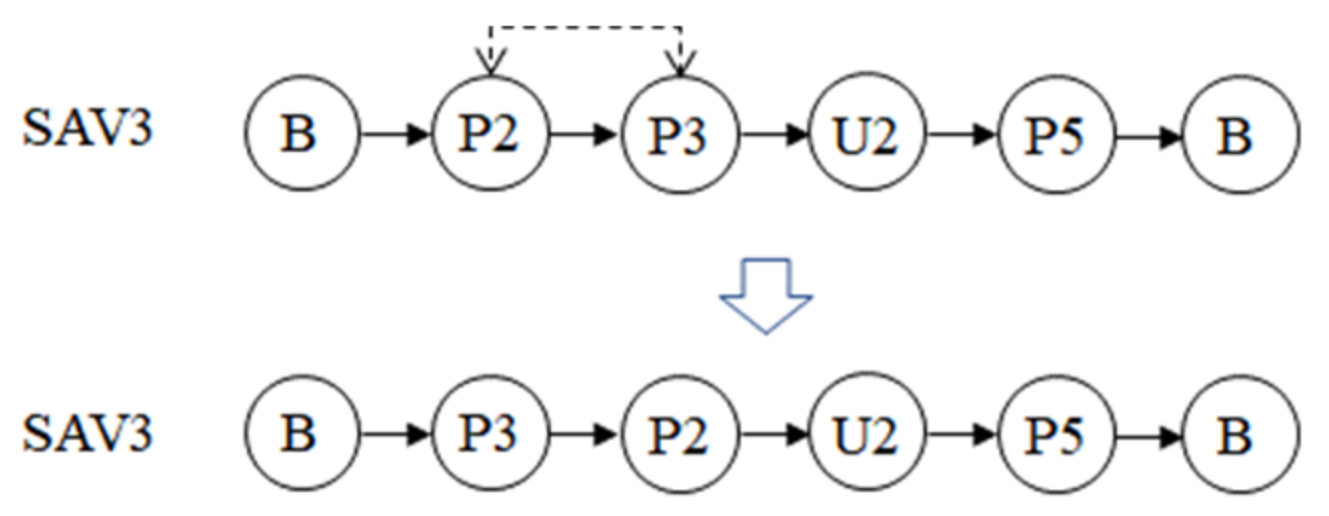
- Parking label removal operator. This kind of operator randomly removes several parking labels on several randomly selected sequences. The removed parking labels include parking lots and the base that is not in the first and last position. Figure 3 shows an example. In this study, there are five operators of this type, each operating on 1, 2, 3, 4, and 5 parking labels.
- 2.
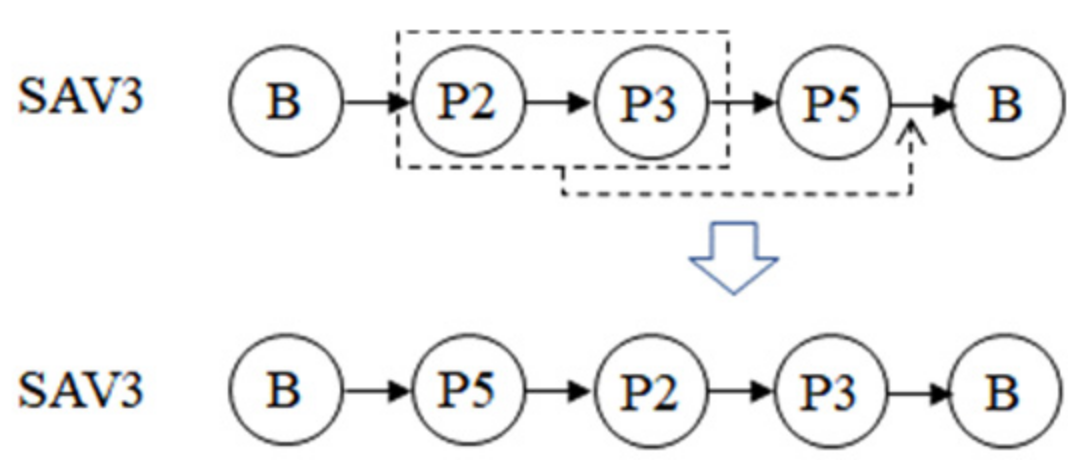
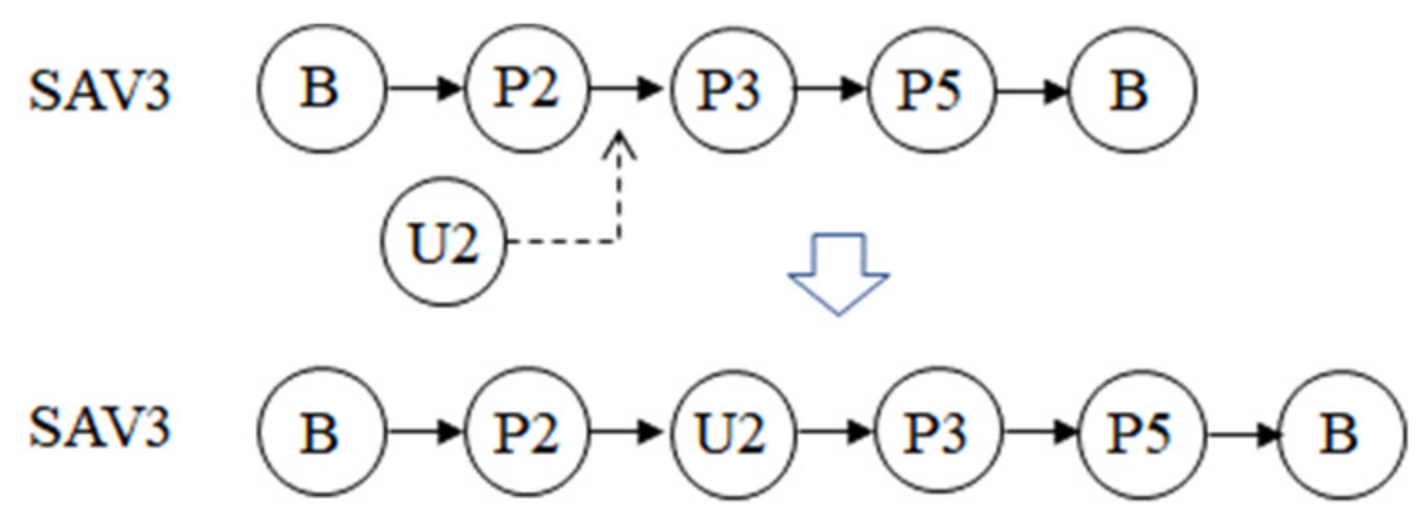
- Parking label replacement operator. This kind of operator randomly replaces several parking labels on several randomly selected sequences. The replaced parking labels include parking lots and the base that is not in the first and last position. Figure 4 shows an example. In this study, there are five operators of this type, each operating on 1, 2, 3, 4, and 5 parking labels.
- 3.
- 4.
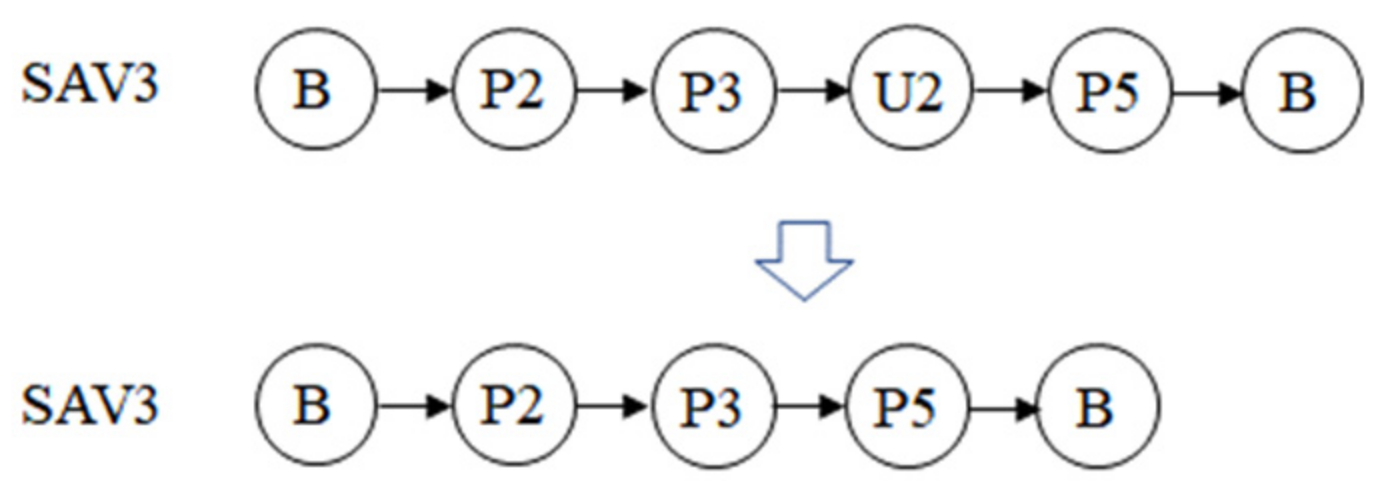
- Or-opt operator [41]. This kind of operator randomly selects a section of labels from a randomly selected sequence and inserts the section into a random position of the sequence. Figure 6 shows an example. In this study, there are four operators of this type, each operating on the section with 2, 3, 4, and 5 adjacent travel demands.
- 5.
- 6.
- 7.
- Exchange operator. This operator swaps two random travel demand labels from two randomly selected sequences. Figure 9 shows an example.
- 8.
- Cross operator. This operator swaps two random sections of labels from two randomly selected sequences. The section does not include the first and last base labels. Figure 10 shows an example.
- 9.
- Icross operator. This operator swaps two random sections of labels from two randomly selected sequences in reverse order. The section does not include the first and last base labels. Figure 11 shows an example.
4.4. Local Search
| Algorithm 2. First improvement (first descent) heuristic. | |
| Input | the set of neighborhood structures , the solution |
| Output | The optimized solution |
| 1 | repeat |
| 2 | ; |
| 3 | repeat |
| 4 | |
| 5 | , |
| 6 | until or |
| 7 | until |
- Single-sequence parking label removal operator. This operator removes one parking label (including the parking lot and the base that is not in the first and last position) on one sequence. Figure 12 shows an example.
- 2.
- Single-sequence parking label replacement operator. This operator replaces one parking label on one sequence and the operator execution should avoid continuous parking labels. The replaced parking labels include parking lots and the base that is not in the first and last position. Figure 13 shows an example.
- 3.
- Single-sequence parking label insertion operator. This operator inserts one parking label into one sequence. Figure 14 shows an example.
5. Numerical Results
5.1. Small-Size Instances
5.2. Large-Size Instances
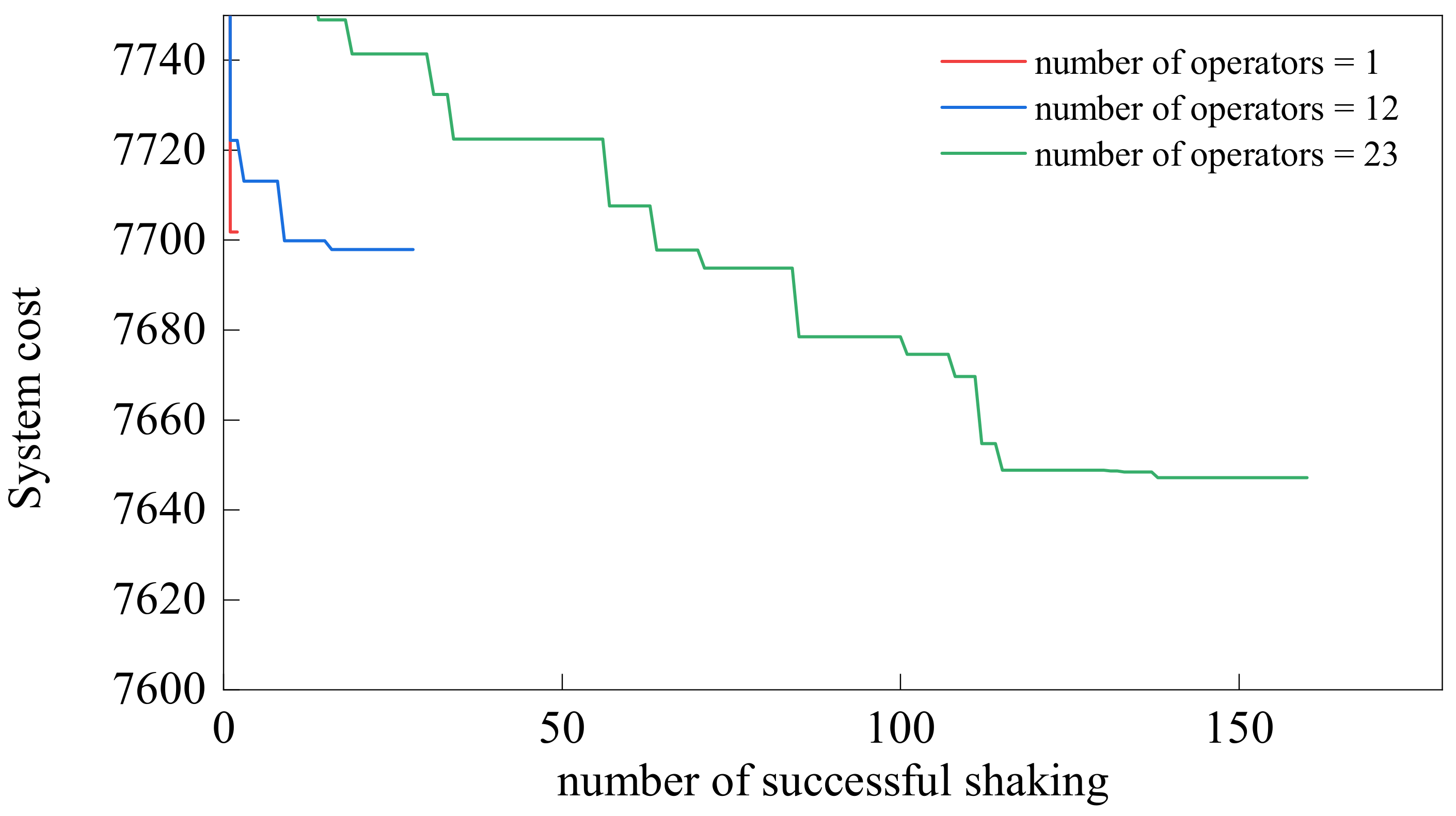
5.2.1. Effect of the Number of Operators in Shaking Procedure
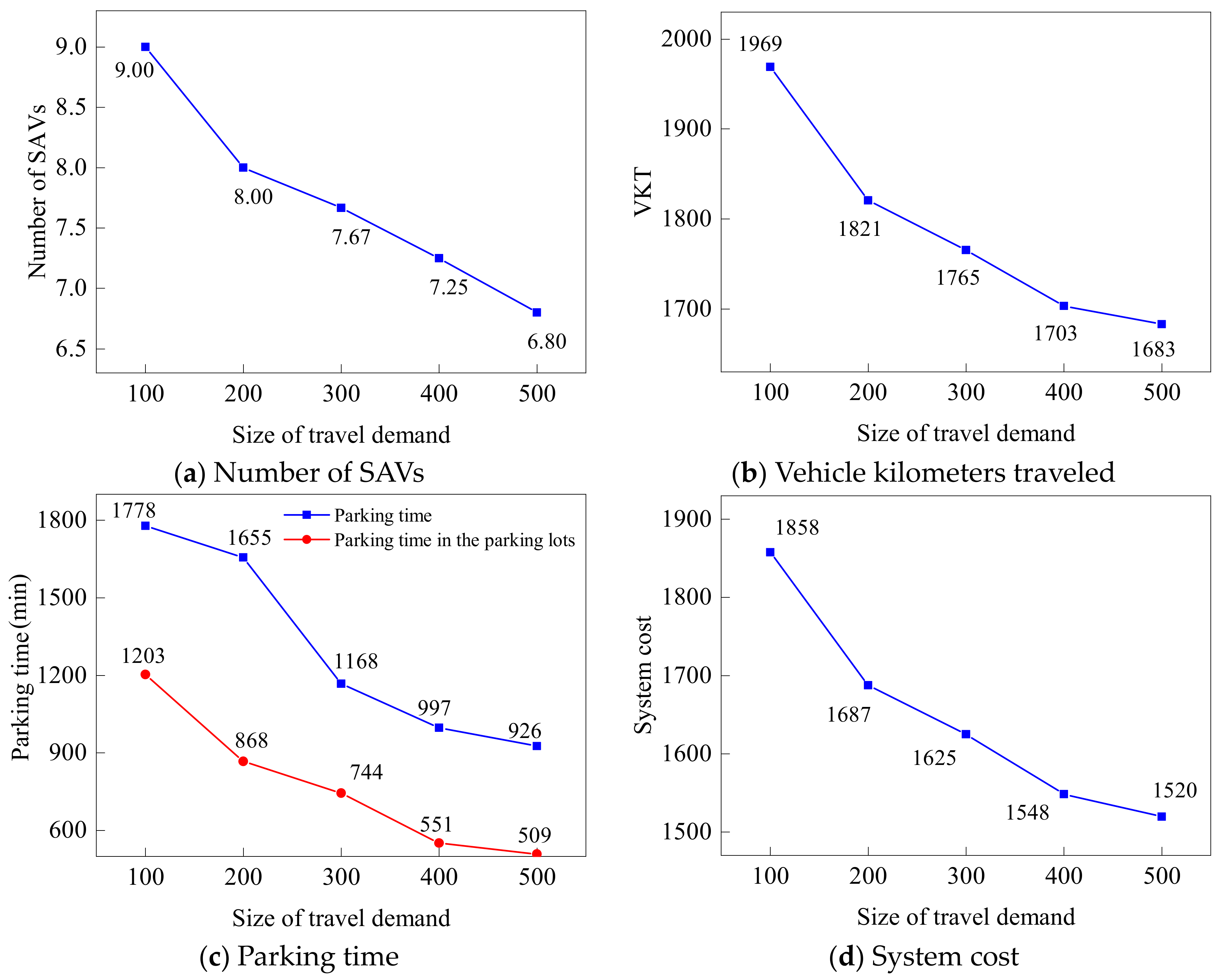
5.2.2. Effect of the Travel Demand
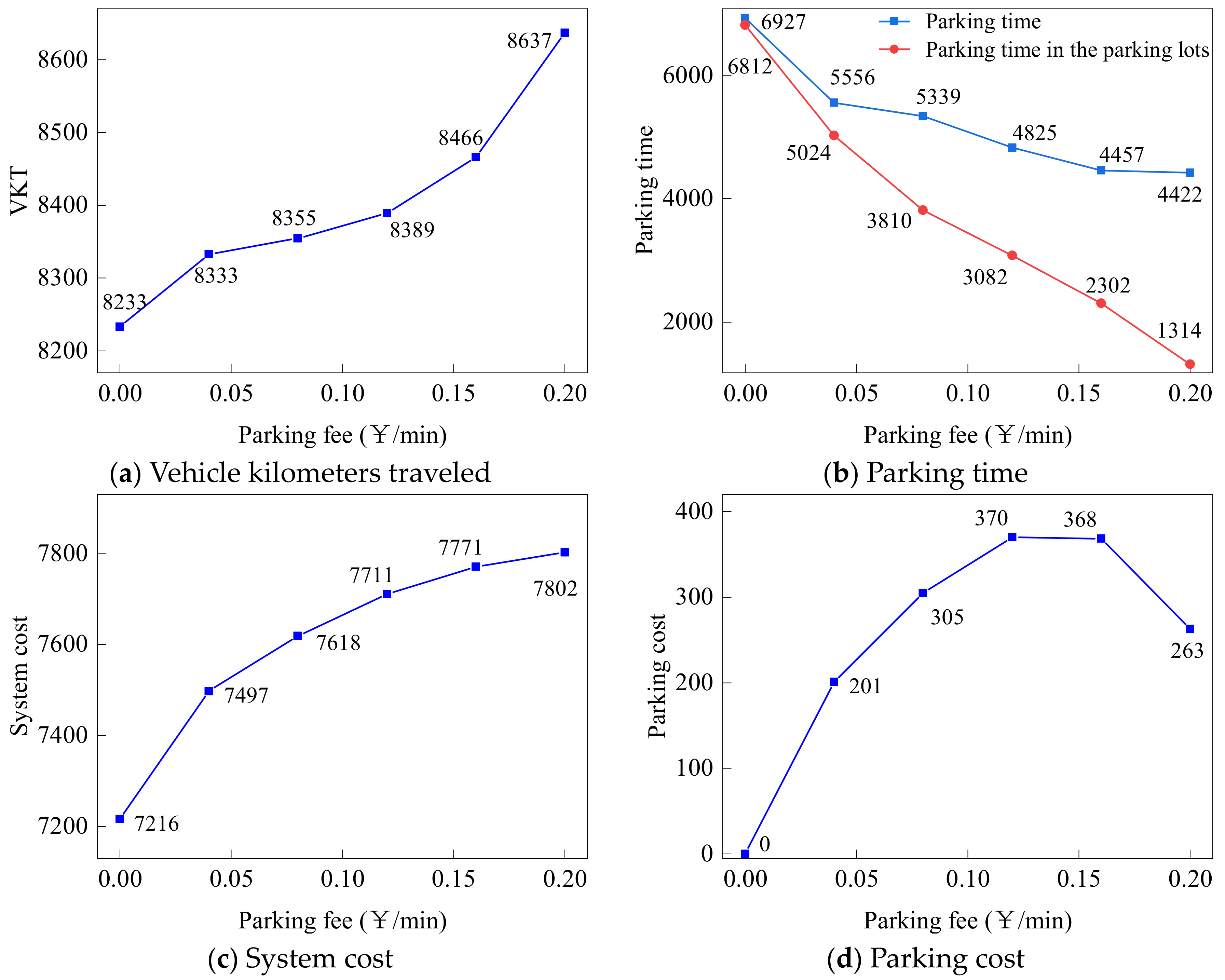
5.2.3. Effect of the Parking Fee
6. Conclusions and Future Work
- The adaptive variable neighborhood search (AVNS) selects the operator in the shaking step by incorporating an adaptive mechanism. It helps to improve the efficiency and quality of the solution. This is the direction of improvement for our algorithm;
- Apply other heuristics to this problem and compare their advantages and disadvantages of problem-solving;
- This study only considers car-sharing. We hope to include ride-sharing in our research, which will reduce costs to a greater extent;
- Travel demand in this study is static, i.e., all demand is known in advance. In fact, previously unknown demand will appear after SAVs operations begin. This is also worth further exploration.
Author Contributions
Funding
Conflicts of Interest
References
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixão, T.M.; Mutz, F.; et al. Self-Driving Cars: A Survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Rahman, M.M.; Thill, J.-C. Impacts of Connected and Autonomous Vehicles on Urban Transportation and Environment: A Comprehensive Review. Sustain. Cities Soc. 2023, 96, 104649. [Google Scholar] [CrossRef]
- Fagnant, D.J.; Kockelman, K. Preparing a Nation for Autonomous Vehicles: Opportunities, Barriers and Policy Recommendations. Transp. Res. Part A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Nunes, A.; Hernandez, K.D. Autonomous Taxis & Public Health: High Cost or High Opportunity Cost? Transp. Res. Part A Policy Pract. 2020, 138, 28–36. [Google Scholar] [CrossRef]
- Kockelman, K.; Boyles, S.; Stone, P.; Fagnant, D.; Patel, R.; Levin, M.W.; Sharon, G.; Simoni, M.; Albert, M.; Fritz, H.; et al. An Assessment of Autonomous Vehicles: Traffic Impacts and Infrastructure Needs: Final Report; University of Texas at Austin: Austin, TX, USA, 2017. [Google Scholar]
- Amirgholy, M.; Shahabi, M.; Oliver Gao, H. Traffic Automation and Lane Management for Communicant, Autonomous, and Human-Driven Vehicles. Transp. Res. Part C Emerg. Technol. 2020, 111, 477–495. [Google Scholar] [CrossRef]
- Chehri, A.; Mouftah, H.T. Autonomous Vehicles in the Sustainable Cities, the Beginning of a Green Adventure. Sustain. Cities Soc. 2019, 51, 101751. [Google Scholar] [CrossRef]
- Milakis, D.; van Arem, B.; van Wee, B. Policy and Society Related Implications of Automated Driving: A Review of Literature and Directions for Future Research. J. Intell. Transp. Syst. 2017, 21, 324–348. [Google Scholar] [CrossRef]
- Gelauff, G.; Ossokina, I.; Teulings, C. Spatial and Welfare Effects of Automated Driving: Will Cities Grow, Decline or Both? Transp. Res. Part A Policy Pract. 2019, 121, 277–294. [Google Scholar] [CrossRef]
- Millard-Ball, A. The Autonomous Vehicle Parking Problem. Transp. Policy 2019, 75, 99–108. [Google Scholar] [CrossRef]
- Hörl, S. Agent-Based Simulation of Autonomous Taxi Services with Dynamic Demand Responses. Procedia Comput. Sci. 2017, 109, 899–904. [Google Scholar] [CrossRef]
- Shaheen, S.; Chan, N.; Bansal, A.; Cohen, A. Shared Mobility: A Sustainability & Technologies Workshop: Definitions, Industry Developments, and Early Understanding; UC Berkeley Transportation Sustainability Research Center: Berkeley, CA, USA, 2015. [Google Scholar]
- Shaheen, S.; Chan, N. Mobility and the Sharing Economy: Potential to Overcome First- and Last-Mile Public Transit Connections; UC Berkeley Transportation Sustainability Research Center: Berkeley, CA, USA, 2016. [Google Scholar] [CrossRef]
- Shoup, D. The High Cost of Free Parking; Taylor & Francis: New York, NY, USA, 2011. [Google Scholar]
- Fagnant, D.J.; Kockelman, K.M. The Travel and Environmental Implications of Shared Autonomous Vehicles, Using Agent-Based Model Scenarios. Transp. Res. Part C Emerg. Technol. 2014, 40, 1–13. [Google Scholar] [CrossRef]
- Iacobucci, R.; McLellan, B.; Tezuka, T. Modeling Shared Autonomous Electric Vehicles: Potential for Transport and Power Grid Integration. Energy 2018, 158, 148–163. [Google Scholar] [CrossRef]
- Spieser, K.; Treleaven, K.; Zhang, R.; Frazzoli, E.; Morton, D.; Pavone, M. Toward a Systematic Approach to the Design and Evaluation of Automated Mobility-on-Demand Systems: A Case Study in Singapore. In Road Vehicle Automation; Meyer, G., Beiker, S., Eds.; Lecture Notes in Mobility; Springer International Publishing: Cham, Switzerland, 2014; pp. 229–245. ISBN 978-3-319-05990-7. [Google Scholar]
- Zhang, R.; Pavone, M. Control of Robotic Mobility-on-Demand Systems: A Queueing-Theoretical Prspective. Int. J. Robot. Res. 2016, 35, 186–203. [Google Scholar] [CrossRef]
- Boesch, P.M.; Ciari, F.; Axhausen, K.W. Autonomous Vehicle Fleet Sizes Required to Serve Different Levels of Demand. Transp. Res. Rec. 2016, 2542, 111–119. [Google Scholar] [CrossRef]
- Brownell, C.; Kornhauser, A. A Driverless Alternative: Fleet Size and Cost Requirements for a Statewide Autonomous Taxi Network in New Jersey. Transp. Res. Rec. 2014, 2416, 73–81. [Google Scholar] [CrossRef]
- Loeb, B.; Kockelman, K.M.; Liu, J. Shared Autonomous Electric Vehicle (SAEV) Operations across the Austin, Texas Network with Charging Infrastructure Decisions. Transp. Res. Part C Emerg. Technol. 2018, 89, 222–233. [Google Scholar] [CrossRef]
- Salazar, M.; Rossi, F.; Schiffer, M.; Onder, C.H.; Pavone, M. On the Interaction between Autonomous Mobility-on-Demand and Public Transportation Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2262–2269. [Google Scholar]
- Taeihagh, A.; Lim, H.S.M. Governing Autonomous Vehicles: Emerging Responses for Safety, Liability, Privacy, Cybersecurity, and Industry Risks. Transp. Rev. 2019, 39, 103–128. [Google Scholar] [CrossRef]
- Greenblatt, J.B.; Saxena, S. Autonomous Taxis Could Greatly Reduce Greenhouse-Gas Emissions of US Light-Duty Vehicles. Nat. Clim. Chang. 2015, 5, 860–863. [Google Scholar] [CrossRef]
- Fournier, G.; Pfeiffer, C.; Baumann, M.; Wörner, R. Individual Mobility by Shared Autonomous Electric Vehicle Fleets: Cost and CO2 Comparison with Internal Combustion Engine Vehicles in Berlin, Germany. In Proceedings of the 2017 International Conference on Engineering, Technology and Innovation (ICE/ITMC), Madeira Island, Portugal, 27–29 June 2017; pp. 368–376. [Google Scholar]
- Bauer, G.S.; Greenblatt, J.B.; Gerke, B.F. Cost, Energy, and Environmental Impact of Automated Electric Taxi Fleets in Manhattan. Environ. Sci. Technol. 2018, 52, 4920–4928. [Google Scholar] [CrossRef]
- Zhang, W.; Guhathakurta, S.; Fang, J.; Zhang, G. Exploring the Impact of Shared Autonomous Vehicles on Urban Parking Demand: An Agent-Based Simulation Approach. Sustain. Cities Soc. 2015, 19, 34–45. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, K. Parking Futures: Shared Automated Vehicles and Parking Demand Reduction Trajectories in Atlanta. Land Use Policy 2020, 91, 103963. [Google Scholar] [CrossRef]
- Schiffer, M.; Schneider, M.; Walther, G.; Laporte, G. Vehicle Routing and Location Routing with Intermediate Stops: A Review. Transp. Sci. 2019, 53, 319–343. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A Green Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Goel, A.; Irnich, S. An Exact Method for Vehicle Routing and Truck Driver Scheduling Problems. Transp. Sci. 2017, 51, 737–754. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.H.G.R. Complexity of Vehicle Routing and Scheduling Problems. Networks 1981, 11, 221–227. [Google Scholar] [CrossRef]
- Lu, F.; Chen, W.; Feng, W.; Bi, H. 4PL Routing Problem Using Hybrid Beetle Swarm Optimization. Soft Comput. 2023. [Google Scholar] [CrossRef]
- Lu, F.; Feng, W.; Gao, M.; Bi, H.; Wang, S. The Fourth-Party Logistics Routing Problem Using Ant Colony System-Improved Grey Wolf Optimization. J. Adv. Transp. 2020, 2020, e8831746. [Google Scholar] [CrossRef]
- Yan, T.; Lu, F.; Wang, S.; Wang, L.; Bi, H. A Hybrid Metaheuristic Algorithm for the Multi-Objective Location-Routing Problem in the Early Post-Disaster Stage. JIMO 2023, 19, 4663–4691. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Brimberg, J.; Pérez, J.A.M. Variable Neighborhood Search. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.-Y., Eds.; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2010; pp. 61–86. ISBN 978-1-4419-1665-5. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable Neighborhood Search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Del Pia, A.; Filippi, C. A Variable Neighborhood Descent Algorithm for a Real Waste Collection Problem with Mobile Depots. Int. Trans. Oper. Res. 2006, 13, 125–141. [Google Scholar] [CrossRef]
- Divsalar, A.; Vansteenwegen, P.; Cattrysse, D. A Variable Neighborhood Search Method for the Orienteering Problem with Hotel Selection. Int. J. Prod. Econ. 2013, 145, 150–160. [Google Scholar] [CrossRef]
- Croes, G.A. A Method for Solving Traveling-Salesman Problems. Oper. Res. 1958, 6, 791–812. [Google Scholar] [CrossRef]
- Or, I. Traveling Salesman Type Combinatorial Problems and Their Relation to the Logistics of Regional Blood Banking; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 1976. [Google Scholar]
- Potvin, J.-Y.; Rousseau, J.-M. An Exchange Heuristic for Routeing Problems with Time Windows. J. Oper. Res. Soc. 1995, 46, 1433–1446. [Google Scholar] [CrossRef]
- Cassani, L.; Righini, G. Heuristic Algorithms for the TSP with Rear-Loading; Springer Nature Switzerland AG: Lecce, Italy, 2004. [Google Scholar]










| Notation | Definition |
|---|---|
| Set | |
| The initial depot, i.e., the base, | |
| The final depot, i.e., the base, | |
| Set of travel demands which indicate the pick-up points, | |
| Set of the dummy bases for park between service intervals, | |
| Set of parking lots, | |
| Set of dummy parking lots in the parking lot , , for example, | |
| Set of all dummy parking lots, | |
| Set of all nodes, | |
| Set of SAVs | |
| Parameter | |
| Energy cost per unit distance | |
| Basic usage cost per SAV | |
| Parking cost per unit time in a parking lot | |
| Weight coefficient of | |
| Weight coefficient of | |
| Weight coefficient of | |
| Size of the travel demand | |
| Number of parking lots, | |
| Number of the dummy bases for the base and dummy parking lots for each parking lot, | |
| Maximum number of available SAVs, | |
| Travel speed | |
| Travel time from to . If , contains the time for delivering passengers to the drop-off point i.e., and the time from the drop-off point to | |
| The earliest acceptable boarding time for the travel demand | |
| The time window for travel demands | |
| The latest acceptable boarding time for the travel demand, , | |
| Service time for SAVs to complete the travel demand | |
| Start time | |
| End time | |
| A sufficiently large number | |
| Variable | |
| Decision variable specifying the arrival time of the SAV at the vertex | |
| Decision variable specifying the departure time of the SAV at the vertex | |
| Decision variable specifying the starting serve time of SAV for the travel demand | |
| Binary decision variable indicating if SAV travel from vertex to vertex | |
| Binary decision variable indicating if SAV participated in the service mission |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 0.4 | ¥/min | 1 | |||
| 60 | ¥ | 0.3 | |||
| 0.1 | ¥/min | 1 | |||
| 10 | min | 30 | km/h | ||
| 0 | min | 1440 | min |
| Demand | Gurobi | VNS | |||
|---|---|---|---|---|---|
| Optimal Value | Runtime (s) | Optimal Value | Ave. Value | Ave. Runtime (s) | |
| 10 | 277.4 | 401.65 | 277.4 | 280.0 | 4.64 |
| 10 | 275.3 | 4.96 | 275.3 | 275.3 | 2.10 |
| 10 | 285.2 | 2.52 | 285.2 | 285.2 | 4.48 |
| 10 | 243.0 | 36.87 | 243.0 | 243.0 | 2.50 |
| 10 | 314.6 | 23.23 | 314.9 | 316.9 | 10.16 |
| 20 | 487.7 | 3600.00 | 462.3 | 462.3 | 7.28 |
| 20 | - | 3600.00 | 500.2 | 505.3 | 3.66 |
| 20 | 544.4 | 3600.00 | 474.6 | 477.7 | 4.77 |
| 20 | 688.4 | 3600.00 | 575.6 | 581.0 | 4.88 |
| 20 | - | 3600.00 | 497.5 | 498.9 | 4.12 |
| 30 | - | 3600.00 | 707.4 | 707.6 | 8.58 |
| 30 | - | 3600.00 | 643.5 | 650.4 | 19.90 |
| 30 | - | 3600.00 | 647.5 | 658.8 | 6.18 |
| 30 | - | 3600.00 | 698.4 | 703.1 | 25.57 |
| 30 | - | 3600.00 | 666.4 | 678.3 | 16.12 |
| Demand | VNS | CV (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Optimal Value | No. SAV | VKT | PTP (min) | PT (min) | Ave. Optimal Value | Ave. Runtime (s) | ||
| 100 | 1858 | 9 | 1969 | 1203 | 1778 | 1859 | 233 | 1.02% |
| 200 | 3375 | 16 | 3642 | 1735 | 3310 | 3399 | 534 | 0.79% |
| 300 | 4874 | 23 | 5296 | 2233 | 3503 | 4898 | 1541 | 0.44% |
| 400 | 6193 | 29 | 6813 | 2205 | 3989 | 6226 | 2017 | 0.66% |
| 500 | 7598 | 34 | 8415 | 2544 | 4631 | 7656 | 3823 | 0.69% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, C.; Mei, Z. Optimization of Shared Autonomous Vehicles Routing Problem: From the View of Parking. Sustainability 2023, 15, 12303. https://doi.org/10.3390/su151612303
Feng C, Mei Z. Optimization of Shared Autonomous Vehicles Routing Problem: From the View of Parking. Sustainability. 2023; 15(16):12303. https://doi.org/10.3390/su151612303
Chicago/Turabian StyleFeng, Chi, and Zhenyu Mei. 2023. "Optimization of Shared Autonomous Vehicles Routing Problem: From the View of Parking" Sustainability 15, no. 16: 12303. https://doi.org/10.3390/su151612303
APA StyleFeng, C., & Mei, Z. (2023). Optimization of Shared Autonomous Vehicles Routing Problem: From the View of Parking. Sustainability, 15(16), 12303. https://doi.org/10.3390/su151612303








