Hybrid Particle Swarm and Gravitational Search Algorithm-Based Optimal Fractional Order PID Control Scheme for Performance Enhancement of Offshore Wind Farms
Abstract
:1. Introduction
1.1. Literature Review
1.2. Paper Main Contribution and Organization
- Introducing a novel application of the hybrid particle swarm and gravitational search algorithm for tuning the FOPID controller;
- Verifying results obtained from HPSOGSA-based FOPID and compared with PI controller tuned using GA and GWO;
- FRT capabilities of variable speed wind turbine-based PMSG is enhanced using the proposed controller with the selected tuning algorithm;
- We demonstrated the strength of the proposed controller with an HPSOGSA optimizer.
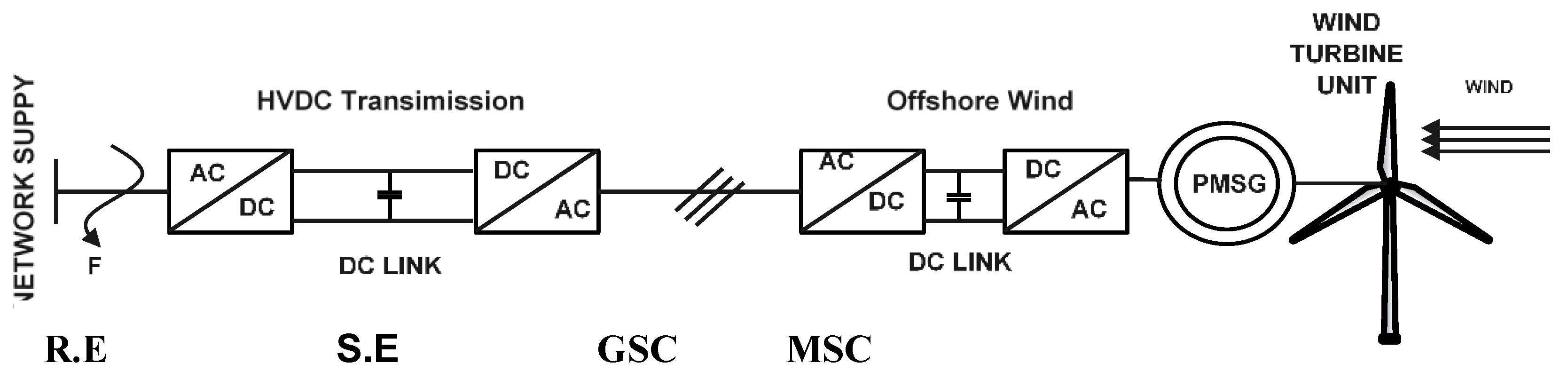
2. System Topology
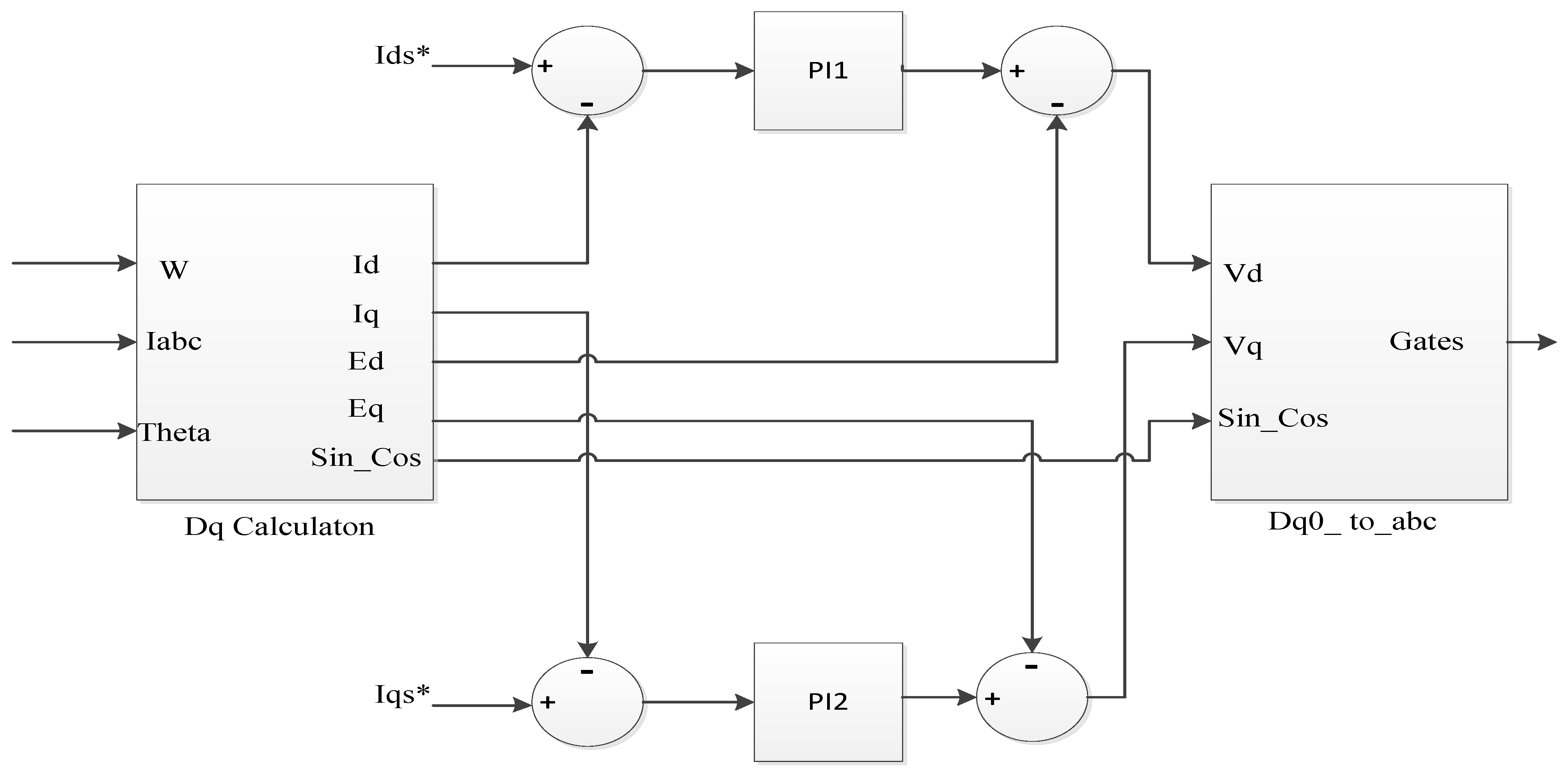
2.1. VSC’s Based VSWT-PMSG Construction
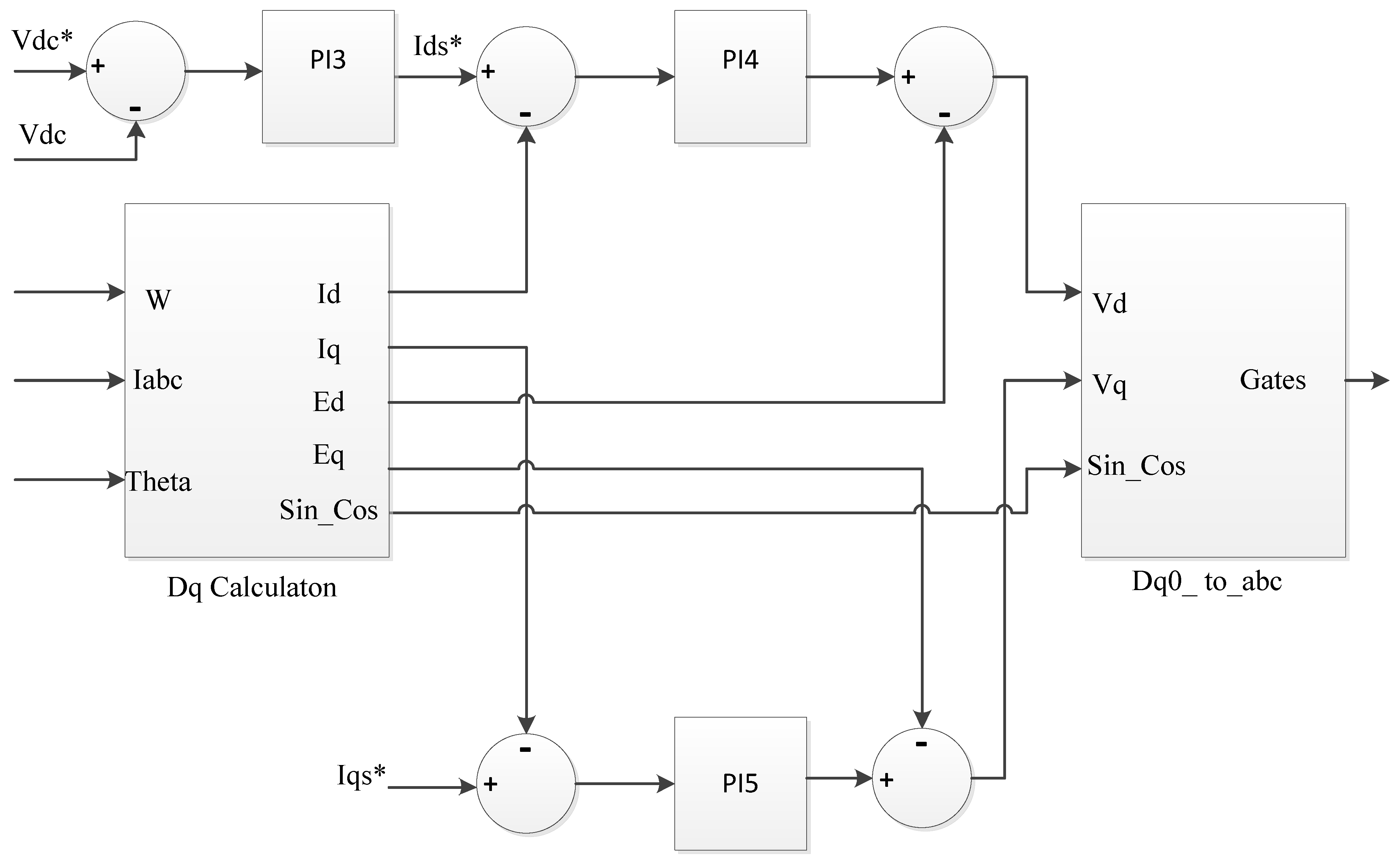
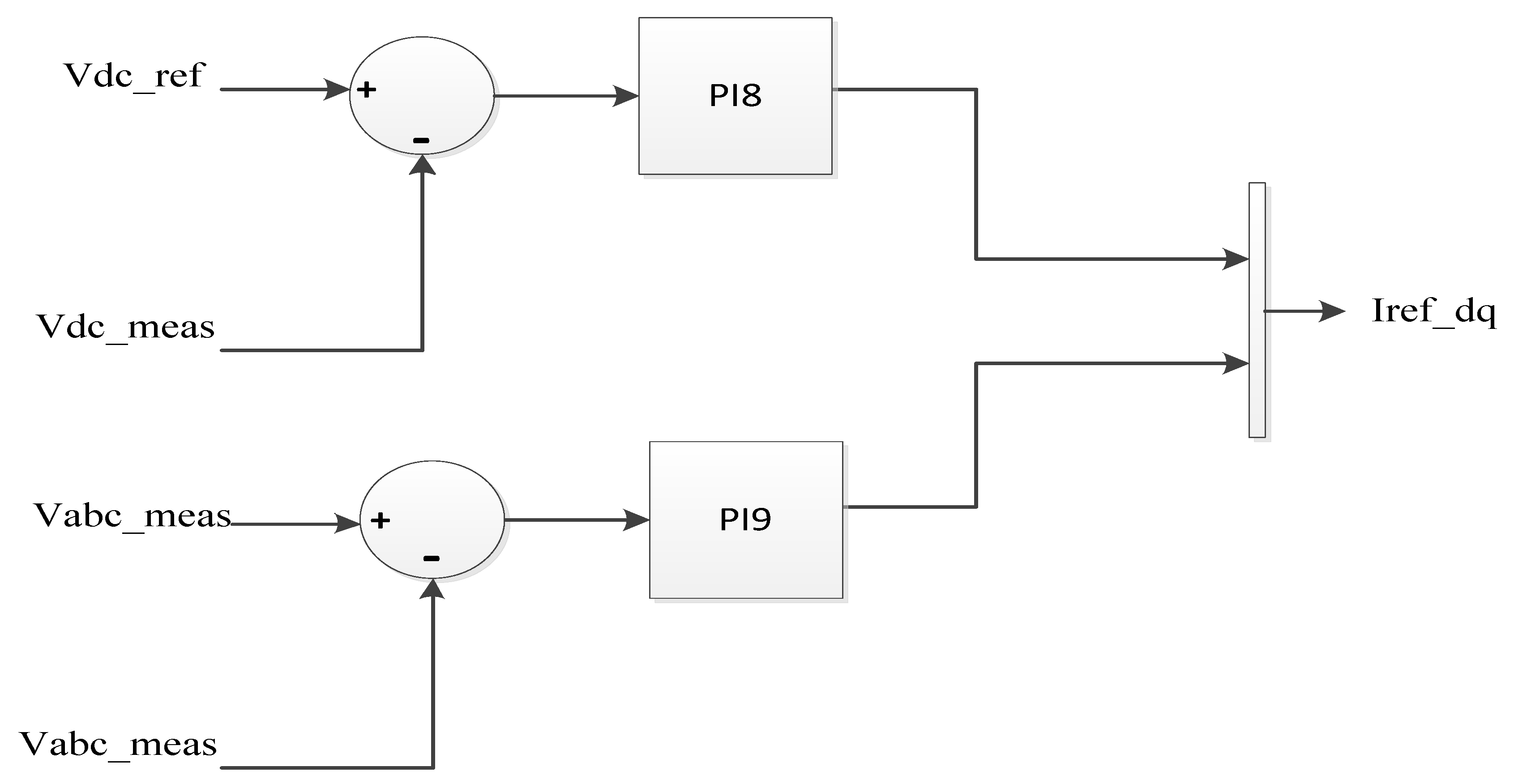
2.2. VSC-BASED HVDC Transmission Construction
3. Optimization Algorithms
3.1. HPSOGSA Overview
3.2. HPSOGSA Procedure
- Initiate population;
- Calculate the fitness function for all candidates;
- Update G and gbest for the population;
- Calculate M, forces and acceleration for all agents;
- Update velocity and positions;
- Check meeting criterion;
- Return the best optimal solution.

4. FOPID Settings
5. Simulation Results
5.1. Comparison between FOPID-Based HPSOGSA and PI-Based GA and GWO
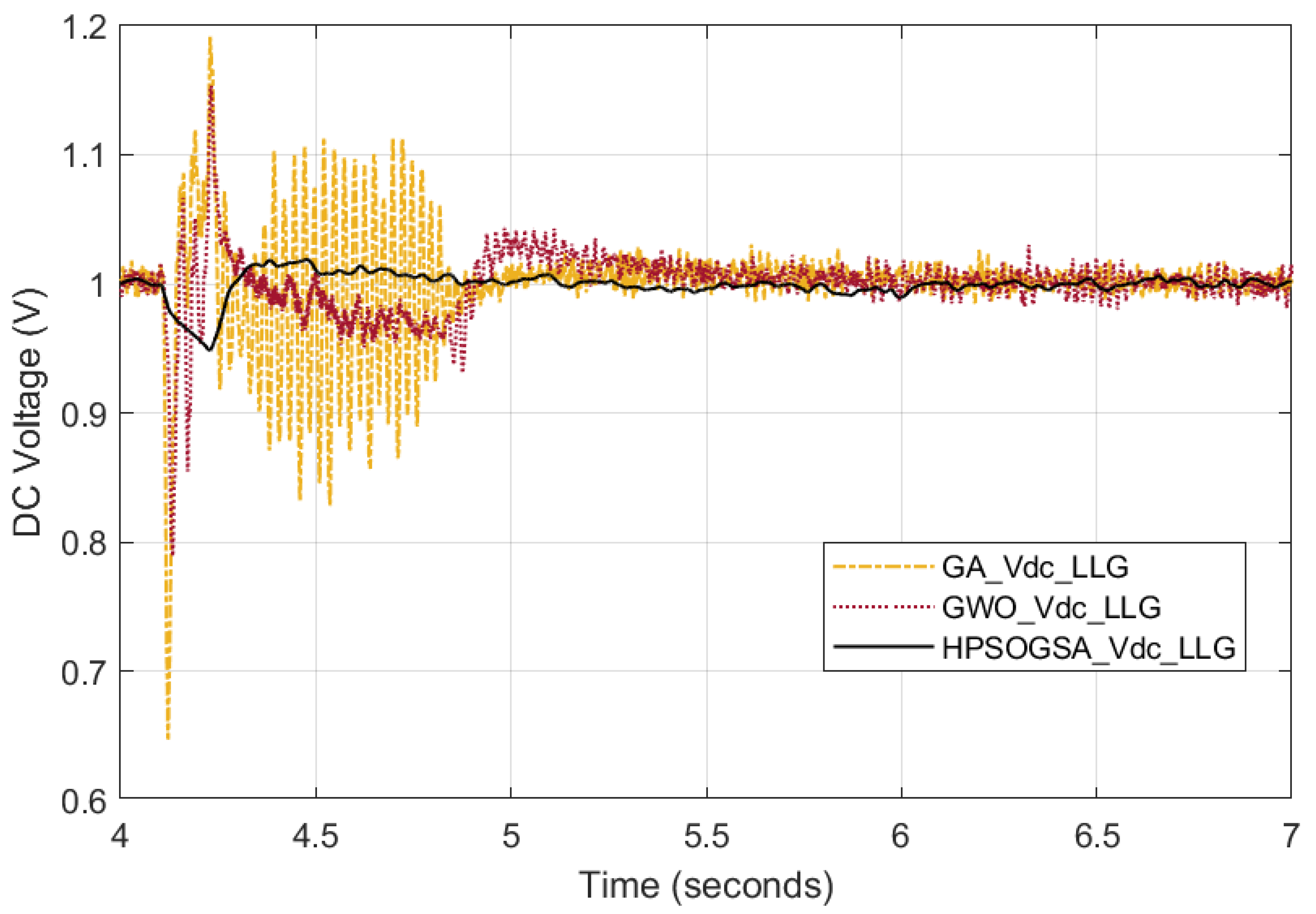
5.1.1. Case 1 Symmetrical Fault (3 Line to Ground Fault)
5.1.2. Case 2 Asymmetrical Fault (2 Line to Ground Fault)
5.1.3. Case 3 Asymmetrical Fault (Line to Ground Fault)
5.1.4. Case 4 Asymmetrical Fault (Line to Line Fault)
5.2. Comparison between FOPID-Based HPSOGSA and PI-Based GA and GWO
5.2.1. Case 1 Symmetrical Fault (3 Line to Ground Fault)
5.2.2. Case 2 Asymmetrical Fault (2 Line to Ground Fault)
5.2.3. Case 3 Asymmetrical Fault (Line to Ground Fault)
5.2.4. Case 4 Asymmetrical Fault (Line to Line Fault)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| LCC | Line Commutated Converter |
| DFIG | Doubly Fed Induction Generator |
| MPPT | Maximum PowerPoint Tracking |
| WECS | Wind Energy Conversion System |
| PI | Proportional Integral Controller |
| PID | Proportional Integral Differential Controller |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimizer |
| FRT | Fault Ride Through |
| EO | Equilibrium Optimizer |
| HVDC | High Voltage Direct Current Transmission |
| FOPID | Fractional Order PID Controller |
| VSC | Voltage Source Converter |
| OWF | Offshore Wind Farm |
| IAE | Integral Absolute Error |
| ITAE | Integral Time Absolute Error |
| ITSE | Integral Time Square Error |
| FLC | Fuzzy Logic Controller |
| CMPN | Continuous Mixed P-Norm |
| CNN | Convolutional Neural Networks |
| ANN | Artificial Neural Network |
| SMES | Superconducting Magnetic Energy System |
| LMS | Least Mean Square |
| LMSRE | Least Mean Square Root Error |
| PCC | Point of Common Coupling |
| S.E | Sending End |
| GSC | Grid Side Converter |
| MSC | Machine Side Converter |
| VSWT | Variable Speed Wind Turbine |
| ITLO | Interactive Teaching Learning Optimizer |
| TLBO | Teaching Learning Based Optimizer |
| HPSOGSA | Hybrid Particle Swarm and Gravitational Search Algorithm |
References
- Xia, S.; Zhang, Q.; Hussain, S.T.; Hong, B.; Zou, W. Impacts of integration of wind farms on power system transient stability. Appl. Sci. 2018, 8, 1289. [Google Scholar] [CrossRef] [Green Version]
- GWEC. Global Wind Report 2021 | Global Wind Energy Council; Global Wind Energy Council: New York, NY, USA, 2021. [Google Scholar]
- Liu, X.; Xu, Z. Coordinated Frequency Control Scheme of Offshore Wind Farm Connected to VSC-HVDC. Electr. Power Components Syst. 2019, 47, 757–771. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, Y. Improved Frequency Control Strategy for Offshore Wind Farm Integration via VSC-HVDC. Energies 2022, 15, 6363. [Google Scholar] [CrossRef]
- Rabie, D.; Senjyu, T.; Alkhalaf, S.; Mohamed, Y.S.; Shehata, E.G. Study and analysis of voltage source converter control stability for HVDC system using different control techniques. Ain Shams Eng. J. 2021, 12, 2763–2779. [Google Scholar] [CrossRef]
- Jing, T.; Maklakov, A.S. A Review of Voltage Source Converters for Energy Applications. In Proceedings of the 2018 International Ural Conference on Green Energy (UralCon), Chelyabinsk, Russia, 4–6 October 2018; pp. 275–281. [Google Scholar] [CrossRef]
- Hassoine, M.A.; Lahlou, F.; Addaim, A.; Madi, A.A. Wind farm layout optimization using real coded multi-population genetic algorithm. In Proceedings of the 2019 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS), Fez, Morocco, 3–4 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, D.-D.; Zhu, Y.-J.; Zeng, T.; Jiang, B.-X.; Tang, C.-X.; Zhou, Y.; He, J.-L. Effect of charge transport on electrical degradation in polypropylene/organic molecular semiconductor composites for HVDC cable insulation. Appl. Phys. Lett. 2023, 122, 112904. [Google Scholar] [CrossRef]
- Oni, O.E.; Mbangula, K.I.; Davidson, I.E. A Review of LCC-HVDC and VSC-HVDC Technologies and Applications. Trans. Environ. Electr. Eng. 2016, 1, 68. [Google Scholar] [CrossRef] [Green Version]
- Ju, Y.F.; Zhu, C.W. The control method and experimental study of HVDC light inverter part. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010; pp. 2–5. [Google Scholar] [CrossRef]
- Bozhko, S.; Blasko-Gimenez, R.; Li, R.; Clare, J.C.; Asher, G.M. Control of offshore DFIG-based wind farm grid with line-commutated HVDC connection. In IEEE Transactions on Energy Conversion; IEEE: Piscateville, NJ, USA, 2007; pp. 1563–1568. [Google Scholar] [CrossRef]
- Ma, X.; Liao, Z.; Wang, Y.; Zhao, J. Fast Dynamic Phasor Estimation Algorithm Considering DC Offset for PMU Applications. In IEEE Transactions on Power Delivery; IEEE: Piscateville, NJ, USA, 2023. [Google Scholar]
- Chaithanya, S.; Reddy, V.N.B.; Kiranmayi, R. Modeling & analysis of grid-tied PMA based offshore wind energy system using PSCAD/EMTDC. Ain Shams Eng. J. 2019, 10, 411–417. [Google Scholar] [CrossRef]
- Alaboudy, A.H.K.; Daoud, A.A.; Desouky, S.S.; Salem, A.A. Converter controls and flicker study of PMSG-based grid connected wind turbines. Ain Shams Eng. J. 2013, 4, 75–91. [Google Scholar] [CrossRef] [Green Version]
- Basak, R.; Bhuvaneswari, G.; Pillai, R.R. Low-Voltage Ride-Through of a Synchronous Generator-Based Variable Speed Grid-Interfaced Wind Energy Conversion System. IEEE Trans. Ind. Appl. 2020, 56, 752–762. [Google Scholar] [CrossRef]
- Ma, X.; Wan, Y.; Wang, Y.; Dong, X.; Shi, S.; Liang, J.; Zhao, Y.; Mi, H. Multi-Parameter Practical Stability Region Analysis of Wind Power System Based on Limit Cycle Amplitude Tracing. IEEE Trans. Energy Convers. 2023. [Google Scholar] [CrossRef]
- Xu, L.; Andersen, B.R. Grid connection of large offshore wind farms using HVDC. Wind. Energy 2006, 9, 371–382. [Google Scholar] [CrossRef]
- Mahvash, H.; Taher, S.A.; Rahimi, M. A new approach for power quality improvement of DFIG based wind farms connected to weak utility grid. Ain Shams Eng. J. 2017, 8, 415–430. [Google Scholar] [CrossRef] [Green Version]
- Nasiri, M.; Milimonfared, J.; Fathi, S.H. Modeling, analysis and comparison of TSR and OTC methods for MPPT and power smoothing in permanent magnet synchronous generator-based wind turbines. Energy Convers. Manag. 2014, 86, 892–900. [Google Scholar] [CrossRef]
- Mishra, S.; Shukla, S.; Verma, N.; Ritu, R. Comprehensive review on Maximum Power Point Tracking techniques: Wind Energy. In Proceedings of the 2015 Communication, Control and Intelligent Systems (CCIS), Mathura, India, 7–8 November 2015; pp. 464–469. [Google Scholar] [CrossRef]
- Jeba, P.; Selvakumar, A.I. FOPID based MPPT for photovoltaic system. Energy Sources Part A Recover. Util. Environ. Eff. 2018, 40, 1591–1603. [Google Scholar] [CrossRef]
- Chaib, L.; Choucha, A.; Arif, S. Optimal design and tuning of novel fractional order PID power system stabilizer using a new metaheuristic Bat algorithm. Ain Shams Eng. J. 2017, 8, 113–125. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud, E.A.; Nasrallah, M.; Soliman, H.F.; Hasanien, H.M. Fractional order PI controller based on hill climbing technique for improving MPPT of the BDF-RG driven by wind turbine. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017. [Google Scholar] [CrossRef]
- Pradhan, R.; Majhi, S.K.; Pradhan, J.K.; Pati, B.B. Optimal fractional order PID controller design using Ant Lion Optimizer. Ain Shams Eng. J. 2010, 11, 281–291. [Google Scholar] [CrossRef]
- Shawqran, A.M.; El-Marhomy, A.; Attia, M.A.; Kamh, M.Z. Novel blade angle controllers techniques based on heuristics algorithms. Ain Shams Eng. J. 2022, 13, 101782. [Google Scholar] [CrossRef]
- Gouda, M.M.; Danaher, S.; Underwood, C.P. Fuzzy Logic Control Versus Conventional PID Control for Controlling Indoor Temperature of a Building Space. IFAC Proc. Vol. 2000, 33, 249–254. [Google Scholar] [CrossRef]
- Rubaai, A.; Castro-Sitiriche, M.J.; Ofoli, A.R. Design and implementation of parallel fuzzy PID controller for high-performance brushless motor drives: An integrated environment for rapid control prototyping. IEEE Trans. Ind. Appl. 2008, 44, 1090–1098. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Al-Durra, A. Modeling and control strategies of fuzzy logic controlled inverter system for grid interconnected variable speed wind generator. IEEE Syst. J. 2013, 7, 817–824. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.; Zhao, X. Deep Neural Learning Based Distributed Predictive Control for Offshore Wind Farm Using High-Fidelity les Data. IEEE Trans. Ind. Electron. 2021, 68, 3251–3261. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. A novel LMSRE-based adaptive PI control scheme for grid-integrated PMSG-based variable-speed wind turbine. Int. J. Electr. Power Energy Syst. 2021, 125, 106505. [Google Scholar] [CrossRef]
- Hasanien, H.M.; Muyeen, S.M. Affine projection algorithm based adaptive control scheme for operation of variable-speed wind generator. IET Gener. Transm. Distrib. 2015, 9, 2611–2616. [Google Scholar] [CrossRef]
- Hussien, A.M.; Kim, J.; Alkuhayli, A.; Alharbi, M.; Hasanien, H.M.; Tostado-Véliz, M.; Turky, R.A.; Jurado, F. Adaptive PI Control Strategy for Optimal Microgrid Autonomous Operation. Sustainability 2022, 14, 14928. [Google Scholar] [CrossRef]
- Soliman, M.A.; Hasanien, H.M.; Al-Durra, A.; Alsaidan, I. A novel adaptive control method for performance enhancement of grid-connected variable-speed wind generators. IEEE Access 2020, 8, 82617–82629. [Google Scholar] [CrossRef]
- Amin, M.N.; Soliman, M.A.; Hasanien, H.M.; Abdelaziz, A.Y. Hybrid CSA-GWO Algorithm-Based Optimal Control Strategy for Efficient Operation of Variable-Speed Wind Generators; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- El-Naggar, M.F.; Mosaad, M.I.; Hasanien, H.M.; AbdulFattah, T.A.; Bendary, A.F. Elephant herding algorithm-based optimal PI controller for LVRT enhancement of wind energy conversion systems. Ain Shams Eng. J. 2021, 12, 599–608. [Google Scholar] [CrossRef]
- Younes, Z.; Alhamrouni, I.; Mekhilef, S.; Reyasudin, M. A memory-based gravitational search algorithm for solving economic dispatch problem in micro-grid. Ain Shams Eng. J. 2021, 12, 1985–1994. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Zhang, X.; Huang, L.; Shu, H.; Jiang, L. Interactive teaching-learning optimiser for parameter tuning of VSC-HVDC systems with offshore wind farm integration. IET Gener. Transm. Distrib. 2018, 12, 678–687. [Google Scholar] [CrossRef] [Green Version]
- Muyeen, S.M.; Takahashi, R.; Tamura, J. Operation and control of HVDC-connected offshore wind farm. IEEE Trans. Sustain. Energy 2010, 1, 30–37. [Google Scholar] [CrossRef]
- Mohamed, N.A.; Hasanien, H.M.; Al-Ammar, E.A.; Tostado-Véliz, M.; Turky, R.A.; Jurado, F.; Badr, A.O. Gorilla tropical optimization algorithm solution for performance enhancement of offshore wind farm. IET Gener. Transm. Distrib. 2022, 17, 2388–2400. [Google Scholar] [CrossRef]
- Behera, S.; Sahoo, S.; Pati, B.B. A review on optimization algorithms and application to wind energy integration to grid. Renew. Sustain. Energy Rev. 2015, 48, 214–227. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2010, 191, 105190. [Google Scholar] [CrossRef]
- Nguyen, T.N.A.; Pham, D.C.; Huu, C.T.N.; Nguyen, A.N. Implementation of equilibrium optimizer algorithm for mppt in a wind turbine with pmsg. WSEAS Trans. Syst. Control. 2021, 16, 216–223. [Google Scholar] [CrossRef]
- Bakry, O.M.; Alhabeeb, A.; Ahmed, M.; Alkhalaf, S.; Senjyu, T.; Mandal, P.; Dardeer, M. Improvement of distribution networks performance using renewable energy sources based hybrid optimization techniques. Ain Shams Eng. J. 2022, 13, 101786. [Google Scholar] [CrossRef]
- Berus, L.; Hernavs, J.; Peršak, T.; Potočnik, D.; Klančnik, S.; Gotlih, J.; Karner, T.; Ficko, M. A New Hybrid PSO-JAYA Algorithm for Function Optimization. Lect. Notes Netw. Syst. 2023, 687, 62–68. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
















| Lower Boundary | 0 |
| Upper Boundary | 100 |
| Population | 10 |
| Maximum Iteration | 20 |
| FOPID | Kp | Ki | KD | λ | μ | |
|---|---|---|---|---|---|---|
| MSC | 1 | 7.322 | 26.332 | 2.23 | 0.8 | 0.8 |
| 2 | 7.322 | 26.332 | 2.23 | 0.8 | 0.8 | |
| GSC | 3 | 0.7 | 2.4 | 0.1123 | 0.92 | 0.95 |
| 4 | 17.335 | 18.242 | 0.2 | 0.88 | 0.98 | |
| 5 | 17.335 | 18.242 | 0.2 | 0.88 | 0.98 | |
| Offhsore | 6 | 12.145 | 60.223 | 0.298 | 0.89 | 1.05 |
| 7 | 27.52 | 6.9 | 0.514 | 0.83 | 0.93 | |
| 8 | 3.75 | 30.442 | 0.1184 | 0.934 | 0.95 | |
| 9 | 3.75 | 30.442 | 0.1184 | 0.934 | 0.95 | |
| Onshore | 10 | 6.7851 | 100 | 0.423 | 0.88 | 0.92 |
| 11 | 2.1 | 0.54 | 0.699 | 0.9 | 0.9 | |
| 12 | 12.778 | 48.225 | 0.194 | 0.972 | 0.95 | |
| 13 | 12.778 | 48.225 | 0.194 | 0.972 | 0.95 |
| FOPID | Kp | Ki | KD | λ | μ | |
|---|---|---|---|---|---|---|
| MSC | 1 | 17.253 | 7.556 | 4.25 | 0.92 | 0.83 |
| 2 | 17.253 | 7.556 | 4.25 | 0.92 | 0.82 | |
| GSC | 3 | 0.9 | 2.5 | 0.2 | 0.88 | 1.05 |
| 4 | 75.224 | 82.846 | 0.256 | 0.9 | 0.95 | |
| 5 | 75.224 | 80.523 | 0.256 | 0.9 | 0.95 | |
| offhsore | 6 | 0.789 | 89.236 | 0.35 | 0.85 | 0.98 |
| 7 | 0.789 | 89.236 | 0.56 | 0.8 | 0.9 | |
| 8 | 15.785 | 20.223 | 0.223 | 0.9 | 0.88 | |
| 9 | 2.523 | 11.225 | 0.223 | 0.9 | 0.88 | |
| Onshore | 10 | 39.25 | 65.778 | 0.421 | 0.88 | 0.92 |
| 11 | 39.25 | 65.778 | 0.5 | 0.92 | 0.88 | |
| 12 | 10 | 6.223 | 0.3 | 0.95 | 0.9 | |
| 13 | 2.25 | 15 | 0.3 | 0.95 | 0.9 |
| PI | GWO | GA | |||
|---|---|---|---|---|---|
| Kp | Ki | Kp | Ki | ||
| Wind Station | PI 1 | 5.2557 | 27.3747 | 15.6187 | 5.6171 |
| PI 2 | 5.2557 | 27.3747 | 15.6187 | 5.6171 | |
| PI 3 | 0.3986 | 2.9042 | 0.858 | 1.959 | |
| PI 4 | 67.1374 | 87.8442 | 74.31 | 82.846 | |
| PI 5 | 67.1374 | 87.8442 | 74.31 | 82.846 | |
| Offshore Station | PI 6 | 1.846 | 35.8433 | 0.589 | 87.937 |
| PI 7 | 1.846 | 35.8433 | 0.589 | 87.937 | |
| PI 8 | 8.0622 | 96.9977 | 13.835 | 18.179 | |
| PI 9 | 2.7042 | 15.3277 | 1.587 | 9.689 | |
| Onshore Station | PI 10 | 34.8745 | 100 | 37.828 | 61.81 |
| PI 11 | 34.8745 | 100 | 37.828 | 61.81 | |
| PI 12 | 2.8052 | 32.2411 | 8.955 | 7.995 | |
| PI 13 | 0.587 | 14.9644 | 1.6 | 10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, N.A.; Hasanien, H.M.; Alkuhayli, A.; Akmaral, T.; Jurado, F.; Badr, A.O. Hybrid Particle Swarm and Gravitational Search Algorithm-Based Optimal Fractional Order PID Control Scheme for Performance Enhancement of Offshore Wind Farms. Sustainability 2023, 15, 11912. https://doi.org/10.3390/su151511912
Mohamed NA, Hasanien HM, Alkuhayli A, Akmaral T, Jurado F, Badr AO. Hybrid Particle Swarm and Gravitational Search Algorithm-Based Optimal Fractional Order PID Control Scheme for Performance Enhancement of Offshore Wind Farms. Sustainability. 2023; 15(15):11912. https://doi.org/10.3390/su151511912
Chicago/Turabian StyleMohamed, Nour A., Hany M. Hasanien, Abdulaziz Alkuhayli, Tlenshiyeva Akmaral, Francisco Jurado, and Ahmed O. Badr. 2023. "Hybrid Particle Swarm and Gravitational Search Algorithm-Based Optimal Fractional Order PID Control Scheme for Performance Enhancement of Offshore Wind Farms" Sustainability 15, no. 15: 11912. https://doi.org/10.3390/su151511912
APA StyleMohamed, N. A., Hasanien, H. M., Alkuhayli, A., Akmaral, T., Jurado, F., & Badr, A. O. (2023). Hybrid Particle Swarm and Gravitational Search Algorithm-Based Optimal Fractional Order PID Control Scheme for Performance Enhancement of Offshore Wind Farms. Sustainability, 15(15), 11912. https://doi.org/10.3390/su151511912








