A New EWMA Control Chart for Monitoring Multinomial Proportions

Abstract

Control charts have been widely used for monitoring process quality in manufacturing and have played an important role in triggering a signal in time when detecting a change in process quality. Many control charts in literature assume that the in-control distribution of the univariate or multivariate process data is continuous. This research develops two exponentially weighted moving average (EWMA) proportion control charts to monitor a process with multinomial proportions under large and small sample sizes, respectively. For a large sample size, the charting statistic depends on the well-known Pearson’s chi-square statistic, and the control limit of the EWMA proportion chart is determined by an asymptotical chi-square distribution. For a small sample size, we derive the exact mean and variance of the Pearson$\mathrm{’}\mathrm{s}$ chi-square statistic. Hence, the exact EWMA proportion chart is determined. The proportion chart can also be applied to monitor the distribution-free continuous multivariate process as long as each categorical proportion associated with specification limits of each quality variable is known or estimated. Lastly, we examine simulation studies and real data analysis to conduct the detection performance of the proposed EWMA proportion chart.

1. Introduction

Process control plays a critical role in fostering sustainable practices within industries. It establishes a connection and enables the attainment of secure and efficient process operation and energy systems. Sustainability encompasses the integration of economic, social, and environmental systems, necessitating a well-rounded approach to resource management [1,2,3]. From the standpoint of process control, several factors contribute to sustainable practices, including the minimization of raw material costs, reduction of product and material scrap/waste expenses, optimization of capital costs, enhancement of process and energy efficiency, mitigation of carbon and water footprints, and maximization of eco-efficiency and process safety. Therefore, process control plays a pivotal role in offering sustainability solutions for developing and implementing efficient technology (refer to Daoutidis et al. [4]). In other words, the practice of sustainability introduces new operational challenges in the development of process control methods. So far, few papers have discussed developing or utilizing control charts to offer sustainability solutions. For example, Anderson et al. [5] applied multivariate control charts to monitor ecological and environmental measurement indices; Morrison [6] used control charts to interpret and monitor environmental data; Gove et al. [7] adopted control charts to catch water supply in south–west Western Australia; Oliveira da Silva et al. [8] constructed control charts to help in stability and reliability of water quality; Shafqat et al. [9] provided triple EWMA mean control chart to monitor and compare Air and Green House Gases Emissions of various countries and identified the critical countries. Control charts serve as effective tools in process control, aiming to enhance the quality and yield of products/parts while reducing scrap/waste of raw materials, minimizing carbon and water footprints, and increasing profits/eco-efficiency and energy efficiency of products.

Among statistical process control tools, control charts are effective tools for monitoring and improving the manufacturing or service process quality. Compared to many process controls with continuous quality variables, less attention has been paid to control charts designed with categorical quality characteristic. The well-known charts for monitoring two-categorical process units are $\mathrm{p},\mathrm{c},\mathrm{n}\mathrm{p},$ and $\mathrm{u}$ charts for monitoring nonconforming fraction and defects and for more details refer to Montgomery [10], Reynolds et al. [11,12] and Qiu [13]. However, only considering two categories is not enough to characterize the more general situation of process control. For example, an item can be classified into the three grades of best, better, or good and not just nonconforming and conforming grades. Consequently, the study of process control for categorical data following a multinomial distribution is required to explore carefully.

Up until now, many control charts monitoring multinomial-proportion process are constructed based on Pearson’s chi-square statistic, but its variant heavily depends on a large sample size (e.g., Marcucci [14] and Nelson et al. [15]). The asymptotic chi-square distribution of Pearson’s chi-square statistic is specifically known for an infinite sample size. When the sample size is small, it is not appropriate to adopt the asymptotic chi-square distribution of Pearson’s chi-square statistic to construct the multinomial-proportion control chart because the calculated average run length (ARL) of the asymptotic control charts may seriously deviate from the pre-specified ARL. It thus leads to an over- or under-adjustment of the process.

We note that many papers of multinomial-proportion control charts are designed based on the asymptotic distribution of Pearson’s chi-square statistic even when the sample size is small, such as Crosier [16] and Qiu [17]. Moreover, Ryan et al. [18] established the multinomial-proportion CUSUM chart that relies on pre-specified out-of-control multinomial proportions, which consequently leads to worse detection performance compared with multiple one-sided Bernoulli CUSUM charts. Li et al. [19] followed the idea of Qiu [17] to propose an EWMA-type control chart for monitoring the proportions of a multivariate binomial distribution under a large sample size. Huang et al. [20,21] and Lee et al. [22] extended the control chart in Li et al. [19] to monitor the multinomial-proportion process with a large sample size.

From those existing methods, we find that monitoring the multinomial-proportion process with a small sample size has not been discussed. Though the exact distribution of Pearson’s chi-square statistic is difficult to know, we may derive its exact mean and variance whether the sample size is small or large. According to the results, we thus provide an exact EWMA-proportion control chart to monitor the multinomial-proportion process. The control limit of the proposed exact control chart can be determined and implemented not only for a small sample size but also for a large sample size and even an individual sample. So far, the literature has not yet discussed the exact EWMA-proportion control chart.

In this study, we have devised a novel, efficient, and accurate method for monitoring and controlling a multinomial-proportion process. The proposed method holds the potential to provide multiple sustainability solutions across industries.

This rest of the paper is organized as follows. Section 2 derives the exact means and variances of Pearson’s chi-square statistic under in-control process proportions and studies the properties of Pearson’s chi-square statistic. Section 3 constructs the exact and asymptotic EWMA-proportion charts and determine their control limits by satisfying the pre-specified ARL₀ and considering small and large sample sizes. Section 4 evaluates and compares the out-of-control proportions’ detection performance of the proposed exact and asymptotic EWMA-proportion charts. Section 5 shows how the proposed exact EWMA-proportion chart can be applied to monitor the identify proportions of all categories of a distribution-free continuous multivariate process using a real example of semiconductor data obtained from UCI database. Finally, we offer conclusions of the study.

2. Investigation of the Property of Pearson’s Chi-Square Statistic for Correlated Quality Variables following a Multinomial Distribution

We first denote X = (X₁, X₂, …, X_m) as the count vector of m categories in n independent trials, where X_i is the count number of the ith category, i = 1, 2,…, m. Let p₀ = (p_0,1, p_0,2, …, p_0,m) be a vector of the in-control proportion associated with X = (X₁, X₂, …, X_m), where p_{0, i}, i = 1, …, m, is the in-control proportion of the $\mathrm{i}$-th category, and ${\displaystyle \sum _{i=1}^m{p}_{0,i}}=1$. Next,

• X follows a multinomial distribution with probability mass function

  $$p(X_1=x_1,X_2=x_2,\dots ,X_m=x_m)=\frac{n!}{x_1!x_2!\dots x_m!}{p}_{0,1}^{x_1}{p}_{0,2}^{x_2}\dots p_{0,m}^{x_m},$$

  where ${\displaystyle \sum _{i=1}^m{x}_i}=n$, and x_i is the realization value of X_i for i = 1, …, m.

To know whether there is a change in the in-control proportion vector p₀, a natural idea is to adopt the Pearson’s chi-square statistic to make a test. The in-control Pearson’s chi-square statistic:

$${\chi }^2={\displaystyle \sum _{i=1}^m\frac{{(X_i-e_{0,i})}^2}{e_{0,i}}},$$

(1)

where $e_{0,i}=n{p}_{0,i}$ is the in control expected number of the $\mathrm{i}$th category.

We now study the in-control distribution of the Pearson’s chi-square statistic and derive its exact mean and variance by considering various sample size and in-control proportion vector. When n is large enough, the Pearson’s chi-square statistic ${\chi }^2$ follows an asymptotical chi-square distribution with degree of freedom (df) m − 1; that is, ${\chi }^2$~${\chi }^2(m-1)$. This is a well-known asymptotical distribution. When n is small, the distribution of Pearson’s chi-square statistic does not follow the ${\chi }^2(m-1)$ distribution. Hence, it is better to know the distribution of the Pearson’s chi-square statistic for a small sample size. However, it is impossible to know the exact distribution of the Pearson’s chi-square statistic, but we may derive its exact mean and variance as follows.

First, it is easy to derive the in-control mean of Pearson’s chi-square statistics ${\chi }^2$ given the in-control proportion as follows.

$$\begin{gathered} E({\chi }^2)={\displaystyle \sum _{i=1}^m\frac{p_{0,i}(1-p_{0,i})}{p_{0,i}}}={\displaystyle \sum _{i=1}^m(1-p_{0,i}}) \\ =m-1 \end{gathered}$$

(2)

As per our best knowledge, the variance of the Pearson’s chi-square statistic has not been derived. We derive the in-control exact variance of Pearson’s chi-square statistic ${\chi }^2$ as follows.

$$Var({\chi }^2)={\displaystyle \sum _{i=1}^m\frac{1}{n{p}_{0,i}}}-\frac{m^2+2m-2}{n}+2(m-1)$$

(3)

The Appendix A presents the derivation process. From (3), we find the variance value differs along with sample size n given m and p₀, that is, the variance value is not fixed for various n.

To investigate how the mean and variance change under different n and in-control proportion vectors, without loss of generality, we consider two scenarios of in-control proportion vectors. In practice, the proportions could be all the same or not. It is the reason that we consider the proportion vector with the two scenarios. The two scenarios of in-control proportion vectors, each with four proportions for four categories are as follows.

Scenario (1): The in-control four proportions are the same,

$p_0=(0.25,0.25,0.25,0.25)$.

Scenario (2): The in-control four proportions are not all the same,

$p_0=(0.1,0.1,0.4,0.4)$.

Table 1 shows the calculated exact means and variances under different n and two scenarios of in-control proportion vectors. We find the following results in Table 1:

(i)

Under scenario (1), the exact means are all fixed at 3 whether n is small or large. However, the exact variance increases when n increases but converges to 5.999 when n is equal to 6000.

(ii)

Under scenario (2), the exact mean are all fixed at 3 whether n is small or large. However, the exact variance decreases when n increases but converges to 6.0 when n is equal to 6000.

(iii)

The exact variance increases or decreases heavily due to the in-control proportion vector. We can see that the change behavior of the exact variance for increasing n is different in scenarios (1) and (2).

The above results present clear evidence and show that the variance of the Pearson’s chi-square statistic is not fixed for a small sample size. However, the variance converges to 2(m − 1) when the sample size is large enough.

Table 1. The exact mean and variance of the Pearson’s chi-square statistic for various n under scenarios (1) and (2) with in-control proportion vectors.

n	Scenario (1)		Scenario (2)
	$\mathit{E}({\mathit{\chi }}^2)$	$\mathit{V}\mathit{a}\mathit{r}({\mathit{\chi }}^2)$	$\mathit{E}({\mathit{\chi }}^2)$	$\mathit{V}\mathit{a}\mathit{r}({\mathit{\chi }}^2)$
1	3.000	0.000	3.000	9.000
2	3.000	3.000	3.000	7.500
3	3.000	4.000	3.000	7.000
4	3.000	4.500	3.000	6.750
5	3.000	4.800	3.000	6.600
6	3.000	5.000	3.000	6.500
7	3.000	5.143	3.000	6.429
8	3.000	5.250	3.000	6.375
9	3.000	5.333	3.000	6.333
10	3.000	5.400	3.000	6.300
11	3.000	5.455	3.000	6.273
12	3.000	5.500	3.000	6.250
13	3.000	5.538	3.000	6.231
14	3.000	5.571	3.000	6.214
15	3.000	5.600	3.000	6.200
16	3.000	5.625	3.000	6.188
17	3.000	5.647	3.000	6.176
18	3.000	5.667	3.000	6.167
19	3.000	5.684	3.000	6.158
20	3.000	5.700	3.000	6.150
50	3.000	5.880	3.000	6.060
100	3.000	5.940	3.000	6.030
200	3.000	5.970	3.000	6.015
400	3.000	5.985	3.000	6.008
600	3.000	5.990	3.000	6.005
800	3.000	5.993	3.000	6.004
1000	3.000	5.994	3.000	6.003
2000	3.000	5.997	3.000	6.002
4000	3.000	5.999	3.000	6.001
5000	3.000	5.999	3.000	6.000
6000	3.000	5.999	3.000	6.000

Table 1. The exact mean and variance of the Pearson’s chi-square statistic for various n under scenarios (1) and (2) with in-control proportion vectors.

n	Scenario (1)		Scenario (2)
	$\mathit{E}({\mathit{\chi }}^2)$	$\mathit{V}\mathit{a}\mathit{r}({\mathit{\chi }}^2)$	$\mathit{E}({\mathit{\chi }}^2)$	$\mathit{V}\mathit{a}\mathit{r}({\mathit{\chi }}^2)$
1	3.000	0.000	3.000	9.000
2	3.000	3.000	3.000	7.500
3	3.000	4.000	3.000	7.000
4	3.000	4.500	3.000	6.750
5	3.000	4.800	3.000	6.600
6	3.000	5.000	3.000	6.500
7	3.000	5.143	3.000	6.429
8	3.000	5.250	3.000	6.375
9	3.000	5.333	3.000	6.333
10	3.000	5.400	3.000	6.300
11	3.000	5.455	3.000	6.273
12	3.000	5.500	3.000	6.250
13	3.000	5.538	3.000	6.231
14	3.000	5.571	3.000	6.214
15	3.000	5.600	3.000	6.200
16	3.000	5.625	3.000	6.188
17	3.000	5.647	3.000	6.176
18	3.000	5.667	3.000	6.167
19	3.000	5.684	3.000	6.158
20	3.000	5.700	3.000	6.150
50	3.000	5.880	3.000	6.060
100	3.000	5.940	3.000	6.030
200	3.000	5.970	3.000	6.015
400	3.000	5.985	3.000	6.008
600	3.000	5.990	3.000	6.005
800	3.000	5.993	3.000	6.004
1000	3.000	5.994	3.000	6.003
2000	3.000	5.997	3.000	6.002
4000	3.000	5.999	3.000	6.001
5000	3.000	5.999	3.000	6.000
6000	3.000	5.999	3.000	6.000

From Table 1, we can construct the exact EWMA-proportion control chart whether n is small or large.

3. A Pearson’s Chi-Square ${(\mathit{\chi }}^2)$ Statistic-Based EWMA Chart for Monitoring the Multinomial Proportions

In statistical process control, sample size is usually small and not large. When n is not large enough, the distribution of Pearson’s chi-square statistic does not follow the well-known ${\chi }^2(m-1)$ distribution. The resulting variances of the Pearson’s chi-square statistic for various n in Section 2 exhibit this situation. Hence, it is not appropriate to adopt the ${\chi }^2(m-1)$ distribution to construct the EWMA-${\chi }^2$ control chart so as to monitor the multinomial-proportion process. The misuse of the EWMA-${\chi }^2$ control chart results in worse out-of-control detection performance.

We are able to derive the exact mean and variance of the Pearson’s chi-square statistic whether the sample size is small or not in Section 2, although it is impossible to know the distribution of the Pearson’s chi-square statistic. Based on (2) and (3), we may construct the exact EWMA-proportion control chart to monitor the changes in proportion vector of the multinomial quality variables for a small sample size. When sample size n is large enough, the in-control Pearson’s chi-square statistic is approximately distributed as ${\chi }^2(m-1)$ distribution with df m − 1. Thus, the monitoring statistic is independent of the original multinomial distribution and sample size n. Hence, we construct the asymptotic EWMA-proportion control chart. The detection performance of the two proposed EWMA-proportion control charts is then compared.

3.1. The Exact Multinomial-Proportion Control Chart

With the derived exact mean and variance of the in-control Pearson’s chi-square statistic, we may construct an exact EWMA-proportion control chart with the upper control limit (UCL), center line (CL), and lower control limit (LCL) as follows; see (5), for various sample size. In other words, the EWMA-proportion control chart has the control limit depending the value of n given the m categories. Here, we let LCL be zero since the out-of-control proportion vector leads to an increase in the value of the Pearson’s chi-square statistic.

We let the EWMA chart with monitoring statistic $EWM{A}_{{\chi }_t^2}$ at time t be the weighted average of the Pearson’s chi-square statistic ${\chi }^2$ at time t:

$$EWM{A}_{{\chi }_t^2}=\lambda {\chi }_t^2+(1-\lambda )EWM{A}_{{\chi }_{t-1}^2},t=1,2,\dots ,$$

(4)

where $\lambda \in (0,1)$ is a smooth parameter.

The in-control mean and variance of monitoring statistic $EWM{A}_{{\chi }_t^2}$ at time t are $E(EWM{A}_{{\chi }_t^2})=m-1$, and $Var(EWM{A}_{{\chi }_t^2})=\left({\displaystyle \sum _{i=1}^m\frac{1}{n{p}_{0i}}}-\frac{m^2+2m-2}{n}+2(m-1)\right)\lambda (1-{(1-\lambda )}^{2t})/(2-\lambda )$, respectively.

We let $EWM{A}_{{\chi }_{t=0}^2}$ = m − 1.

The control limits of the exact EWMA-proportion control chart are consequently:

$$\begin{array}{l}UC{L}_t=m-1+L_n\sqrt{\left({\displaystyle \sum _{i=1}^m\frac{1}{n{p}_{0i}}}-\frac{m^2+2m-2}{n}+2(m-1)\right)\lambda (1-{(1-\lambda )}^{2t})/(2-\lambda )},\\ C{L}_t=m-1,\\ LC{L}_t=0,\end{array}$$

(5)

where the coefficient L_n should be chosen to satisfy the specified ARL₀.

To determine L_n satisfying a specified ARL₀, we use the Monte Carlo method and follow Yang et al. [23]. The Monte Carlo procedure using R program language is applied to calculate L_n, by satisfying a specified ARL₀ (see Appendix B, Algorithm A1).

Based on the Monte Carlo procedure,

Table 2. The coefficient (L_n) of UCL with specified ARL₀ = 370.4 for various n and two scenarios of in-control proportion vectors.

n	Ln
	Scenario (1)	Scenario (2)
1	-	2.414
2	2.382	2.605
3	2.377	2.600
4	2.388	2.550
5	2.401	2.537
6	2.388	2.525
7	2.394	2.513
8	2.398	2.501
9	2.403	2.492
10	2.395	2.489
11	2.404	2.485
12	2.409	2.474
13	2.403	2.471
14	2.403	2.467
15	2.409	2.468
16	2.407	2.464
17	2.406	2.456
18	2.408	2.452
19	2.408	2.454
20	2.406	2.453
50	2.413	2.430
100	2.414	2.423
200	2.416	2.419
400	2.418	2.419
600	2.419	2.419
800	2.419	2.420
1000	2.419	2.420
2000	2.418	2.419
4000	2.416	2.418
5000	2.416	2.417
6000	2.416	2.417

lists the resulting L_n of the exact EWMA-proportion control charts with specified ARL₀ = 370.4 for various combinations of setting n and $\lambda$ under the aforementioned two scenarios with in-control proportion vectors. We find that the L_n value increases slowly as n increases and converges to 2.416 or 2.417 when n is equal to 6000 under scenario (1) or (2).

3.2. The Asymptotic Multinomial-Proportion Control Chart

When $n$ is large enough, the Pearson’s chi-square statistic ${\chi }^2$ follows an asymptotical chi-square distribution with df m − 1 for an in-control process, that is, ${\chi }^2$~${\chi }^2(m-1)$ with mean m − 1 and variance 2(m − 1). Thus, the monitoring statistic is independent of the original multinomial distribution and sample size n.

Based on the in-control asymptotical chi-square distribution, we may establish an EWMA multinomial-proportion control chart to monitor whether the proportion vector changes or not.

We let the EWMA chart with monitoring statistic $EWM{A}_{{\chi }_t^2}$ at time $t$ be

$$EWM{A}_{{\chi }_t^2}=\lambda {\chi }_t^2+(1-\lambda )EWM{A}_{{\chi }_{t-1}^2},t=1,2,\dots ,$$

(6)

where $EWM{A}_{{\chi }_0^2}$ = $E({\chi }^2)$ = m − 1, and $\lambda \in (0,1)$ is a smooth parameter.

The mean and variance of monitoring statistic $EWM{A}_{{\chi }_t^2}$ at time $t$ are $E(EWM{A}_{{\chi }_t^2})=m-1$ and $Var(EWM{A}_{{\chi }_t^2})=2(m-1)\lambda (1-{(1-\lambda )}^{2t})/(2-\lambda )$, respectively. We may find that the mean and variance of the monitoring statistic $EWM{A}_{{\chi }_t^2}$ are independent on n.

Hence, the dynamic control limits of the EWMA-${\chi }^2$ control chart are constructed as

$$\begin{array}{l}UC{L}_t=m-1+L\sqrt{2(m-1)\lambda (1-{(1-\lambda )}^{2t})/(2-\lambda )},\\ C{L}_t=m-1,\\ LC{L}_t=0,\end{array}$$

(7)

where $L$ is a coefficient of UCL and should be chosen to achieve a specified ARL₀.

To determine L satisfying a specified ARL₀, we refer to the Markov chain method in Lucas and Saccucci [24] or Chandrasekaran et al. [25]. We describe the ARL₀ calculation procedure as follows.

Step 1. For a given $L$, at time $t$, the region $(0,UC{L}_t]$ is partitioned into $k$(e.g., $k=101$) subsets $\mathrm{or}\mathrm{state}{A}_i,i=1,2,\dots ,k$, where $A_i=(UC{L}_t(i-1)/k,UC{L}_t(i)/k]$.

Step 2. Denote the transition probability matrix with transition probabilities $p_{i,j}{}^t$, from state $A_i$ to state $A_j$ at time $t$, as $B_t={(p_{i,j}{}^t)}_{k\times k},t\ge 2$, where

$p_{i,j}{}^t=p({\chi }^2(m-1)\le (UC{L}_t(j)/k-(1-\lambda )UC{L}_{t-1}(i-0.5)/k)/\lambda )-$

$p({\chi }^2(m-1)\le (UC{L}_t(j-1)/k-(1-\lambda )UC{L}_{t-1}(i-0.5)/k)/\lambda )$.

For $t=1$,

$p_{i,j}{}^1=p({\chi }^2(m-1)\le (UC{L}_1(j)/k-(1-\lambda )UC{L}_1(i-0.5)/k)/\lambda )-$

$p({\chi }^2(m-1)\le (UC{L}_1(j-1)/k-(1-\lambda )UC{L}_1(i-0.5)/k)/\lambda )$.

Step 3. $AR{L}_0(L)=p^T(Q_1+2B_1{Q}_2+3B_1{B}_2{Q}_3+\dots +n{B}_1{B}_2{B}_3\dots B_{n-1}{Q}_n+\dots )$, where $Q_t=(I_k-B_t)1$, $1$ is a column vector of ones, and the initial state probability is

$p={(0,\dots ,1,\dots ,0)}^T$.

To obtain the coefficient of the UCL, $L$, of the asymptotical control chart we next adopt the bisection algorithm. The calculation procedure is described as follows.

Step 1. For a given in-control $AR{L}_0$, consider an interval $[L_1,L_2]$ of L such that

$AR{L}_0(L_1)<AR{L}_0<AR{L}_0(L_2)$, and a threshold error $\epsilon >0$ (e.g., $\epsilon =0.5$),

• where $AR{L}_0(L_1)$ and $AR{L}_0(L_2)$ are computed by the above-mentioned procedure.

Step 2. Let $L_{middle}=(L_1+L_2)/2$.

Step 3. If $(AR{L}_0(L_{middle})-AR{L}_0)(AR{L}_0(L_1)-AR{L}_0)\le 0$, then

$L_2=L_{middle}$, else $L_1=L_{middle}$.

Step 4. Repeat step 2 and step 3 until $|AR{L}_0(L_{middle})-AR{L}_0|\le \epsilon$.

Hence, $L=L_{middle}$.

Based on the Markov chain method and bisection algorithm described above, the calculated coefficient (L) of the UCL with specified ARL₀ = 370.4 under scenario (1) or (2) is 2.416. The result is obvious since L is a fixed value and independent of sample size n.

3.3. Comparison of the Exact and Asymptotic Multinomial-Proportion Control Charts

The resulting L and $L_n$ of the exact and asymptotic EWMA-proportion control charts for the two scenarios show that L_n converges to L (=2.416) when n ($\ge$6000) is large enough. However, when n is not large enough, estimated L_n and L exhibit obvious difference. This is evidence that it is incorrect to adopt the asymptotic EWMA-proportion control chart to monitor the multinomial proportion vector when n is small or not large enough. Hence, the exact EWMA-proportion control chart is recommended for small and not large enough n.

4. Detection Performance Measurement of the Proposed Exact and Asymptotic EWMA-Proportion Control Charts

Without loss of generality, to measure the out-of-control detection performance of the proposed exact and asymptotic EWMA-proportion charts, we consider the following two scenarios with six out-of-control proportion vectors for setting n = 2(1)20, 50, 100(100), $\lambda =0.05$, and ARL₀ = 370.

Scenario (1) has in-control proportion vector, $p_0=(0.25,0.25,0.25,0.25)$, and six out-of-control proportion vectors as follows. The six out-of-control proportion vectors:

$p_1=(0.2,0.3,0.25,0.25)$, $p_2=(0.1,0.4,0.25,0.25),$ $p_3=(0.05,0.45,0.25,0.25),$ $p_4=(0.2,0.2,0.35,0.25),$ $p_5=(0.1,0.1,0.55,0.25)$, and $p_6=(0.05,0.05,0.65,0.25)$.

Scenario (2) with in-control proportion vector, $p_0=(0.1,0.1,0.4,0.4)$, and six out-of-control proportion vectors run as follows. The six out-of-control proportion vectors:

$p_1=(0.15,0.05,0.4,0.4)$, $p_2=(0.2,0,0.4,0.4),$ $p_3=(0.25,0.25,0.1,0.4)$, $p_4=(0.2,0.2,0.35,0.25)$, $p_5=(0.15,0.15,0.3,0.4)$, and $p_6=(0.25,0.25,0.25,0.25)$.

4.1. Detection Performance of the Proposed Exact EWMA-Proportion Chart

Applying the calculated control limit coefficient, $L_n$, of the proposed exact chart and the given scenarios (1) and (2) with the six out-of-control proportion vectors and sample size, we can calculate out-of-control average run length (ARL₁). The Monte Carlo procedure is also applied to calculate ARL₁ using R program language, see Appendix C (Algorithm A2). A smaller ARL₁ indicates better detection performance of a control chart. ARL₁ is always a popular detection performance index in the study of statistical process control.

The resulting Table 3 and Table 4 illustrate the calculated ARL₁ (first row) and SDRL (standard deviation of run length; second row) of the proposed exact chart for various n and scenarios (1) and (2), respectively. We find the following results in Table 3 and Table 4:

(i)

For detecting any out-of-control proportion vector, ARL₁ decreases when n increases;

(ii)

The larger the difference is between p₀ and p_i, the smaller is ARL₁ under each n. The result is reasonable.

Table 3. ARLs of the proposed exact control chart for various n under scenario (1) with the six out-of-control proportion vectors.

$\mathit{n}$	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$
2	369.956 402.099	321.682 351.861	121.808 130.346	65.69 69.036	243.704 264.746	32.476 32.604	13.582 12.771
3	372.065 416.056	287.588 323.047	69.136 75.999	32.504 34.156	183.376 205.704	14.306 15.077	5.923 5.942
4	369.232 393.303	261.716 278.589	47.220 47.005	21.347 19.678	144.940 153.794	9.817 8.761	4.451 3.444
5	370.177 405.620	238.209 263.725	32.446 33.244	14.187 13.570	114.307 125.545	6.370 6.160	2.813 2.369
6	368.793 394.082	218.664 232.241	25.131 23.899	11.102 9.574	95.834 100.353	5.307 4.421	2.577 1.693
7	374.458 398.754	203.780 217.250	20.065 18.688	8.840 7.366	81.281 84.604	4.339 3.463	2.127 1.325
8	369.532 399.416	185.235 197.368	16.036 14.924	6.974 5.832	67.638 70.737	3.475 2.815	1.737 1.051
9	367.247 395.453	170.07 184.802	13.245 12.332	5.749 4.824	57.690 60.603	2.899 2.343	1.487 0.846
10	370.275 396.203	158.746 167.584	11.551 10.170	5.181 3.947	50.98 52.264	2.762 1.965	1.509 0.754
11	370.450 400.534	146.869 157.557	9.862 8.811	4.438 3.391	44.622 45.979	2.359 1.715	1.350 0.635
12	368.108 398.165	135.948 146.166	8.451 7.626	3.764 2.968	39.605 41.012	2.106 1.503	1.215 0.504
13	370.740 398.013	127.254 134.882	7.674 6.678	3.482 2.524	35.619 36.202	1.973 1.331	1.195 0.461
14	369.888 396.682	119.230 125.792	6.936 5.874	3.178 2.246	32.176 32.313	1.887 1.183	1.170 0.418
15	371.409 399.734	110.564 117.402	6.162 5.318	2.785 2.025	29.037 29.353	1.697 1.058	1.110 0.341
16	368.316 396.150	103.902 110.434	5.658 4.771	2.643 1.791	26.366 26.366	1.619 0.957	1.086 0.300
17	372.261 398.352	97.635 102.595	5.250 4.308	2.476 1.609	24.342 24.132	1.557 0.875	1.074 0.274
18	368.650 397.644	92.060 97.515	4.764 3.962	2.225 1.466	22.313 22.202	1.458 0.801	1.050 0.225
19	369.787 396.360	86.608 91.298	4.394 3.594	2.102 1.345	20.668 20.551	1.402 0.726	1.035 0.189
20	368.262 395.554	81.618 85.676	4.127 3.323	2.004 1.236	19.156 18.807	1.359 0.675	1.030 0.173
50	370.723 398.263	24.540 24.130	1.476 0.778	1.045 0.211	5.338 4.713	1.008 0.675	1.000 0.001
100	370.097 398.439	9.079 8.360	1.041 0.203	1.000 0.009	2.309 1.678	1.000 0.002	1.000 0.000
200	371.126 400.019	3.564 2.916	1.000 0.011	1.000 0.000	1.286 0.587	1.000 0.000	1.000 0.000
400	369.493 398.541	1.692 1.028	1.000 0.000	1.000 0.000	1.021 0.143	1.000 0.000	1.000 0.000
600	370.632 398.363	1.256 0.542	1.000 0.000	1.000 0.000	1.001 0.033	1.000 0.000	1.000 0.000
800	369.187 397.229	1.101 0.324	1.000 0.000	1.000 0.000	1.000 0.007	1.000 0.000	1.000 0.000
1000	369.751 398.334	1.038 0.196	1.000 0.000	1.000 0.000	1.000 0.001	1.000 0.000	1.000 0.000
2000	369.708 398.510	1.000 0.013	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
4000	369.557 397.351	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
5000	369.657 398.279	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
6000	369.736 398.101	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000

Table 3. ARLs of the proposed exact control chart for various n under scenario (1) with the six out-of-control proportion vectors.

$\mathit{n}$	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$
2	369.956 402.099	321.682 351.861	121.808 130.346	65.69 69.036	243.704 264.746	32.476 32.604	13.582 12.771
3	372.065 416.056	287.588 323.047	69.136 75.999	32.504 34.156	183.376 205.704	14.306 15.077	5.923 5.942
4	369.232 393.303	261.716 278.589	47.220 47.005	21.347 19.678	144.940 153.794	9.817 8.761	4.451 3.444
5	370.177 405.620	238.209 263.725	32.446 33.244	14.187 13.570	114.307 125.545	6.370 6.160	2.813 2.369
6	368.793 394.082	218.664 232.241	25.131 23.899	11.102 9.574	95.834 100.353	5.307 4.421	2.577 1.693
7	374.458 398.754	203.780 217.250	20.065 18.688	8.840 7.366	81.281 84.604	4.339 3.463	2.127 1.325
8	369.532 399.416	185.235 197.368	16.036 14.924	6.974 5.832	67.638 70.737	3.475 2.815	1.737 1.051
9	367.247 395.453	170.07 184.802	13.245 12.332	5.749 4.824	57.690 60.603	2.899 2.343	1.487 0.846
10	370.275 396.203	158.746 167.584	11.551 10.170	5.181 3.947	50.98 52.264	2.762 1.965	1.509 0.754
11	370.450 400.534	146.869 157.557	9.862 8.811	4.438 3.391	44.622 45.979	2.359 1.715	1.350 0.635
12	368.108 398.165	135.948 146.166	8.451 7.626	3.764 2.968	39.605 41.012	2.106 1.503	1.215 0.504
13	370.740 398.013	127.254 134.882	7.674 6.678	3.482 2.524	35.619 36.202	1.973 1.331	1.195 0.461
14	369.888 396.682	119.230 125.792	6.936 5.874	3.178 2.246	32.176 32.313	1.887 1.183	1.170 0.418
15	371.409 399.734	110.564 117.402	6.162 5.318	2.785 2.025	29.037 29.353	1.697 1.058	1.110 0.341
16	368.316 396.150	103.902 110.434	5.658 4.771	2.643 1.791	26.366 26.366	1.619 0.957	1.086 0.300
17	372.261 398.352	97.635 102.595	5.250 4.308	2.476 1.609	24.342 24.132	1.557 0.875	1.074 0.274
18	368.650 397.644	92.060 97.515	4.764 3.962	2.225 1.466	22.313 22.202	1.458 0.801	1.050 0.225
19	369.787 396.360	86.608 91.298	4.394 3.594	2.102 1.345	20.668 20.551	1.402 0.726	1.035 0.189
20	368.262 395.554	81.618 85.676	4.127 3.323	2.004 1.236	19.156 18.807	1.359 0.675	1.030 0.173
50	370.723 398.263	24.540 24.130	1.476 0.778	1.045 0.211	5.338 4.713	1.008 0.675	1.000 0.001
100	370.097 398.439	9.079 8.360	1.041 0.203	1.000 0.009	2.309 1.678	1.000 0.002	1.000 0.000
200	371.126 400.019	3.564 2.916	1.000 0.011	1.000 0.000	1.286 0.587	1.000 0.000	1.000 0.000
400	369.493 398.541	1.692 1.028	1.000 0.000	1.000 0.000	1.021 0.143	1.000 0.000	1.000 0.000
600	370.632 398.363	1.256 0.542	1.000 0.000	1.000 0.000	1.001 0.033	1.000 0.000	1.000 0.000
800	369.187 397.229	1.101 0.324	1.000 0.000	1.000 0.000	1.000 0.007	1.000 0.000	1.000 0.000
1000	369.751 398.334	1.038 0.196	1.000 0.000	1.000 0.000	1.000 0.001	1.000 0.000	1.000 0.000
2000	369.708 398.510	1.000 0.013	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
4000	369.557 397.351	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
5000	369.657 398.279	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
6000	369.736 398.101	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000

Table 4. ARLs of the proposed exact control chart for various n under scenario (2) with the six out-of-control proportion vectors.

$\mathit{n}$	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$
1	369.314 395.079	371.081 394.476	370.828 394.501	9.320 7.951	17.190 15.914	45.580 45.433	9.318 7.973
2	368.283 400.411	258.404 283.917	123.075 138.227	7.802 6.934	15.158 14.770	42.878 44.518	8.120 7.384
3	369.013 405.564	207.565 229.870	74.424 83.969	4.972 4.754	11.054 11.299	34.678 36.799	5.396 5.359
4	368.840 390.956	173.702 185.024	51.568 54.552	4.441 3.391	9.838 9.003	31.085 30.668	4.930 4.078
5	370.999 395.305	144.832 157.049	36.937 38.928	3.570 2.746	8.096 7.597	26.724 26.895	3.966 3.395
6	370.222 398.943	123.071 133.663	27.592 28.795	2.904 2.217	6.842 6.532	23.593 23.916	3.302 2.841
7	368.671 398.112	107.071 114.893	21.611 22.220	2.494 1.823	6.081 5.613	21.262 21.481	2.970 2.394
8	370.126 395.952	93.134 99.214	17.970 17.581	2.167 1.546	5.363 4.940	19.289 19.300	2.592 2.081
9	370.868 396.084	81.428 86.310	14.823 14.296	2.029 1.318	4.915 4.388	17.743 17.596	2.446 1.829
10	369.120 398.684	71.317 76.376	12.402 11.947	1.789 1.151	4.354 3.959	16.071 16.203	2.139 1.630
11	370.757 398.200	63.001 67.485	10.537 10.107	1.671 1.004	4.013 3.569	14.954 14.947	2.026 1.454
12	368.926 396.388	57.180 59.868	9.521 8.605	1.595 0.889	3.802 3.222	14.066 13.791	1.960 1.306
13	371.755 398.458	51.611 53.654	8.408 7.491	1.449 0.792	3.475 2.966	12.980 12.832	1.782 1.190
14	369.361 398.027	46.467 48.400	7.471 6.571	1.406 0.715	3.292 2.725	12.146 11.953	1.741 1.096
15	366.476 398.999	42.014 43.662	6.654 5.823	1.331 0.641	3.002 2.526	11.312 11.217	1.599 0.998
16	369.623 398.93	38.371 39.606	5.875 1.197	1.268 0.57	2.852 2.342	10.702 10.512	1.536 0.915
17	372.149 397.024	35.721 36.112	5.585 4.611	1.249 0.531	2.783 2.171	10.282 9.860	1.537 0.862
18	369.494 397.07	32.851 33.070	5.151 4.163	1.215 0.486	2.634 2.03	9.769 9.296	1.461 0.794
19	369.044 398.317	30.160 30.550	4.714 3.802	1.185 0.442	2.441 1.907	9.156 8.822	1.369 0.726
20	369.159 399.616	27.988 28.106	4.392 3.473	1.159 0.410	2.365 1.797	8.657 8.356	1.365 0.690
50	370.314 397.494	7.236 6.396	1.420 0.618	1.000 0.025	1.242 0.532	3.407 2.825	1.019 0.136
100	369.737 398.007	2.819 2.120	1.000 0.000	1.000 0.000	1.018 0.135	1.757 1.119	1.000 0.007
200	369.376 397.284	1.405 0.709	1.000 0.000	1.000 0.000	1.000 0.007	1.141 0.391	1.000 0.000
400	370.64 399.136	1.031 0.170	1.000 0.000	1.000 0.000	1.000 0.000	1.005 0.069	1.000 0.000
600	370.225 398.276	1.002 0.041	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.009	1.000 0.000
800	370.060 397.990	1.000 0.008	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.001	1.000 0.000
1000	369.657 398.683	1.000 0.001	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
2000	370.317 398.111	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
4000	370.794 399.123	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
5000	370.790 399.038	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
6000	369.862 398.246	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000

Table 4. ARLs of the proposed exact control chart for various n under scenario (2) with the six out-of-control proportion vectors.

$\mathit{n}$	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$
1	369.314 395.079	371.081 394.476	370.828 394.501	9.320 7.951	17.190 15.914	45.580 45.433	9.318 7.973
2	368.283 400.411	258.404 283.917	123.075 138.227	7.802 6.934	15.158 14.770	42.878 44.518	8.120 7.384
3	369.013 405.564	207.565 229.870	74.424 83.969	4.972 4.754	11.054 11.299	34.678 36.799	5.396 5.359
4	368.840 390.956	173.702 185.024	51.568 54.552	4.441 3.391	9.838 9.003	31.085 30.668	4.930 4.078
5	370.999 395.305	144.832 157.049	36.937 38.928	3.570 2.746	8.096 7.597	26.724 26.895	3.966 3.395
6	370.222 398.943	123.071 133.663	27.592 28.795	2.904 2.217	6.842 6.532	23.593 23.916	3.302 2.841
7	368.671 398.112	107.071 114.893	21.611 22.220	2.494 1.823	6.081 5.613	21.262 21.481	2.970 2.394
8	370.126 395.952	93.134 99.214	17.970 17.581	2.167 1.546	5.363 4.940	19.289 19.300	2.592 2.081
9	370.868 396.084	81.428 86.310	14.823 14.296	2.029 1.318	4.915 4.388	17.743 17.596	2.446 1.829
10	369.120 398.684	71.317 76.376	12.402 11.947	1.789 1.151	4.354 3.959	16.071 16.203	2.139 1.630
11	370.757 398.200	63.001 67.485	10.537 10.107	1.671 1.004	4.013 3.569	14.954 14.947	2.026 1.454
12	368.926 396.388	57.180 59.868	9.521 8.605	1.595 0.889	3.802 3.222	14.066 13.791	1.960 1.306
13	371.755 398.458	51.611 53.654	8.408 7.491	1.449 0.792	3.475 2.966	12.980 12.832	1.782 1.190
14	369.361 398.027	46.467 48.400	7.471 6.571	1.406 0.715	3.292 2.725	12.146 11.953	1.741 1.096
15	366.476 398.999	42.014 43.662	6.654 5.823	1.331 0.641	3.002 2.526	11.312 11.217	1.599 0.998
16	369.623 398.93	38.371 39.606	5.875 1.197	1.268 0.57	2.852 2.342	10.702 10.512	1.536 0.915
17	372.149 397.024	35.721 36.112	5.585 4.611	1.249 0.531	2.783 2.171	10.282 9.860	1.537 0.862
18	369.494 397.07	32.851 33.070	5.151 4.163	1.215 0.486	2.634 2.03	9.769 9.296	1.461 0.794
19	369.044 398.317	30.160 30.550	4.714 3.802	1.185 0.442	2.441 1.907	9.156 8.822	1.369 0.726
20	369.159 399.616	27.988 28.106	4.392 3.473	1.159 0.410	2.365 1.797	8.657 8.356	1.365 0.690
50	370.314 397.494	7.236 6.396	1.420 0.618	1.000 0.025	1.242 0.532	3.407 2.825	1.019 0.136
100	369.737 398.007	2.819 2.120	1.000 0.000	1.000 0.000	1.018 0.135	1.757 1.119	1.000 0.007
200	369.376 397.284	1.405 0.709	1.000 0.000	1.000 0.000	1.000 0.007	1.141 0.391	1.000 0.000
400	370.64 399.136	1.031 0.170	1.000 0.000	1.000 0.000	1.000 0.000	1.005 0.069	1.000 0.000
600	370.225 398.276	1.002 0.041	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.009	1.000 0.000
800	370.060 397.990	1.000 0.008	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.001	1.000 0.000
1000	369.657 398.683	1.000 0.001	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
2000	370.317 398.111	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
4000	370.794 399.123	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
5000	370.790 399.038	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
6000	369.862 398.246	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000

4.2. Detection Performance of the Asymptotic EWMA-Proportion Chart

Applying the calculated control limit coefficient, L, of the asymptotic chart and the given scenarios (1) and (2) with the six out-of-control proportion vectors, we can calculate ARL₁.

The resulting

Table 5. ARLs of the asymptotic control chart under various n for scenario (1) with the six out-of-control proportion vectors.

n	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$
2	3880.926 3896.139	3123.472 3131.111	720.986 713.365	280.329 267.982	2074.137 2077.971	100.033 87.278	32.574 23.585
3	1078.071 1157.757	791.313 852.399	135.773 143.038	54.859 54.858	449.865 486.158	21.522 20.860	8.127 7.673
4	757.384 789.150	509.243 530.552	69.903 67.986	29.123 25.865	255.223 264.734	12.387 10.735	5.275 4.127
5	648.207 671.590	398.79 412.093	44.919 41.702	18.887 15.778	178.058 181.867	8.516 6.820	3.906 2.517
6	569.374 600.160	321.301 338.397	30.593 28.619	12.860 10.987	129.408 134.551	5.840 4.960	2.674 1.853
7	535.804 565.679	277.828 292.373	23.219 21.278	9.835 8.174	102.369 105.892	4.649 3.783	2.184 1.425
8	506.336 538.152	241.435 255.351	18.239 16.578	7.768 6.409	82.654 85.335	3.753 3.033	1.818 1.155
9	483.561 518.434	212.767 227.899	14.599 13.408	6.212 5.205	68.121 71.033	3.058 2.507	1.524 0.909
10	476.051 503.278	194.730 204.614	12.641 11.060	5.506 4.240	59.056 59.678	2.837 2.081	1.515 0.774
11	458.735 490.911	173.615 184.745	10.581 9.367	4.643 3.601	50.003 51.157	2.415 1.800	1.356 0.653
12	455.017 481.168	160.708 168.485	9.410 8.035	4.172 3.048	44.605 44.578	2.298 1.549	1.322 0.577
13	446.672 476.889	146.102 154.694	8.163 7.040	3.641 2.673	38.955 39.251	2.015 1.383	1.200 0.475
14	439.888 468.259	134.735 141.612	7.318 6.176	3.300 2.341	34.911 34.699	1.919 1.230	1.173 0.427
15	437.203 465.765	125.143 131.462	6.589 5.493	3.032 2.066	31.407 31.184	1.775 1.100	1.134 0.372
16	428.399 458.844	115.217 121.453	5.884 4.944	2.715 1.867	28.267 28.076	1.636 0.989	1.086 0.302
17	425.681 454.903	107.603 112.808	5.423 4.465	2.523 1.674	25.919 25.447	1.573 0.902	1.073 0.274
18	420.922 451.455	100.071 105.644	4.913 4.088	2.287 1.532	23.522 23.301	1.465 0.815	1.050 0.228
19	417.849 448.075	93.837 98.522	4.547 3.733	2.148 1.394	21.729 21.368	1.411 0.745	1.036 0.192
20	416.766 445.050	88.216 92.002	4.277 3.407	2.062 1.270	20.240 19.673	1.385 0.692	1.035 0.187
50	386.868 415.975	25.082 24.631	1.480 0.785	1.044 0.21	5.391 4.773	1.008 0.090	1.000 0.000
100	378.202 406.259	9.145 8.405	9.082 0.204	1.000 0.009	2.319 1.688	1.000 0.002	1.000 0.000
200	374.087 403.003	3.575 2.921	1.000 0.011	1.000 0.000	1.288 0.590	1.000 0.000	1.000 0.000
400	370.638 399.267	1.692 1.028	1.000 0.000	1.000 0.000	1.020 0.143	1.000 0.000	1.000 0.000
600	369.798 398.157	1.256 0.543	1.000 0.000	1.000 0.000	1.001 0.032	1.000 0.000	1.000 0.000
800	369.017 397.659	1.100 0.323	1.000 0.000	1.000 0.000	1.000 0.005	1.000 0.000	1.000 0.000
1000	368.672 397.161	1.038 0.197	1.000 0.000	1.000 0.000	1.000 0.002	1.000 0.000	1.000 0.000
2000	369.183 398.185	1.000 0.013	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
4000	369.313 398.385	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
5000	369.596 398.369	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
6000	369.646 397.875	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000

(scenario (1)) and

Table 6. ARLs of the asymptotic control chart under various n for scenario (2) with the six out-of-control proportion vectors.

$\mathit{n}$	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$
1	149.100 190.427	149.131 190.656	149.435 190.444	5.099 6.226	9.434 11.788	23.891 30.444	5.091 6.220
2	211.107 232.441	156.108 174.418	81.979 94.030	6.891 5.926	12.582 12.043	31.619 32.925	7.071 6.270
3	234.377 261.884	141.543 160.014	56.129 64.268	4.239 4.098	9.132 9.570	26.670 28.990	4.632 4.644
4	254.595 278.088	128.980 140.884	42.294 45.288	3.612 3.110	8.095 8.012	24.825 25.974	4.000 3.723
5	270.693 292.512	114.659 124.793	31.555 33.353	3.292 2.500	7.366 6.881	23.010 23.390	3.731 3.122
6	278.487 305.263	100.133 110.100	24.204 25.650	2.654 2.071	6.237 6.021	20.532 21.291	3.071 2.669
7	287.245 315.190	88.690 97.624	19.511 20.162	2.287 1.712	5.416 5.256	18.594 19.448	2.658 2.267
8	297.024 320.759	80.086 85.897	16.506 16.214	2.091 1.454	5.043 4.642	17.515 17.787	2.494 1.970
9	300.812 326.830	70.928 76.427	13.705 13.386	1.919 1.251	4.657 4.157	16.204 16.357	2.369 1.746
10	306.108 331.928	63.493 68.176	11.661 11.222	1.724 1.097	4.157 3.778	14.883 15.099	2.087 1.564
11	309.943 337.242	56.698 60.932	9.940 9.547	1.580 0.959	3.788 3.422	13.764 14.016	1.934 1.400
12	316.717 342.484	52.133 55.010	9.015 8.221	1.539 0.860	3.694 3.120	13.238 13.089	1.936 1.271
13	320.280 346.034	47.283 49.674	7.963 7.166	1.435 0.762	3.361 2.858	12.291 12.203	1.753 1.151
14	321.785 348.787	42.931 44.946	7.119 6.303	1.360 0.683	3.138 2.637	11.508 11.437	1.672 1.055
15	324.025 351.660	39.232 40.889	6.411 5.595	1.324 0.623	2.937 2.449	10.800 10.737	1.583 0.971
16	326.148 353.893	35.968 37.359	5.705 5.013	1.262 0.559	2.775 2.274	10.223 10.121	1.510 0.890
17	329.612 356.022	33.574 34.347	5.438 4.462	1.232 0.514	2.665 2.118	9.756 9.515	1.474 0.830
18	331.238 357.644	31.008 31.556	4.978 4.048	1.189 0.463	2.541 1.986	9.284 9.023	1.432 0.774
19	331.958 359.795	28.646 29.015	4.585 3.687	1.165 0.426	2.400 1.866	8.792 8.556	1.360 0.712
20	333.886 361.667	26.651 26.966	4.261 3.367	1.147 0.395	2.318 1.751	8.365 8.096	1.350 0.675
50	355.057 381.753	7.161 6.34	1.417 0.611	1.001 0.025	1.241 0.529	3.38 2.797	1.019 0.137
100	362.178 391.087	2.801 2.107	1.000 0.000	1.000 0.000	1.018 0.134	1.751 1.113	1.000 0.007
200	366.135 393.971	1.404 0.708	1.000 0.000	1.000 0.000	1.000 0.007	1.140 0.390	1.000 0.000
400	367.412 396.169	1.031 0.177	1.000 0.000	1.000 0.000	1.000 0.000	1.005 0.000	1.000 0.000
600	367.196 396.301	1.002 0.042	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.009	1.000 0.000
800	367.608 396.326	1.000 0.008	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.001	1.000 0.000
1000	367.333 395.985	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
2000	367.691 396.363	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
4000	368.637 397.286	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
5000	368.955 397.586	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000
6000	370.236 399.095	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000	1.000 0.000

(scenario (2)) illustrate the calculated ARL₁ (first row) and SDRL (second row) of the asymptotic chart, respectively.

We find the following results in Table 5 and Table 6:

(i)

Most ARL₀s are far away from the specified 370.4 for small n. In Table 5, we find many ARL₀s are larger than the specified 370.4 for n < 400, and some ARL₁s are larger than the specified 370.4 for very small n. However, in Table 6, we find all ARL₀s are smaller than the specified 370.4 for n < 6000. These results indicate that the proposed asymptotic control chart is not in-control robust, it becomes ARL biased, and its detection performance is worse for small n.

(ii)

When n is large (n $\ge$ 400 for scenario (1) or n = 6000 for scenario (2)), the calculated ARL₀ close to the specified ARL₀, and ARL₁ decreases when n increases for detecting any out-of-control proportion vector.

(iii)

The larger the difference is between p₀ and p_i, i = 1, 2, …, 6, the smaller is ARL₁ under each n.

All those phenomena indicate the asymptotic control chart should be adopted in process control by taking n $\ge$ 400 or 6000 in scenario (1) or (2) for the correcting control process; otherwise, the detection performance of the asymptotic control chart would be worse and result in an incorrect process adjustment.

Compared with the resulting Table 3, Table 4, Table 5 and Table 6, we find that the two charts do have almost the same in-control and out-of-control process control performances for n $\ge$ 6000. However, the exact EWMA-proportion chart offers correct results compared to the asymptotic control chart, especially for small n. Hence, the proposed exact EWMA-proportion chart is recommended whether the sample size is small or not.

5. Monitoring Under-Specification Proportions of a Continuous Multivariate Process Using the Proposed EWMA-Proportion Chart and Its Application

The proposed exact EWMA-proportion chart can not only be applied to monitor the proportion vector of a multinomial process but also the proportion vector of multiple categories in a distribution-free or an unknown distributed continuous multivariate process.

In this section, we provide an example to describe how to apply our proposed exact chart to monitor the proportion vector of four categories in a distribution-free or an unknown distributed continuous bivariate process. We adopt a semiconductor manufacturing data-set that can be found in a data depository maintained by the University of California, Irvine (McCann and Johnston [26]). The data-set spans from July 2008 to October 2008 and contains 591 continuous quality variables. Each variable has 1567 observations, including 1463 in-control observations and 104 out-of-control observations.

To demonstrate the detection performance of the proposed exact chart, we select 2 of the 591 continuous correlated quality variables, $X$ = (X3, X12)^T. Based on the respective specifications of X3 and X12, they can be classified into four categories. The four categories: (1) X3 and X12 are all under specifications, (2) X3 is under specification, but X12 is not, (3) X3 and X12 are all out of specifications, and (4) X3 is out of specification, but X12 is under specification. By examining the 1463 in-control population observations, we classify their categories and obtain the proportion vector of the four categories as p₀ = (0.4, 0.08, 0.07, 0.45). For the 104 out-of-control population observations, the proportion vector of the four categories is p₁ = (0.00, 0.00, 0.2167, 0.7833). To demonstrate the detection performance of the proposed exact chart, we take the first 100 in-control observations and the first 60 out-of-control observations, respectively. We let the sample size be five, then there are 20 in-control samples and 12 out-of-control samples. To monitor the process proportion vector, we construct the exact control chart applying the aforementioned method.

From (5), we know that the control limit of the proposed exact control chart is variable when sampling time changes. Hence, for each sampling time t, we list $UC{L}_t$, the number of observations in each category (n_ij), the in-control statistic value (${\chi }_t^2$), and charting statistic value ($EWM{A}_{{\chi }_t^2}$) for the 20 in-control subgroup data. The results are illustrated in

Table 7. The in-control statistics and UCL of the exact control chart.

Number $\mathit{t}$	${\mathit{n}}_{11}$	${\mathit{n}}_{12}$	${\mathit{n}}_{21}$	${\mathit{n}}_{22}$	${\mathit{\chi }}_{\mathit{t}}^2$	$\mathit{E}\mathit{W}\mathit{M}{\mathit{A}}_{{\mathit{\chi }}_{\mathit{t}}^2}$	$\mathit{U}\mathit{C}{\mathit{L}}_{\mathit{t}}$
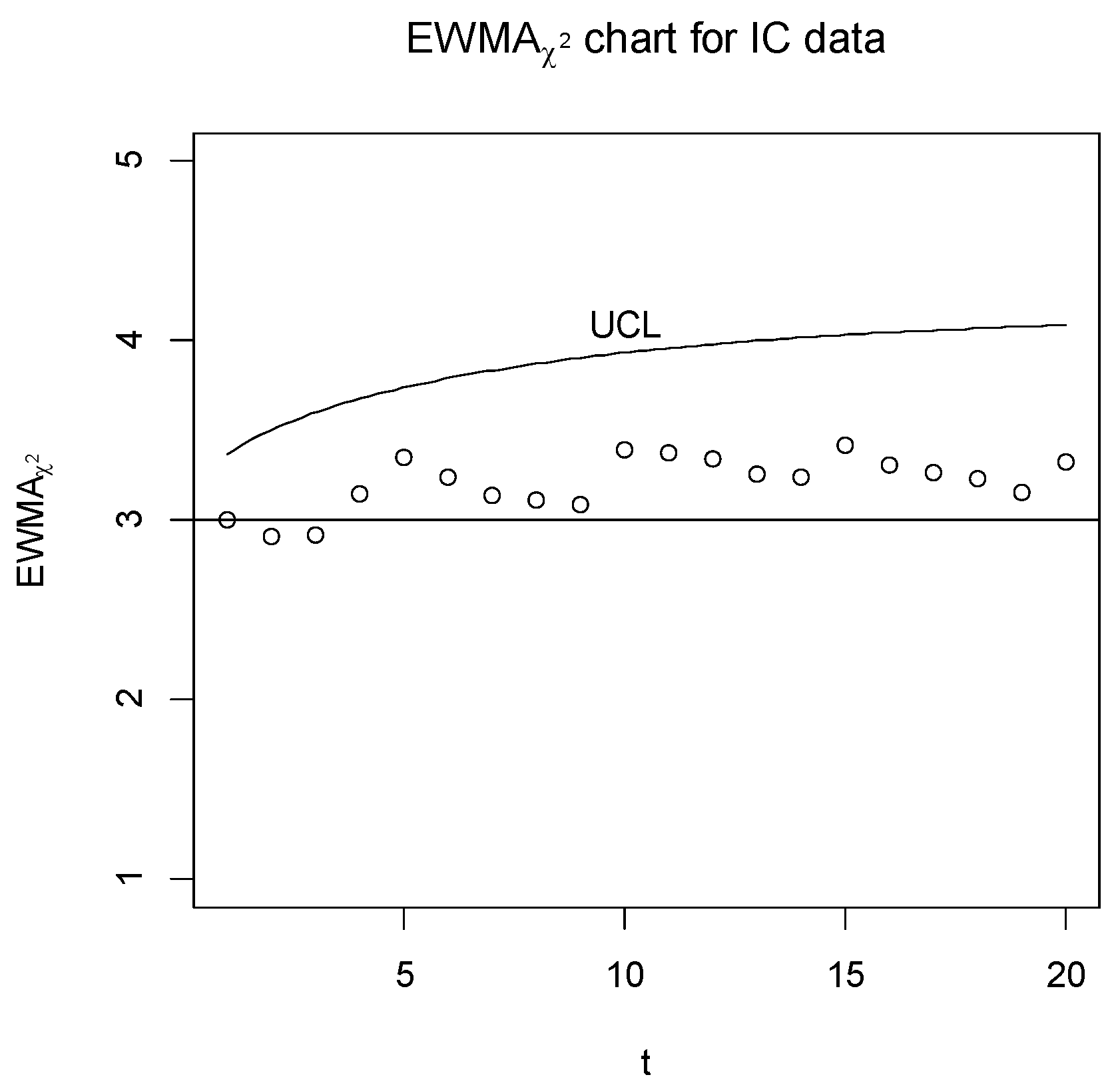
1	4	0	0	1	3.084	3.004	3.363
2	3	0	0	2	1.146	2.911	3.500
3	4	0	0	1	3.084	2.92	3.598
4	2	2	0	1	7.37	3.142	3.674
5	1	2	0	2	7.337	3.352	3.735
6	2	0	0	3	1.091	3.239	3.787
7	3	0	0	2	1.146	3.134	3.831
8	1	1	1	2	2.694	3.112	3.869
9	1	0	1	3	2.519	3.083	3.901
10	0	2	0	3	9.186	3.388	3.930
11	4	0	0	1	3.084	3.373	3.955
12	1	1	1	2	2.694	3.339	3.977
13	2	0	1	2	1.622	3.253	3.999
14	1	0	0	4	2.918	3.236	4.017
15	5	0	0	0	6.905	3.42	4.032
16	2	0	0	3	1.091	3.303	4.046
17	1	0	1	3	2.519	3.264	4.058
18	3	0	1	1	2.608	3.231	4.069
19	2	0	1	2	1.622	3.151	4.078
20	0	0	0	5	6.628	3.325	4.087

. We then plot the in-control $EWM{A}_{{\chi }_t^2}$ values in the constructed exact control chart; see Figure 1. We find all $EWM{A}_{{\chi }_t^2}$ values fall within $UC{L}_t$ demonstrating that the first 20 samples are all from the population with the in-control proportion vector. Furthermore, we calculate n_ij, the out-of-control statistic value (${\chi }_t^2$), and charting statistic value ($EWM{A}_{{\chi }_t^2}$) using the 12 out-of-control subgroup data. The results appear in

Table 8. The out-of-control statistics of the exact EWMA control chart.

Sampling Time $\mathit{t}$	${\mathit{n}}_{11}$	${\mathit{n}}_{12}$	${\mathit{n}}_{21}$	${\mathit{n}}_{22}$	${\mathit{\chi }}_{\mathit{t}}^2$	$\mathit{E}\mathit{W}\mathit{M}{\mathit{A}}_{{\mathit{\chi }}_{\mathit{t}}^2}$
1	0	0	2	3	10.615	3.381
2	0	0	1	4	5.299	3.477
3	0	0	1	4	5.299	3.568
4	0	0	2	3	10.615	3.92
5	0	0	2	3	10.615	4.255
6	0	0	2	3	10.615	4.573
7	0	0	0	5	6.628	4.676
8	0	0	2	3	10.615	4.973
9	0	0	1	4	5.299	4.989
10	0	0	0	5	6.628	5.071
11	0	0	0	5	6.628	5.149
12	0	0	0	5	6.628	5.223

. We display the out-of-control $EWM{A}_{{\chi }_t^2}$ values in the constructed exact control chart in Figure 2. We find that the first $EWM{A}_{{\chi }_t^2}$ value falls outside of $UC{L}_t$, and ten out of the twelve $EWM{A}_{{\chi }_t^2}$ values create signals. It demonstrates that the proposed exact control chart performs well in detecting the out-of-control proportion vector.

6. Conclusions

This paper develops the exact and asymptotic EWMA-proportion control charts to monitor the multinomial-proportions process. Based on the derived in-control exact mean and variance of the chi-square statistic, we calculate the control limits of the exact EWMA-proportion control chart for various small and large sample sizes using the Monte Carlo method. Based on the asymptotic chi-square distribution with df m − 1, we calculate the control limits of the asymptotic EWMA-proportion control chart for a large enough sample size using the Markov chain method.

From numerical analyses, we find that control limits (5) and (7) with the same preset in-control ARL and out-of-control detection ability are nearly the same when the sample size is large enough, e.g., n $\ge$ 6000 under scenarios (1) and (2). For small or moderate sample size, the exact EWMA-proportion control chart is in-control robust, but the asymptotic control chart’s in-control ARL is more or less than the preset ALR₀ = 370.4. The misuse of the asymptotic control chart results in worse out-of-control detection performance. Thus, we strongly suggest to adopt the proposed exact control chart to monitor a multinomial-proportions process. Moreover, the proposed exact EWMA proportion chart can be adopted to monitor the change in proportions of categories of a distribution-free or unknown continuous distributed multivariate process. A numerical example utilizing semiconductor manufacturing data was discussed to illustrate the application of the proposed exact EWMA proportion chart. The illustration of real data example shows good detection performance of the proposed chart.

In this study, we have developed a novel, efficient, and exact EWMA-proportion control chart specifically designed for monitoring a multinomial-proportion process. Unlike existing literature, which focuses on control charts for multinomial proportions with large or infinite sample sizes, our proposed method is tailored for small and medium sample sizes. Our exact EWMA-proportion control chart offers significant potential for providing sustainable solutions across various industries. We recommend applying this method not only for monitoring multinomial proportions in a multinomial process but also for distribution-free or unknown continuous distributed multivariate processes. By utilizing the proposed exact EWMA-proportion control chart, organizations can effectively monitor and control their processes, enabling them to identify and address deviations or shifts in the multinomial proportions. This approach holds promise for enhancing quality assurance, process optimization, and overall operational performance in diverse industrial settings.