Butterfly Algorithm for Sustainable Lot Size Optimization
Abstract
1. Introduction
2. Literature Review
2.1. Lot Sizing
2.2. Optimization Algorithms and BA
- -
- ABC is based on honeybee swarm intelligence, which divides the bees in a hive into three types: scout bees, worker bees, and onlooker bees. Scout bees fly at random. Worker bees investigate the area around their sites for food sources and relay this information to spectator bees. Onlooker bees employ population fitness to choose a guiding solution for exploitation. These onlooker bees prefer to pick good food sources from those found by the employed bees. The higher-quality food sources are more likely to be chosen by onlooker bees than lesser-quality food sources (Karaboga and Basturk 2007) [35]. The scout bees are derived from a few employed bees that quit their food sources in the quest for new ones. This technique is mostly used for multifunctional service optimizing (Karaboga and Basturk 2008) [42].
- -
- CS is an algorithm known as a metaheuristic based on some cuckoo species’ obligatory brood parasite behavior, in which cuckoo birds deposit their eggs in the nests of other birds (Gandomi et al. 2013a) [43]. Every answer is represented by an egg, and a new solution with an egg of the cuckoo. The primary concept of the algorithm is built on replacing a subpar answer with fresh or potentially superior options. Cuckoo looks to optimize like a breeding technique (Arora and Singh 2013b) [44].
- -
- DE is an easy-to-use but effective community-based stochastic-looking approach that employs vector differences to disrupt the population of vectors and generates a population of potential solutions that are exposed to repeats of recombination, assessment, and selection (Storn and Price 1997) [36]. The weighted difference between two randomly chosen people joined to a third population participant, using a recurrence technique, makes it easier to create novel approaches. In relation to the distribution of the larger population, this disturbs members of the population. The hyper-search space’s sample is further self-organized by the perturbation impact at choosing, restricting it to known regions of interest.
- -
- FA, used to find the best answers to any given challenge, is an algorithmic model of the communal moving conduct of fireflies (Arora and Singh 2013a) [45]. The fundamental principle is that each firefly is drawn to the distinctive flashing pattern made by the other fireflies due to bioluminescence. The individual’s fitness has a direct correlation with the flash’s intensity (Gupta and Arora 2015) [46]. FA takes advantage of the idea of attraction, whereby a less bright object attracts a brighter one, enabling people to move around from one spot to another. This mobility allows the swarm to seek the search space for the best option (Yang 2009) [47].
- -
- GA is where a person’s chromosome is thought of as a problem-solving mechanism, and a population of such people tries to live in hostile environments (Holland 1992 [48]; The Darwinian notion of “survival of the fittest” is the foundation of GA. Three operators—selection, crossover, and mutation—form the foundation of GA (Goldberg and Holland 1988) [39]. Highly-matched people are chosen through selection to produce offspring that the crossover operator uses. Depending on the kind of chromosomal encoding utilized, a specific site within the chromosome is chosen for mutation, and its value is altered.
- -
- MBO is built on the eastern North American monarch population’s southern migration to Mexico. The butterfly population is split into two groups in this algorithm: southern Canada and the northern United States (Land 1), and Mexico (Land 2). Two operators, namely the migratory operator and the butterfly adjustment operator, are used to update the location of individual butterflies. While the butterfly adjusting operator is used to alter the placements of other butterfly individuals, the migration operator’s function is to produce new progeny. The movement rate serves as the determining element for the movement operator, which produces new monarch butterfly progeny (Wang et al. 2015) [41].
- -
- PSO method simulates how different species interact such as fish and birds to identify the best answer in challenging search areas (Eberhart and Shi 2001) [49]. A swarm of particles is used to symbolize the group, and the method explains how the particles move as their neighbors discover more effective search solutions. People gravitate toward one another’s accomplishments over time, which causes them to group together in advantageous parts of the environment. PSO makes use of two different types of knowledge: (first) cognitive learning, in which the particle gains knowledge from itself prior experiences, and (second) social learning, in which the particle gains knowledge from the experiences of others. The method incorporates both, with the learning phenomena causing the answer to improve as the algorithm runs [50].
3. Methodology of the Study
3.1. Lot Size Optimization
3.2. Sustainable Lot Size Optimization
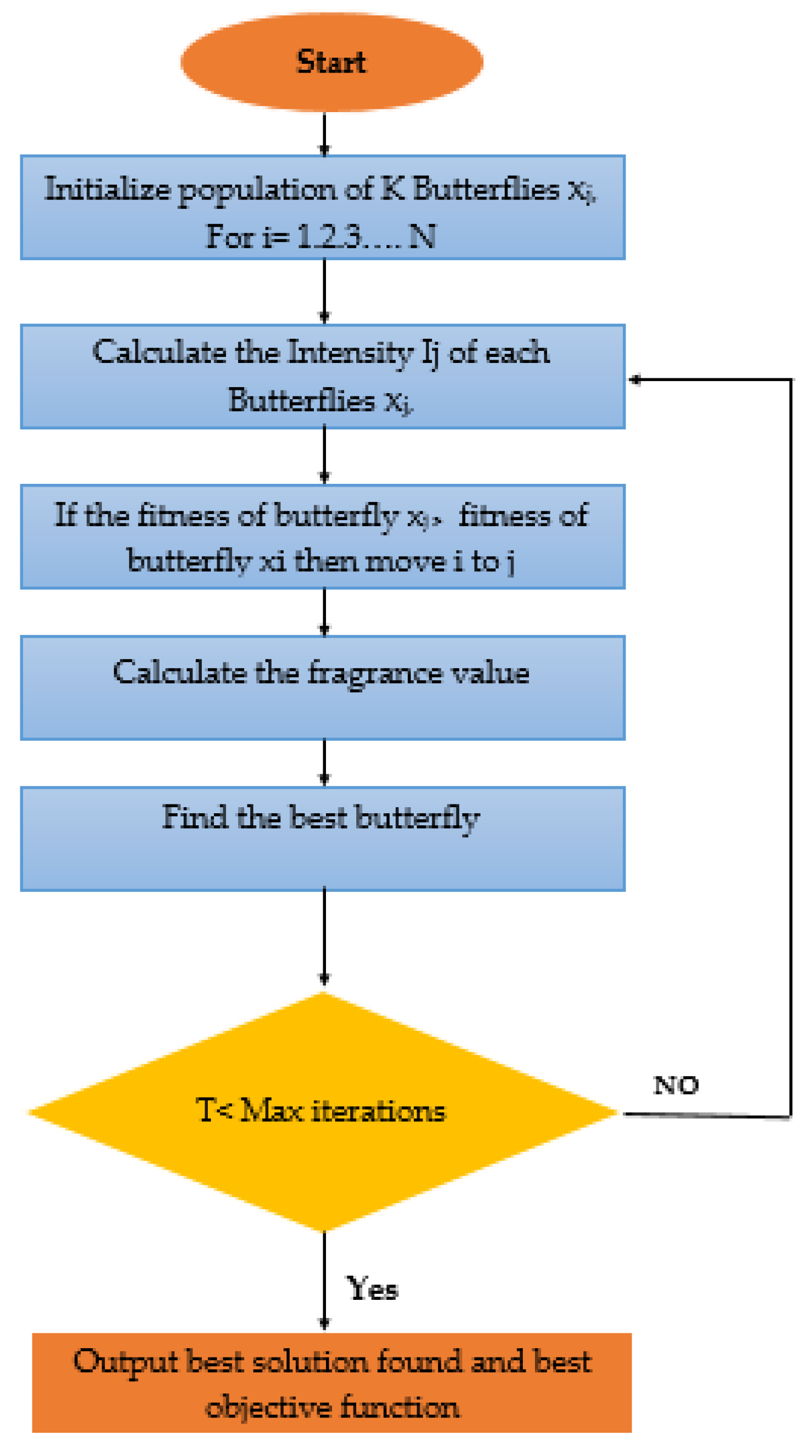
3.3. Butterfly Algorithm
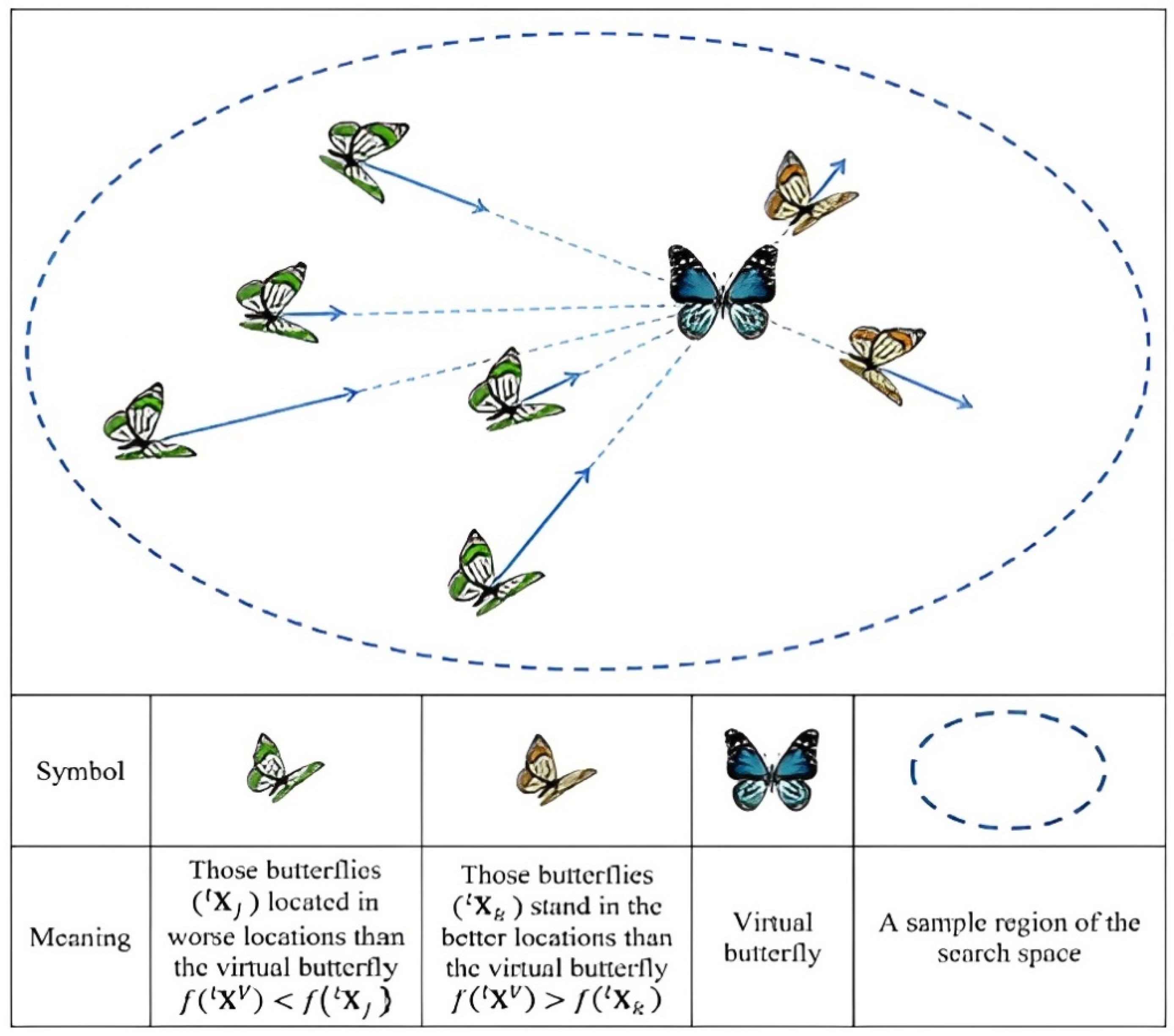
3.4. Butterflies Movement
| Algorithm 1: Btteterly Optimization Algorithm |
| 1: for i = 1,2…, NPF do 2: Generate the initial population P0 of butterflies 3: Generate weight vector 𝜔i 4: fitness F(x)= (f(x1), f(x2),…, f(xNf)) 5: Stimulus Intensity Ij at xj is determined using F(xj) 6: Define the parameters of the algorithm Ps, c and a 7: while sopping criteria is not saisfied do 8: for each butterfly k in the population do 9: Calculate the fagrance value hk by (3). 10: end for 11: Find the best butterfly k that minimizes λ 12: for each butterfly k in the population do 13: Generate a rand(r) from [0, 1] 14: if rand()< Ps then 15: Move towards best solution using (4) 16: else 17: Move randomly by (5) 18: end if 19: end for 20: Update the value of a. 21: end while new optima data found. 22: end for 23: return The Pareto front is extracted from the data set. |
3.5. Simulations and Comparison
4. Case Study
4.1. Data Description
4.2. Model and Parameter Setting
4.3. Algorithm and Parameter Setting
- Population size: 8000
- Number of iterations: 500
4.4. Experimental Environment
4.5. Results and Analysis
4.6. Managerial Insights
5. Conclusions
6. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, L.D.; Xu, E.L.; Li, L. Industry 4.0: State of the art and future trends. Int. J. Prod. Res. 2018, 56, 2941–2962. [Google Scholar] [CrossRef]
- Benmamoun, Z.; Hachimi, H.; Amine, A. Comparison of Inventory Models for Optimal Working Capital; Case of Aeronautics Company. Int. J. Eng. 2018, 31, 605–611. [Google Scholar]
- Harris, F.W. How many parts to make at once. Fact. Mag. Manag. 1913, 10, 135–136. [Google Scholar] [CrossRef]
- Sboui, S. Unsold and Excess Inventory: Between optimization and management: A New challenge for the Supply Chain Management. In Proceedings of the 2006 International Conference on Service Systems and Service Management, Troyes, France, 25–27 October 2006; pp. 283–289. [Google Scholar]
- Benmamoun, Z.; Hachimi, H.; Amine, A. Green logistics practices. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7 December 2017; pp. 1–5. [Google Scholar]
- Cherrafi, A.; Elfezazi, S.; Chiarini, A.; Mokhlis, A.; Benhida, K. The integration of lean manufacturing, Six Sigma and sustainability: A literature. J. Clean. Prod. 2016, 139, 828–846. [Google Scholar] [CrossRef]
- Baryannis, G.; Dani, S.; Antoniou, G. Predicting supply chain risks using machine learning: The trade-off between performance and interpretability, Future Gener. Comput. Syst. 2019, 101, 993–1004. [Google Scholar] [CrossRef]
- Tseng, M.-L.; Islam, M.S.; Karia, N.; Fauzi, F.A.; Afrin, S. A literature review on green supply chain management: Trends and future challenges. Resour. Conserv. Recycl. 2019, 141, 145–162. [Google Scholar] [CrossRef]
- Elkhechafi, M.; Benmamoun, Z.; Hachimi, H.; Amine, A.; Elkettani, Y. Firefly Algorithm for Supply Chain Optimization. Lobachevskii J. Math. 2018, 39, 355–367. [Google Scholar] [CrossRef]
- Mujkic, Z.; Qorri, A.; Kraslawski, A. Sustainability and Optimization of Supply Chains: A Literature Review. OSCM Int. J. 2018, 11, 186–199. [Google Scholar] [CrossRef]
- Bressanelli, G.; Perona, M.; Saccani, N. Challenges in supply chain redesign for the Circular Economy: A literature review and a multiple case study. Int. J. Prod. Res. 2019, 57, 7395–7422. [Google Scholar] [CrossRef]
- Ghobakhloo, M. Industry 4.0, digitization, and opportunities for sustainability. J. Clean. Prod. 2020, 252, 119869. [Google Scholar] [CrossRef]
- Plambeck, E.L. Reducing greenhouse gas emissions through operations and supply chain management. Energy Econ. 2012, 34, S64–S74. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.; Chung, S.H.; Lam, H.Y. Survey of green vehicle routing problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Edwards, J.; McKinnon, A.; Cullinane, S. Comparative carbon auditing of conventional and online retail supply chains: A review of methodological issues. Supply Chain Manag. Int. J. 2011, 16, 57–63. [Google Scholar] [CrossRef]
- Jensen, J.K. Product carbon footprint developments and gaps. Int. J. Phys. Distrib. Logist. Manag. 2012, 42, 338–354. [Google Scholar] [CrossRef]
- Gaussin, M.; Hu, G.; Abolghasem, S.; Basu, S.; Shankar, M.R.; Bidanda, B. Assessing the environmental footprint of manufactured products: A survey of current literature. Int. J. Prod. Econ. 2013, 146, 515–523. [Google Scholar] [CrossRef]
- Subramanian, N.; Gunasekaran, A. Cleaner supply-chain management practices for twenty-first-century organizational competitiveness: Practice-performance framework and research propositions. Int. J. Prod. Econ. 2015, 164, 216–233. [Google Scholar] [CrossRef]
- Jemai, J.; Chung, B.D.; Sarkar, B. Environmental effect for a complex green supply-chain management to control waste: A sustainable approach. J. Clean. Prod. 2020, 278, 12219. [Google Scholar] [CrossRef]
- Yadav, D.; Kumari, R.; Kumar, N.; Sarkar, B. Reduction of waste and carbon emission through the selection of items with cross-price elasticity of demand to form a sustainable supply chain with preservation technology. J. Clean. Prod. 2020, 297, 126298. [Google Scholar] [CrossRef]
- Sarkar, B.; Sarkar, M.; Ganguly, B.; Cárdenas-Barrón, L.E. Combined effects of carbon emission and production quality improvement for fixed lifetime products in a sustainable supply chain management. Int. J. Prod. Econ. 2021, 231, 107867. [Google Scholar] [CrossRef]
- Vandana; Singh, S.R.; Yadav, D.; Sarkar, B.; Sarkar, M. Impact of energy and carbon emission of a supply chain management with two-level trade-credit policy. Energies 2021, 14, 1569. [Google Scholar] [CrossRef]
- Husna, A.; Amin, S.H.; Shah, B. Demand Forecasting in Supply Chain Management Using Different Deep Learning Methods. In Demand Forecasting and Order Planning in Supply Chains and Humanitarian Logistics; IGI Global: Hershey, PA, USA, 2021; pp. 140–170. [Google Scholar]
- Wagner, H.M.; Whitin, T.M. Dynamic version of the economic lot size model. Manag. Sci. 1958, 5, 89–96. [Google Scholar] [CrossRef]
- Suprayoga, G.B.; Witte, P.; Spit, T. Identifying barriers to implementing a sustainability assessment tool for road project planning:An institutional perspective from practitioners in Indonesia. J. Environ. Plan. Manag. 2020, 63, 2380–2401. [Google Scholar] [CrossRef]
- Robinson, K.F.; Fuller, A.K.; Stedman, R.C.; Siemer, W.F.; Decker, D.J. Integration of social and ecological sciences for natural resource decision making: Challenges and opportunities. Environ. Manag. 2019, 63, 565–573. [Google Scholar] [CrossRef] [PubMed]
- Poplawska, J.; Labib, A.; Reed, D.M. From vicious to virtuous circles: Problem structuring for quantified decision making in operationalization of corporate social responsibility. J. Oper. Res. Soc. 2017, 68, 291–307. [Google Scholar] [CrossRef][Green Version]
- Zadjafar, M.A.; Gholamian, M.R. A sustainable inventory model by considering environmental ergonomics and environmental pollution, case study: Pulp and paper mills. J. Clean. Prod. 2018, 199, 444–458. [Google Scholar] [CrossRef]
- Elkington, J. Partnerships from cannibals with forks: The triple bottom line of 21st-century business. Environ. Qual. Manag. 1998, 8, 37–51. [Google Scholar] [CrossRef]
- Yıldızbaşi, A.; Öztürk, C.; Efendioğlu, D.; Bulkan, S. Assessing the social sustainable supply chain indicators using an integrated fuzzy multi-criteria decision-making method: A case study of Turkey. Environ. Dev. Sustain. 2021, 23, 4285–4320. [Google Scholar] [CrossRef]
- Raza, F.; Alshameri, B.; Jamil, S.M. Assessment of triple bottom line of sustainability for geotechnical projects. Environ. Dev. Sustain. 2021, 23, 4521–4558. [Google Scholar] [CrossRef]
- Bouazza, S.; Benmamoun, Z.; Hachimi, H. Maritime Bilateral Connectivity Analysis for Sustainable Maritime Growth: Case of Morocco. Sustainability 2023, 15, 4993. [Google Scholar] [CrossRef]
- Benchekroun, H.T.; Benmamoun, Z.; Hachimi, H. Implementation and Sustainability Assessment of a Public Procurement Strategy. Sustainability 2022, 14, 15565. [Google Scholar] [CrossRef]
- Jokar, A.; Hosseini-Motlagh, S.-M. Simultaneous coordination of order quantity and corporate social responsibility in a two- Echelon supply chain: A combined contract approach. J. Oper. Res. Soc. 2020, 71, 69–84. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (abc) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the World Congress on Nature and Biologically Inspired Computing, NaBIC 2009, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.-S. Firefly algorithm, levy flights and global optimization. In Research and Development in Inteligent Systems XXVI; Bramer, M., Ellis, R., Petridis, M., Eds.; Springer: Berlin, Germany, 2010; pp. 209–218. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2015, 31, 1995–2014. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (abc) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. A conceptual comparison of firefly algorithm, bat algorithm and cuckoo search. In Proceedings of the 2013 International Conference on Control Computing Communication and Materials (ICCCCM), Allahabad, India, 3–4 August 2013; pp. 1–4. [Google Scholar]
- Arora, S.; Singh, S. The firefly optimization algorithm: Convergence analysis and parameter selection. Int. J. Comput. Appl. 2013, 69, 48–52. [Google Scholar] [CrossRef]
- Gupta, S.; Arora, S. A hybrid firefly algorithm and social spider algorithm for multimodal function. Intell. Syst. Technol. Appl. 2015, 1, 17. [Google Scholar]
- Yang, X.-S. Firefly algorithms for multimodal optimization. In Stochastic algorithms: Foundations and Applications, SAGA 2009; Lecture Notes in Computer Science; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5792. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010. [Google Scholar]
- Arora, S.; Singh, S. Butterfly algorithm with l’evy flights for global optimization. In Proceedings of the 2015 International Conference on Signal Processing, Computing and Control (ISPCC), Waknaghat, India, 24–26 September 2015. [Google Scholar]
- RBlair, B.; Launer, A.E. Butterfly diversity and human land use: Species assemblages along an urban grandient. Biol. Conserv. 1997, 80, 113–125. [Google Scholar]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S.; Yetilmezsoy, K. A modified butterfly optimization algorithm for mechanical design optimization problems. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 21. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Li, W.; Li, N. Multi-strategy monarch butterfly optimization algorithm for discounted {0–1} knapsack problem. Neural Comput. Appl. 2018, 30, 3019–3036. [Google Scholar] [CrossRef]
- Hu, H.; Cai, Z.; Hu, S.; Cai, Y.; Chen, J.; Huang, S. Improving monarch butterfly optimization algorithm with self-adaptive population. Algorithms 2018, 11, 71. [Google Scholar] [CrossRef]
- Singh, B.; Anand, P. A novel adaptive butterfly optimization algorithm. Int. J. Comput. Mater. Sci. Eng. 2018, 7, 4. [Google Scholar] [CrossRef]
- Dhanya, K.M.; Kanmani, S. Mutated butterfly optimization algorithm. Int. J. Eng. Adv. Technol. 2019, 8, 375–381. [Google Scholar]
- Li, G.; Shuang, F.; Zhao, P.; Le, C. An improved butterfly optimization algorithm for engineering design problems using the cross-entropy method. Symmetry 2019, 11, 1049. [Google Scholar] [CrossRef]
- Sharma, T.K.; Sahoo, A.K.; Goyal, P. Bidirectional butterfly optimization algorithm and engineering applications. Mater. Today: Proc. 2019, 34, 736–741. [Google Scholar] [CrossRef]
- Sun, L.; Chen, S.; Xu, J.; Tian, Y.; Zhou, Y. Improved Monarch Butterfly Optimization Algorithm Based on Opposition-Based Learning and Random Local Perturbation. Complexity 2019, 2019, 4182148. [Google Scholar] [CrossRef]
- Yazdani, S.; Hadavandi, E. LMBO-DE: A linearized monarch butterfly optimization algorithm improved with differential evolution. Soft Comput. 2019, 23, 8029–8043. [Google Scholar] [CrossRef]
- Sharma, S.; Saha, A.K. m-MBOA: A novel butterfly optimization algorithm enhanced with mutualism scheme. Soft Comput. 2020, 24, 4809–4827. [Google Scholar] [CrossRef]
- Tubishat, M.; Alswaitti, M.; Mirjalili, S.; Al-Garadi, M.A.; Alrashdan, M.T.; Rana, T.A. Dynamic butterfly optimization algorithm for feature selection. IEEE Access 2020, 8, 194303–194314. [Google Scholar] [CrossRef]
- Utama, D.M.; Widodo, D.S.; Ibrahim, M.F.; Dewi, S.K. A New Hybrid Butterfly Optimization Algorithm for Green Vehicle Routing Problem. J. Adv. Transp. 2020, 2020, 8834502. [Google Scholar] [CrossRef]
- Zhang, M.; Long, D.; Qin, T.; Yang, J. A chaotic hybrid butterfly optimization algorithm with particle swarm optimization for high-dimensional optimization problems. Symmetry 2020, 12, 1800. [Google Scholar] [CrossRef]
- Zhi, Y.; Wang, W.; Wang, H.; Khodaei, H. Improved butterfly optimization algorithm for CCHP driven by PEMFC. Appl. Therm. Eng. 2020, 173, 114766. [Google Scholar] [CrossRef]
- Hu, K.; Jiang, H.; Ji, C.-G.; Pan, Z. A modified butterfly optimization algorithm: An adaptive algorithm for global optimization and the support vector machine. Expert Syst. 2021, 38, e12642. [Google Scholar] [CrossRef]
- Geetha, J.; Raja, J.B. An Advanced Circular Adaptive Search Butterfly Optimization Algorithm for the CNN-based Sleep Apnea Detection Approach. IETE J. Res. 2022. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Wu, T.; Xu, M.; Cai, S. A balanced butterfly optimization algorithm for numerical optimization and feature selection. Soft Comput. 2022, 26, 11505–11523. [Google Scholar] [CrossRef]
- Rajesh, B.M.; Thanamani, A.S.; Chithra, B.; FinnyBelwin, A.; LindaSherin, A. Adaptive weight butterfly optimization algorithm (AWBOA) based cluster head selection (CHS) and optimized energy efficient cluster based scheduling (OEECS) approach in wireless sensor networks (WSNS). Int. J. Syst. Assur. Eng. Manag. 2022. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Panigrahi, T.K.; Das, S.R.; Behera, A. Chaotic Butterfly Optimization Algorithm Applied to Multi-objective Economic and Emission Dispatch in Modern Power System. Recent Adv. Comput. Sci. Commun. 2022, 15, 170–185. [Google Scholar] [CrossRef]
- Sharma, S.; Chakraborty, S.; Saha, A.K.; Nama, S.; Sahoo, S.K. mLBOA: A Modified Butterfly Optimization Algorithm with Lagrange Interpolation for Global Optimization. J. Bionic Eng. 2022, 19, 1161–1176. [Google Scholar] [CrossRef]
- Sihwail, R.; Solaiman, O.S.; Ariffin, K.A.Z. New robust hybrid Jarratt-Butterfly optimization algorithm for nonlinear models. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 8207–8220. [Google Scholar] [CrossRef]
- Xu, H.; Lu, Y.; Guo, Q. Application of Improved Butterfly Optimization Algorithm Combined with Black Widow Optimization in Feature Selection of Network Intrusion Detection. Electronics 2022, 11, 3531. [Google Scholar] [CrossRef]
- Yadav, P.; Kumar, S.; Saini, D.K.J. A Novel Method of Butterfly Optimization Algorithm for Load Balancing in Cloud Computing. Int. J. Recent Innov. Trends Comput. Commun. 2022, 10, 110–115. [Google Scholar] [CrossRef]
- Rao, U.; Scheller-Wolf, A.; Tayur, S. Development of a rapid-response supply chain at Caterpillar. Oper. Res. 2000, 48, 189–204. [Google Scholar] [CrossRef]
- Benmamoun, Z.; Hachimi, H.; Amine, A. Inventory management optimization using lean six-sigma. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Rabat, Morocco, 11–13 April 2017; pp. 1722–1730. [Google Scholar]
- Zhang, D.-Z.; Liu, X.-H.; Li, S.-Y. An optimization model for multi-period collaborative inventory control based on target performance management. In Proceedings of the 2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Wuhan, China, 23–25 May 2012. [Google Scholar]
- Caballero-Morales, S.-O.; Martínez-Flores, J.-L. Analysis and Reduction of CO2 Emissions and Costs Associated to Inventory Replenishment Strategies with Uncertain Demand. Polish J. Environ. Stud. 2020, 29, 3997–4005. [Google Scholar] [CrossRef]
- Benmamoun, Z.; Fethallah, W.; Bouazza, S.; Abdo, A.A.; Serrou, D.; Benchekroun, H. A framework for sustainability evaluation and improvement of radiology service. J. Clean. Prod. 2023, 401, 136796. [Google Scholar] [CrossRef]
- Ahlaqqach, M.; Benhra, J.; Mouatassim, S.; Lamrani, S. Closed loop location routing supply chain network design in the end of life pharmaceutical products. Supply Chain Forum 2020, 21, 79–92. [Google Scholar] [CrossRef]
- Zarbakhshnia, N.; Soleimani, H.; Goh, M.; Razavi, S.S. A novel multi-objective model for green forward and reverse logistics network design. J. Clean. Prod. 2019, 208, 1304–1316. [Google Scholar] [CrossRef]
- Bonilla-Enriquez, G.; Cano-Olivos, P.; Peng, L.Q.; Gan, W.; Martinez-Flores, J.L.; Partida, D.S. Modelling Sustainable Development Aspects within Inventory Supply Strategies. Model. Simul. Eng. 2021, 2021, 5232814. [Google Scholar] [CrossRef]
- Mortazavi, A.; Moloodpoor, M. Enhanced butterfly optimization algorithm with a new fuzzy regulator strategy and virtual butterfly concept. Knowl. Based Syst. 2021, 228, 107291. [Google Scholar] [CrossRef]
- Pasha, J.; Nwodu, A.L.; Fathollahi-Fard, A.M.; Tian, G.; Li, Z.; Wang, H.; Dulebenets, M.A. Exact and metaheuristic algorithms for the vehicle routing problem with a factory-in-a-box in multi-objective settings. Adv. Eng. Inform. 2022, 52, 101623. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Fazlollahtabar, H.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Preventive maintenance for the flexible flowshop scheduling under uncertainty: A waste-to-energy system. Environ. Sci. Pollut. Res. 2021, 1–20. [Google Scholar] [CrossRef]
- Singh, E.; Pillay, N. A study of ant-based pheromone spaces for generation constructive hyper-heuristics. Swarm Evol. Comput. 2022, 72, 101095. [Google Scholar] [CrossRef]
- Chen, M.; Tan, Y. SF-FWA: A Self-Adaptive Fast Fireworks Algorithm for effective large-scale optimization. Swarm Evol. Comput. 2023, 80, 101314. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for scheduling trucks at a cross-docking terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A Diffused Memetic Optimizer for reactive berth allocation and scheduling at marine container terminals in response to disruptions. Swarm Evol. Comput. 2023, 80, 101334. [Google Scholar] [CrossRef]

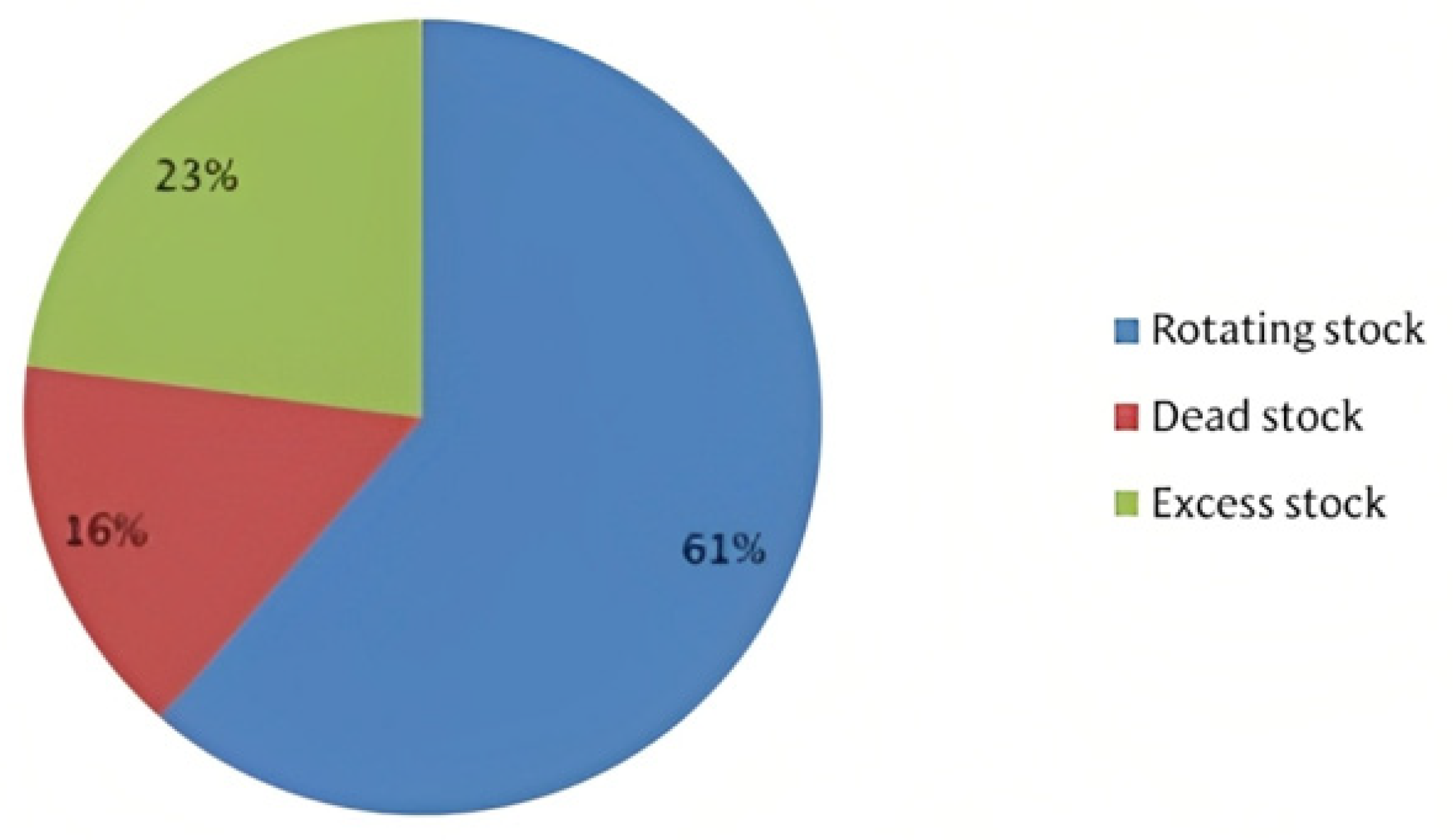
| Authors | Year | Journal | Review |
|---|---|---|---|
| Arora et al. | 2018 | Brazilian Society of Mechanical Sciences and Engineering | An improved butterfly algorithm for the purpose of solving optimization issues in mechanical engineering [54]. |
| Feng, Y., Wang et al. | 2018 | Neural Computing and Applications | Discounted 0–1 knapsack issue optimization using a proposed improved-strategy monarch butterfly algorithm [55]. |
| Hu, H., Cai, Z. et al. | 2018 | Algorithms | Enhanced the algorithm for optimization of the monarch butterfly with a population that can adapt to itself [56]. |
| Singh, B. and Anand, P. | 2018 | International Journal of Computational Materials Science and Engineering | A novel adaptive butterfly optimization algorithm [57]. |
| Dhanya, K. M. et al. | 2019 | International Journal of Engineering and Advanced Technology | Mutated butterfly optimization algorithm [58]. |
| Li, G., Shuang et al. | 2019 | Symmetry | Applied the cross-entropy approach, an enhanced butterfly algorithm for optimization of the design in engineering issues [59]. |
| Sharma, T. K. et al. | 2019 | Materials Today: Proceedings | Bidirectional butterfly optimization algorithm and engineering applications [60]. |
| Sun, L. et al. | 2019 | Complexity | On the basis of opposition-based learning and random local perturbation, a better algorithm for the monarch butterfly optimization method was developed [61]. |
| Yazdani, S. et al. | 2019 | Soft Computing | A linear algorithm for monarch butterfly optimization using differential evolution (DE) is known as “LMBO-DE” [62]. |
| Sharma, S. et al. | 2020 | Soft Computing | m-MBOA: A novel butterfly optimization algorithm enhanced with a mutualism scheme [63]. |
| Tubishat, M., Alswaitti et al. | 2020 | IEEE Access | Algorithm of dynamic butterfly optimization for the selection of features [64]. |
| Utama, D. M. et al. | 2020 | Journal of Advanced Transportation | A new hybrid butterfly optimization algorithm for green vehicle routing problem [65] |
| Zhang, M. et al. | 2020 | Symmetry | The algorithm for a chaotic hybrid particle swarm optimization combined with the algorithm of butterfly optimization for highly dimensional optimization issues [66]. |
| Zhi, Y., Weiqing et al. | 2020 | Applied Thermal Engineering | The algorithm of butterfly optimization for CCHP powered by PEMFC improved [67]. |
| Hu, K., Jiang et al. | 2021 | Expert Systems | An adjustable algorithm for assistance vector machines and global optimization [68]. |
| Geetha, J. et al. | 2022 | IETE Journal of Research | An enhanced algorithm of butterfly optimization for circular adaptive searching for the CNN-based sleep apnea diagnosis method [69]. |
| Long, W., Jiao et al. | 2022 | Soft Computing | An algorithm balanced for feature selection and numerical optimization [70]. |
| Rajesh, B. M. et al. | 2022 | System Assurance Engineering and Management International Journal | CHS and OEECS techniques are both based on the algorithm of the adaptive weight butterfly optimization in wireless sensing networks [71]. |
| Sahoo, A. K. et al. | 2022 | Recent Advances in Computer Science and Communications | Multi-objective economic and emission dispatching using the algorithm of chaotic butterfly optimization in an advanced power system [72]. |
| Sharma, S. et al. | 2022 | Journal of Bionic Engineering | Lagrange interpolation was added to a modified algorithm of butterfly optimization for overall optimization [73]. |
| Sihwail, R. et al. | 2022 | King Saud University—Computer and Information Sciences | A new efficient algorithm for hybrid Jarratt–butterfly optimization was used for nonlinear theories [74]. |
| Xu, H., Lu, Y. et al. | 2022 | Electronics (Switzerland) | To choose attributes for the detection of network intrusions, an updated algorithm of butterfly optimization was paired with black widow optimization [75]. |
| Yadav, P., Kumar et al. | 2022 | International Journal on Recent and Innovation Trends in Computing and Communication | Balanced load in cloud-based computing using a new algorithm for butterfly optimization [76]. |
| Function | GA | PSO | FA | BA |
|---|---|---|---|---|
| Michalewicz | 90,025 ± 8011 (93%) | 6012 ± 488 (99%) | 2890 ± 709 (100%) | 2898 ± 688 (100%) |
| Rosenbrock | 55,644 ± 8973 (89%) | 34,312 ± 5015 (97%) | 6121 ± 501 (100%) | 6023 ± 420 (100%) |
| De Jong | 26,355 ± 1025 (98%) | 17,144 ± 2126 (100%) | 5701 ± 706 (100%) | 5688 ± 696 (100%) |
| Schwefel | 206,005 ± 8321 (95%) | 261,333 ± 1188 (99%) | 79,961 ± 3536 (97%) | 7920 ± 521 (100%) |
| Ackley | 36,356 ± 3422 (91%) | 2720 ± 4356 (98%) | 4398 ± 2730 (100%) | 4388 ± 2680 (100%) |
| Rastrigin | 112,265 ± 6089 (75%) | 77,323± 3025 (92%) | 12,055 ± 3830 (100%) | 9005 ± 859 (100%) |
| Easom | 20,036 ± 3405 (93%) | 16,418± 2011 (98%) | 14,042 ± 2550 (95%) | 6100 ±1598 (100%) |
| Griewank | 68,863 ± 7704 (94%) | 54,800± 3966 (95%) | 13,995 ± 4973 (97%) | 10,800 ± 2950 (100%) |
| Yang | 37,198 ± 7625 (90%) | 20,004± 3104 (98%) | 5162 ± 2485 (100%) | 5122 ± 2456 (100%) |
| Shubert | 55,144 ± 5001 (91%) | 24,885 ± 3536 (93%) | 9937 ± 2510 (100%) | 9907 ± 2517 (100%) |
| Part | TC | TC_Firefly | IC_Butterfly | TC_PSO | TC_GA | Best Value |
|---|---|---|---|---|---|---|
| Part1 | 1,015,112 | 518,627.74 | 508,627.74 | 519,663.74 | 508,827.74 | BOA |
| Part2 | 95,241.98 | 49,564.17 | 49,526.02 | 49,487.86 | 49,487.86 | GA |
| Part3 | 392,067.8 | 211,768.25 | 212,460.96 | 211,868.25 | 211,968.25 | FA |
| PART4 | 479,668.83 | 258,055.98 | 371,729.62 | 257,477.24 | 257,477.24 | PSO |
| Part5 | 1,021,387.52 | 511,322.56 | 511,398.78 | 511,412.56 | 5,034,696.40 | GA |
| Part6 | 1,679,063.76 | 855,397.67 | 845,090.37 | 855,397.67 | 855,397.67 | BOA |
| Part7 | 517,979.04 | 275,045.63 | 276,286.56 | 275,005.22 | 275,115.22 | PSO |
| Part8 | 125,647.72 | 67,256.03 | 6618.38 | 71,309.45 | 67,256.03 | BOA |
| Part9 | 5607.99 | 5132.90 | 5049.09 | 5060.58 | 5051.09 | BOA |
| Part10 | 90,380.62 | 55,253.97 | 47,419.46 | 47,526.46 | 47,623.46 | BOA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benmamoun, Z.; Fethallah, W.; Ahlaqqach, M.; Jebbor, I.; Benmamoun, M.; Elkhechafi, M. Butterfly Algorithm for Sustainable Lot Size Optimization. Sustainability 2023, 15, 11761. https://doi.org/10.3390/su151511761
Benmamoun Z, Fethallah W, Ahlaqqach M, Jebbor I, Benmamoun M, Elkhechafi M. Butterfly Algorithm for Sustainable Lot Size Optimization. Sustainability. 2023; 15(15):11761. https://doi.org/10.3390/su151511761
Chicago/Turabian StyleBenmamoun, Zoubida, Widad Fethallah, Mustapha Ahlaqqach, Ikhlef Jebbor, Mouad Benmamoun, and Mariam Elkhechafi. 2023. "Butterfly Algorithm for Sustainable Lot Size Optimization" Sustainability 15, no. 15: 11761. https://doi.org/10.3390/su151511761
APA StyleBenmamoun, Z., Fethallah, W., Ahlaqqach, M., Jebbor, I., Benmamoun, M., & Elkhechafi, M. (2023). Butterfly Algorithm for Sustainable Lot Size Optimization. Sustainability, 15(15), 11761. https://doi.org/10.3390/su151511761








