Sustainable Design of Circular Reinforced Concrete Column Sections via Multi-Objective Optimization
Abstract
:1. Introduction
2. Optimization Model: Reinforced Circular Concrete Section (RCCS)
2.1. Objective Functions of the Optimization Model RCCS
2.2. Structural Analysis of a Reinforced Circular Concrete Section and Design Constraints
| Symbol | Description | Value |
|---|---|---|
| ccon | unit price of concrete C30/37 | 115 EUR/m3 |
| csteel | unit price of the steel reinforcement S500 | 1.45 EUR/kg |
| CO2,con * | unit emissions of CO2 for concrete | 308.2 kgCO2/m3 |
| CO2,steel * | unit emissions of CO2 for steel reinforcement | 0.87 kgCO2/kg |
| ρsteel | steel density | 7850 kg/m3 |
| L | length of the column section | 1 m |
| fck | the compressive strength of the concrete | 30 MPa |
| fyk | tensile strength of the steel | 500 MPa |
| Es | modulus of elasticity of steel | 200,000 MPa |
| γc | safety factor for concrete | 1.5 |
| γs | safety factor for steel | 1.15 |
| αcc | coefficient for sustained compression | 0.85 |
| Φlink | diameter of shear reinforcement | 6 mm |
| ccon | concrete cover | 30 mm |
| Variable | Discrete Alternatives |
|---|---|
| Φ (mm) | 400, 450, 500, 550, 600, 650, 700, 750, 800, 850, 900, 950, 1000 |
| n (-) | 6, 8, 10, 12, 14, 16, 18, 20, 22 |
| Φmain (mm) | 12, 14, 16, 18, 20, 22, 24, 26, 28 |
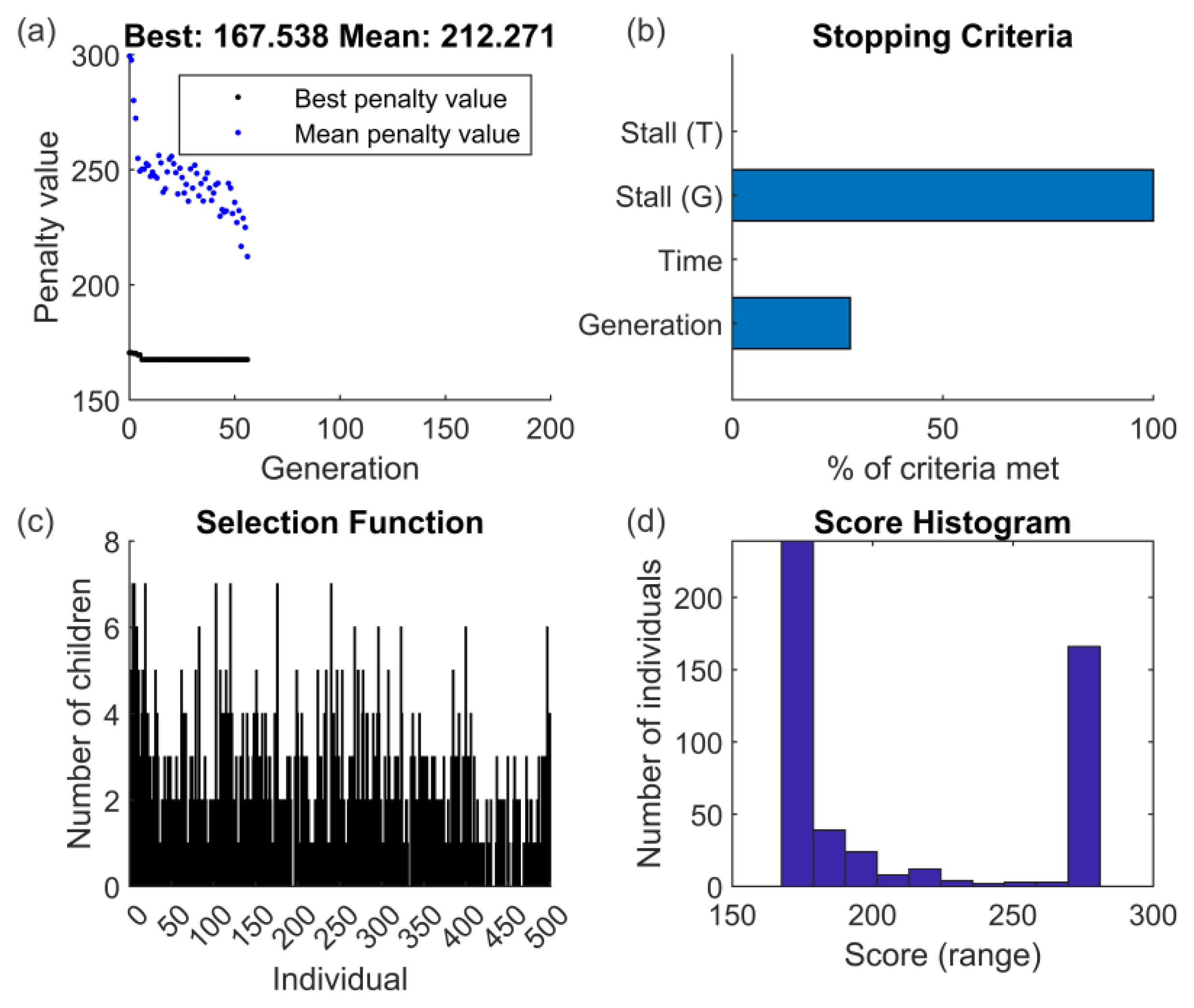
2.3. Genetic Algorithm
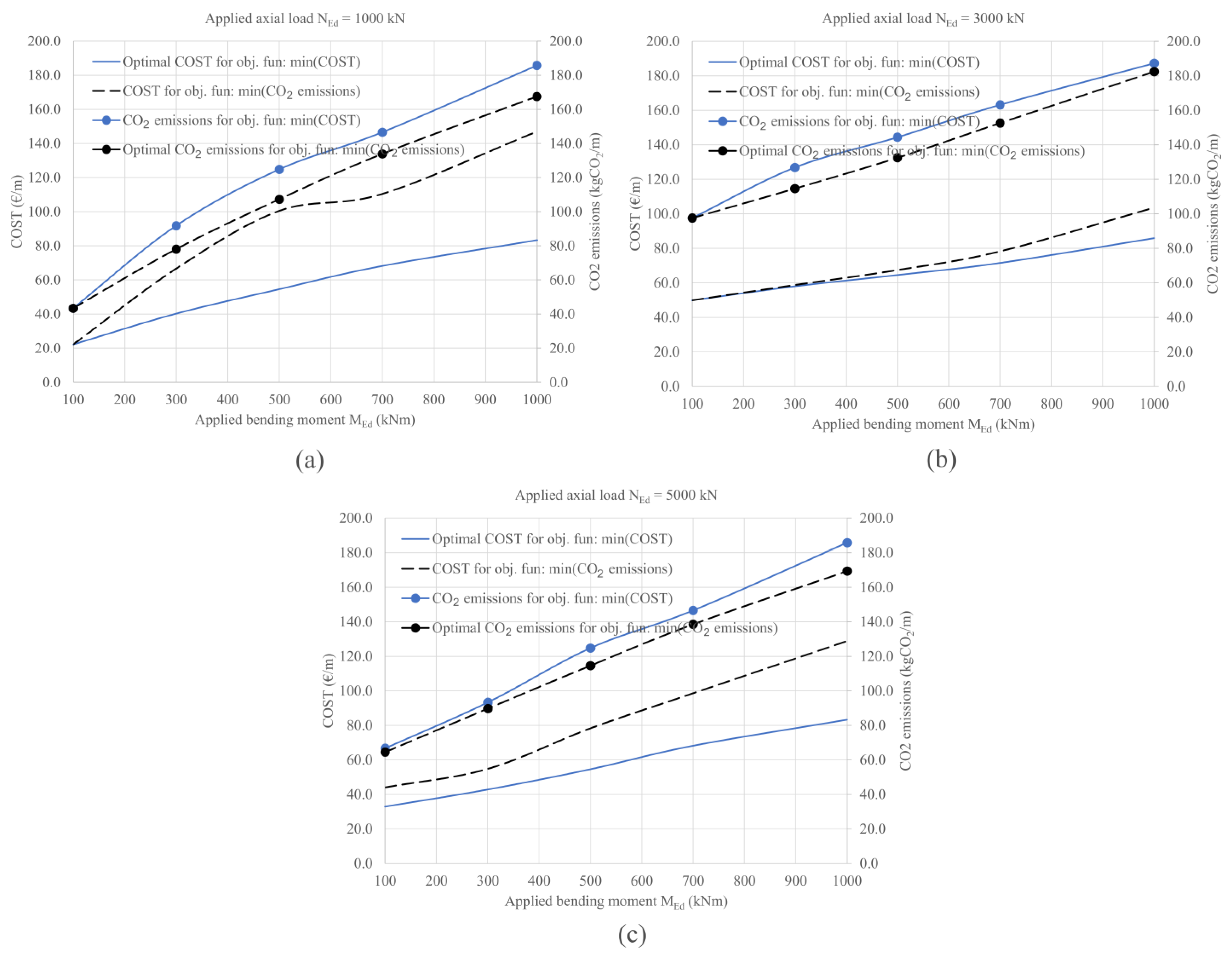
3. Multiparametric Optimization
- Three different axial loads: 1000 kN, 3000 kN, and 5000 kN;
- Five different bending moments: 100 kNm, 300 kNm, 500 kNm, 700 kNm, and 1000 kNm;
- Two objective functions: material cost and quantity of CO2 emissions.
4. Multi-Objective Optimization
5. Summery and Conclusions
- -
- The optimal design of the reinforced concrete cross section, considering the material cost as the objective function, results in a larger cross-sectional area of concrete and a smaller area of steel compared with the optimization results when CO2 emissions are considered as the objective function;
- -
- The optimal solution obtained with material cost as the objective function exhibits a significantly higher reserve in axial load capacity than the optimal design when CO2 emissions are selected as the objective function;
- -
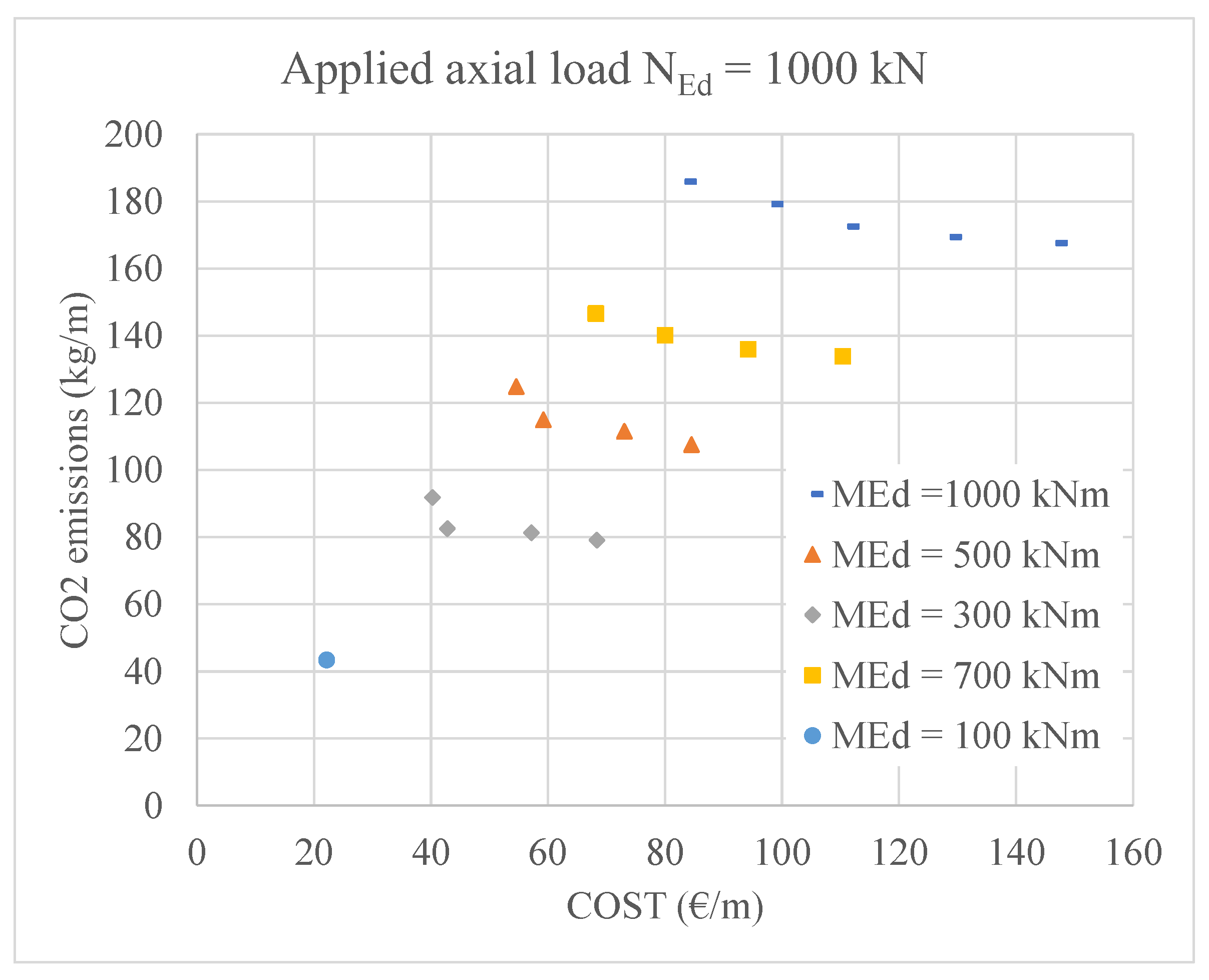
- Analyzing the Pareto front reveals that a marginal decrease in CO2 emissions is accompanied by a substantial increase in material costs;
- -
- In addition, the model can be integrated into the design of structural elements such as columns and piles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kanagasundaram, S.; Karihaloo, B.L. Minimum-cost design of reinforced concrete structures. Comput. Struct. 1991, 41, 1357–1364. [Google Scholar] [CrossRef]
- Menezes, I.S.; Tinoco, V.N.V.; Christoforo, A.L.; Bomfim Junior, F.C.; Narques, T.V.N. Optimization of reinforced concrete columns via genetic algorithm. Acta Sci. Technol. 2022, 45, e61562. [Google Scholar] [CrossRef]
- de Oliveira, L.C.; de Almeida, F.S.; Gomes, H.M. Optimization of RC polygonal cross-sections under compression and biaxial bending with QPSO. Comput. Concr. 2022, 30, 127–141. [Google Scholar] [CrossRef]
- Paya-Zaforteza, I.; Yepes, V.; Hospitaler, A.; González-Vidosa, F. CO2-optimization of reinforced concrete frames by simulated annealing. Eng. Struct. 2009, 31, 1501–1508. [Google Scholar] [CrossRef]
- Camp, C.V.; Huq, F. CO2 and cost optimization of reinforced concrete frames using a big bang-big crunch algorithm. Eng. Struct. 2013, 48, 363–372. [Google Scholar] [CrossRef]
- Trinh, H.T.M.K.; Chowdhury, S.; Nguyen, M.T.; Liu, T. Optimising flat plate buildings based on carbon footprint using Branch-and-Reduce deterministic algorithm. J. Clean. Prod. 2021, 320, 128780. [Google Scholar] [CrossRef]
- Martínez-Alonso, C.; Berdasco, L. Carbon footprint of sawn timber products of Castanea sativa Mill. in the north of Spain. J. Clean. Prod. 2015, 102, 127–135. [Google Scholar] [CrossRef]
- Yeo, D.; Gabbai, R.D. Sustainable design of reinforced concrete structures through embodied energy optimization. Energy Build. 2011, 43, 2028–2033. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. Sustainable design of reinforced concrete structural members using embodied carbon emission and cost optimization. J. Build. Eng. 2021, 44, 102940. [Google Scholar] [CrossRef]
- Jayasinghe, A.; Orr, J.; Ibell, T.; Boshoff, W.P. Minimising embodied carbon in reinforced concrete beams. Eng. Struct. 2021, 242, 112590. [Google Scholar] [CrossRef]
- Sahebi, M.; Dehestani, M. Sustainability assessment of reinforced concrete beams under corrosion in life-span utilizing design optimization. J. Build. Eng. 2023, 65, 105737. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Amin, A.H.; Khalil, A.B.I. Optimal circular reinforced concrete columns. J. Eng. Appl. Sci. 1997, 44, 69–84. [Google Scholar]
- Tayem, A.; Najmi, A. Design of Round Reinforced-Concrete Columns. J. Struct. Eng. 1996, 122, 1062–1071. [Google Scholar] [CrossRef]
- Bekdaş, G.; Cakiroglu, C.; Kim, S.; Geem, Z.W. Optimization and Predictive Modeling of Reinforced Concrete Circular Columns. Materials 2022, 15, 6624. [Google Scholar] [CrossRef]
- Camp, C.V.; Assadollahi, A. CO2 and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
- Zhao, X.; Lu, Y.; Liang, H.; Wang, Y.; Yan, Y. Optimal design of reinforced concrete columns strengthened with square steel tubes and sandwiched concrete. Eng. Struct. 2021, 244, 112723. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Determining optimal designs for conventional and geothermal energy piles. Renew. Energy 2020, 147, 2633–2642. [Google Scholar] [CrossRef]
- Payá-Zaforteza, I.; Yepes, V.; González-Vidosa, F.; Hospitaler, A. Cost versus sustainability of reinforced concrete building frames by multiobjective optimization. In Proceedings of the Life-Cycle Civil Engineering—1st International Symposium on Life-Cycle Civil Engineering, IALCCE ’08, Commo, Italy, 10–14 June 2008; pp. 953–958. [Google Scholar]
- Hong, W.-K.; Le, T.-A.; Nguyen, M.C.; Pham, T.D. ANN-based Lagrange optimization for RC circular columns having multiobjective functions. J. Asian Archit. Build. Eng. 2023, 22, 961–976. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, B.; Wang, P.; Gan, Z.; Han, P.; Wang, Y. Multi-Objective Parametric Optimization Design for Mirrors Combined with Non-Dominated Sorting Genetic Algorithm. Appl. Sci. 2023, 13, 3346. [Google Scholar] [CrossRef]
- Khouri Chalouhi, E.; Zelmanovitz Ciulla, G.; García-Brioles Bueno, J.; Pacoste, C.; Karoumi, R. Environmental and economical optimization of reinforced concrete overhang bridge slabs. Struct. Multidiscip. Optim. 2023, 66, 66. [Google Scholar] [CrossRef]
- Di, L.; Sun, Z.; Zhi, F.; Wan, T.; Yang, Q. Assessment of an Optimal Design Method for a High-Energy Ultrasonic Igniter Based on Multi-Objective Robustness Optimization. Sustainability 2023, 15, 1841. [Google Scholar] [CrossRef]
- The MathWorks, Inc., R. How the Genetic Algorithm Works. 2021. Available online: https://se.mathworks.com/help/gads/how-the-genetic-algorithmworks.html (accessed on 5 May 2023).
- EN1992-1-1 2004; CEN Eurocode 2 Design of Concrete Structures–Part 1-1: General Rules and Rules for Buildings. EU: Brussels, Belgium, 2004.
- The Model of the Eco-costs/Value Ratio (EVR). Available online: www.ecocostsvalue.com/eco-costs/eco-costs-emissions/ (accessed on 5 May 2023).

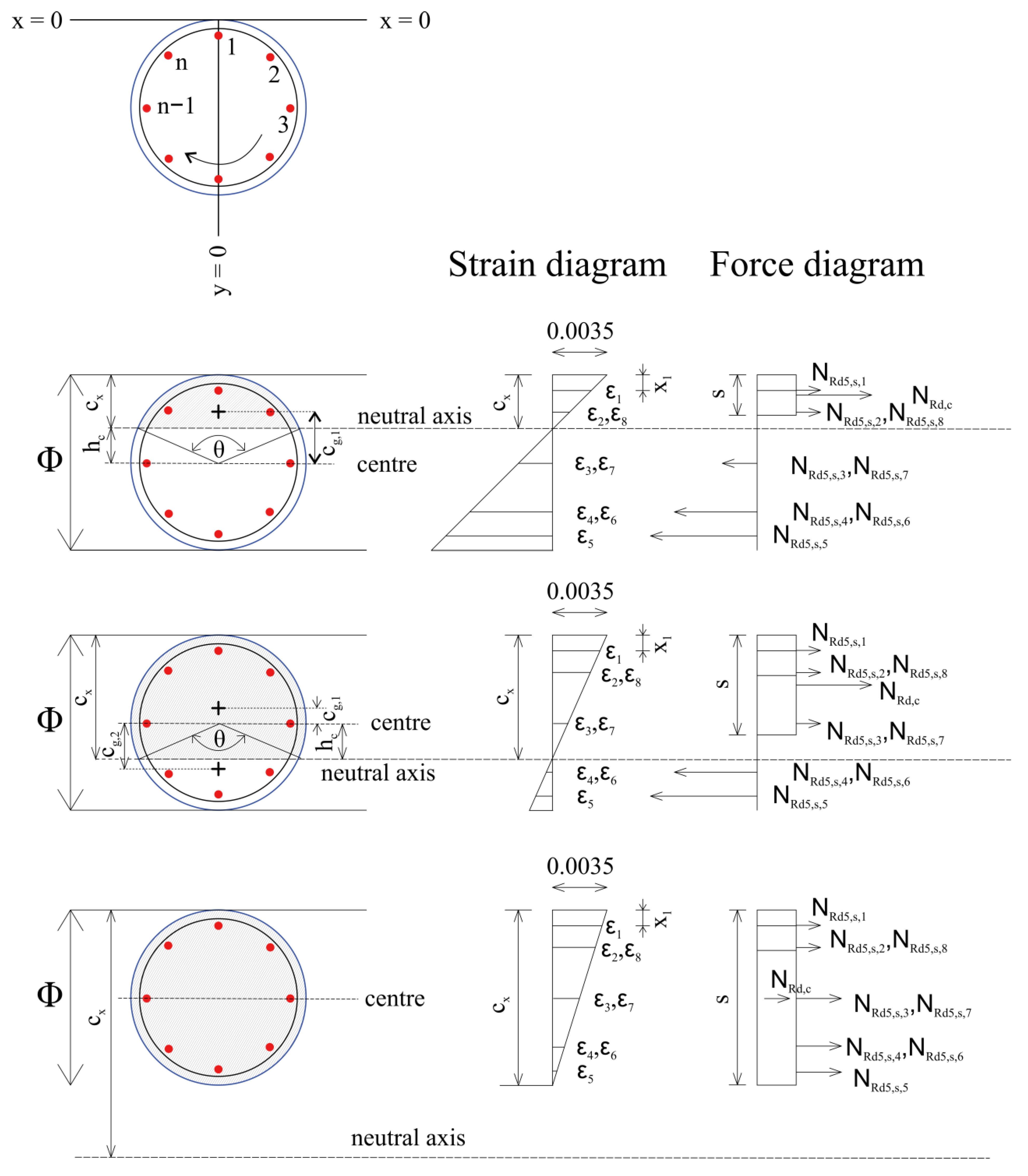

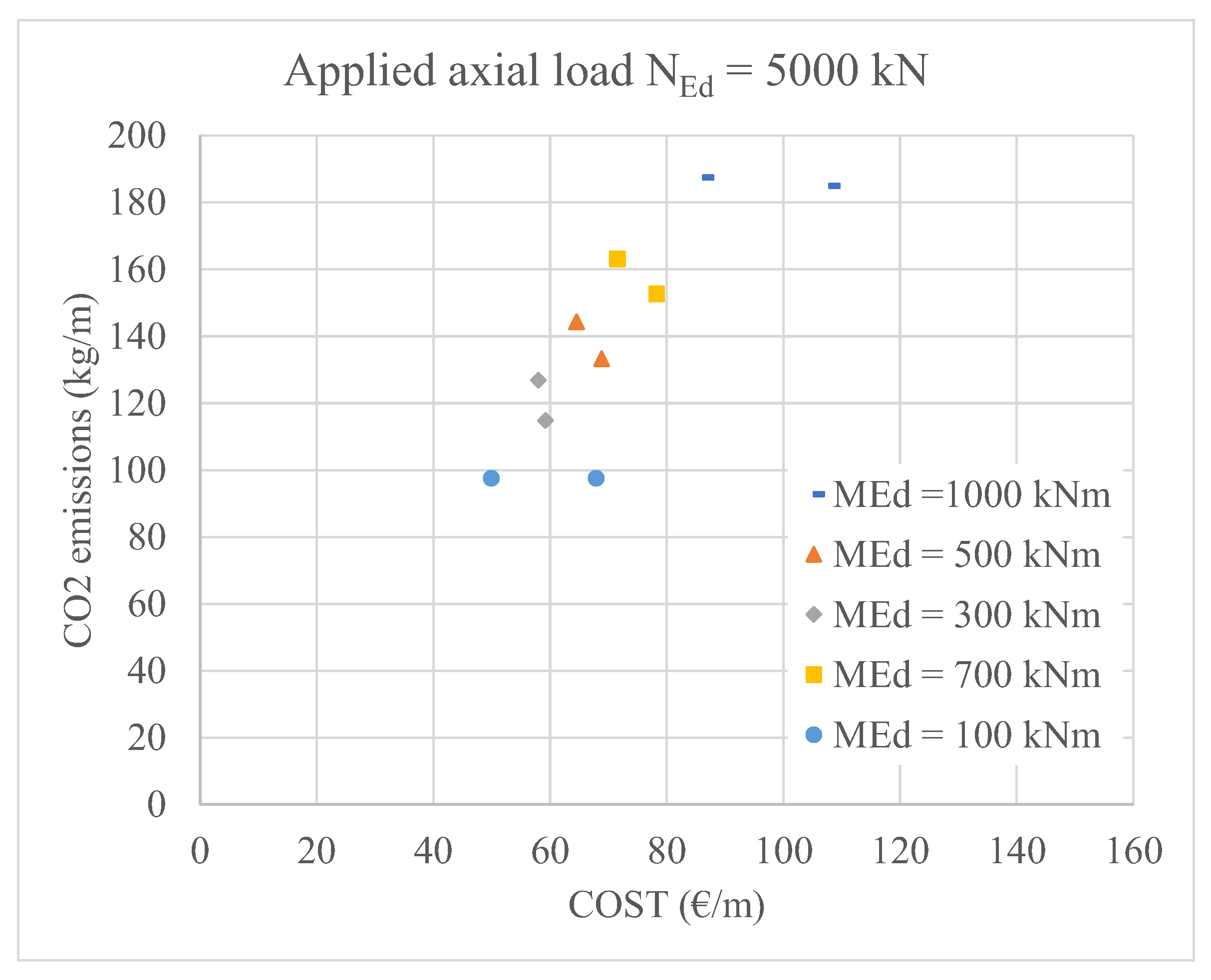
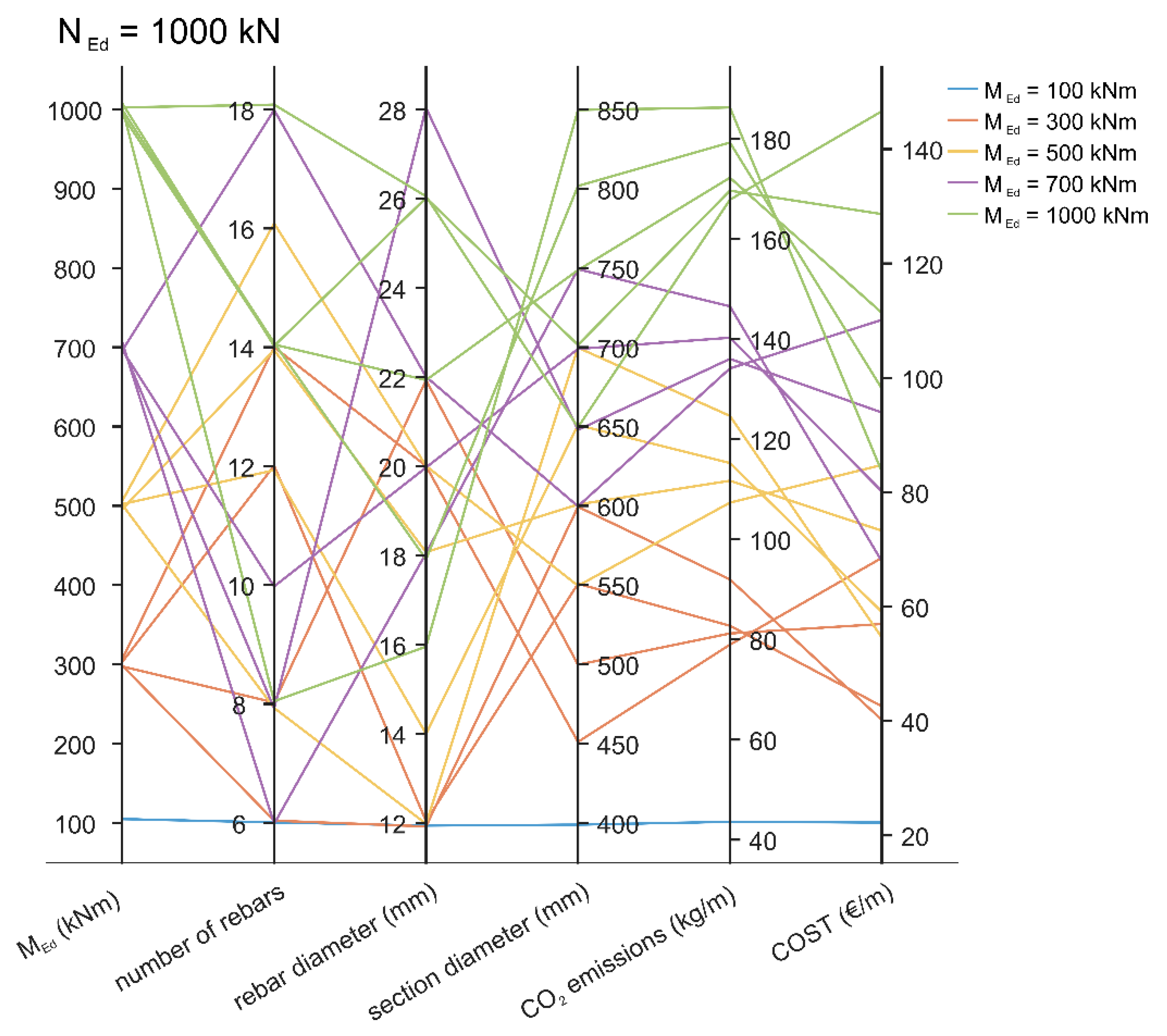
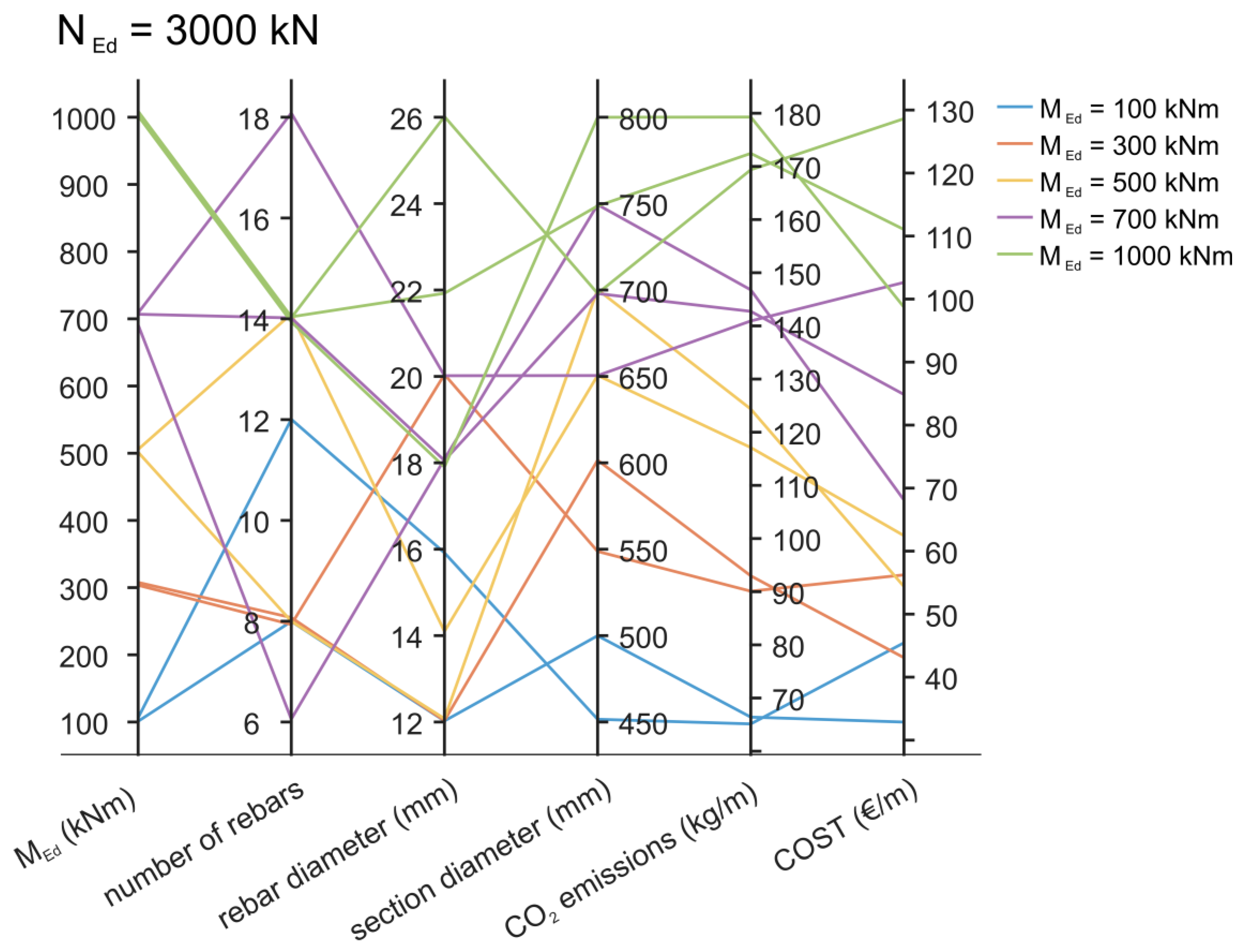
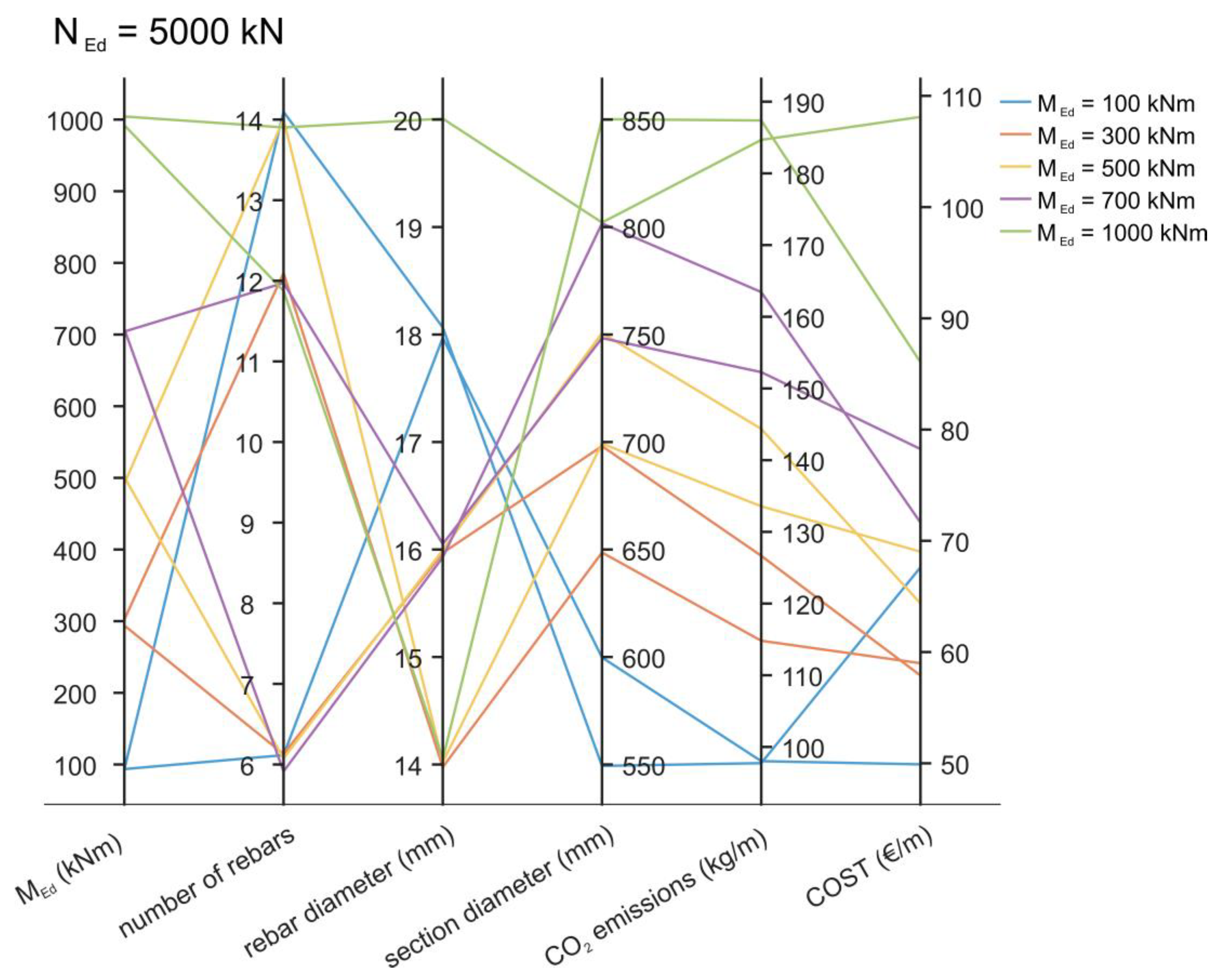
| NEd (kN) | MEd (kNm) | cx (mm) | n (-) | Φmain (mm) | Φ (mm) | NRd (kN) | MRd (kNm) | As,min (cm2) | As,total (cm2) | COST (€/m) | CO2 (kg/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 100 | 274.13 | 6 | 12 | 400 | 1304.0 | 107.6 | 2.51 | 6.79 | 22.18 | 43.36 |
| 1000 | 300 | 345.24 | 6 | 12 | 600 | 2196.8 | 342.7 | 5.65 | 6.79 | 40.24 | 91.78 |
| 1000 | 500 | 420.77 | 8 | 12 | 700 | 3180.4 | 545.8 | 7.70 | 9.05 | 54.56 | 124.79 |
| 1000 | 700 | 412.14 | 6 | 18 | 750 | 3230.4 | 701.9 | 8.84 | 15.27 | 68.18 | 146.59 |
| 1000 | 1000 | 518.16 | 14 | 12 | 850 | 4795.6 | 1000.8 | 11.35 | 15.83 | 83.28 | 185.70 |
| 3000 | 100 | 484.11 | 8 | 12 | 500 | 3021.5 | 122.0 | 6.90 | 9.05 | 32.88 | 66.69 |
| 3000 | 300 | 433.11 | 8 | 12 | 600 | 3021.3 | 333.7 | 6.90 | 9.05 | 42.81 | 93.32 |
| 3000 | 500 | 457.15 | 8 | 12 | 700 | 3560.1 | 538.6 | 7.70 | 9.05 | 54.56 | 124.79 |
| 3000 | 700 | 470.55 | 6 | 18 | 750 | 3927.1 | 701.8 | 8.84 | 15.27 | 68.18 | 146.59 |
| 3000 | 1000 | 487.00 | 14 | 12 | 850 | 4385.9 | 1002.8 | 11.35 | 15.83 | 83.28 | 185.70 |
| 5000 | 100 | 670.25 | 6 | 18 | 600 | 5002.9 | 102.8 | 11.50 | 15.27 | 49.89 | 97.57 |
| 5000 | 300 | 670.67 | 6 | 16 | 700 | 5699.5 | 335.1 | 11.50 | 12.06 | 57.99 | 126.85 |
| 5000 | 500 | 623.14 | 6 | 16 | 750 | 5571.6 | 558.7 | 11.50 | 12.06 | 64.54 | 144.40 |
| 5000 | 700 | 559.91 | 6 | 16 | 800 | 5111.5 | 787.9 | 11.50 | 12.06 | 71.54 | 163.16 |
| 5000 | 1000 | 539.41 | 16 | 12 | 850 | 5091.3 | 1011.3 | 11.50 | 18.10 | 85.85 | 187.25 |
| NEd (kN) | MEd (kNm) | cx (mm) | n (-) | Φmain (mm) | Φ (mm) | NRd (kN) | MRd (kNm) | As,min (cm2) | As,total (cm2) | COST (€/m) | CO2 (kg/m) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000 | 100 | 301.79 | 6 | 12 | 400 | 1483.3 | 100.9 | 2.51 | 6.79 | 22.18 | 43.36 |
| 1000 | 300 | 231.21 | 8 | 26 | 450 | 1080.1 | 300.0 | 3.18 | 42.47 | 66.64 | 78.02 |
| 1000 | 500 | 241.57 | 18 | 22 | 500 | 1064.8 | 502.3 | 3.93 | 68.42 | 100.46 | 107.25 |
| 1000 | 700 | 276.92 | 18 | 22 | 600 | 1387.2 | 703.7 | 5.65 | 68.42 | 110.40 | 133.87 |
| 1000 | 1000 | 353.53 | 18 | 26 | 650 | 2591.7 | 1000.5 | 6.64 | 95.57 | 146.94 | 167.54 |
| 3000 | 100 | 455.84 | 20 | 12 | 450 | 3001.1 | 100.2 | 6.90 | 22.62 | 44.04 | 64.47 |
| 3000 | 300 | 421.93 | 12 | 16 | 550 | 3067.8 | 301.2 | 6.90 | 24.13 | 54.79 | 89.70 |
| 3000 | 500 | 391.52 | 20 | 16 | 600 | 3015.0 | 501.2 | 6.90 | 40.21 | 78.29 | 114.60 |
| 3000 | 700 | 386.66 | 10 | 26 | 650 | 3015.2 | 700.6 | 6.90 | 53.09 | 98.59 | 138.53 |
| 3000 | 1000 | 387.00 | 14 | 26 | 700 | 3024.4 | 1002.7 | 7.70 | 74.33 | 128.86 | 169.37 |
| 5000 | 100 | 671.73 | 6 | 18 | 600 | 5011.1 | 100.9 | 11.50 | 15.27 | 49.89 | 97.57 |
| 5000 | 300 | 615.70 | 16 | 12 | 650 | 5063.0 | 300.4 | 11.50 | 18.10 | 58.76 | 114.63 |
| 5000 | 500 | 575.86 | 18 | 12 | 700 | 5001.6 | 501.3 | 11.50 | 20.36 | 67.43 | 132.51 |
| 5000 | 700 | 551.17 | 12 | 16 | 750 | 5003.8 | 702.2 | 11.50 | 24.13 | 78.27 | 152.64 |
| 5000 | 1000 | 524.82 | 20 | 16 | 800 | 5008.2 | 1000.8 | 11.50 | 40.21 | 103.58 | 182.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jelušič, P.; Žula, T. Sustainable Design of Circular Reinforced Concrete Column Sections via Multi-Objective Optimization. Sustainability 2023, 15, 11689. https://doi.org/10.3390/su151511689
Jelušič P, Žula T. Sustainable Design of Circular Reinforced Concrete Column Sections via Multi-Objective Optimization. Sustainability. 2023; 15(15):11689. https://doi.org/10.3390/su151511689
Chicago/Turabian StyleJelušič, Primož, and Tomaž Žula. 2023. "Sustainable Design of Circular Reinforced Concrete Column Sections via Multi-Objective Optimization" Sustainability 15, no. 15: 11689. https://doi.org/10.3390/su151511689
APA StyleJelušič, P., & Žula, T. (2023). Sustainable Design of Circular Reinforced Concrete Column Sections via Multi-Objective Optimization. Sustainability, 15(15), 11689. https://doi.org/10.3390/su151511689







