Novel TIλDND2N2 Controller Application with Equilibrium Optimizer for Automatic Voltage Regulator
Abstract
:1. Introduction
1.1. Background
1.2. Literature Survey
1.3. Limitations and Motivations
1.4. Main Contributions
- -
- TIλDND2N2 controller is recommended for the first time in order to increase the control performance of AVR systems. The successful result of the proposed controller on AVR control, which is one of the main subjects of electrical engineering, paves the way for its use in other engineering subjects.
- -
- The compatibility of the EO algorithm, which has been successfully applied in engineering problems with the proposed controller and AVR is evaluated.
- -
- The superior control performance of the proposed controller has been demonstrated by comparing it with PID-type controllers such as PID, FOPID, PIDA, PIDD2, and hybrid controllers.
- -
- The achievement of the proposed controller in the frequency domain is shown.
- -
- The robustness of the proposed controller against perturbed system parameters is demonstrated.
1.5. Organization of Paper
2. Modelling of the AVR System
3. Control Methodologies
3.1. A Brief Overview of Fractional Calculus
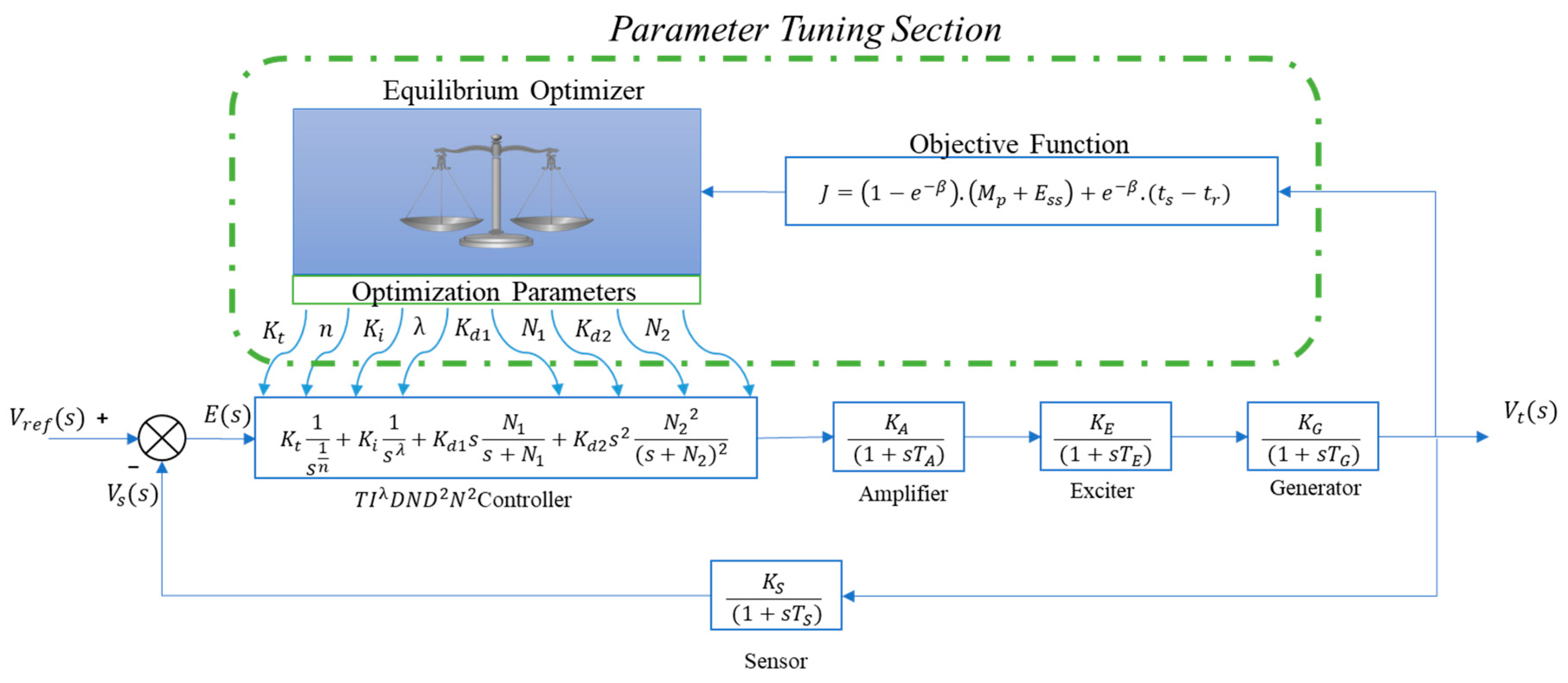
3.2. Proposed Controller
4. Optimization Algorithm
4.1. Initialization
4.2. Equilibrium Pool and Candidates (Ceq)
4.3. Exponential Term
4.4. Generation Rate
5. Objective Function
6. Results and Discussion
6.1. The Performance Achievement of the TIλDND2N2 Controller
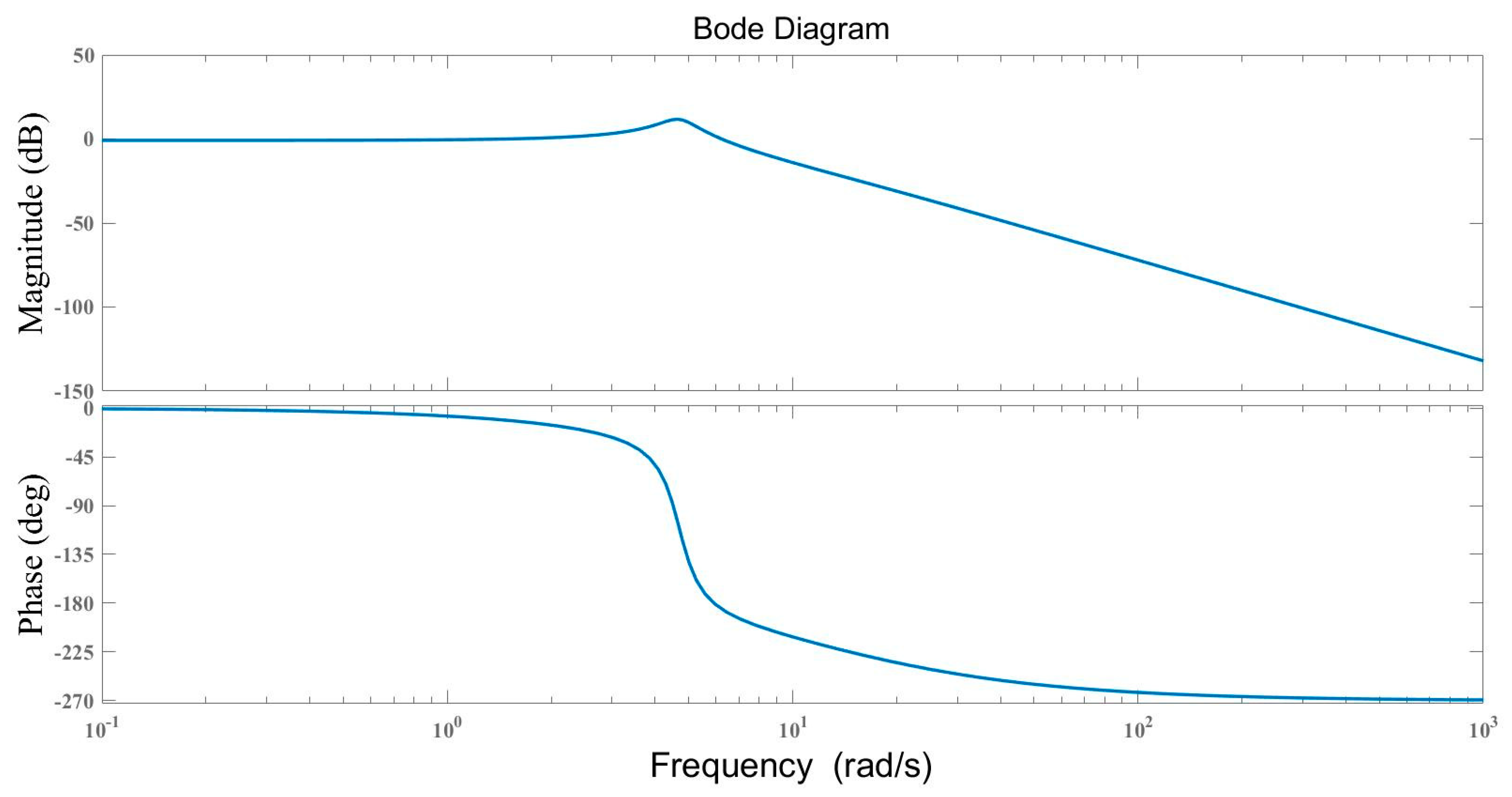
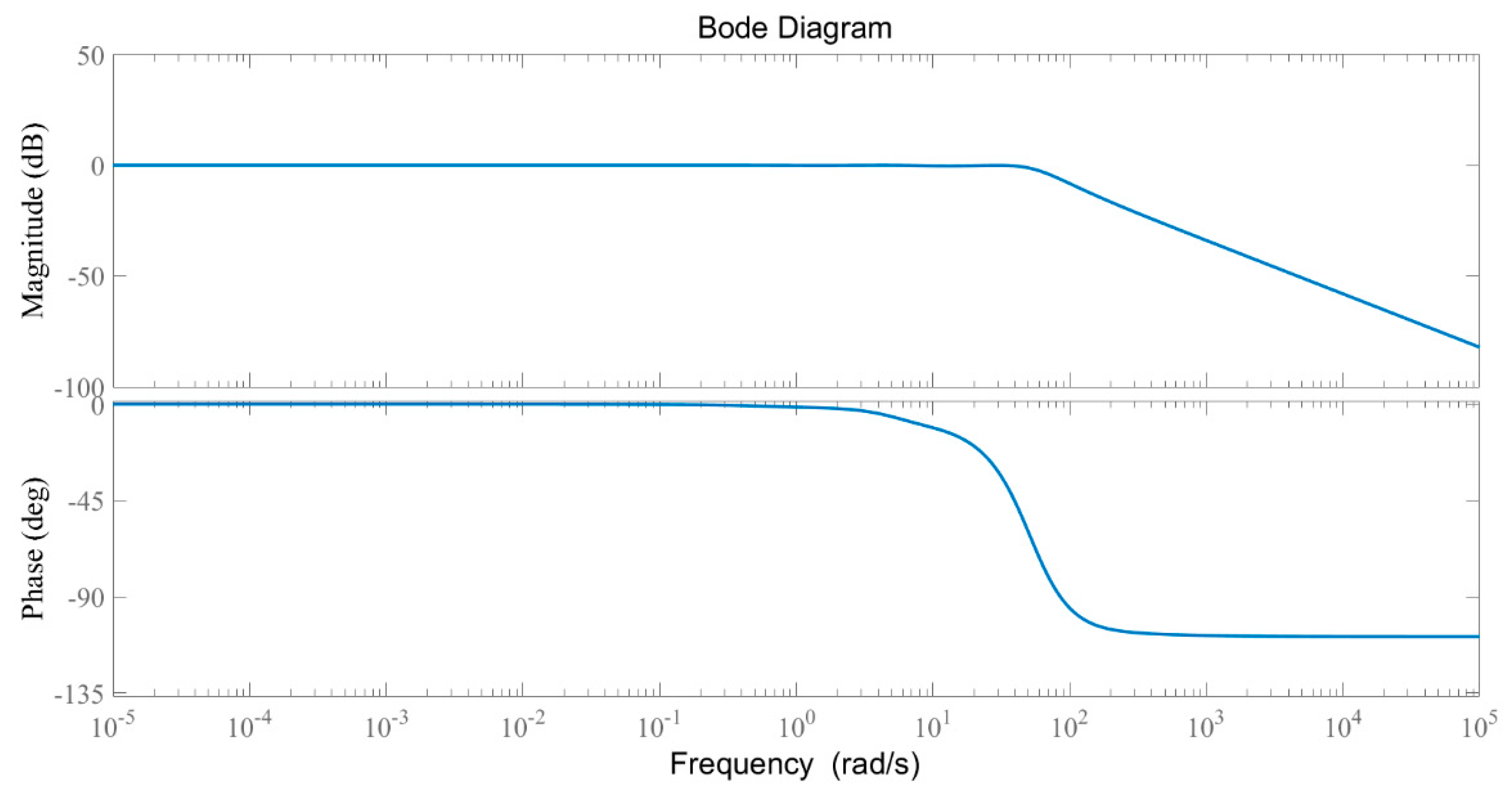
6.2. Frequency Domain Analysis
6.3. Robustness Analysis
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sedighizadeh, M.; Esmaili, M.; Eisapour-Moarref, A. Voltage and frequency regulation in autonomous microgrids using Hybrid Big Bang-Big Crunch algorithm. Appl. Soft Comput. 2017, 52, 176–189. [Google Scholar] [CrossRef]
- Boldea, I. Synchronous Generators, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Ula, A.; Hasan, A.R. Design and Implementation of a Personal Computer Based Automatic Voltage Regulator for a Synchronous Generator. IEEE Trans. Energy Convers. 1992, 7, 125–131. [Google Scholar] [CrossRef]
- Duman, S.; Yörükeren, N.; Altaş, İ. Gravitational search algorithm for determining controller parameters in an automatic voltage regulator system. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 2387–2400. [Google Scholar] [CrossRef] [Green Version]
- Furat, M.; Cucu, G.G. Design, Implementation, and Optimization of Sliding Mode Controller for Automatic Voltage Regulator System. IEEE Access 2022, 10, 55650–55674. [Google Scholar] [CrossRef]
- Gupta, T.; Sambariya, D.K. Optimal design of fuzzy logic controller for automatic voltage regulator. In Proceedings of the 2017 International Conference on Information, Communication, Instrumentation and Control (ICICIC), Indore, India, 17–19 August 2017; Volume 2018, pp. 1–6. [Google Scholar] [CrossRef]
- Yavarian, K.; Mohammadian, A.; Hashemi, F. Adaptive neuro fuzzy inference system PID controller for AVR system using SNR-PSO optimization. Int. J. Electr. Eng. Inform. 2015, 7, 394–408. [Google Scholar] [CrossRef]
- Tabak, A.; İlhan, İ. An effective method based on simulated annealing for automatic generation control of power systems. Appl. Soft Comput. 2022, 126, 109277. [Google Scholar] [CrossRef]
- Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y.; Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y.; Mosaad, A.M.; Attia, M.A. Comparative Performance Analysis of AVR Controllers Using Modern Optimization Techniques. Electr. Power Compon. Syst. 2018, 46, 2117–2130. [Google Scholar] [CrossRef]
- Bhookya, J.; Jatoth, R.K. Optimal FOPID / PID controller parameters tuning for the AVR system based on sine–cosine-algorithm. Evol. Intell. 2019, 12, 725–733. [Google Scholar] [CrossRef]
- Pachauri, N. Water cycle algorithm-based PID controller for AVR. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 551–567. [Google Scholar] [CrossRef]
- Mosaad, A.M.; Attia, M.A.; Abdelaziz, A.Y. Whale optimization algorithm to tune PID and PIDA controllers on AVR system. Ain Shams Eng. J. 2019, 10, 755–767. [Google Scholar] [CrossRef]
- Sikander, A.; Thakur, P. A new control design strategy for automatic voltage regulator in power system. ISA Trans. 2020, 100, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Micev, M.; Calasan, M.; Ali, Z.M.; Hasanien, H.M.; Abdel, S.H.E. Optimal design of automatic voltage regulation controller using hybrid simulated annealing–Manta ray foraging optimization algorithm. Ain Shams Eng. J. 2021, 12, 641–657. [Google Scholar] [CrossRef]
- Miavagh, F.M.; Miavaghi, E.A.A.; Ghiasi, A.R.; Asadollahi, M. Applying of PID, FPID, TID and ITID controllers on AVR system using particle swarm optimization (PSO). In Proceedings of the 2015 2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 5–6 November 2015; pp. 866–871. [Google Scholar] [CrossRef]
- Shukla, H.; Nikolovski, S.; Raju, M.; Rana, A.S.; Kumar, P. A Particle Swarm Optimization Technique Tuned TID Controller for Frequency and Voltage Regulation with Penetration of Electric Vehicles and Distributed Generations. Energies 2022, 15, 8225. [Google Scholar] [CrossRef]
- Verma, S.K.; Devarapalli, R. Fractional order PIλDμ controller with optimal parameters using Modified Grey Wolf Optimizer for AVR system. Arch. Control Sci. 2022, 32, 429–450. [Google Scholar] [CrossRef]
- Moschos, I.; Parisses, C. A novel optimal PIλDND2N2 controller using coyote optimization algorithm for an AVR system. Eng. Sci. Technol. Int. J. 2022, 26, 100991. [Google Scholar] [CrossRef]
- Khan, I.A.; Alghamdi, A.S.; Jumani, T.A.; Alamgir, A.; Awan, A.B.; Khidrani, A. Salp Swarm Optimization Algorithm-Based Fractional Order PID Controller for Dynamic Response and Stability Enhancement of an Automatic Voltage Regulator System. Electronics 2019, 8, 1472. [Google Scholar] [CrossRef] [Green Version]
- Sikander, A.; Thakur, P.; Bansal, R.C.; Rajasekar, S. A novel technique to design cuckoo search based FOPID controller for AVR in power systems R. Comput. Electr. Eng. 2018, 70, 261–274. [Google Scholar] [CrossRef]
- Sahib, M.A. A novel optimal PID plus second order derivative controller for AVR system. Eng. Sci. Technol. Int. J. 2015, 18, 194–206. [Google Scholar] [CrossRef] [Green Version]
- Tabak, A. Maiden application of fractional order PID plus second order derivative controller in automatic voltage regulator. Int. Trans. Electr. Energy Syst. 2021, 31, e13211. [Google Scholar] [CrossRef]
- Tabak, A. A novel fractional order PID plus derivative (PIλDµDµ2) controller for AVR system using equilibrium optimizer. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2021, 40, 722–743. [Google Scholar] [CrossRef]
- Paliwal, N.; Srivastava, L.; Pandit, M. Rao algorithm based optimal Multi-term FOPID controller for automatic voltage regulator system. Optim. Control Appl. Methods 2022, 43, 1707–1734. [Google Scholar] [CrossRef]
- Agwa, A.; Elsayed, S.; Ahmed, M. Design of Optimal Controllers for Automatic Voltage Regulation Using Archimedes Optimizer. Intell. Autom. Soft Comput. 2021, 31, 799–815. [Google Scholar] [CrossRef]
- Suid, M.H.; Ahmad, M.A. Optimal tuning of sigmoid PID controller using Nonlinear Sine Cosine Algorithm for the Automatic Voltage Regulator system. ISA Trans. 2022, 128, 265–286. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.W.; Zohaib, H.; Rasid, M.M.; Saeed, M.S.; Memon, M.M.; Khan, I.; Nisar, K.S. Jaya optimization algorithm for transient response and stability enhancement of a fractional-order PID based automatic voltage regulator system. Alex. Eng. J. 2020, 59, 2429–2440. [Google Scholar] [CrossRef]
- Gozde, H.; Taplamacioglu, M.C. Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system. J. Frankl. Inst. 2011, 348, 1927–1946. [Google Scholar] [CrossRef]
- Ayas, M.S.; Sahin, E. FOPID controller with fractional filter for an automatic voltage regulator. Comput. Electr. Eng. 2020, 90, 106895. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Oliva, D. Fractional Order PID Controller Design for an AVR System Using Chaotic Yellow Saddle Goatfish Algorithm. Mathematics 2020, 8, 1182. [Google Scholar] [CrossRef]
- Puangdownreong, D. Application of Current Search to Optimum PIDA Controller Design. Intell. Control Autom. 2012, 3, 303–312. [Google Scholar] [CrossRef] [Green Version]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Gaing, Z. A Particle Swarm Optimization Approach for Optimum Design of PID Controller in AVR System. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef] [Green Version]
- Kose, E. Optimal Control of AVR System with Tree Seed Algorithm-Based PID Controller. IEEE Access 2020, 8, 89457–89467. [Google Scholar] [CrossRef]
- Habib, S.; Abbas, G.; Jumani, T.A.; Bhutto, A.A.; Mirsaeidi, S.; Ahmed, E.M. Improved Whale Optimization Algorithm for Transient Response, Robustness, and Stability Enhancement of an Automatic Voltage Regulator System. Energies 2022, 15, 5037. [Google Scholar] [CrossRef]
- Jegatheesh, A.; Thiyagarajan, V.; Selvan, N.B.M.; Raj, M.D. Voltage Regulation and Stability Enhancement in AVR System Based on SOA-FOPID Controller. J. Electr. Eng. Technol. 2023, 1–14. [Google Scholar] [CrossRef]
- Munagala, V.K.; Jatoth, R.K. Improved fractional PIλDμ controller for AVR system using Chaotic Black Widow algorithm. Comput. Electr. Eng. 2022, 97, 107600. [Google Scholar] [CrossRef]
- Ayas, M.S.; Sahin, A.K. A reinforcement learning approach to Automatic Voltage Regulator system. Eng. Appl. Artif. Intell. 2023, 121, 106050. [Google Scholar] [CrossRef]
- Priyambada, S.; Sahu, B.K.; Mohanty, P.K. Fuzzy-PID controller optimized TLBO approach on automatic voltage regulator. In Proceedings of the 2015 International Conference on Energy, Power and Environment: Towards Sustainable Growth (ICEPE), Shillong, India, 12–13 June 2015; IEEE: Piscateville, NJ, USA, 2015. [Google Scholar]
- Al Gizi, A.J.H.; Mustafa, M.W.; Al-geelani, N.A.; Alsaedi, M.A. Sugeno fuzzy PID tuning, by genetic-neutral for AVR in electrical power generation. Appl. Soft Comput. J. 2015, 28, 226–236. [Google Scholar] [CrossRef] [Green Version]
- Oziablo, P.; Mozyrska, D.; Wyrwas, M. Fractional-variable-order digital controller design tuned with the chaotic yellow saddle goatfish algorithm for the AVR system. ISA Trans. 2022, 125, 260–267. [Google Scholar] [CrossRef]





| Units | Transfer Function | Range of Gain (K) | Range of Time Constant (Ts) | Gain Values Used (K) | Time Constants Used (Ts) |
|---|---|---|---|---|---|
| Amplifier | 10–40 | 0.02–0.1 | 10 | 0. 1 | |
| Exciter | 1–10 | 0.4–1 | 1 | 0.4 | |
| Generator | 0.7–1 | 1–2 | 1 | 1 | |
| Sensor | 0.9–1.1 | 0.001–0.06 | 1 | 0.01 |
| System | Peak Gain (dB) | Phase Margin (deg) | Delay Margin (s) |
|---|---|---|---|
| AVR (without controller) | 11.8 (at 4.64 rad/s) | −5.43 | 0.994 |
| Parameters | Values/Ranges |
|---|---|
| Iteration number | 100 |
| Population number | 50 |
| Variables number | 8 |
| Constant controlling the exploration phase () | 2 |
| Constant controlling the exploitation phase () | 1 |
| Generation Probability (GP) | 0.5 |
| , | [0, 1] |
| Method | λ/α | μ/β | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TIλDND2N2 EO | 2.1792 | 2.6626 | 1.5658 | 0.1365 | 2.3438 | 0.1099 | -- | 36.2387 | 246.8546 |
| PID IWOA [34] | 0.8167 | 0.6898 | 0.2799 | -- | -- | -- | -- | -- | -- |
| PID MVO [21] | 0.5971 | 0.4057 | 0.1980 | -- | -- | -- | -- | -- | -- |
| PID WCA [10] | 0.6158 | 0.4410 | 0.2158 | -- | -- | -- | -- | -- | -- |
| FOPID SOA [35] | 0.9697 | 0. 4918 | 0. 2210 | -- | -- | 1.1522 | 1.1524 | -- | -- |
| FOPID hSA-MRFO [13] | 1.8931 | 0.8699 | 0.3595 | -- | -- | 1.0408 | 1.278 | -- | -- |
| FOPID ChBWO [36] | 2.8204 | 0.7387 | 0.428 | -- | -- | 1.1294 | 1.3558 | -- | -- |
| PIDD2 EO [22] | 3 | 2.0058 | 1.0936 | 0.0789 | -- | -- | -- | -- | -- |
| PIDD2 PSO [20] | 2.7784 | 1.8521 | 0.9997 | 0.0739 | -- | -- | -- | -- | -- |
| PIDA WOA [11] | 777.401 | 397.741 | 500.652 | -- | 103.02 | 550.118 | 915.041 | -- | -- |
| PIDA TLBO [8] | 850 | 421.601 | 550 | -- | 150 | 550 | 900 | -- | -- |
| Controller-Algorithm | (s) | (s) | (%) | |
|---|---|---|---|---|
| Proposed | TIλDND2N2-EO | 0.0596 | 0.03752 | 0.4128 |
| PID | PID MVO [22] | 0.5074 | 0.3264 | 0.0018 |
| PID EO [23] | 0.4478 | 0.2954 | 1.0004 | |
| PID SCA [10] | 0.665 | 0.3935 | 0.019 | |
| PID TSA [34] | 0.758 | 0.1310 | 15.57 | |
| PID WOA [12] | 2.1359 | 0.2152 | 7.2570 | |
| PID WCA [11] | 0.4620 | 0.3000 | 0.4760 | |
| PID IWOA [35] | 0.6420 | 0.2120 | 9.56 | |
| Sigmoid PID Nonlinar SCA [26] | 0.579 | 0.498 | 1.022 | |
| PIDA | PIDA LUS [9] | 1.1725 | 0.3465 | 1.8049 |
| PIDA TLBO [9] | 1.1023 | 0.2758 | 0.6332 | |
| PIDA HSA [9] | 1.09838 | 0.3073 | 0.4899 | |
| PIDA WOA [12] | 0.4996 | 0.3295 | 1.4087 | |
| PIDD2 | PIDD2 PSO [21] | 0.1635 | 0.0929 | 0.0027 |
| PIDD2 EO [23] | 0.1399 | 0.0829 | 0.0041 | |
| FOPID | MFOPID RAO [24] | 0.170 | 0.0965 | 0.01 |
| FOPID SCA [10] | 0.2260 | 0.1660 | 2.4223 | |
| FOPID C-YSGA [30] | 0.2 | 0.1347 | 1.89 | |
| FOPID hSA MRFO [14] | 0.1909 | 0.1309 | 1.9765 | |
| FOPID COA [18] | 0.1474 | 0.1011 | 1.952 | |
| FOPID EO [23] | 0.4596 | 0.1442 | 0.1849 | |
| FOPID MVO [22] | 0.3493 | 0.1075 | 1.0295 | |
| FOPID SOA [36] | 0.4459 | 0.2745 | 0.1516 | |
| ChBWO-FOPID [37] | 0.1586 | 0.1101 | 1.2714 | |
| Hybrid Controllers | A reinforcement learning approach [38] | 0.55 | 0.34 | 0.2064 |
| Sliding Mode Control [5] | 0.8812 | 0.2998 | 0.08 | |
| Fuzzy TLBO-PID [39] | 0.86 | 0.73 | 0.0001 | |
| Fuzzy PSO PID [39] | 1.9500 | 1.3400 | 0.2510 | |
| GNFPID [40] | 1.3766 | 1.0024 | 0.0017 | |
| YSGA FVOPID [41] | n/a | 0.09820 | 0.71987 | |
| YSGA FVOPID V2 [41] | n/a | 0.09808 | 1.35453 |
| Controller-Method | Peak Gain (dB) | Phase Margin (deg) | Delay Margin (s) |
|---|---|---|---|
| TIλDND2N2-EO | 0. 0233 (at 2.16 rad/s) | 175 | 1.14 |
| PID-ABC [28] | 2.87 (at 7.54 rad/s) | 69.4 | 0.111 |
| POD-PSO [28] | 3.75 (at 7.16 rad/s) | 62.2 | 0.103 |
| PID-EO [23] | 0.00178 (0.31 rad/s) | 175 | 7.01 |
| PID-WOA [12] | 0.569 (n/a) | 155 | 1.04 |
| PIDD2- EO [23] | 0 (0 rad/s) | 180 | Inf |
| PIDA-LUS [9] | 0.159 (n/a) | 162 | 2.42 |
| FOPID-SOA [36] | 0.0259 (n/a) | 176 | 1.38 |
| FOPID-SCA [29] | 0.0379 (0.263 rad/s) | 165 | 1.24 |
| FOPID-EO [23] | 0.0618 (0.242 rad/s) | 177 | 7.34 |
| Perturbation Variation (%) | Peak Value (p.u) | (s) | (s) | (s) | |
| Nominal Values | 0.9937138 | 0.0596 | 0.03752 | 0.1827 | |
| −50 | 1.142358 | 0.2637 | 0.01808 | 0.0412 | |
| −25 | 1.03247 | 0.15194 | 0.02686 | 0.05371 | |
| +25 | 1.02067 | 0.2250 | 0.04915 | 0.16243 | |
| +50 | 1.04847 | 0.2905 | 0.05987 | 0.17193 | |
| −50 | 1.27087 | 0.30788 | 0.01669 | 0.04075 | |
| −25 | 1.07934 | 0.12966 | 0.02539 | 0.05257 | |
| +25 | 1.00453 | 0.10158 | 0.05433 | 0.1996 | |
| +50 | 1.01394 | 0.30182 | 0.07306 | 0.2133 | |
| −50 | 1.30404 | 0.13815 | 0.016417 | 0.04137 | |
| −25 | 1.09113 | 0.11917 | 0.02512 | 0.05263 | |
| +25 | 0.99731 | 0.11430 | 0.05603 | 0.75282 | |
| +50 | 1.0029 | 0.14260 | 0.078498 | 0.72093 | |
| −50 | 0.99424 | 0.11751 | 0.04972 | 0.67725 | |
| −25 | 0.99403 | 0.10542 | 0.04162 | 0.70737 | |
| +25 | 1.030779 | 0.09614 | 0.035358 | 0.075396 | |
| +50 | 1.06998 | 0.11272 | 0.033879 | 0.07659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabak, A. Novel TIλDND2N2 Controller Application with Equilibrium Optimizer for Automatic Voltage Regulator. Sustainability 2023, 15, 11640. https://doi.org/10.3390/su151511640
Tabak A. Novel TIλDND2N2 Controller Application with Equilibrium Optimizer for Automatic Voltage Regulator. Sustainability. 2023; 15(15):11640. https://doi.org/10.3390/su151511640
Chicago/Turabian StyleTabak, Abdulsamed. 2023. "Novel TIλDND2N2 Controller Application with Equilibrium Optimizer for Automatic Voltage Regulator" Sustainability 15, no. 15: 11640. https://doi.org/10.3390/su151511640
APA StyleTabak, A. (2023). Novel TIλDND2N2 Controller Application with Equilibrium Optimizer for Automatic Voltage Regulator. Sustainability, 15(15), 11640. https://doi.org/10.3390/su151511640








