A Comprehensive Review of Recent Maximum Power Point Tracking Techniques for Photovoltaic Systems under Partial Shading
Abstract
1. Introduction
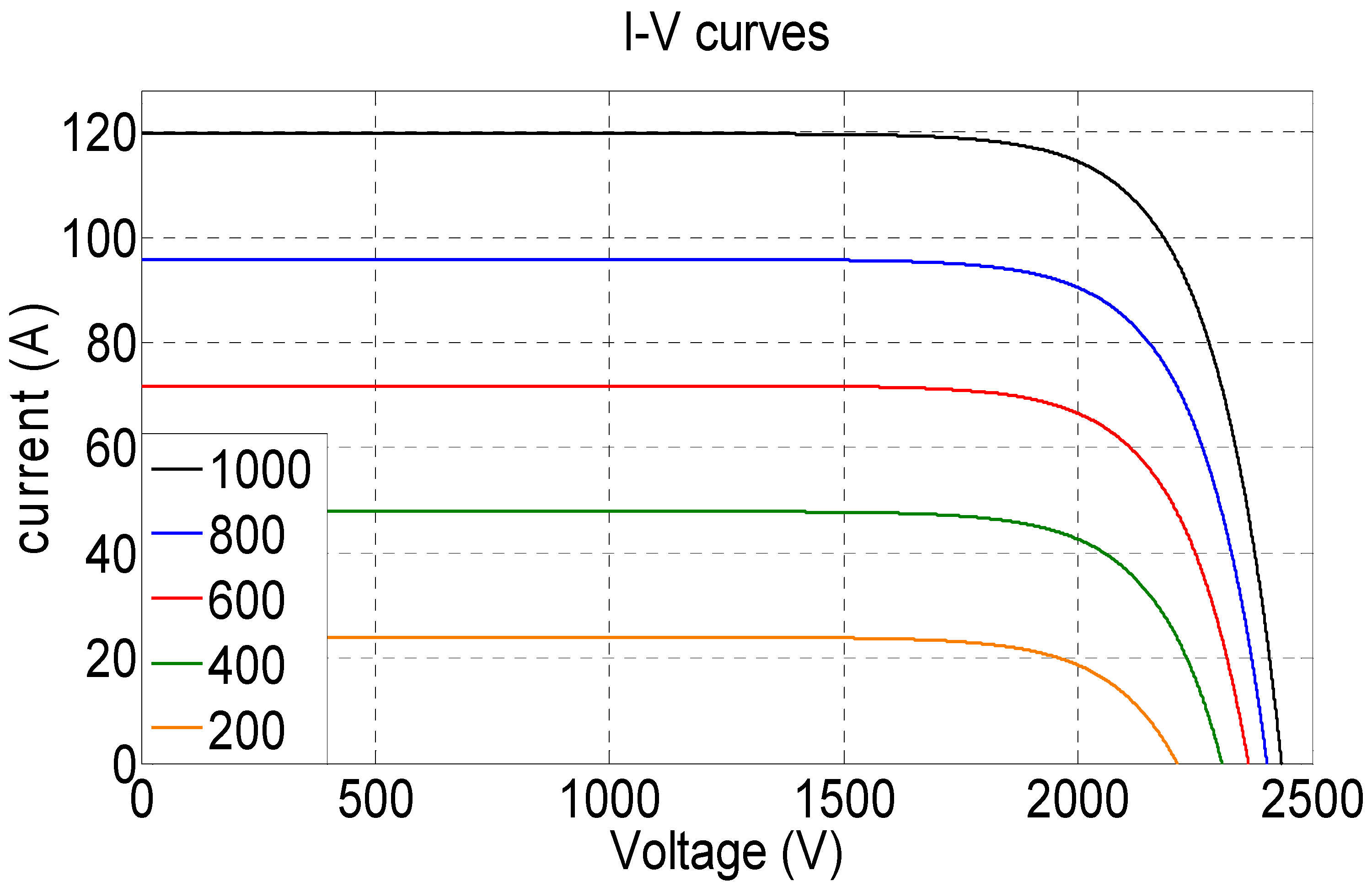
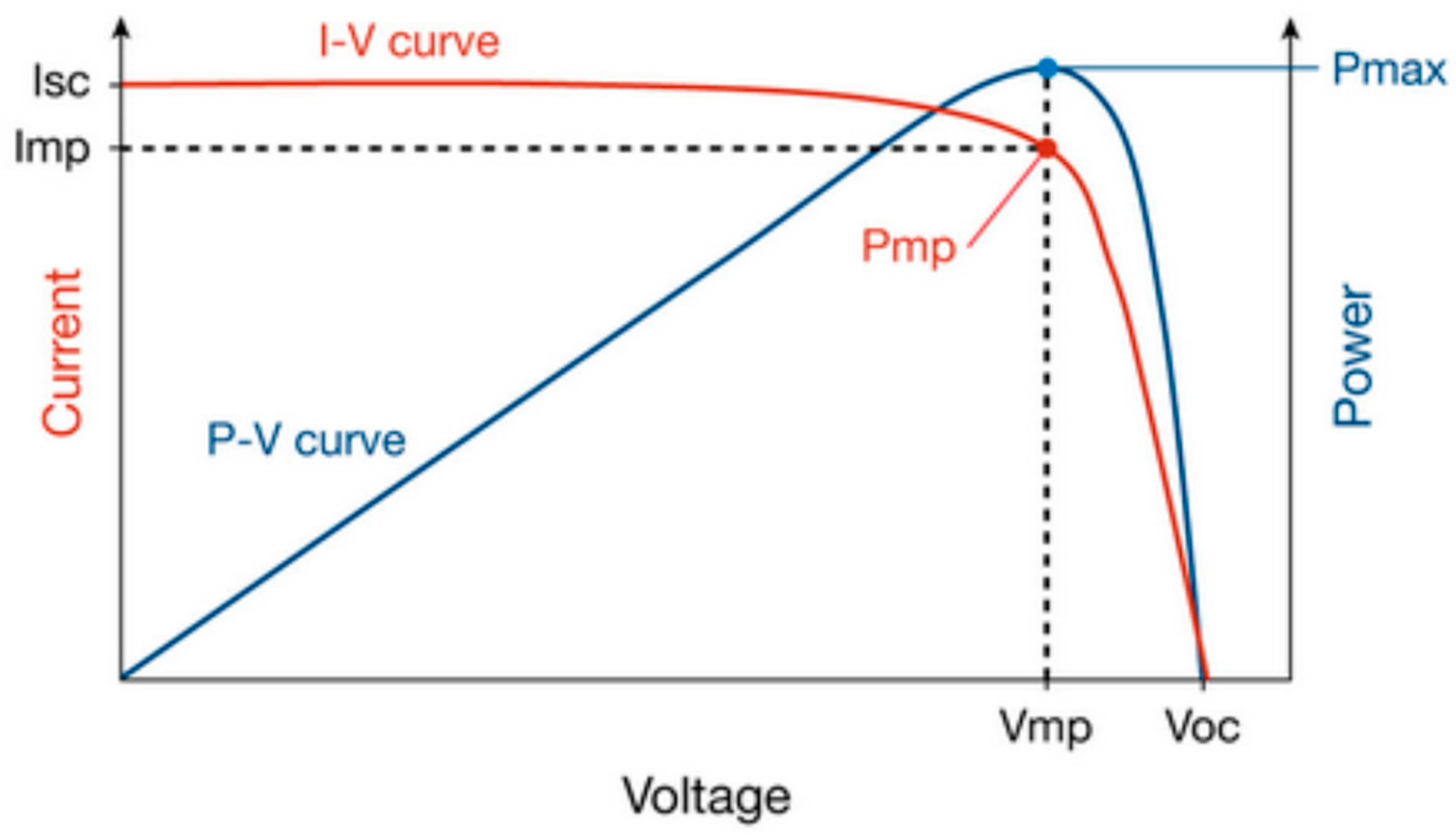
2. PV Configuration
3. Maximum Power Point Tracking (MPPT) Methods for Partial Shading
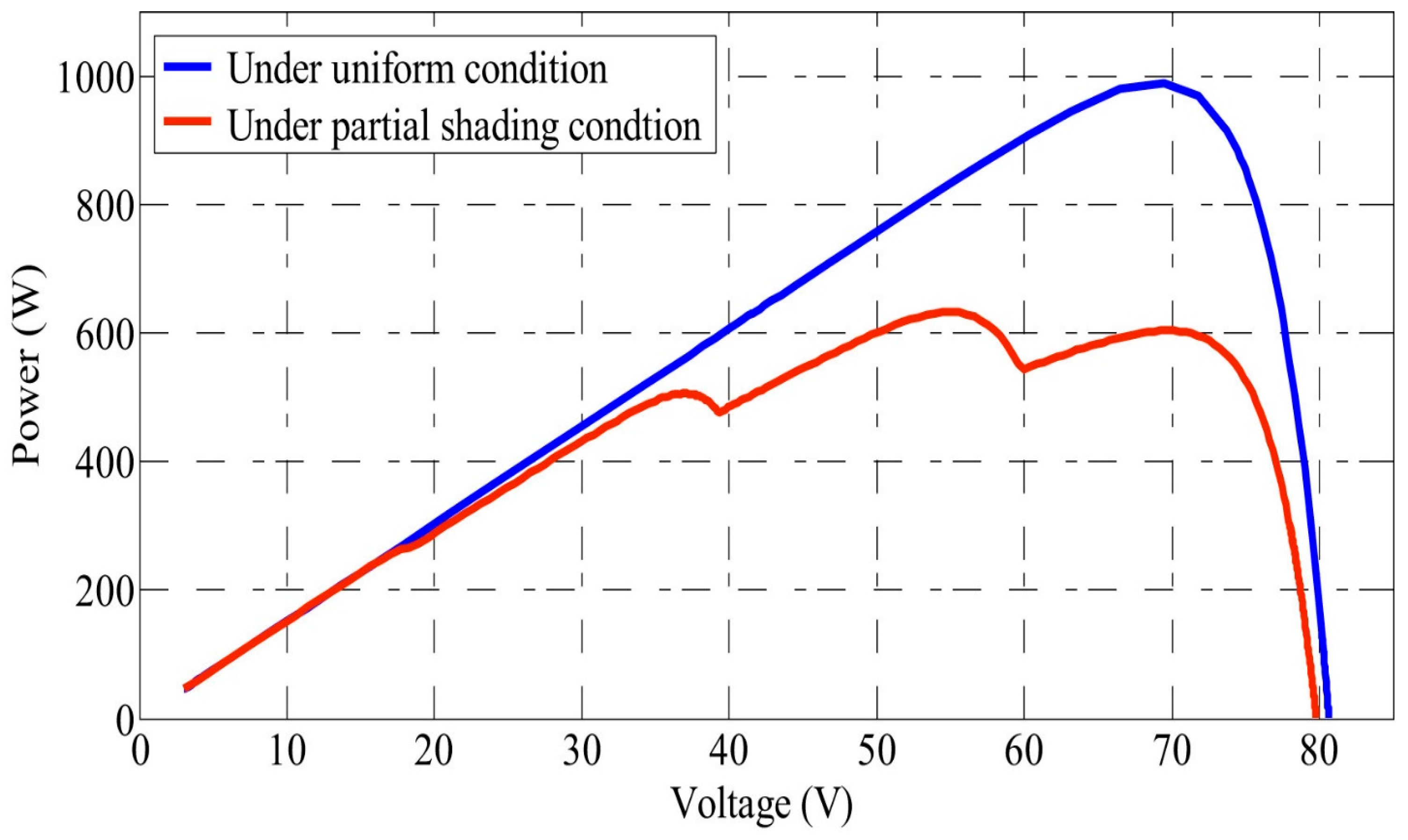
4. Dynamic Tracking under Partial Shading
4.1. MPPT-Based Techniques
4.1.1. Conventional MPPT
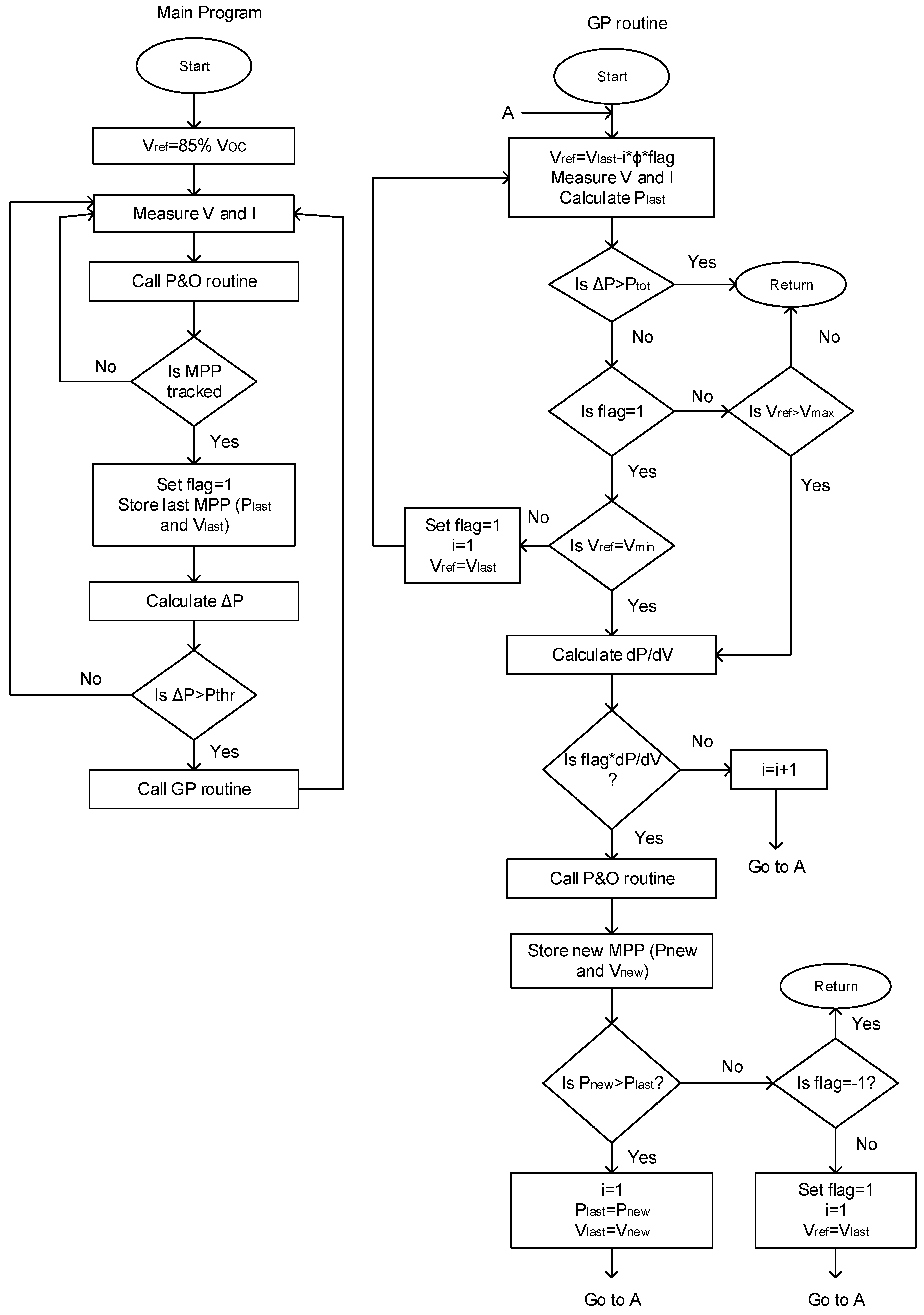
- Modified Perturb and Observe (P&O) technique
- Pm(t) is the instantaneous measured power and
- Pref(t) is the instantaneous reference maximum power.
- 2.
- Modified Incremental Conductance (IC)
- k is the correction factor, and
- VMP and IMP are approximately 80% of VOC and 90% of ISC, respectively.
- VOC and ISC are the open circuit voltage and short circuit current, respectively.
- Vgrid is the output grid voltage and
- Iout is the output grid current.
- 3.
- Modified Hill Climbing (HC)
4.1.2. Soft Computing MPPT Techniques
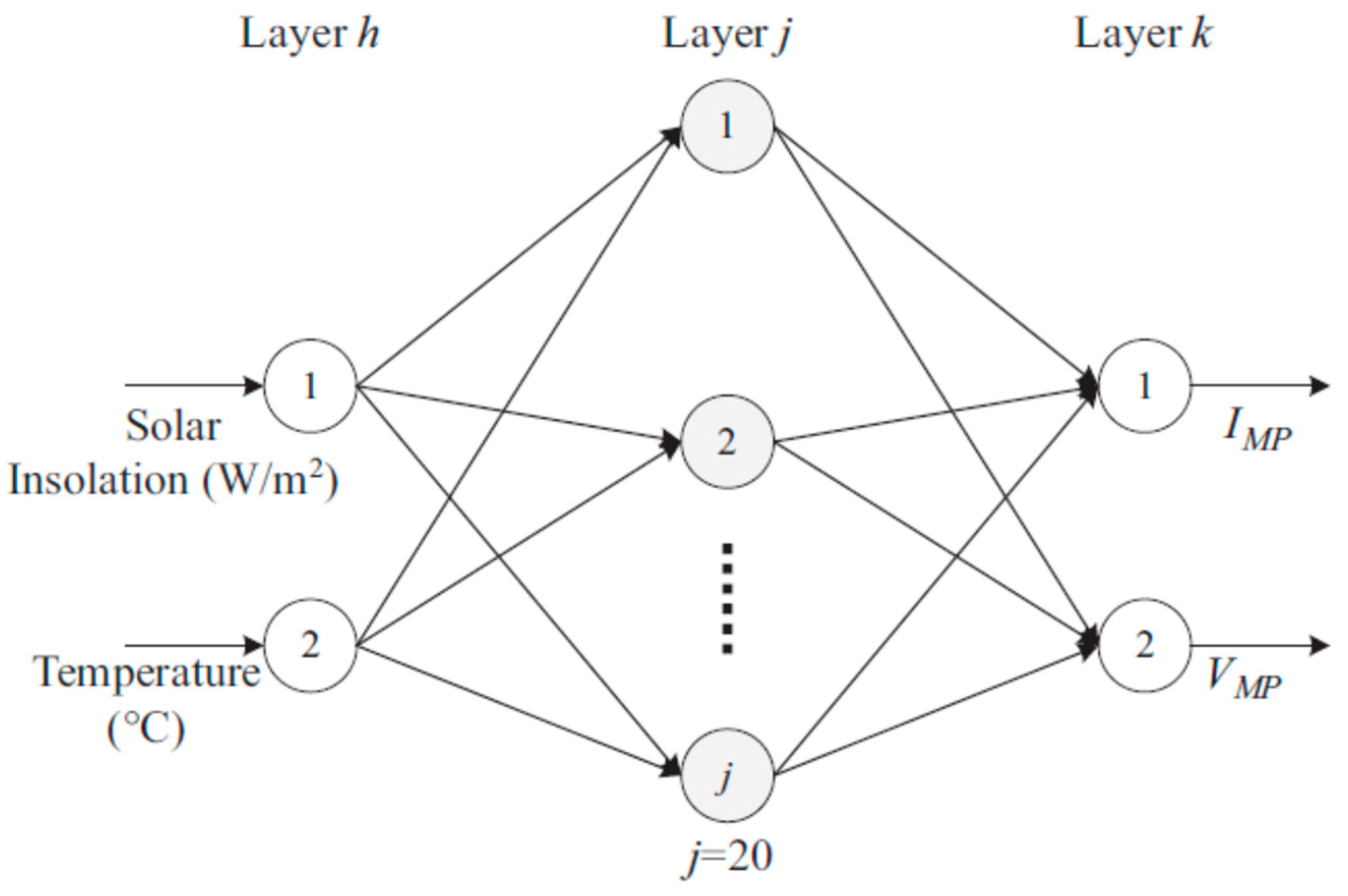
- Artificial Neural Network (ANN)
- 2.
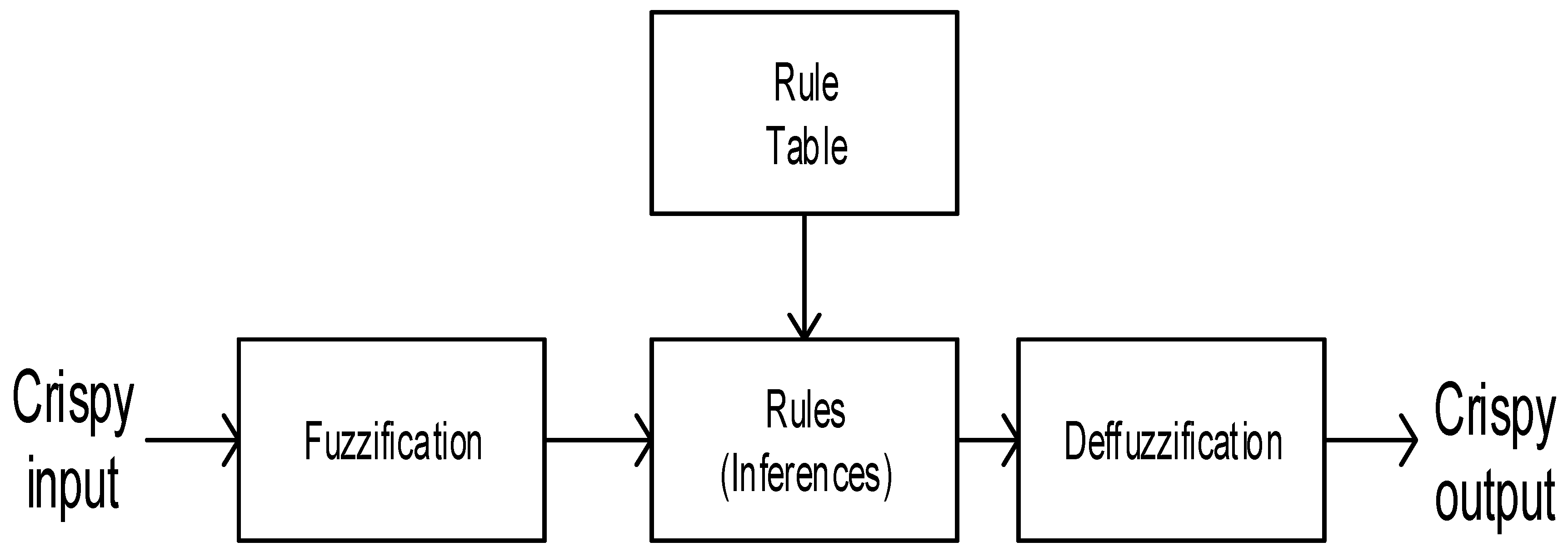
- Fuzzy Logic Control (FLC)
- 3.
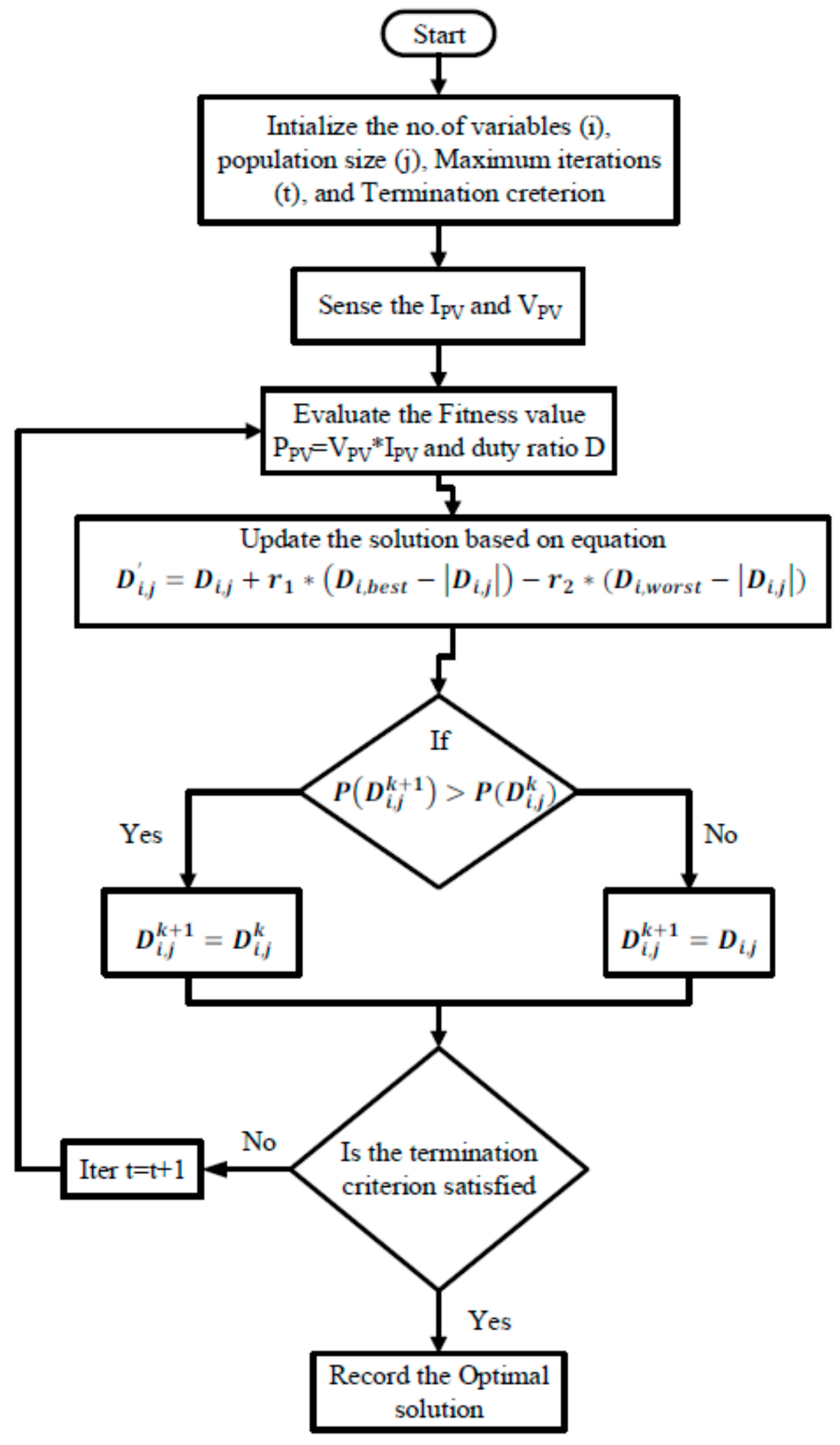
- Particle Swarm Optimization (PSO)
- Vi(k + 1) is the particle velocity at k + 1th iteration,
- W is the inertia weight,
- Vi(k) is the particle velocity at the kth iteration,
- C1 is the acceleration component associated with Gbest,
- Xi(k + 1) is the particle position at (k + 1)th iteration,
- Xi(k) is the particle position at the kth iteration,
- C2 is the acceleration component associated with Pbest,
- rand1 and rand2 are random numbers from zero to one,
- Gbest is the best position of all particles, and Pbest is the best position of the particle.
- 4.
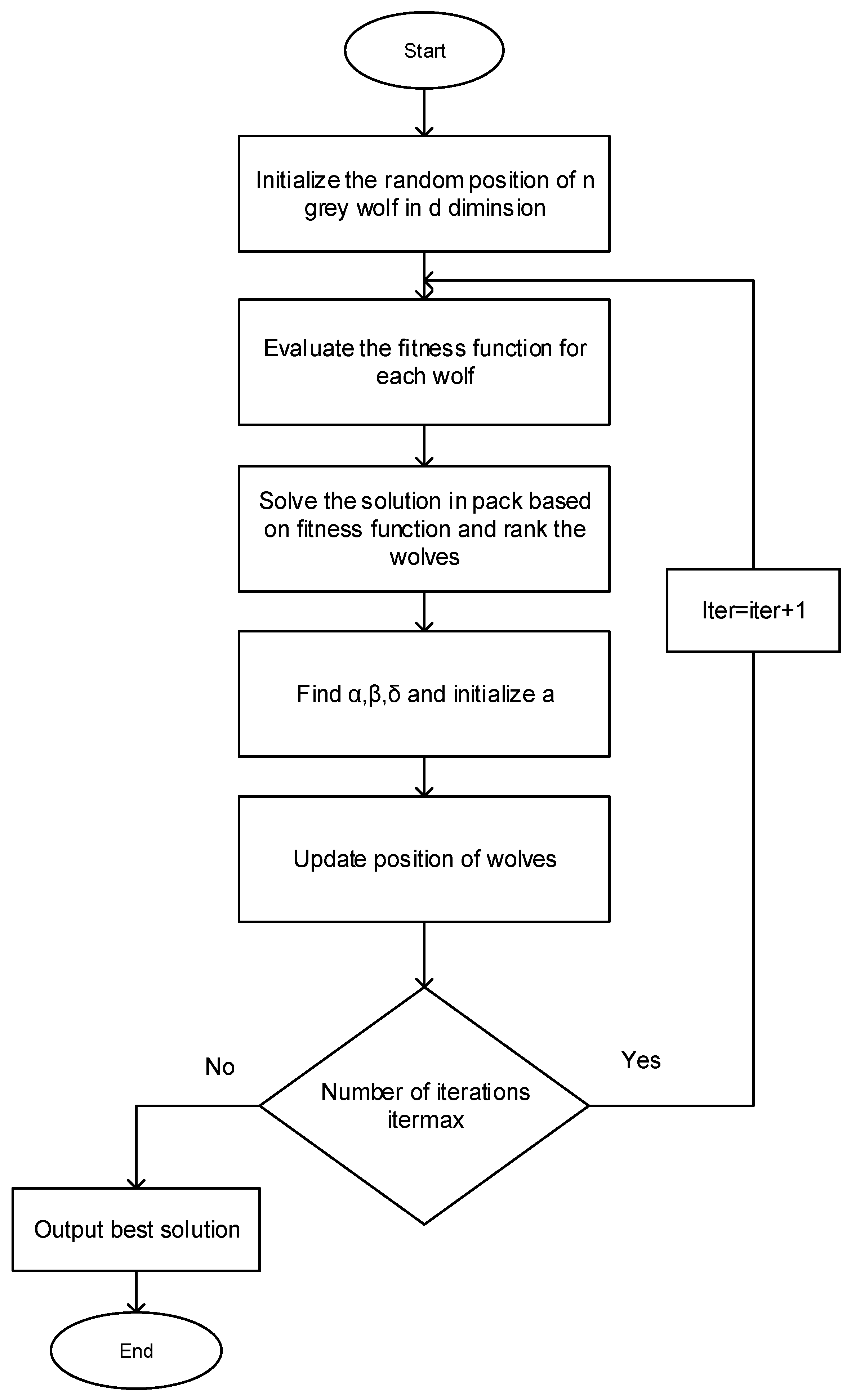
- Grey Wolf Optimization (GWO)
- E, F, and C are the coefficient vectors,
- Xp is the position vector of the hunting prey,
- X is the position vector for the Grey wolf, and
- t is the current iteration.
- d is the duty cycle,
- k represents the iteration count,
- i is the number of the current individual grey wolves, and P is the power.
- 5.
- Firefly Algorithm (FA)
- Xi represents the position of the less bright firefly,
- Xj represents the position of the brighter firefly, and
- β is the firefly attractiveness factor.
- 6.
- Ant Colony Optimization (ACO)
- 7.
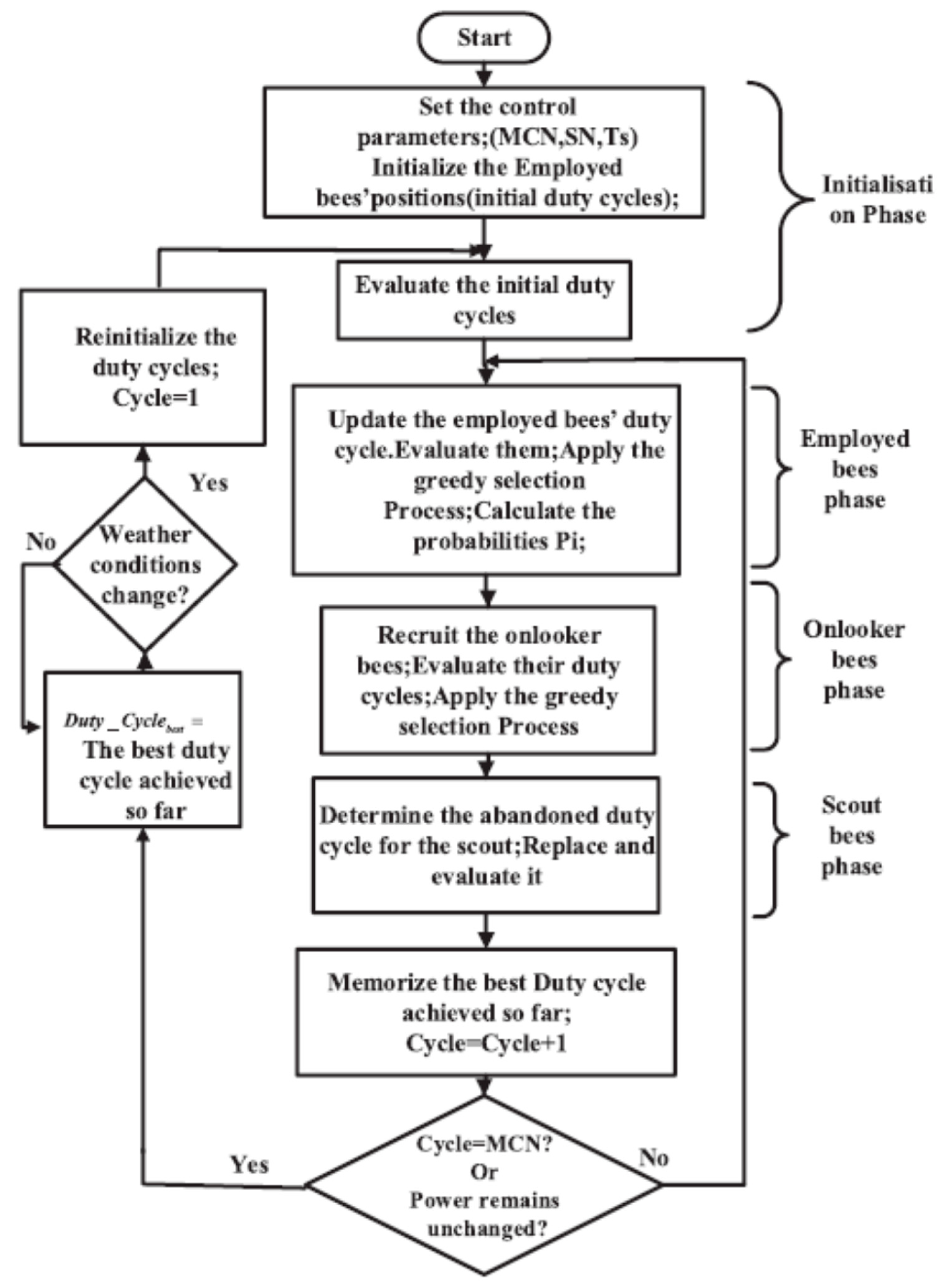
- Artificial Bee Colony (ABC)
- d is the current duty cycle,
- dmin is the minimum value of the duty cycle,
- dmax is the maximum value of the duty cycle),
- ϕe is a constant between [−1, 1], and
- dp is the previous duty cycle.
- 8.
- Cuckoo Search (CS)
- 9.
- Jaya Algorithm (JA)
4.1.3. Hybrid MPPT Techniques
- Hybrid GWO and P&O MPPT Algorithm
- 2.
- P&O combined with PSO
- 3.
- Differential Evolution and PSO (DEPSO)
4.2. Circuit-Based Approach
4.2.1. Monitoring Bypass Diode Voltages
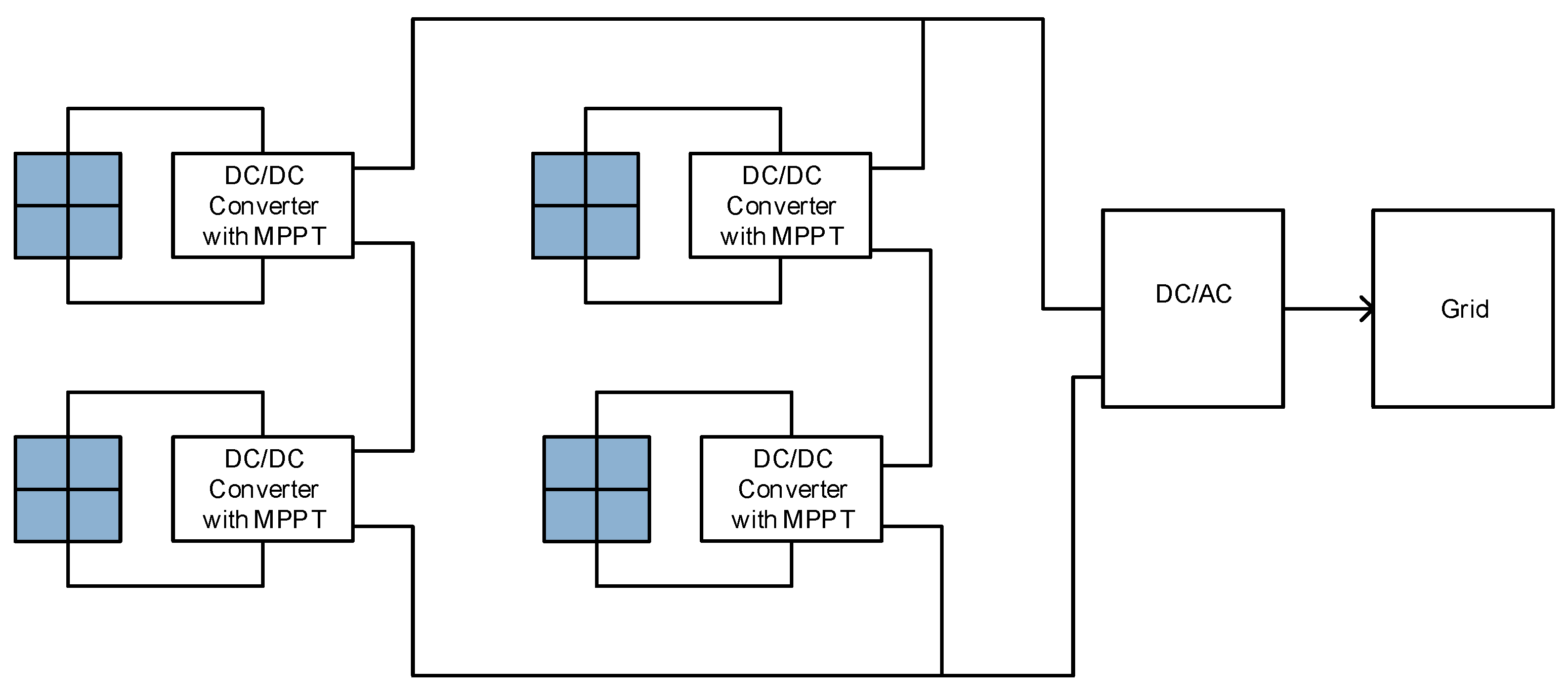
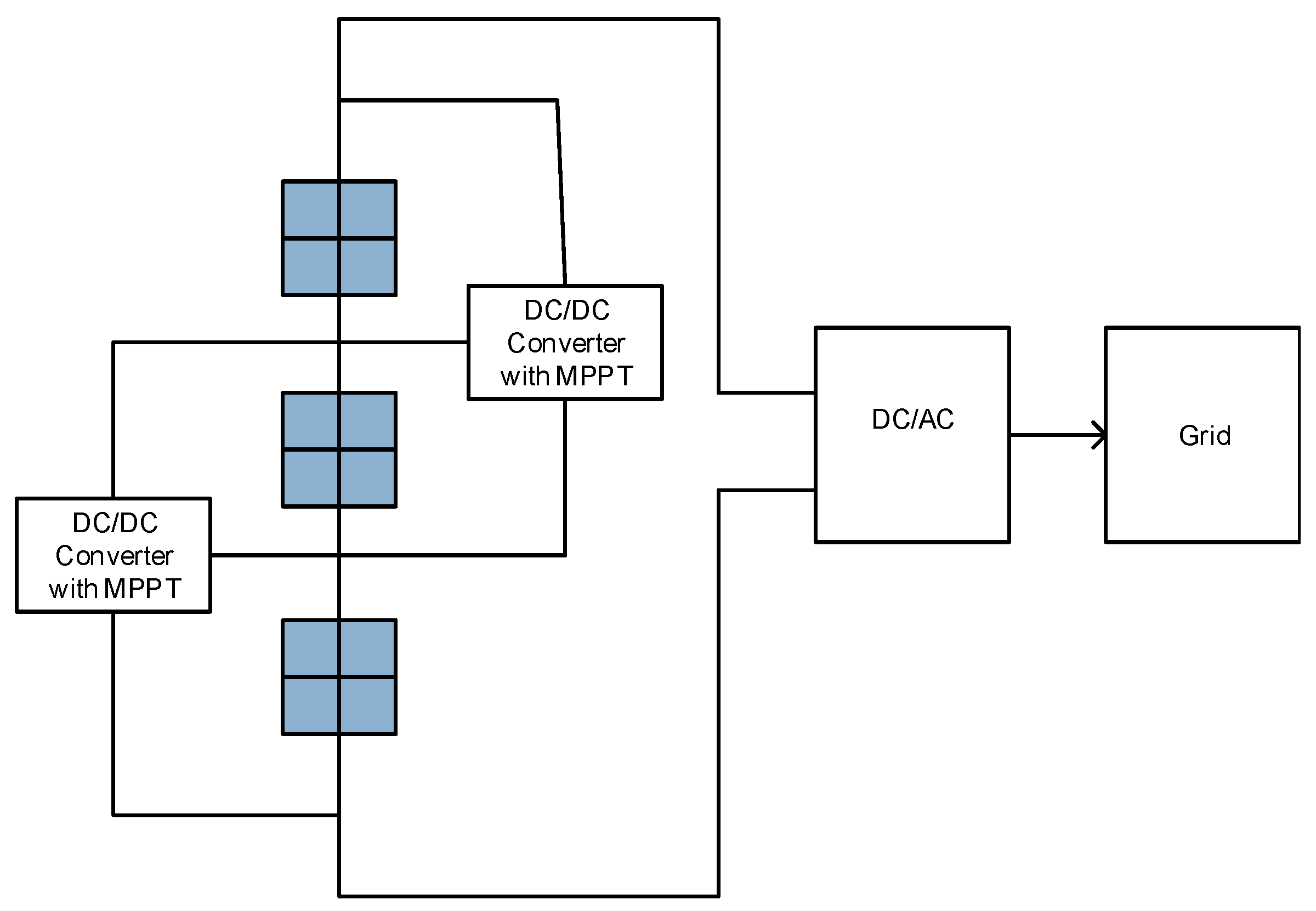
4.2.2. Distributed MPPT
4.2.3. Differential Power Processing
4.2.4. Power Electronics Equalizer
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Asghar, R.; Ullah, Z.; Azeem, B.; Aslam, S.; Hashmi, M.H.; Rasool, E.; Shaker, B.; Anwar, M.J.; Mustafa, K. Wind Energy Potential in Pakistan: A Feasibility Study in Sindh Province. Energies 2022, 15, 8333. [Google Scholar] [CrossRef]
- Asghar, M.; Anwar, J.; Wadood, H.; Saleem, H.; Rasul, N.; Ullah, Z. Promising Features of Wind Energy: A Glance Overview. In Proceedings of the 2023 4th International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 17–18 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gupta, A.; Likozar, B.; Jana, R.; Chanu, W.C.; Singh, M.K. A review of hydrogen production processes by photocatalytic water splitting—From atomistic catalysis design to optimal reactor engineering. Int. J. Hydrog. Energy 2022, 47, 33282–33307. [Google Scholar] [CrossRef]
- Ješić, D.; Jurković, D.L.; Pohar, A.; Suhadolnik, L.; Likozar, B. Engineering photocatalytic and photoelectrocatalytic CO2 reduction reactions: Mechanisms, intrinsic kinetics, mass transfer resistances, reactors and multi-scale modelling simulations. Chem. Eng. J. 2021, 407, 126799. [Google Scholar] [CrossRef]
- Kržmanc, M.M.; Daneu, N.; Čontala, A.; Santra, S.; Kamal, K.M.; Likozar, B.; Spreitzer, M. SrTiO3/Bi4Ti3O12 Nanoheterostructural Platelets Synthesized by Topotactic Epitaxy as Effective Noble-Metal-Free Photocatalysts for pH-Neutral Hydrogen Evolution. ACS Appl. Mater. Interfaces 2021, 13, 370–381. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelrahem, M.; Kennel, R. Highly Efficient and Robust Grid Connected Photovoltaic System Based Model Predictive Control with Kalman Filtering Capability. Sustainability 2020, 12, 4542. [Google Scholar] [CrossRef]
- Bubalo, M.; Bašić, M.; Vukadinović, D.; Grgić, I. Hybrid Wind-Solar Power System with a Battery-Assisted Quasi-Z-Source Inverter: Optimal Power Generation by Deploying Minimum Sensors. Energies 2023, 16, 1488. [Google Scholar] [CrossRef]
- Ludin, N.A.; Affandi, N.A.A.; Purvis-Roberts, K.; Ahmad, A.; Ibrahim, M.A.; Sopian, K.; Jusoh, S. Environmental Impact and Levelised Cost of Energy Analysis of Solar Photovoltaic Systems in Selected Asia Pacific Region: A Cradle-to-Grave Approach. Sustainability 2021, 13, 396. [Google Scholar] [CrossRef]
- Uoya, M.; Koizumi, H. A Calculation Method of Photovoltaic Array’s Operating Point for MPPT Evaluation Based on One-Dimensional Newton–Raphson Method. IEEE Trans. Ind. Appl. 2015, 51, 567–575. [Google Scholar] [CrossRef]
- El-Khozondar, H.J.; El-Khozondar, R.J.; Matter, K.; Suntio, T. A review study of photovoltaic array maximum power tracking algorithms. Renew. Wind Water Sol. 2016, 3, 1. [Google Scholar] [CrossRef]
- Jafarkazemi, F.; Saadabadi, S.A. Optimum tilt angle and orientation of solar surfaces in Abu Dhabi, UAE. Renew. Energy 2013, 56, 44–49. [Google Scholar] [CrossRef]
- Almasoud, A.H.; Gandayh, H.M. Future of solar energy in Saudi Arabia. J. King Saud. Univ. Eng. Sci. 2014, 27, 153–157. [Google Scholar] [CrossRef]
- SAKAKA PV IPP. Available online: https://acwapower.com/en/projects/sakaka-pv-ipp/ (accessed on 14 March 2023).
- Liu, L.; Wang, Z.; Zhang, H.; Xue, Y. Solar energy development in China—A review. Renew. Sustain. Energy Rev. 2010, 14, 301–311. [Google Scholar] [CrossRef]
- Ahmed, S.U.; Affan, M.; Raza, M.I.; Hashmi, M.H. Inspecting Mega Solar Plants through Computer Vision and Drone Technologies. In Proceedings of the 2022 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 11–12 December 2022; pp. 18–23. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Chiaberge, M. An intelligent control strategy of fractional short circuit current maximum power point tracking technique for photovoltaic applications. J. Renew. Sustain. Energy 2015, 7, 013114. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A New Sensorless Hybrid MPPT Algorithm Based on Fractional Short-Circuit Current Measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar]
- Baimel, D.; Tapuchi, S.; Levron, Y.; Belikov, J. Improved Fractional Open Circuit Voltage MPPT Methods for PV Systems. Electronics 2019, 8, 321. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An improved perturb and observe (P&O) maximum power point tracking (MPPT) algorithm for higher efficiency. Appl. Energy 2015, 150, 97–108. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, optimization, intelligent and classical PV MPPT techniques: A Review. CSEE J. Power Energy Syst. 2021, 7, 9–33. [Google Scholar]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, K. Framework of maximum power extraction from solar PV panel using self predictive perturb and observe algorithm. IEEE Trans. Sustain. Energy. 2018, 9, 895–903. [Google Scholar] [CrossRef]
- Jiang, J.-A.; Su, Y.-L.; Kuo, K.-C.; Wang, C.-H.; Liao, M.-S.; Wang, J.-C.; Huang, C.-K.; Chou, C.-Y.; Lee, C.-H.; Shieh, J.-C. On a hybrid MPPT control scheme to improve energy harvesting performance of traditional two-stage inverters used in photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 69, 1113–1128. [Google Scholar] [CrossRef]
- Mousa, H.H.; Youssef, A.-R.; Mohamed, E.E. State of the art perturb and observe MPPT algorithms based wind energy conversion systems: A technology review. Int. J. Electr. Power Energy Syst. 2020, 126, 106598. [Google Scholar] [CrossRef]
- Alik, R.; Jusoh, A.; Sutikno, T. A Review on Perturb and Observe Maximum Power Point Tracking in Photovoltaic System. TELKOMNIKA (Telecommun. Comput. Electron. Control.) 2015, 13, 745–751. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M.; Nassef, A.M.; Rezk, H.; Nisar, K.S. Optimal parameter design of fractional order control based INC-MPPT for PV system. Sol. Energy 2018, 159, 650–664. [Google Scholar] [CrossRef]
- Zakzouk, N.E.; Williams, B.W.; Helal, A.A.; Elsaharty, M.A.; Abdelsalam, A.K. Improved performance low-cost incremental conductance PV MPPT technique. IET Renew. Power Gener. 2016, 10, 561–574. [Google Scholar] [CrossRef]
- Tozlu, Ö.F.; Çalik, H. A Review and Classification of Most Used MPPT Algorithms for Photovoltaic Systems. Hittite J. Sci. Eng. 2021, 8, 207–220. [Google Scholar] [CrossRef]
- Huynh, D.C.; Dunnigan, M.W. Development and Comparison of an Improved Incremental Conductance Algorithm for Tracking the MPP of a Solar PV Panel. IEEE Trans. Sustain. Energy 2016, 7, 1421–1429. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Atkinson, D.J.; Zahawi, B. Experimental investigation of the incremental conductance maximum power point tracking algorithm at high perturbation rates. IET Renew. Power Gener. 2016, 10, 133–139. [Google Scholar] [CrossRef]
- Worku, M.Y.; Abido, M.A. Real-Time Implementation of Grid-Connected PV System with Decoupled P-Q Controllers. In Proceedings of the 22nd Mediterranean Conference on Control & Automation (MED’14), Palermo, Italy, 16–19 June 2014. [Google Scholar]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Self-Adaptive Incremental Conductance Algorithm for Swift and Ripple-Free Maximum Power Harvesting from PV Array. IEEE Trans. Ind. Inform. 2018, 14, 2031–2041. [Google Scholar] [CrossRef]
- Kandemir, E.; Cetin, N.S.; Borekci, S.A. A comprehensive overview of maximum power extraction methods for PV systems. Renew. Sustain. Energy Rev. 2017, 78, 93–112. [Google Scholar] [CrossRef]
- Jately, V.; Azzopardi, B.; Joshi, J.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Verma, D.; Nema, S.; Shandilya, A.M.; Dash, S.K. Maximum power point tracking (MPPT) techniques: Recapitulation in solar photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Twaha, S.; Ishaque, K.; Al-Turki, Y.A. A review on maximum power point tracking for photovoltaic systems with and without shading conditions. Renew. Sustain. Energy Rev. 2017, 67, 144–159. [Google Scholar] [CrossRef]
- Farayola, A.M.; Hasan, A.N.; Ali, A. Curve Fitting Polynomial Technique Compared to ANFIS Technique for Maximum Power Point Tracking. In Proceedings of the 2017 8th International Renewable Energy Congress (IREC), Amman, Jordan, 21–23 March 2017; pp. 1–6. [Google Scholar]
- Lasheen, M.; Rahman, A.K.A.; Abdel-Salam, M.; Ookawara, S. Performance Enhancement of Constant Voltage Based MPPT for Photovoltaic Applications Using Genetic Algorithm. Energy Procedia 2016, 100, 217–222. [Google Scholar] [CrossRef]
- Leedy, A.W.; Guo, L.P.; Aganah, K.A. A constant voltage MPPT method for a solar powered boost converter with DC motor load. In Proceedings of the 2012 IEEE Southeastcon, Orlando, FL, USA, 15–18 March 2012; pp. 1–6. [Google Scholar]
- Kimball, J.W.; Krein, P.T. Digital ripple correlation control for photovoltaic applications. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007. [Google Scholar]
- Li, G.; Jin, Y.; Akram, M.W.; Chen, X.; Ji, J.I. Application of bio-inspired algorithms in maximum power point tracking for PV systems under partial shading conditions—A review. Renew. Sustain. Energy Rev. 2018, 81, 840–873. [Google Scholar] [CrossRef]
- Balamurugan, M.; Sahoo, S.K.; Sukchai, S. Application of soft computing methods for grid connected PV system: A technological and status review. Renew. Sustain. Energy Rev. 2017, 75, 1493–1508. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2015, 7, 181–188. [Google Scholar] [CrossRef]
- Shams, I.; Mekhilef, S.; Tey, K.S. Improved Social Ski Driver-Based MPPT for Partial Shading Conditions Hybridized with Constant Voltage Method for Fast Response to Load Variations. IEEE Trans. Sustain. Energy 2021, 12, 2255–2267. [Google Scholar] [CrossRef]
- Li, X.; Wen, H.; Hu, Y.; Jiang, L. A novel beta parameter based fuzzy-logic controller for photovoltaic MPPT application. Renew. Energy 2019, 130, 416–427. [Google Scholar] [CrossRef]
- Tang, S.; Sun, Y.; Chen, Y.; Zhao, Y.; Yang, Y.; Szeto, W. An Enhanced MPPT Method Combining Fractional-Order and Fuzzy Logic Control. IEEE J. Photovolt. 2017, 7, 640–650. [Google Scholar] [CrossRef]
- Craciunescu, D.; Fara, L. Investigation of the Partial Shading Effect of Photovoltaic Panels and Optimization of Their Performance Based on High-Efficiency FLC Algorithm. Energies 2023, 16, 1169. [Google Scholar] [CrossRef]
- Aly, M.; Rezk, H. An improved fuzzy logic control-based MPPT method to enhance the performance of PEM fuel cell system. Neural Comput. Appl. 2022, 34, 4555–4566. [Google Scholar] [CrossRef]
- Ram, J.P.; Babu, T.S.; Rajasekar, N. A comprehensive review on solar PV maximum power point tracking techniques. Renew. Sustain. Energy Rev. 2017, 67, 826–847. [Google Scholar] [CrossRef]
- Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial neural network-based photovoltaic maximum power point tracking techniques: A survey. IET Renew. Power Gener. 2015, 9, 1043–1063. [Google Scholar] [CrossRef]
- Srinivasan, S.; Tiwari, R.; Krishnamoorthy, M.; Lalitha, M.P.; Raj, K.K. Neural network based MPPT control with reconfigured quadratic boost converter for fuel cell application. Int. J. Hydrogen Energy 2020, 46, 6709–6719. [Google Scholar] [CrossRef]
- Messalti, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Zhanga, R.; Ong, S.K.; Nee, A.Y.C. A simulation-based genetic algorithm approach for re manufacturing process planning and scheduling. Appl. Soft Comput. 2015, 37, 521–532. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Wang, S. A novel case adaptation method based on an improved integrated genetic algorithm for power grid wind disaster emergencies. Expert Syst. Appl. 2015, 42, 7812–7824. [Google Scholar] [CrossRef]
- Dou, R.; Zong, C.; Nan, G. Multi-stage interactive genetic algorithm for collaborative product customization. Knowl. Based Syst. 2016, 92, 43–54. [Google Scholar] [CrossRef]
- Daraban, S.; Petreus, D.; Morel, C. Anovel MPPT algorithm based on a modified genetic algorithm specialized on tracking the global maximum power point in photovoltaic systems affected by partial shading. Energy 2014, 74, 374–388. [Google Scholar] [CrossRef]
- Koad, R.B.; Zobaa, A.F.; El-Shahat, A. A Novel MPPT Algorithm Based on Particle Swarm Optimization for Photovoltaic Systems. IEEE Trans. Sustain. Energy 2016, 8, 468–476. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Palani, S. Application of a combined particle swarm optimization and perturb and observe method for MPPT in PV systems under partial shading conditions. Renew. Energy 2015, 75, 308–317. [Google Scholar] [CrossRef]
- Luta, D.N.; Raji, A.K. Fuzzy Rule-Based and Particle Swarm Optimisation MPPT Techniques for a Fuel Cell Stack. Energies 2019, 12, 936. [Google Scholar] [CrossRef]
- Li, H.; Yang, D.; Su, W.; Lü, J.; Yu, X. An Overall Distribution Particle Swarm Optimization MPPT Algorithm for Photovoltaic System Under Partial Shading. IEEE Trans. Ind. Electron. 2018, 66, 265–275. [Google Scholar] [CrossRef]
- Chen, M.; Ma, S.; Wu, J.; Huang, L. Analysis of MPPT Failure and Development of an Augmented Nonlinear Controller fo MPPT of Photovoltaic Systems under Partial Shading Conditions. Appl. Sci. 2017, 7, 95. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, Y.; Liu, Q.; Wu, J. Maximum power point tracking (MPPT) control of a photovoltaic system based on dual carrier chaotic search. J. Control Theory Appl. 2012, 10, 244–250. [Google Scholar] [CrossRef]
- Ramli Makbul, A.M.; Kashif, I.; Faizan, J.; Al-Turki Yusuf, A.; Zainal, S. A modified differential evolution based maximum power point tracker for photovoltaic system under partial shading condition. Energy Build. 2015, 103, 175–184. [Google Scholar] [CrossRef]
- Naim, T.M.F.; Md, A.S.; Zainal, S.; Sazli, S.M. Evolutionary based maximum power point tracking technique using differential evolution algorithm. Energy Build. 2013, 67, 245–252. [Google Scholar]
- Ramasamy, S.; Dash, S.S.; Selvan, T. An Intelligent Differential Evolution Based Maximum Power Point Tracking (MPPT) Technique for Partially Shaded Photo Voltaic (PV) Array. Int. J. Adv. Soft Comput. Its Appl. 2014, 6, 1–16. [Google Scholar]
- Azam, M.A.; Abdullah-Al-Nahid, S.; Kabir, M.A.; Chowdhury, S.M.H. Microcontroller based maximum power tracking of PV using stimulated annealing algorithm. In Proceedings of the International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 18–19 May 2012; pp. 298–303. [Google Scholar]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 2017, 9512741. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Rezk, H. Optimal Sizing and Placement of Capacitors in Radial Distribution Systems Based on Grey Wolf, Dragonfly and Moth–Flame Optimization Algorithms. Iran. J. Sci. Technol. Trans. Electr. Eng. 2018, 43, 77–96. [Google Scholar] [CrossRef]
- Cherukuri, S.K.; Rayapudi, S.R. Enhanced Grey Wolf Optimizer based MPPT Algorithm of PV system under Partial Shaded Condition. Int. J. Renew. Energy Dev. 2017, 6, 203–212. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A.; Abdelaziz, A.Y. A comparison of different global MPPT techniques based on meta-heuristic algorithms for photovoltaic system subjected to partial shading conditions. Renew. Sustain. Energy Rev. 2017, 74, 377–386. [Google Scholar] [CrossRef]
- Jubaer, A.; Zainal, S. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar]
- Alshareef, M.J. An Effective Falcon Optimization Algorithm Based MPPT Under Partial Shaded Photovoltaic Systems. IEEE Access 2022, 10, 131345–131360. [Google Scholar] [CrossRef]
- Abousoufyane, B.; Aissa, C.; Kamel, K.; Santiago, S.; Ait, S.O. Artificial bee colony based algorithm for maximum power point tracking (MPPT) for PV systems operating under partial shaded conditions. Appl. Soft Comput. 2015, 32, 38–48. [Google Scholar]
- González-Castaño, C.; Restrepo, C.; Kouro, S.; Rodriguez, J. MPPT Algorithm Based on Artificial Bee Colony for PV System. IEEE Access 2021, 9, 43121–43133. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. A review of global maximum power point tracking techniques of photovoltaic system under partial shading conditions. Renew. Sustain. Energy Rev. 2018, 92, 513–553. [Google Scholar] [CrossRef]
- Titri, S.; Larbes, C.; Toumi, K.Y.; Benatchba, K. A new MPPT controller based on the Ant colony optimization algorithm for Photovoltaic systems under partial shading conditions. Appl. Soft Comput. 2017, 58, 465–479. [Google Scholar] [CrossRef]
- Besheer, A.H. Ant Colony System Based PI Maximum Power Point Tracking for Stand Alone Photovoltaic System. In Proceedings of the IEEE International Conference on Industrial Technology, ICIT-2012, Athens, Greece, 19–21 March 2012. [Google Scholar]
- Priyadarshi, N.; Ramachandaramurthy, V.K.; Padmanaban, S.; Azam, F. An Ant Colony Optimized MPPT for Standalone Hybrid PV-Wind Power System with Single Cuk Converter. Energies 2019, 12, 167. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Peddapati, S.; Palani, S. MPPT of PV Systems Under Partial Shaded Conditions through a Colony of Flashing Fireflies. IEEE Trans. Energy Convers. 2014, 29, 463–472. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Peddapati, S.; Palani, S. Application of random search method for maximum power point tracking in partially shaded photovoltaic systems. IET Renew. Power Gener. 2014, 8, 670–678. [Google Scholar] [CrossRef]
- Shi, J.Y.; Ling, L.T.; Xue, F.; Qin, Z.J.; Li, Y.J.; Lai, Z.X.; Yang, T. Combining incremental conductance and firefly algorithm for tracking the global MPP of PV arrays. J. Renew. Sustain. Energy 2017, 9, 023501. [Google Scholar] [CrossRef]
- El-Helw, H.M.; Magdy, A.; Marei, M.I. A Hybrid Maximum Power Point Tracking Technique for Partially Shaded Photovoltaic Arrays. IEEE Access 2017, 5, 11900–11908. [Google Scholar] [CrossRef]
- Chakkarapani, M.; Raman, G.P.; Raman, G.R.; Ganesan, S.I.; Chilakapati, N. Fireworks Enriched P&O Algorithm for GMPPT and Detection of Partial Shading in PV Systems. IEEE Trans. Power Electron. 2017, 32, 4432–4443. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A Grey Wolf-Assisted Perturb & Observe MPPT Algorithm for a Photovoltaic Power System. IEEE Trans. Energy Convers. 2017, 32, 340–347. [Google Scholar] [CrossRef]
- Abdelghani, H.; Sabir, M. Variable step size modified P&OMPPT algorithm using GA-based hybrid offline/online PID controller. Renew. Sustain. Energy Rev. 2015, 491, 1247–1260. [Google Scholar]
- Karagoz, M.K.; Demirel, H. A novel MPPT method for PV arrays based on modified Bat algorithm with partial shading capability. Int. J. Comput. Sci. Netw. Secur. 2017, 17, 61–66. [Google Scholar]
- Hanafiah, S.; Ayad, A.; Hehn, A.; Kennel, R. A hybrid MPPT for quasi-Z-source inverters in PV applications under partial shading condition. In Proceedings of the 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering, Cadiz, Spain, 4–6 April 2017. [Google Scholar]
- Yang, Z.; Duan, Q.; Zhong, J.; Mao, M.; Xun, Z. Analysis of improved PSO and perturb & observe global MPPT algorithm for PV array under partial shading condition. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar]
- Guan, T.; Zhuo, F. An improved SA-PSO global maximum power point tracking method of photovoltaic system under partial shading conditions. In Proceedings of the IEEE Conference on Environment and Electrical Engineering, Milan, Italy, 6–9 June 2017. [Google Scholar]
- Duan, Q.; Mao, M.; Duan, P.; Hu, B. An intelligent algorithm for maximum power point tracking in photovoltaic system under partial shading conditions. Trans. Inst. Meas. Control. 2016, 39, 244–256. [Google Scholar] [CrossRef]
- Mao, M.; Duan, Q.; Duan, P.; Hu, B. Comprehensive improvement of artificial fish swarm algorithm for global MPPT in PV system under partial shading conditions. Trans. Inst. Meas. Control. 2017, 40, 2178–2199. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Rapid MPPT for Uniformly and Partial Shaded PV System by Using JayaDE Algorithm in Highly Fluctuating Atmospheric Conditions. IEEE Trans. Ind. Inform. 2017, 13, 2406–2416. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. MPPT in Dynamic Condition of Partially Shaded PV System by Using WODE Technique. IEEE Trans. Sustain. Energy 2017, 8, 1204–1214. [Google Scholar] [CrossRef]
- Rajasekar, N.; Neeraja, K.K.; Venugopalan, R. Bacterial Foraging Algorithm based solar PV parameter estimation. Sol. Energy 2013, 97, 255–265. [Google Scholar] [CrossRef]
- Worku, M.Y.; Abido, M.A. Grid Connected PV System Using ANFIS Based MPPT Controller in Real Time. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’16), Madrid, Spain, 4–6 May 2016. [Google Scholar]
- Alam, D.F.; Yousri, D.A.; Eteiba, M.B. Flower Pollination Algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Gao, L.; Dougal, R.A.; Liu, S.; Iotova, A.P. Parallel-Connected Solar PV System to Address Partial and Rapidly Fluctuating Shadow Conditions. IEEE Trans. Ind. Electron. 2009, 56, 1548–1556. [Google Scholar] [CrossRef]
- Abido, M.A.; Sheraz, M.; Worku, M.Y. An Efficient ANFIS-Based PI Controller for Maximum Power Point Tracking of PV Systems. Arab. J. Sci. Eng. 2015, 40, 2641–2651. [Google Scholar] [CrossRef]
- Kamarzaman, N.A.; WeiTan, C. A comprehensive review of maximum power point tracking algorithms for photovoltaic systems. Renew. Sustain. Energy Rev. 2014, 37, 585–598. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Syafaruddin Tahei, H. Modeling and simulation of pho- tovoltaic (PV) system during partial shading based on a two-diode model. Simul. Model Pract. Theory 2011, 19, 1613–1626. [Google Scholar] [CrossRef]
- Kadri, R.; Andrei, H.; Gaubert, J.P.; Ivanovici, T.; Champenois, G.; Andrei, P. Modeling of the photovoltaic cell circuit parameters for optimum connection model and real-time emulator with partial shadow conditions. Energy 2012, 42, 57–67. [Google Scholar] [CrossRef]
- Sánchez Reinoso, C.R.; Milone, D.H.; Buitrago, R.H. Simulation of photovoltaic centrals with dynamic shading. Appl. Energy 2013, 103, 278–289. [Google Scholar] [CrossRef]
- Rajalakshmi, M.; Chandramohan, S.; Kannadasan, R.; Alsharif, M.H.; Kim, M.-K.; Nebhen, J. Design and Validation of BAT Algorithm-Based Photovoltaic System Using Simplified High Gain Quasi Boost Inverter. Energies 2021, 14, 1086. [Google Scholar] [CrossRef]
- Alturki, F.A.; Al-Shamma’a, A.; Farh, H.M.H. Simulations and dSPACE Real-Time Implementation of Photovoltaic Global Maximum Power Extraction under Partial Shading. Sustainability 2020, 12, 3652. [Google Scholar] [CrossRef]
- Ali, A.; Almutairi, K.; Padmanaban, S.; Tirth, V.; Algarni, S.; Irshad, K.; Islam, S.; Zahir, M.H.; Shafiullah, M.; Malik, M.Z. Investigation of MPPT Techniques Under Uniform and Non-Uniform Solar Irradiation Condition–A Retrospection. IEEE Access 2020, 8, 127368–127392. [Google Scholar] [CrossRef]
- Almutairi, A.; Abo-Khalil, A.; Sayed, K.; Albagami, N. MPPT for a PV Grid-Connected System to Improve Efficiency under Partial Shading Conditions. Sustainability 2020, 12, 10310. [Google Scholar] [CrossRef]
- Islam, H.; Mekhilef, S.; Shah, N.; Soon, T.; Wahyudie, A.; Ahmed, M. IImproved Proportional-Integral Coordinated MPPT Controller with Fast Tracking Speed for Grid-Tied PV Systems under Partially Shaded Conditions. Sustainability 2021, 13, 830. [Google Scholar] [CrossRef]
- Pandiyan, P.; Saravanan, S.; Prabaharan, N.; Tiwari, R.; Chinnadurai, T.; Babu, N.; Hossain, E. Implementation of Different MPPT Techniques in Solar PV Tree under Partial Shading Conditions. Sustainability 2021, 13, 7208. [Google Scholar] [CrossRef]
- Patel, H.; Agarwal, V. Maximum power point tracking scheme for PV systemsoperating under partially shaded conditions, industrial electronics. IEEE Trans. 2008, 55, 1689–1698. [Google Scholar]
- Carannante, G.; Fraddanno, C.; Pagano, M.; Piegari, L. Experimental performanceof MPPT algorithm for photovoltaic sources subject to in homogeneous insolation. IEEE Trans. Ind. Electron. 2009, 56, 7. [Google Scholar] [CrossRef]
- Koutroulis, E.; Blaabjerg, F. A New Technique for Tracking the Global Maximum Power Point of PV Arrays Operating Under Partial-Shading Conditions. IEEE J. Photovoltaics 2012, 2, 184–190. [Google Scholar] [CrossRef]
- Kobayashi, K.; Takano, I.; Sawada, Y. A study of a two stage maximum power point tracking control of a photovoltaic system under partially shaded insolation conditions. Sol. Energy Mater. Sol. Cells 2006, 90, 2975–2988. [Google Scholar] [CrossRef]
- Young-Hyok, J.; Doo-Yong, J.; Jun-Gu, K.; Jae-Hyung, K.; Tae-Won, L.; Chung-Yuen, W. A Real maximum power point tracking method for mismatching compensation in PV array under partially shaded conditions, power electronics. IEEE Trans. 2011, 26, 1001–1009. [Google Scholar]
- Lie, M.; Yaojie, S.; Yandan, L.; Zhifeng, B.; Liqin, T.; Jieqiong, S. A high performance MPPT control method. In Proceedings of the 2011 International Conference on Materials for Renewable Energy & Environment (ICMREE), Shanghai, China, 20–22 May 2011; pp. 195–199. [Google Scholar]
- Dhople, S.V.; Ehlmann, J.L.; Davoudi, A.; Chapman, P.L. Multiple-input boost converter to minimize power losses due to partial shading in photovoltaic modules. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 2633–2636. [Google Scholar]
- Kiran, S.R.; Basha, C.H.H.; Singh, V.P.; Dhanamjayulu, C.; Prusty, B.R.; Khan, B. Reduced Simulative Performance Analysis of Variable Step Size ANN Based MPPT Techniques for Partially Shaded Solar PV Systems. IEEE Access 2022, 10, 48875–48889. [Google Scholar] [CrossRef]
- Roy, R.B.; Rokonuzzaman, M.; Amin, N.; Mishu, M.K.; Alahakoon, S.; Rahman, S.; Mithulananthan, N.; Rahman, K.S.; Shakeri, M.; Pasupuleti, J. A Comparative Performance Analysis of ANN Algorithms for MPPT Energy Harvesting in Solar PV System. IEEE Access 2021, 9, 102137–102152. [Google Scholar] [CrossRef]
- Allahabadi, S.; Iman-Eini, H.; Farhangi, S. Fast Artificial Neural Network Based Method for Estimation of the Global Maximum Power Point in Photovoltaic Systems. IEEE Trans. Ind. Electron. 2022, 69, 5879–5888. [Google Scholar] [CrossRef]
- Sheraz, M.; Abido, M.A. An Efficient MPPT Controller Using Differential Evolution and Neural Network. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 378–383. [Google Scholar]
- Padmanaban, S.; Dhanamjayulu, C.; Khan, B. Artificial Neural Network and Newton Raphson (ANN-NR) Algorithm Based Selective Harmonic Elimination in Cascaded Multilevel Inverter for PV Applications. IEEE Access 2021, 9, 75058–75070. [Google Scholar] [CrossRef]
- Alabedin, A.M.; El-Saadany, E.F.; Salama, M.M. Maximum power point tracking for Photovoltaic systems using fuzzy logic and artificial neural networks. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–18 July 2011; pp. 1–9. [Google Scholar]
- Jinbang, X.; Anwen, S.; Cheng, Y.; Wenpei, R.; Xuan, Y. ANN based on IncCond algorithm for MPP tracker. In Proceedings of the 2011 Sixth International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA), Penang, Malaysia, 27–29 September 2011; pp. 129–134. [Google Scholar]
- Islam, M.A.; Kabir, M.A. Neural network based maximum power point tracking of photovoltaic arrays. In Proceedings of the TENCON 2011–2011 IEEE Region 10 Conference, Bali, Indonesia, 21–24 November 2011; pp. 79–82. [Google Scholar]
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar] [CrossRef]
- Bendib, B.; Belmili, H.; Krim, F. A survey of the most used MPPT methods: Conventional and advanced algorithms applied for photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 45, 637–648. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An Efficient Fuzzy-Logic Based Variable-Step Incremental Conductance MPPT Method for Grid-Connected PV Systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
- Miyatake, M.; Veerachary, M. Maximum Power Point Tracking of Multiple Photovoltaic Arrays: A PSO Approach. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 367–380. [Google Scholar] [CrossRef]
- Ibrahim, A.W.; Shafik, M.B.; Ding, M.; Sarhan, M.A.; Fang, Z.; Alareqi, A.G.; Almoqri, T.; Al-Rassas, A.M. PV maximum power-point tracking using modified particle swarm optimization under partial shading conditions. Chin. J. Electr. Eng. 2020, 6, 106–121. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Huang, S.-C.; Huang, J.-W.; Liang, W.-C. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating Under Partially Shaded Conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- Ballaji, A.; Dash, R.; Subburaj, V.; Kalvakurthi, J.R.; Swain, D.; Swain, S.C. Design & Development of MPPT Using PSO with Predefined Search Space Based on Fuzzy Fokker Planck Solution. IEEE Access 2022, 10, 80764–80783. [Google Scholar]
- Kashif, I.; Zainal, S. An improved Particle Swarm Optimization (PSO)–based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electron. 2013, 27, 3627–3638. [Google Scholar]
- Millah, I.S.; Chang, P.C.; Teshome, D.F.; Subroto, R.K.; Lian, K.L.; Lin, J.-F. An Enhanced Grey Wolf Optimization Algorithm for Photovoltaic Maximum Power Point Tracking Control under Partial Shading Conditions. IEEE Open J. Ind. Electron. Soc. 2022, 3, 392–408. [Google Scholar] [CrossRef]
- Rajkumar, M.V.; Mahakumar, M.; Manojkumar, M.; Hemaraj, M.; Kumaravel, E. A New DC-DC Converter topology with grey wolf MPPT algorithm for photovoltaic system. Int. J. Emerg. Technol. Eng. Res. 2017, 5, 54–59. [Google Scholar]
- Rezaei, H.; Bozorg-Haddad, O.; Chu, X. Grey Wolf Optimization (GWO) Algorithm. In Advanced Optimization by Nature-Inspired Algorithms; Springer: Berlin/Heidelberg, Germany, 2018; pp. 81–91. [Google Scholar]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. A Grey Wolf Optimizer for Optimum Parameters of Multiple PI Controllers of a Grid-Connected PMSG Driven by Variable Speed Wind Turbine. IEEE Access 2018, 6, 44120–44128. [Google Scholar] [CrossRef]
- Guo, K.; Cui, L.; Mao, M.; Zhou, L.; Zhang, Q. An Improved Gray Wolf Optimizer MPPT Algorithm for PV System with BFBIC Converter Under Partial Shading. IEEE Access 2020, 8, 103476–103490. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.P.; Rosas-Caro, J.C.; Valderrabano-Gonzalez, A.; Panda, G. Comprehensive Review of Conventional and Emerging Maximum Power Point Tracking Algorithms for Uniformly and Partially Shaded Solar Photovoltaic Systems. IEEE Access 2023, 11, 31778–31812. [Google Scholar] [CrossRef]
- OmPrakash, V.; Deepti, A.; Tejna, P. Opposition and dimensional based modified firefly algorithm. Exp. Syst. Appl. 2016, 44, 168–176. [Google Scholar]
- Huang, Y.P.; Huang, M.Y.; Ye, C.E. A Fusion Firefly Algorithm with Simplified Propagation for Photovoltaic MPPT Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2020, 11, 2641–2652. [Google Scholar] [CrossRef]
- Safarudin, Y.M.; Priyadi, A.; Purnomo, M.H.; Pujiantara, M. Maximum power point tracking algsorithm for photovoltaic system under partial shaded condition by means updating β firefly technique. In Proceedings of the 6th International Conference on Information Technology and Electrical Engineering (ICITEE 2014), Yogyakarta, Indonesia, 7–8 October 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Yun-Chia, L.; Smith, A.E. An Ant Colony Optimization Algorithm for the Redundancy Allocation Problem (RAP). IEEE Trans. Reliab. 2004, 53, 417–423. [Google Scholar]
- Lian, L.; Maskell, D.L.; Patra, J.C. A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A Comprehensive Review of Maximum Power Point Tracking (MPPT) Techniques Used in Solar PV Systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Vigneshkumar, V.; Sankar, P.; Simon, S.P.; Nayak, P.S.R.; Palani, S. Development of an Improved P&O Algorithm Assisted through a Colony of Foraging Ants for MPPT in PV System. IEEE Trans. Ind. Inform. 2016, 12, 187–200. [Google Scholar]
- Ghasemi, M.A.; Foroushani, H.M.; Parniani, M. Partial Shading Detection and Smooth Maximum Power Point Tracking of PV Arrays under PSC. IEEE Trans. Power Electron. 2016, 31, 6281–6292. [Google Scholar] [CrossRef]
- Ramin, R. Cuckoo Optimization Algorithm. Appl. Soft Comput. 2011, 11, 5508–5518. [Google Scholar]
- Liu, L.; Meng, X.; Liu, C. A review of maximum power point tracking methods of PV power system at uniform and partial shading. Renew. Sustain. Energy Rev. 2016, 53, 1500–1507. [Google Scholar] [CrossRef]
- Nugraha, D.A.; Lian, K.L.; Suwarno. A Novel MPPT Method Based on Cuckoo Search Algorithm and Golden Section Search Algorithm for Partially Shaded PV System. Can. J. Electr. Comput. Eng. 2019, 42, 173–182. [Google Scholar] [CrossRef]
- Rao, R.V.; Saroj, A. A self-adaptive multi-population based Jaya algorithm for engineering optimization. Swarm Evol. Comput. 2017, 37, 1–26. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N.I. Optimal Power Flow Using the Jaya Algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef]
- Bhukya, L.; Annamraju, A.; Nandiraju, S. A novel maximum power point tracking technique based on Rao-1 algorithm for solar PV system under partial shading conditions. Int. Trans. Electr. Energy Syst. 2021, 31, e13028. [Google Scholar] [CrossRef]
- Bhukya, L.; Kedika, N.R.; Salkuti, S.R. Enhanced Maximum Power Point Techniques for Solar Photovoltaic System under Uniform Insolation and Partial Shading Conditions: A Review. Algorithms 2022, 15, 365. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Lian, K.L.; Jhang, J.H.; Tian, I.S. A Maximum Power Point Tracking Method Based on Perturb-and-Observe Combined with Particle Swarm Optimization. IEEE J. Photovolt. 2014, 4, 626–633. [Google Scholar] [CrossRef]
- Manickam, C.; Raman, G.R.; Raman, G.P.; Ganesan, S.I.; Nagamani, C. A Hybrid Algorithm for Tracking of GMPP Based on P&O and PSO with Reduced Power Oscillation in String Inverters. IEEE Trans. Ind. Electron. 2016, 63, 6097–6106. [Google Scholar]
- Seyedmahmoudian, M.; Rahmani, R.; Mekhilef, S.; Maung Than, O.A.; Stojcevski, A.; Soon, T.K.; Ghandhari, A.S. Simulation and hardware implementation of new maximum power point tracking technique for partially shaded PV system using hybrid DEPSO method. IEEE Trans. Sustain. Energy 2015, 6, 850–862. [Google Scholar] [CrossRef]
- Lyden, S.; Haque, M.E. Maximum Power Point Tracking techniques for photovoltaic systems: A comprehensive review and comparative analysis. Renew. Sustain. Energy Rev. 2015, 52, 1504–1518. [Google Scholar] [CrossRef]
- Dhople, S.V.; Bell, R.; Ehlmann, J.; Davoudi, A.; Chapman, P.L.; Domínguez-García, A.D. A global maximum power point tracking method for PV module integrated converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 4762–4767. [Google Scholar]
- Elasser, A.; Agamy, M.; Sabate, J.; Steigerwald, R.; Fisher, R.; Harfman-Todorovic, M. A comparative study of central and distributed MPPT architectures for megawatt utility and large scale commercial photovoltaic plants. In Proceedings of the IEEE Industrial Electronics Society Conference (IECON), Glendale, AZ, USA, 7–10 November 2010; pp. 2753–2758. [Google Scholar]
- Poshtkouhi, S.; Palaniappan, V.; Fard, M.; Trescases, O. A General Approach for Quantifying the Benefit of Distributed Power Electronics for Fine Grained MPPT in Photovoltaic Applications Using 3-D Modeling. IEEE Trans. Power Electron. 2012, 27, 4656–4666. [Google Scholar] [CrossRef]
- Shenoy, P.S.; Kim, K.A.; Johnson, B.B.; Krein, P.T. Differential power processing for increased energy production and reliability of photovoltaic systems. IEEE Trans. Power Electron. 2013, 28, 2968–2979. [Google Scholar] [CrossRef]
- Olalla, C.; Deline, C.; Clement, D.; Levron, Y.; Rodriguez, M.; Maksimovic, D. Performance of Power-Limited Differential Power Processing Architectures in Mismatched PV Systems. IEEE Trans. Power Electron. 2015, 30, 618–631. [Google Scholar] [CrossRef]
- Villa, L.F.L.; Tien-Phu, H.; Crebier, J.C.; Raison, B. A Power Electronics Equalizer Application for Partially Shaded Photovoltaic Modules. IEEE Trans. Ind. Electron. 2013, 60, 1179–1190. [Google Scholar] [CrossRef]
- Salam, Z.R.; Amli, M.Z. A simple circuit to improve the power yield of PV array during partial shading. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1622–1626. [Google Scholar]
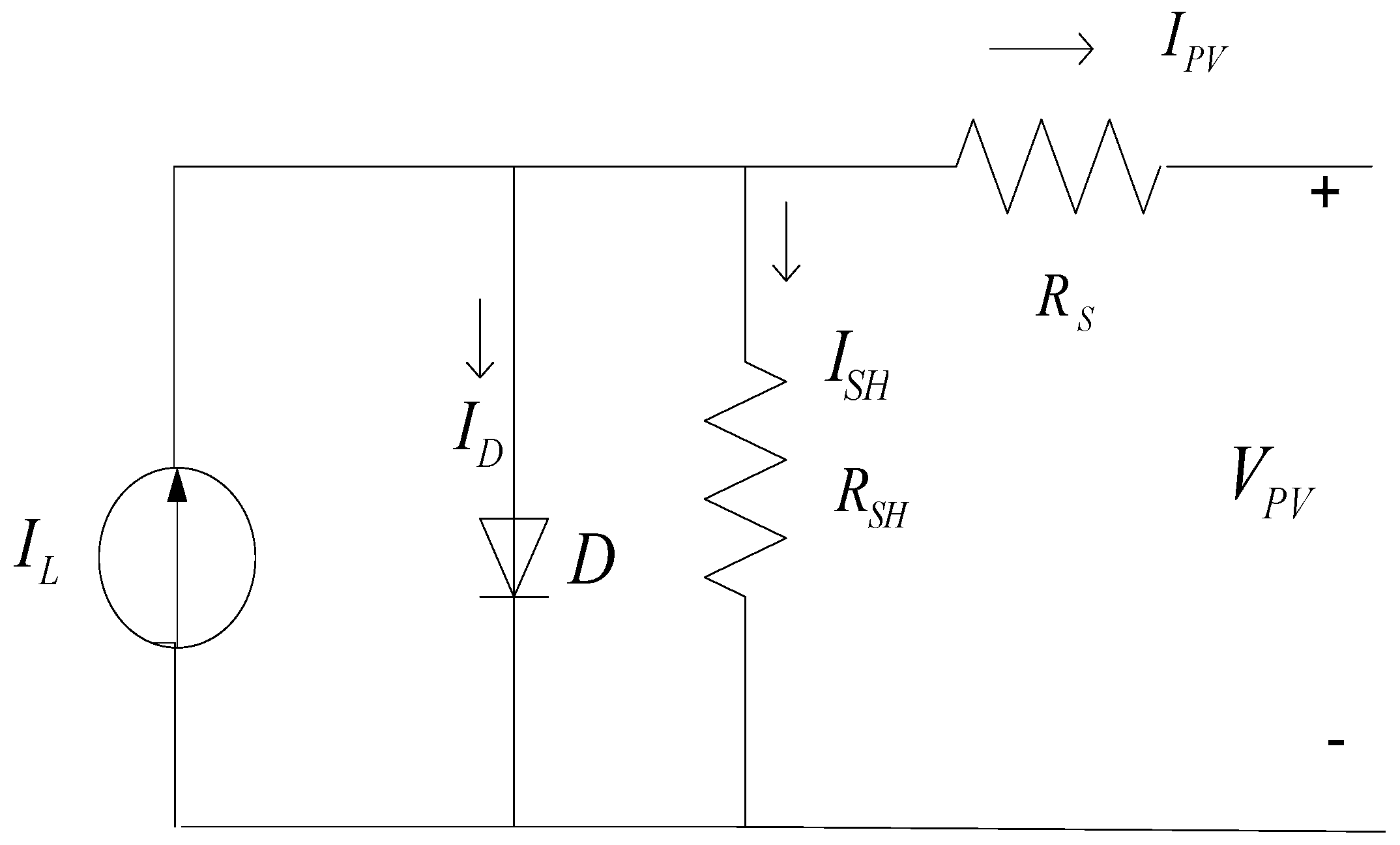




| Method | Complexity | Tracking Speed (s) | Efficiency (%) | Converter | Application |
|---|---|---|---|---|---|
| ANN | High | - | - | Boost | Island mode |
| FLC | High | 0.3 | - | Boost | Island mode |
| PSO | Medium | 1.5 | - | Buck-boost | Island mode |
| ABC | Low | 0.2 | - | Boost | Island mode |
| ACO | Low | 1.1 | ≈100 | Boost | Island mode |
| Jaya | Low | 1.18 | 99.99 | Boost | Island mode |
| FA | Low to medium | 1.3 | 98.8 | Boost | Island mode |
| GWO | High | - | 99.92 | Boost | Island mode |
| CS | Medium | 0.3 | - | Boost | Island mode |
| DE-PSO | Medium | 0.44 | - | Boost | Island mode |
| PSO-P&O | Medium | 0.9 | - | Boost | Island mode |
| GWO-P&O | Medium | 0.015 | 100 | Boost | Island mode |
| Method | Complexity | Tracking Speed | Steady-State Oscillation | Dependency on System Parameter |
|---|---|---|---|---|
| Bypass diode | High | Slow | No | No |
| Distributed MPPT | Moderate | Variable | Sometimes | No |
| Differential Power Processing | Moderate | Variable | Sometimes | No |
| Power Electronics Equalizer | High | Fast | No | Yes |
| Method | Advantages | Disadvantages |
|---|---|---|
| Conventional Methods | ||
| P&O |
|
|
| IC |
|
|
| HC |
|
|
| Soft Computing Methods | ||
| Fuzzy Logic Control |
|
|
| Artificial Neural Network |
|
|
| Artificial Bee Colony |
|
|
| Particle Swarm Optimization |
|
|
| Cuckoo Search |
|
|
| Ant Colony Optimization |
|
|
| Grey Wolf Optimization |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Worku, M.Y.; Hassan, M.A.; Maraaba, L.S.; Shafiullah, M.; Elkadeem, M.R.; Hossain, M.I.; Abido, M.A. A Comprehensive Review of Recent Maximum Power Point Tracking Techniques for Photovoltaic Systems under Partial Shading. Sustainability 2023, 15, 11132. https://doi.org/10.3390/su151411132
Worku MY, Hassan MA, Maraaba LS, Shafiullah M, Elkadeem MR, Hossain MI, Abido MA. A Comprehensive Review of Recent Maximum Power Point Tracking Techniques for Photovoltaic Systems under Partial Shading. Sustainability. 2023; 15(14):11132. https://doi.org/10.3390/su151411132
Chicago/Turabian StyleWorku, Muhammed Y., Mohamed A. Hassan, Luqman S. Maraaba, Md Shafiullah, Mohamed R. Elkadeem, Md Ismail Hossain, and Mohamed A. Abido. 2023. "A Comprehensive Review of Recent Maximum Power Point Tracking Techniques for Photovoltaic Systems under Partial Shading" Sustainability 15, no. 14: 11132. https://doi.org/10.3390/su151411132
APA StyleWorku, M. Y., Hassan, M. A., Maraaba, L. S., Shafiullah, M., Elkadeem, M. R., Hossain, M. I., & Abido, M. A. (2023). A Comprehensive Review of Recent Maximum Power Point Tracking Techniques for Photovoltaic Systems under Partial Shading. Sustainability, 15(14), 11132. https://doi.org/10.3390/su151411132










