Thermal Bridges Monitoring and Energy Optimization of Rural Residences in China’s Cold Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Project Overview
2.1.1. Site Selection and Layout
2.1.2. Materials of Walls
2.1.3. Construction Methods
2.2. Methods for Environmental Analysis
2.3. On-Site Methods for Identifying Thermal Bridges in Building Envelope Structures
2.4. Numerical Simulation Methods for Evaluating the Thermal Performance of Building Envelope Structures
2.5. Building Energy Analysis and Energy-Saving Optimization
2.5.1. Comprehensive Calculation of Building Energy Consumption
2.5.2. Single-Parameter Analysis of Building Energy Consumption
2.5.3. Analysis of Building Energy Consumption Sensitivity and Optimization of Energy-Saving Measures
- A coefficient close to +1 indicates a strong positive correlation, suggesting that the two variables change in the same direction, either increasing or decreasing simultaneously;
- A coefficient close to 0 signifies no correlation, indicating that there is no apparent relationship between the two variables;
- A coefficient close to −1 signifies a strong negative correlation, indicating that when one variable increases, the other variable decreases.
3. Results
3.1. Climate and Environmental Characteristics
3.2. Thermal Bridge Identification in Buildings
3.3. Analysis and Optimization of Building Thermal Bridges
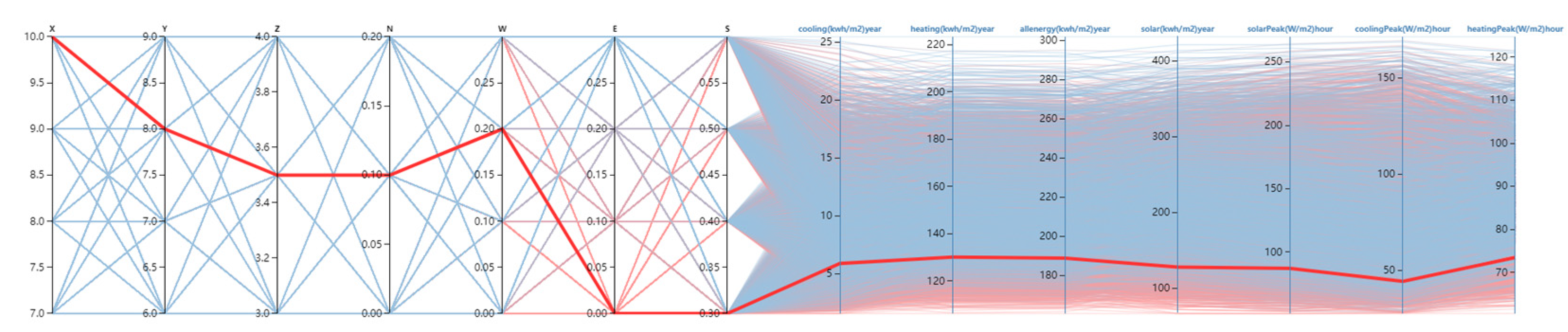
3.4. Single-Parameter Analysis of Building Energy Consumption
3.5. Sensitivity Analysis of Building Energy Consumption and Optimization for Energy Savings
4. Discussion
- This article offers a comprehensive analysis of the climatic conditions in the Nenjiang region and provides pertinent suggestions for integrating local climatic characteristics into architectural design. The proposed strategies, including harnessing winter solar radiation and leveraging summer natural ventilation, possess broad applicability.
- This article presents structural enhancements to the thermal bridging areas of large-scale insulated block buildings, resulting in a significant improvement in insulation performance and a reduction in thermal bridging effects. Furthermore, the refined construction methods have effectively increased construction efficiency. In practical applications, the proposed enhancements were implemented by the authors, and the primary structural elements were constructed using demountable formwork, achieving a remarkable completion time of just one day with a 100% formwork utilization rate. Additionally, the load-bearing capacity of the beams was enhanced by 3–6 times. The construction of the enclosure structure was efficiently accomplished in a mere three days, significantly expediting the overall construction process.
- Furthermore, there is still room for further improvement in this type of insulated block. In practical applications, the authors have replaced the EPS (expanded polystyrene) in the blocks with XPS (extruded polystyrene), resulting in a thermal resistance of 10 m2·K/W. Considering actual energy usage conditions (equipment not running all day), simulated calculations indicate a comprehensive energy consumption value of 43.8 kWh/m2·a, which is 73.45% lower than the ideal load value mentioned in this article (assuming equipment runs all day). This design achieves a 32.62% energy savings compared to the requirements outlined in the “Heilongjiang Province Ultra-Low Energy Residential Building Energy Efficiency Design Standard” (DB23/T 3337-2022) [18], thus fully meeting the standard’s requirements.
- In comparison to the ultra-low energy consumption residential system utilizing porous bricks and EPS insulation boards [19], the rural housing system proposed in this study exhibits a thermal load of 29.3 kwh/m2·a, representing a 51.32% reduction compared to the thermal load of 60.19 kwh/m2·a, observed in such ultra-low energy consumption rural housing with porous bricks. Moreover, compared to ultra-low energy consumption rural housing equipped with a solar-air source heat pump coupled heating system, the annual cumulative thermal load index achieves a similar level [20]. This demonstrates that in practical applications, houses built with these improved insulated blocks will deliver even better performance and possess significant energy-saving potential.
5. Conclusions
- The cold climate conditions in the Nenjiang region play a crucial role in the absence of comfort during winter, resulting in a 0% comfort time. Conversely, summer offers a relatively higher comfort time, constituting 76.3% of the total annual comfort time. Hence, it is essential to prioritize the utilization of natural ventilation during the design phase, particularly in the summer. While ensuring effective insulation in the enclosure structure for winter, equal attention should be given to maximizing solar radiation heat gain to reduce the building’s energy demand.
- Corresponding solutions have been proposed for three types of thermal bridging in large-scale insulated block residential buildings, leading to a remarkable 54.82% reduction in the overall heat transfer coefficient of the walls compared to the original design. Moreover, the overall heat transfer coefficient at the beam and column locations has been significantly reduced by 97%. These solutions have not only enhanced the construction efficiency of the main structure and enclosure but also yielded significant improvements in thermal performance.
- The impact of building scale on energy consumption load surpasses that of window size. In the case of residential buildings in extremely cold regions, ample solar radiation aids in reducing the building load. Hence, it is recommended to incorporate larger windows on the south side. Conversely, smaller windows with a window-to-wall ratio of approximately 0.1 are advisable on the north side. Windows on the west side are not recommended.
- To improve energy-saving effectiveness in building forms like insulated blocks, which already exhibit good insulation performance, it is essential to use more efficient insulation materials, implement measures to reduce thermal bridges, adopt a more suitable architectural exterior design, and establish a rational energy utilization plan. These collective efforts will contribute to further enhancing energy efficiency on the existing foundation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsinghua University Research Center for Building Energy Efficiency. Annual Development Research Report on Building Energy Efficiency in China; China Architecture & Building Press: Beijing, China, 2022. [Google Scholar]
- Dumitrescu, L.; Baran, I.; Pescaru, R.A. The Influence of Thermal Bridges in the Process of Buildings Thermal Rehabilitation. Procedia Eng. 2017, 181, 682–689. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Rossi, F.D.; Turni, G.; Vanoli, G.P. Different methods for the modelling of thermal bridges into energy simulation programs: Comparisons of accuracy for flat heterogeneous roofs in Italian climates. Appl. Energy 2012, 97, 405–418. [Google Scholar] [CrossRef]
- Baldinelli, G.; Bianchi, F.; Rotili, A.; Costarelli, D.; Seracini, M.; Vinti, G.; Asdrubali, F.; Evangelisti, L. A model for the improvement of thermal bridges quantitative assessment by infrared thermography. Appl. Energy 2018, 211, 854–864. [Google Scholar] [CrossRef]
- Garay, R.; Uriarte, A.; Apraiz, I. Performance assessment of thermal bridge elements into a full scale experimental study of a building façade. Energy Build. 2014, 85, 579–591. [Google Scholar] [CrossRef]
- Zalewski, L.; Lassue, S.; Rousse, D.; Boukhalfa, K. Experimental and numerical characterization of thermal bridges in prefabricated building walls. Energy Convers. Manag. 2010, 51, 2869–2877. [Google Scholar] [CrossRef]
- Santos, P.; Martins, C.; Simoes, D.S.L. Thermal Performance of Lightweight Steel-Framed Construction Systems; Metallurgical Research & Technology|Cambridge Core: Cambridge, UK, 2014; pp. 329–338. [Google Scholar]
- Soares, N.; Santos, P.; Gervasio, H.; Costa, J.J.; Da Silva, L. Energy efficiency and thermal performance of lightweight steel-framed (LSF) construction: A review. Renew. Sustain. Energy Rev. 2017, 78, 194–209. [Google Scholar] [CrossRef]
- Mithraratne, N.; Vale, B. Life cycle analysis model for New Zealand houses. Build. Environ. 2004, 39, 483–492. [Google Scholar] [CrossRef]
- Sartori, I.; Hestnes, A.G. Energy use in the life cycle of conventional and low-energy buildings: A review article. Energy Build. 2007, 39, 249–257. [Google Scholar] [CrossRef]
- Fang, Y.; Cho, S. Design optimization of building geometry and fenestration for daylighting and energy performance. Sol. Energy 2019, 191, 7–18. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, N.; Wang, S. A parametric approach for performance optimization of residential building design in Beijing. Build. Simul. 2020, 13, 223–235. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H.; Lu, L. A comprehensive review on passive design approaches in green building rating tools. Renew. Sustain. Energy Rev. 2015, 50, 1425–1436. [Google Scholar] [CrossRef]
- Verbeeck, G.; Hens, H. Energy savings in retrofitted dwellings: Economically viable? Energy Build. 2005, 37, 747–754. [Google Scholar] [CrossRef]
- Payyanapotta, A.; Thomas, A. An analytical hierarchy based optimization framework to aid sustainable assessment of buildings. J. Build. Eng. 2021, 35, 102003. [Google Scholar] [CrossRef]
- GB50176-2016; Code for Thermal Design of Civil Building. China Building Industry Press: Beijing, China, 2016.
- GB55015-2021; General Specification for Building Energy Efficiency and Renewable Energy Utilization. China Building Industry Press: Beijing, China, 2021.
- DB23/T 3337-2022; Energy-Saving Design Standard for Ultra-Low Energy Consumption Residential Buildings in Heilongjiang Province. Heilongjiang Provincial Department of Housing and Urban-Rural Development Press: Heilongjiang, China, 2022.
- Deng, Q.Q.; Song, B.; Zhang, S.N. Study on Thermal Parameters of Enclosure Structure in Ultra-Low Energy Consumption Rural Housing. Build. Energy Effic. 2022, 50, 46–49. [Google Scholar]
- Li, X.L.; Hao, M. Construction and Operation Research of Multi-Energy Coupled Heating System for Ultra-Low Energy Consumption Rural Housing. Energy Sav. 2023, 42, 22–25. [Google Scholar]
























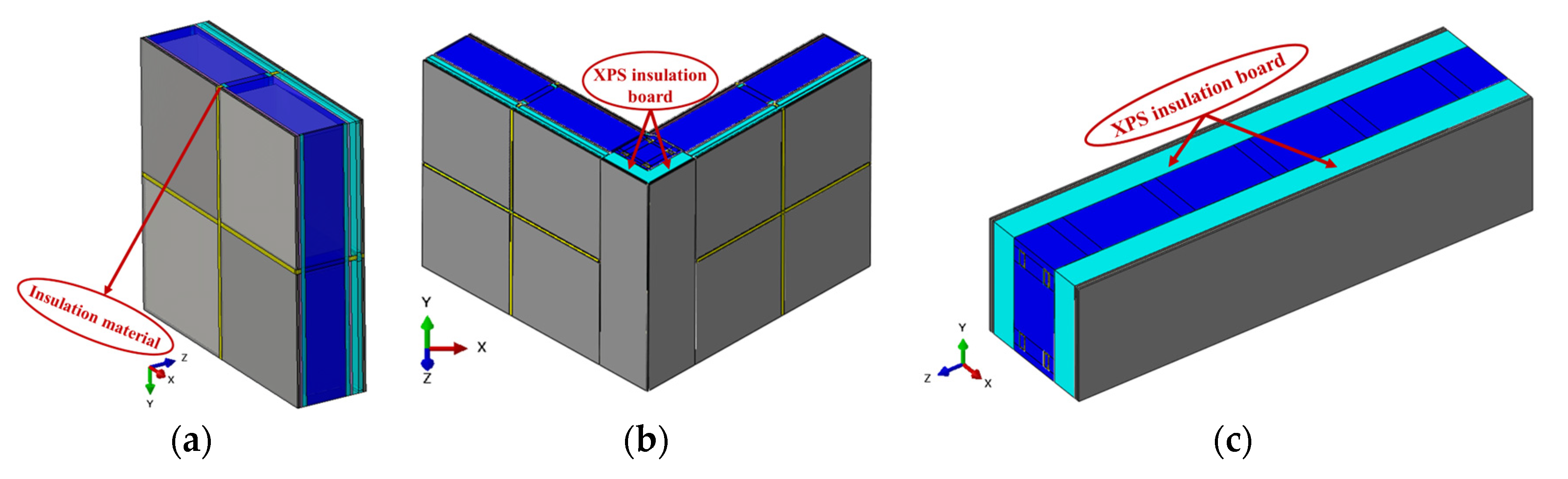






| Name | Density (kg/m3) | Thermal Conductivity (W/m·K) | Specific Heat Capacity (J/Kg·K) | Heat Storage Coefficient W/(m2·K) |
|---|---|---|---|---|
| XPS | 30 | 0.03 | 4455 | 0.54 |
| EPS | 20 | 0.04 | 1380 | 0.29 |
| Thermal insulation mortar | 800 | 0.29 | 1050 | 4.44 |
| Phenolic foam adhesive | 350 | 0.07 | 1380 | 1.57 |
| Cement mortar | 1800 | 0.93 | 1050 | 11.37 |
| C20 | 2300 | 1.51 | 920 | 15.24 |
| C30 | 2420 | 1.62 | 970 | 15 |
| Parameter Name | Range of Parameter Values |
|---|---|
| Building Orientation | 0~3.1 rad |
| Window-to-Wall Ratio | 0~0.9 |
| Building Depth | 6~20 m |
| Building Span | |
| Building Height | 2.8~4.4 m |
| Name | X/m | Y/m | Z/m | N | W | S | E |
|---|---|---|---|---|---|---|---|
| Range | 7–10 | 6–9 | 3–4 | 0–0.2 | 0–0.3 | 0.3–0.6 | 0–0.3 |
| Min-T | Max-T | Comfort | Min-H | Max-H | Comfort | Min-Wind | Max-Wind | Comfort | Overall Comfort | |
|---|---|---|---|---|---|---|---|---|---|---|
| All year | −38.4 °C | 36 °C | 22.4% | 6% | 100% | 26.2% | 0 m/s | 12 m/s | 59.9% | 3.2% |
| Winter | −38.4 °C | 2.2 °C | 0% | 26% | 96% | 31.4% | 0 m/s | 12 m/s | 28.9% | 0% |
| Summer | 4.3 °C | 36 °C | 76.3% | 19% | 100% | 20.6% | 0 m/s | 12 m/s | 29.8% | 74.9% |
| Name | Wall | Column | Beam |
|---|---|---|---|
| Value-W/(m2·K) | 0.54 | 10.24 | 7.25 |
| Name | Wall | Column | Beam |
|---|---|---|---|
| Value-W/(m2·K) | 0.24 | 0.27 | 0.20 |
| Cooling (kwh/m2) | Heating (kwh/m2) | All Energy (kwh/m2) | Solar (kwh/m2) | |
|---|---|---|---|---|
| X | −0.203 ** | −0.317 ** | −0.303 ** | −0.122 ** |
| Y | −0.351 ** | −0.441 ** | −0.435 ** | −0.398 ** |
| Z | 0.426 ** | 0.629 ** | 0.606 ** | 0.410 ** |
| N | 0.100 ** | 0.293 ** | 0.265 ** | 0.107 ** |
| W | 0.618 ** | 0.299 ** | 0.365 ** | 0.389 ** |
| S | 0.449 ** | 0.178 ** | 0.233 ** | 0.620 ** |
| E | 0.132 ** | 0.273 ** | 0.253 ** | 0.292 ** |
| Heating (kwh/m2) | Solar (kwh/m2) | |
|---|---|---|
| N | 0.796 ** | 0.061 ** |
| W | 0.404 ** | 0.174 ** |
| S | 0.025 * | 0.965 ** |
| E | 0.425 ** | 0.163 ** |
| X | Y | Z | N | W | S | E | Energy (kwh/m2) | Solar (kwh/m2) |
|---|---|---|---|---|---|---|---|---|
| 10 | 7 | 3 | 0 | 0 | 0.3 | 0 | 168 | 86 |
| 10 | 9 | 3 | 0 | 0 | 0.4 | 0 | 162 | 89 |
| 10 | 9 | 3 | 0.1 | 0 | 0.4 | 0 | 166 | 94 |
| 10 | 8 | 3 | 0 | 0 | 0.3 | 0.1 | 167 | 86 |
| 10 | 9 | 3 | 0 | 0 | 0.4 | 0.1 | 165 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Wu, Y.; Miao, X. Thermal Bridges Monitoring and Energy Optimization of Rural Residences in China’s Cold Regions. Sustainability 2023, 15, 11015. https://doi.org/10.3390/su151411015
Guo M, Wu Y, Miao X. Thermal Bridges Monitoring and Energy Optimization of Rural Residences in China’s Cold Regions. Sustainability. 2023; 15(14):11015. https://doi.org/10.3390/su151411015
Chicago/Turabian StyleGuo, Mingqian, Yue Wu, and Xinran Miao. 2023. "Thermal Bridges Monitoring and Energy Optimization of Rural Residences in China’s Cold Regions" Sustainability 15, no. 14: 11015. https://doi.org/10.3390/su151411015
APA StyleGuo, M., Wu, Y., & Miao, X. (2023). Thermal Bridges Monitoring and Energy Optimization of Rural Residences in China’s Cold Regions. Sustainability, 15(14), 11015. https://doi.org/10.3390/su151411015






