How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Urban Morphology Indicators and Data Preparation
2.2. Urban Heat Island Intensity Calculation
2.3. Interpreting Machine Learning Models
2.3.1. XGBoost Regression
2.3.2. Shapley Additive Explanations (SHAP) Method
3. Results
3.1. Experimental Area
3.2. Distribution of UHII and Correlation of Multiple Indicators
3.3. XGBoost Regression between Multi-Indicator and UHII
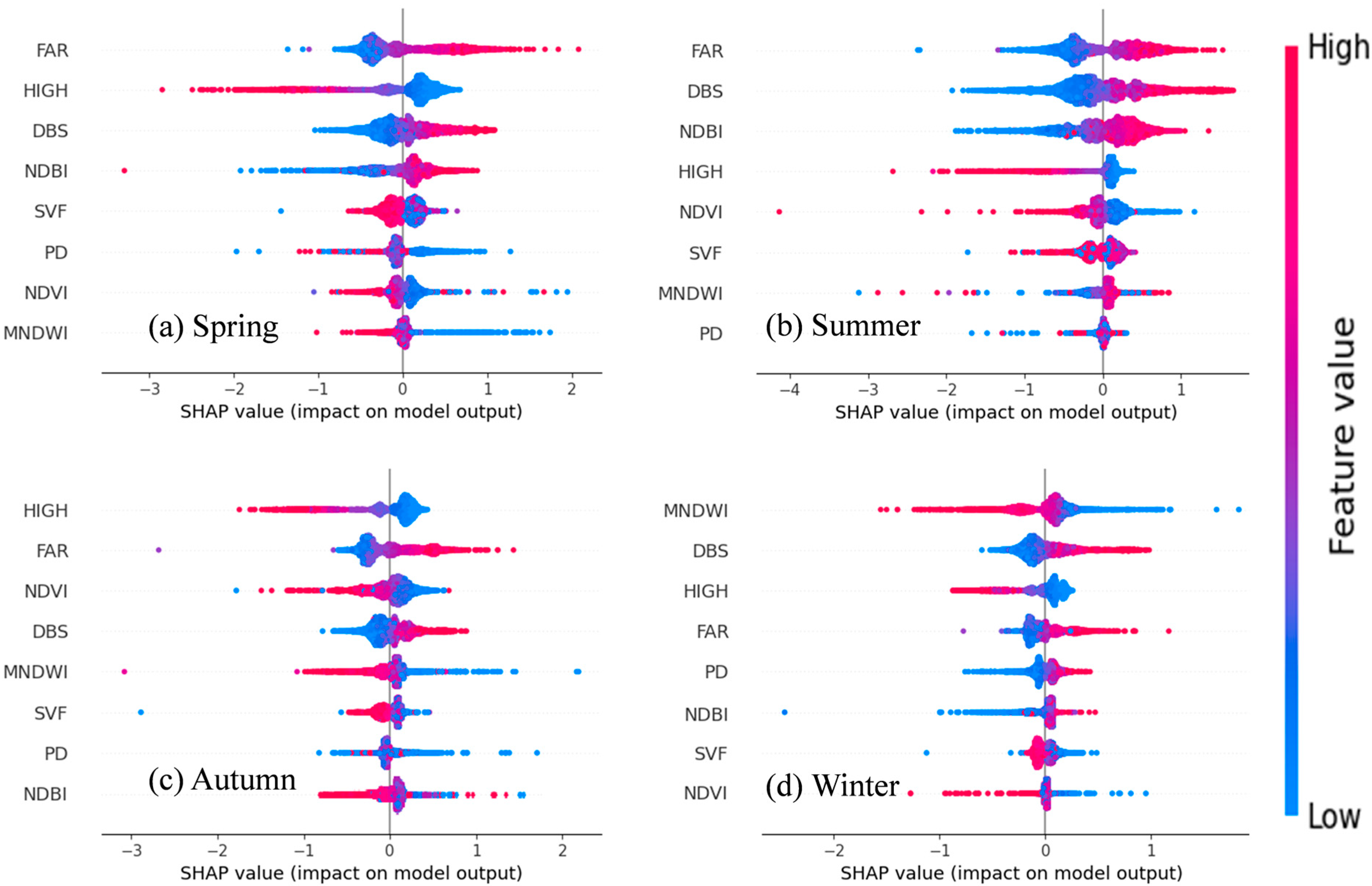
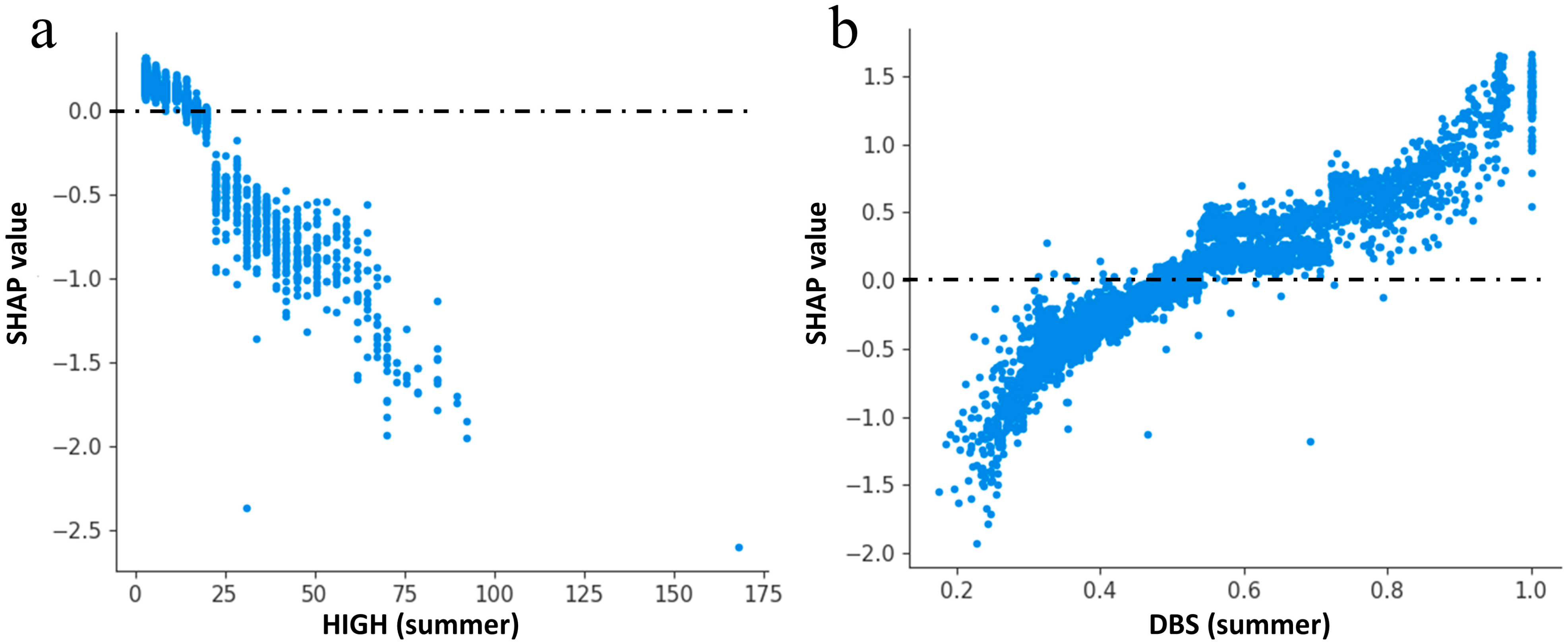
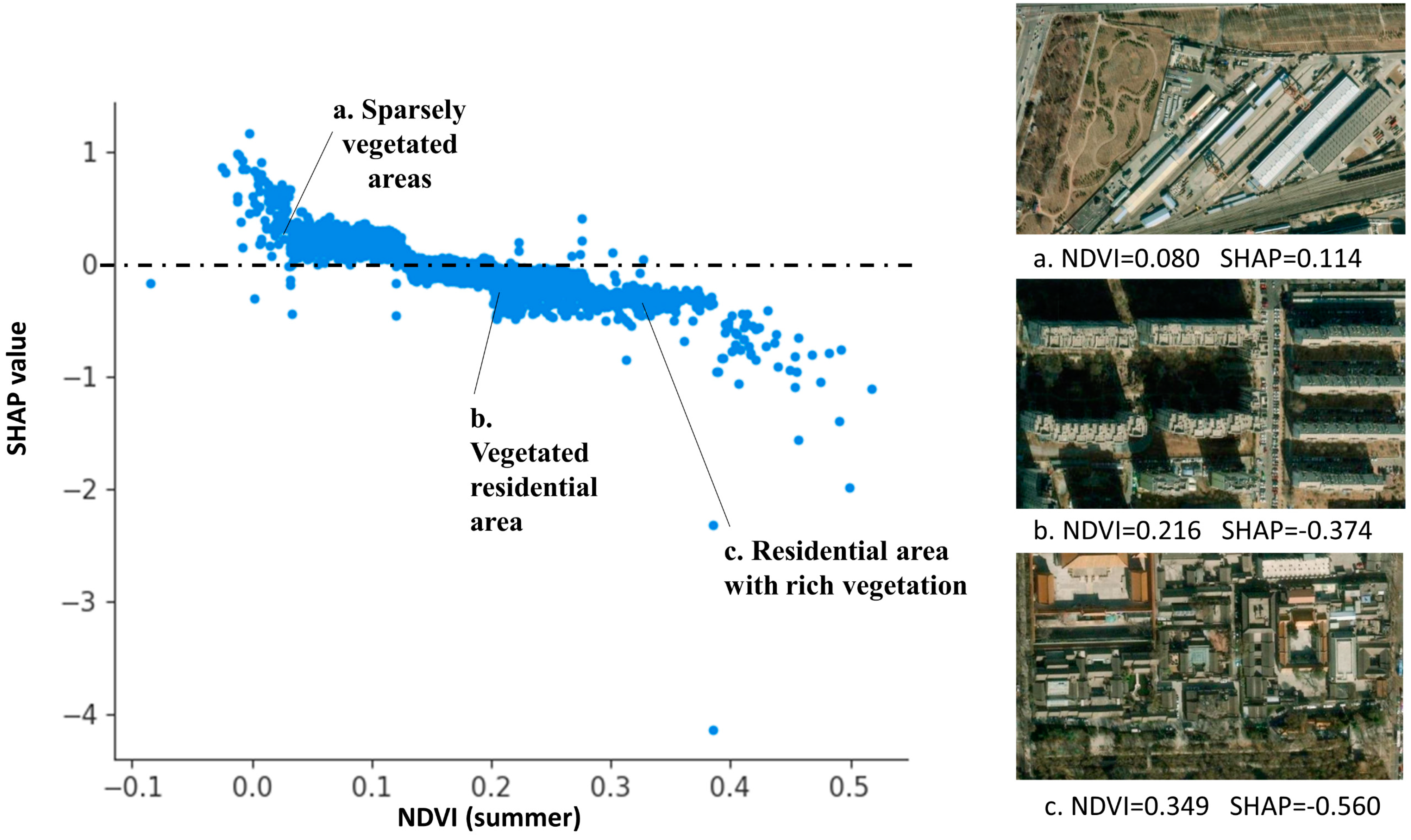
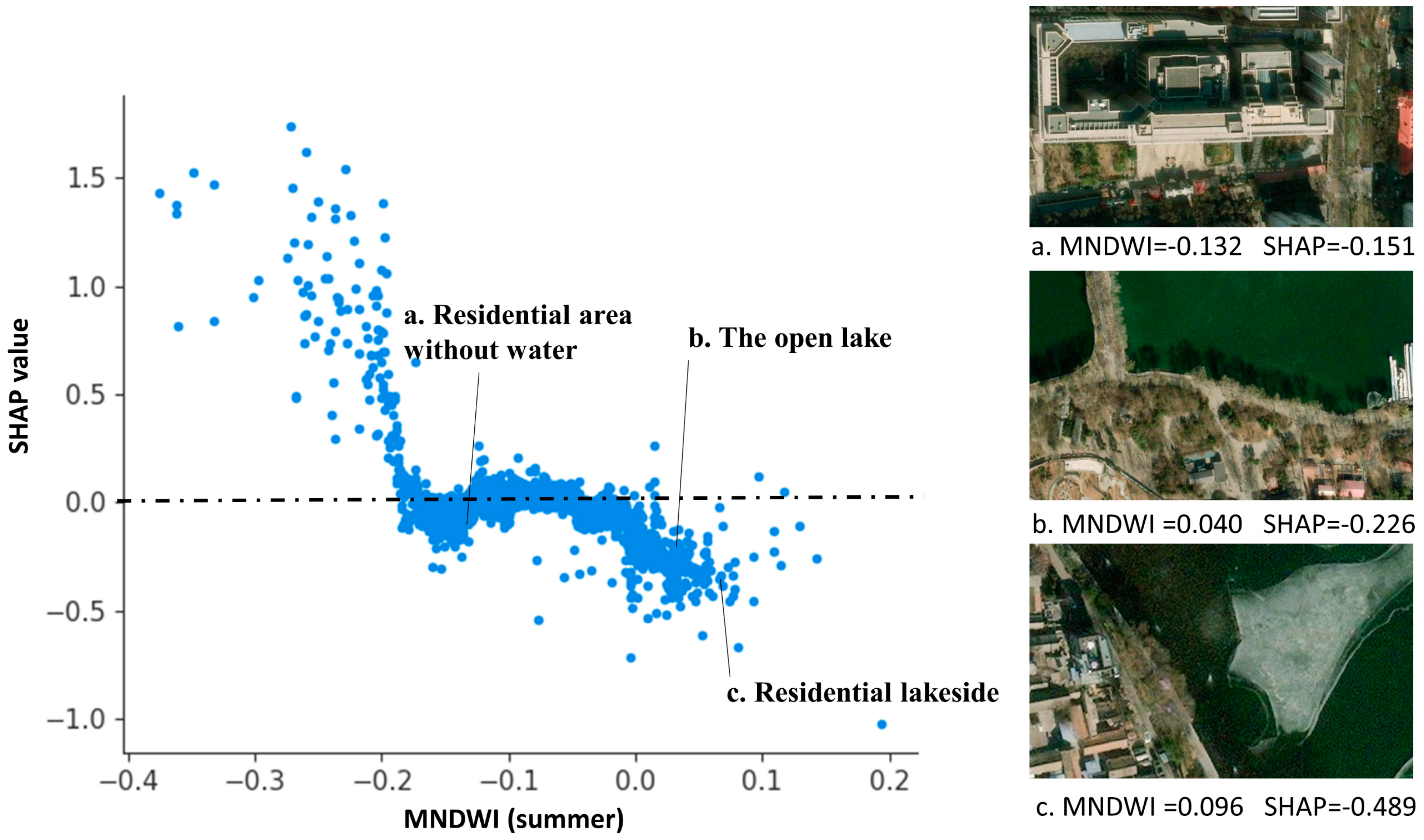
3.4. Contributions from Multi-Indicators Based on SHAP Summary Plots
4. Discussion
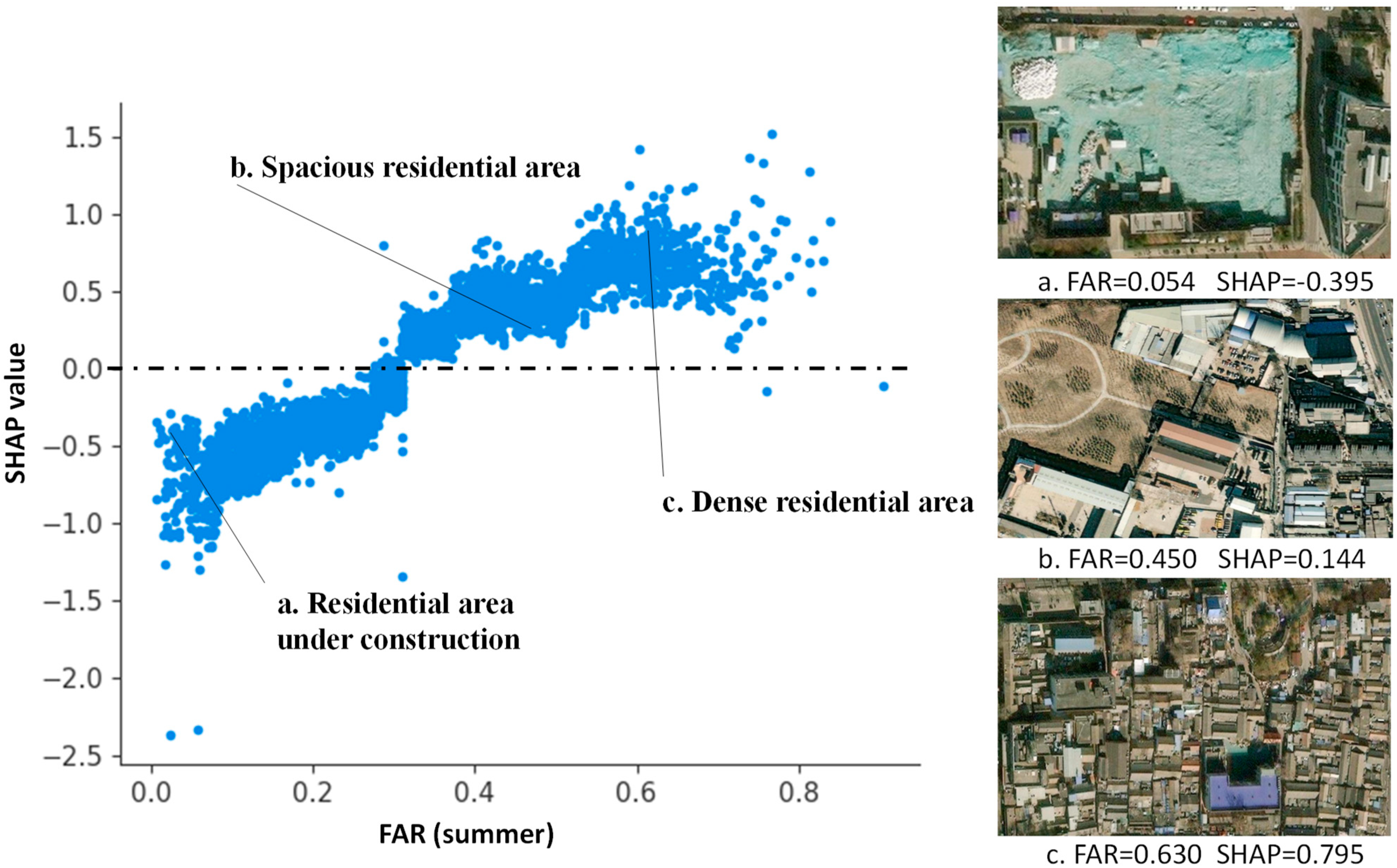
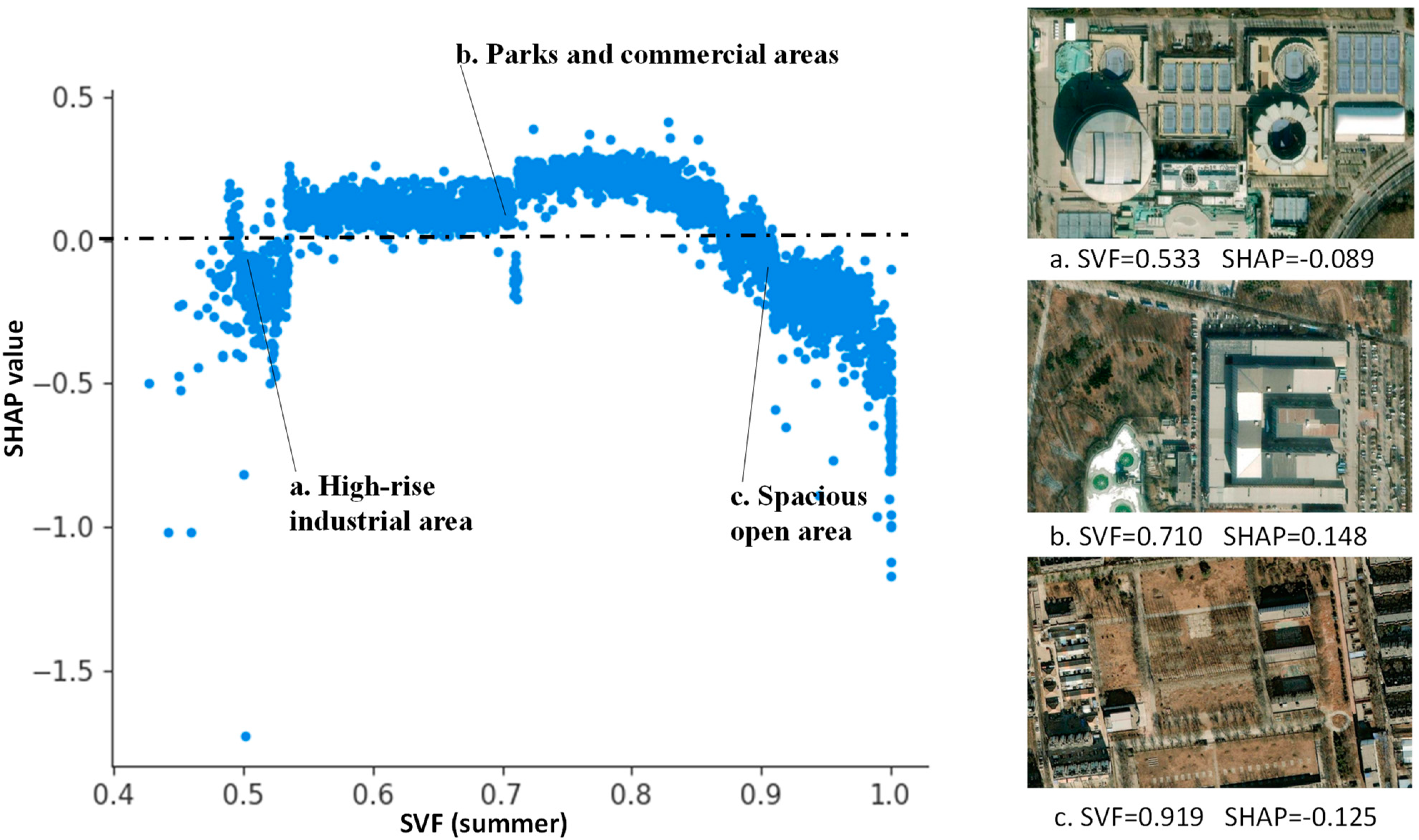
4.1. Influences of Multi-Indicators on UHII
4.1.1. The Influence of Building in 2D/3D Space
4.1.2. The Influence of Vegetation and Water Bodies in 2D/3D Space
4.2. Implications for Urban Planning and Management
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohajerani, A.; Bakaric, J.; Jeffrey-Bailey, T. The urban heat island effect, its causes, and mitigation, with reference to the thermal properties of asphalt concrete. J. Environ. Manag. 2017, 197, 522–538. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, J.; Yang, G. How to build a heat network to alleviate surface heat island effect? Sustain. Cities Soc. 2021, 74, 103135. [Google Scholar] [CrossRef]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef]
- Lo, C.P.; Quattrochi, D.A.; Luvall, J.C. Application of high-resolution thermal infrared remote sensing and GIS to assess the urban heat island effect. Int. J. Remote Sens. 1997, 18, 287–304. [Google Scholar] [CrossRef]
- Adeyemi, A.; Ramoelo, A.; Cho, M.A.; Strydom, J. Spatio-temporal analysis of built-up impervious surface area and interplay with land surface temperature in Pretoria, South Africa. Geocarto Int. 2022, 37, 7618–7638. [Google Scholar] [CrossRef]
- Allegrini, J.; Carmeliet, J. Coupled CFD and building energy simulations for studying the impacts of building height topology and buoyancy on local urban microclimates. Urban Clim. 2017, 21, 278–305. [Google Scholar] [CrossRef]
- Zheng, B.H.; Bedra, K.B.; Zheng, J.; Wang, G.G. Combination of Tree Configuration with Street Configuration for Thermal Comfort Optimization under Extreme Summer Conditions in the Urban Center of Shantou City, China. Sustainability 2018, 10, 4192. [Google Scholar] [CrossRef]
- Tran, D.X.; Pla, F.; Latorre-Carmona, P.; Myint, S.W.; Caetano, M.; Kieu, H.V. Characterizing the relationship between land use land cover change and land surface temperature. ISPRS J. Photogramm. Remote Sens. 2017, 124, 119–132. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y. Investigating the effects of 3D urban morphology on the surface urban heat island effect in urban functional zones by using high-resolution remote sensing data: A case study of Wuhan, Central China. ISPRS J. Photogramm. Remote Sens. 2019, 152, 119–131. [Google Scholar] [CrossRef]
- Guo, G.; Wu, Z.; Xiao, R.; Chen, Y.; Liu, X.; Zhang, X. Impacts of urban biophysical composition on land surface temperature in urban heat island clusters. Landsc. Urban Plan. 2015, 135, 1–10. [Google Scholar] [CrossRef]
- Liang, Z.; Wu, S.Y.; Wang, Y.Y.; Wei, F.L.; Huang, J.; Shen, J.S.; Li, S.C. The relationship between urban form and heat island intensity along the urban development gradients. Sci. Total Environ. 2020, 708, 135011. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Monteiro, M.V.; Doick, K.J.; Handley, P.; Peace, A. The impact of greenspace size on the extent of local nocturnal air temperature cooling in London. Urban For. Urban Green. 2016, 16, 160–169. [Google Scholar] [CrossRef]
- Scarano, M.; Mancini, F. Assessing the relationship between sky view factor and land surface temperature to the spatial resolution. Int. J. Remote Sens. 2017, 38, 6910–6929. [Google Scholar] [CrossRef]
- Huang, X.; Chen, H.; Gong, J. Angular difference feature extraction for urban scene classification using ZY-3 multi-angle high-resolution satellite imagery. ISPRS J. Photogramm. Remote Sens. 2018, 135, 127–141. [Google Scholar] [CrossRef]
- Guan, Q.; Yao, Y.; Ma, T.; Hong, Y.; Bie, Y.; Lyu, J. Under the Dome: A 3D Urban Texture Model and Its Relationship with Urban Land Surface Temperature. Ann. Am. Assoc. Geogr. 2021, 112, 1369–1389. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, H.; Mao, S.; Zhang, G.; Jin, Y.; Luo, Y.; Huo, W.; Pan, Z.; An, P.; Lun, F. Exploring surface urban heat island (SUHI) intensity and its implications based on urban 3D neighborhood metrics: An investigation of 57 Chinese cities. Sci. Total Environ. 2022, 847, 157662. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Wu, C.-D.; Lung, S.-C.C. Application of 3-D urbanization index to assess impact of urbanization on air temperature. Sci. Rep. 2016, 6, 24351. [Google Scholar] [CrossRef]
- Berger, C.; Rosentreter, J.; Voltersen, M.; Baumgart, C.; Schmullius, C.; Hese, S. Spatio-temporal analysis of the relationship between 2D/3D urban site characteristics and land surface temperature. Remote Sens. Environ. 2017, 193, 225–243. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A study on multiple linear regression analysis. Procedia-Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Ostertagová, E. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef]
- Mahesh, B. Machine learning algorithms-a review. Int. J. Sci. Res. IJSR 2020, 9, 381–386. [Google Scholar]
- Molnar, C. Interpretable Machine Learning; Lulu Press: Morrisville, NC, USA, 2020. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. CSUR 2018, 51, 1–42. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, J.; Han, L. Quantifying the nonlinear relationship between block morphology and the surrounding thermal environment using random forest method. Sustain. Cities Soc. 2023, 91, 104443. [Google Scholar] [CrossRef]
- Kim, M.; Kim, G. Modeling and Predicting Urban Expansion in South Korea Using Explainable Artificial Intelligence (XAI) Model. Appl. Sci. 2022, 12, 9169. [Google Scholar] [CrossRef]
- Du, Y.; McNestry, C.; Wei, L.; Antoniadi, A.M.; McAuliffe, F.M.; Mooney, C. Machine learning-based clinical decision support systems: A systematic review. Appl. Sci. 2021, 11, 5088. [Google Scholar] [CrossRef]
- Iban, M.C. An explainable model for the mass appraisal of residences: The application of tree-based Machine Learning algorithms and interpretation of value determinants. Habitat Int. 2022, 128, 102660. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, X.; Tang, Q. The footprint of urban heat island effect in 302 Chinese cities: Temporal trends and associated factors. Sci. Total Environ. 2019, 655, 652–662. [Google Scholar] [CrossRef]
- Middel, A.; Häb, K.; Brazel, A.J.; Martin, C.A.; Guhathakurta, S. Impact of urban form and design on mid-afternoon microclimate in Phoenix Local Climate Zones. Landsc. Urban Plan. 2014, 122, 16–28. [Google Scholar] [CrossRef]
- Alobaydi, D.; Bakarman, M.A.; Obeidat, B. The Impact of Urban Form Configuration on the Urban Heat Island: The Case Study of Baghdad, Iraq. Procedia Eng. 2016, 145, 820–827. [Google Scholar] [CrossRef]
- Bourdic, L.; Salat, S.; Nowacki, C. Assessing cities: A new system of cross-scale spatial indicators. Build. Res. Inf. 2012, 40, 592–605. [Google Scholar] [CrossRef]
- Qin, Z.; Wenjuan, L.; Minghua, Z.; Karnieli, A.; Berliner, P. Estimating of the essential atmospheric parameters of mono-window algorithm for land surface temperature retrieval from lanDSAT TM6. Remote Sens. Land Resour. 2003, 15, 37–43. [Google Scholar]
- Howard, L. The Climate of London: Deduced from Meteorological Observations; Cambridge University Press: Cambridge, UK, 2012; Volume 1. [Google Scholar]
- Quan, J.; Zhan, W.; Chen, Y.; Wang, M.; Wang, J. Time series decomposition of remotely sensed land surface temperature and investigation of trends and seasonal variations in surface urban heat islands. J. Geophys. Res. Atmos. 2016, 121, 2638–2657. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, Y.; Guo, X.; Qu, T. Calculation and Expression of the Urban Heat Island Indices Based on GeoSOT Grid. Sustainability 2022, 14, 2588. [Google Scholar] [CrossRef]
- Li, K.; Chen, Y.; Wang, M.; Gong, A. Spatial-temporal variations of surface urban heat island intensity induced by different definitions of rural extents in China. Sci. Total Environ. 2019, 669, 229–247. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liu, L.; Wu, C.; Chen, X.; Gao, Y.; Xie, S.; Zhang, B. Development of a global 30 m impervious surface map using multisource and multitemporal remote sensing datasets with the Google Earth Engine platform. Earth Syst. Sci. Data 2020, 12, 1625–1648. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface urban heat island across 419 global big cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Yu, S.; Chen, Z.; Yu, B.; Wang, L.; Wu, B.; Wu, J.; Zhao, F. Exploring the relationship between 2D/3D landscape pattern and land surface temperature based on explainable eXtreme Gradient Boosting tree: A case study of Shanghai, China. Sci. Total Environ. 2020, 725, 138229. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Yu, B.L.; Liu, Y.; Chen, Z.Q.; Li, Q.X.; Wang, C.X.; Wu, J.P. Estimation of Poverty Using Random Forest Regression with Multi-Source Data: A Case Study in Bangladesh. Remote Sens. 2019, 11, 375. [Google Scholar] [CrossRef]
- Molnar, C.; Casalicchio, G.; Bischl, B. Interpretable machine learning—A brief history, state-of-the-art and challenges. In Proceedings of the ECML PKDD 2020 Workshops: Workshops of the European Conference on Machine Learning and Knowledge Discovery in Databases (ECML PKDD 2020): SoGood 2020, PDFL 2020, MLCS 2020, NFMCP 2020, DINA 2020, EDML 2020, XKDD 2020 and INRA 2020, Ghent, Belgium, 14–18 September 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 417–431. [Google Scholar]
- Dabkowski, P.; Gal, Y. Real time image saliency for black box classifiers. In Proceedings of the Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Shapley, L.S. A Value for n-Person Games; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Lundberg, S.M.; Erion, G.G.; Lee, S.-I. Consistent Individualized Feature Attribution for Tree Ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Beijing Overview. Available online: http://www.beijing.gov.cn/renwen/bjgk (accessed on 15 March 2023).
- Beijing Municipal Bureau of Statistics. Available online: http://tjj.beijing.gov.cn (accessed on 15 March 2023).
- Li, Z.; Zhao, Y.; Hu, D. Evaluating the impacts of three-dimensional building morphology on urban near-surface energy fluxes: A case study in Beijing, China. Energy Build. 2023, 279, 112690. [Google Scholar] [CrossRef]
- Jenks, G.F. Optimal Data Classification for Choropleth Maps; Occasional Paper; Department of Geography, University of Kansas: Lawrence, KS, USA, 1977. [Google Scholar]
- Peng, W.C.Y.; Wang, R.; Duan, J.; Gao, W.J.; Fan, Z.X. Surface and canopy urban heat islands: Does urban morphology result in the spatiotemporal differences? Urban Clim. 2022, 42, 101136. [Google Scholar] [CrossRef]
- Cai, Z.; Han, G.F.; Chen, M.C. Do water bodies play an important role in the relationship between urban form and land surface temperature? Sustain. Cities Soc. 2018, 39, 487–498. [Google Scholar] [CrossRef]
- Murakawa, S.; Sekine, T.; Narita, K.-I.; Nishina, D. Study of the effects of a river on the thermal environment in an urban area. Energy Build. 1991, 16, 993–1001. [Google Scholar] [CrossRef]
- Xi, C.; Ren, C.; Wang, J.; Feng, Z.; Cao, S.-J. Impacts of urban-scale building height diversity on urban climates: A case study of Nanjing, China. Energy Build. 2021, 251, 111350. [Google Scholar] [CrossRef]
- Chen, J.; Du, P.; Jin, S.; Ding, H.; Chen, C.; Xu, Y.; Feng, L.; Guo, G.; Zheng, H.; Huang, M. Unravelling the multilevel and multi-dimensional impacts of building and tree on surface urban heat islands. Energy Build. 2022, 259, 111843. [Google Scholar] [CrossRef]
- Wang, Q.; Fan, Y.; Hang, J.; Li, Y. Interacting urban heat island circulations as affected by weak background wind. Build. Environ. 2019, 160, 106224. [Google Scholar] [CrossRef]
- Chun, B.; Guldmann, J.M. Impact of greening on the urban heat island: Seasonal variations and mitigation strategies. Comput. Environ. Urban Syst. 2018, 71, 165–176. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Oke, T.R. The urban energy balance. Prog. Phys. Geogr. 1988, 12, 471–508. [Google Scholar] [CrossRef]
- Guo, G.; Zhou, X.; Wu, Z.; Xiao, R.; Chen, Y. Characterizing the impact of urban morphology heterogeneity on land surface temperature in Guangzhou, China. Environ. Model. Softw. 2016, 84, 427–439. [Google Scholar] [CrossRef]
- Lan, Y.; Zhan, Q. How do urban buildings impact summer air temperature? The effects of building configurations in space and time. Build. Environ. 2017, 125, 88–98. [Google Scholar] [CrossRef]
- Yang, F.; Lau, S.S.Y.; Qian, F. Summertime heat island intensities in three high-rise housing quarters in inner-city Shanghai China: Building layout, density and greenery. Build. Environ. 2010, 45, 115–134. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y. The impact of building density and building height heterogeneity on average urban albedo and street surface temperature. Build. Environ. 2015, 90, 146–156. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Gao, Y.; Yao, R.; Li, B.; Turkbeyler, E.; Luo, Q.; Short, A. Field studies on the effect of built forms on urban wind environments. Renew. Energy 2012, 46, 148–154. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, C.; Teng, M. Impact of residential building layouts on microclimate in a high temperature and high humidity region. Sustainability 2020, 12, 1046. [Google Scholar] [CrossRef]
- Cheng, X.; Wei, B.; Chen, G.; Li, J.; Song, C. Influence of park size and its surrounding urban landscape patterns on the park cooling effect. J. Urban Plan. Dev. 2015, 141, A4014002. [Google Scholar] [CrossRef]
- Al-Saadi, L.M.; Jaber, S.H.; Al-Jiboori, M.H. Variation of urban vegetation cover and its impact on minimum and maximum heat islands. Urban Clim. 2020, 34, 100707. [Google Scholar] [CrossRef]
- Park, Y.; Guldmann, J.-M.; Liu, D. Impacts of tree and building shades on the urban heat island: Combining remote sensing, 3D digital city and spatial regression approaches. Comput. Environ. Urban Syst. 2021, 88, 101655. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhan, Y.; Yu, T.; Ren, X. Urban green effects on land surface temperature caused by surface characteristics: A case study of summer Beijing metropolitan region. Infrared Phys. Technol. 2017, 86, 35–43. [Google Scholar] [CrossRef]
- Das, M.; Das, A.; Momin, S. Quantifying the cooling effect of urban green space: A case from urban parks in a tropical mega metropolitan area (India). Sustain. Cities Soc. 2022, 87, 104062. [Google Scholar] [CrossRef]
- Armson, D.; Stringer, P.; Ennos, A. The effect of tree shade and grass on surface and globe temperatures in an urban area. Urban For. Urban Green. 2012, 11, 245–255. [Google Scholar] [CrossRef]
- Tan, J.K.; Belcher, R.N.; Tan, H.T.; Menz, S.; Schroepfer, T. The urban heat island mitigation potential of vegetation depends on local surface type and shade. Urban For. Urban Green. 2021, 62, 127128. [Google Scholar] [CrossRef]
- Wang, X.; Dallimer, M.; Scott, C.E.; Shi, W.; Gao, J. Tree species richness and diversity predicts the magnitude of urban heat island mitigation effects of greenspaces. Sci. Total Environ. 2021, 770, 145211. [Google Scholar] [CrossRef]
- Oberndorfer, E.; Lundholm, J.; Bass, B.; Coffman, R.R.; Doshi, H.; Dunnett, N.; Gaffin, S.; Köhler, M.; Liu, K.K.; Rowe, B. Green roofs as urban ecosystems: Ecological structures, functions, and services. BioScience 2007, 57, 823–833. [Google Scholar] [CrossRef]
- Gober, P.; Brazel, A.; Quay, R.; Myint, S.; Grossman-Clarke, S.; Miller, A.; Rossi, S. Using watered landscapes to manipulate urban heat island effects: How much water will it take to cool Phoenix? J. Am. Plan. Assoc. 2009, 76, 109–121. [Google Scholar] [CrossRef]
- Deilami, K.; Kamruzzaman, M.; Liu, Y. Urban heat island effect: A systematic review of spatio-temporal factors, data, methods, and mitigation measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]

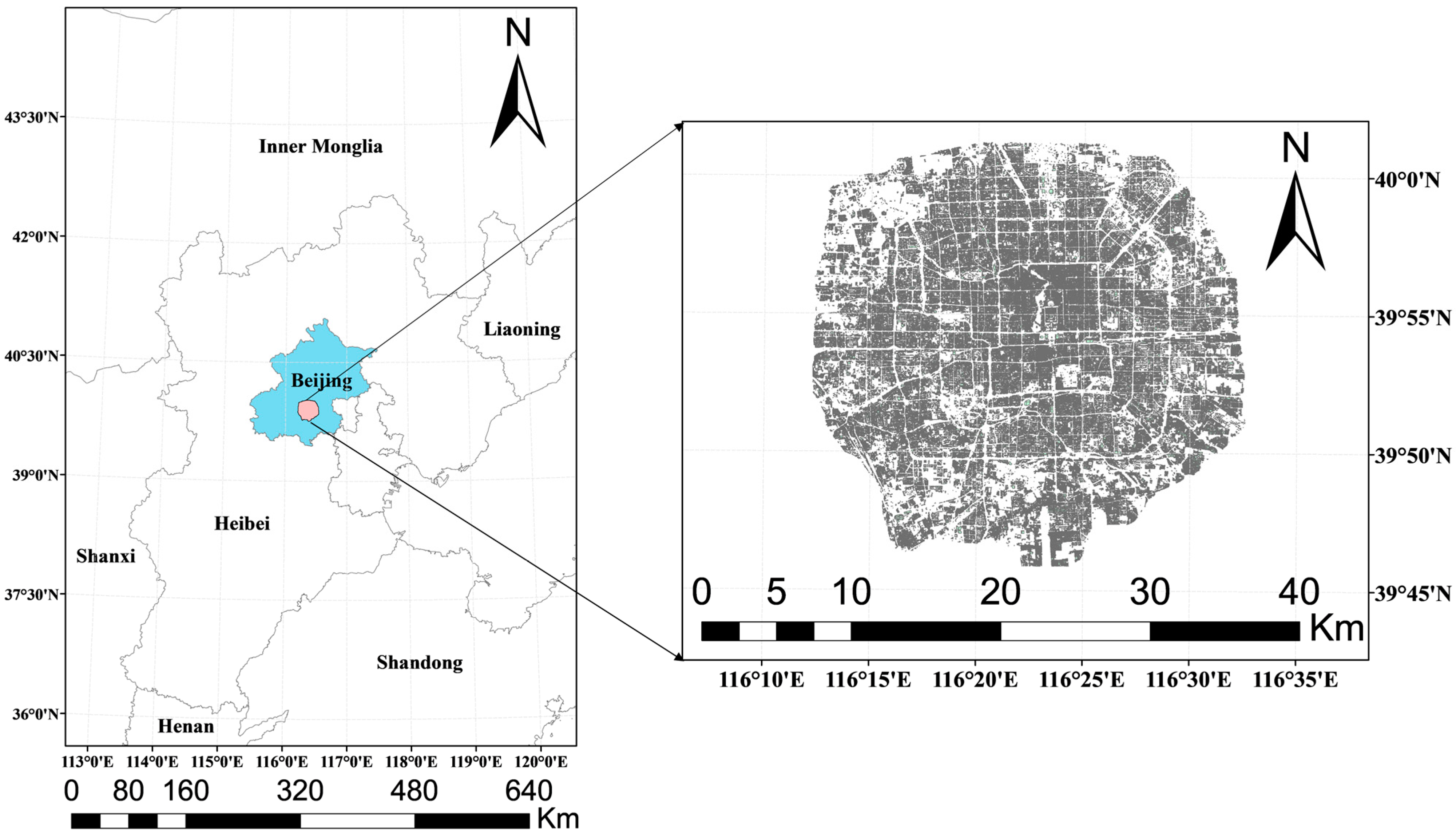

| Type | Name | Description | Calculation |
|---|---|---|---|
| 2D building form indicators | Diversity of building shapes (DBS) | The diversity of building shapes in the area | |
| Floor area ratio (FAR) | The density of the horizontal distribution of buildings | ||
| Normalized difference built-up index (NDBI) | Building and impermeable surface coverage | ||
| 3D building form indicators | Sky view factor (SVF) | The extent to which the sky is blocked by buildings | |
| Building height (HIGH) | The average height of buildings in the area | ||
| Ecological infrastructure | Normalized difference vegetation index (NDVI) | Growth, abundance, and coverage of vegetation | |
| Modified normalized difference water index (MNDWI) | Coverage of water bodies | ||
| Human activities | Population density (PD) | The density of population in the area | / |
| Data Type | Resolution | Time | Use |
|---|---|---|---|
| Landsat 8 satellite imagery | Thermal infrared band 30 m Multispectral band 100 m | 17 December 2017 (Winter) 27 June 2018 (Summer) 8 April 2018 (Spring) 17 October 2018 (Autumn) | Surface temperature inversion |
| Building vector | - | 2018 | Calculation of morphological indicators |
| Population raster | 100 m | 2018 | Population density calculations |
| Resources Satellite Three imagery | 2.1 m | 2018 | Auxiliary data |
| Nighttime light data | 30 m | 2015 | Auxiliary data |
| Impervious surface data | 30 m | 2015 | Auxiliary data |
| Date | Values |
|---|---|
| Winter—December 2017 | 2.07 °C |
| Spring—April 2018 | 23.12 °C |
| Summer—June 2018 | 36.33 °C |
| Autumn—October 2018 | 17.57 °C |
| UHII | FAR | DBS | HIGH | SVF | PD | NDVI | NDBI | MNDWI |
|---|---|---|---|---|---|---|---|---|
| Spring | 0.418 ** | 0.398 ** | −0.426 ** | −0.237 ** | 0.092 ** | −0.125 ** | 0.339 ** | −0.179 ** |
| Summer | 0.410 ** | 0.426 ** | −0.298 ** | −0.222 ** | 0.005 | −0.364 ** | 0.339 ** | −0.072 ** |
| Autumn | 0.378 ** | 0.338 ** | −0.384 ** | −0.213 ** | 0.064 ** | −0.115 ** | 0.215 ** | −0.209 ** |
| Winter | 0.289 ** | 0.355 ** | −0.348 ** | −0.173 ** | 0.008 | 0.245 ** | 0.171 ** | −0.321 ** |
| Variable Group | Percentage of Explained Variance of UHII | |||
|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | |
| 2D building indicators | 48.10% | 45.60% | 39.00% | 38.10% |
| 3D building indicators | 35.10% | 28.90% | 30.70% | 28.50% |
| all building indicators | 56.30% | 57.50% | 49.10% | 47.20% |
| ecological infrastructure indicators | 29.50% | 23.20% | 30.50% | 31.00% |
| all multi-indicators | 60.60% | 61.20% | 53.70% | 54.50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Guo, X.; Jiang, J. How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study. Sustainability 2023, 15, 10787. https://doi.org/10.3390/su151410787
Liu B, Guo X, Jiang J. How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study. Sustainability. 2023; 15(14):10787. https://doi.org/10.3390/su151410787
Chicago/Turabian StyleLiu, Biao, Xian Guo, and Jie Jiang. 2023. "How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study" Sustainability 15, no. 14: 10787. https://doi.org/10.3390/su151410787
APA StyleLiu, B., Guo, X., & Jiang, J. (2023). How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study. Sustainability, 15(14), 10787. https://doi.org/10.3390/su151410787







