Abstract
With the spread of compulsory education emerged continuous school management problems, and the quality of school management in compulsory education has attracted a great deal of attention in China. However, the application of information technology in the field is not yet detailed and wide, resulting in problems concerning heavy workloads and high difficulty in the whole evaluation process. As such, we have utilized big data technologies, including Apache Spark, Apache Hive, and SPSS, to effectively carry out data cleaning, correlation analysis, dynamic factor analysis, principal component analysis, and visual display on a sample of 1760 data points from 40 primary and secondary schools located in the Q Province of China. This has enabled us to construct a model for evaluating school management quality in the compulsory education stage, reducing the previous 22 management tasks required for evaluation down to just 5. Such streamlining has greatly reduced the workload and difficulty previously associated with evaluation, providing a more efficient and effective solution for assessing quality management in schools. It has improved the efficiency and accuracy of evaluation and further promoted the simultaneous development of education and education equity in the compulsory education stage.
1. Introduction
With the rapid development of the education industry, the evaluation of school management quality has emerged as a pivotal tool for promoting educational equity, improving education quality, and fostering sustainable education development [1]. School evaluation can be defined as the process of collecting, analyzing, and interpreting information on various aspects related to improving educational plans [2,3]. Particularly important during the primary and secondary education stage, school management quality evaluation carries significant implications for the growth and future of children [4]. Consequently, research into the school management quality evaluation model within compulsory education is of utmost importance. In accordance with the principle of global education equity, we require standardized data and evaluation methods to undertake comprehensive, fair, and efficient assessments of the quality of education management [5]. This is an ongoing process of sustainability, continuity, and gradual improvement.
In 2002, the South African Department of Education [6] stated that school management quality evaluation is the cornerstone of the school quality assurance system. It assists schools and external inspectors in reviewing the current performance of schools and demonstrating how they fulfill international, regional, and local education goals. In 2016, Ireland outlined guidelines for implementing self-evaluation in primary and secondary schools with the aim of achieving independent improvement and sustainable development in education [7]. In 2022, the Education Bureau of Hong Kong emphasized that the school management quality evaluation of primary and secondary schools should be guided by evaluation, be based on data, and promote sustainable development through strategic and targeted planning [8]. Since 1990, the Chinese government has increased its investment in school management quality evaluation for primary and secondary schools, which are referred to as compulsory education in China, and made continuous efforts to improve relevant policies and standards. These include the Provisional Regulations on Education Evaluation of General Institutions of Higher Education [9], School Management Standards for Compulsory Education (for Trial Implementation) [10], Several Opinions of the Ministry of Education on Further Promoting the Separation of Education Administration and Evaluation to Promote the Transformation of Government Functions [11], Outline of the National Medium- and Long-term Education Reform and Development Plan (2010–2020) [12], and School Management Standards for Compulsory Education [13]. These have pointed out that the management level of compulsory education schools directly relates to the school’s teaching quality and education equity issues. Therefore, the national education supervision departments should carry out supervisory evaluations to promote scientific management, fair education, and sustainable educational reform and development in schools. At present, although the use of information technology and systems is widespread, there is a lack of refinement and widespread investment in big data technology, and there is no effective evaluation of educational technology in the place where it is used. Based on the “School Management Standards for Compulsory Education” issued by the Ministry of Education, there are 88 “Management Contents” that must be evaluated. Given the current 213,000 compulsory education schools in China, the quality evaluation process for school management in the compulsory education stage requires the submission of a staggering 18,744,000 evaluation materials each year. Furthermore, each evaluation expert must assess, assign scores, and provide recommendations for improvement for these 18,744,000 evaluation materials. The whole evaluation process is extremely difficult for schools, evaluation experts, and the government in terms of workload and assessment accuracy.
In 2015, the United Nations summit adopted the “2030 Agenda for Sustainable Development” and proposed the Sustainable Development Goals (SDGs) [1]. The fourth goal of SDGs is to provide quality education. It emphasizes that obtaining high-quality education is fundamental to improving people’s lives and achieving sustainable development. Evaluation of school management quality, especially in primary and secondary schools, is essential for achieving improved and sustainable education quality. Regarding global research on school management quality evaluation in primary and secondary schools, most studies focus on various evaluation models and frameworks and lack research on the informationization implementation of these models. The CIPP model of school management quality evaluation was proposed by Stufflebeam [14] in the United States in 1983. The implementation of this model includes background analysis, input, process, and product evaluation, with the most important goal being improvement rather than proof. In 2018, Aziz [15] from Turkey improved the CIPP evaluation model to provide more accurate evaluation of school management quality in primary and secondary schools. In 2017, Zhang Shanmei [16] from China proposed a research framework for evaluating the management quality of primary and secondary schools based on resource theory. This evaluation framework includes four secondary dimensions and eighteen tertiary dimensions. In 2018, Şahin and Kılıç [17] from Turkey proposed a self-evaluation model for the management quality of primary and secondary schools that includes five stages: preparation, monitoring, evaluation, planning, and implementation. In 2020, Nancy Bouranta [18] from South Africa used affinity diagrams and Pareto charts to classify the study of school management quality in primary and secondary schools. The results showed that the most prominent themes of research on school quality management were principal leadership, quality management and assurance, relationships and cooperation among stakeholders, school performance and education quality, and government roles.
To address the aforementioned issues both domestically and internationally, we take 40 primary and secondary schools in Q province as a case study. We utilize big data technologies such as Apache Spark, Apache Hive, and IBM SPSS Statistics to clean data, analyze correlation, create visualizations, and perform dynamic factor analysis and principal component analysis of the 1760 sample data points collected. Based on this, we construct a school management quality evaluation model and corresponding scoring standards for compulsory education stages. As compared to the previous evaluation, this model reduces the required number of management tasks from 22 to 5, significantly reducing evaluation workload and difficulty while improving efficiency and accuracy. Additionally, it promotes education equity and sustainable development in compulsory education stages. Furthermore, the result of the study can serve as a reference for other countries’ primary and secondary school management quality evaluation indicators and methods.
2. Big Data Research Methods and Tool Selection
Faced with massive data in the information age, big data has become an indispensable technology. After Google released open source technology for big data in 2004, big data technology has become popular all over the world [19]. Commonly used big data technologies include distributed computing, distributed storage, and visualization techniques [20]. With the continuous maturation of big data technology, big data technology has been used more and more in the field of educational evaluation and has achieved remarkable results. Zhang, Rongbo [21], Wu Guangzhi [22], Islam, A. Y. M. Atiquil [23], Lyu, Bu [24], Li Lianzhi [25], and others have constructed several construction paradigms of education evaluation models and a series of education evaluation models from the macro and micro levels, playing an active role in research, policy making, practice, and evaluation in related fields. Liu Hai-ling [26], Jiang, Jie [27], Li, Yuqian [28], and others proposed design and implementation schemes for several big data evaluation systems applied to online learning, which not only provide help for school administrators, teachers, and students, but also change the old model of learning behavior analysis and contribute to the construction of the intelligent campus. With certain flexibility and expansibility, it provides a more comprehensive and objective basis for the analysis and optimization of online learning. Yu and Wenhua [29] proposed a scholar co-authorship network and citation evaluation system based on big data technology. Mao and Chen-Lei [30] improved the teaching effectiveness of ideological and political courses based on big data a priori genetic algorithms. Bai, Xiaomei [31], Jiang, Cheng [32], and others comprehensively analyzed the application and practice of big data technology in education evaluation, prediction, and recommendation.
3. Evaluation Model Construction
The research conducted analyzed the school management quality of 40 primary and secondary schools in Q Province in 2020 utilizing the evaluation methods and criteria for standardization of management in compulsory education outlined by the “Fujian Provincial Department of Education” [33]. A total of 1760 sample data points were collected through the evaluation. Using advanced big data technology from Apache Spark 3.2.1, data cleaning was performed on the sample data. Subsequently, dynamic factor analysis and principal component analysis were carried out using Apache Hive 3.1.2. IBM SPSS Statistics 26 was also utilized for correlation analysis and the visual display of results in order to construct a comprehensive school management quality evaluation model and corresponding scoring criteria for the compulsory education stage. These efforts sought to streamline the evaluation process and establish more efficient and accurate methods for assessing school management quality. Finally, the model was tested using expert evaluation data concerning these 40 primary and secondary schools in 2021. The detailed process is shown in Figure 1.
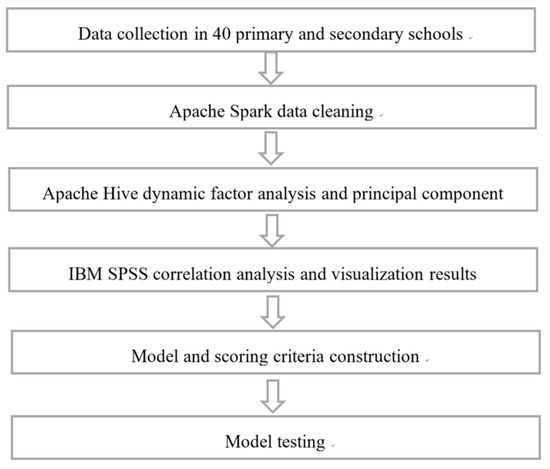
Figure 1.
The process of constructing a model for evaluating the quality of school management in the compulsory education stage.
3.1. Sample Data Collection, Cleaning, and Standardized Processing
Firstly, the data source of the sample in the study was selected from school quality evaluation results in data from 40 primary and secondary schools in Q Province in 2020, including data from 13 junior high schools and 27 primary schools. Secondly, the 1760 sample data points collected were cleaned by Apache Spark, Hive, and SPSS, which included dirty data filtering, text evaluation data deletion, missing data completion and final result counting, aggregation, global sorting, secondary sorting, etc. Finally, the cleaned data items included six management responsibilities, 22 management tasks, 88 evaluation rules, standard score details, school self-evaluation scores, expert 1 scoring results, and expert 2 scoring results.
The collection criteria of sample data in the study were based on the regulations of Fujian Provincial Department of Education on the Issuance of Evaluation Methods and Criteria for Standardization of Management in Compulsory Education [20] issued by the Department of Education, which stipulated 6 first-level indicators, 22 second-level indicators, and 88 third-level indicators. In the study, the management quality evaluation indicators of schools in the compulsory education stage are constructed based on 22 secondary indicators, and the variables are defined in the model construction process as follows: : safeguarding students’ equal right to enter schools (score); : establishing a working mechanism for “dropout control and school protection” (score); : meeting the needs of students (score); : improving students’ moral quality (score); : helping students learn to learn (score); : enhancing students’ physical fitness (score); : improving students’ artistic qualities (score); : developing students’ life skills (score); : strengthening teachers’ management and professional ethics (score); : improving teachers’ educational and teaching abilities (score); : establishing a professional development support system for teachers (score); : building a curriculum suitable for students’ development (score); : implementing student development-based teaching (score); : establishing an assessment system to promote students’ development (score); : providing convenient and practical teaching resources (score); : establishing a practical safety and health management system (score); : building a safe and hygienic school infrastructure (score); : providing life skills-based safety and health education (score); : creating a respectful and inclusive school culture (score); : enhancing the capacity for scientific management in accordance with the law (score); : establishing a sound democratic management system (score); : building a harmonious family, school, and community partnership (score); : overall expert score (score); : total model score (score). Since the evaluation results of the 40 primary and secondary schools were consistent in the three variables related to safeguarding the equal access rights of students establishing a mechanism for controlling dropouts and ensuring education, and meeting the needs of students requiring attention/focus on individual needs, , , and are constants without correlation. As a result, these three variables have been excluded from factor analysis.
3.2. KMO Sample Measures and Bartlett Sphere Tests
The KMO measure (Kaiser–Meyer–Olkin measure of sampling adequacy) is one of the statistical test methods used to determine the suitability of the original variables for factor analysis. It compares the magnitude of the observed correlation coefficient and partial correlation coefficient between the original variables. A KMO measure value > 0.5 means that factor analysis can be performed, while a value above 0.7 is a satisfactory value [34]. Bartlett’s test of sphericity is used to test the correlation between variables in the correlation matrix. In factor analysis, if the original hypothesis is rejected, it means that factor analysis can be performed. If the original hypothesis is not rejected, it means that these variables may provide some information independently and are not suitable for factor analysis [35].
We used Apache Hive and SPSS to analyze the KMO measure in the sample and the Bartlett’s sphere tests that were performed on the sample data of 40 primary and secondary school departmental management quality assessment results cleaned by Apache Spark, and the results are shown in Table 1. According to Table 1, the KMO measure for the sample is 0.664 > 0.5, while the Bartlett sphere test result of Sig = 0.000 < 0.05 rejects the original hypothesis, indicating that factor analysis can be conducted between variables …. The correlation coefficients and the common factor variance analysis between variables … revealed that three variables (, and ) had low correlation with other variables, while common factor variance was also low; thus, these three variables were deleted and the remaining sixteen variables were re-tested for the KMO measures and Bartlett’s test of sphericity. The test results are shown in Table 2.

Table 1.
Variable … KMO measures and Bartlett’s test of sphericity results.

Table 2.
KMO measures for the 16 variables and Bartlett sphere test results.
According to Table 2, the KMO measure for the sample was 0.710 > 0.664 > 0.5, while the result for Bartlett’s test of sphericity was Sig = 0.000 < 0.05, rejecting the original hypothesis. The correlation coefficients between the variables are higher after optimization, and the variance of the extracted common factors is also higher. All of the above indicates that after removing the three variables , and , the remaining sixteen variables have a stronger correlation, which is more suitable for factor analysis.
3.3. Analysis of the Commonality of Each Factor
The total explained variance demonstrates the contribution of factors to the explanation of the variables. Table 3 displays the total explained variance of the 16 variables as determined by principal component analysis. It reveals that five components have initial eigenvalues greater than 1, with values of 4.576, 2.695, 1.616, 1.390, and 1.185, respectively. These components account for a cumulative contribution of 71.635%, surpassing the threshold of 50%. This suggests that these five key components effectively represent the variations in the 16 variables under consideration. The dynamic factor analysis gravel map of 16 variables like Figure 2. The red line distinguishes between the primary and secondary influencing variables, with the left side being the primary influencing variable and the right side being the secondary influencing factor

Table 3.
Total explained variance in the 16 variables.
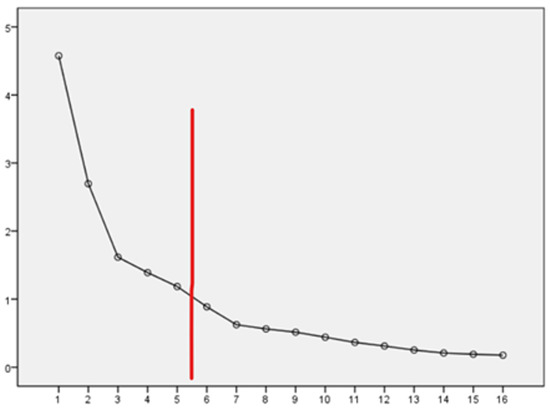
Figure 2.
Dynamic factor analysis gravel map of 16 variables. Note: the x-axis is the fraction and the y-axis is the characteristic value.
Component score coefficients are shown in Table 4, which represents the score coefficients of each variable in the five major components. At the same time, Sig = 0.000 < 0.05 between each component in the covariance matrix of the five components’ scores represents its high significance and illustrates the accuracy of the component score coefficient table in Table 4.

Table 4.
Component score coefficient matrix of the 16 variables.
The factor load matrix is obtained by orthogonal rotation with the criterion of “variance maximization”, while the cumulative contribution rate of the variance of the overall factor remains unchanged after rotation. The main common factors of the 16 variables can be obtained from the rotated factor load matrix. The corresponding main common factors are shown in Table 5. According to Table 5, the larger values of the corresponding variable of principal component 1 are , , . Principal component 2 corresponds to variables with larger values for , , , and . The variable values corresponding to principal component 3 are , , and . The larger values of the corresponding variable of principal component 4 are , , and . Principal component 5 corresponds to variables with larger values for and .

Table 5.
Main common factors corresponding to the five major components.
3.4. Evaluation Model Construction
Based on correlation analysis of the above 16 assessment indicators, the components and the representative secondary indicators of the primary indicators are calculated using the formula , where is the correlation coefficient among indicators within a class, n is the number of indicators within a class, and the largest value is the representative indicator between classes. At the same time, the weights of the representative secondary indicators of each component factor are determined based on the ratio of the rotated eigenvalues of the 16 secondary indicators to the sum of the rotated eigenvalues of each factor, and the calculated results are shown in Table 6.

Table 6.
Representative secondary indicators of each principal component and the primary indicator.
As can be seen from Table 6, the ranking results for within each group in component 1 are , of which is the maximum value; thus, the representative secondary indicator chosen is the ninth indicator (“Strengthening teacher management and professional ethics”), with a weighting coefficient of 0.339, and the corresponding primary indicator is “Leading teacher professional development”. In component 2, the sorting result of in each group is , where is the maximum value within the group; thus, the 14th second-level indicator (“Establishing an evaluation system to promote students’ development”) is selected as a representative indicator of the corresponding first-level indicator with a weight coefficient of 0.235, corresponding to the first-level indicator “Improving the quality of education and teaching”. In component 3, the ranking result of in each group’s internal value is . Although is the maximum value, there is little difference in the values of . Considering the representative secondary indicators of the other four components, the 19th secondary indicator (“Building a respectful and inclusive school culture”) is selected as the representative indicator of the corresponding first-level indicator in component 3 with a weight coefficient of 0.141, and the corresponding first-level indicator is “Building a harmonious and safe environment”. The ranking result of in each group in component 4 is , with having the highest value; thus, the fourth second-level indicator (“Promoting students’ all-round development”) is selected as the representative indicator of the corresponding first-level indicator, with a weight coefficient of 0.121, and the corresponding first-level indicator is “Promoting the overall development of students”. In component 5, the ranking result of within each group is , of which has the largest value; thus, the second-level indicator of the 20th item (“Enhancing the capacity of scientific management according to law”) is selected as the representative indicator of the corresponding first-level indicator with a weight coefficient of 0.121, and the corresponding first-level indicator is “Building a modern school system”.
Based on each secondary representative indicator and the corresponding weighting coefficients, the comprehensive evaluation model of the first-level indicator can be obtained as follows:
From the perspective of the evaluation model, the two first-level indicators that are most relevant to the final evaluation results are “Leading the professional development of teachers” and “Improving the quality of education and teaching”. The corresponding second-level indicators are “Strengthening the management of teachers and the construction of professional ethics” and “Establishing the evaluation system to promote the development of students”, indicating that the evaluation of school management quality at the stage of compulsory education in China focuses on the development of teachers and students.
4. Evaluation Model Test
4.1. Expert Scoring Results Test the Evaluation Model
The scores of the corresponding second-level indicators of 40 primary and secondary schools in 2021 were calculated using the first-level comprehensive evaluation model, resulting in first-level comprehensive evaluation model scores for each school, as shown in Table 7.

Table 7.
Scoring results of the comprehensive evaluation model of first-level indicators.
The validity and reliability of the comprehensive evaluation model of the first-level indicators can be tested by conducting a correlation analysis between the model scoring results and the expert scoring results. In the study, IBM SPSS Statistics 26 was adopted to conduct correlation analysis between model scoring results and expert scoring results. According to the previous definitions of the variables, the new variables were defined as follows: : total expert score (marks); : total model score (marks). The next step is to import the data into SPPS 19.0 for Pearson correlation analysis based on the defined variables. The analysis results are shown in Table 8.

Table 8.
Correlation analysis results for model scoring results and expert scoring results.
According to Table 8, and are significantly correlated at the 0.01 level, indicating that the model scores are very strongly correlated with the expert scores (correlation coefficient of 0.813). To explore the specific correlation between the two, the study used IBM SPSS Statistics 26 to draw a scatter diagram of them, and we can preliminarily infer that the two are linearly correlated. Based on the inferred linear correlation between the two, the study continued to use IBM SPSS Statistics 26 to perform regression analysis and curve fitting, resulting in a summary of the two models and a table of parameter estimates shown in Table 9, where is the dependent variable and is the independent variable.

Table 9.
Model summary and parameter estimates for model scoring results and expert scoring results.
Based on Table 9, it can be seen that the model summary Sig = 0.000 < 0.01 for the model scoring results and that the expert scoring results are significant at the 0.01 level, representing the very significant relationship of the curve fitting. At the same time, according to the parameter estimates, the linear model of the two can be obtained as follows: = 41.063 + 10.809.
Meanwhile, the fitting curve of the two is shown in Figure 3, where the horizontal coordinate is , the model scoring result, and the vertical coordinate is , the expert scoring result. Based on Figure 3, it can be seen that there is a linear relationship between the two. It further illustrates the correlation between the model scoring results and the expert scoring results and further tests the validity and reliability of the comprehensive evaluation model of the first-level indicators.
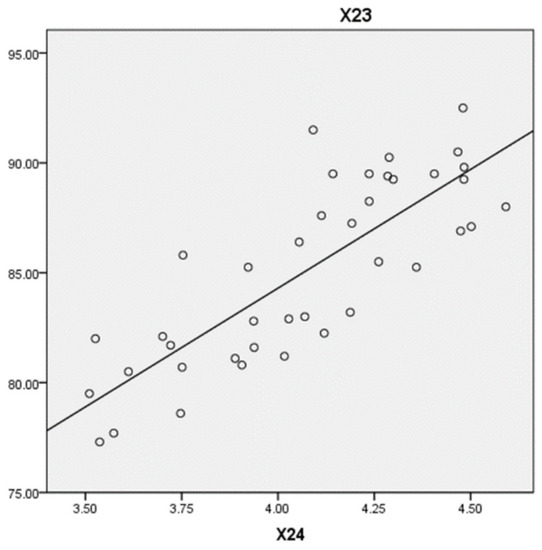
Figure 3.
Linear fitting diagram of model scoring results and expert scoring results.
4.2. Evaluation Model Test Findings
Based on the expert evaluation results in 2021, validation of the evaluation model showed that the correlation between the 2021 evaluation scores and the evaluation model scores reached a significance level of 0.01, with significant coefficients of 0.813 and 0.758. This indicated that the evaluation results and the model evaluation results were highly consistent for the past two years, further demonstrating the validity and reliability of the model.
5. Discussion and Conclusions
5.1. Discussion
Although the evaluation indicators for the management quality of primary and secondary schools are relatively comprehensive in many countries, the complex nature of these indicators often results in significant expenditure in terms of human, material, and financial resources during the evaluation process. For instance, China’s “Management Standards for Compulsory Education Schools” [13] includes 22 second-level evaluation indicators covering areas such as leadership design, faculty team, student development, curriculum and teaching, school management, parent and community participation, and safety and security. Similarly, France’s “Education Regulations” [36] incorporate 21 second-level evaluation indicators for school leadership, faculty team, curriculum design and teaching quality, school environment and facilities, and student management. Likewise, the US’s “Education policy in the United States” [37] entails 25 second-level evaluation indicators for school management, teacher quality, curriculum design and teaching quality, student management, parent and community involvement, and equity and diversity. Further, the UK’s “Education inspection framework in England” [38] includes 23 evaluation indicators for teaching quality and student achievement, creating a positive learning environment, student behavior and discipline, school leadership, management and efficiency, parent and community involvement, school culture, and social responsibility. Lastly, Japan’s “Principles Guide Japan’s Educational System” [39] comprises of 20 second-level evaluation indicators on teaching quality and student development, school management and operation, faculty team building, parent and community involvement, school culture, and social responsibility. We have proposed a structurally scientific and easy-to-use estimation method that avoids the heavy task load typically associated with evaluation processes related to the management quality of primary and secondary schools. On the basis of not affecting the evaluation results, this method reduces the previous 22 evaluation indicators to 5 indicators, enabling rapid estimation of the management quality of primary and secondary schools. This approach not only reduces the burden of the evaluation process but also enhances the overall efficiency of evaluating the management quality of primary and secondary schools, thereby further promoting the evaluation, reform, and development of education equity and sustainability. Finally, based on analysis of the current situation of global primary and secondary school assessments, the following recommendations are proposed:
- (1)
- Optimize evaluation methods and improve evaluation efficiency and accuracy.
The evaluation of school management quality in the compulsory education stage is characterized by a heavy workload, complex content, a long evaluation cycle, and a large amount of human, material, and financial resources. In this context, we should optimize the entire assessment process and link methods in order to achieve the highest evaluation efficiency and accuracy at the lowest cost. In 2022, the Ministry of Education officially issued the Guidelines for Quality Evaluation of General High School [40], which pointed out that in the process of evaluating the quality of secondary school education, it is important to focus on optimizing and improving the methods and techniques of evaluation to continuously enhance the efficiency and accuracy of the evaluation process. In today’s era of information technology development, such as the Internet of Things, the Internet, big data, and artificial intelligence, we should pay attention to the application and implementation of information technology, especially big data, in the assessment of school management quality at the compulsory education stage. Leveraging information technology can help reduce the workload, difficulty, and duration of the entire evaluation process, improve the efficiency and scientific nature of the evaluation process, and ensure the accuracy and precision of the evaluation results. This will ultimately contribute to sustainable development of the evaluation of primary and secondary school management quality.
- (2)
- Streamline the evaluation process and reduce assessment costs without compromising accuracy.
When dealing with the complex evaluation process for the quality of compulsory education schools, it is essential to simplify evaluation criteria, materials, human resources, and financial expenses without compromising the quality of the evaluation. Currently, the evaluation process follows the 88 management requirements outlined in the “Standard for School Management Quality of Compulsory Education,” with 2.8744 million evaluation materials submitted annually by the 213,000 compulsory education schools nationwide. This creates a huge workload, a high level of difficulty, and the significant consumption of human, material, and financial resources. Therefore, it is necessary to continuously optimize the methods and techniques of evaluation, streamline the complexity and difficulty of the evaluation process, and achieve accurate evaluations of school management quality at a lower cost, ultimately promoting the rational, fair, and just distribution of compulsory education resources. By adhering to the principles of objectivity and fairness, evaluating to promote development, and promoting education equity, we can facilitate the healthy, sustainable development and progress of compulsory education schools in China. At the same time, the evaluation indicators and processes of school management in the compulsory education stage of all countries in the world are just as complex. In terms of evaluation indicators, the United States has nine first-level indicators, the United Kingdom has seven first-level indicators, and Japan has eight first-level indicators. We should try to simplify the complex evaluation indicators without affecting evaluation results to improve evaluation efficiency and reduce evaluation costs.
- (3)
- Countries should attach importance to the evaluation of teacher development.
By comparing the evaluation indicators and processes of school management in the current compulsory education stage around the world, we found that China focuses on evaluation of the development of teachers and students, mainly in leading the professional development of teachers and improving the quality of education and teaching. The focus of evaluation in the United States is dynamic, including school tasks, school objectives, financial conditions, teaching facilities, libraries and collections, teaching plans, teaching staff and level, student admission conditions, and degree awarding. The UK focuses on evaluation of the teaching effect of the curriculum, including curriculum teaching, evaluation and feedback, academic support, organization and management, learning resources, personal development, and overall satisfaction. Japan focuses on evaluation of students’ personal development, including respecting students’ individual choices, cultivating students’ personalities, and guiding students to learn actively. From the perspective of school management evaluation at the compulsory education stage in various countries, it is a people-oriented evaluation; However, it mainly focuses on the evaluation of students and curriculum learning effects, ignoring the evaluation of teachers’ development because, for school education, teachers are still in the leading position. Although the student-centered learning method has been advocated, students at the compulsory education stage cannot learn independently, and the habit of independent learning has not been formed yet. Thus, the guidance, supervision, and management role of teachers is particularly important at this stage. Therefore, when evaluating the quality of school management, we should not ignore the importance of teacher development evaluation.
5.2. Conclusions
- (1)
- Research conclusion
We analyzed data from 40 primary and secondary schools in Q province using big data technology and based analysis on the 22 school management quality evaluation indicators in the “Management Standards for Compulsory Education Schools” issued by the Chinese Ministry of Education. The estimation results showed that 5 main indicators had a significant impact on the estimated results among the 22 indicators: improving students’ moral quality (), strengthening teachers’ management and professional ethics (), establishing an evaluation system to promote students’ development (), creating a respectful and inclusive school culture (), and improving the capacity for scientific management according to law (). Furthermore, a rapid estimation model for school management quality in primary and secondary schools was constructed based on these five main indicators using the formula = 0.121 + 0.399 + 0.235 + 0.141 + 0.103. Finally, the model’s validity and reliability were further confirmed by testing it with 2021 data, which showed that the evaluation results were highly consistent with the model results.
- (2)
- Research Limitations
The study’s sample data were obtained from the school management quality evaluation data of 40 primary and secondary schools in Q province, which limits the generalizability of the research findings and may result in regional differences. Additionally, the evaluation model requires more data to be continuously trained by the machine and achieve higher evaluation accuracy. In the next phase of our research, we plan to expand our research subjects to include school management quality evaluation data from primary and secondary schools in other provinces to avoid any errors in the evaluation results that might arise due to regional differences or insufficient sample size.
Author Contributions
Conceptualization, G.M.; methodology, G.M.; software, G.M.; formal analysis, G.M.; investigation, G.M. and Y.L.; writing—original draft, G.M.; writing—review and editing, G.M. and Z.L.; supervision, M.L., N.Y. and Z.L.; funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the Key Special Project for the High-Quality Development of Basic Education in Fujian Province Education Science Planning (FJWTZD21-06) and the Fujian Social Science Foundation (FJ2022BF015).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful for the help and technical support of other authors and appreciate the financial support provided by the foundation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- United States THE 17 GOALS of SDGs. Available online: https://sdgs.un.org/goals (accessed on 5 June 2023).
- Ellington, H. Handbook of Educational Technology; Kogan Page: London, UK, 1993. [Google Scholar]
- Jerrim, J.; Sims, S. School accountability and teacher stress: International evidence from the OECD TALIS study. Educ. Assess. Eval. Account. 2022, 34, 5–32. [Google Scholar] [CrossRef]
- Sanders, J.R. A vision for evaluation. Am. J. Eval. 2001, 22, 363–366. [Google Scholar] [CrossRef]
- McNamara, G.; Brown, M.; Gardezi, S.; O Hara, J.; O Brien, S.; Skerritt, C. Embedding Self-Evaluation in School Routines. Sage Open 2021, 11, 1915385864. [Google Scholar] [CrossRef]
- European Education Area Quality Education and Training for All. Available online: https://education.ec.europa.eu/education-levels/school-education/quality-assurance#:~:text=Quality%20assurance%20involves%20the%20systematic%20review%20of%20educational,of%20teachers%20and%20school%20leaders%2C%20and%20student%20assessments (accessed on 5 June 2023).
- Department of Education and Skills in Ireland School Self-Evaluation Guidelines 2016–2020. Available online: https://assets.gov.ie/25263/dcc85452ad6d451f89ed8e7b1967f200.pdf (accessed on 5 June 2023).
- Hong Kong Education Bureau School Self-Evaluation. Available online: https://www.edb.gov.hk/en/sch-admin/sch-quality-assurance/sse/sse.html#guideline (accessed on 5 June 2023).
- The Chinese Ministry of Education. Provisional Regulations on the Evaluation of Education in Ordinary Higher Education Institutions. Available online: http://www-moe-gov-cn.vpn.sdnu.edu.cn/srcsite/A02/s5911/moe_621/199010/t19901031_81932.html (accessed on 1 July 2022).
- The Chinese Ministry of Education. Opinions of the Ministry of Education on Strengthening and Improving the Comprehensive Quality Evaluation of Ordinary High School Students. Available online: http://www.moe.gov.cn/srcsite/A06/s3732/201808/t20180807_344612.html (accessed on 1 July 2020).
- The Chinese Ministry of Education. Notice of the Ministry of Education on Issuing the “Management Standards for Compulsory Education Schools (Trial)”. Available online: http://www.moe.gov.cn/srcsite/A06/s3321/201408/t20140804_172861.html (accessed on 5 June 2023).
- The State Council of China. Outline of the National Medium and Long Term Education Reform and Development Plan (2010–2020). Available online: http://www.gov.cn/jrzg/2010-07/29/content_1667143.htm (accessed on 5 June 2023).
- The Chinese Ministry of Education. Notice of the Ministry of Education on Issuing the “Management Standards for Compulsory Education Schools”. Available online: http://www.moe.gov.cn/srcsite/A06/s3321/201712/t20171211_321026.html (accessed on 5 June 2023).
- Stufflebeam, D.L. The CIPP Model for Program Evaluation. In Evaluation Models: Viewpoints on Educational and Human Services Evaluation; Madaus, G.F., Scriven, M.S., Stufflebeam, D.L., Eds.; Springer: Dordrecht, The Netherlands, 1983; pp. 117–141. [Google Scholar]
- Aziz, S.; Mahmood, M.; Rehman, Z. Implementation of CIPP Model for Quality Evaluation at School Level: A Case Study. J. Educ. Educ. Dev. 2018, 5, 189. [Google Scholar] [CrossRef]
- Zhang, S. Study of the Evaluation Framework of Management Quality of Primary and Secondary Schools Based on Resource-Based Theory. Creat. Educ. 2017, 8, 893–900. [Google Scholar] [CrossRef]
- Şahin, S.; Kılıç, A. School Self Evaluation Model Suggestion. Int. J. Instr. 2018, 11, 193–206. [Google Scholar] [CrossRef]
- Bouranta, N.; Psomas, E.; Antony, J. Findings of quality management studies in primary and secondary education: A systematic literature review. TQM J. 2020, 33, 729–769. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Du, X.; Li, C.; Lu, J.; Zhao, S.; Zhou, X. Big data challenge: A data management perspective. Front. Comput. Sci.-China 2013, 7, 157–164. [Google Scholar] [CrossRef]
- Chandarana, P.; Vijayalakshmi, M. IEEE Big Data Analytics Frameworks. In Proceedings of the 2014 International Conference on Circuits, Systems, Communication and Information Technology Applications (CSCITA), Mumbai, India, 4–5 April 2014; pp. 430–434. [Google Scholar]
- Zhang, R.; Zhao, W.; Wang, Y. Big data analytics for intelligent online education. J. Intell. Fuzzy Syst. 2021, 40, 2815–2825. [Google Scholar] [CrossRef]
- Wu, G. A New Paradigm of Educational Technology Research based on Big Data. Agro. Food Ind. Hi-Tech 2017, 28, 599–603. [Google Scholar]
- Islam, A.Y.M.A.; Ahmad, K.; Rafi, M.; Ming, Z.J. Performance-based evaluation of academic libraries in the big data era. J. Inf. Sci. 2021, 47, 458–471. [Google Scholar] [CrossRef]
- Lyu, B.; Chen, J.; Wang, N. IEEE Teaching Quality Evaluation Model for Human Resource Development and Management Major under the Background of Big Data. In Proceedings of the 5th International Conference on Smart Grid and Electrical Automation (ICSGEA), Zhangjiajie, China, 13–14 June 2020; pp. 529–533. [Google Scholar]
- Li, L. IEEE Evaluation Model of Education Service Quality Satisfaction in Colleges and Universities Dependent on Classification Attribute Big Data Feature Selection Algorithm. In Proceedings of the International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019; pp. 645–649. [Google Scholar]
- Liu, H.; Li, J.; Peng, J. IEEE Big Data Technology Applied to Learning Behavior Evaluation System. In Proceedings of the International Conference on Big Data and Artificial Intelligence (BDAI), Beijing, China, 22–24 June 2018; pp. 10–17. [Google Scholar]
- Jiang, J.; Zeng, L.; Zhi, L. IEEE Research on the Process Data Mining of Online Wisdom Learning. In Proceedings of the 4th IEEE International Conference on Big Data Analytics (ICBDA), Suzhou, China, 15–18 March 2019; pp. 135–139. [Google Scholar]
- Li, Y.; Zhu, F.; Li, P.; Wang, R. IEEE Design of Higher Education Quality Monitoring and Evaluation Platform Based on Big Data. In Proceedings of the 12th International Conference on Computer Science and Education (ICCSE), London, UK, 22–25 August 2017; pp. 337–342. [Google Scholar]
- Yu, W.; Zhao, L.; He, X.; Zhou, J.; Cheng, T.; Xue, C.; Yang, F. IEEE A New Evaluation System for Scholars and Majors Based on Big-Data Techniques. In Proceedings of the 30th IEEE International Parallel and Distributed Processing Symposium (IPDPS), Chicago, IL, USA, 23–27 May 2016; pp. 1477–1480. [Google Scholar]
- Mao, C.; Zou, S.; Yin, J. Educational Evaluation Based on Apriori-Gen Algorithm. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 6555–6564. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Zhang, F.; Li, J.; Guo, T.; Aziz, A.; Jin, A.; Xia, F. Educational Big Data: Predictions, Applications and Challenges. Big Data Res. 2021, 26, 100270. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, Q.; Qing, W.; Zhu, L.; Cheng, S.; Wang, H. IOP The Present of Education Big Data Research in China: Base on the Bibliometric Analysis and Knowledge Mapping. In Proceedings of the International Symposium on Power Electronics and Control Engineering (ISPECE), Tianjin, China, 22–24 November 2019; Volume 1187. [Google Scholar]
- Fujian Provincial Department of Education Notice of the Education Department of Fujian Province on the Construction and Evaluation of “Standardized Schools for Compulsory Education Management”. Available online: http://www.fuzhou.gov.cn/zgfzzt/jy/zdjy/201611/t20161115_116591.htm (accessed on 17 November 2020).
- Wu, J.; Otsuka, Y. Adaptation of leadership competence to climate change education: Conceptual foundations, validation, and applications of a new measure. Leadership 2022, 18, 247–265. [Google Scholar] [CrossRef]
- Bai, P. Sphericity test in a GMANOVA-MANOVA model with normal error. J. Multivar. Anal. 2009, 100, 2305–2312. [Google Scholar] [CrossRef]
- French Civil Service Legislation and Official Policy Documents. Available online: https://eurydice.eacea.ec.europa.eu/national-education-systems/france/legislation-and-official-policy-documents (accessed on 6 June 2023).
- The Federal Government Education Policy in the United States. Available online: https://ballotpedia.org/Education_policy_in_the_United_States (accessed on 6 June 2023).
- UK Government. Education Inspection Framework in England. Available online: https://www.gov.uk/government/publications/education-inspection-framework/education-inspection-framework (accessed on 6 June 2023).
- The Japanese Department of Education Principles Guide Japan’s Educational System. Available online: https://www.mext.go.jp/en/policy/education/overview/index.htm (accessed on 6 June 2023).
- The Chinese Ministry of Education. The Ministry of Education Has Issued the “Guidelines for Evaluating the Quality of Regular High School Education”. Available online: http://www.moe.gov.cn/jyb_xwfb/gzdt_gzdt/s5987/202201/t20220110_593455.html (accessed on 5 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).