Research on Energy Absorption Characteristics of Bouligand Biomimetic Structure Based on CFRP Composite Materials
Abstract
1. Introduction
1.1. Overview of CFRP Materials
1.2. Application of CFRP in the Field of Protection
1.3. Common CFRP Lamination Angles
1.4. Overview of Bouligand Structure
1.5. Overview of Bouligand Structure
1.6. Limitations of the Current Study
2. Model and Damage Criterion
2.1. Verification of Model Validity
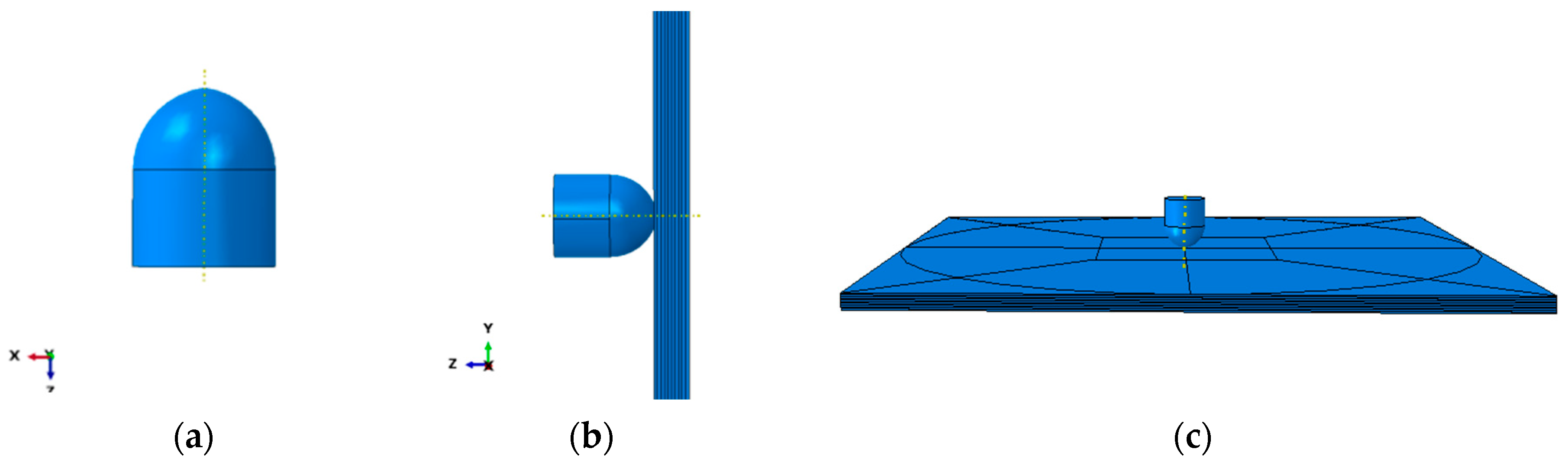
2.2. Preliminary Modeling Process
2.3. The Hashin 3D Criterion for Fiber-Reinforced Composites
2.3.1. Hashin Damage Criteria
2.3.2. Quads Damage Criteria
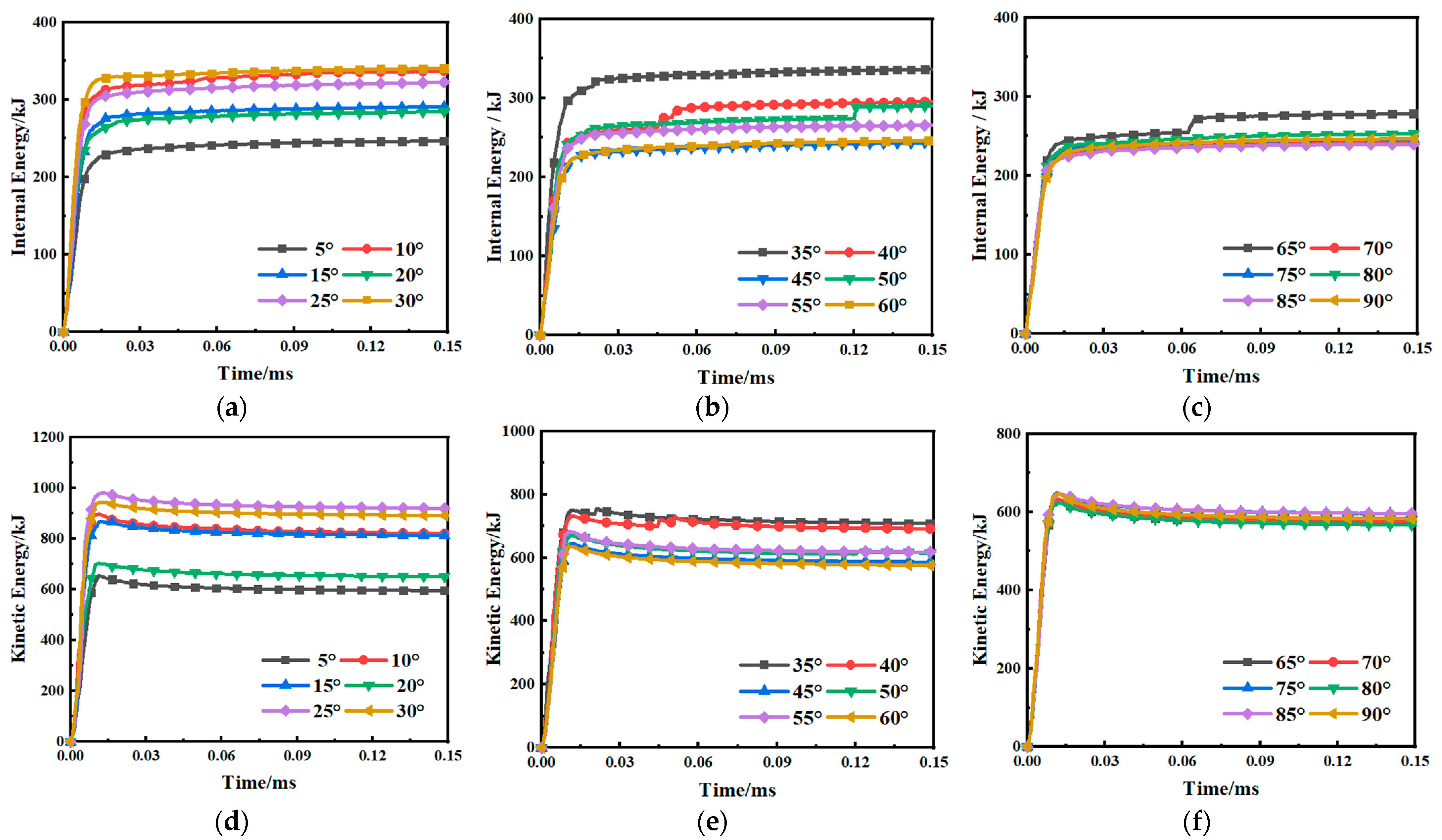
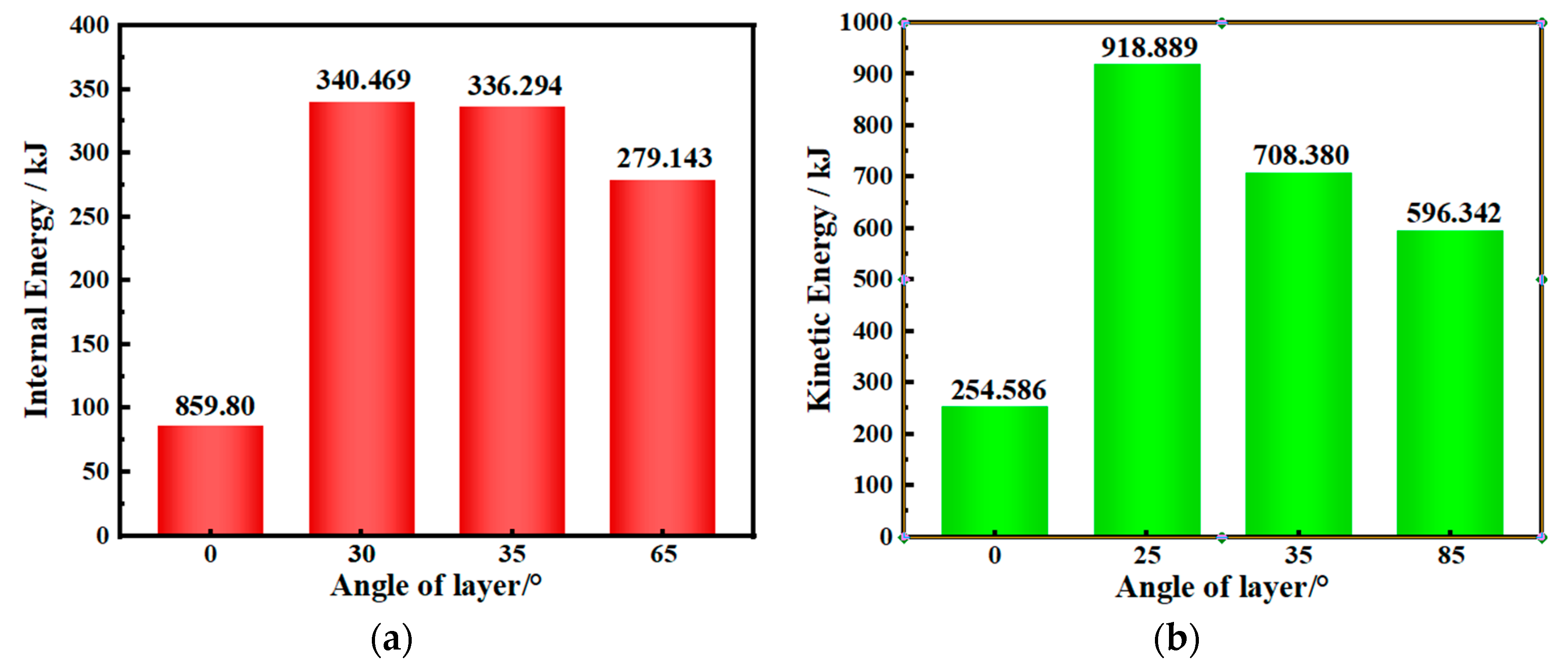
3. Numerical Simulation Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- González, E.V.; Maimí, P.; Martín-Santos, E.; Soto, A.; Cruz, P.; Martín de la Escalera, F.; Sainz de Aja, J.R. Simulating drop-weight impact and compression after impact tests on composite laminates using conventional shell finite elements. Int. J. Solids Struct. 2018, 144–145, 230–247. [Google Scholar] [CrossRef]
- Byar, A.D.; Pang, J.K.; Iqbal, J.; Ko, J.; Rassaian, M. Determination of Ballistic Limit for IM7/8552 Using LS-DYNA. In Proceedings of the 2018 AIAA SciTech Forum, Kissimmee, FL, USA, 8–12 January 2018; p. 11. [Google Scholar]
- Nassiraei, H.; Rezadoost, P. SCFs in tubular X-connections retrofitted with FRP under in-plane bending load. Compos. Struct. 2021, 274, 114314. [Google Scholar] [CrossRef]
- Melis, M.; Pereira, M.; Goldberg, R.K.; Rassaian, M. Dynamic Impact Testing and Model Development in Support of NASA’s Advanced Composites Program. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Kissimmee, FL, USA, 2018. [Google Scholar]
- Nassiraei, H.; Rezadoost, P. Static capacity of tubular X-joints reinforced with fiber reinforced polymer subjected to compressive load. Eng. Struct. 2021, 236, 112041. [Google Scholar] [CrossRef]
- Hoffarth, C.; Khaled, B.; Rajan, S.D.; Goldberg, R.; Carney, K.; DuBois, P.; Blankenhorn, G. Using Tabulated Experimental Data to Drive an Orthotropic Elasto-Plastic Three-Dimensional Model for Impact Analysis. In Proceedings of the LS-DYNA International Conference, Detroit, MI, USA, 14–16 May 2014. [Google Scholar]
- Ogihara, S.; Takeda, N.; Kobayashi, S.; Kobayashi, A. Effects of stacking sequence on microscopic fatigue damage development in quasi-isotropic CFRP laminates with interlaminar-toughened layers. Compos. Sci. Technol. 1999, 59, 1387–1398. [Google Scholar] [CrossRef]
- Hoffarth, C.; Khaled, B.; Shyamsunder, L.; Rajan, S.D. Development of a Tabulated Material Model for Composite Material Failure, MAT213: Part 1: Theory, Implementation, Verification & Validation; U.S. Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2020.
- Shyamsunder, L.; Khaled, B.; Rajan, S.D.; Pereira, J.M.; DuBois, P.; Blankenhorn, G. Numerical validation of composite panel impact tests. Int. J. Impact Eng. 2022, 159, 104032. [Google Scholar] [CrossRef]
- Meola, C.; Carlomagno, G.M. Infrared thermography of impact-driven thermal effects. Appl. Phys. A 2009, 96, 759–762. [Google Scholar] [CrossRef]
- Meola, C.; Carlomagno, G.M. Impact damage in GFRP: New insights with infrared thermography. Compos. Part. Appl. Sci. Manuf. 2010, 41, 1839–1847. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. Life prediction of metals undergoing fatigue load based on temperature evolution. Mater. Sci. Eng. A 2010, 527, 1555–1559. [Google Scholar] [CrossRef]
- Meola, C.; Carlomagno, G.M. Infrared thermography to evaluate impact damage in glass/epoxy with manufacturing defects. Int. J. Impact Eng. 2014, 67, 1–11. [Google Scholar] [CrossRef]
- Boccardi, S.; Carlomagno, G.M.; Simeoli, G.; Russo, P.; Meola, C. Evaluation of impact-affected areas of glass fibre thermoplastic composites from thermographic images. Meas. Sci. Technol. 2016, 27, 075602. [Google Scholar] [CrossRef]
- Koyanagi, J.; Mochizuki, A.; Higuchi, R.; Tan, V.B.C.; Tay, T.E. Finite element model for simulating entropy-based strength-degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings. Int. J. Fatigue 2022, 165, 107204. [Google Scholar] [CrossRef]
- Lawrence Sy, B.; Oguamanam, D.; Bougherara, H. Impact response of a new kevlar/flax/epoxy hybrid composite using infrared thermography and high-speed imaging. Compos. Struct. 2022, 280, 114885. [Google Scholar] [CrossRef]
- Goto, K.; Arai, M.; Kano, Y.; Hara, E.; Ishikawa, T. Compressive fracture aspect of thick quasi-isotropic carbon fiber reinforced plastic laminates. Compos. Sci. Technol. 2019, 181, 107706. [Google Scholar] [CrossRef]
- Kramer, S.L.B.; Tighe, R. (Eds.) Conference Proceedings of the Society for Experimental Mechanics Series; Springer International Publishing: Cham, Switzerland, 2021; pp. 99–104. [Google Scholar]
- Ogihara, S.; Takeda, N.; Kobayashi, S.; Kobayashi, A. Damage mechanics characterization of transverse cracking behavior in quasi-isotropic CFRP laminates with interlaminar-toughened layers. Int. J. Fatigue 2002, 24, 93–98. [Google Scholar] [CrossRef]
- Roberts-Wollmann, C.L.; Kreger, M.E.; Rogowsky, D.M.; Breen, J.E. Stresses in External Tendons at Ultimate. ACI Struct. J. 2005, 102, 206–213. [Google Scholar]
- Tian, D.; Zhou, X. A continuum-kinematics-inspired peridynamic model of anisotropic continua: Elasticity, damage, and fracture. Int. J. Mech. Sci. 2021, 199, 106413. [Google Scholar] [CrossRef]
- Yamada, Y.; Iwata, K.; Kadowaki, T.; Sumiya, T. Method of reduced variables for stiffness degradation process of unidirectional CFRP composites subjected to alternating bending. Compos. Sci. Technol. 2017, 138, 117–123. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation. Compos. Part. Appl. Sci. 2006, 37, 766–777. [Google Scholar] [CrossRef]
- Cantwell, W.J.; Morton, J. Impact perforation of carbon fibre reinforced plastic. Compos. Sci. Technol. 1990, 38, 119–141. [Google Scholar] [CrossRef]
- Lee, S.W.R.; Sun, C.T. Dynamic penetration of gahite/epoxy laminates impacted byablunt-ended projectil. Compos. Sci. Technol. 1993, 49, 369–380. [Google Scholar] [CrossRef]
- Goldsmith, W. Dharan CKH and Chang H. Quasi-static and ballsi perfration of carbonfiber laminates. Int. J. Solids Struct. 1995, 32, 89–103. [Google Scholar] [CrossRef]
- Ulven, C.; Vaidya, U.K.; Hosur, M.V. Efect of prjctile shape during baliii pefrationo of VARTM carbon/epoxy composite panels. Compos. Struct. 2003, 61, 143–150. [Google Scholar] [CrossRef]
- Wen, H.M. Preicting the pentraion and peforarion of FRP laminates struck normally by pojectles with dffrer nose shapes. Compos. Struct. 2000, 49, 321–329. [Google Scholar] [CrossRef]
- Wen, H.M. Penetration and perfration of thick FRP laminates. Compos. Sci. Technol. 2001, 61, 1163–1172. [Google Scholar] [CrossRef]
- Sokolović, N.M.; Gavrilović-Grmuša, I.; Zdravković, V.; Ivanović-Šekularac, J.; Pavićević, D.; Šekularac, N. Flexural Properties in Edgewise Bending of LVL Reinforced with Woven Carbon Fibers. Materials 2023, 16, 3346. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Kim, S.J.; Min, K.J.; Choi, J.C.; Eun, H.S.; Song, B.K. A Study on Tensile Behavior According to the Design Method for the CFRP/GFRP Grid for Reinforced Concrete. Materials 2022, 15, 357. [Google Scholar] [CrossRef]
- Zhang, J.; Rao, J.; Ma, L.; Wen, X. Investigation of the Damping Capacity of CFRP Raft Frames. Materials 2022, 15, 653. [Google Scholar] [CrossRef]
- Abdellah, M.Y.; Zuwawi, A.-R.; Azam, S.A.; Hassan, M.K. A Comparative Study to Evaluate the Essential Work of Fracture to Measure the Fracture Toughness of Quasi-Brittle Material. Materials 2022, 15, 4514. [Google Scholar] [CrossRef]
- Khozeimeh, M.A.; Fotouhi, R.; Moazed, R. Static and Vibration Analyses of a Composite CFRP Robot Manipulator. J. Compos. Sci. 2022, 6, 196. [Google Scholar] [CrossRef]
- Ge, F.; Lin, Y.; Zhang, F.; Zhang, Z.; Wang, M. Crushing Characteristics Comparison between Aluminum/CFRP and Aluminum/CFRP/Aluminum Hybrid Tubes. Polymers 2022, 14, 4034. [Google Scholar] [CrossRef]
- Abdellah, M.Y.; Hassan, M.K.; AlMalki, A.-A.; Mohamed, A.F.; Backar, A.H. Finite Element Modelling of Wear Behaviors of Composite Laminated Structure. Lubricants 2022, 10, 317. [Google Scholar] [CrossRef]
- Rao, K.S.; Varadarajan, Y.; Rajendra, N. Erosive Wear Behaviour of Carbon Fiber-reinforced Epoxy Composite. Mater. Today Proc. 2015, 2, 2975–2983. [Google Scholar] [CrossRef]
- Korim, N.S.; Abdellah, M.Y.; Dewidar, M.; Abdelhaleem, A.M. Crushable finite element modeling of mechanical properties of titanium foam. Int. J. Sci. Eng. Res. 2015, 6, 1221–1227. [Google Scholar]
- Abdellah, M.Y. Essential work of fracture assessment for thin aluminium strips using finite element analysis. Eng. Fract. Mech. 2017, 179, 190–202. [Google Scholar] [CrossRef]
- Fabritius, H.O.; Sachs, C.; Triguero, P.R.; Raabe, D. Influence of structural principles on the mechanics of a biological fiber-based composite material with hierarchical organization: The exoskeleton of the lobster Homarus americanus. Adv. Mater. 2009, 21, 391–400. [Google Scholar] [CrossRef]
- Grunenfelder, L.K.; Suksangpanya, N.; Salinas, C.; Milliron, G.; Yaraghi, N.; Herrera, S.; Evans-Lutterodt, K.; Nutt, S.R.; Zavattieri, P.; Kisailus, D. Bio-inspired impact-resistant composites. Acta Biomater. 2014, 10, 3997–4008. [Google Scholar] [CrossRef]
- Whitney, J. Structural Analysis of Laminated Anisotropic Plates; CRC Press: Lancaster, PA, USA, 1987. [Google Scholar]
- Alqam, M.; Alkhairi, F.; Naaman, A. An Improved Methodology for the Prediction of the Stress at Ultimate in Unbonded Internal and External Steel Tendons. Arab. J. Sci. Eng. 2020, 45, 7915–7954. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Ashby, M.F. The mechanical efficiency of natural materials. The mechanical efficiency of natural materials. Phil. Mag. 2004, 84, 2167–2186. [Google Scholar] [CrossRef]
- Apichattrabrut, T.; Ravi-Chandar, K. Helicoidal composites. Mech. Adv. Mater. Struct. 2006, 13, 61–76. [Google Scholar] [CrossRef]
- Mencattelli, L.; Pinho, S.T. Realising bio-inspired impact damage-tolerant thin-ply CFRP Bouligand structures via promoting diffused sub-critical helicoidal damage. Compos. Sci. Technol. 2019, 182, 107684. [Google Scholar] [CrossRef]
- Mencattelli, L.; Pinho, S.T. Herringbone-bouligand cfrp structures: A new tailorable damage-tolerant solution for damage containment and reduced delaminations. Compos. Sci. Technol. 2020, 190, 108047. [Google Scholar] [CrossRef]
- Yang, W.; Chen, I.H.; Mckittrick, J.; Meyers, M.A. Flexible Dermal Armor in Nature. JOM 2012, 64, 475–485. [Google Scholar] [CrossRef]
- Luz, G.M.; Mano, J.F. Biomimetic design of materials and biomaterials inspired by the structure of nacre. Philos. Trans. A Math. Phys. Eng. Sci. 2009, 367, 1587–1605. [Google Scholar] [CrossRef] [PubMed]
- Bouligand, Y. Twisted fifibrous arrangements in biological materials and cholesteric mesophases. Tissue Cell 1972, 4, 189–217. [Google Scholar] [CrossRef] [PubMed]
- Weaver, J.C.; Milliron, G.W.; Miserez, A.; Evans-Lutterodt, K.; Herrera, S.; Gallana, I.; Mershon, W.J.; Swanson, B.; Zavattieri, P.; DiMasi, E.; et al. The stomatopod dactyl club: A formidable damage-tolerant biological hammer. Science 2012, 336, 1275–1280. [Google Scholar] [CrossRef]
- Giraud, M.M.; Castanet, J.; Meunier, F.J.; Bouligand, Y. The fifibrous structure of coelacanth scales: A twisted ‘Plywood’. Tissue Cell. 1978, 10, 671–686. [Google Scholar] [CrossRef]
- Ginzburg, D.; Pinto, F.; Iervolino, O.; Meo, M. Damage tolerance of bio-inspired helicoidal composites under low velocity impact. Compos. Struct. 2017, 161, 187–203. [Google Scholar] [CrossRef]
- Xingyuan, Z.; Zhen, W.; Yongcun, L.; Yunbo, L.; Zhang, Q. Improved strength and toughness of bioinspired Bouligand architecture composite by discontinuous carbon fiber. J. Phys. Conf. Ser. 2021, 1906, 012030. [Google Scholar]
- An, Y.; Yang, Y.; Jia, Y.; Han, W.; Cheng, Y. Mechanical properties of biomimetic ceramic with Bouligand architecture. J. Am. Ceram. Soc. 2022, 105, 2385–2391. [Google Scholar] [CrossRef]
- Yuan, Z.; Guoqi, T.; Mingyang, Z.; Qin, Y.; Zengqian, L.; Yanyan, L.; Jian, Z.; Da, J.; Faheng, W.; Longchao, Z.; et al. Bioinspired tungsten-copper composites with Bouligand-type architectures mimicking fish scales. J. Mater. Sci. Technol. 2022, 96, 21–30. [Google Scholar]
- Lorenzo, M.; Silvestre, T.P. Ultra-thin-ply CFRP Bouligand bio-inspired structures with enhanced load-bearing capacity, delayed catastrophic failure and high energy dissipation capability. Pinho Compos. Part A 2020, 129, 105655. [Google Scholar]
- Ouyang, W.; Gong, B.; Wang, H.; Scarpa, F.; So, B.; Peng, H.X. Identifying optimal rotating pitch angles in composites with Bouligand structure. Compos. Commun. 2021, 23, 100602. [Google Scholar] [CrossRef]
- Xu, S.; Chen, P.H. Prediction of low velocity impact damage in carbon–epoxy laminates. Compos. Part A Appl. Sci. Manuf. 2002, 33, 361. [Google Scholar] [CrossRef]
- Nuruzzaman, D.M.; Chowdhury, M.A.; Rahaman, M.L. Effect of duration of rubbing and normal load on friction coefficient for polymer and composite materials. Ind. Lubr. Tribol. 2011, 63, 320–326. [Google Scholar] [CrossRef]
- Mohagheghian, I.; Wang, Y.; Zhou, J.; Yu, L.; Guo, X.; Yan, Y.; Charalambides, M.N.; Dear, J.P. Deformation and damage mechanisms of laminated glass windows subjected to high velocity soft impact. Int. J. Solids. Struct. 2017, 109, 46. [Google Scholar] [CrossRef]
- Palomar, M.; Lozano-Mínguez, E.; Rodríguez-Millán, M.; Miguélez, M.H.; Giner, E. Relevant factors in the design of composite ballistic helmets. Compos. Struct. 2018, 201, 49. [Google Scholar] [CrossRef]
- Heimbs, S.; Heller, S.; Middendorf, P.; Hähnel, F.C.; Weiße, J. Low velocity impact on CFRP plates with compressive preload:test and modelling. Int. J. Impact. Eng. 2009, 36, 1182–1193. [Google Scholar] [CrossRef]
- Schwab, M.; Todt, M.; Tauchner, J.; Schlie, D.; Pettermann, H.E. Modeling, simulation, and experiments of high velocity impact on laminated composites. Compos. Struct. 2018, 205, 42. [Google Scholar] [CrossRef]
- Duarte, A.; Herszberg, I.; Paton, R. Impact resistance and tolerance of interleavedtape laminates. Compos. Struct. 1999, 47, 753–758. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Shor, O.; Vazir, R. Adaptive insertion of cohesive elements for simulation of delamination in laminated composite materials. Eng. Fract. Mech. 2015, 146, 121–138. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear Strength of Joints in Precast Posttensioned Segmental Bridges During 1959–2019, Review and Analysis. Structures 2019, 20, 527–542. [Google Scholar] [CrossRef]

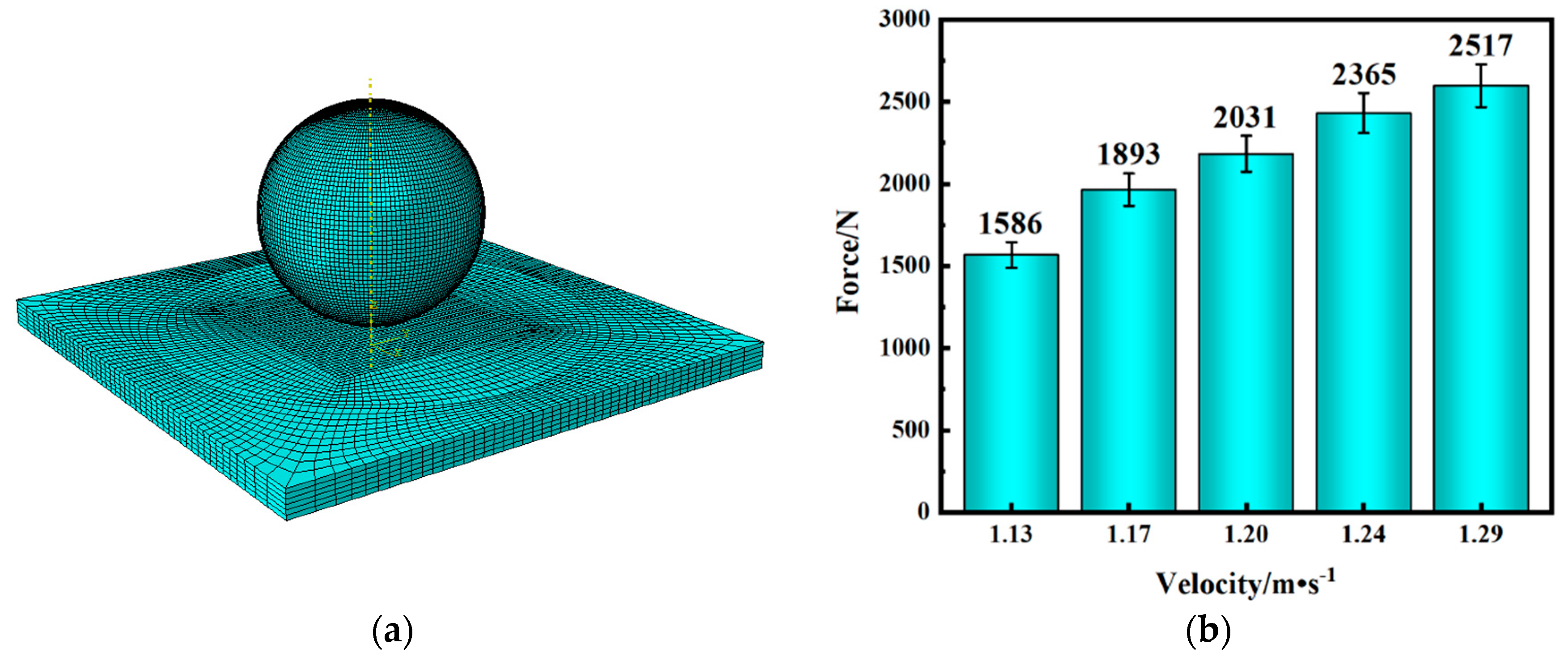
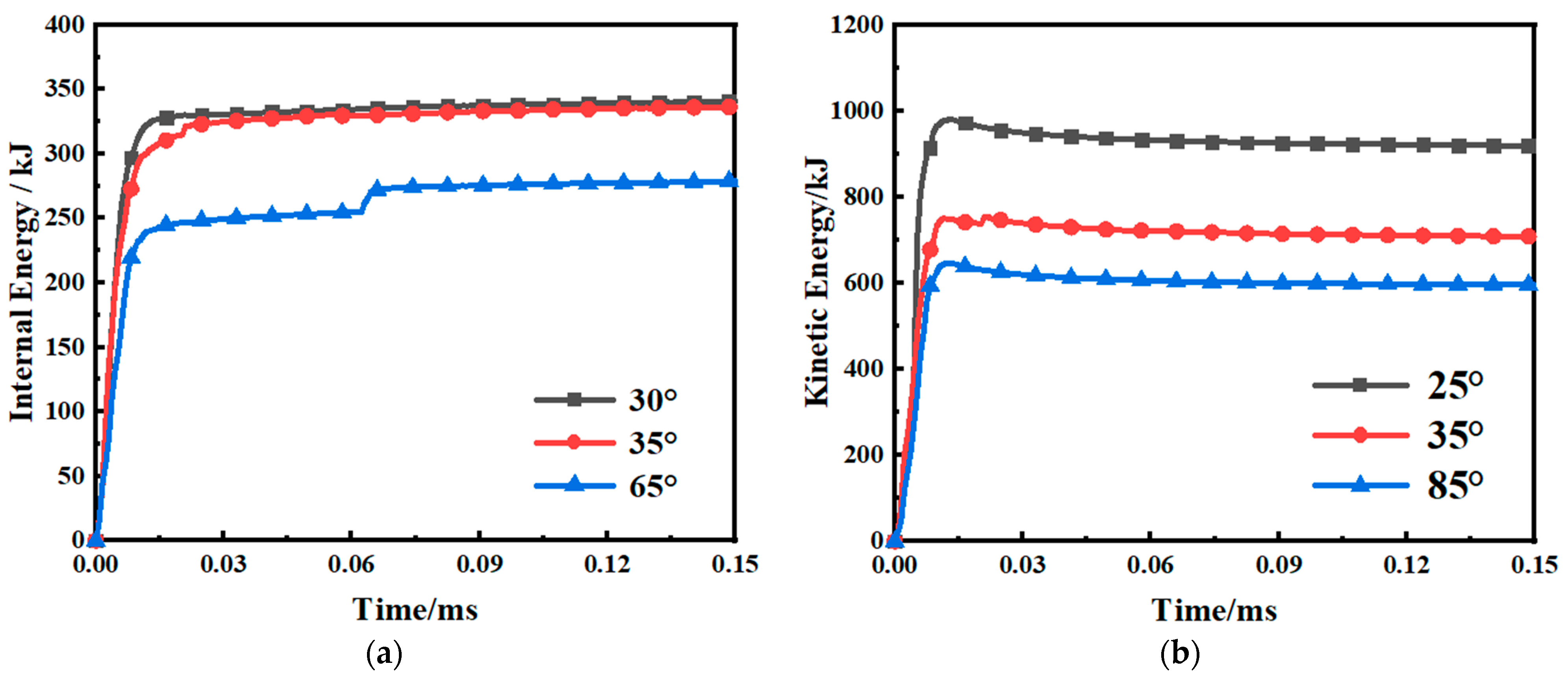
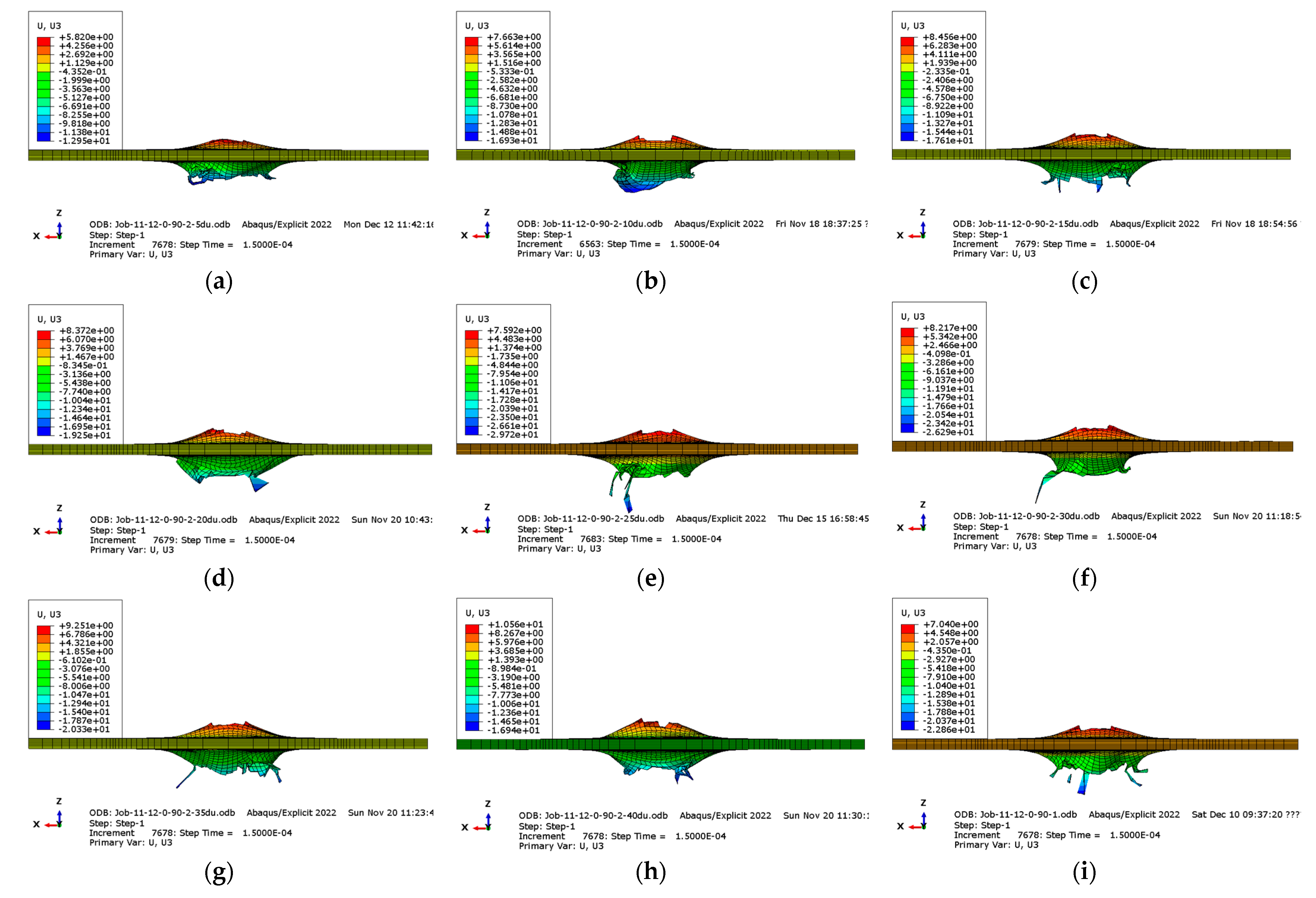
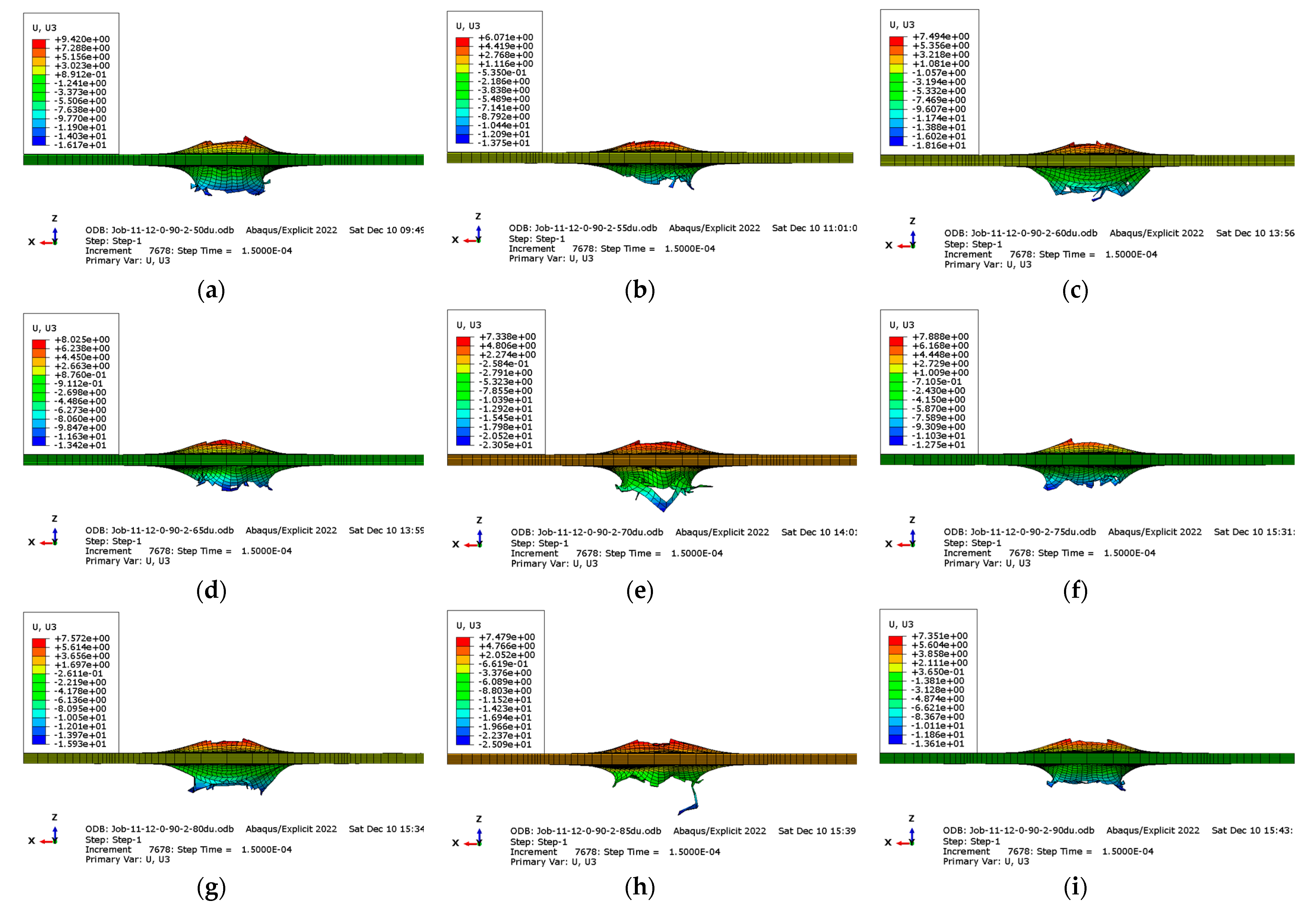
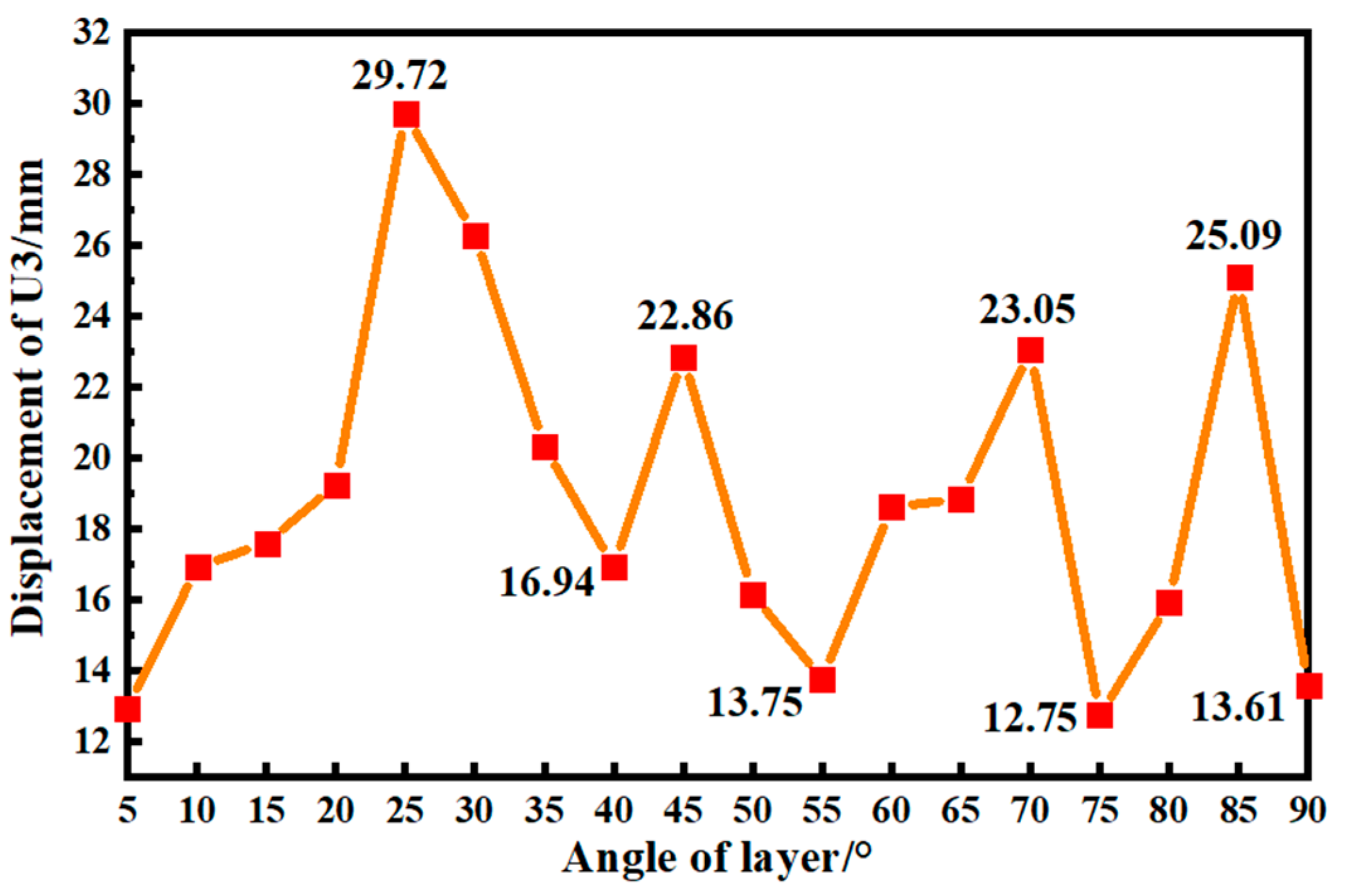
| Impact Velocity (m·s−1) | Experimental Maximum Force (N) | Simulated Maximum Force (N) | Average Error (%) |
|---|---|---|---|
| 1.13 | 1608 | 1567 | 2.55 |
| 1.17 | 1840 | 1965 | 6.79 |
| 1.20 | 1986 | 2183 | 9.92 |
| 1.24 | 2247 | 2431 | 8.19 |
| 1.29 | 2501 | 2597 | 3.84 |
| Parameter | Numerical Value | Parameter | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|---|---|
| E1/MPa | 138,000 | E2/MPa | 9040 | µ12 | 0.305 |
| G12/MPa | 4710 | G13/MPa | 4710 | G23/MPa | 4000 |
| YC/MPa | 202 | YT/MPa | 71.4 | XC/MPa | 1188 |
| XT/MPa | 1696 | S1/MPa | 102 | S2/MPa | 90 |
| ρ/(t∙m−3) | 2.7 × 10−9 |
| Parameter | Numerical Value | Parameter | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|---|---|
| Enn/MPa | 3000 | Ess/MPa | 1154 | Ett/MPa | 1154 |
| σn | 20 | σs | 25 | σt | 25 |
| GI | 0.249 | GII | 0.733 | GIII | 0.733 |
| σs | 25 | σt | 25 | GI | 0.249 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Z.; Xu, W.; Liu, D.; Duan, J. Research on Energy Absorption Characteristics of Bouligand Biomimetic Structure Based on CFRP Composite Materials. Sustainability 2023, 15, 9911. https://doi.org/10.3390/su15139911
Xin Z, Xu W, Liu D, Duan J. Research on Energy Absorption Characteristics of Bouligand Biomimetic Structure Based on CFRP Composite Materials. Sustainability. 2023; 15(13):9911. https://doi.org/10.3390/su15139911
Chicago/Turabian StyleXin, Zhuangzhuang, Wei Xu, Defa Liu, and Jilu Duan. 2023. "Research on Energy Absorption Characteristics of Bouligand Biomimetic Structure Based on CFRP Composite Materials" Sustainability 15, no. 13: 9911. https://doi.org/10.3390/su15139911
APA StyleXin, Z., Xu, W., Liu, D., & Duan, J. (2023). Research on Energy Absorption Characteristics of Bouligand Biomimetic Structure Based on CFRP Composite Materials. Sustainability, 15(13), 9911. https://doi.org/10.3390/su15139911







