A Novel Odd Beta Prime-Logistic Distribution: Desirable Mathematical Properties and Applications to Engineering and Environmental Data
Abstract
1. Introduction
- (i)
- To define novel FPDs using the BP distribution.
- (ii)
- To develop new PD that can accommodate both monotonic and non-monotonic hazard rates.
- (iii)
- To establish heavy-tailed models for different data sets.
- (iv)
- To generate a PD that can provide suitable shapes to fit symmetric and skewed real data sets that are commonly found in practical disciplines, including environment, engineering, and finance.
- (v)
- To obtain a flexible PD that can consistently provide more realistic fits to given data sets when tested against known competing PDs.
2. Literature Review
3. Development of Odd Beta Prime Generalized Family of Distributions
Mixture Representations of the pdf of OBP-G FPDs
4. Development of Odd Beta Prime-Logistic Distribution
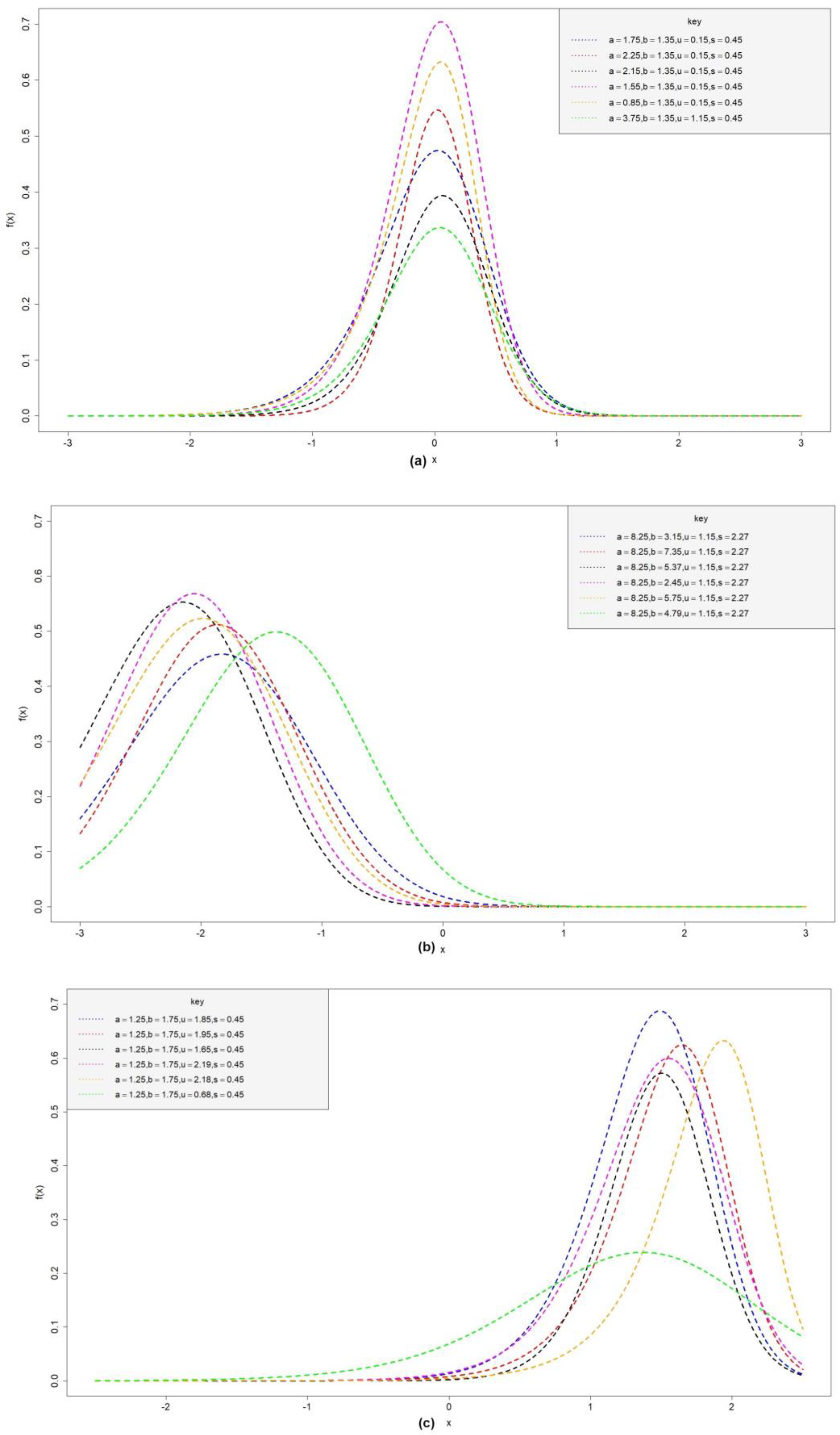
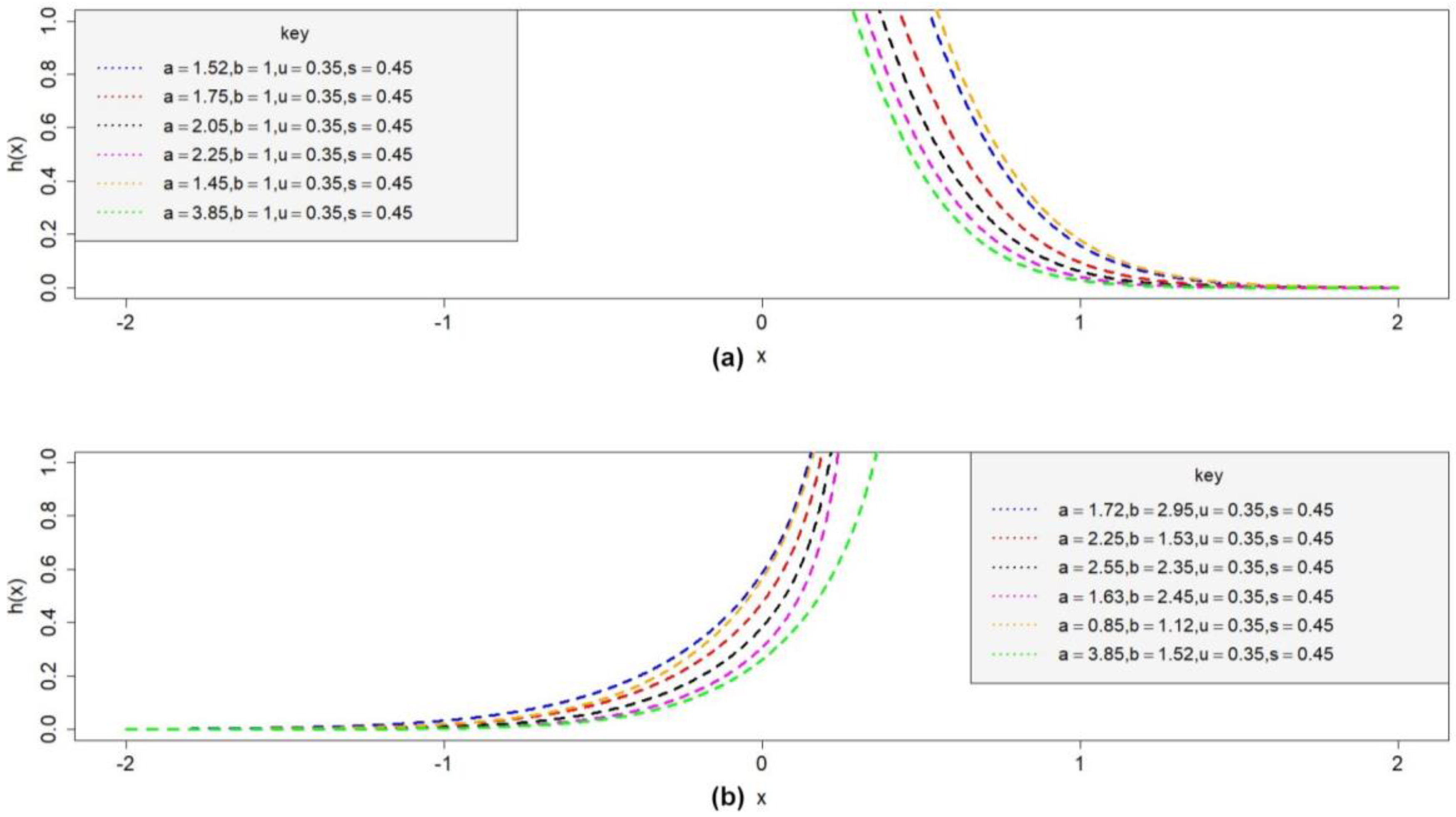
5. Statistical Features of OBP-Logistic Distribution
5.1. Moments
5.2. Moment-Generating Function (mgf)
5.3. Information-Generating Function (IGF)
5.4. Quantile Function
5.5. Stress–Strength
5.6. Order Statistics
5.7. Entropies
6. Maximum Likelihood Estimation
7. Monte Carlo Simulation Study
8. Applications
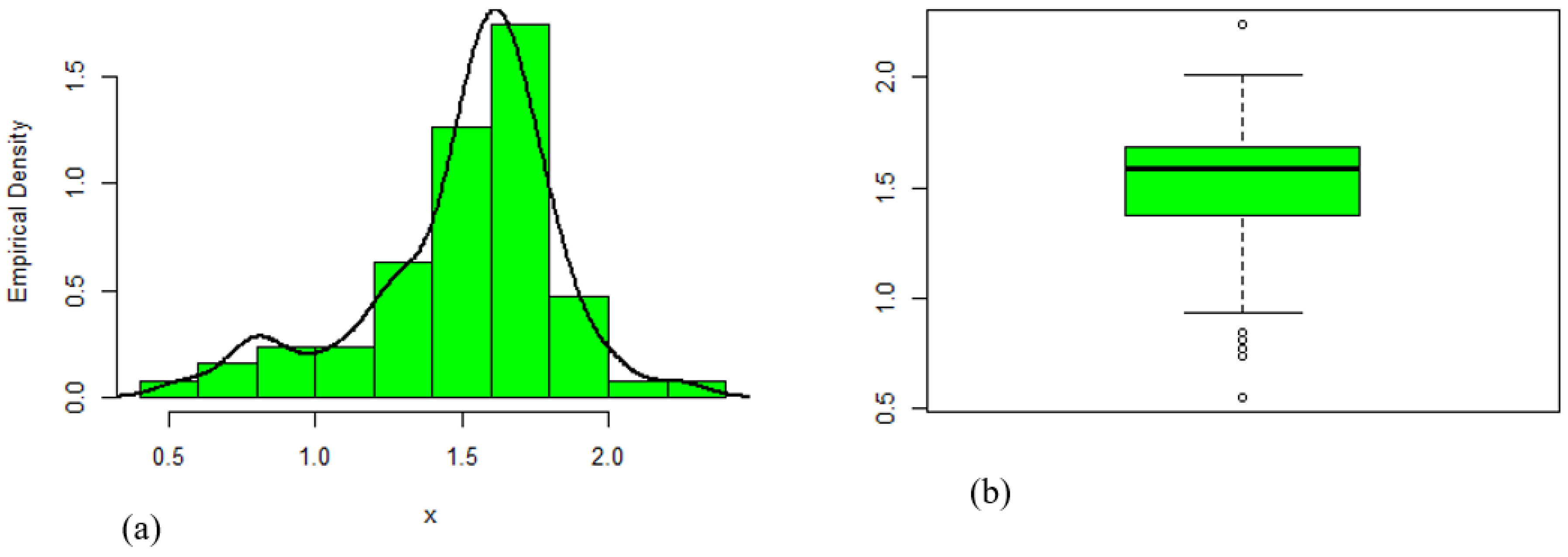
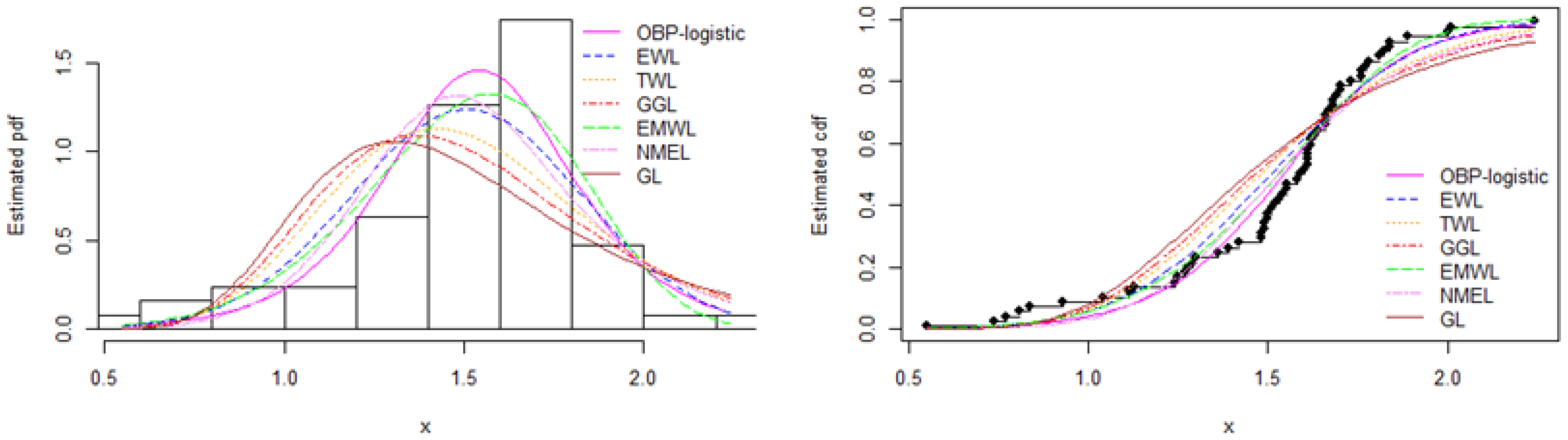
8.1. Data Set 1: Glass Fiber Data
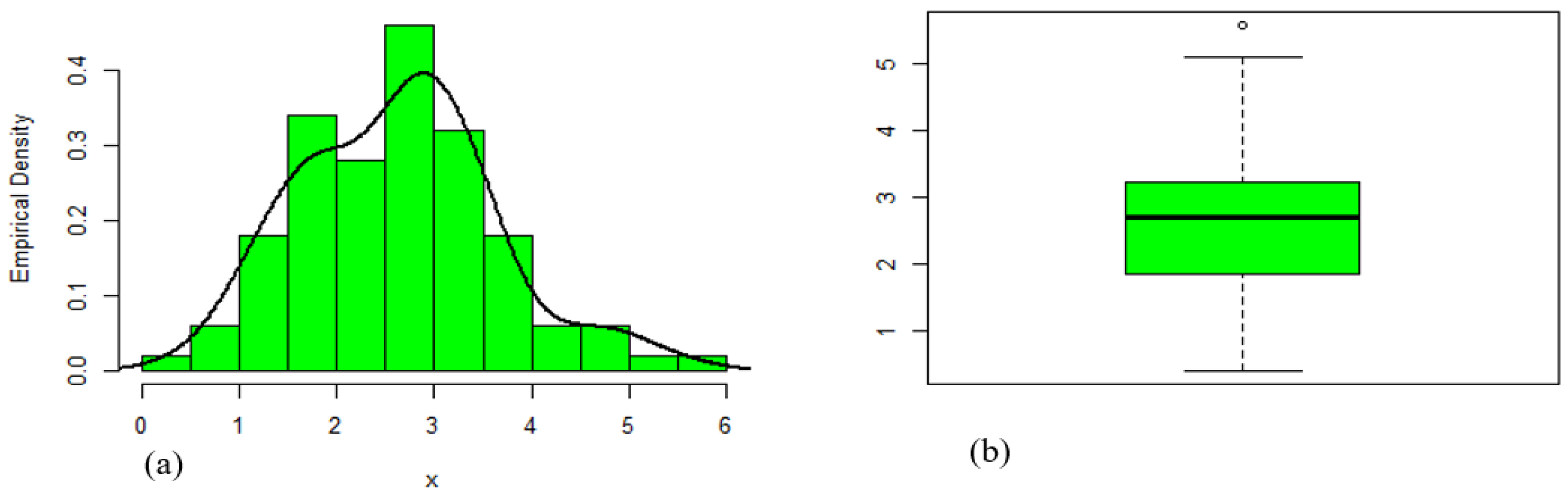
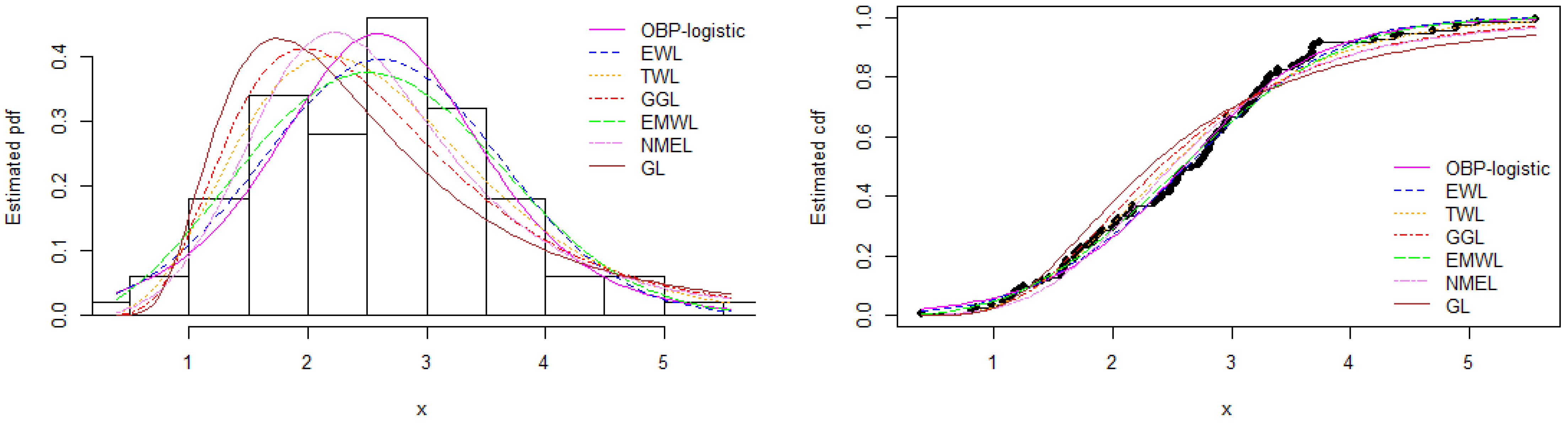
8.2. Data Set 2: Carbon Fiber Data
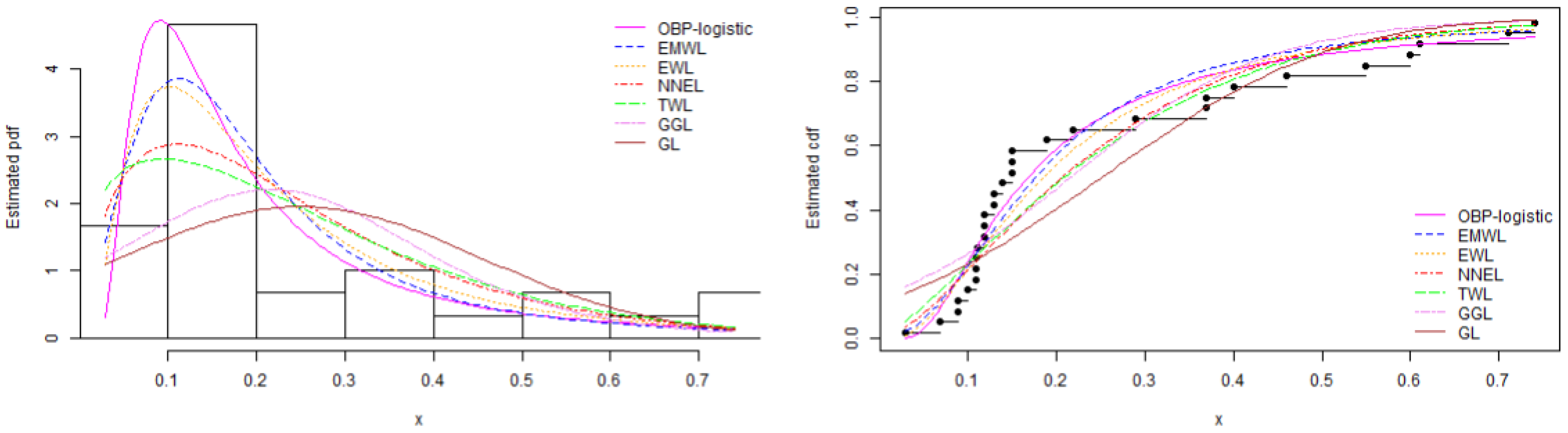
8.3. Data Set 3: Magnesium Concentration Data
9. Discussion
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cumulative distribution function of beta of the second kind | |
| Incomplete beta function ratio | |
| , | Shape parameters of beta of the second kind |
| Beta function | |
| Incomplete beta function | |
| Probability density function of beta of the second kind | |
| Cumulative distribution function of logistic distribution | |
| Location parameter of logistic distribution | |
| Scale parameter of logistic distribution | |
| Cumulative distribution function of family of distributions | |
| Odds ration | |
| Vector parameter | |
| Probability density function of the baseline distribution | |
| Survival function | |
| Hazard function | |
| moment | |
| Moment-generating function | |
| Information-generating function | |
| Stress–Strength function | |
| Order statistics | |
| Probability density function of OBP-logistic distribution | |
| Cumulative density function of OBP-logistic distribution | |
| Rényi entropy | |
| q-entropy | |
| Sample size | |
| , | Vector of parameters |
| Likelihood function | |
| Log-likelihood function | |
| Digamma function | |
| Information-generating function | |
| Inverted cumulative distribution function | |
| Uniform random variable on the interval (0,1) |
References
- Eliwa, M.S.; Altun, E.; Alhussain, Z.A.; Ahmed, E.A.; Salah, M.M.; Ahmed, H.H.; El-Morshedy, M. A new one-parameter lifetime distribution and its regression model with applications. PLoS ONE 2021, 16, e0246969. [Google Scholar] [CrossRef] [PubMed]
- Nasiru, S. Extended Odd Fréchet-G Family of Distributions. J. Probab. Stat. 2018, 2018, 2931326. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Alshammari, F.S.; Hamed, Y.S.; Eliwa, M.S.; Yousof, H.M. A New Family of Continuous Probability Distributions. Entropy 2021, 23, 194. [Google Scholar] [CrossRef]
- Yousof, H.M.; Altun, E.; Ramires, T.G.; Alizadeh, M.; Rasekhi, M. A new family of distributions with properties, regression models and applications. J. Stat. Manag. Syst. 2018, 21, 163–188. [Google Scholar] [CrossRef]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat.-Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Zografos, K.; Balakrishnan, N. On families of beta-and generalized gamma-generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Nadarajah, S.; Cordeiro, G.M.; Ortega, E.M. General results for the Kumaraswamy-G distribution. J. Stat. Comput. Simul. 2012, 82, 951–979. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; da Cunha, D.C. The exponentiated generalized class of distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Alzaatreh, A.Y. Methods for generating families of univariate continuous distributions in the recent decades. Wiley Interdiscip. Rev. Comput. Stat. 2013, 5, 219–238. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Ortega, E.M. The exponentiated half-logistic family of distributions: Properties and applications. J. Probab. Stat. 2014, 2014. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M.; Hamedani, G.G. The odd generalized exponential family of distributions with applications. J. Stat. Distrib. Appl. 2015, 2, 1–28. [Google Scholar] [CrossRef]
- Amal, S.H.; Elgarhy, M. A New Family of Exponentiated Weibull-Generated Distributions. Int. J. Math. Its Appl. 2016, 4, 135–148. [Google Scholar]
- Afify, A.Z.; Altun, E.; Alizadeh, M.; Ozel, G.; Hamedani, G. The odd exponentiated half-logistic-G family: Properties, characterizations and applications. Chil. J. Stat. 2017, 8, 65–91. [Google Scholar]
- Gomes-Silva, F.S.; Percontini, A.; de Brito, E.; Ramos, M.W.; Venâncio, R.; Cordeiro, G.M. The odd Lindley-G family of distributions. Austrian J. Stat. 2017, 46, 65–87. [Google Scholar] [CrossRef]
- Reyad, H.; Alizadeh, M.; Jamal, F.; Othman, S. The Topp Leone odd Lindley-G family of distributions: Properties and applications. J. Stat. Manag. Syst. 2018, 21, 1273–1297. [Google Scholar] [CrossRef]
- ul Haq, M.A.; Elgarhy, M. The odd Frèchet-G family of probability distributions. J. Stat. Appl. Probab. 2018, 7, 189–203. [Google Scholar] [CrossRef]
- Alizadeh, M.; Rasekhi, M.; Yousof, H.M.; Hamedani, G. The transmuted Weibull-G family of distributions. Hacet. J. Math. Stat. 2018, 47, 1671–1689. [Google Scholar] [CrossRef]
- Oluyede, B. The gamma-Weibull-G Family of distributions with applications. Austrian J. Stat. 2018, 47, 45–76. [Google Scholar] [CrossRef]
- Hassan, A.S.; Nassr, S.G. Power Lindley-G family of distributions. Ann. Data Sci. 2019, 6, 189–210. [Google Scholar] [CrossRef]
- Ahmad, Z.; Elgarhy, M.; Hamedani, G.; Butt, N.S. Odd generalized NH generated family of distributions with application to exponential model. Pak. J. Stat. Oper. Res. 2020, 16, 53–71. [Google Scholar] [CrossRef]
- Jamal, F.; Reyad, H.; Chesneau, C.; Nasir, M.A.; Othman, S. The Marshall-Olkin odd Lindley-G family of distributions: Theory and applications. Punjab Univ. J. Math. 2020, 51, 7. [Google Scholar]
- Ishaq, A.I.; Abiodun, A.A. The Maxwell–Weibull distribution in modeling lifetime datasets. Ann. Data Sci. 2020, 7, 639–662. [Google Scholar] [CrossRef]
- Al-Moisheer, A.S.; Elbatal, I.; Almutiry, W.; Elgarhy, M. Odd Inverse Power Generalized Weibull Generated Family of Distributions: Properties and Applications. Math. Probl. Eng. 2021, 2021, 5082192. [Google Scholar] [CrossRef]
- Barranco-Chamorro, I.; Iriarte, Y.A.; Gómez, Y.M.; Astorga, J.M.; Gómez, H.W. A Generalized Rayleigh Family of Distributions Based on the Modified Slash Model. Symmetry 2021, 13, 1226. [Google Scholar] [CrossRef]
- Jamal, F.; Handique, L.; Ahmed, A.H.N.; Khan, S.; Shafiq, S.; Marzouk, W. The Generalized Odd Linear Exponential Family of Distributions with Applications to Reliability Theory. Math. Comput. Appl. 2022, 27, 55. [Google Scholar] [CrossRef]
- Hussain, S.; Sajid Rashid, M.; Ul Hassan, M.; Ahmed, R. The Generalized Exponential Extended Exponentiated Family of Distributions: Theory, Properties, and Applications. Mathematics 2022, 10, 3419. [Google Scholar] [CrossRef]
- Hussain, S.; Rashid, M.S.; Ul Hassan, M.; Ahmed, R. The Generalized Alpha Exponent Power Family of Distributions: Properties and Applications. Mathematics 2022, 10, 1421. [Google Scholar] [CrossRef]
- Bourguignon, M.; Santos-Neto, M.; de Castro, M. A new regression model for positive random variables with skewed and long tail. Metron 2021, 79, 33–55. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Venter, G. Transformed beta and gamma distributions and aggregate losses. In Proceedings of Casualty Actuarial Society; Casualty Actuarial Society: Arlington, VA, USA, 1983; Volume 70, pp. 289–308. [Google Scholar]
- Vartia, P.; Vartia, Y.O. Description of the Income Distribution by the Scaled F Distribution Model; Elinkeinoelämän Tutkimuslaitos: Helsinki, Finland, 1981. [Google Scholar]
- McDonald, J.B.; Ransom, M.R. Functional forms, estimation techniques and the distribution of income. Econom. J. Econom. Soc. 1979, 47, 1513–1525. [Google Scholar] [CrossRef]
- McDonald, J.B. Model selection: Some generalized distributions. Commun. Stat.-Theory Methods 1987, 16, 1049–1074. [Google Scholar] [CrossRef]
- McDonald, J.B.; Butler, R.J. Regression models for positive random variables. J. Econom. 1990, 43, 227–251. [Google Scholar] [CrossRef]
- Tulupyev, A.; Suvorova, A.; Sousa, J.; Zelterman, D. Beta prime regression with application to risky behavior frequency screening. Stat. Med. 2013, 32, 4044–4056. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, J.; Soares, C.G. Modelling the long-term distribution of significant wave height with the Beta and Gamma models. Ocean. Eng. 1999, 26, 713–725. [Google Scholar] [CrossRef]
- Dubey, S.D. Compound gamma, beta and F distributions. Metrika 1970, 16, 27–31. [Google Scholar] [CrossRef]
- Joshi, R.K.; Kumar, V. The Logistic Gompertz Distribution with Properties and Applications. Bull. Math. Stat. Res. 2020, 8, 81–94. [Google Scholar]
- Brown, R.Z. Social behavior, reproduction, and population changes in the house mouse (Mus musculus L.). Ecol. Monogr. 1953, 23, 218–240. [Google Scholar] [CrossRef]
- Schultz, H. The standard error of a forecast from a curve. J. Am. Stat. Assoc. 1930, 25, 139–185. [Google Scholar] [CrossRef]
- Oliver, F. Methods of estimating the logistic growth function. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1964, 13, 57–66. [Google Scholar] [CrossRef]
- Ravikumar, K. Negative Binomial Logistic Distribution. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 5963–5976. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Alzaatreh, A.; Ghosh, I.; Said, H. On the gamma-logistic distribution. J. Mod. Appl. Stat. Methods 2014, 13, 5. [Google Scholar] [CrossRef]
- Morais, A.L.; Cordeiro, G.M.; Cysneiros, A.H. The beta generalized logistic distribution. Braz. J. Probab. Stat. 2013, 27, 185–200. [Google Scholar] [CrossRef]
- Prentice, R.L. A generalization of the probit and logit methods for dose response curves. Biometrics 1976, 32, 761–768. [Google Scholar] [CrossRef] [PubMed]
- Stukel, T.A. Generalized logistic models. J. Am. Stat. Assoc. 1988, 83, 426–431. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Leung, M. Order statistics from the type I generalized logistic distribution. Commun. Stat.-Simul. Comput. 1988, 17, 25–50. [Google Scholar] [CrossRef]
- Wahed, A.; Ali, M.M. The skew-logistic distribution. J. Statist. Res 2001, 35, 71–80. [Google Scholar]
- Nadarajah, S. The skew logistic distribution. AStA Adv. Stat. Anal. 2009, 93, 187–203. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized logistic distributions. J. Appl. Stat. Sci. 2010, 18, 51. [Google Scholar]
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Aljarrah, M.A.; Famoye, F.; Lee, C. Generalized logistic distribution and its regression model. J. Stat. Distrib. Appl. 2020, 7, 1–21. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Aljarrah, M.A.; Lee, C.; Famoye, F. On generating TX family of distributions using quantile functions. J. Stat. Distrib. Appl. 2014, 1, 1–17. [Google Scholar] [CrossRef]
- Ghosh, I.; Alzaatreh, A. A new class of generalized logistic distribution. Commun. Stat.-Theory Methods 2018, 47, 2043–2055. [Google Scholar] [CrossRef]
- Suleiman, A.; Othman, M.; Ishaq, A.; Daud, H.; Indawati, R.; Abdullah, M.L.; Husin, A. The Odd Beta Prime-G Family of Probability Distributions: Properties and Applications. In Proceedings of the 1st International Online Conference on Mathematics and Applications, Online, 1–15 May 2023; MDPI: Basel, Switzerland, 2023. [Google Scholar] [CrossRef]
- Alsadat, N.; Ahmad, A.; Jallal, M.; Gemeay, A.M.; Meraou, M.A.; Hussam, E.; Elmetwally, E.M.; Hossain, M.M. The novel Kumaraswamy power Frechet distribution with data analysis related to diverse scientific areas. Alex. Eng. J. 2023, 70, 651–664. [Google Scholar] [CrossRef]
- Alghamdi, S.M.; Shrahili, M.; Hassan, A.S.; Mohamed, R.E.; Elbatal, I.; Elgarhy, M. Analysis of Milk Production and Failure Data: Using Unit Exponentiated Half Logistic Power Series Class of Distributions. Symmetry 2023, 15, 714. [Google Scholar] [CrossRef]
- Muhammad, M.; Bantan, R.A.R.; Liu, L.; Chesneau, C.; Tahir, M.H.; Jamal, F.; Elgarhy, M. A New Extended Cosine—G Distributions for Lifetime Studies. Mathematics 2021, 9, 2758. [Google Scholar] [CrossRef]
- Alyami, S.A.; Elbatal, I.; Alotaibi, N.; Almetwally, E.M.; Elgarhy, M. Modeling to Factor Productivity of the United Kingdom Food Chain: Using a New Lifetime-Generated Family of Distributions. Sustainability 2022, 14, 8942. [Google Scholar] [CrossRef]
- Alyami, S.A.; Babu, M.G.; Elbatal, I.; Alotaibi, N.; Elgarhy, M. Type II Half-Logistic Odd Fréchet Class of Distributions: Statistical Theory and Applications. Symmetry 2022, 14, 1222. [Google Scholar]
- Elbatal, I.; Alotaibi, N.; Almetwally, E.M.; Alyami, S.A.; Elgarhy, M. On Odd Perks-G Class of Distributions: Properties, Regression Model, Discretization, Bayesian and Non-Bayesian Estimation, and Applications. Symmetry 2022, 14, 883. [Google Scholar] [CrossRef]
- Alotaibi, N.; Elbatal, I.; Almetwally, E.M.; Alyami, S.A.; Al-Moisheer, A.S.; Elgarhy, M. Truncated Cauchy Power Weibull-G Class of Distributions: Bayesian and Non-Bayesian Inference Modelling for COVID-19 and Carbon Fiber Data. Mathematics 2022, 10, 1565. [Google Scholar] [CrossRef]
- Algarni, A.; Almarashi, A.M.; Elbatal, I.; Hassan, A.S.; Almetwally, E.M.; Daghistani, A.M.; Elgarhy, M. Type I Half Logistic Burr X-G Family: Properties, Bayesian, and Non-Bayesian Estimation under Censored Samples and Applications to COVID-19 Data. Math. Probl. Eng. 2021, 2021, 5461130. [Google Scholar] [CrossRef]
- David Sam Jayakumar, G.S.; Sulthan, A.; Samuel, W. A new bivariate beta distribution of Kind-1 of Type-A. J. Stat. Manag. Syst. 2019, 22, 141–158. [Google Scholar] [CrossRef]
- Baro-Tijerina, M.; Pina-Monarrez, M.R.; Villa-Covarrubias, B. Stress-strength Weibull analysis with different shape parameter and probabilistic safety factor. DYNA 2020, 87, 28–33. [Google Scholar] [CrossRef]
- Gauss, M.C.; Saralees, N. Closed-form expressions for moments of a class of beta generalized distributions. Braz. J. Probab. Stat. 2011, 25, 14–33. [Google Scholar] [CrossRef]
- Verma, A. Finite summation formulas of generalized Kampé de Fériet series. arXiv 2020, arXiv:2003.07530. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA; Volume 1, pp. 547–561. [Google Scholar]
- Khammash, G.S.; Agarwal, P.; Choi, J. Extended k-Gamma and k-Beta Functions of Matrix Arguments. Mathematics 2020, 8, 1715. Available online: https://www.mdpi.com/2227-7390/8/10/1715 (accessed on 16 March 2023). [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://cir.nii.ac.jp/crid/1574231874043578752 (accessed on 5 April 2023).
- Kumar, C.S.; Manju, L. Gamma Generalized Logistic Distribution: Properties and Applications. J. Stat. Theory Appl. 2022, 21, 155–174. [Google Scholar] [CrossRef]
- Ahmad, Z.; Almaspoor, Z.; Khan, F.; Alhazmi, S.E.; El-Morshedy, M.; Ababneh, O.; Al-Omari, A.I. On fitting and forecasting the log-returns of cryptocurrency exchange rates using a new logistic model and machine learning algorithms. AIMS Math. 2022, 7, 18031–18049. [Google Scholar] [CrossRef]
- Nassar, M.M.; Radwan, S.S.; Elmasry, A.S. the Exponential Modified Weibull Logistic Distribution (EMWL). EPH-Int. J. Math. Stat. 2018, 4, 22–38. [Google Scholar] [CrossRef]
- MURAT, U.; Gamze, Ö. Exponentiated Weibull-logistic distribution. Bilge Int. J. Sci. Technol. Res. 2020, 4, 55–62. [Google Scholar]
- Nassar, M.; Radwan, S.; Elmasry, A. Transmuted Weibull logistic distribution. Int. J. Innov. Res. Dev. 2017, 6, 122–131. [Google Scholar] [CrossRef]
- Abdullahi, U.A.; Suleiman, A.A.; Ishaq, A.I.; Usman, A.; Suleiman, A. The Maxwell–Exponential Distribution: Theory and Application to Lifetime Data. J. Stat. Model. Anal. (JOSMA) 2021, 3, 2. [Google Scholar] [CrossRef]
- Singh, V.V.; Suleman, A.A.; Ibrahim, A.; Abdullahi, U.A.; Suleiman, S.A. Assessment of probability distributions of groundwater quality data in Gwale area, north-western Nigeria. Ann. Optim. Theory Pract. 2020, 3, 37–46. [Google Scholar]
- Eferhonore, E.-E.; Thomas, J.; Zelibe, S.C. Theoretical analysis of the Weibull alpha power inverted exponential distribution: Properties and applications. Gazi Univ. J. Sci. 2020, 33, 265–277. [Google Scholar]
- Ceren, Ü.; Cakmakyapan, S.; Gamze, Ö. Alpha power inverted exponential distribution: Properties and application. Gazi Univ. J. Sci. 2018, 31, 954–965. [Google Scholar]
- Merovci, F.; Khaleel, M.A.; Ibrahim, N.A.; Shitan, M. The beta Burr type X distribution properties with application. SpringerPlus 2016, 5, 697. [Google Scholar] [CrossRef]
- Maxwell, O.; Oyamakin, S.O.; Th, E.J. The Gompertz Length Biased Exponential Distribution and its application to Uncensored Data. Curr. Trends Biostat. Biom. 2018, 1, 52–57. [Google Scholar] [CrossRef]
- Suleiman, A.A.; Abdullahi, U.A.; Suleiman, A.; Yunus, R.B.; Suleiman, S.A. Assessment of Groundwater Quality Using Multivariate Statistical Techniques. In Intelligent Systems Modeling and Simulation II: Machine Learning, Neural Networks, Efficient Numerical Algorithm and Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2022; pp. 567–579. [Google Scholar]

| Set 2: | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | n | Mean | Bias | MSE | Mean | Bias | MSE |
| 50 | 1.021639 | 0.421634 | 0.323464 | 0.376896 | 0.069939 | 0.051017 | |
| 150 | 0.783206 | 0.283205 | 0.159113 | 0.415324 | 0.154217 | 0.051843 | |
| 300 | 0.705664 | 0.205666 | 0.088489 | 0.387839 | 0.097845 | 0.026851 | |
| 750 | 0.632203 | 0.132208 | 0.053510 | 0.377562 | 0.070852 | 0.018937 | |
| 1050 | 0.579878 | 0.079871 | 0.024855 | 0.369832 | 0.059126 | 0.013711 | |
| 1550 | 0.534531 | 0.064537 | 0.016711 | 0.360532 | 0.047211 | 0.008374 | |
| 2050 | 0.511279 | 0.061279 | 0.015390 | 0.356891 | 0.036824 | 0.004921 | |
| 50 | 3.071120 | 2.051126 | 6.501042 | 2.757921 | 1.057934 | 8.337832 | |
| 150 | 2.335925 | 1.315927 | 4.281831 | 1.903067 | 0.203953 | 1.077834 | |
| 300 | 1.916825 | 0.896823 | 2.927313 | 1.815383 | 0.115848 | 0.662473 | |
| 750 | 1.853472 | 0.533476 | 1.630027 | 1.725902 | 0.025954 | 0.398832 | |
| 1050 | 1.801139 | 0.265113 | 0.727289 | 1.724942 | 0.290710 | 0.024529 | |
| 1550 | 1.795770 | 0.178776 | 0.410361 | 1.717291 | 0.004975 | 0.193952 | |
| 2050 | 1.628714 | 0.156718 | 0.363602 | 1.704701 | 0.002562 | 0.009541 | |
| 50 | 0.526858 | −0.273106 | 0.104449 | 1.875402 | 0.780864 | 3.704327 | |
| 150 | 0.620049 | −0.179951 | 0.060271 | 1.460174 | 0.208016 | 0.877854 | |
| 300 | 0.662551 | −0.137446 | 0.039444 | 1.386421 | 0.072756 | 0.392853 | |
| 750 | 0.709550 | −0.090441 | 0.023709 | 1.283419 | 0.049643 | 0.270834 | |
| 1050 | 0.715512 | −0.074489 | 0.017091 | 1.247242 | 0.015953 | 0.174934 | |
| 1550 | 0.739470 | −0.057208 | 0.010584 | 1.227641 | 0.010261 | 0.118342 | |
| 2050 | 0.757674 | −0.042325 | 0.007179 | 1.207845 | 0.007834 | 0.111962 | |
| 50 | 0.657450 | 0.089643 | 0.010547 | 0.234628 | 0.012999 | 0.009617 | |
| 150 | 0.579762 | 0.019884 | 0.005913 | 0.238917 | 0.038921 | 0.005998 | |
| 300 | 0.546031 | 0.009546 | 0.001750 | 0.233610 | 0.023610 | 0.004892 | |
| 750 | 0.536545 | 0.006575 | 0.001147 | 0.229828 | 0.019721 | 0.003671 | |
| 1050 | 0.524567 | 0.004567 | 0.000756 | 0.222611 | 0.016963 | 0.002930 | |
| 1550 | 0.534541 | 0.003454 | 0.000471 | 0.218936 | 0.012953 | 0.002538 | |
| 2050 | 0.546522 | 0.002622 | 0.000242 | 0.204097 | 0.009618 | 0.001273 | |
| 0.55 | 0.74 | 0.77 | 0.81 | 0.84 | 1.24 | 0.93 | 1.04 | 1.11 | 1.13 | 1.30 |
| 1.25 | 1.27 | 1.28 | 1.29 | 1.48 | 1.36 | 1.39 | 1.42 | 1.48 | 1.51 | 1.49 |
| 1.49 | 1.50 | 1.50 | 1.55 | 1.52 | 1.53 | 1.54 | 1.55 | 1.61 | 1.58 | 1.59 |
| 1.60 | 1.61 | 1.63 | 1.61 | 1.61 | 1.62 | 1.62 | 1.67 | 1.64 | 1.66 | 1.66 |
| 1.66 | 1.70 | 1.68 | 1.69 | 1.70 | 1.78 | 1.73 | 1.76 | 1.76 | 1.77 | 1.89 |
| 1.81 | 1.82 | 1.84 | 1.84 | 2.00 | 2.01 | 2.24 |
| 3.70 | 2.74 | 2.73 | 2.50 | 3.60 | 3.11 | 3.27 | 2.87 | 1.47 | 3.11 |
| 2.41 | 3.19 | 3.22 | 1.69 | 3.28 | 3.09 | 1.87 | 3.15 | 4.90 | 3.75 |
| 2.95 | 2.97 | 3.39 | 2.96 | 2.53 | 2.67 | 2.93 | 3.22 | 3.39 | 2.81 |
| 3.33 | 2.55 | 3.31 | 3.31 | 2.85 | 2.56 | 3.56 | 3.15 | 2.35 | 2.55 |
| 2.38 | 2.81 | 2.77 | 2.17 | 2.83 | 1.92 | 1.41 | 3.68 | 2.97 | 1.36 |
| 2.76 | 4.91 | 3.68 | 1.84 | 1.59 | 3.19 | 1.57 | 0.81 | 5.56 | 1.73 |
| 2.00 | 1.22 | 1.12 | 1.71 | 2.17 | 1.17 | 5.08 | 2.48 | 1.18 | 3.51 |
| 1.69 | 1.25 | 4.38 | 1.84 | 0.39 | 3.68 | 2.48 | 0.85 | 1.61 | 2.79 |
| 2.03 | 1.80 | 1.57 | 1.08 | 2.03 | 1.61 | 2.12 | 1.89 | 2.88 | 2.82 |
| 2.05 | 2.43 | 4.20 | 2.59 | 0.98 | 1.59 | 2.17 | 4.70 | 4.42 | 3.65 |
| 0.74 | 0.15 | 0.37 | 0.07 | 0.12 | 0.03 | 0.29 | 0.11 | 0.11 | 0.37 |
| 0.12 | 0.09 | 0.61 | 0.13 | 0.15 | 0.19 | 0.11 | 0.15 | 0.10 | 0.60 |
| 0.09 | 0.71 | 0.12 | 0.40 | 0.55 | 0.11 | 0.14 | 0.13 | 0.46 | 0.22 |
| Data | Min. | Q1 | Median | Mean | Q3 | Max. | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.550 | 1.375 | 1.590 | 1.507 | 1.685 | 2.240 | 0.105 | −0.879 | 0.800 |
| 2 | 0.390 | 1.840 | 2.700 | 2.621 | 3.220 | 5.560 | 1.028 | 0.363 | 0.043 |
| 3 | 0.030 | 0.110 | 0.145 | 0.251 | 0.370 | 0.740 | 0.043 | 1.077 | −0.269 |
| Model | ||||||
|---|---|---|---|---|---|---|
| OBP-logistic | 0.6345 (0.1279) | 0.7346 (0.1671) | 1.5415 (0.0368) | 0.1708 (0.0184) | _ | _ |
| GGL | 0.3811 (0.0325) | 0.2578 (0.0229) | _ | 0.2854 (0.0425) | 0.1764 (0.0124) | _ |
| NMEL | _ | 7.9262 (0.8735) | 1.5262 (0.0408) | 0.5286 (0.0437) | 0.8543 (0.0267) | _ |
| GL | 13.1164 (2.3079) | 18.4734 (3.3134) | _ | 4.8783 (0.8954) | 2.6508 (0.7354) | _ |
| EMWL | 5.7806 (0.5761) | 1.62813 (0.0371) | _ | 1.2532 (0.0192) | 0.3518 (0.0113) | _ |
| EWL | 0.2791 (0.0274) | 0.3215 (0.0286) | _ | 0.4176 (0.0210) | 1.5068 (0.0405) | _ |
| TWL | 17.4410 (3.0783) | _ | _ | 8.3092 (1.7391) | 11.5746 (2.0725) | 2.6301 (0.6390) |
| Model | ||||||
|---|---|---|---|---|---|---|
| OBP-logistic | 0.5876 (0.1134) | 0.6753 (0.3452) | 2.5975 (0.1001) | 0.5732 (0.0475) | _ | _ |
| GGL | 0.8774 (0.0444) | 0.4439 (0.0314) | _ | 0.7354 (0.0649) | 0.2763 (0.0873) | _ |
| NMEL | _ | 4.1184 (0.3441) | 2.4985 (0.1053) | 1.8534 (0.0342) | 0.5285 (0.0263) | _ |
| GL | 4.4477 (0.6068) | 9.5189 (1.3750) | _ | 1.4567 (0.0326) | 3.0653 (0.4375) | _ |
| EMWL | 2.7929 (0.2141) | 2.9438 (0.1110) | _ | 0.7393 (0.0741) | 0.2481 (0.0173) | _ |
| EWL | 1.4502 (0.0807) | 2.6214 (0.1008) | _ | 1.3092 (0.0981) | 1.0088 (0.0713) | _ |
| TWL | 5.9529 (0.8194) | _ | _ | 3.7407 (0.3681) | 2.2711 (0.3264) | 0.7622 (0.0137) |
| Model | ||||||
|---|---|---|---|---|---|---|
| OBP-logistic | 1.3290 (0.1827) | 0.2756 (0.0401) | 1.7834 (0.0854) | 0.1964 (0.0543) | _ | _ |
| GGL | 0.2162 (0.0360) | 0.1129 (0.017) | _ | 1.9743 (0.6342) | 0.3714 (0.0302) | _ |
| NMEL | 3.5783 (1.0428) | 1.7937 (0.4270) | 7.1363 (1.957) | 1.6453 (0.4943) | _ | _ |
| GL | 0.2513 (0.037) | 0.2040 (0.0263) | _ | 1.5462 (0.3648) | 0.6328 (0.0843) | _ |
| EMWL | 2.2019 (0.3317) | 0.1765 (0.0258) | _ | 1.7845 (0.1534) | 0.5281 (0.0848) | _ |
| EWL | 1.6847 (0.1418) | 0.7768 (0.1002) | _ | 2.4271 (0.5832) | 1.3977 (0.1143) | _ |
| TWL | 1.3290 (0.1827) | _ | _ | 0.2756 (0.0402) | 3.8262 (1.9436) | 1.6749 (0.5483) |
| Model | AIC | BIC | KS | CM | AD | p-Value (KS) | |
|---|---|---|---|---|---|---|---|
| OBP-logistic | 15.0212 | 34.0419 | 38.3281 | 0.12529 | 0.17247 | 1.21460 | 0.83122 |
| GGL | 28.0055 | 60.0098 | 64.2961 | 0.23127 | 0.69182 | 3.77362 | 0.29976 |
| NMEL | 23.7893 | 51.5799 | 56.8662 | 0.22365 | 0.50593 | 2.37584 | 0.36177 |
| GL | 33.1273 | 70.2546 | 74.5409 | 0.24835 | 0.86135 | 4.63834 | 0.20137 |
| EMWL | 17.2067 | 39.4136 | 44.6999 | 0.20221 | 0.27504 | 1.28061 | 0.71306 |
| EWL | 16.9118 | 36.8236 | 40.1099 | 0.13127 | 0.24538 | 1.24988 | 0.76951 |
| TWL | 22.9515 | 49.9030 | 53.1893 | 0.21636 | 0.36580 | 3.08700 | 0.53102 |
| Model | AIC | BIC | KS | CM | AD | p-Value (KS) | |
|---|---|---|---|---|---|---|---|
| OBP-logistic | 141.310 | 287.621 | 291.831 | 0.05753 | 0.06165 | 0.42792 | 0.90347 |
| GGL | 148.419 | 300.839 | 306.050 | 0.11773 | 0.27528 | 1.46502 | 0.60725 |
| NMEL | 143.779 | 293.559 | 301.769 | 0.09025 | 0.15750 | 0.73771 | 0.68425 |
| GL | 158.737 | 321.474 | 326.684 | 0.14673 | 0.51933 | 2.84714 | 0.54792 |
| EMWL | 141.529 | 288.058 | 292.268 | 0.06049 | 0.06331 | 0.43769 | 0.73061 |
| EWL | 143.270 | 290.540 | 294.751 | 0.06306 | 0.06806 | 0.46805 | 0.72370 |
| TWL | 146.233 | 296.467 | 302.677 | 0.09339 | 0.16002 | 1.07584 | 0.62563 |
| Model | AIC | BIC | KS | CM | AD | p-Value (KS) | |
|---|---|---|---|---|---|---|---|
| OBP-logistic | 14.1082 | −26.2164 | −23.4140 | 0.15834 | 0.13164 | 0.83862 | 0.88436 |
| GGL | 18.7392 | −6.38254 | −3.5801 | 0.24248 | 0.38390 | 2.39556 | 0.25342 |
| NMEL | 14.8236 | −24.1073 | −21.2049 | 0.24678 | 0.29601 | 1.52516 | 0.46418 |
| GL | 22.7643 | −6.21814 | −3.4157 | 0.29029 | 0.49237 | 2.65561 | 0.20345 |
| EMWL | 14.8047 | −25.6695 | −22.8671 | 0.18878 | 0.18968 | 1.10471 | 0.75396 |
| EWL | 15.5494 | −24.0988 | −22.9964 | 0.20769 | 0.20388 | 1.09361 | 0.69807 |
| TWL | 16.2846 | −22.5692 | −19.7668 | 0.24051 | 0.28781 | 1.50597 | 0.37649 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suleiman, A.A.; Daud, H.; Singh, N.S.S.; Othman, M.; Ishaq, A.I.; Sokkalingam, R. A Novel Odd Beta Prime-Logistic Distribution: Desirable Mathematical Properties and Applications to Engineering and Environmental Data. Sustainability 2023, 15, 10239. https://doi.org/10.3390/su151310239
Suleiman AA, Daud H, Singh NSS, Othman M, Ishaq AI, Sokkalingam R. A Novel Odd Beta Prime-Logistic Distribution: Desirable Mathematical Properties and Applications to Engineering and Environmental Data. Sustainability. 2023; 15(13):10239. https://doi.org/10.3390/su151310239
Chicago/Turabian StyleSuleiman, Ahmad Abubakar, Hanita Daud, Narinderjit Singh Sawaran Singh, Mahmod Othman, Aliyu Ismail Ishaq, and Rajalingam Sokkalingam. 2023. "A Novel Odd Beta Prime-Logistic Distribution: Desirable Mathematical Properties and Applications to Engineering and Environmental Data" Sustainability 15, no. 13: 10239. https://doi.org/10.3390/su151310239
APA StyleSuleiman, A. A., Daud, H., Singh, N. S. S., Othman, M., Ishaq, A. I., & Sokkalingam, R. (2023). A Novel Odd Beta Prime-Logistic Distribution: Desirable Mathematical Properties and Applications to Engineering and Environmental Data. Sustainability, 15(13), 10239. https://doi.org/10.3390/su151310239







