Modeling Structural Changes in Intra-Asian Maritime Container Shipping Networks Considering Their Characteristics

Abstract

In East Asia, where several large hub ports exist, maritime container shipping (MCS) has developed rapidly, and the MCS network has become more complex. This study develops a link prediction model that reproduces the changes in the structure of the intra-Asian oceangoing MCS network using graph theory. To improve the prediction accuracy, we propose a method that reflects the generation of a link considering the node and link characteristics of the MCS network, including the port performance and shipping distance between ports. Consequently, we conclude: (1) The intra-Asian oceangoing MCS network has expanded from 2011 to 2021 as the trading partners and trade volume have increased. (2) The usefulness of the proposed model is confirmed. In particular, the proposed model is good at predicting the new links between ports with short distances. (3) The prediction accuracy of link disappearance remains to be improved.

1. Introduction

Maritime shipping accounts for more than 80% of the world’s transportation demand. In particular, global trade has expanded with economic globalization since the first use of containers in the 1950s, and 815.6 million twenty-feet equivalent units (TEUs) of containers were handled in ports worldwide in 2020 [1]. Maritime container shipping (MCS) networks have maintained a high growth rate and become increasingly complex with the enlargement of vessel sizes [2,3]. In order to focus on the structure of MCS networks, some studies have applied network theory [3,4]. However, the network structure changes with time because of interactions among nodes, and changes in the direction and weight of links lead to the generation of new links or the disappearance of links in the existing network. Analyzing these network structure changes is essential from both academic and practical viewpoints. Academically, the organizational mechanism for MCS has attracted researchers’ attention because maritime shipping affords most of the worldwide trade, and the development of trade networks contributes to the sustainable growth of the global economy. From a practical viewpoint, it is also significant because adding new routes and ports of call to the existing liner network requires significant and time-consuming investment for shipping companies in building and chartering new vessels and for ports in constructing new and improving existing container terminals [2]. Therefore, predicting the future network structure by developing a link prediction model in advance is crucial for the sustainable growth of these industries.

In East Asia, the demand for MCS is drastically increasing because of the rapid economic growth of many countries, the international division of labor, and the global optimization of procurement and production locations [2]. As described in Section 3, the increase in intra-Asian trade is also remarkable. The increase in trade in intermediate goods between Northeast Asian countries such as China, Japan, Korea, and Taiwan and Southeast Asian countries has raised intra-Asian MCS demand. As a result, many hub ports have grown in East Asia; particularly, ports in China and Singapore boast the world’s largest container handling volumes. In summary, there is a need to analyze the evolution process of intra-Asian complex MCS networks quantitatively.

As summarized in Section 2, the link prediction problem was first defined and solved by Barabasi and Albert [5], and several studies applied it to maritime shipping. However, most of them did not reflect node characteristics unique to shipping, such as port performance, or link characteristics, such as distance between ports. Among them, Kaluza et al. [6] and Kosowska-Stamirowska [7] focused on the effect of shipping distance and developed the gravity model, although they did not consider node and link characteristics simultaneously. Therefore, this study aims to construct a model that reproduces changes in the structure of the intra-Asian MCS networks using link prediction theory for quantitatively analyzing the evolution process of the MCS networks by considering the characteristics of the MCS network and geographical constraints such as port performance and distance between ports to support the sustainable growth of the maritime industry.

2. Literature Review

2.1. Development of MCS Network in East Asia

Since the commercial use of containers began in the 1950s, the volume of containers handled has rapidly increased with the development of world trade, and a global MCS network has been formed and becomes increasingly complex because of the enlargement of vessel sizes and the increasing number of ports available for port calls and services [2,3]. In the MCS networks, various factors cause the generation of new links and the deletion of existing links. Liner shipping companies may cooperate with other shipping companies by periodically (e.g., three to six months) reallocating vessels or changing their service network to respond to various economic, social, and technological changes [8]. Notteboom et al. [9] also pointed out that forming alliances and vertical integration of container terminal operators affect the choice of ports of call.

Hub ports have also grown in recent years. The progressive increase in the size of containerships has led to a decrease in the frequency of port calls, which has intensified competition among ports. The ports must invest in accommodating the larger vessels, threatening their sustainable development. Consequently, the operating entities of ports have become privatized and strengthened their market dominance as mega-terminal operators through repeated mergers and acquisitions [10]. In the East Asian region, many hub ports have been born following this global trend. The top 10 ports in the world in terms of container handling volume included only three Asian ports in 1980, but in 2020, eight are in East Asia [11]. Southeast Asian ports, besides Singapore, have also seen significant growth in handling volumes in recent years.

2.2. Analysis of MCS Network

The literature on quantitative MCS network analysis can be classified into network assignment methodology of cargo flows, such as Tavasszy et al. [12], Lee and Meng [13], and Shibasaki et al. [14], and network analysis based on graph theory. The latter approach can effectively analyze the evolutionary process of networks; for example, regarding the quantitative analysis of the structure of static MCS networks, statistical parameters of the network, such as the degree, network density, and centralities, are mainly used to express the characteristics of the MCS network [15]. Hu and Zhu [16] used betweenness centrality to study the worldwide maritime transportation network. Ducruet et al. [17,18] analyzed the Atlantic shipping network, revealing that the scale-free characteristic gradually decreased with emerging new ports. Liu et al. [19,20] focused on the scale-free properties of the centrality indices of global shipping networks and concluded that the connectivity of a port is influenced by the connectivity of its directly connected ports, the shipping distance, and the hinterland economic scale. In these studies, the static maritime shipping network was reduced to a graph, and the properties of the mathematical topology were statistically analyzed.

Meanwhile, studies analyzing the time-series evolution of complex shipping networks are more important from the viewpoint of the sustainable development of the maritime industry. Several recent studies analyzed dynamic network change by focusing on detecting evolutionary patterns in maritime shipping networks by examining network stability and connectivity changes over time. Fang et al. [21] used automatic identification system data to analyze changes in maritime networks before and after interstate events, such as the military conflict between India and Pakistan, economic sanctions against Iran, and government elections in Sri Lanka. Yu et al. [22] simulated changes in shipping networks and traffic flow due to oil price fluctuations using a system-based approach that constructs maritime shipping networks based on trajectory data. Some studies analyzed time-series changes in MCS networks. Ducruet and Notteboom [23] analyzed the global liner network in 1996 and 2006, when the port hierarchy changed rapidly, and concluded that some East Asian and Mediterranean ports gained a high position in the port hierarchy between 1996 and 2006. Li et al. [24] analyzed changes in the positioning of each area using a centrality index for the MCS networks from 2001 to 2012. Wang et al. [25] analyzed the container service networks of liner shipping companies between Taiwan and mainland China in 2004, 2009, and 2013 using weighted networks. Wang et al. [26] empirically analyzed the spatial patterns of China’s international maritime linkages using graph theory based on navigation data from the mid-1990s to 2016. Saito et al. [3] focused on the MCS networks in the 1970s. They examined the changes in the overall structure of the networks over the medium to long term using graph theory. Sugimura et al. [27] examined the impact of Japanese port policies through network analysis with historical MCS network data from 1998 to 2019. These examples of dynamic analysis studies only analyze time-series parameter changes such as network centrality and do not predict link generation. The creation or disappearance of links significantly impacts network connectivity and should be analyzed.

2.3. Link Prediction Models and Applications to MCS Network

Studies on the link prediction problem have been conducted as a problem to reproduce the evolutionary process of networks. An early study of the link prediction problem is by Barabasi and Albert [5], using node degree to predict the existence of links. Newman [28] constructed common neighbors to calculate the probability of link generation. Jaccard [29] proposed an index to measure the structural equivalence of sets, and some studies, such as Gu et al. [30] and Ge et al. [31], applied the Jaccard index to link prediction assuming that the rate of CNs determines the probability of link generation to the total number of neighbors. Adamic and Adar [32] developed an index defining the probability of link generation by the number of shared links between two nodes. Thus, various algorithms have been constructed to calculate the probability of link generation. Among link prediction problems, some studies have analyzed the structure of transportation networks, which have developed rapidly with economic globalization and the development of various transportation systems. Gu et al. [30] developed a link prediction algorithm for China’s railroad and highway networks that considers network characteristics such as node degree and economic indicators such as GDP.

Some studies applied the link prediction problem to maritime shipping. Jeon et al. [33] proposed the hub-centrality and authority-centrality indices to analyze the centrality transition in the Asian cruise ship market. Ge et al. [31] quantitatively showed the hierarchical structure of ports and proposed four indices that developed the existing link prediction model. Kanrak and Nguyen [34] analyzed the structure, characteristics, and connectivity of cruise ship networks in Asia and Australasia using a random network model. Tagawa et al. [35] dealt with the link prediction problem using Node2vec, a graph embedding method and evaluated the impact of port alliances on port hierarchy. These studies proposed algorithms to predict the probability of link generation based on network characteristics. However, they did not reflect node characteristics unique to shipping, such as port performance, or link characteristics, such as distance between ports. If geographical constraints affect the link generation in shipping, the link prediction models of previous studies are inadequate. Based on the results of Kaluza et al. [6], who focused on the effect of shipping distance and developed the gravity model, Kosowska-Stamirowska [7] developed a prediction model for opening new routes and trade volume on links and concluded that the number of common neighbors between a pair of ports tempered by sea distance between them is better at predicting future links than the gravity model. However, her gravity models did not consider node and link characteristics simultaneously.

This study focuses on the intra-Asia container transport network, having a high concentration of ports with relatively homogeneous economies, which is different from Kosowska-Stamirowska [7] considering the entire world. Therefore, a model that considers geographical constraints such as port performance and distance between ports can be introduced.

3. Trends in Intra-Asian Container Shipping

3.1. Data Overview

This section analyzes the current intra-Asian oceangoing MCS trends using the MDS Containership Databank data provided by MDS Transmodal Inc. (hereinafter, ‘MDS data’) from 2011 to 2021 regarding the number of services and vessel sizes. The MDS data includes the name of service, operator, co-operating company, port of call list, annual service frequency, capacity (TEU and dead-weight tonnage), and speed for each containership but does not include any cargo information such as shipping amount. In addition, it also provides major and minor route classifications in the world for each liner service. This study focuses on oceangoing services classified into intra-Asia as the major category and Northeast and Southeast Asia as the minor categories. Notably, services that call only in Hong Kong and Chinese ports are also regarded as oceangoing services. Consequently, during the research period, the data on liner services, including 226 ports in 20 countries, are extracted (see Table 1).

Table 1. Countries and number of ports included in this study.

	Year
	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021
Australia	0	0	0	0	0	0	0	0	0	1	1
Bangladesh	0	1	1	1	2	2	2	1	0	0	1
Brunei	2	2	2	2	2	2	1	1	1	1	1
Cambodia	1	1	1	1	1	1	1	1	1	1	1
China	40	41	38	37	39	40	43	37	40	42	39
East Timor	1	1	1	1	1	1	1	1	1	1	1
Hong Kong	1	1	1	1	1	1	1	1	1	1	1
Indonesia	11	9	12	13	13	13	13	12	12	12	12
Japan	58	59	60	58	62	62	60	59	63	60	63
Malaysia	14	15	14	14	15	14	12	12	12	11	9
Myanmar	1	1	1	1	1	1	1	2	2	2	2
North Korea	1	1	0	0	0	0	0	0	0	0	0
Papua New Guinea	1	1	1	0	0	0	0	0	0	0	0
Philippines	7	7	8	7	7	7	7	7	7	7	7
Russia	4	3	4	5	5	5	6	5	5	4	3
Singapore	1	1	1	1	1	1	1	1	1	1	1
South Korea	12	12	10	10	10	11	10	11	12	11	11
Taiwan	5	5	5	4	4	4	4	4	4	4	4
Thailand	3	4	5	4	4	3	3	4	4	4	4
Vietnam	6	6	5	7	7	7	6	8	6	7	7
Total	169	171	170	167	175	175	172	167	172	170	168

3.2. Trend Analysis

First, Table 1 shows the countries and number of ports included in this study. The table shows that the total number of ports was approximately 170 in a given year. The number of ports in each country was also significantly unchanged.

Figure 1 shows the number of intra-Asian (Northeast and Southeast Asia) oceangoing MCS services in major East Asian countries. The figure indicates that the number of intra-Asian MCS services to/from China and Vietnam has been increasing, while the number of services to/from other countries has generally remained unchanged. Figure 2 shows the number of services if intra-Asian MCS services are further divided into those within Northeast Asia (China, Japan, Korea, Taiwan, and Far East Russia), those within Southeast Asia (ten member countries of the Association of Southeast Asian Nations and East Timor), and those between the two regions. The figure indicates that the number of services within Southeast Asia has been decreasing; in contrast, the number of services within Northeast and connecting Northeast and Southeast Asia has increased significantly, indicating a trend toward long-distance intra-Asia services.

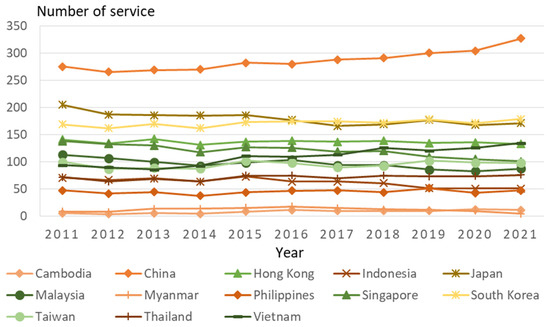
Figure 1. Number of intra-Asian oceangoing MCS services in major East Asian countries (2011–2021).

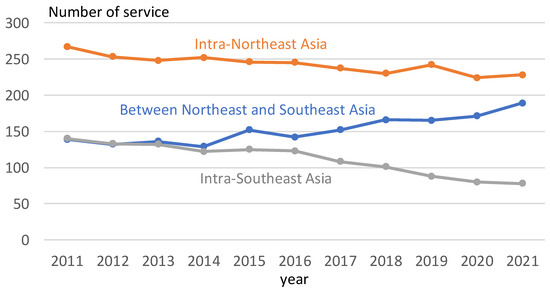
Figure 2. Number of intra-Asian oceangoing MCS services by region (2011–2021).

Figure 3 shows the average vessel size for intra-Asian MCS services by major countries. There is a clear trend toward increasing the average size of vessels. Moreover, the size of vessels in Southeast Asian island countries such as Indonesia, Singapore, Malaysia, and the Philippines is relatively large. Figure 4 shows the trend of average vessel sizes within and between Northeast and Southeast Asia. The figure indicates that the average vessel size within Northeast Asia is the smallest, followed by Southeast Asia. The average vessel size between the two regions is considerably larger than within them because they are long-distance services. The significant increase in vessel size is mainly caused by increasing competition among shipping companies and a cascade effect that larger vessels were shifted from the trunk routes [36], in addition to the increase in cargo shipping demand.

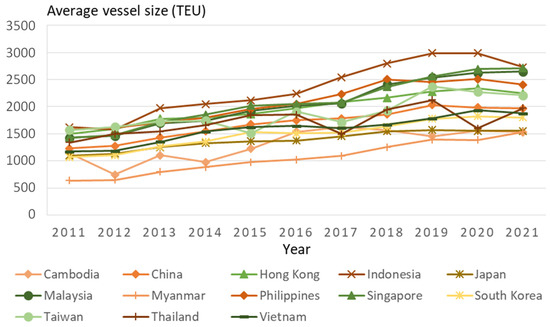
Figure 3. Average vessel size of intra-Asian oceangoing MCS services in major East Asian countries (2011–2021).

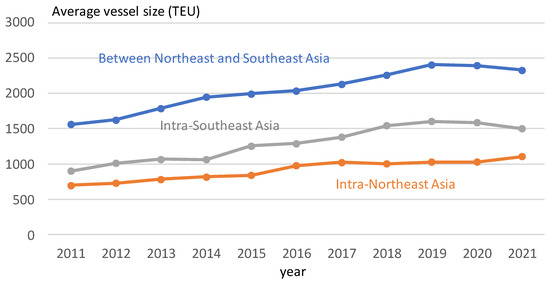
Figure 4. Average vessel size of intra-Asian oceangoing MCS services by region (2011–2021).

4. Model

This study represents the intra-Asian oceangoing MCS networks for 11 years from 2011 to 2021 as a weighted undirected graph using NetworkX, a Python library, based on the MDS data used in Section 3, and analyzes its characteristics. Ports are nodes, and MCS services are links. The links are weighted according to their annual shipping capacities. The annual capacity is calculated by multiplying a single vessel’s capacity by the annual service frequency. In this study, links are established only between ports of MCS services in consecutive order to call.

Furthermore, we construct a link prediction model that predicts the target year’s network structure based on the previous year’s structure. In addition to the methods of existing studies, we develop a link prediction method that considers the characteristics of MCS: the port size and the shipping distance between ports.

4.1. Network Topologies

The weighted undirected graph consists of two elements: nodes representing ports (N) and links representing MCS capacity between ports (L). If we define the number of ports as P, The set of nodes is denoted as N = {1, 2,…P}. Each link in a link set L is defined by two nodes (i, j) denoted l_ij. Two nodes connected by a link are represented as neighbor nodes. The network (N, L) is represented by a P × P square adjacency matrix A (each element is a_ij), where a_ij = 1 if there is a link between nodes i and j and a_ij = 0 otherwise. The weight of link l_ij is represented as w_ij and follows the MCS capacity between nodes ij. The following topology represents the configuration of the network.

The degree (k_i) of node i represents the number of links connecting to node i, expressed as follows:

$$k_i=\sum _{i,j\in \mathbb{N}}{a}_{ij}$$

(1)

The strength (s_i) of node i represents the sum of the weights of the links connected to node i, expressed as follows:

$$s_i=\sum _{i,j\in \mathbb{N}}{w}_{ij}$$

(2)

The disparity quantity (v_i) of node i is expressed using Equation (3). If all links have the same weights, the weights w_ij of all links are calculated by dividing the strength s_i of the node by the degree k_i, and thus the disparity is 1/k_i. On the other hand, if there is a large difference in the weights of the links, the disparity approaches 1 [37].

$${\mathit{v}}_{\mathit{i}}=\sum _{\mathit{i},\mathit{j}\in \mathbb{N}}{\left(\frac{{\mathit{w}}_{\mathit{i}\mathit{j}}}{{\mathit{s}}_{\mathit{i}}}\right)}^2$$

(3)

Betweenness centrality (b_i) represents the degree to which a node is on the shortest path connecting two other nodes, expressed using Equation (4). Betweenness centrality indicates the strength of a node as a hub or bridge connecting other nodes that are independent in the graph. Notably, the weights of the links do not affect betweenness centrality.

$$b_i=\frac{1}{\left(P-1\right)\left(P-2\right)}\sum _{j,h\in \mathbb{N}}\frac{{\sigma }_{jh}\left(i\right)}{{\sigma }_{jh}}$$

(4)

where σ_jh is the number of shortest paths connecting nodes j and h, and σ_jh(i) is the number of shortest paths connecting nodes j and h that pass through node i.

4.2. Link Prediction Models

The link prediction problem predicts the generation (or disappearance) of a link between two nodes in the target year based on available network information. Namely, c is the number of new links that will appear (or the number of links that will disappear) in the target year. A score S_ij, which is differently defined for each model, is calculated for each missing (or existing) link in the target year, and then the links included within the cth link, counting from the one with the highest (or lowest) score calculated by the link prediction model, is regarded as the set of new (or disappearing) links in the target year.

Link prediction models have been developed and are widely applied as an efficient tool for analyzing the evolutionary process of networks. In addition to the existing link prediction models, this study develops a link prediction method that considers the significance of ports (the sum of the weights of the links connected to ports) and the distance between ports.

4.2.1. Existing Models

First, common neighbors (CNs) [28] is an index representing that the more neighbors nodes i and j have in common, the more likely a link connecting these two nodes will appear, expressed as follows:

$$S_{ij}^{CN}=\left|\mathsf{\Gamma }\left(i\right)\cap \mathsf{\Gamma }\left(j\right)\right|$$

(5)

where Γ(i) and Γ(j) are the set of neighboring nodes of nodes i and j, respectively.

Second, the Jaccard coefficient (JC) [29] is an index to measure the structural equivalence of sets. In link prediction, the index is determined by the number of CNs and adjacent nodes, expressed as follows:

$$S_{ij}^{JC}=\frac{\mathsf{\Gamma }\left(i\right)\cap \mathsf{\Gamma }\left(j\right)}{\mathsf{\Gamma }\left(i\right)\cup \mathsf{\Gamma }\left(j\right)}$$

(6)

Third, Adamic Adar (AA) [32] is an index representing that the probability of link generation is determined by the number of nodes adjacent to CNs of two nodes, expressed as follows:

$$S_{ij}^{AA}=\sum _{u\in \mathsf{\Gamma }\left(i\right)\cap \mathsf{\Gamma }\left(j\right)}\frac{1}{\log \left|\mathsf{\Gamma }\left(u\right)\right|}$$

(7)

Fourth, preferential attachment (PA) [5] is an index representing that the degree of two nodes affects the probability of link generation, expressed as follows.

$$S_{ij}^{PA}=k_i\times k_j$$

(8)

4.2.2. A New Model for MCS Network Analysis

This study develops a new link generation model, an MCS network (MCN) model, that considers the evolutionary characteristics of MCS networks as follows. (1) Node characteristics: In an MCS network, new services are likely to be launched between ports with many cargo or vessel capacities to call at. (2) Link characteristics: New services are more likely to be launched between ports nearby in an MCS network.

Points (1) and (2) reflect the hub-and-spoke structure in the MCS networks, where cargo generated in each region is collected at a hub port by feeder services and allocated and shipped by destination direction without direct inter-regional shipping between small ports. This system can reduce the number of routes required to develop an MCS network and improve shipping efficiency.

Based on the above assumptions and referring to the structure of the gravity model, which is often used in the trade research field, the MCN model uses the following index. One of the important features of this model is its applicability to both existing and non-existent links, different from other indices such as transport volume by link.

$$S_{ij}^{MCN}=\frac{{{(s}_i\times s_j)}^a}{{d_{ij}}^b}$$

(9)

where d_ij is the distance between nodes i and j, a is the parameter for intensity, and b is the parameter for distance.

Regarding the shipping distance data between ports, we used the data [38] used in the global logistics intermodal network simulation (GLINS) model [14], as shown in the following steps. Of the 226 ports included in the model in this study, 117 ports were also included in the GLINS model (referred to as port group A), and 109 ports were not included (referred to as port group B).

• Regarding the shipping distance between ports in port group A, the distances used in the GLINS model are adopted.
• Regarding the shipping distance $d_{p_A{p}_B}$ between port p_A of port group A and port p_B of port group B, let p′_A be the port in port group A that is closest to port p_B in port group B. $d_{p_A{p}_B}$ is expressed as

  $$d_{p_A{p}_B}=d_{p_A{p\prime }_A}+d_{{p\prime }_A{p}_B}$$

  (10)
• Regarding the shipping distance $d_{p_{B1}{p}_{B2}}$ between ports p_B1 and p_B2 of port group B, let p′_A1 be the closest port in port group A to port p_B1 in port group B and p′_A2 be the closest port in port group A to port p_B2 in port group B. $d_{p_{B1}{p}_{B2}}$ is expressed as

  $$d_{p_{B1}{p}_{B2}}=d_{{p\prime }_{A1}{p\prime }_{A2}}+d_{{p\prime }_{A1}{p}_{B1}}+d_{{p\prime }_{A2}{p}_{B2}}$$

  (11)

Figure 5 shows an illustration of how the distance between ports is generated.

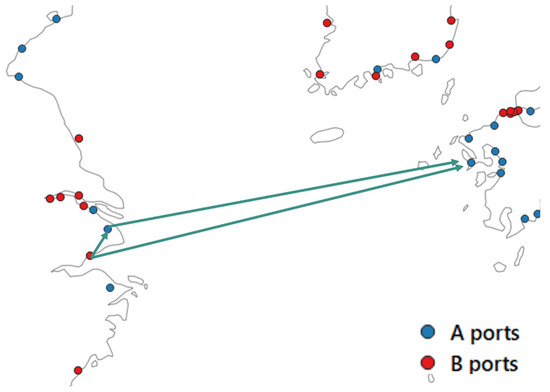
Figure 5. Image of creating shipping distance between ports.

4.3. Model Evaluation Methodology

As an evaluation index for the link prediction method, this study adopts the area under the receiver operating characteristic (ROC) curve (AUC) as in previous studies [30,31]. The ROC curve is a coordinate graph with sensitivity on the vertical axis and a false positive rate on the horizontal axis. AUC is the probability that a randomly selected missing link will score higher than a randomly selected non-existent link in each link prediction method. The AUC takes values from 0.5 to 1.0; the closer to 1.0, the higher the link prediction accuracy.

$$AUC=\frac{n^{\prime }+0.5n^{″}}{n}$$

(12)

where n is the number of links, n’ is the number of missing links that obtained a higher score than the randomly selected non-existent link, and n″ is the number of missing links that obtained the same score as a randomly selected non-existent link.

5. Results

This section presents the results of the network structure analysis and link prediction. Section 5.1 describes the topological characteristics of the intra-Asian MCS service from 2011 to 2021; Section 5.2 explains the parameter calibration of the MCN model; Section 5.3 compares the prediction results of each model; then Section 5.4 presents a discussion based on the results.

5.1. Basic Configurations of the MCS Network

Table 2 shows the basic configurations of the intra-Asian oceangoing MCS network from 2011 to 2021. As shown in the table, the number of links, average degree, and average strength increased from 2011 to 2021, indicating that the intra-Asian oceangoing MCS networks have expanded as the number of trading partner ports and volume have increased. In contrast, the average disparity quantity has decreased from 2011 to 2021, indicating that the difference in shipping capacity between the links is decreasing.

Table 2. Basic configurations of intra-Asian oceangoing MCS networks (2011–2021).

	Year
	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021
Number of nodes (N)	169	171	170	167	175	175	172	167	172	170	168
Number of links (L)	1765	1780	1756	1818	2025	2118	2068	2105	2222	2227	2329
Average degrees (ki)	20.888	20.819	20.659	21.772	23.143	24.206	24.047	25.210	25.837	26.200	27.726
Average betweenness centrality (bi)	0.007	0.007	0.007	0.007	0.006	0.006	0.006	0.006	0.006	0.006	0.006
Average strength (si) (10,000)	541	503	573	596	667	757	761	867	926	979	1015
Average disparity quantity (vi)	0.188	0.181	0.190	0.180	0.166	0.153	0.154	0.148	0.142	0.142	0.131
Max. degrees	107	108	104	100	115	114	115	117	125	109	113
Max. betweenness centrality	0.201	0.202	0.190	0.177	0.182	0.182	0.195	0.206	0.216	0.160	0.154
Max. strength	6510	6286	7578	6851	7853	8890	8895	9306	9817	10,892	10,283

Figure 6 shows the intra-Asian oceangoing MCS networks in 2011 and 2021. The size of a node is weighted according to each node’s degree, and the link thickness is weighted according to the annual vessel capacity. As shown in the figure, the links connecting ports in China and those in Southeast Asia are particularly thick. This result indicates that the container trade volume between Southeast Asia and China increased from 2011 to 2021.

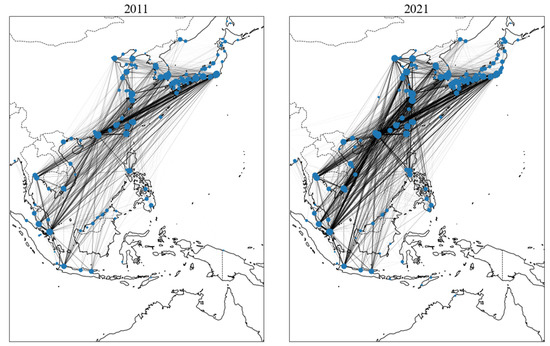
Figure 6. Intra-Asian oceangoing MCS networks (left: 2011, right: 2021). The size of each blue circle represents a degree of each port.

5.2. Model Calibration

This section presents the results of calibrating the MCN model constructed in this study. For each year from 2012 to 2021, we predict the presence or absence of links for all port combinations in the network, given the previous year’s network, and obtain the average for nine years of AUC that the MCN model estimates for each year.

Table 3 shows the calibration results to compare the average AUC with different combinations of parameters, indicating that the model performs best for a = 1 and b = 2 (the same AUC for a = 2 and b = 4 due to the model’s cost function specification). Therefore, this study uses a = 1 and b = 2 as the parameters of the MCN model for further analysis.

Table 3. Average AUCs for nine years with different combinations of parameters.

a	b	AUC
1	1	0.9202
1	2	0.9271
1	3	0.9161
1	4	0.8982
1	5	0.8792
2	1	0.9062
2	2	0.9202
2	3	0.9267
2	4	0.9271
2	5	0.9230

5.3. Link Prediction Results

This section presents the link prediction results for each model and compares the accuracy of the MCN model with that of other models. Furthermore, we analyze the prediction accuracy of each model from a geographic perspective. This study defines “the correct link” for each model to compare the model accuracy as follows. Namely, m is defined as the total number of new links that actually appeared in the network in year Y (or the total number of disappeared links in the network in year Y). Among these new (or disappeared) links, the correct link in year Y is defined as the one included within the mth link, counting from the one with the highest (or lowest) score calculated by the link prediction model. We define the set of the correct links by summing the correct links in all research years.

In the following part of this section, we discuss the prediction accuracy of all links (links for the entire network), new links, and disappearing links. The prediction accuracy of all links is obtained by computing S_ij from all possible node combinations in the network of year Y-1, regardless of their existence. In contrast, regarding the new (or disappearing) links, S_ij is computed from all missing (or existing) links in the network of year Y-1.

5.3.1. Prediction of the Entire Network

Figure 7 shows the prediction accuracy of links for the entire network for each model. The figure indicates that the AA model has the highest prediction accuracy for all pairs except for 2015 and that the MCN model has the second-highest accuracy in many years.

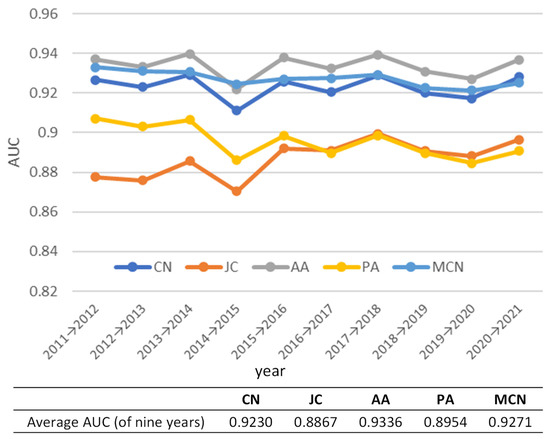
Figure 7. AUC calculated by each model (prediction of all links).

5.3.2. Prediction of New Links

Figure 8 shows the prediction accuracy of new links for each model. The figure indicates that the MCN model performs the best on average and consistently performs higher than the other models except for in 2020. In contrast, other models are less accurate, especially in 2015 and 2020. There are fewer accuracies in 2015 because these models cannot predict the generation of links between Southeast and Northeast Asia, which appeared in large numbers from 2014 to 2015. On the other hand, there are fewer accuracies in 2020 because all models failed to predict the generation of links between small ports, which appeared in large numbers in 2020.

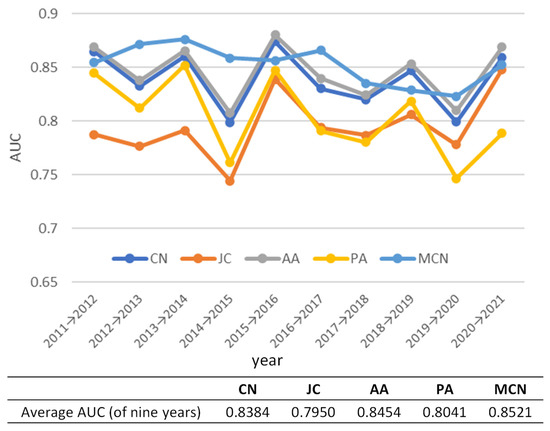
Figure 8. AUC calculated by each model (prediction of new links).

Figure 9 shows the geographical characteristics of the correctly predicted new links. As summarized in the figure, 308 correct new links for the MCN model are found. This number is the lowest of all of the models. Regarding the breakdown of domestic/international links, the MCN model has the highest percentage of domestic links (148/308 = 48%) out of all the models. Furthermore, the MCN model has the shortest average distance of 543 nautical miles for the correct new links out of all the models. This observation indicates that the MCN model predicts new links between nearby ports well. In contrast, the MCN model has the lowest number of correct new links for new international links connecting ports far from each other. Regarding new links in the intra-Asia container transport network, there is a characteristic that many links appear between a large number of ports located in Japan and China, which are densely located within a short distance from each other. Therefore, the MCN model, which assumes that the shorter the distance between ports, the higher the probability of link generation, acquires more correct links than other models.

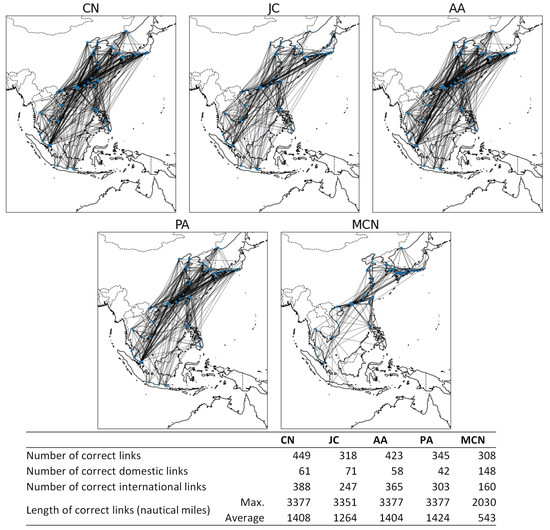
Figure 9. Geographic characteristics of correct links (prediction of new links).

5.3.3. Prediction of Disappearing Links

Figure 10 shows the prediction accuracy of each model in predicting the disappearing links, which is lower than the prediction accuracy for new links shown in Figure 8. Furthermore, Figure 10 indicates that the MCN model performs the best on average and consistently performs higher than the other models except for 2014 and 2017.

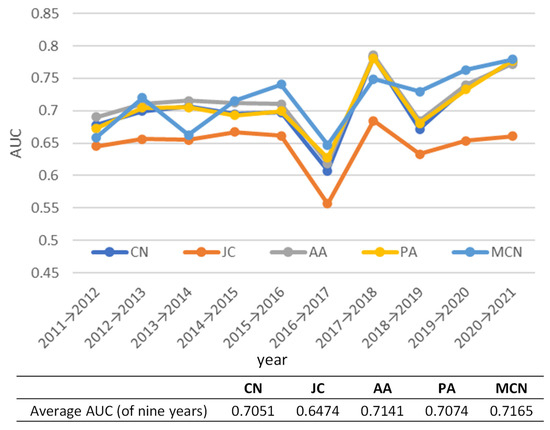
Figure 10. AUC calculated by each model (prediction of disappearing links).

Figure 11 shows the geographical characteristics of the correctly predicted disappearing links for each model. The MCN model predicts 640 correct disappearing links, the largest number of all of the models. Moreover, the MCN model predicts an average distance of 1360 nautical miles for the correct disappearing links, and international links account for 68% of the correct disappearing links. This observation indicates that the MCN model performs well in predicting disappearing links between ports far from each other. As vessels’ sizes increase, especially for longer-distance intra-Asian services between Southeast and Northeast Asia, as shown in Figure 4 of Section 3, they tend to be consolidated into large-scale transport between major ports. Therefore, the MCN model, which assumes that the farther the distance between ports is, the higher the probability of link disappearance, fits well.

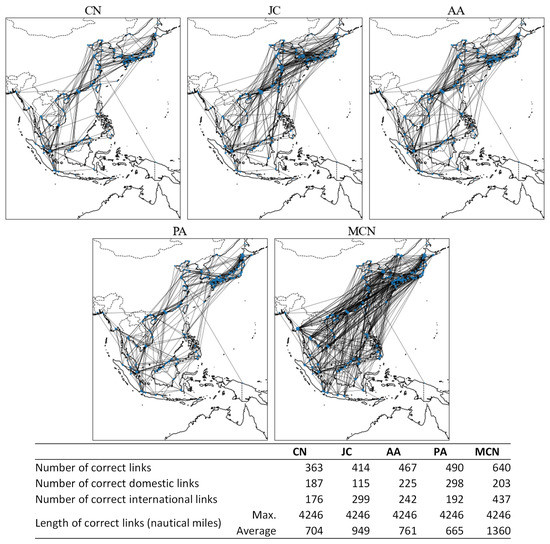
Figure 11. Geographic characteristic of correct links (prediction of disappearing links).

5.4. Discussion

This study examined the link prediction accuracy of the MCN model compared to the existing link prediction models. In summary, the MCN model predicted new links well in all years except 2020. However, Kosowska-Stamirowska [7] showed that the CN model, considering the distance between ports, had a higher prediction accuracy than the gravity model, which corresponds to the MCN model in this study. There are two possible reasons for this discrepancy in results: first, both studies applied their models to different regions; while Kosowska-Stamirowska [7] predicted links in the worldwide MCS network, this study applied the model only to the intra-Asian MCS network, which has a high concentration of ports with relatively homogeneous economies. Second, unlike the gravity model in Kosowska-Stamirowska [7], the MCN model incorporates node strength. Simultaneous consideration of both node and link characteristics improves the prediction accuracy of the model.

Moreover, compared with the MCN model, other models showed a particularly decreased accuracy for 2015. Figure 12 indicates a frequency distribution of the new links which appeared in 2015 in the rank of link generation probability for each model. The figure shows that the MCN model predicts 88 links (28.6% of the total correct new links) as having a probability of link generation in the top 500 and 285 links (92.5%) in the top 4500. These results indicate that the MCN model’s assumption that new links are more likely to appear between ports of larger size and closer distance is valid.

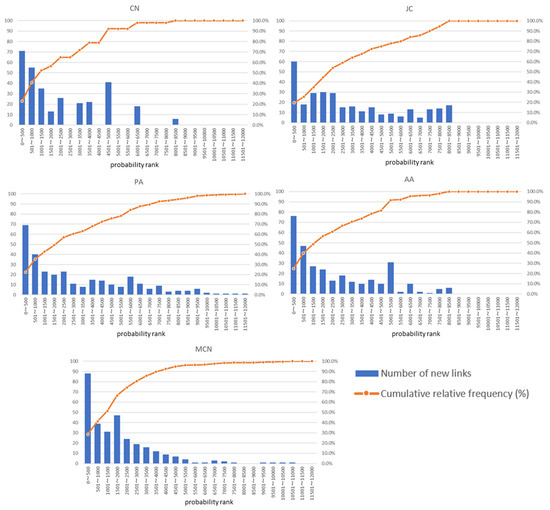
Figure 12. Frequency distribution of new links appearing in 2015 in the link generation probability rank.

If focusing on the CN and AA models, which have similar trends, the number of links with a probability of link generation in the top 500 is smaller than that of the MCN model, at 71 links (23.1%) and 76 links (24.7%), respectively. Moreover, the CN model predicts 41 links (13.3%) with a probability of link generation between 4501 and 5000, whereas the AA model predicts 31 links (10.1%) with a probability of link generation of 5001 to 5500, which are larger than that of the MCN model. Among them, significant portions (25 of the 41 links predicted by the CN model as having a probability of link generation between 4501 and 5000, and 25 of the 31 new links predicted by the AA model as having a probability of link generation between 5001 and 5500) are occupied with the links connected to the Subic Bay port in the Philippines. These results indicate that the CN and AA models are less accurate in predicting the new links between ports with few neighboring nodes in common in the previous year, such as the new links from the Subic Bay port. In particular, in Kosowska-Stamirowska [7], the CN model considering distances showed higher accuracy than that of the gravity model. In the intra-Asian MCS network, small ports such as Subic Bay port often connect to hub ports, and containers are transported to other ports by transshipment. Therefore, the number of common neighbors, an indicator used in the CN model, is small, and the probability of link generation is likely to be underestimated.

The JC model predicts 60 links (19.5%) with a probability of link generation in the top 500, fewer than the MCN model, and 85 links (27.6%) with a probability of link generation above 4501. Furthermore, the frequency of links in each class is smaller than that of the MCN model. This is because it is difficult for the JC model to show differences in the index among the ports. In other words, there is a correlation between the number of adjacent nodes in each port, the denominator of the index used in the JC model, and the number of common adjacent nodes, which is the numerator.

The PA model predicts 69 links (22.4%) as having a probability of link generation in the top 500, fewer than the MCN model, and 85 links (27.6%) as having a probability of link generation above the 4501. Furthermore, as with the JC model, the frequency difference for each class is smaller than that of the MCN model. This is because the node degree used in the PA model does not differ easily among ports, except for some large ports.

Meanwhile, in predicting disappearing links, each model’s accuracy was lower than that of the prediction of new links. In this study, we assumed that links with smaller link generation probabilities calculated using the indicators of each model are more likely to disappear. However, in the hub-and-spoke shipping network, the number of small ports is much larger than that of large ports. Among the links with small link generation probabilities calculated by the models, many links disappear and do not disappear. Therefore, setting the threshold to increase the model’s sensitivity will likely increase the false positive rate, resulting in the ROC curve approaching a 45-degree straight line and a smaller value for the AUC, the lower area of the curve.

Figure 13 shows a frequency distribution of the links that disappeared in 2017 in the rank of link disappearance probability (the smaller the probability, the higher the ranking) for each model. The figure indicates that the prediction accuracies of the existing models are low: the links that disappeared in 2017 are dispersed within 1 to 2000th place in the link disappearance probability ranking calculated by the model of the previous study. This indicates that the indices of the existing models do not include enough variables to correlate with link disappearance. Meanwhile, there is a slight correlation between the link disappearance probability rank calculated by the MCN model and the number of links that disappeared, suggesting that the MCN model may be more accurate in predicting the disappearing links than other models. However, the AUC of the MCN model is not as high as that of other models. Therefore, improving the prediction accuracy by identifying factors that correlate with link disappearance and incorporating them into the model is a further issue.

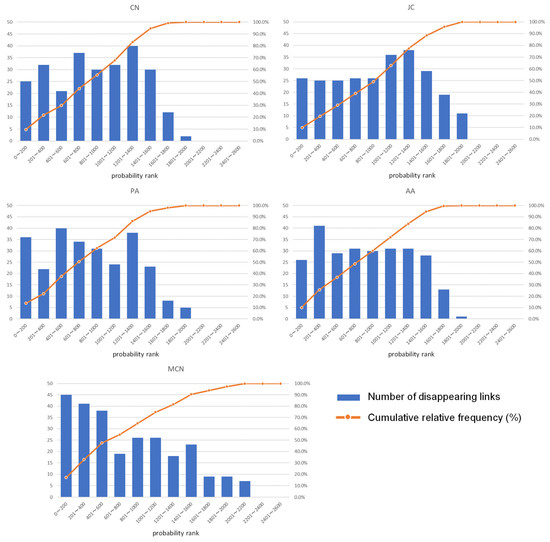
Figure 13. Frequency distribution of new links appearing in 2017 in the link generation probability rank.

6. Conclusions

This study proposed a link prediction model for the intra-Asian oceangoing MCS networks to realize the sustainable growth of the MCS market. The model can calculate the probability of link generation by considering the characteristics of MCS, including the port size and shipping distance between ports that cause the generation of new shipping routes in the MCS industry. We compared the prediction accuracy of the proposed model with other models considered in previous studies. Consequently, the following were found.

(1)

The intra-Asian oceangoing MCS networks have expanded from 2011 to 2021 as the trading partners and trade volume have increased.

(2)

The assumptions of the MCN model that new links are likely to be generated between closer or larger ports were suitable as a link prediction method. In particular, the MCN model is good at predicting the new links between ports with short distances. Unlike Kosowska-Stamirowska [7], the MCN model showed the highest prediction accuracy, indicating that the link prediction model should be created with the geographical characteristics for both nodes and links of the region to which it is applied, especially for those having a high concentration of ports with relatively homogeneous economies such as the intra-Asian shipping network.

(3)

Regarding the prediction of disappearing links, the accuracy of all the models remained an issue because of a high proportion of small ports characterized by the hub-and-spoke shipping network.

These results support the development process and characteristics of the intra-Asian container transport network. In particular, the results fit the trend toward consolidating into longer-distance services between major ports or multiple port-calling services because of vessel enlargement and the generation of many local links connecting closer ports. Furthermore, the difference from the results of Kosowska-Stamirowska [7] suggests that a link prediction model that considers distance is helpful in Asia, where ports are densely located over short distances and intra-regional transport is flourishing. In building a more sophisticated link prediction model, it is necessary to consider the characteristics of shipping networks in each region.

The following are possible future research directions.

(1)

Adding other variables

The MCN model can be improved further. In this study, we proposed a model that depends on the shipping distance between ports and the significance of ports. However, in the shipping industry, in addition to these factors, various factors, such as the regional characteristics of each shipping company and economic growth rate, may affect the emergence of new networks. Reflecting more factors in the model is necessary to develop a more accurate model.

(2)

Improvement of accuracy of shipping distance data between ports

The shipping distance data for ports not treated in previous studies was calculated based on nearby ports in this study. However, there is still a possibility to improve the model’s accuracy if we make distance data between ports more accurate.

(3)

Analysis using time-series data

In this study, we developed a model for MDS data from 2011 to 2021 that predicts the network in a year from the network in the previous year. However, we may also develop a model to predict the future network by inputting multiple past years of network data that reflects the time-series evolution process of the network more accurately.

(4)

Improvement of the structure of the MCN model

In this study, we calculated the MCN model by employing annual capacity as the link weights. However, the prediction accuracy may be improved by adopting different indicators, such as the number of annual services, as weights. Furthermore, by analyzing the effect of vessel size on each link, it is possible to verify the cascade effect, which can explain the rapid increase in the size of containerships in the intra-Asian MCS services as a result of the diversion of vessels from the main trunk routes when large containerships are replaced there. Considering the cascade effect is also important from the viewpoint of realizing the sustainable MCS and shipbuilding markets factoring in the entire life of vessels. In addition, a model that combines the assumptions of other models with the MCN model could also be considered.