Spatial Distribution of Soil Heavy Metal Concentrations in Road-Neighboring Areas Using UAV-Based Hyperspectral Remote Sensing and GIS Technology
Abstract
1. Introduction
2. Study Area and Materials
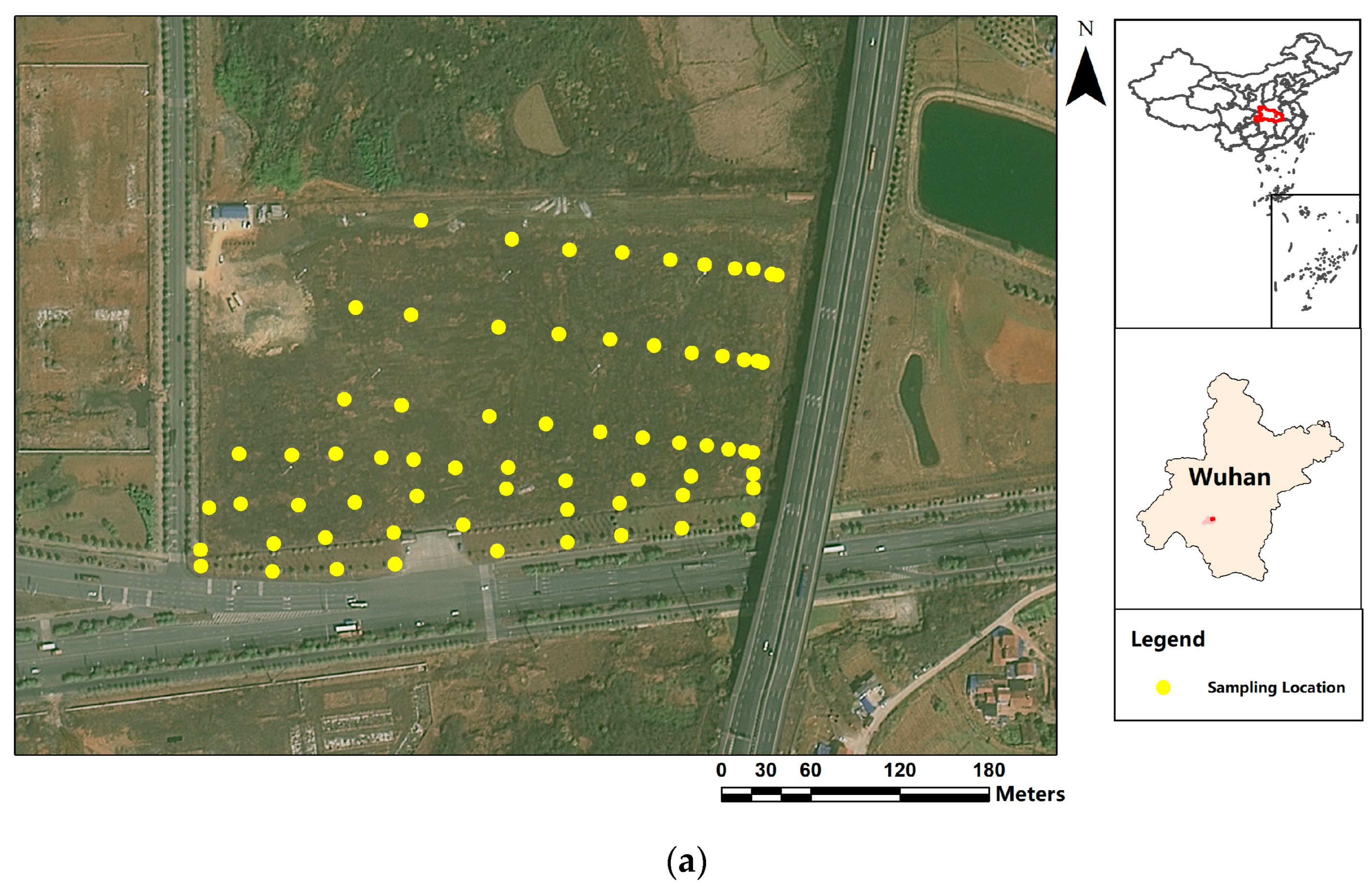
2.1. Study Area
2.2. Materials
2.2.1. UAV Hyperspectral Remote Sensing Image Data Collection and Image Preprocessing
- (a)
- Geometric registration: Images from different flights were geometrically registered using the quadratic polynomial calculation model to eliminate the geometric distortions.
- (b)
- Radiometrical normalization: This process was used to eliminate the radiometrical inconsistency among the images acquired by different flights.
- (c)
- Image mosaic: The images acquired from different flights were mosaicked into a seamless wide-field image.
- (d)
- Geometric correction: The mosaicked image was geometrically corrected based on the ground control points.
2.2.2. On-Site Soil Data Collection and Processing
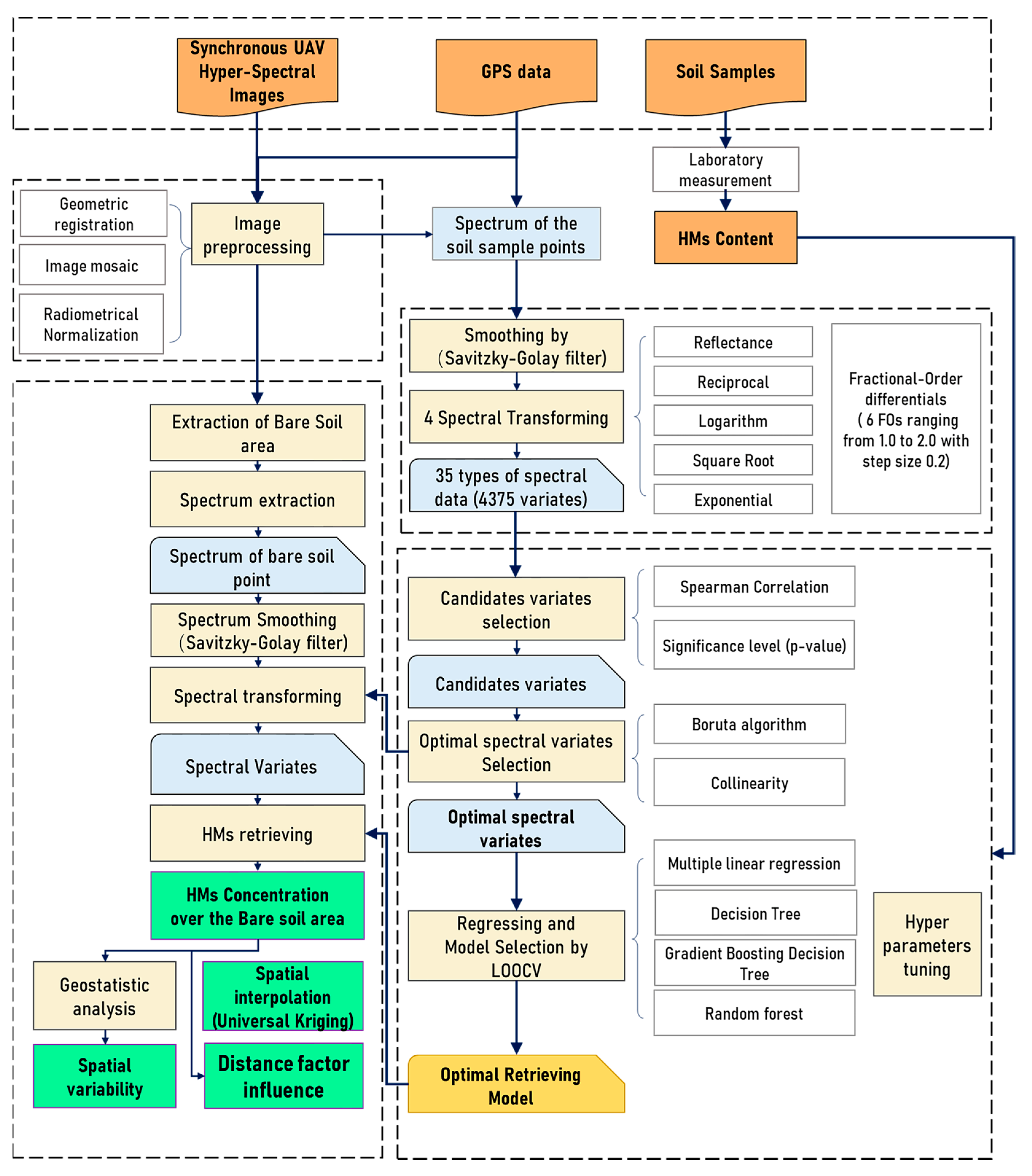
3. Method
3.1. Retrieval of Soil Heavy Metal Concentrations
3.1.1. Pretreatment of the Hyperspectral Data
3.1.2. Optimal Spectral Variates Selection
3.1.3. Model Development and Selecting for Retrieving Soil HM Concentrations
- (1)
- The modeling methods.
- 1.
- Multivariate Linear Regressor (MLR)
- 2.
- Decision Tree Regressor (DT)
- 3.
- Gradient-Boosted Decision Trees Regressor (GBDT)
- 4.
- Random Forest Regressor (RF)
- (2)
- Metrics for Evaluating Regression Models
- (3)
- Model selection
3.2. Analysis of Soil Heavy Metal Concentrations Characteristics
- (1)
- Correlation Analysis: Correlation analysis was conducted to reveal the inter-correlations among different HMs. A strong correlation may indicate that two types of heavy metals come from the same source [52,53]. In this study, the Pearson correlation coefficient was calculated to measure the degree of association between the concentrations of Cr and Cu in the soil samples [54].
- (2)
- Spatial Interpolation: Since only the HM concentrations over the bare soil pixels were retrieved, interpolation was employed to map the distribution of HM concentrations in the entire study area to provide a qualitative understanding of spatial trends and patterns, enabling visual interpretation and exploration of the data. The universal kriging (UK) interpolation tool in ArcGIS software (version 10.7.1, ESRI, Redlands, CA, USA) was used for this purpose. Kriging is a geostatistical interpolation method that considers both the distance and degree of variation between known data points when estimating values in unknown areas. UK, a kriging method with a local trend or drift, was used because it is appropriate for analyzing data with a specific trend [55].
- (3)
- Influence of Perpendicular Distance to the Road: The spatial distribution of HMs in the road-neighboring area is affected by various factors. In this study, the perpendicular distance of bare soil points from Jin-Long Avenue was calculated and analyzed as an external environmental factor. The relationship between this distance and soil HM concentrations was analyzed using the Data Management Tool in ArcMap 10.7 and a self-developed Python program.
4. Results and Discussion
4.1. Descriptive Statistics of Soil HMs Concentrations
4.2. Model Development and Selection for Heavy Metal Concentration Retrieval
4.2.1. Spectral Transformations
4.2.2. Selection of Optimal Spectral Variates
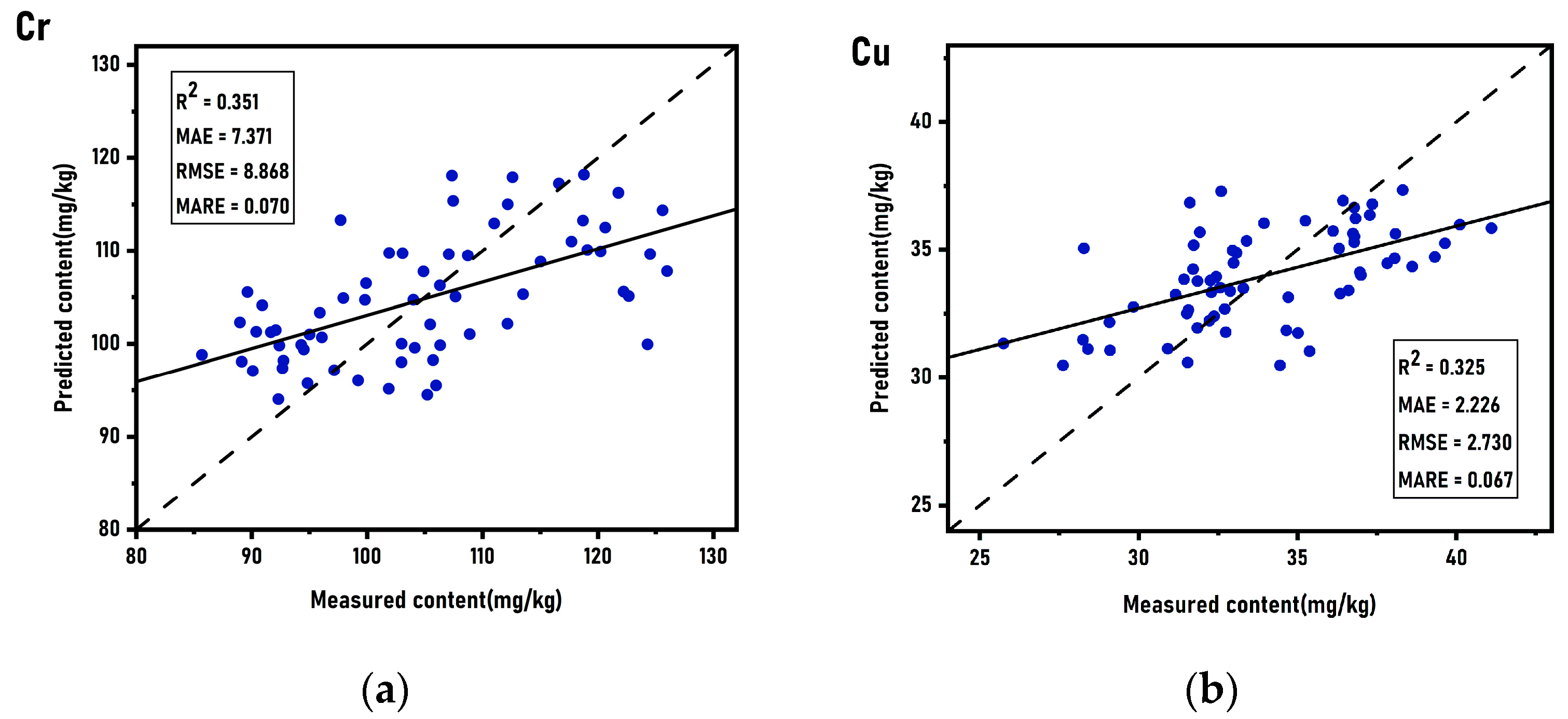
4.2.3. Model Development and Selection for Heavy Metal Concentration Retrieval
4.3. The Spatial Character of the Soil HMs Concentrations
4.3.1. Spatial Distribution of HMs Concentrations
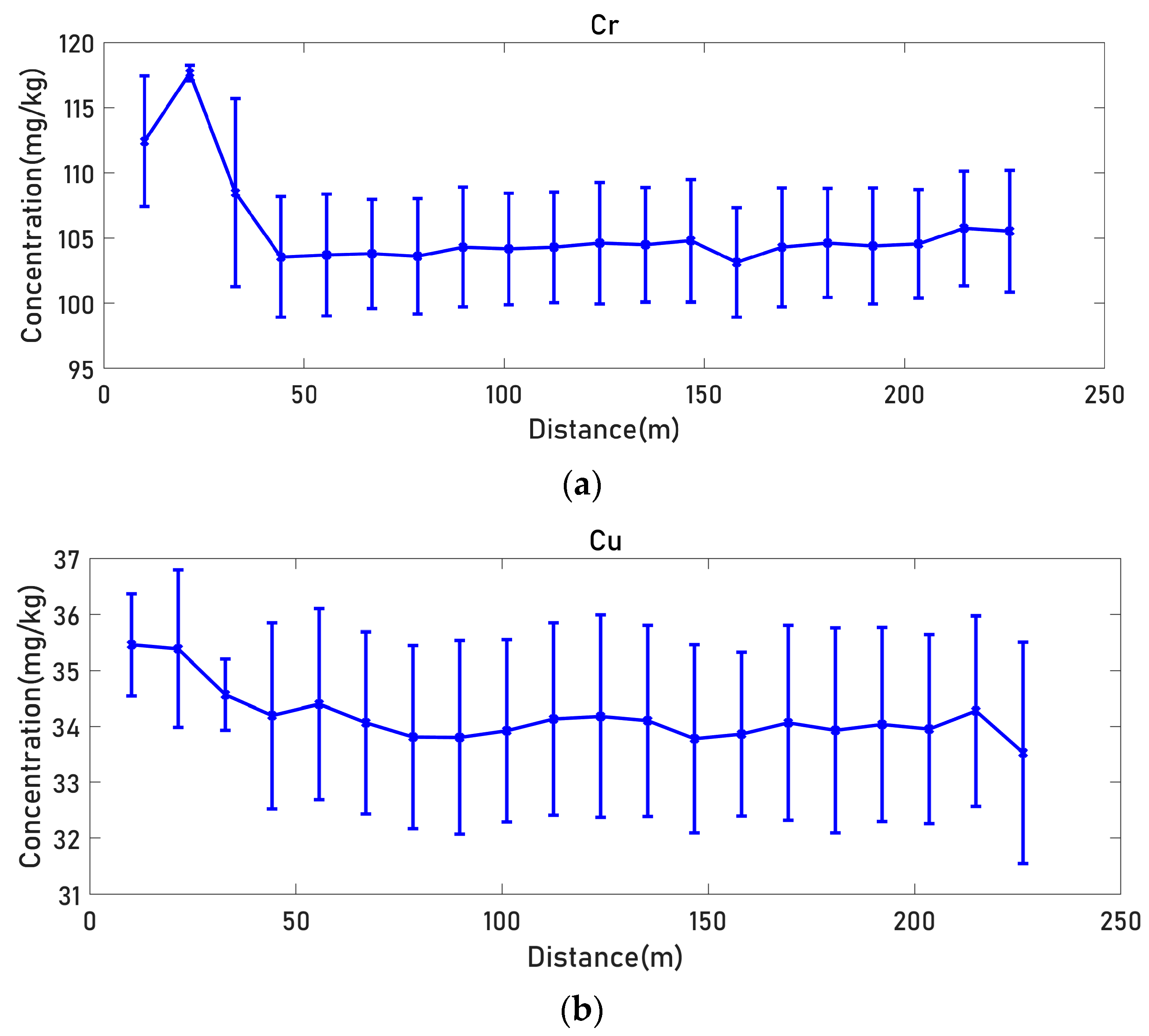
4.3.2. Influence of the Perpendicular Distance to the Road
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, T.; Guo, L.; Chen, Y.; Wang, W.; Shi, Z.; Li, Q.; Wu, G. Proximal and Remote Sensing Techniques for Mapping of Soil Contamination with Heavy Metals. Appl. Spectrosc. Rev. 2018, 53, 783–805. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, R.; Li, H.; Zhao, X.; Liu, X. Heavy Metal Pollution and Soil Quality Assessment under Different Land Uses in the Red Soil Region, Southern China. Int. J. Environ. Res. Public Health 2022, 19, 4125. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, Y.; Hu, Q.; Han, M.; Li, X.; Zhang, Y.; Li, Z.; Shi, R. Accumulation Characteristics and Pollution Evaluation of Soil Heavy Metals in Different Land Use Types: Study on the Whole Region of Tianjin. Int. J. Environ. Res. Public Health 2022, 19, 10013. [Google Scholar] [CrossRef]
- Sert, E.B.; Turkmen, M.; Cetin, M. Heavy Metal Accumulation in Rosemary Leaves and Stems Exposed to Traffic-Related Pollution near Adana-İskenderun Highway (Hatay, Turkey). Environ Monit Assess 2019, 191, 553. [Google Scholar] [CrossRef]
- Hamzeh, M.A.; Aftabi, A.; Mirzaee, M. Assessing Geochemical Influence of Traffic and Other Vehicle-Related Activities on Heavy Metal Contamination in Urban Soils of Kerman City, Using a GIS-Based Approach. Environ Geochem Health 2011, 33, 577–594. [Google Scholar] [CrossRef]
- Khalifa, A.A.; Darwish, M. Estimation of Lead Concentration in Settled Dust at Gharian City, Libya. MAYFEB J. Environ. Sci. 2017, 1, 6–10. [Google Scholar]
- Heidari, M.; Darijani, T.; Alipour, V. Heavy Metal Pollution of Road Dust in a City and Its Highly Polluted Suburb; Quantitative Source Apportionment and Source-Specific Ecological and Health Risk Assessment. Chemosphere 2021, 273, 129656. [Google Scholar] [CrossRef]
- Wang, G.; Zeng, C.; Zhang, F.; Zhang, Y.; Scott, C.A.; Yan, X. Traffic-Related Trace Elements in Soils along Six Highway Segments on the Tibetan Plateau: Influence Factors and Spatial Variation—ScienceDirect. Sci. Total Environ. 2017, 581–582, 811–821. [Google Scholar] [CrossRef]
- Nikolaeva, O.; Rozanova, M.; Karpukhin, M. Distribution of Traffic-Related Contaminants in Urban Topsoils across a Highway in Moscow. J. Soils Sediments 2017, 17, 1045–1053. [Google Scholar] [CrossRef]
- She, W.; Guo, L.; Gao, J.; Zhang, C.; Wu, S.; Jiao, Y.; Zhu, G. Spatial Distribution of Soil Heavy Metals and Associated Environmental Risks near Major Roads in Southern Tibet, China. Int. J. Environ. Res. Public Health 2022, 19, 8380. [Google Scholar] [CrossRef]
- Sutherland, R.A. Lead in Grain Size Fractions of Road-Deposited Sediment. Environ. Pollut. 2003, 121, 229–237. [Google Scholar] [CrossRef] [PubMed]
- Hua, M.; Zhu, B.W.; Liao, Q.L.; Pan, Y.M.; Yang, J.; Feng, J.S. Preliminary Research on Pollution Level of Heavy Metals in Farmland Soils along Both Sides of Main Roads in Jiangsu. J. Geol. 2008, 32, 165–171. [Google Scholar]
- Yan, X.; Gao, D.; Zhang, F.; Zeng, C.; Xiang, W.; Zhang, M. Relationships between Heavy Metal Concentrations in Roadside Topsoil and Distance to Road Edge Based on Field Observations in the Qinghai-Tibet Plateau, China. Int. J. Environ. Res. Public Health 2013, 10, 762–775. [Google Scholar] [CrossRef]
- Enuneku, A.; Biose, E.; Ezemonye, L. Levels, Distribution, Characterization and Ecological Risk Assessment of Heavy Metals in Road Side Soils and Earthworms from Urban High Traffic Areas in Benin Metropolis, Southern Nigeria. J. Environ. Chem. Eng. 2017, 5, 2773–2781. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, Y.; Peng, Y.; Zhao, L.; Hu, Y. Estimation of Soil Heavy Metal Content Using Hyperspectral Data. Remote. Sens. 2019, 11, 1464. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, A.; Kaur, P.; Singh Sidhu, G.P.; Bali, A.S.; Bhardwaj, R.; Thukral, A.K.; Cerda, A. Pollution Assessment of Heavy Metals in Soils of India and Ecological Risk Assessment: A State-of-the-Art. Chemosphere 2019, 216, 449–462. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral Sensing of Heavy Metals in Soil and Vegetation: Feasibility and Challenges. ISPRS J. Photogramm. Remote. Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Mulder, V.L.; de Bruin, S.; Schaepman, M.E.; Mayr, T.R. The Use of Remote Sensing in Soil and Terrain Mapping—A Review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Gan, W.; Xu, J.; Feng, S.; Xiaodi, H.U.; Anna, X.; Suxun, S. Spatial Statistical Characteristics of the Heavy Metal Pollution at the Road Side Soil-A Case in Jiang-Xia District of Wuhan. J. Geomat. 2022, 47, 49–53. [Google Scholar]
- Mouazen, A.M.; Nyarko, F.; Qaswar, M.; Tóth, G.; Gobin, A.; Moshou, D. Spatiotemporal Prediction and Mapping of Heavy Metals at Regional Scale Using Regression Methods and Landsat 7. Remote. Sens. 2021, 13, 4615. [Google Scholar] [CrossRef]
- Chen, H.W.; Chen, C.-Y.; Nguyen, K.L.P.; Chen, B.-J.; Tsai, C.-H. Hyperspectral Sensing of Heavy Metals in Soil by Integrating AI and UAV Technology. Environ. Monit. Assess. 2022, 194, 518. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Y.; Lu, Q.; Yuan, Z.; Li, H.; Huang, Q. Estimating the Spatial Distribution of Soil Total Arsenic in the Suspected Contaminated Area Using UAV-Borne Hyperspectral Imagery and Deep Learning. Ecol. Indic. 2021, 133, 108384. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, L.; Lu, Q.; Zhong, Y.; Yuan, Z.; Wang, Z.; Li, Z.; Yang, Y. Mapping Soil Available Copper Content in the Mine Tailings Pond with Combined Simulated Annealing Deep Neural Network and UAV Hyperspectral Images. Environ. Pollut. 2023, 320, 120962. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Alelyani, S.; Liu, H. Feature Selection for Classification: A Review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kemper, T.; Sommer, S. Estimate of Heavy Metal Contamination in Soils after a Mining Accident Using Reflectance Spectroscopy. Environ. Sci. Technol. 2002, 36, 2742. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic Determination of Leaf Biochemistry Using Band-Depth Analysis of Absorption Features and Stepwise Multiple Linear Regression. Remote. Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Wu, X.; Tian, Q.; Ji, J.; Qin, Z. Possibilities of Reflectance Spectroscopy for the Assessment of Contaminant Elements in Suburban Soils. Appl. Geochem. 2005, 20, 1051–1059. [Google Scholar] [CrossRef]
- Mi, L. Based on the Spectral Variation of Vegetation Monitoring the Heavy Metal Pollution of Soil. Earth Sci. Front. 2009, 3, 17. [Google Scholar]
- Nagaraju, T.V.; Mantena, S.; Azab, M.; Alisha, S.S.; El Hachem, C.; Adamu, M.; Rama Murthy, P.S. Prediction of High Strength Ternary Blended Concrete Containing Different Silica Proportions Using Machine Learning Approaches. Results Eng. 2023, 17, 100973. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Fathizad, H.; Ali Hakimzadeh Ardakani, M.; Sodaiezadeh, H.; Kerry, R.; Heung, B.; Scholten, T. Spatio-Temporal Analysis of Heavy Metals in Arid Soils at the Catchment Scale Using Digital Soil Assessment and a Random Forest Model. Remote. Sens. 2021, 13, 1698. [Google Scholar] [CrossRef]
- Fang, Y.; Xu, L.; Wong, A.; Clausi, D.A. Multi-Temporal Landsat-8 Images for Retrieval and Broad Scale Mapping of Soil Copper Concentration Using Empirical Models. Remote. Sens. 2022, 14, 2311. [Google Scholar] [CrossRef]
- Copyright 2021 Cubert GmbH. Available online: https://www.cubert-hyperspectral.com/Products/Firefleye-185 (accessed on 15 September 2022).
- UAV Calibration Board: Radiation Calibration and Reflectance Calibration. Available online: https://www.gzchanghui.com/product_view_37_163.html (accessed on 18 May 2023).
- Gan, W.; Shen, H.; Zhang, L.; Gong, W. Normalization of Medium-Resolution NDVI by the Use of Coarser Reference Data: Method and Evaluation. Int. J. Remote. Sens. 2014, 35, 7400–7429. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Yang, G.; Yang, H.; Feng, H.; Xu, X.; Wang, J.; Li, X.; Luo, J. Winter Wheat Yield Estimation Based on Multi-Source Medium Resolution Optical and Radar Imaging Data and the AquaCrop Model Using the Particle Swarm Optimization Algorithm. ISPRS J. Photogramm. Remote. Sens. 2017, 126, 24–37. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Ji, J.; Gong, P.; Liao, Q.; Tian, Q.; Ma, H. A Mechanism Study of Reflectance Spectroscopy for Investigating Heavy Metals in Soils. Soil. Sci. Soc. Am. J. 2007, 71, 918–926. [Google Scholar] [CrossRef]
- Public Laboratory Platform. Available online: http://www.wbg.cas.cn/Gglabplat/Index.Html. (accessed on 15 September 2022).
- Lei, W.; You-lu, B.A.; Yan-li, L.U.; He, W.A. Effect on Retrieval Precision for Corn N Content by Spectrum Data. Remote. Sens. Technol. Appl. 2011, 26, 220–225. [Google Scholar]
- Xu, X.; Chen, S.; Ren, L.; Han, C.; Lv, D.; Zhang, Y.; Ai, F. Estimation of Heavy Metals in Agricultural Soils Using Vis-Nir Spectroscopy with Fractional-Order Derivative and Generalized Regression Neural Network. Remote. Sens. 2021, 13, 2718. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.T.; Johnson, V.C. New Methods for Improving the Remote Sensing Estimation of Soil Organic Matter Content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in Northwest China. Remote. Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Xiao, C.; Ye, J.; Esteves, R.M.; Rong, C. Using Spearman’s Correlation Coefficients for Exploratory Data Analysis on Big Dataset. In Concurrency and Computation: Practice and Experience; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2016; Volume 28, pp. 3866–3878. [Google Scholar]
- Sedgwick, P. Spearman’s Rank Correlation Coefficient. BMJ 2014, 349, g7327. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Rudnicki, W.R.; Wrzesień, M.; Paja, W. All Relevant Feature Selection Methods and Applications. Stud. Comput. Intell. 2015, 584, 11–28. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Song, Y.; Niu, R.; Xu, S.; Ye, R.; Peng, L.; Guo, T.; Li, S.; Chen, T. Landslide Susceptibility Mapping Based on Weighted Gradient Boosting Decision Tree in Wanzhou Section of the Three Gorges Reservoir Area (China). ISPRS Int. J. Geoinf. 2019, 8, 4. [Google Scholar] [CrossRef]
- Ho, K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995. [Google Scholar]
- Varma, S.; Simon, R. Bias in Error Estimation When Using Cross-Validation for Model Selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Zhang, J.; Hua, P.; Krebs, P. Influences of Land Use and Antecedent Dry-Weather Period on Pollution Level and Ecological Risk of Heavy Metals in Road-Deposited Sediment. Environ. Pollut. 2017, 228, 158. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. On the Importance of the Pearson Correlation Coefficient in Noise Reduction. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 757–765. [Google Scholar] [CrossRef]
- Borjac, J.; El Joumaa, M.; Kawach, R.; Youssef, L.; Blake, D.A. Heavy Metals and Organic Compounds Contamination in Leachates Collected from Deir Kanoun Ras El Ain Dump and Its Adjacent Canal in South Lebanon. Heliyon 2019, 5, e02212. [Google Scholar] [CrossRef]
- ArcMap. Available online: https://www.esri.com/zh-cn/arcgis/products/arcgis-desktop/resources (accessed on 15 September 2022).
- China Environmental Monitoring Station. Chinese Soil Element Background Value; China Environmental Science Press: Beijing, China, 1990. [Google Scholar]
- Hair, J.; Black, W.; Babin, B.; Anderson, R. Multivarite Data Analysis, 7th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2010. [Google Scholar]
- Neter, J.; Kutner, H.; Nachtsheim, C. Applied Linear Statistical Models; McGraw-Hill/Irwin: New York, NY, USA, 1996; Volume 4. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Shi, T.; Chen, Y.; Liu, Y.; Wu, G. Visible and Near-Infrared Reflectance Spectroscopy—An Alternative for Monitoring Soil Contamination by Heavy Metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Li, Y.; Li, L.; Tang, M.; Hu, W.; Chen, L.; Ai, S. Speciation of Heavy Metals in Soils and Their Immobilization at Micro-Scale Interfaces among Diverse Soil Components. Sci. Total Environ. 2022, 825, 153862. [Google Scholar] [CrossRef]
- China Meteorological Science Data Sharing Service Network. Available online: https://www.cdc.cma.gov.cn (accessed on 15 September 2022).





| Spectral Transformation | Formula |
|---|---|
| Reciprocal transformation | |
| Logarithmic transformation | |
| Square Root transformation | |
| Exponential transformation |
| Heavy Metal | n 1 | Min (mg/kg) | Max (mg/kg) | Mean (mg/kg) | Standard Deviation | C.V. 2 (%) | SBV 3 | Pearson Correlation Coefficients | |
|---|---|---|---|---|---|---|---|---|---|
| Cr | Total | 70 | 68.034 | 133.843 | 104.987 | 11.091 | 10.564% | 86.000 | 0.770 * |
| <SBV | 4 | 68.034 | 85.686 | 74.315 | 6.740 | 9.070% | |||
| >SBV | 66 | 88.975 | 133.843 | 105.539 | 11.314 | 10.720% | |||
| Cu | Total | 70 | 24.952 | 41.109 | 33.920 | 3.349 | 9.879% | 30.700 | |
| <SBV | 12 | 24.952 | 29.879 | 28.144 | 1.464 | 5.202% | |||
| >SBV | 58 | 30.918 | 41.109 | 34.729 | 2.688 | 7.740% |
| Soil Heavy Metals | The Optimal Spectral Variables | Spearman Correlation Coefficient |
|---|---|---|
| Cr | Sqrt, FOD-1.2, 518 nm | 0.433 |
| Exponential, 946 nm | 0.405 | |
| Reciprocal, FOD-1.0, 658 nm | −0.478 | |
| Reciprocal, FOD-1.2, 742 nm | −0.427 | |
| Reciprocal, FOD-1.4, 658 nm | −0.331 | |
| Reciprocal, FOD-1.6, 710 nm | −0.514 | |
| Cu | Sqrt, FOD-1.8, 706 nm | −0.399 |
| Sqrt, FOD-2.0, 946 nm | −0.365 | |
| Reciprocal, FOD-1.8, 510 nm | 0.362 | |
| Reciprocal, FOD-1.8, 666 nm | 0.447 | |
| Reciprocal, FOD-1.8, 702 nm | −0.421 |
| Parameter | Method | R2 | MAE | RMSE | MARE | |
|---|---|---|---|---|---|---|
| Cr | RF | Train | 0.621 | 5.535 | 6.766 | 0.053 |
| Test | 0.325 | 7.322 | 9.043 | 0.070 | ||
| Decision Tree | Train | 0.338 | 7.242 | 8.930 | 0.069 | |
| Test | 0.252 | 7.925 | 9.516 | 0.076 | ||
| MLR | Train | 0.397 | 7.011 | 8.546 | 0.067 | |
| Test | 0.264 | 7.738 | 9.442 | 0.074 | ||
| GBDT | Train | 0.668 | 5.224 | 6.315 | 0.050 | |
| Test | 0.351 | 7.371 | 8.868 | 0.070 | ||
| Parameter | Method | R2 | MAE | RMSE | MARE | |
|---|---|---|---|---|---|---|
| Cu | RF | Train | 0.608 | 1.655 | 2.078 | 0.050 |
| Test | 0.324 | 2.185 | 2.733 | 0.065 | ||
| Decision Tree | Train | 0.311 | 2.237 | 2.752 | 0.067 | |
| Test | 0.116 | 2.479 | 3.124 | 0.074 | ||
| MLR | Train | 0.380 | 2.139 | 2.615 | 0.064 | |
| Test | 0.246 | 2.377 | 2.886 | 0.071 | ||
| GBDT | Train | 0.643 | 1.610 | 1.978 | 0.048 | |
| Test | 0.325 | 2.226 | 2.730 | 0.067 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, W.; Zhang, Y.; Xu, J.; Yang, R.; Xiao, A.; Hu, X. Spatial Distribution of Soil Heavy Metal Concentrations in Road-Neighboring Areas Using UAV-Based Hyperspectral Remote Sensing and GIS Technology. Sustainability 2023, 15, 10043. https://doi.org/10.3390/su151310043
Gan W, Zhang Y, Xu J, Yang R, Xiao A, Hu X. Spatial Distribution of Soil Heavy Metal Concentrations in Road-Neighboring Areas Using UAV-Based Hyperspectral Remote Sensing and GIS Technology. Sustainability. 2023; 15(13):10043. https://doi.org/10.3390/su151310043
Chicago/Turabian StyleGan, Wenxia, Yuxuan Zhang, Jinying Xu, Ruqin Yang, Anna Xiao, and Xiaodi Hu. 2023. "Spatial Distribution of Soil Heavy Metal Concentrations in Road-Neighboring Areas Using UAV-Based Hyperspectral Remote Sensing and GIS Technology" Sustainability 15, no. 13: 10043. https://doi.org/10.3390/su151310043
APA StyleGan, W., Zhang, Y., Xu, J., Yang, R., Xiao, A., & Hu, X. (2023). Spatial Distribution of Soil Heavy Metal Concentrations in Road-Neighboring Areas Using UAV-Based Hyperspectral Remote Sensing and GIS Technology. Sustainability, 15(13), 10043. https://doi.org/10.3390/su151310043





