Exergo–Economic and Parametric Analysis of Waste Heat Recovery from Taji Gas Turbines Power Plant Using Rankine Cycle and Organic Rankine Cycle

Abstract

This study focused on exergo–conomic and parametric analysis for Taji station in Baghdad. This station was chosen to reduce the emission of waste gases that pollute the environment, as it is located in a residential area, and to increase the production of electric power, since for a long time, Iraq has been a country that has suffered from a shortage of electricity. The main objective of this work is to integrate the Taji gas turbine’s power plant, which is in Baghdad, with the Rankine cycle and organic Rankine cycle to verify waste heat recovery to produce extra electricity and reduce emissions into the environment. Thermodynamic and exergoeconomic assessment of the combined Brayton cycle–Rankine cycle/Organic Rankin cycle (GSO CC) system, considering the three objective functions of the First- and Second-Law efficiencies and the total cost rates of the system, were applied. According to the findings, 258.2 MW of power is produced from the GSO CC system, whereas 167.3 MW of power is created for the Brayton cycle (BC) under the optimum operating conditions. It was demonstrated that the overall energy and exergy efficiencies, respectively, are 44.37% and 42.84% for the GSO CC system, while they are 28.74% and 27.75%, respectively, for the Brayton cycle. The findings indicate that the combustion chamber has the highest exergy degradation rate. The exergo–economic factor for the entire cycle is 37%, demonstrating that the cost of exergy destruction exceeds the cost of capital investment. Moreover, the cost of the energy produced by the GSO CC system is USD 9.03/MWh, whereas it is USD 8.24/MWh for BC. The results also indicate that the network of the GSO CC system decreases as the pressure ratio increases. Nonetheless, the GSO CC system’s efficiencies and costs increase with a rise in the pressure ratio until they reach a maximum and then decrease with further pressure ratio increases. The increase in the gas turbine inlet temperature and isentropic efficiency of the air compressor and gas turbine enhances the thermodynamic performance of the system; however, a further increase in these parameters increases the overall cost rates.

1. Introduction

Today, power is produced either through the combustion of fossil fuels in power cycles or via renewable energy sources, such as solar [1,2], wind, and water [3]. Increasing the efficiency of power generation systems is usually desirable for achieving energy sustainability and addressing the constraints of many conventional energy sources [4]. The use of fossil fuels to generate electricity was crucial to the success of the industrial revolution, and it has continued to play this role ever since, enabling important advances in society, science, and culture [5]. However, the widespread application of fossil fuels has contributed to the rising air pollution levels and CO₂ emissions, leading to the greenhouse effect, and has exacerbated climate change generally [6]. Further, fossil fuel reserves are delimited and are eventually predicted to run out. As a result, it is crucial to lessen reliance on fossil fuels while boosting the effectiveness of energy infrastructure [7,8]. Combined cycles can assist in achieving such objectives by increasing net electrical power output, decreasing fuel consumption, and enhancing efficiency [9].

Exergy is a key term connected to the second law of thermodynamics and is defined as the greatest amount of useful work that can be extracted from a flow of matter or energy in a reference environment [10,11]. The engineering field known as exergoeconomics or thermo economics combines exergy analysis and economics [12]. This method assists the designer in discovering information that cannot be found with economic evaluation and regular energy analysis [13]. Modern Combined Cycle Gas Turbines (CCGTs) are a dependable method for producing energy with a thermal efficiency of at least 60% [14]. There have been several articles published over the years that provide energy, exergy, and economic analyses of the integration of ORC with the CCGT with the combined cycle power plant. According to Roy et al. [15], the integration of ORC with power plants resulted in lower emissions, improved thermal efficiency, and a lower power load. Parametric optimization of an SRC and ORC integrated with the GT for the variable turbine input pressure and temperature was carried out by Kose et al. [16]. According to the findings, R141b outperformed the other working fluids tested. Qui et al. [17] concluded that ORC improved energy efficiency, producing 14 kW of thermal output and 0.65 kW of electrical power output for combined heat and power application. Hemadri et al. [18] evaluated the influence of reheat on combined cycle performance in the context of repowering and found that integrating reheat in the ORC boosted specific thermal work output. Balanesscu et al. [19] conducted an analysis on the effect of ORC integration into the gas steam combined cycle and found that the thermal efficiency of the combined cycle improved by 1.1% due to decreased SFC (specific fuel consumption, kg/kWh). Exergo–environmental analysis of an integrated organic Rankine cycle for tri-generation purposes by Ahmadi et al. [20] showed that the input temperature, the compressor pressure ratio, and the isentropic efficiency of the gas turbine are the most influential factors in the system’s overall performance. Koç et al. [21] presented a GT-ORC hybrid power unit with and without HR for the Rankine portion. Several organic fluids were studied, and an exergy assessment was performed. The exergy efficiency of the organic Rankine cycle (ORC) with heat recovery is improved by approximately 13.5 percent, and the total power output is increased by almost 41.1 percent compared to the GT. Heat recovery for energy production was suggested by Salehi et al. [22] by combining the ORC with the Kalina cycle. Combined, the two organic fluids boost output from 250 kW (pure fluid) to 280 kW (mixed) under ideal circumstances. Cao et al. [23] performed a thermodynamic study of a gas turbine and ORC combined cycle with recuperators. They discovered that when the ORC turbine intake pressure increased, the power ratio of the GT-ORC combined cycle and thermal efficiency improved. Fernández-Guillamón et al. [24] describe the ORC under analysis considering a steady-state and two cycles, excluding and including irreversibility, and all of the data analyzed [25]. The summary in Table 1 illustrates the methods and relationships studied by many researchers.

Table 1. Summary illustrates the methods and relationships studied by many researchers.

Authors	Method and Technique	Remarked
Sahoo [13]	Exergy analysis and economics	New method for regular energy analysis
Woudstra et al. [14]	Used modern Combined Cycle Gas Turbines (CCGTs)	Thermal efficiency of at least 60%
Roy et al. [15]	The integration of ORC	lower emissions, improved thermal efficiency, and a lower power load
Kose et al. [16] & Qui et al. [17]	Used an SRC and ORC integrated with the GT for the variable turbine input pressure and temperature	Improved thermal efficiency
Hemadri et al. [18] & Balanesscu et al. [19]	studied the influence of reheat on combined cycle performance and integrated with steam	thermal efficiency of the combined cycle improved by 1.1%
Salehi et al. [22] & Cao et al. [23]	Thermodynamic study of a gas turbine and ORC	pressure increased, improved thermal efficiency

Organic Rankine cycles (ORCs) were chosen because they are most suitable for converting low-quality thermal energy into electricity. In order to avoid the release of exhaust gases into the atmosphere, the main objective of this work is to integrate the Ghazi plant in Baghdad with the Rankine cycle and the organic Rankine cycle to increase the production of electricity quantities and reduce environmental emissions. In this novel power plant, the waste heat of the GT units is first utilized in the HRSG and later in the ORC as the heat source. The EES program is used to model the novel triple cycle. On the basis of the first and second laws, a comprehensive and exhaustive thermodynamic analysis and optimization of the GSO CC cycle was conducted with a focus on the irreversibility distribution within the plant. In addition, a parametric study was conducted to determine the effects of key parameters, such as compressor pressure ratio, compressor isentropic efficiency, turbine isentropic efficiency, gas turbine inlet temperature, boiler pressure, and condenser temperature, on cycle performance and cost.

2. Description of the GSOCC Cycle

A model is prepared and discussed for the steady-state analysis of the natural gas combined cycle, which is integrated with the organic Rankine cycle (GSO CC). It includes three main parts. The first part is the Brayton cycle, which consists of a gas turbine (GT), a combustion chamber (CC), and an air compressor (AC). The second part, which represents the Rankine cycle, consists of two pumps (P1 and P2), a deaerator, a condenser (CON1), a steam turbine (ST), and heat recovery steam generation (HRSG). The third and final part of the Organic Rankine cycle consists of a heat exchanger (HE), an organic Rankine turbine (ORT), a condenser (CON2), a pump (P3), and a heat recovery boiler (HRB) (see Figure 1). The principle of operation of the embedded system can be summarized as follows.

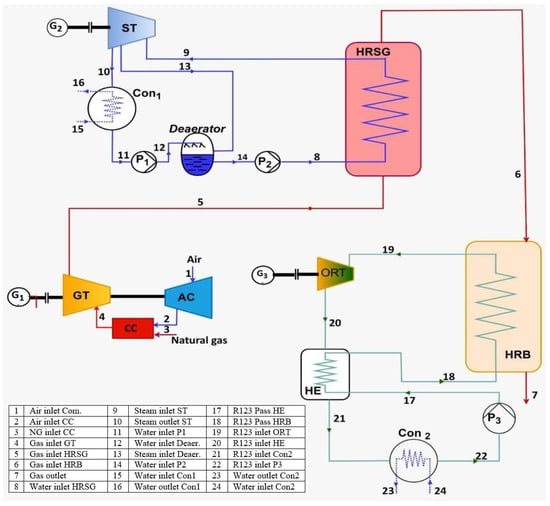
Figure 1. Schematic diagram of the GSOCC system.

Air is compressed to operating pressure and heated as it enters an air compressor (AC). The air is then transported to the CC, reacting with the natural gas fuel to create high-pressure, high-temperature exhaust gases. Through the GT, the exhaust gases expand to produce mechanical power. The HRSG converts compressed water into steam at high temperatures using the temperature of the exhaust gases. To generate more mechanical power, the steam expands as it passes through the ST. The water is pressurized through the pump after entering the condenser, which turns all the vapor into saturated liquid.

The working principle of the organic Rankine cycle is similar to that of the Rankine cycle: the working fluid is pumped into a heat recovery boiler where it evaporates, passes through an expansion device (the turbine), then through a condenser heat exchanger where it is finally re-condensed.

The selection of the working fluid is essential. R123 was chosen as the working fluid in this current work because it is the most suitable fluid dynamically and economically. It is environmentally friendly with an acceptable value of ODP and low global warming value compared to other working fluids. Additionally, R123 falls into the category of dry working fluids with a higher critical temperature value (in relatively lower certainty ranges), which makes it a suitable working fluid in ORC applications. Moreover, R123 is the most suitable working fluid in ORCs for engine or gas turbine WHRT applications and is highly recommended by many researchers, given all of the above R123 environmental and technical advantages [26,27].

3. Mathematical Analysis

The EES program was used to solve the mass, energy, and exergy balance equations for all of the GSOCC system’s components. The basic input parameters of the GSOCC system are provided in Table 2, the parameters were adopted on the basis of the design values of the station, and the average weather rates in Baghdad were also adopted from the ambient temperature and relative humidity. These parameters selected depend on periodic statistics of the performance of the station’s units, where 4 units were stable in terms of their performance; therefore, they were chosen to conduct the analysis. Table 3 illustrates the thermodynamic modeling as well as the energetic and energetic relationships of the GSOCC system’s components. The general assumptions made for the simulation of the combined system are listed as follows:

Table 2. Operation condition used for the GSOCC model.

	Parameter	Value
GT cycle	Number of units	4
	Compression ratio	12.1
	Air mass flow rate (kg/s)	142.6 × 4
	GTIT (°C)	1177
	Ambient temperature (°C)	27
	LHV of fuel (Natural Gas (NG)) (kJ/kg)	50,056
	${\eta }_{AC}$ (%)	84
	${\eta }_{GT}$ (%)	88
	${\eta }_{CC}$ (%)	99.5
RC cycle	ST inlet pressure (bar)	100
	Condenser Temperature (°C)	50
	${\eta }_{ST}$ (%)	90
	${\eta }_P$ (%)	80
	Effectiveness of HRSG (%)	70
ORC cycle	ORT inlet pressure (kPa)	800
	Condenser pressure (bar)	1.2
	Effectiveness of evaporator (%)	70
	Working fluid	R123

Table 3. Energetic and exergetic relations for the subsystems of GSOCC [28].

Subsystem	Energy Balances	Exergy Balances
Air compressor	${\dot{W}}_{AC}={\dot{m}}_{\mathrm{air} }\left(h_2-h_1\right)$	${\dot{E}}_{D,AC}=\left({\dot{E}}_1-{\dot{E}}_2\right)+{\dot{W}}_{AC}$
Combustion chamber	${\dot{m}}_2{h}_2+{\eta }_{CC}{\dot{m}}_3\mathrm{LHV}={\dot{m}}_4{h}_4$	${\dot{E}}_{\mathrm{D}, \mathrm{CC}}={\dot{E}}_2+{\dot{E}}_3-{\dot{E}}_4$
Gas turbine	${\dot{W}}_{GT}={\dot{m}}_{gas}\left(h_4-h_5\right)$	${\dot{E}}_{D,GT}=\left({\dot{E}}_4-{\dot{E}}_5\right)-{\dot{W}}_{GT}$
HRSG	${\dot{m}}_5\left(h_5-h_6\right)={\dot{m}}_8\left(h_9-h_8\right)$	${\dot{E}}_{\mathrm{D}, \mathrm{HRSG}}={\dot{E}}_5-{\dot{E}}_6+{\dot{E}}_8-{\dot{E}}_9$
Steam Turbine	${\dot{W}}_{\mathrm{ST}}={\dot{m}}_9\left(h_9-h_{13}\right)+{\dot{m}}_{10}\left(h_{13}-h_{10}\right)$	${\dot{E}}_{\mathrm{D}, \mathrm{ST}}=\left({\dot{E}}_9-{\dot{E}}_{13}-{\dot{E}}_{10}\right)-{\dot{W}}_{\mathrm{ST}}$
Condenser	${\dot{Q}}_{COND1}={\dot{m}}_{10}\left(h_{11}-h_{10}\right)$	${\dot{E}}_{\mathrm{D}, COND1}=\left({\dot{E}}_{10}-{\dot{E}}_{11}\right)+\left({\dot{E}}_{15}-{\dot{E}}_{16}\right)$
Pump1	${\dot{W}}_{\mathrm{Pump}1 }={\dot{m}}_{11}\left(h_{12}-h_{11}\right)$	${\dot{E}}_{\mathrm{D}, \mathrm{Pump}1 }={\dot{W}}_{\mathrm{Pump}1 }-\left({\dot{E}}_{11}-{\dot{E}}_{12}\right)$
Pump2	${\dot{W}}_{\mathrm{Pump}2 }={\dot{m}}_8\left(h_{14}-h_8\right)$	${\dot{E}}_{\mathrm{D}, \mathrm{Pump}2 }={\dot{W}}_{\mathrm{Pump}2 }-\left({\dot{E}}_{14}-{\dot{E}}_8\right)$
Deaerator	${\dot{m}}_{13}{h}_{13}+{\dot{m}}_{12}{h}_{12}={\dot{m}}_{14}{h}_{14}$	${\dot{E}}_{\mathrm{D}, \mathrm{Deaerator} }={\dot{E}}_{13}+{\dot{E}}_{12}-{\dot{E}}_{14}$
HRB	${\dot{Q}}_{HRB}={\dot{m}}_{18}\left(h_{19}-h_{18}\right)$	${\dot{E}}_{\mathrm{D},HRB}={\dot{E}}_6-{\dot{E}}_7+{\dot{E}}_{18}-{\dot{E}}_{19}$
ORT	${\dot{W}}_{\mathrm{ORT}}={\dot{m}}_{19}\left(h_{20}-h_{19}\right)$	${\dot{E}}_{\mathrm{D}, \mathrm{ORT}}=\left({\dot{E}}_{19}-{\dot{E}}_{20}\right)-{\dot{W}}_{\mathrm{ORT}}$
ORC Condenser	${\dot{Q}}_{COND2}={\dot{m}}_{21}\left(h_{22}-h_{21}\right)$	${\dot{E}}_{\mathrm{D}, COND2}=\left({\dot{E}}_{21}-{\dot{E}}_{22}\right)+\left({\dot{E}}_{23}-{\dot{E}}_{24}\right)$
ORC Pump	${\dot{W}}_{\mathrm{Pump}3 }={\dot{m}}_{22}\left(h_{17}-h_{22}\right)$	${\dot{E}}_{\mathrm{D}, \mathrm{Pump}3 }={\dot{W}}_{\mathrm{Pump}3 }-\left({\dot{E}}_{22}-{\dot{E}}_{17}\right)$
Heat exchanger	${\dot{Q}}_{HE}={\dot{m}}_{17}\left(h_{18}-h_{17}\right)$	${\dot{E}}_{\mathrm{D},\mathrm{HE}}={\dot{E}}_{17}-{\dot{E}}_{18}+{\dot{E}}_{20}-{\dot{E}}_{21}$

• All components of the combined system operate under steady-state conditions.
• Compositions of air at the inlet of the AC are 79% N₂ and 21% O₂.
• Natural gas is completely oxidized in the CC.
• Ideal gas principles apply to the exhaust gases.
• The CC is insulated completely.
• The relations utilized to assess the thermodynamic performance of the triple combined cycle are shown in Table 4.
  Table 4. Exergetic performance criteria of GSOCC system.

  first-law efficiency	${\mathsf{\eta }}_{\mathrm{overall}}=\left({\dot{W}}_{BC}+{\dot{W}}_{RC}+{\dot{W}}_{ORC}\right)/{\dot{Q}}_{CC}$
  Second-law efficiency	${\Psi }_{overall}=\left({\dot{W}}_{BC}+{\dot{W}}_{RC}+{\dot{W}}_{ORC}\right)/\left({\dot{E}}_1+{\dot{W}}_3\right)$
  Components exergy efficiency	${\epsilon }_k={\dot{E}}_P/{\dot{E}}_F$
  Exergy destructio ratio	$E_{d,k\%}={\dot{E}}_{d,k}/{\dot{E}}_{d, total}$

The cost balance and auxiliary equations for each part must be written as follows [28]:

$$\begin{array}{c}{\displaystyle \sum }_e{\dot{C}}_{e,k}+{\dot{C}}_{w,k}={\dot{C}}_{q,k}+{\displaystyle \sum }_i{\dot{C}}_{i,k}+{\dot{Z}}_k\\ \end{array}$$

(1)

$${\dot{C}}_j=c_j{\dot{E}}_j$$

(2)

where C is the cost rate (USD/h), and ${\dot{Z}}_k$ represents the entire cost rate related to the capital investment and operation and maintenance costs component k. Table 5 presents the relevant parameters for the exergoeconomic assessment of the system, and Table 6 contains the cost balances and auxiliary equations for every system component. The total capital investment in the plant is given by [29,30]:

$${\dot{Z}}_k=\frac{Z_k\times CRF\times \varphi }{N\times 3600}$$

(3)

where PEC is the equipment purchase cost in US dollars, 𝜑 is the maintenance factor (1.06), and CRF is the Capital Recovery Factor, which can be calculated as follows:

$$CRF=\frac{i{(1+i)}^n}{{(1+i)}^n-1}$$

(4)

Table 5. Exergoeconomic evaluation parameters of GSO CC [31,32].

Average costs per exergy unit of fuel	${\mathrm{c}}_{\mathrm{F},\mathrm{k}}={ \mathrm{Ċ} }_{\mathrm{F},\mathrm{k}}/{ \mathrm{Ė} }_{\mathrm{F},\mathrm{k}}$
Average costs per exergy unit of product	${\mathrm{c}}_{\mathrm{P},\mathrm{k}}={ \mathrm{Ċ} }_{\mathrm{P},\mathrm{k}}/{ \mathrm{Ė} }_{\mathrm{P},\mathrm{k}}$
Cost rate of exergy destruction	${ \mathrm{Ċ} }_{\mathrm{D},\mathrm{k}}={\mathrm{c}}_{\mathrm{F},\mathrm{k}}{ \mathrm{Ė} }_{\mathrm{D},\mathrm{k}}$
Relative Cost Difference	${\mathrm{r}}_{\mathrm{k}}=\left({\mathrm{c}}_{\mathrm{P},\mathrm{k}}-{\mathrm{c}}_{\mathrm{F},\mathrm{k}}\right)/{\mathrm{c}}_{\mathrm{F},\mathrm{k}}$
Exergoeconomic factor	${\mathrm{f}}_{\mathrm{k}}={ \mathrm{Ż} }_{\mathrm{k}}/\left({ \mathrm{Ż} }_{\mathrm{k}}+{\mathrm{c}}_{\mathrm{F},\mathrm{k}}{ \mathrm{Ė} }_{\mathrm{D},\mathrm{k}}+{ \mathrm{Ė} }_{\mathrm{L},\mathrm{k}}\right))$
The overall cost	${\dot{C}}_{\mathrm{system}}={\displaystyle \sum }_{k=1}^N{Z}_{\mathrm{k}}$+${\displaystyle \sum }_{k=1}^N{\dot{C}}_{\mathrm{D},\mathrm{k}}$
Total electricity cost	${ \mathrm{Ċ} }_{\mathrm{electricity}, \mathrm{Total}}={\dot{C}}_{\mathrm{system}}/{\dot{W}}_{\mathrm{net} }$

Table 6. Cost balance and auxiliary equations for the components of GSO CC system.

Subsystem	Exergy Cost Rate Balance Equation	Exergy Balances
Air compressor	${ \mathrm{Ċ} }_1+{ \mathrm{Ċ} }_{\mathrm{AC}}+{ \mathrm{Ż} }_{\mathrm{AC}}={ \mathrm{Ċ} }_2$	$\frac{{ \mathrm{Ċ} }_1}{{ \mathrm{W} }_{\mathrm{C},\mathrm{LP}}}=\frac{{ \mathrm{Ċ} }_2}{{ \mathrm{W} }_{\mathrm{T}}}$        ${\mathrm{c}}_1$= 0
Combustion chamber	${ \mathrm{Ċ} }_2+{ \mathrm{Ċ} }_3+{ \mathrm{Ż} }_{\mathrm{CC}}={ \mathrm{Ċ} }_4$	$\frac{{ \mathrm{Ċ} }_2}{{\mathrm{Ex}}_2}=\frac{{ \mathrm{Ċ} }_4}{{\mathrm{Ex}}_4}$       ${\mathrm{c}}_2$=${ \mathrm{c}}_4$        ${\mathrm{c}}_3$=12
Gas turbine	${ \mathrm{Ċ} }_4+{ \mathrm{Ż} }_{GT}={ \mathrm{Ċ} }_5$ $+{ \mathrm{Ċ} }_{GT}$	$\frac{{ \mathrm{Ċ} }_4}{{\mathrm{Ex}}_4}=\frac{{ \mathrm{Ċ} }_5}{{\mathrm{Ex}}_5}$       ${\mathrm{c}}_4$=${\mathrm{c}}_5$
HRSG	${ \mathrm{Ċ} }_5+{\dot{{ \mathrm{Ċ} }_8+\mathrm{Ż}}}_{\mathrm{HRSG}}={ \mathrm{Ċ} }_6+{ \mathrm{Ċ} }_9$	$\frac{{ \mathrm{Ċ} }_5}{{\mathrm{Ex}}_5}=\frac{{ \mathrm{Ċ} }_6}{{\mathrm{Ex}}_6}$         ${\mathrm{c}}_5={ \mathrm{c}}_6$
Steam Turbine	${ \mathrm{Ċ} }_9+{ \mathrm{Ż} }_{\mathrm{ST}}={ \mathrm{Ċ} }_{10}+{ \mathrm{Ċ} }_{13}+$ ${ \mathrm{Ċ} }_{\mathrm{ST}}$	$\frac{{ \mathrm{Ċ} }_9}{{\mathrm{Ex}}_9}=\frac{{ \mathrm{Ċ} }_{10}}{{\mathrm{Ex}}_{10}}$     ${\mathrm{c}}_9={ \mathrm{c}}_{10}$      ${\mathrm{c}}_{10}={ \mathrm{c}}_{13}$
Condenser	${ \mathrm{Ċ} }_{10}+{\dot{{ \mathrm{Ċ} }_{15}+\mathrm{Ż}}}_{\mathrm{cond}1}={ \mathrm{Ċ} }_{11}+{ \mathrm{Ċ} }_{16}$	$\frac{{ \mathrm{Ċ} }_{10}}{{\mathrm{Ex}}_{10}}=\frac{{ \mathrm{Ċ} }_{11}}{{\mathrm{Ex}}_{11}}$       ${\mathrm{c}}_{10}={ \mathrm{c}}_{11}$        ${\mathrm{c}}_{15}=0$
Pump1	${ \mathrm{Ċ} }_{11}+{\dot{{ \mathrm{Ċ} }_{\mathrm{ST}}+\mathrm{Ż}}}_{\mathrm{Pump}1}={ \mathrm{Ċ} }_{12}$	$\frac{{ \mathrm{Ċ} }_{\mathrm{Pump}1}}{{ \mathrm{W} }_{\mathrm{Pump}1}}=\frac{{ \mathrm{Ċ} }_{\mathrm{ST}}}{{ \mathrm{W} }_{\mathrm{ST}}}$
Deaerator	${ \mathrm{Ċ} }_{12}+{\dot{{ \mathrm{Ċ} }_{13}+\mathrm{Ż}}}_{\mathrm{Derea}}={ \mathrm{Ċ} }_{14}$	$\frac{{ \mathrm{Ċ} }_{12}}{{\mathrm{Ex}}_{12}}=\frac{{ \mathrm{Ċ} }_{14}}{{\mathrm{Ex}}_{14}}$
Pump2	${ \mathrm{Ċ} }_{14}+{\dot{{ \mathrm{Ċ} }_{\mathrm{ST}}+\mathrm{Ż}}}_{\mathrm{Pump}2}={ \mathrm{Ċ} }_8$	$\frac{{ \mathrm{Ċ} }_{\mathrm{Pump}2}}{{ \mathrm{W} }_{\mathrm{Pump}2}}=\frac{{ \mathrm{Ċ} }_{\mathrm{ST}}}{{ \mathrm{W} }_{\mathrm{ST}}}$
HRB	${ \mathrm{Ċ} }_6+{\dot{{ \mathrm{Ċ} }_{18}+\mathrm{Ż}}}_{\mathrm{HRB}}={ \mathrm{Ċ} }_7+{ \mathrm{Ċ} }_{19}$	$\frac{{ \mathrm{Ċ} }_6}{{\mathrm{Ex}}_6}=\frac{{ \mathrm{Ċ} }_7}{{\mathrm{Ex}}_7}$        ${\mathrm{c}}_{10}={ \mathrm{c}}_{11}$
ORT	${ \mathrm{Ċ} }_{19}{\dot{+\mathrm{Ż}}}_{\mathrm{ORT}}={ \mathrm{Ċ} }_{20}+{ \mathrm{Ċ} }_{\mathrm{ORT}}$	$\frac{{ \mathrm{Ċ} }_{19}}{{\mathrm{Ex}}_{19}}=\frac{{ \mathrm{Ċ} }_{20}}{{\mathrm{Ex}}_{20}}$        ${\mathrm{c}}_{19}={ \mathrm{c}}_{20}$
ORC Condenser	${ \mathrm{Ċ} }_{21}+{\dot{{ \mathrm{Ċ} }_{24}+\mathrm{Ż}}}_{\mathrm{cond}2}={ \mathrm{Ċ} }_{22}+{ \mathrm{Ċ} }_{23}$	$\frac{{ \mathrm{Ċ} }_{21}}{{\mathrm{Ex}}_{21}}=\frac{{ \mathrm{Ċ} }_{22}}{{\mathrm{Ex}}_{22}}$          ${\mathrm{c}}_{21}={ \mathrm{c}}_{22}$
ORP	${ \mathrm{Ċ} }_{22}+{\dot{{ \mathrm{Ċ} }_{\mathrm{ORP}}+\mathrm{Ż}}}_{\mathrm{ORP}}={ \mathrm{Ċ} }_{17}$	$\frac{{ \mathrm{Ċ} }_{\mathrm{ORP}}}{{ \mathrm{W} }_{\mathrm{ORP}}}=\frac{{ \mathrm{Ċ} }_{\mathrm{ORT}}}{{ \mathrm{W} }_{\mathrm{ORT}}}$
Heat exchanger	${ \mathrm{Ċ} }_{20}+{\dot{{ \mathrm{Ċ} }_{17}+\mathrm{Ż}}}_{\mathrm{HE}}={ \mathrm{Ċ} }_{21}+{ \mathrm{Ċ} }_{18}$	$\frac{{ \mathrm{Ċ} }_{20}}{{\mathrm{Ex}}_{20}}=\frac{{ \mathrm{Ċ} }_{21}}{{\mathrm{Ex}}_{21}}$       ${\mathrm{c}}_{20}={ \mathrm{c}}_{21}$

The purchase equipment cost (PEC) for the GSO CC components is provided in Table 7.

Table 7. Purchased cost equations for the components of GSOCC system.

Subsystem	Cost Equation
Air compressor	$\left(71.1\times { \dot{\mathrm{m}}}_{\mathrm{air}}/0.9-{\mathsf{\eta }}_{\mathrm{comp}}\right)\left({\mathrm{p}}_2/{\mathrm{p}}_1\right)\mathrm{Ln}\left({\mathrm{p}}_2/{\mathrm{p}}_1\right)$ [32]
Combustion chamber	$\left(46.08\times { \dot{\mathrm{m}}}_{\mathrm{air}}/0.996-\left({\mathrm{p}}_4/{\mathrm{p}}_2\right)\right)\left(1+\exp \left(0.018\times {\mathrm{T}}_4-26.4\right)\right)$ [32]
Gas turbine	$\left(479.34\times { \dot{\mathrm{m}}}_4/0.92-{\mathsf{\eta }}_{\mathrm{GT}}\right)\mathrm{Ln}\left({\mathrm{p}}_4/{\mathrm{p}}_5\right) \left(1+\exp \left(0.036\times {\mathrm{T}}_4-54.4\right)\right)$ [32]
HRSG	$6570 \left[{\frac{{ \dot{\mathrm{Q}}}_{\mathrm{ec}}}{\Delta {\mathrm{T}}_{\mathrm{LMTD},\mathrm{ec}}}}^{0.8}+{\frac{{ \dot{\mathrm{Q}}}_{\mathrm{ev}}}{\Delta {\mathrm{T}}_{\mathrm{LMTD},\mathrm{ev}}}}^{0.8}+{\frac{{ \dot{\mathrm{Q}}}_{\sup }}{\Delta {\mathrm{T}}_{\mathrm{LMTD},\sup }}}^{0.8}\right]+21276{ \dot{\mathrm{m}}}_8+1184.4{ \dot{\mathrm{m}}}_4$ [32]
Steam Turbine	$6000{ \dot{\mathrm{W}}}_{\mathrm{ST}}^{0.7}$ [33]
Condenser	$1773{ \dot{\mathrm{m}}}_{\mathrm{steam}}$ [34]
Pump1	$2100{ \dot{\mathrm{W}}}_{\mathrm{pump}1}{}^{0.26}{\left(1-{\mathsf{\eta }}_{\mathrm{Pump}}/{\mathsf{\eta }}_{\mathrm{Pump}}\right)}^{0.5}$ [34]
Deaerator	$\mathrm{52,000}{ \dot{\mathrm{m}}}_9$ [34]
Pump2	$2100{ \dot{\mathrm{W}}}_{\mathrm{pump}2}{}^{0.26}{\left(1-{\mathsf{\eta }}_{\mathrm{Pump}}/{\mathsf{\eta }}_{\mathrm{Pump}}\right)}^{0.5}$ [34]
HRB	$235{ \dot{\mathrm{Q}}}_{\mathrm{HRB}}$ [35]
ORT	$\left(479.3{ \dot{\mathrm{m}}}_{19}/0.92-{\mathsf{\eta }}_{\mathrm{ORT}}\right)\mathrm{Ln}\left({\mathrm{p}}_{19}/{\mathrm{p}}_{20}\right) \left(1+\exp \left(0.036\times {\mathrm{T}}_4-54.4\right)\right)$ [30]
ORC Condenser	$1773{ \dot{\mathrm{m}}}_{\mathrm{organic}}$ [34]
ORP	$2100{ \dot{\mathrm{W}}}_{\mathrm{ORP}}{}^{0.26}{\left(1-{\mathsf{\eta }}_{\mathrm{ORP}}/{\mathsf{\eta }}_{\mathrm{ORP}}\right)}^{0.5}$ [34]
Heat exchanger	$235{ \dot{\mathrm{Q}}}_{\mathrm{HE}}$ [35]

4. Results and Discussion

This section describes the outcomes of thermodynamics, economic modeling, and the impact of different design factors on the performance of the GSO CC cycle. The suggested heat and power combined cycle system of this research consists of four 160 MW gas turbine cycles with exhaust gases directed into a single-pressure heat recovery steam generator (HRSG) to generate heat. The HRSG receives water, which exists as a superheated vapor. The superheated vapor is introduced into the ST to create additional electricity. Ultimately, a bottoming cycle of the ORC is added to boost system efficiency and maximize the benefit of heat losses [36,37], in which the gases ejected from the HRSG are sent to the ORC evaporator. The BC’s power production and thermal efficiency are verified after thermodynamic modeling of the GSO CC model, using the values presented in [21] as the standard [38]. Table 8 displays the results of the validation. Table 9 details the suggested model’s thermodynamic parameters, including each state’s mass, enthalpy, entropy, and exergy flow rates.

Table 8. Validation of the Brayton cycle model.

Parameter	Literature Model [21]	Present Model
Pressure ratio	15	15
Fuel type of gas turbine cycle	Natural gas	Natural gas
Air mass flow rate (kg/s)	21.4	21.4
Air mass flow rate (kg/s)	0.4	0.41
Exhaust Flow (kg/s)	21.8	21.9
Power output (kW)	6200	6203
Thermal efficiency	33.8	32.7

Table 9. Properties for each state for the GSO CC model at the optimum condition.

State	m (kg/s)	P (kPa)	T (K)	h (kJ/kg)	s (KJ/kg K)	E (MW)	c ($/GJ)	$\dot{\mathbf{C}}$ ($/h)
1	498.4	101.3	300	233.6	5.762	0	0	0
2	498.4	1226	679.2	627.8	5.886	203.7	22.53	16,522
3	11.2	101.3	288	−4672	11.53	518.2	12	26,035
4	509.6	1165	1450	235.2	8.164	508.8	18.9	42,578
5	509.6	107.7	919.8	−425.5	8.3	200.72	18.9	14,284
6	509.6	104.5	500	−904	7.617	41.52	18.9	2873
7	509.6	101.3	400	−1012	7.386	19.4	18.9	1364
8	67.56	10,133	445.7	735.5	2.055	11.77	43.72	1931
9	67.56	9829	869.8	3619	6.904	140.5	25.46	13,475
10	54.04	12.26	323	2339	7.298	36.89	25.46	3496
11	54.04	12.26	323	208.7	0.7019	2.889	25.46	273.3
12	54.04	100	323	208.8	0.702	2.893	25.48	273.9
13	13.51	100	372.8	2617	7.203	13.36	25.46	1269
14	67.56	100	372.8	690.4	2.035	9.136	46.83	1599
15	637.1	100	300	2028	7.082	0	0	0
16	637.1	100	310	2781	9.551	7.854	99.85	3225
17	177.2	800	306.4	235	1.119	0.1125	64.34	26.12
18	177.2	800	359.6	292.9	1.292	1.222	140	617.2
19	177.2	800	480	540	1.92	11.86	50.07	2141
20	177.2	121.6	428.4	499.3	1.931	4.088	50.07	738.4
21	177.2	121.6	306.1	402.8	1.669	0.8161	50.07	147.4
22	177.2	121.6	306.1	234.4	1.119	0.02848	50.07	5.144
23	39.62	100	300	2028	7.082	0	0	0
24	39.62	100	305	2404	8.326	0.1238	329.5	147.2

Table 10 presents the findings of an energy analysis performed on the components of the GSO CC model under the input parameters listed in Table 1. The Ẇ_net of the BC model is 167.3 MW, with a First-Law efficiency (${\mathsf{\eta }}_{BC}$) of 28.74% and a Second-Law efficiency (${\Psi }_{BC}$) of 27.74%. The RC/ORC model generates 258.2 MW of power by adding RC and ORC cycles. Therefore, the ${\mathsf{\eta }}_{overall}$ of the RC/ORC cycle increases to 44.37%, and ${\Psi }_{overall}$ increases to 42.84%.

Table 10. Performance of the GSO CC model.

	BC Model	ORC Model
Net output power	167.3	258.2
Overall exergy efficiency	27.75	42.84
Overall thermal efficiency	28.74	44.37

As shown in Table 11, the total exergy input and exergy destruction for the RC/ORC model are illustrated. The total exergy destruction for all components is approximately 315.3 MW, accounting for 52.31% of the total exergy input to the GT-RC/ORC. Therefore, the valuable work of the GSO CC is 258.2 MW, and its percentage is almost 42.84%. The remaining part of the exergy is released with the exhaust gases to the surrounding environment, and its percentage is nearly 4.85%.

Table 11. Exergy input, output, losses of the model, and active indicator.

Exergy	Values (MW)	Percentage (%)	Station	I
Input	602.7	100%	GT cycle	7.2
Output (network)	258.2	42.84%	RC cycle	9.6
Exergy destruction	315.3	52.31%	ORC cycle	3.4
Exergy losses	29.2	4.85%	Combined	7.1
Total	602.7	100%

Depending on the interaction analysis of the technical, economic, and social effects, new data can be collected. The thermodynamic quantities have been introduced in order to describe the socio-economic system as a biosystem, based on Grisolia et al. [39,40].

$$I=\frac{exergy lost}{quantity related to required effect}$$

(5)

when I is an active indicator.

The exergy analysis findings for the GSO CC system components under ideal conditions are shown in Table 12. This table demonstrates that the combustion chambers are where the greatest exergy is lost due to the highly irreversible nature of the combustion process (approx. 57.3%). The HRSG and condenser 1 have the second and third ranks, respectively, whereas pump 1 experiences the most negligible exergy loss (0.0004%). According to Table 12, the highest exergy efficiency is associated with the gas turbine (94.2%).

Table 12. Exergy analysis and the entropy change rate for each component of the (GSO CC) model.

Component	${\dot{\mathbf{E}}}_{\mathbf{i}\mathbf{n}\mathbf{p}\mathbf{u}\mathbf{t}}$ (MW)	${\dot{\mathbf{E}}}_{\mathbf{o}\mathbf{u}\mathbf{t}\mathbf{p}\mathbf{u}\mathbf{t}}$ (MW)	${\dot{\mathbf{E}}}_{\mathbf{d}\mathbf{e}\mathbf{s}\mathbf{t}\mathbf{r}\mathbf{u}\mathbf{c}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}}$ (MW)	${\dot{\mathbf{E}}}_{\mathbf{d}\mathbf{e}\mathbf{s}\mathbf{t}\mathbf{r}\mathbf{u}\mathbf{c}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}}$ (%)	${\dot{\mathbf{s}}}_{\mathbf{g}\mathbf{e}\mathbf{n}\mathbf{e}\mathbf{r}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}}$ (Kw/K)	Δs (KJ/Kg.K)	Exergy Effi. (%)
AC	224.8	203.7	21.17	6.9	71.04	11.654	90.6
CC	784.8	608.7	176.1	57.3	590.9	9.252	77.6
GT	408	384.3	23.73	7.7	79.3	0.136	94.2
HRSG	159.2	128.8	30.39	9.88	101.98	4.166	80.9
ST	90.3	82.69	7.6	2.5	2.5	7.597	91.85
Condenser 1	34	7.85	26.16	8.5	87.78	4.1271	23.1
Deaerator	16.25	9.14	7.12	2.31	23.89	5.87	56.22
Pump 1	0.006	0.005	0.001	0.0004	0	0	81.4
Pump 2	3.05	2.63	0.411	0.134	0	0	86.5
ORB	22.14	10.63	11.5	3.74	38.59	0.04	48
ORT	7.77	7.21	0.55	0.18	1.845	0.397	92.86
HE	3.27	1.11	2.16	0.7	7.25	0.089	34
Condenser 2	0.79	0.124	0.66	0.22	2.215	1.794	15.72
ORP	0.104	0.084	0.02	0.0066	0	0	80.6

Exergoeconomic analysis is a valuable method for assessing the performance of a thermal system. The findings of the exergoeconomic study for the GSO CC system are shown in Table 13. The results indicate that the combustion chamber and steam generator had the highest $\dot{Z}{ }_K+\dot{C}{ }_D$ values, correspondingly. It is clear that condensers have a more considerable relative cost difference than other components because they are less efficient. Evaluating the exergoeconomic factor demonstrates that 63% of this cost is attributable to the cost of exergy destruction, whereas only 37% is attributable to investment costs.

Table 13. Exergoeconomic results of components of the GSO CC system.

Component	${\mathbf{c}}_{\mathbf{f}}$ ($/GJ)	${\mathbf{c}}_{\mathbf{p}}$ ($/GJ)	$\dot{\mathbf{C}}{ }_{\mathbf{D}}$ ($/h)	$\dot{\mathbf{Z}}{ }_{\mathbf{K}}$ ($/h)	$\dot{\mathbf{Z}}{ }_{\mathbf{K}}+\dot{\mathbf{C}}{ }_{\mathbf{D}}$ ($/h)	$\mathbf{r}$ (%)	$\mathbf{f}$ (%)
AC	20.41	22.27	120	190.4	310.4	9.12	61.33
CC	14.66	18.9	735.8	20.1	755.9	28.94	2.65
GT	18.9	20.18	124.2	187.9	312.1	6.75	60.22
HRSG	18.9	23.8	172.9	133	305.9	25.98	43.46
ST	25.46	28.65	56.56	268	324.5	12.55	82.75
Condenser 1	25.46	99.85	185.3	1.5	186.8	292.2	0.82
Deaerator	25.46	46.83	51.94	56.46	108.4	83.91	52.07
Pump 1	28.65	35.99	0.0091	0.014	0.0236	25.95	61.18
Pump 2	28.65	33.12	3.439	0.074	3.513	15.58	2.1
ORB	18.9	39.73	60.53	14.5	75.02	110.2	19.31
ORT	50.07	55.28	7.728	35.65	43.38	10.42	82.19
HE	50.07	147.7	30.14	0.08	30.22	195	0.254
Condenser 2	50.07	329.5	9.251	4.9	14.15	558	34.62
ORP	55.28	69.18	0.311	0.181	0.492	25.13	36.82
Total system	-	-	1558.0	912.4	2470.4	-	37

The effects of the changing pressure ratio (Pr), compressor isentropic efficiency (${\eta }_{AC}$), gas turbine isentropic efficiency (${\eta }_{GT}$), gas turbine inlet temperature (GTIT), boiler pressure ($P_{boiler}$), and condenser temperature ($T_{condenser}$) on the performance and cost of the GSO CC system are analyzed here.

Figure 2a presents the impact of the pressure ratio (Pr) on the GSO CC system’s performance and cost. The findings demonstrate that Ẇ_BC increases with an increase in Pr until it reaches a maximum point and then decreases with further increases in Pr. At high values of Pr, the power consumed by the compressors increases and affects Ẇ_BC negatively. The maximum Ẇ_BC was obtained at 10 bar (169.3 MW). The curves also illustrate that Ẇ_net for the GSO CC system decreases with an increase in Pr. At the lower value of Pr, the exhaust temperature from the BC is very high and positively affects Ẇ_RC and Ẇ_ORC. The findings reveal that when Pr increases from 4 to 18 bar, Ẇ_net decreases from 288/6 MW to 229.3 MW for the GSO CC system.

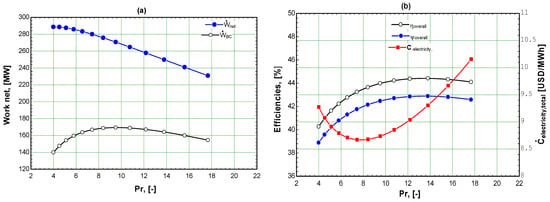
Figure 2. Variation of Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$, and ${\dot{C}}_{\mathrm{electricity}}$ with pressure ratio (Pr); (a) for performance and cost; (b) for efficiencies and cost.

Figure 2b reveals the effect of Pr on the efficiencies and cost of the GSO CC system. The GSO CC system’s efficiency and cost improve with a rise in Pr until it peaks and then decline with additional increases in Pr. At high values of Pr, Ẇ_net decreases and negatively affects the efficiencies of the GSO CC system. The maximum ${\eta }_{overall}$ and ${\Psi }_{overall}$ were obtained at 13 bar (44.41% and 42.88%, respectively). The results also showed that the lower GSO CC system cost was obtained at lower Pr. For the GSO CC system, the lowest ${\dot{C}}_{\mathrm{electricity} }$ is obtained at 7.5 bar (USD 8.67/MWh), and then ${\dot{C}}_{\mathrm{electricity} }$ jumps to USD 10.24/MWh at 18 bar.

The influence of air compressor isentropic efficiency (${\eta }_{AC}$) on system performance and total cost rate is shown in Figure 3. The figures revealed that a rise in ${\eta }_{AC}$ results in an increase in both Ẇ_net and the efficiencies of the GSO CC system. If the airflow rates remain constant, increasing the ${\eta }_{AC}$ will reduce the power consumption of the compressor, increasing the gas turbine’s power production. Figure 3a shows that a change in ${\eta }_{AC}$ from 70% to approximately 88% increases total Ẇ_net from 215.6 MW to 275 MW. Figure 3b shows that when ${\eta }_{AC}$ was raised, the First- and Second-Law efficiencies of the cycle would improve. The results indicate that increasing ${\eta }_{AC}$ is needed in order to attain greater efficiency. However, this is not economical. Based on these findings, increasing ${\eta }_{AC}$ from 70% to approximately 84% results in a lower cycle’s overall cost. However, further raising ${\eta }_{AC}$ to beyond 84% increases the cycle’s overall cost [41,42].

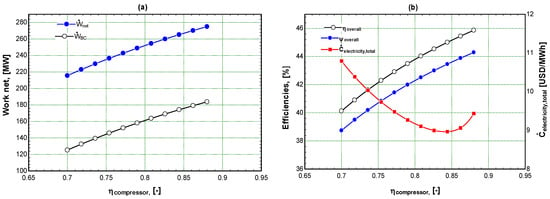
Figure 3. Variation of Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$, and ${\dot{C}}_{\mathrm{electricity}}$ with ${\eta }_{AC}$. (a) for performance and cost; (b) for efficiencies and cost.

Figure 4 shows how the isentropic efficiency of gas turbines (${\eta }_{GT}$) affects the performance of the GSO CC system and the rate of total costs. Ẇ_net and the efficiencies of the suggested system improved by increasing ${\eta }_{GT}$. By maximizing η_GT, the exergy destruction rate of the system was reduced and hence boosted the overall net and efficiencies of the proposed system. Figure 4a presents that when η_GT increases from 0.7 to 0.9, Ẇ_net improves from 212.1 MW to 270 MW for the system. Additionally, the ${\eta }_{overall}$ of the GSO CC system increases from 36.45% to 46.37 % and ${\Psi }_{overall}$ rises from 35.2% to 44.78%, as seen in Figure 4b. By increasing ${\eta }_{GT}$, the overall cost rate of the system initially drops and subsequently rises. As the gas turbine’s isentropic efficiency rises, the investment cost rate of the ORC components increases by growing the mass flow rate of the working fluid. As a result of these variations, the overall cost rate will initially fall and then rise [43,44]. With an increase in ${\eta }_{GT}$, ${\dot{C}}_{\mathrm{electricity} }$ drops significantly from USD 12.4/MWh until it reaches a minimum value of USD 9.03/MWh at ${\eta }_{GT}$ of 86%, and then it increases to USD 9.24/MWh at ${\eta }_{GT}$ of 90%.

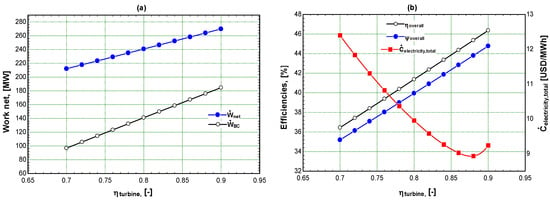
Figure 4. Variation of ${\dot{w}}_{\mathrm{net}}$, ${\eta }_{overall}$, ${\Psi }_{overall}$, and ${\dot{C}}_{\mathrm{electricity}}$ with ${\eta }_{GT}$. (a) for performance and cost; (b) for efficiencies and cost.

Figure 5 shows the variation in Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$_, and ${\dot{C}}_{\mathrm{electricity}}$ with GTIT. These figures demonstrate that a change in GTIT has a substantial effect on the values of Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$_, and ${\dot{C}}_{\mathrm{electricity}}$. With a rise in GTIT, the temperature of the exhaust gases leaving the gas turbine rises, increasing the thermal energy transferred from the exhaust gases in the HRSG to the RC [38,45]. This produces an increase in the Ẇ_net of the RC and ORC. Additionally, when the GTIT increases, the overall system becomes more efficient. Therefore, an increase in the GTIT from 1200 K to 1525 K dramatically increases Ẇ_net from 133.2 MW to 282.6 MW, and ${\eta }_{overall}$ improves substantially from 36.74% to 45.29%, while ${\Psi }_{overall}$ increases from 35.74% to 43.73%. Figure 5b also illustrates how a change in the GTIT affects the entire cost of the cycle. ${\dot{C}}_{\mathrm{electricity} }$ first declines drastically when the GTIT rises but subsequently considerably increases at higher GTIT levels [36,37,46]. ${\dot{C}}_{\mathrm{electricity} }$ becomes minimal at a GTIT of 1475 K, leading to minimum ${\dot{C}}_{\mathrm{electricity} }$ at 8.24 USD/MWh. With an increase in the GTIT, ${\dot{C}}_{\mathrm{electricity} }$ reduces significantly from 14.86 USD/MWh until it falls to a minimum value of 8.24 USD/MWh at a GTIT of 1475 K and then increases to 8.86 USD/MWh at a GTIT of 1525 K.

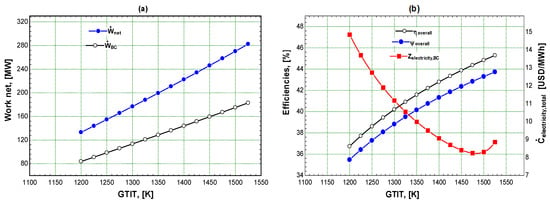
Figure 5. Variation of Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$, and ${\dot{C}}_{\mathrm{electricity}}$ with GTIT; (a) for performance and cost; (b) for efficiencies and cost.

Figure 6 shows how the boiler pressure ($P_{boiler}$) affects the performance of the GSO CC system and the rate of total costs. Since the network of the BC cycle remains constant regardless of the value of $P_{boiler}$, the network of the RC improves when $P_{boiler}$ rises due to the higher enthalpy of the water leaving the boiler, as seen in Figure 6a. Consequently, when $P_{boiler}$ climbs from 75 bar to 275 bar, Ẇ_net for the GSO CC system increases from 244 MW to 262.3 MW. Likewise, the efficiencies of the GSO CC system also increase at high $P_{boiler}$. Figure 6b shows that as $P_{boiler}$ increases, ${\eta }_{overall}$ increases from 43.6% to 44.9%, ${\Psi }_{overall}$ increases from 42.15% to 43.4%. The graph also shows that when P_boiler decreases from 275 bar to 75 bar, ${\dot{C}}_{\mathrm{electricity} }$ rises from USD 8.87/MWh to USD 9.27/MWh. The decreased power output of the GSO CC system at a lower $P_{boiler}$ is the fundamental cause of the rise in ${\dot{C}}_{\mathrm{electricity} }$.

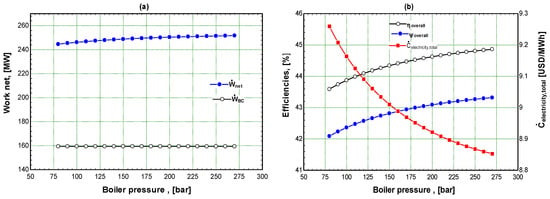
Figure 6. Variation of Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$, and ${\dot{C}}_{\mathrm{electricity}}$ with boiler pressure ($P_{boiler}$); (a) for performance and cost; (b) for efficiencies and cost.

The influence of Rankine cycle condenser temperature ($T_{condenser}$) on system performance and the total cost rate is shown in Figure 7. The finding demonstrates that when $T_{condenser}$ rises, the RC’s power output decreases, limiting Ẇ_net, ${\eta }_{overall}$, and ${\Psi }_{overall}$ of the GSO CC system. Ẇ_net drops from 2513 MW to 239.6 MW (approximately 11.7 MW) when $T_{condenser}$ increases from 303 K to 348 K, as seen in Figure 7a. Figure 7b also shows how ${\eta }_{overall}$ falls from 44.77 to 42.7%, while ${\Psi }_{overall}$ decreases from 43.23% to 41.23%. The results also show that the diminishment in the Ẇ_net of the GSO CC leads to an increase in ${\dot{C}}_{\mathrm{electricity} }$ at high $T_{condenser}$. ${\dot{C}}_{\mathrm{electricity} }$ increases from USD 8.83/MWh to USD 9.665/MWh with variations of $T_{condenser}$ between 303 K and 348 K.

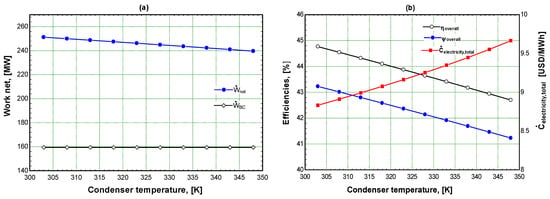
Figure 7. Variation in Ẇ_net, ${\eta }_{overall}$, ${\Psi }_{overall}$ _, and ${\dot{C}}_{\mathrm{electricity}}$ with condenser temperature ($T_{condenser}$); (a) for performance and cost; (b) for efficiencies and cost.

5. Conclusions

In this paper, the Rankine and organic Rankine cycles are integrated with the Taji gas turbine’s power plant to produce extra electricity and reduce environmental emissions by using waste heat recovery from the existing power plant. The novel triple trigeneration cycle has been investigated from a thermodynamic and economic standpoint. The entire processes for the cycle were investigated parametrically and optimized using thermodynamic principles and EES software V10.561-3D. The power plant’s overall efficiency and cost as a function of the primary operational parameters are examined. The obtained results can be discussed in the following conclusions:

• The combustion chamber is where the most exergy is lost (about 57.3%), and the pumps destroy the least amount of exergy compared to the other parts of the cycle.
• The highest total cost rate parts are the combustion chamber, the gas turbine, the steam turbine, and the heat recovery steam generator. Therefore, from the point of view of energy–economic analysis, these are the most important parts.
• Overall, the cost of exergy destruction for the cycle is 63%, indicating that 37% of the system’s total cost is attributable to the initial investment. This would mean that optimizing the system should focus on minimizing the cost of exergy destruction.
• According to the findings of the parametric analysis of the base case, the thermodynamic performance and cost of the system are enhanced by increasing the gas turbine inlet temperature and the isentropic efficiencies of the gas turbine and the air compressor. However, as these parameters are increased, the total cost of the system increases. Additionally, the increase in the pressure ratio will benefit the system. Additionally, the increase in pressure ratio will be thermodynamically and exergo–economically beneficial to the system. The increase in boiler pressure increases the First- and Second-Law efficiencies and decreases the system’s total cost rate. The increase in condenser temperature decreases the First- and Second-Law efficiencies and raises the system’s total cost rate.

These results may be a suitable contribution to future investigations on the Taji gas turbine’s power plant development and enhancement.