The Asymmetric Effects of Extreme Climate Risk Perception on Coal Futures Return Dynamics: Evidence from Nonparametric Causality-In-Quantiles Tests
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Nonparametric Causality-In-Quantiles Tests
3.2. Coal Futures Return Dynamics
3.2.1. Price Return
3.2.2. Realized Volatility
3.2.3. Jump and Continuous Variations
3.2.4. Realized Semi-Variance
3.2.5. Signed Realized Jump
4. Data and Empirical Findings
4.1. Data
4.2. Empirical Results
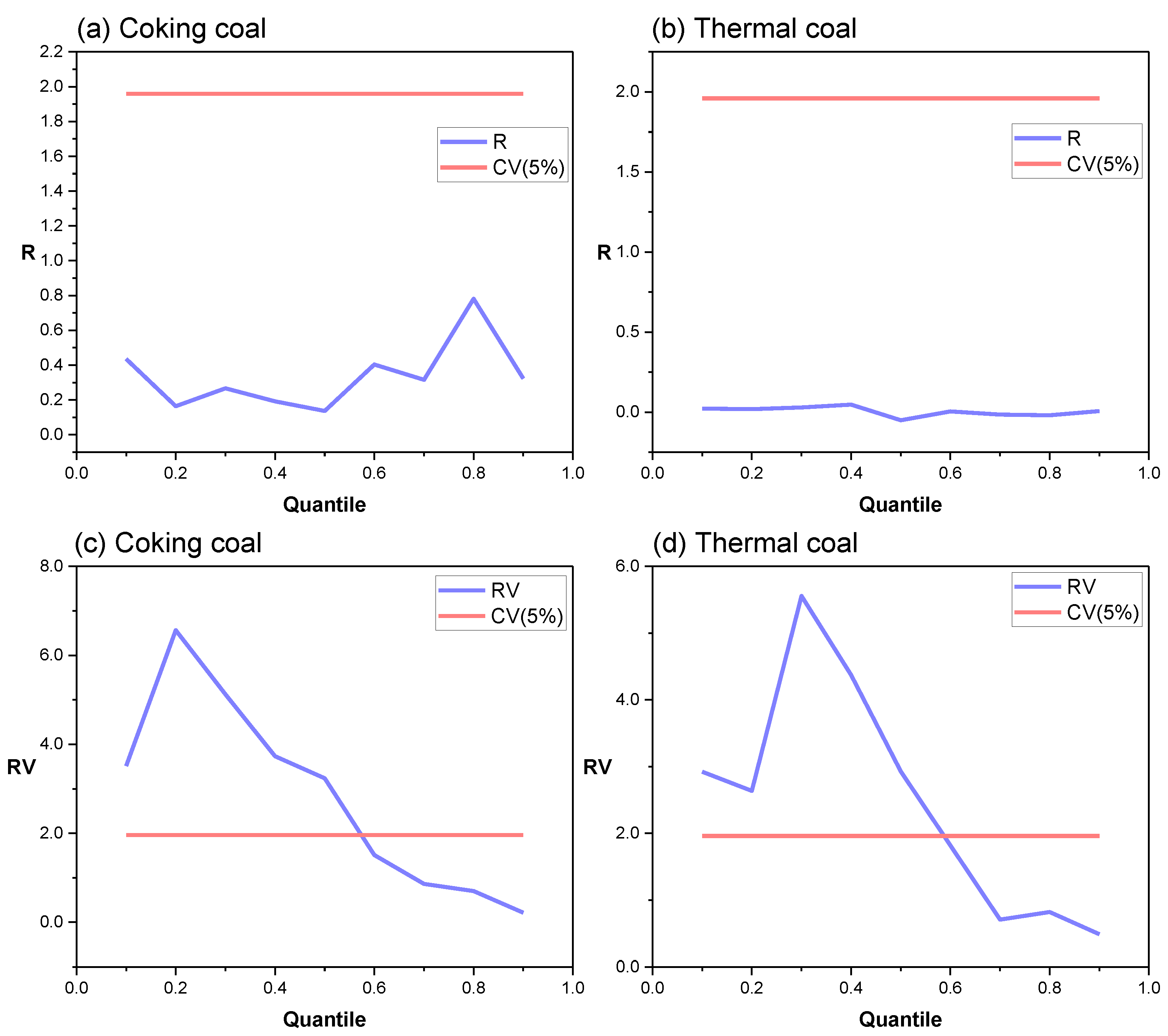
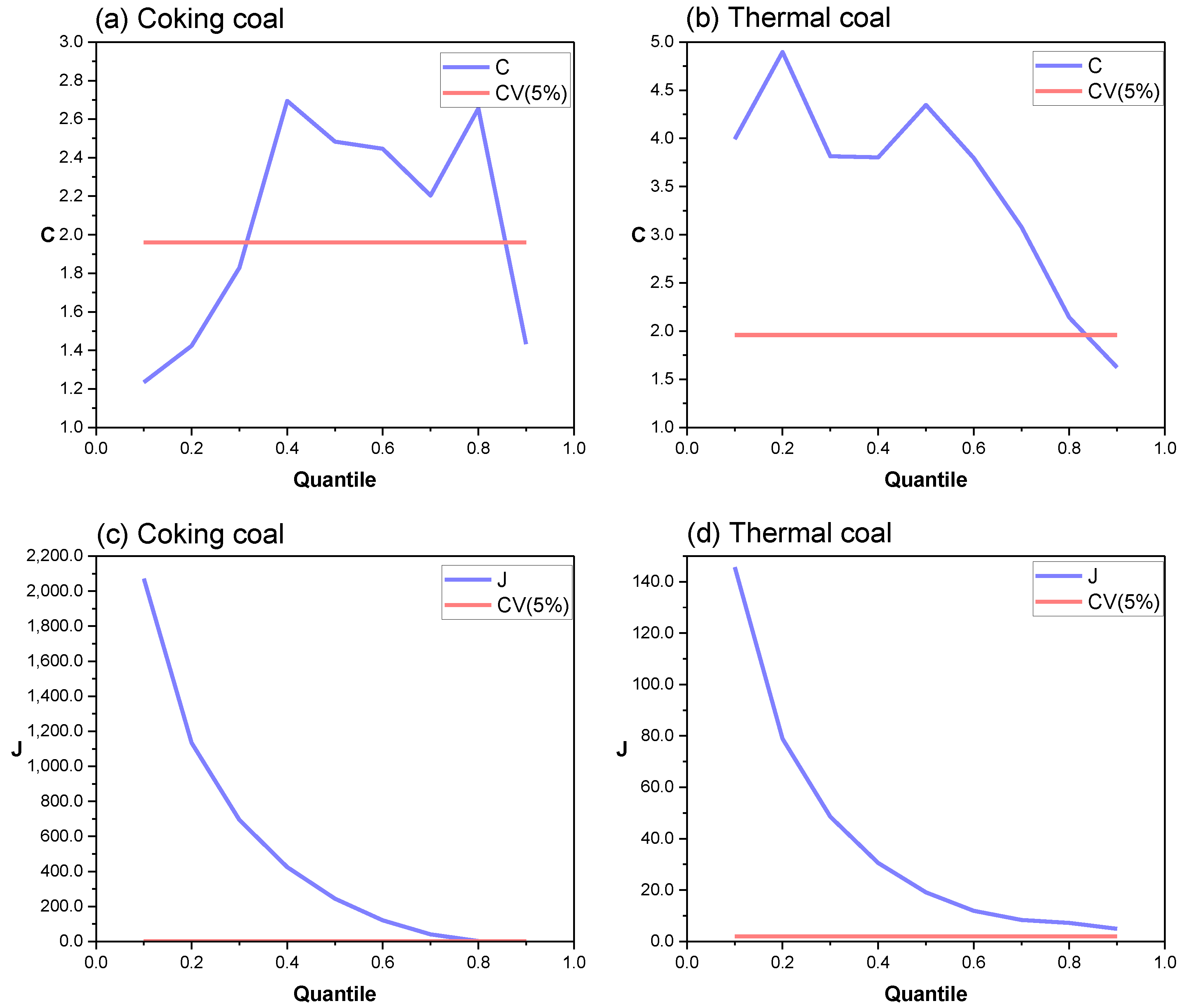
4.2.1. The Effects of CRP on Coal Returns and Realized Volatility
4.2.2. The Effects of CRP on Jumps in Coal Volatility
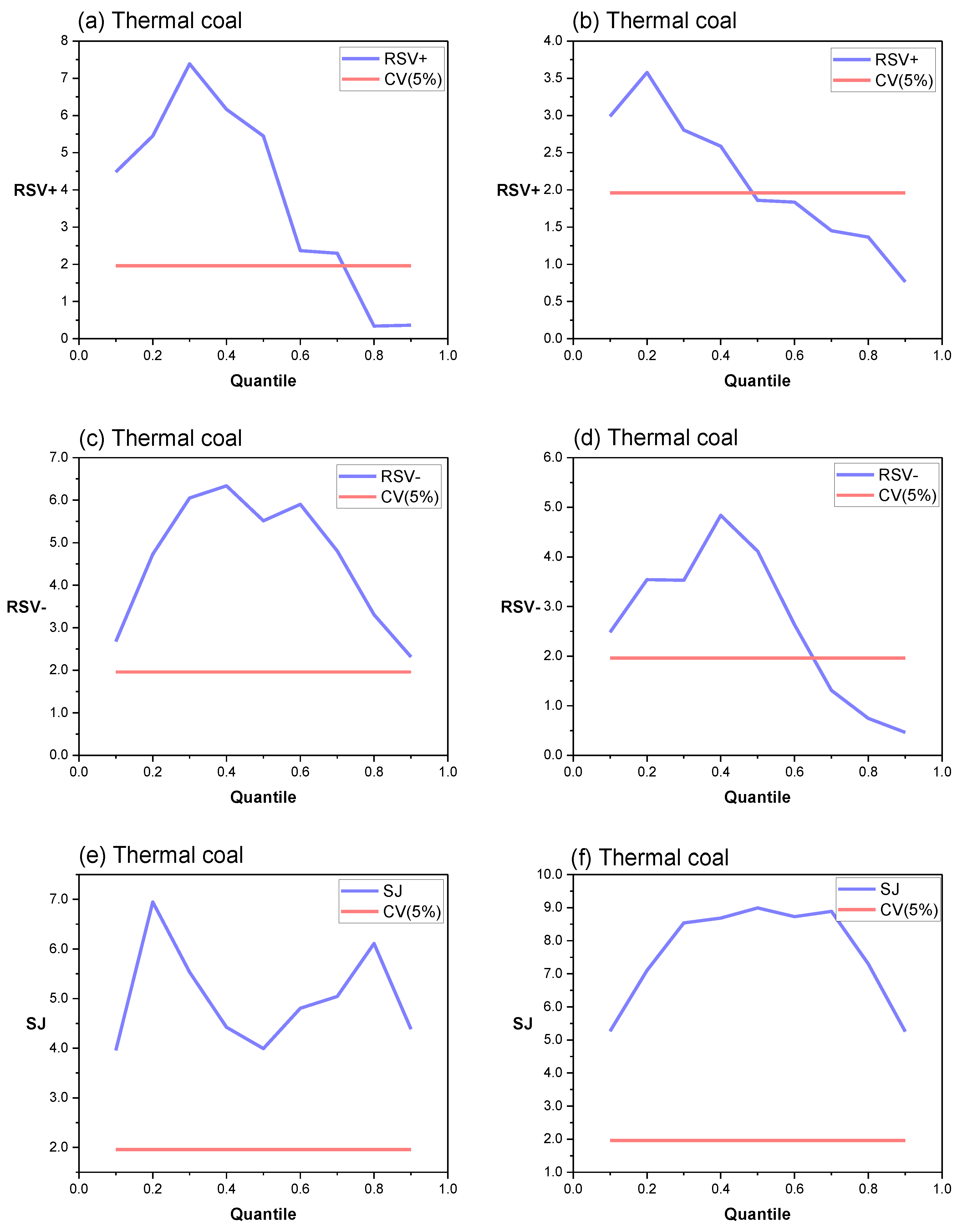
4.2.3. Asymmetric Effects of CRP
4.3. Robustness Test
5. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burke, M.; Hsiang, S.M.; Miguel, E. Global non-linear effect of temperature on economic production. Nature 2015, 527, 235–239. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Mondal, S.K.; Zhai, J.; Fischer, T.; Wang, Y.; Su, B.; Wang, G.; Gao, M.; Jiang, S.; Tao, H.; et al. Intensity-area-duration-based drought analysis under 1.5 °C–4.0 °C warming using CMIP6 over a climate hotspot in South Asia. J. Clean. Prod. 2022, 345, 131106. [Google Scholar] [CrossRef]
- Elkouk, A.; Pokhrel, Y.; Satoh, Y.; Bouchaou, L. Implications of changes in climate and human development on 21st-century global drought risk. J. Environ. Manag. 2022, 317, 115378. [Google Scholar] [CrossRef] [PubMed]
- Rohde, M.M. Floods and droughts are intensifying globally. Nat. Water 2023, 1, 226–227. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Wang, M. Flood detection using Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage and extreme precipitation data. Earth Syst. Sci. Data 2023, 15, 521–540. [Google Scholar] [CrossRef]
- Liu, W.; McKibbin, W.J.; Morris, A.C.; Wilcoxen, P.J. Global economic and environmental outcomes of the Paris Agreement. Energy Econ. 2020, 90, 104838. [Google Scholar] [CrossRef]
- Huang, M.-T.; Zhai, P.-M. Achieving Paris Agreement temperature goals requires carbon neutrality by middle century with far-reaching transitions in the whole society. Adv. Clim. Chang. Res. 2021, 12, 281–286. [Google Scholar] [CrossRef]
- MMurshed, M.; Ahmed, R.; Kumpamool, C.; Bassim, M.; Elheddad, M. The effects of regional trade integration and renewable energy transition on environmental quality: Evidence from South Asian neighbors. Bus. Strategy Environ. 2021, 30, 4154–4170. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Yan, L.-Z. Volatility spillover and hedging strategies between the European carbon emissions and energy markets. Energy Strategy Rev. 2023, 46, 101058. [Google Scholar] [CrossRef]
- Alola, A.A.; Adebayo, T.S. Analysing the waste management, industrial and agriculture greenhouse gas emissions of biomass, fossil fuel, and metallic ores utilization in Iceland. Sci. Total Environ. 2023, 164115, in press. [Google Scholar] [CrossRef]
- McCollum, D.L.; Zhou, W.; Bertram, C. Energy investment needs for fulfilling the Paris Agreement and achieving the Sustainable Development Goals. Nat. Energy 2018, 3, 589–599. [Google Scholar] [CrossRef]
- Ren, X.; Li, Y.; Shahbaz, M. Climate risk and corporate environmental performance: Empirical evidence from China. Sustain. Prod. Consum. 2022, 30, 467–477. [Google Scholar] [CrossRef]
- Ovaere, M.; Proost, S. Cost-effective reduction of fossil energy use in the European transport sector: An assessment of the Fit for 55 Package. Energy Policy 2022, 168, 113085. [Google Scholar] [CrossRef]
- Jie, D.; Xu, X.; Guo, F. The future of coal supply in China based on non-fossil energy development and carbon price strategies. Energy 2021, 220, 119644. [Google Scholar] [CrossRef]
- Gu, F.; Wang, J.; Guo, J. How the supply and demand of steam coal affect the investment in clean energy industry? Evidence from China. Resour. Policy 2020, 69, 101788. [Google Scholar] [CrossRef]
- Zhang, S.Y. Are investors sensitive to climate-related transition and physical risks? Evidence from global stock markets. Res. Int. Bus. Financ. 2022, 62, 101710. [Google Scholar] [CrossRef]
- Salisu, A.A.; Ndako, U.B.; Vo, X.V. Transition risk, physical risk, and the realized volatility of oil and natural gas prices. Resour. Policy 2023, 81, 103383. [Google Scholar] [CrossRef]
- Qi, X.-L.; Xu, H.-J.; Chen, T.; Shan, S.-Y.; Chen, S.-Y. Effects of climate change, coal mining and grazing on vegetation dynamics in the mountain permafrost regions. Ecol. Inform. 2022, 69, 101684. [Google Scholar] [CrossRef]
- Zamanipour, B.; Ghadaksaz, H.; Keppo, I.; Saboohi, Y. Electricity supply and demand dynamics in Iran considering climate change-induced stresses. Energy 2023, 263, 126118. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, D.; Cai, J. Legal systems, national governance and renewable energy investment: Evidence from around the world. Br. J. Manag. 2021, 32, 579–610. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, X.; Yan, C. Climate policy uncertainty and firm-level total factor productivity: Evidence from China. Energy Econ. 2022, 113, 106209. [Google Scholar] [CrossRef]
- Wong, J.B.; Zhang, Q. Impact of carbon tax on electricity prices and behaviour. Financ. Res. Lett. 2022, 44, 102098. [Google Scholar] [CrossRef]
- Lorente, D.B.; Mohammed, K.S. Dynamic connectedness among climate change index, green financial assets and renewable energy markets: Novel evidence from sustainable development perspective. Renew. Energy 2023, 204, 94–105. [Google Scholar] [CrossRef]
- Fahmy, H. The rise in investors’ awareness of climate risks after the Paris Agreement and the clean energy-oil-technology prices nexus. Energy Econ. 2022, 106, 105738. [Google Scholar] [CrossRef]
- Kung, C.-C.; Cao, X.; Choi, Y.; Kung, S.-S. A stochastic analysis of cropland utilization and resource allocation under climate change. Technol. Forecast. Soc. Chang. 2019, 148, 119711. [Google Scholar] [CrossRef]
- He, W.; Yang, Y.; Gu, W. A comparative analysis of China’s provincial carbon emission allowances allocation schemes by 2030: A resource misallocation perspective. J. Clean. Prod. 2022, 361, 132192. [Google Scholar] [CrossRef]
- Zhao, Y.; Dai, X.; Zhang, D. Do weather conditions drive China’s carbon-coal-electricity markets systemic risk? A multi-timescale analysis. Financ. Res. Lett. 2023, 51, 103432. [Google Scholar] [CrossRef]
- Walk, P.; Stognief, N. From coal phase-out to net zero: Driving factors of UK climate policy. Environ. Sci. Policy 2022, 138, 76–84. [Google Scholar] [CrossRef]
- Ding, Q.; Huang, J.; Zhang, H. Time-frequency spillovers among carbon, fossil energy and clean energy markets: The effects of attention to climate change. Int. Rev. Financ. Anal. 2022, 83, 102222. [Google Scholar] [CrossRef]
- Curran, G. Coal, climate and change: The narrative drivers of Australia’s coal economy. Energy Res. Soc. Sci. 2021, 74, 101955. [Google Scholar] [CrossRef]
- Ren, X.; Li, J.; He, F. Impact of climate policy uncertainty on traditional energy and green markets: Evidence from time-varying granger tests. Renew. Sustain. Energy Rev. 2023, 173, 113058. [Google Scholar] [CrossRef]
- Battiston, S.; Dafermos, Y.; Monasterolo, I. Climate risks and financial stability. J. Financ. Stab. 2021, 54, 100867. [Google Scholar] [CrossRef]
- Caporin, M.; Naeem, M.A. Asymmetric and time-frequency spillovers among commodities using high-frequency data. Resour. Policy 2021, 70, 101958. [Google Scholar] [CrossRef]
- Alam, M.S.; Shahzad, S.J.H. Causal flows between oil and forex markets using high-frequency data: Asymmetries from good and bad volatility. Energy Econ. 2019, 84, 104513. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Hitomi, K.; Kawasaki, Y. A consistent nonparametric test for nonlinear causality—Specification in time series regression. J. Econom. 2011, 165, 112–127. [Google Scholar] [CrossRef]
- Song, Y.; Fang, Z.; Fu, H.-Z. Influence of interdisciplinarity on scientific impact: The case of climate change field. J. Informetr. 2023, 17, 101410. [Google Scholar] [CrossRef]
- Zhou, D.; Siddik, A.B.; Guo, L.; Li, H. Dynamic relationship among climate policy uncertainty, oil price and renewable energy consumption—Findings from TVP-SV-VAR approach. Renew. Energy 2023, 204, 722–732. [Google Scholar] [CrossRef]
- Kyritsis, E.; Andersson, J. Causality in quantiles and dynamic relations in energy markets: (De) tails matter. Energy Policy 2019, 133, 110933. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Raza, N. Can economic policy uncertainty and investors sentiment predict commodities returns and volatility? Resour. Policy 2017, 53, 208–218. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Shephard, N. Power and bipower variation with stochastic volatility and jumps. J. Financ. Econom. 2004, 2, 1–37. [Google Scholar] [CrossRef]
- Barnett, M.; Brock, W.; Hansen, L.P. Pricing uncertainty induced by climate change. Rev. Financ. Stud. 2020, 33, 1024–1066. [Google Scholar] [CrossRef]
- Dafermos, Y.; Nikolaidi, M.; Galanis, G. Climate change, financial stability and monetary policy. Ecol. Econ. 2018, 152, 219–234. [Google Scholar] [CrossRef]
- Choi, D.; Gao, Z.; Jiang, W. Attention to global warming. Rev. Financ. Stud. 2020, 33, 1112–1145. [Google Scholar] [CrossRef]
- Krueger, P.; Sautner, Z.; Starks, L.T. The importance of climate risks for institutional investors. Rev. Financ. Stud. 2020, 33, 1067–1111. [Google Scholar] [CrossRef]
- Zhu, B.; Hu, X.; Deng, Y.; Zhang, B.; Li, X. The differential effects of climate risks on non-fossil and fossil fuel stock markets: Evidence from China. Financ. Res. Lett. 2023, 103962, in press. [Google Scholar] [CrossRef]
- Huynh, T.D.; Nguyen, T.H.; Truong, C. Climate risk: The price of drought. J. Corp. Financ. 2020, 65, 101750. [Google Scholar] [CrossRef]
- Painter, M. An inconvenient cost: The effects of climate change on municipal bonds. J. Financ. Econ. 2020, 135, 468–482. [Google Scholar] [CrossRef]
- Bansal, R.; Kiku, D.; Ochoa, M. Price of Long-Run Temperature Shifts in Capital Markets; National Bureau of Economic Research: Cambridge, MA, USA, 2016. [Google Scholar]
- Guo, K.; Liu, F.; Sun, X.; Zhang, D.; Ji, Q. Predicting natural gas futures’ volatility using climate risks. Financ. Res. Lett. 2023, 103915, in press. [Google Scholar] [CrossRef]
- Nguyen, Q.; Diaz-Rainey, I.; Kuruppuarachchi, D. Predicting corporate carbon footprints for climate finance risk analyses: A machine learning approach. Energy Econ. 2021, 95, 105129. [Google Scholar] [CrossRef]
- Mosquera-López, S.; Uribe, J.M. Nonlinear empirical pricing in electricity markets using fundamental weather factors. Energy 2017, 139, 594–605. [Google Scholar] [CrossRef]
- Balcilar, M.; Bonato, M.; Demirer, R. The effect of investor sentiment on gold market return dynamics: Evidence from a nonparametric causality-in-quantiles approach. Resour. Policy 2017, 51, 77–84. [Google Scholar] [CrossRef]
- Jeong, K.; Härdle, W.K.; Song, S. A consistent nonparametric test for causality in quantile. Econom. Theory 2012, 28, 861–887. [Google Scholar] [CrossRef]
- Batten, J.A.; Brzeszczynski, J.; Ciner, C. Price and volatility spillovers across the international steam coal market. Energy Econ. 2019, 77, 119–138. [Google Scholar] [CrossRef]
- Safarian, S. To what extent could biochar replace coal and coke in steel industries? Fuel 2023, 339, 127401. [Google Scholar] [CrossRef]
- Yu, B.; Liu, J.; Lyu, T.; Li, Z.; Wang, M.; Yang, W. A new detection method to assess the influence of human activities and climate change of CO2 emissions in coal field. Ecol. Indic. 2022, 143, 109417. [Google Scholar] [CrossRef]
- Cao, X.; Yan, J.; Wang, Z.; Lei, Z.; Ren, S.; Kang, S.; Li, Z.; Shui, H. Comparative study on coal blending and coke-making property of two kinds of thermal dissolution soluble fractions from lignite and coking coal. J. Anal. Appl. Pyrolysis 2022, 166, 105585. [Google Scholar] [CrossRef]
- Nishiyama, Y. Causality between government spending and income: The case of Saudi Arabia. Appl. Econ. Lett. 2019, 26, 433–435. [Google Scholar] [CrossRef]
- Andersen, T.G.; Bollerslev, T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. Int. Econ. Rev. 1998, 39, 885–905. [Google Scholar] [CrossRef]
- Benth, F.E. The stochastic volatility model of Barndorff-Nielsen and Shephard in commodity markets. Math. Financ. Int. J. Math. Stat. Financ. Econ. 2011, 21, 595–625. [Google Scholar] [CrossRef]
- Huang, X.; Tauchen, G. The relative contribution of jumps to total price variance. J. Financ. Econom. 2005, 3, 456–499. [Google Scholar]
- Bradley, E.H.; McGraw, S.A.; Curry, L.; Buckser, A.; King, K.L.; Kasl, S.V.; Andersen, R. Expanding the Andersen model: The role of psychosocial factors in long-term care use. Health Serv. Res. 2002, 37, 1221–1242. [Google Scholar] [CrossRef] [PubMed]
- Dunham, L.M.; Friesen, G.C. An empirical examination of jump risk in US equity and bond markets. North Am. Actuar. J. 2007, 11, 76–91. [Google Scholar] [CrossRef]
- Andersen, T.G.; Dobrev, D.; Schaumburg, E. Jump-robust volatility estimation using nearest neighbor truncation. J. Econom. 2012, 169, 75–93. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Hansen, P.R.; Lunde, A.; Shephard, N. Designing realized kernels to measure the ex post variation of equity prices in the presence of noise. Econometrica 2008, 76, 1481–1536. [Google Scholar]
- Patton, A.J.; Sheppard, K. Good volatility, bad volatility: Signed jumps and the persistence of volatility. Rev. Econ. Stat. 2015, 97, 683–697. [Google Scholar] [CrossRef]
- Broock, W.A.; Scheinkman, J.A.; Dechert, W.D.; LeBaron, B. A test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Naeem, M.A.; Peng, Z.; Bouri, E. Asymmetric volatility spillover among Chinese sectors during COVID-19. Int. Rev. Financ. Anal. 2021, 75, 101754. [Google Scholar] [CrossRef]
- Bahloul, W.; Balcilar, M.; Cunado, J.; Gupta, R. The role of economic and financial uncertainties in predicting commodity futures returns and volatility: Evidence from a nonparametric causality-in-quantiles test. J. Multinatl. Financ. Manag. 2018, 45, 52–71. [Google Scholar] [CrossRef]
- Dai, X.; Dai, P.-F.; Wang, Q.; Ouyang, Z.-Y. The impact of energy-exporting countries’ EPUs on China’s energy futures investors: Risk preference, investment position and investment horizon. Res. Int. Bus. Financ. 2023, 64, 101806. [Google Scholar] [CrossRef]
- Jost, F.; Dale, A.; Schwebel, S. How positive is “change” in climate change? A sentiment analysis. Environ. Sci. Policy 2019, 96, 27–36. [Google Scholar] [CrossRef]
- Liu, F.; Kang, Y.; Guo, K. The relationship between air pollution, investor attention and stock prices: Evidence from new energy and polluting sectors. Energy Policy 2021, 156, 112430. [Google Scholar] [CrossRef]
- Grieb, T. Mean and volatility transmission for commodity futures. J. Econ. Financ. 2015, 39, 100–118. [Google Scholar] [CrossRef]
- Zhao, X.; Lyon, T.P.; Wang, F. Why do electricity utilities cooperate with coal suppliers? A theoretical and empirical analysis from China. Energy Policy 2012, 46, 520–529. [Google Scholar] [CrossRef]
- Dao, X.; Ji, D.; Zhang, X.; He, J.; Meng, X.; Wang, Z.; Liu, Y.; Xu, X.; Tang, G.; Wang, Y. Characteristics, sources and health risk assessment of PM2. 5 in China’s coal and coking heartland: Insights gained from the regional observations during the heating season. Atmos. Pollut. Res. 2021, 12, 101237. [Google Scholar] [CrossRef]
- Lei, H.; Xue, M.; Liu, H.; Ye, J. Precious metal as a safe haven for global ESG stocks: Portfolio implications for socially responsible investing. Resour. Policy 2023, 80, 103170. [Google Scholar] [CrossRef]
- Aldieri, L.; Bruno, B.; Lorente, D.B.; Vinci, C.P. Environmental innovation, climate change and knowledge diffusion process: How can spillovers play a role in the goal of sustainable economic performance? Resour. Policy 2022, 79, 103021. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, F.; Zhang, Y. Good, bad cojumps and volatility forecasting: New evidence from crude oil and the U.S. stock markets. Energy Econ. 2019, 81, 52–62. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, H.; Arkorful, G.B.; Peng, Z. The impacts of futures trading on volatility and volatility asymmetry of Bitcoin returns. Int. Rev. Financ. Anal. 2023, 86, 102497. [Google Scholar] [CrossRef]
- Fang, N.; Jiang, W.; Luo, R. Realized semivariances and the variation of signed jumps in China’s stock market. Emerg. Mark. Financ. Trade 2017, 53, 563–586. [Google Scholar] [CrossRef]
- Zhang, H.; Demirer, R.; Huang, J.; Huang, W.; Tahir Suleman, M. Economic policy uncertainty and gold return dynamics: Evidence from high-frequency data. Resour. Policy 2021, 72, 102078. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Kinnebrock, S.; Shephard, N. Measuring Downside Risk-Realised Semivariance. CREATES Research Paper No. 2008-42. 2008. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1262194 (accessed on 23 January 2023).
- Mzoughi, H.; Urom, C.; Guesmi, K. Downside and upside risk spillovers between green finance and energy markets. Financ. Res. Lett. 2022, 47, 102612. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A. Realized variance and market microstructure noise. J. Bus. Econ. Stat. 2006, 24, 127–161. [Google Scholar] [CrossRef]


| Panel A: Coking | Mean | Median | Max | Min | Std | Variance | Skewness | Kurtosis | ADF | PP |
| 0.02 | −0.03 | 8.20 | −10.94 | 1.76 | 3.09 | −0.36 | 6.77 | −45.56 *** | −45.62 *** | |
| 3.45 | 1.82 | 71.80 | 0.04 | 4.85 | 23.53 | 5.64 | 57.81 | −15.02 *** | −14.97 *** | |
| 2.92 | 1.52 | 71.80 | 0.00 | 4.23 | 17.93 | 5.80 | 64.70 | −23.99 *** | −26.91 *** | |
| 0.53 | 0.00 | 70.38 | 0.00 | 2.43 | 5.90 | 15.05 | 359.64 | −30.56 *** | −33.19 *** | |
| 1.65 | 0.88 | 27.45 | 0.00 | 2.07 | 4.28 | 3.59 | 25.58 | −19.64 *** | −20.31 *** | |
| 1.80 | 0.87 | 70.43 | 0.00 | 3.38 | 11.46 | 10.16 | 170.16 | −18.31 *** | −21.16 *** | |
| −1555 | −0.02 | 19.89 | −70.43 | 2.82 | 7.95 | −14.32 | 334.11 | −30.64 *** | −33.54 *** | |
| CRP | 7.11 | 6.72 | 11.81 | 5.65 | 1.09 | 1.19 | 1.34 | 4.23 | −8.85 *** | −8.01 *** |
| Panel B: Thermal | Mean | Median | Max | Min | Std | Variance | Skewness | Kurtosis | ADF | PP |
| 0.04 | 0.00 | 9.32 | −10.66 | 1.52 | 2.31 | −0.76 | 14.00 | −34.80 *** | −35.66 *** | |
| 2.43 | 1.04 | 101.68 | 0.01 | 6.61 | 43.74 | 9.89 | 123.29 | −15.94 *** | −17.58 *** | |
| 1.86 | 0.75 | 101.68 | 0.00 | 4.95 | 24.51 | 10.77 | 163.25 | −15.99 *** | −18.75 *** | |
| 0.57 | 0.00 | 100.33 | 0.00 | 4.31 | 18.38 | 18.38 | 374.90 | −28.87 *** | −28.41 *** | |
| 1.05 | 0.48 | 26.74 | 0.00 | 2.03 | 4.12 | 6.44 | 58.65 | −18.57 *** | −19.82 *** | |
| 1.38 | 0.49 | 100.65 | 0.00 | 5.60 | 31.41 | 13.26 | 205.41 | −18.09 *** | −20.54 *** | |
| −0.33 | −0.01 | 24.43 | −100.34 | 5.23 | 27.33 | −14.55 | 254.02 | −21.75 *** | −23.45 *** | |
| CRP | 7.24 | 6.84 | 11.81 | 5.84 | 1.11 | 1.23 | 1.28 | 4.01 | −7.64 *** | −7.02 *** |
| Panel A: Coking | Chi-Sq. Statistic | Prob | Decision |
| 5.5889 | 0.0610 | No causality | |
| 0.7488 | 0.6880 | No causality | |
| 0.4515 | 0.7980 | No causality | |
| 1.0688 | 0.5860 | No causality | |
| 0.2384 | 0.8880 | No causality | |
| 1.4337 | 0.4880 | No causality | |
| 2.9813 | 0.2250 | No causality | |
| Panel B: Thermal | Chi-Sq. Statistic | Prob | Decision |
| 1.2948 | 0.5230 | No causality | |
| 1.5616 | 0.9170 | No causality | |
| 0.1743 | 0.5230 | No causality | |
| 1.2962 | 0.6310 | No causality | |
| 0.9219 | 0.2460 | No causality | |
| 2.8084 | 0.1490 | No causality | |
| 3.8108 | 0.8950 | No causality |
| Panel A: BDS Test with Coking Coal | |||||
| Embedding Dimension | m = 2 | m = 3 | m = 4 | m = 5 | m = 6 |
| 12.7426 *** | 16.2958 *** | 20.2575 *** | 25.3950 *** | 31.9624 *** | |
| 49.5603 *** | 60.2837 *** | 73.7292 *** | 91.769 *** | 117.3047 *** | |
| 35.2802 *** | 44.4288 *** | 54.4439 *** | 67.0186 *** | 84.4758 *** | |
| 4.7613 *** | 6.6792 *** | 7.5063 *** | 8.1157 *** | 8.9451 *** | |
| 47.2427 *** | 60.0328 *** | 75.8622 *** | 98.3250 *** | 131.2503 *** | |
| 33.4811 *** | 38.5438 *** | 43.6620 *** | 49.3561 *** | 56.7198 *** | |
| 17.4078 *** | 20.8513 *** | 24.0966 *** | 27.5773 *** | 31.1949 *** | |
| Panel B: BDS Test with Thermal Coal | |||||
| Embedding Dimension | m = 2 | m = 3 | m = 4 | m = 5 | m = 6 |
| 9.0246 *** | 11.9894 *** | 15.1983 *** | 20.0970 *** | 26.7040 *** | |
| 27.8075 *** | 28.4370 *** | 28.7493 *** | 29.1148 *** | 29.7465 *** | |
| 23.9704 *** | 27.0302 *** | 28.6262 *** | 30.1882 *** | 31.9588 *** | |
| 2.2465 *** | 2.9593 *** | 3.6069 *** | 4.7288 *** | 5.5339 *** | |
| 26.7867 *** | 31.1099 *** | 34.2424 *** | 37.7584 *** | 42.0198 *** | |
| 20.2393 *** | 20.6914 *** | 20.1458 *** | 19.5741 *** | 19.4708 *** | |
| 17.2931 *** | 17.4312 *** | 17.2163 *** | 16.9062 *** | 16.5965 *** | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Wei, J.; Yang, S. The Asymmetric Effects of Extreme Climate Risk Perception on Coal Futures Return Dynamics: Evidence from Nonparametric Causality-In-Quantiles Tests. Sustainability 2023, 15, 8156. https://doi.org/10.3390/su15108156
Gao W, Wei J, Yang S. The Asymmetric Effects of Extreme Climate Risk Perception on Coal Futures Return Dynamics: Evidence from Nonparametric Causality-In-Quantiles Tests. Sustainability. 2023; 15(10):8156. https://doi.org/10.3390/su15108156
Chicago/Turabian StyleGao, Wang, Jiajia Wei, and Shixiong Yang. 2023. "The Asymmetric Effects of Extreme Climate Risk Perception on Coal Futures Return Dynamics: Evidence from Nonparametric Causality-In-Quantiles Tests" Sustainability 15, no. 10: 8156. https://doi.org/10.3390/su15108156
APA StyleGao, W., Wei, J., & Yang, S. (2023). The Asymmetric Effects of Extreme Climate Risk Perception on Coal Futures Return Dynamics: Evidence from Nonparametric Causality-In-Quantiles Tests. Sustainability, 15(10), 8156. https://doi.org/10.3390/su15108156






