Application of Multicriteria Methods for Improvement of Information Security Metrics

Abstract

Metrics are a set of numbers that are used to obtain information about the operation of a process or system. In our case, metrics are used to assess the level of information security of information and communication infrastructure facilities. Metrics in the field of information security are used to quantify the possibility of damage due to unauthorized hacking of an information system, which make it possible to assess the cyber sustainability of the system. The purpose of the paper is to improve information security metrics using multicriteria decision–making methods (MCDM). This is achieved by proposing aggregated information security metrics and evaluating the effectiveness of their application. Classical information security metrics consist of one size or one variable. We obtained the total value by adding at least two different metrics and evaluating the weighting factors that determine their importance. This is what we call aggregated or multicriteria metrics of information security. Consequently, MCDM methods are applied to compile aggregated metrics of information security. These are derived from expert judgement and are proposed for the three management domains of the ISO/IEC 27001 information security standard. The proposed methods for improving cyber sustainability metrics are also relevant to information security metrics. Using AHP, WASPAS and Fuzzy TOPSIS methods to solve the problem, the weights of classical metrics are calculated and three aggregated metrics are proposed. As a result, to confirm the fulfilment of the task of improving information security metrics, a verification experiment is conducted, during which aggregated and classical information security metrics are compared. The experiment shows that the use of aggregated metrics can be a more convenient and faster process and higher intelligibility is also achieved.

1. Introduction

Information security in the field of informatization (hereinafter, information security) refers to the state of security of electronic information resources, information systems and information and communication infrastructure from external and internal threats [1]. According to the concept of the CIA triad, the main tasks of information security are to ensure the confidentiality, integrity and availability of information–communication infrastructure objects [2].

Most organizations in the world cannot function without information security measures. Working in certain areas, such as the financial sector, requires compliance with various standards and requirements related to information security. Companies from other areas, such as energy, medicine, logistics and national defense, are no exception. To ensure information security, organizations are forced to allocate resources for this. The planning and operation of resources are mainly taken care of by the chief information security officer (CISO). Therefore, the CISO forms the security program and is responsible for its implementation. It is necessary to carry out measurements to verify the effectiveness of the applied program; such measurements are called metrics of information security. Metrics allow one to assess the security situation and, in the long term, understand the effectiveness of the information security program in place. The use of metrics is also determined by the international information security management standard ISO/IEC 27004 [3].

Moreover, cyber sustainability is defined as the ability to continuously achieve the expected results despite negative cybersecurity events [4]. Information security indicators partially include the area of attack sustainability metrics [5]. When choosing cyber sustainability metrics, it is proposed to evaluate a variety of criteria. In order for metrics to be suitable for selection, first of all, it must be possible to evaluate them. It should also be possible to quickly extract the data needed to compile the metrics. The benefits provided by each metric should exceed the losses incurred during its receipt and compilation. There are other requirements that additional metrics must meet. The criteria for selecting metrics should be ordered by priority, which may vary depending on the needs of a particular organization. The specification of metrics is proposed to assess the metrics of cyber sustainability. This allows one to evaluate how a specific metric can be used, what are the values of the metric values or what information a specific numeric value gives [6].

The effectiveness of security programs is usually measured by metrics. Metrics are crucial because they provide direct information about the organization’s information security situation. Using metrics effectively can solve organizations’ security problems [7]. This, accordingly, will reduce the number of crimes in cyberspace [8]. This work aims to improve metrics, which can significantly contribute to improving the organization’s position in the security field [9]. The topic is new and relevant since organizations’ use of information security metrics is not yet a well-established process. The scientific community needs currently applicable metrics to systematize, select the best ones, improve existing ones or offer new ones—aggregated ones. The novelty of the research is the application of a new approach to improving information security metrics through the use of multicriteria decision-making methods. Moreover, it is revealed that previously aggregated metrics were not used in the field of information security in accordance with multicriteria decision-making methods.

In accordance with the current international information security management system standard ISO/IEC 27001, information security metrics are mandatory [10]. It is worth noting that the standard identifies 14 areas of information security management [11]. Consequently, a certain number of classical metrics are allocated for each of these areas. In general, metrics in information security are used to measure and evaluate the effectiveness of the system under study but the application of classical metrics in information security requires a lot of time. In turn, to solve this problem, we propose to build aggregated information security metrics based on classical metrics.

This article describes the application of decision-making methods based on multicriteria methods (MCDM) to improve information security metrics. The goal is to evaluate the current classical information security metrics and propose new aggregated metrics. Aggregated metrics provide a generalized approach to the information security situation of the organization. Their use makes it possible to understand the current security situation more effectively and reduces the resources allocated for monitoring. Using multi-criteria decision-making methods (MCDM) to improve information security metrics. This will be achieved by offering aggregated information security metrics and evaluating the effectiveness of their application.

The article [12] analyzes MCDM methods by application area and indicates the top 25 areas where these methods are used. According to the research data, the largest number of articles relates to the fields of computer science and artificial intelligence. Also, authors [12] indicate that one of the disadvantages of the AHP method is that it requires a large number of inputs. However, in our suggested approach, we use the AHP method without fuzzy sets to avoid requiring a large number of inputs. Consequently, while the AHP method serves primarily to rank the criteria based on the weights, the TOPSIS method is applied in combination with fuzzy theory in order to evaluate the criteria and the selection of an alternative [12]. A review of the MCDM methods used in assessing the sustainability of the system is shown in [13] and it can be concluded that the AHP method takes the leading position in a number of applications. The aggregation techniques have a great effect on MCDM problems and the aggregation operators have been broadly applied to MCDM.

Additionally, in the paper [14], the literature was reviewed for the recent developments in TOPSIS. This article provided a detailed analysis of the methods TOPSIS and Fuzzy TOPSIS for solving many different selection/ranking problems. Based on the research in the paper [14], it was decided to use the Fuzzy TOPSIS method because of its ability to deal with different types of values: crisp, interval, fuzzy or linguistic. The F-TOPSIS algorithm allows all the data to be transformed into a common domain of triangular fuzzy numbers and perform all calculations required using fuzzy arithmetic [14].

The WASPAS method is an MCDM method which integrates the weighted sum model (WSM) and weighted product model (WPM) for decision-making process [15]. WSM and WPM are particularly useful to assess alternatives based on different criteria [16]. WASPAS is based on a weighted linear combination of WSM and WPM for ranking alternatives [17]. In this study, we use linear normalization; in this regard, the classical WASPAS method is applicable.

Section 1 is an introduction to the article. Section 2 defines the concept of information security metrics and summarizes the quantitative approach in information security-related processes. It also provides a classification of security metrics and examples of them. Section 3 provides the classification of MCDM methods and presents a comparison of the advantages and disadvantages of various MCDM methods. Section 4 describes the application of the MCDM methods to create aggregated information security metrics. Expert evaluation is used to apply the method. Section 5 describes the expert evaluation group, the compilation of aggregated metrics and the verification of the reliability of the results.

2. Related Work Analysis on Information Security Metrics

Aggregated Metrics

Ensuring an organization’s information security is necessary due to the constant incidents of information security. In the case of direct hacking of an organization’s information systems, huge damage is caused, which also leads to indirect damage—a decrease in reputation. Such incidents are rare. Quite often, the person responsible for security experiences a sense of insecurity in the company (CIO or CISO), realizing that the protection of the organization’s information may be compromised. It is the use of metrics that can solve this situation. A properly configured metric system should diagnose the information security situation, ensure security, measure the effectiveness of applied metrics and increase security awareness levels [18].

Metrics are sets of numbers that provide information about the operation of a process or system. Information security metrics are a set of interrelated dimensions that allow quantifying the possibility of harm as a result of unauthorized hacking of an information system [19].

Information security metrics are defined in scientific articles quite differently. The concepts and definitions of information security metrics used in scientific papers are given in Table 1.

Table 1. Definitions of information security metrics as used in scientific papers [18].

Reference	Definition of Information Security Metrics in the Paper
[20]	Security metrics consist of three main parts: size, scale and interpretation. The security values of the systems are measured based on a given size and are linked to the scale. The interpretation indicates what the specific security values obtained mean.
[18]	Security metrics are a group of cornerstone metrics that describe the position of both autonomous and dependent systems of information security operations in an organization.
[21]	Security metrics are a quantitative and objective basis for ensuring security. They facilitate business and engineering solutions related to information security.
[22]	Security metrics are tools that allow one to build on information security solutions and improve information security management.
[23]	Security metrics provide a framework for evaluating the security processes included in products and commercial information security services.
[24]	Security metrics are the quantitative value that shows a particular entity’s security level.
[25]	Security metrics are tools that allow one to simplify decision-making and increase productivity and accountability. This is achieved by collecting, analyzing and reporting relevant data related to information security activities.

The above definitions show that information security metrics are defined differently in different sources. Information security metrics can bring several advantages to an organization [18]:

• Understand security threats;
• Notice emerging problems with information security;
• Understand weaknesses in the security infrastructure;
• Measure the effectiveness of applied measures that are used to solve security problems;
• Disclose recommendations for the development of security technologies and processes.

In order for organizations to not face misunderstandings and difficulties, it is believed that metrics should be simple and understandable. Good metrics are those that meet the following criteria [18]:

• A certain parameter is constantly measured using the same methodology;
• Simple and inexpensive data collection;
• Expressed as a digit or percentage expression (“high”, “medium” or “low” is incorrect);
• Expressed by including certain standard units of measurement (for example time or monetary expression);
• Metrics should be specific, speak about a specific process and provide clear data to those who make organizational decisions.

Metrics that are constantly measured by the same methods allow one to draw conclusions and obtain the same results (regardless of the perception or individual assumptions of the measuring person). Obtaining metrics should be simple and inexpensive. Data collection can be both very simple and quite a complex task. To evaluate some metrics, it is enough to write one SQL query, while for others it may not be enough to make an infinite number of phone calls. It is believed that one of the characteristics of a good metric should be a simple extraction of data to calculate the metric. It is also important that the metrics are clear and understandable, describe a specific process well and allow one to make specific decisions. As an example, the metric “average number of corporate attacks” is too abstract; in this case, the metric “average number of attacks to e-commerce servers” should be applied. Accurate metrics allow adoption of more specific mechanisms that can solve the security problem [18].

We can create an effective metric system by knowing which parameters describe the quality of information security metrics. Such a system enables making decisions related to information security while considering numerical parameters. Currently, in some organizations, information security decisions are made only according to information security experts’ personal opinions and experience. This situation should change, as it will significantly improve the information security management process. For instance, in the paper [26], this task was assigned to 141 specialists from around the world who have a direct connection and working or scientific experience with information security metrics. Specialists had to choose the most important of the 19 quality criteria describing information security metrics [26]. Those 19 criteria were taken from the research of [26]. There were respondents from 21 countries: 61 (43%) from Finland, 20 (14%) from the U.S., 9 (6%) from Spain, 7 (5%) from each Italy and Germany and 5 (4%) from each Austria, Ireland and Norway. The remaining respondents were from Belgium, the Czech Republic, France, Greece, Hungary, India, Luxembourg, The Netherlands, Norway, Singapore, South Africa, Sweden and the U.K. This study was aimed at clarifying the main quality criteria that describe good performance. The results of the study showed that three main quality criteria are the most important, according to respondents. These are correctness, the ability to measure (or measurability) and significance [21]. The fourth-most important criterion is the ability to use metrics. Correctness means that the metric is applied correctly and does not give any misinformation; the metric is obtained without errors. Measurable metrics have a range of possible values, i.e., a clear value determined by numerical units. Meaningful metrics justify the needs that are presented to them and the ability to use them describes the practical benefits that the metric provides. This study gives information security professionals a clear idea of what real criteria describe the quality of metrics [27].

Other key metrics characterizing quality criteria can also be found in scientific sources. These quality criteria are given in Table 2.

Table 2. Highlights from the literature of the main criteria for the quality of information security metrics [18].

Reference	The Main Criteria Determining Information Security Metrics
[18]	A certain parameter is constantly measured using the same methodology; Simple and inexpensive data collection, preferably automatically; Expressed by the inclusion of certain standard units of measurement; Metrics should be specific, speak about a specific process and provide clear data to those who make organizational decisions.
[26]	Correctness; Measurability; Significance; Ability to use metrics (usability).
[25]	Measurements should include quantitative data (percentages, averages, numbers); Measurement data should be easily obtainable; Only repetitive information security processes should be measured; Measurements should be useful; they should allow one to monitor the effectiveness of systems and perform resource allocation.
[3]	Here are recommendations for measuring information security parameters: Data are easily collected; Human resources are allocated for data collection and management; The right tools are used; The number of potentially similar metrics are based on the baseline measurement; Easy to interpret; Number of users of measurement results; Compliance with measurements and the need for measured information; Cost of data collection, management and analysis.

Security metrics should be divided into certain groups depending on their origin. One can distinguish such a classification of metrics as follows [18]:

• Perimeter protection. Defines the risks associated with potential security breaches of the organization that come from outside (firewalls, IDS, email, etc.; see the analysis of emails and the resistance of employees to social engineering attacks). Examples of this type of metric are given in Table 3;
  Table 3. Table of information security metrics, based on [18].

  Classification of the Information Security-Level Metrics	Metric Name (Unit of Measurement)	Metric Characteristics, the Purpose of Parameter Tracking
  Perimeter protection: Email	The number of messages received per day (pcs.)	Determines the effectiveness of email filtering system
  	Detected/undetected spam quantity (pcs., %)
  	False positive spam detection (pcs., %)
  	Spam detection errors, which include false positives and malicious emails which are not detected (%)
  	Number of detected viruses and spyware malicious software code (pcs., %)	Determines malicious software code for email contamination
  Perimeter protection: Antivirus software	Viruses and spyware malicious code detected on web pages visited by users (pcs., %)	Determines the propensity of users to visit suspicious websites
  	Malicious program code detected (pcs.): * On servers; * In desktop computers; * On laptops.	Determines the amount of contaminated equipment
  	Viruses and incidents of malicious software code requiring system cleaning (pcs., % compared to all MSC incidents)	Quantity of resources allocated for cleaning malicious software code
  	Tools for cleaning up incidents of spyware malicious software code: Classified by departments of the organization	Assesses the cost of cleaning equipment from viruses and malicious software code
  	The costs of cleaning up viruses and incidents of malicious software code: Classified by departments of the organization
  	The number of malicious software codes sent captured from the organization’s network (pcs.)	Determines the number of contaminated devices in an organization
  Perimeter protection: Firewall and network perimeter	Firewall rule changes (pcs.): * Classified by departments of the organization * Classified by the type of group server	Shows the level of information security of the system
  	The firewall requires working resources (time spent per hour)	Assesses the time to fix firewall needs
  	Incoming logins/sessions on the organization’s servers on the internet (pcs.)	Predicts the size of approximate future consumer traffic
  	Number of open wireless access points	Determines potential vulnerability to external attacks by using Wireless Scanning Tools
  	Network devices directly connected to the main transactional and financial systems, without intermediate firewalls (pcs.)	Determines potential vulnerability to attacks
  Perimeter protection: Attacks	Classification of online attacks into three levels of event danger (%): * Probable attacks (the original IDS event is generated); * Suspects (machine-filtered attack reports); * Attackers (manual investigation of employees).	Determines the level of harm that can be caused by attacks
  	Quantity of attacks (pcs.)	Determines the quantity of successful/unsuccessful attacks
  	Quantity of successful attacks (pcs., %)	Evaluates the effectiveness of perimeter protection
  Scope and management area: Antivirus software	Computer workstations and servers with antivirus software	Determines the number of vulnerable workstations and servers
  	Computer workstations and servers with the latest malicious code database lists	Assesses the security of workstations and servers when using antivirus software
  Scope and management area: Patch management	Hardware has not received critical software updates (%): Classified by hardware type.	Identifies gaps in software updates
  	Quantity of critical updates (pcs.)	Assesses the effectiveness of the software update process
  	Delay in performing a critical security update (time)	Shows how fast the Software Update Management System records critical security updates
  Scope and management area: Host configuration	Percentage of systems corresponding to a certain configuration (%)	Evaluates the organization’s systems for compliance with the configuration standard
  	Remote control of systems (%)	Shows the percentage of systems that can be managed remotely
  	Actively controlled critical systems of the organization (%)	Shows the percentage of ensuring uptime and security of critical informatization objects through the SIEM system
  Scope and management area: Vulnerability management	Systems exposed to software scanning vulnerabilities (%)	Shows percentage of efficiency of vulnerability scanning software
  	The number of vulnerabilities detected per fixed unit of time (pcs.)	Shows the quantity of detected vulnerabilities by vulnerability scanning software
  	Time spent fixing vulnerabilities (time)	Shows how quickly vulnerability scanning software determines gaps and vulnerabilities in systems
  Information availability and system reliability: Working hours (uptime)	System operation time (time, %)	Assesses the availability of critical systems
  	Unplanned failure and consent to unplanned activity due to security incidents (%, time)	Estimates the time of unavailability of the systems due to the security incidents
  	MTBF (time)	Estimates the time of unavailability of system elements
  Information availability and system reliability: System recovery	Staff response time (average time)	Assesses the time to spend for repairing the system by staff
  	MTTR (time)	Shows how long it takes to fix a non-working element of the system

• Scope and management area determine how well an organization succeeds in implementing an application security program. In other words, whether the factors provided for by the security program within the organization are being observed. While CISO can apply a wide range of methods that improve information security parameters in a company, real endpoints (such as computers, servers, or employees) may not be available. Examples of this type of metric are given in Table 3;
• The availability of information and the stability of systems determine the metrics that characterize the operation of systems that generate profit for the organization (for example, metrics such as MTTR and MTBF). Examples of this type of metric are given in Table 3. Table 3 was compiled on the basis of the information provided in [18].

The information security metrics in Table 3 are among the most significant and widely used in the information security industry. Of course, other metrics are successfully used in various organizations that monitor information security processes. The concept of information security metrics can be equated with key performance metrics used in the field of business management [27].

This is not the only way to classify metrics. Other classifications of metrics are presented in other scientific papers. For example, by the type of input data, metrics are classified into analyzing design and development, analyzing performance processes and analysis of support and updates. Design and development describe and measure the effectiveness of the security engineering process and the development of information systems. The scope describes the specifics of already-created and working systems. The area of support and updates describes the effectiveness of information security management and changes in running processes [22].

It is also possible to classify metrics according to information security management standards. For example, the classification of ISO/IEC 27000 metrics can be performed based on the management areas offered by the standard. Management areas are described in part 27001 of the standard and this classification is applied in this part of the study. In addition, the standard itself defines, as part of the monitoring, measurement and analysis of information security, in the highlighted part of the standard 27004 [5]. The standard describes examples of measurement construction and a possible classification covering 30 areas. Some of the areas offered by the standard are resource allocation, policy verification, risk impact, audit program, password quality, PDA protection, firewall rules, device configuration, vulnerability environment and other areas [5].

Classical information security metrics consist of one size or one variable. As an example, one metric is the number of malicious software codes detected on the organization’s servers per day, which is measured in units. This is a metric of one criterion. We can obtain the total value by adding at least two different metrics and evaluating the weighting factors that determine their importance. This is what we call aggregated or multicriteria metrics of information security.

The concept of aggregated information security metrics is not established in the studied articles on information security issues. Researchers offer various methodologies for assessing the information security situation in an organization using metrics. One of the articles presents unconventional multicriteria information security metrics for assessing the overall security of a database management system. This is carried out by measuring the uncertainty that arises from possible attacks on database management systems [28].

Scientific articles also discuss the importance of aggregated information security metrics. They state that combining individual security metrics is useful but is not easy. To aggregate metrics, one needs to evaluate the dependencies between them to obtain a generalized one. Dependency assessment is a decision-making task, since it is necessary to decide how important a certain measurable factor is in relation to others [29]. This can be performed by entering weighting factors that determine the value of traditional metrics in an aggregated multicriteria metric.

The problem of aggregated metrics in the scientific community has not yet been widely studied and, therefore, a generalized concept has not been agreed upon. For business institutions, the use of aggregated metrics is an understudied phenomenon. Such aggregated, generalized data—providing information security of specific areas of activity—and metrics are offered to their clients by business institutions [30].

3. MCDM Methods

3.1. Comparison of MCDM Methods

Multi-criteria decision-making methods (MCDM) are used to make the optimal decision. MCDM is a well-known multicriteria methodological method used in decision-making. This method is used in various fields of science and business, covered by the fields of management sciences, engineering and IT.

Before delving into specific methods of problem-solving, it is important to clarify the classification characteristic of these methods. Classification of methods is carried out based on various factors. MCDMs are divided into two groups: Multi-Objective Decision Making (MODM) and Multi-Attribute Decision Making (MADM). Multi-purpose methods are further classified by the types of data used to rank alternatives. The methods are classified into deterministic, stochastic (probabilistic) and indeterminate sets (fuzzy). Depending on the number of decision-makers involved in the process, the methods can be divided into single-person or group decision methods [31]. Other classifications of multicriteria methods are also proposed, depending on the type of information that is provided to decision-makers. In accordance with this classification, it is possible to distinguish methods of rank correlation, methods based on the comparison of preferences (priority), methods that allow conversion of qualitative estimates into quantitative ones and methods that calculate the distance from the reference point [32].

When solving MCDM tasks, qualitative criteria are often found. Expert assessment is used to solve such problems. In traditional MCDM methods, decisions made by people are converted into certain numerical values. However, it is often difficult for decision-makers to determine the exact numerical value of a particular problem [33]. In this case, one can use indeterminate sets (fuzzy) methods.

There are various multicriteria methods with different decision-making characteristics. The methods are quite different; all have their advantages and disadvantages. Because of these differences, it is quite difficult to make an objective comparison of these methods. A generalized comparison of the methods is given in Table 4.

Table 4. Comparison of multicriteria methods [32].

	AHP	Fuzzy	WSM	WPM	ELECTRE PROMETHEE	TOPSIS	MAUT
World practice in the field of engineering. MCDA issues	+	+/−	−	−	+/−	+/−	+/−
Group decision-making	+/−	+	+	+	+/−	+/−	+/−
Uses a hierarchical task structure	+	−	−	−	−	−	−
Ensures compatibility of ratings	+	−	−	−	+	+	+
Evaluation of quality criteria	+	+	−	−	+	+	+
Various aspects of criterion measurement	+	+	−	+	+	+	+
Legibility of the method	Medium	Medium	Simple	Simple	Difficult	Difficult	Difficult
Labor costs	Medium	Medium	Small	Small	Large	Large	Large

It is worth noting that the AHP method is very often used in scientific articles in the engineering field [34]. This method uses the hierarchical structure of the problem, breaking the problem into smaller parts and, consequently, evaluating all aspects of the problem [35].

A brief description of the MCDM methods is also provided in Table 5. The table describes the advantages and disadvantages of the methods and the most common applications.

Table 5. Description of MCDM methods [35].

Methods	Advantages	Disadvantages	Application Areas
MAUT	Evaluates uncertainty; wishes may be included	A lot of data are required; wishes should be very precise.	Economics, finance, actuarial calculations, agriculture and energy.
AHP	Easy to use; the size-adjustable hierarchical system can be configured so that various problems can be investigated; does not require a lot of data.	Problems caused by interdependencies between criteria and alternatives; may lead to discrepancies between solutions and ranking criteria; changes in the ranking.	To solve problems of efficiency, resource planning, policy and strategy of the organization and public policy.
CBR	Does not require a large amount of data; does not require much maintenance; can improve over time; can adapt to changes in the environment.	Sensitive to conflicting data; required in many cases.	Business, vehicle insurance, medicine and engineering
DEA	Can deal with many inputs and outputs; efficiency can be analyzed and quantified.	Does not deal with inaccurate data; assumes that all incoming and outgoing quantities are accurate and well-known.	Economics, medicine, road security, utilities, agriculture, solving sales and business problems.
Fuzzy	Accepts inaccurate data; takes into account insufficient information.	It is difficult to assemble and develop; it may require a large number of simulations before actual use and obtaining results.	Engineering, economics, ecology, medicine and management
SMART	A simple method; allows one to use any type of weight distribution method; decision-making requires less effort.	When evaluating the structure of the method, the procedure may be inconvenient.	Environment, construction sector, logistics, national defense, production and assembly problems.
GP	Can solve large-scale problems; can create large-scale alternatives.	Coefficient scale system; other MCDM weight gain methods are commonly used coefficients.	Production planning, scheduling, medicine, portfolio selection and energy.
ELECTRE	Assesses uncertainty and unreliability.	The process and its outcome are difficult to describe in simple words; prioritization does not allow one to directly identify the strengths and weaknesses of alternatives.	Energy, economics, ecology and solving logistical problems.
PROMETHEE	Easy to use; does not require the assumption that the criteria are proportional.	Does not provide a clear method of weight distribution.	Ecology, hydrology, business and finance, logistics, production, energy and agriculture.
SAW	Ability to compensate for criteria; intuitive to decision-makers; calculations are simple; does not require complex software.	Calculations do not always reveal the real situation; the results obtained may be illogical.	Business and management of financial institutions.
TOPSIS	Simple process; ease of use and programming; the number of steps in the execution of the method remains the same regardless of the number of attributes.	Euclidean distance underestimates the correlation of attributes; it is difficult to weigh and maintain the constancy of the solution. The method is suitable when the metrics of alternatives do not have very significant differences. Differences can distort the results.	Logistics, engineering, manufacturing, business and marketing, environment and human resources.
WASPAS	A high level of reliability; a fairly simple calculation process.	The method evaluates only the minimum (not for useful criteria) and maximum (for useful criteria) values. Not all alternative values are evaluated.	Engineering, manufacturing and business

From Table 5, three MCDM methods are selected to compile aggregated information security metrics: AHP, WASPAS and Fuzzy TOPSIS. Since the task of compiling aggregated information security metrics involves the use of purely qualitative values, it is necessary to choose the appropriate research methodology. For this reason, two separate methods of solving the problem are used:

• The AHP method is used to determine the weights of the criteria and these weights are then applied to the calculation using the WASPAS method;
• Calculations and weights are determined using the Fuzzy TOPSIS method.

To compile aggregated multi-criteria metrics of information security, classical metrics of information security are needed. In this regard, it is necessary to select the best metrics from the presented areas of the ISO/IEC 27001 standard and assign them weight coefficients. For this, multi-criteria decision-making methods are applied, where expert assessment is used. In multi-criteria decision-making methods, the correct choice of evaluation criteria is very important.

In accordance with the current international information security management system standard ISO/IEC 27001, information security metrics are mandatory [5]. The standard identifies 14 areas of information security management [10]:

• Information security policy—aims to ensure compliance with information security policies;
• Organizational aspects of information security—includes the procedure for performing specific tasks and the distribution of responsibilities;
• Security of human resources—has the purpose of ensuring the responsibility of employees and their performance;
• Value management—includes the protection of information and information values;
• Access control—has the goal of ensuring that employees can only access information related to their immediate tasks. Extended access rights can be a serious threat to information security;
• Cryptography—aims to ensure data encryption and secure management of confidential information;
• Physical security—includes the security of the premises of the organization and the equipment that is stored in them;
• Operation security—one of the broadest areas, covering organization operations, the military–industrial complex, system backup, logging, software integration, technical vulnerability management and information systems audit;
• Communication security—includes the protection of information in computer networks;
• Acquisition, improvement and maintenance of systems—strives to ensure the importance of information security in the organization’s information systems;
• Relations with suppliers—includes the information security of the organization associated with third parties and partners of the organization;
• Information security incident management—defines the responsibilities of employees and an action plan during a security incident;
• Aspects of information security for business continuity management—includes management of business failures, ensuring the availability of information;
• Compliance with standards—ensures that organizations comply with laws and applicable information security standards.

Information security metrics are used to measure the effectiveness of processes occurring in the scope of all these areas. The specifics of the organization determine which program of metrics should be used. The work creates aggregated information security metrics for three management areas defined by the ISO/IEC 27001 standard: security of operations, security of communications and acquisition and improvement and maintenance of systems. These are the ones chosen since the work tends to focus more on the technical aspects of security. Aggregated metrics are also compiled by region by selecting classical information security metrics and then providing them with weighting coefficients.

Based on the scientific literature and business publications, information is provided on recommendations for security metrics and classical information security metrics are selected for each of the selected areas of information security management. From this list, classical metrics are directed to the selection of the best ones, which are included in the aggregated information security metrics. Classical security metrics in the field of security operations, metrics in the field of communications and in the field of management of acquisition and improvement and maintenance of information systems are shown in Table 6.

Table 6. Classical metrics of information security in the fields of operation, communication and information systems security, which are used to compile aggregated metrics, based on [36].

Metric	Description
Operation security: MPC or ensuring the integrity of the operating system
Incidents related to the MPC (pcs.)	Shows the number of all incidents related to the MPC
Malicious program code detected in the mail system (pcs.)	Displays the clogging of the email with the malicious program code of the email
Malicious program code detected on web pages visited by the user (pcs.)	Demonstrates the tendency of employees to visit web pages that distribute malicious code
Malicious program code files detected on the organization’s devices (including all the organization’s devices) (pcs.)	Indicates a malicious program code file found on the organization’s devices
Malicious program code files found on the organization’s servers (pcs.)	Indicates a malicious program code file found on the organization’s servers
Files of malicious program code found on the computers of employees of the organization (pcs.)	Indicates a malicious program code file found on employees’ computers
Incidents with malicious software code requiring mechanical cleaning of the system (pcs.)	Shows the threat posed by malicious code incidents, as well as the number of resources spent on cleaning systems affected by malicious code
Operation security: Vulnerability management
Vulnerability scanning software does not apply to systems (pcs.).	Identifies the degree of vulnerability of the scanning system
Several known vulnerabilities (pcs.)	Shows how many vulnerabilities there are in the organization’s information systems
Time spent on fixing the vulnerabilities (time)	Identifies the level of criticality of vulnerabilities and personnel training
The number of vulnerabilities detected per fixed unit of time (pcs.)	Identifies the effectiveness of the vulnerability scanning system and the overall security of systems
Operation security: Backup
The number of failures in the backup system, including copying and restoring data (pcs.)	Shows how often there are failures in the backup system
Lagging of the backup system from the default values associated with copying and resetting data (time)	Shows the delay in creating copies of data and restoring them
Operation security: Event monitoring
Logs of critical systems of the organization are not actively monitored or maintained (pcs.)	Identifies the effectiveness of the event monitoring system and the scale of monitoring of critical systems
Response time to critical messages from logging and monitoring systems (time)	Shows the speed of staff response to critical messages and the significance of generated messages
Communication security: Email system
Quantity of incoming emails (pcs.)	Regular tracking of email traffic
Quantity of detected spam (pcs.)	Shows the effectiveness of the email filtering system
Quantity of unidentified spam (pcs.)	Shows the effectiveness of the mail filtering system by the number of errors
Communication security: Firewall management
Firewall rule changes (pcs.)	Shows how often firewall rules are changed, created and deleted
Work resources required for firewall operation (time spent, hours)	Shows how long it takes to complete the firewall settings
Communication security: Session and traffic monitoring
Inputs (sessions) to the online servers and services of the organization (pcs.)	Shows the normal number of connections to the services provided by the organization and allows one to conclude as traffic grows
Network traffic of the organization (B)	Shows the average network traffic of the organization and allows one to conclude as traffic grows
Quantity of devices in the internal network of the enterprise (pcs.)	Reveals a potential threat; newly appeared devices can be used for attack purposes
Communication security: Network attacks (triggering firewall rules, IPS, IDS systems)
Quantity of network attacks (including successful and unsuccessful) (pcs.)	Shows how often an organization faces successful and unsuccessful hacker attacks
Quantity of successful network attacks (pcs.)	Shows how often an organization faces successful hacker attacks
MTTD network attacks (mean time to detect) (time)	Shows how quickly one manages to detect an attack on an organization’s computer network
MTTR network attacks (mean time to repair) (time)	Shows how quickly it is possible to correct the consequences of the attack that occurred
Quantity of incidents of external scanning of the organization’s network devices (pcs.)	Reveals the scale of scanning of the organization’s network devices and allows one to predict the number of future network attacks
Acquisition, improvement and maintenance of information systems: System configuration
Quantity of systems that do not correspond to a specific configuration (pcs.)	Identifies the effectiveness of the system configuration
Quantity of system configuration changes (pcs.)	Identifies the frequency of changes in system configurations
Quantity of configuration security tightening parameters for a specific system (pcs.)	Reveals the scope of application of tightening configuration settings
Acquisition, improvement and maintenance of information systems: System failures
System inactivity time, which includes planned and unplanned system inactivity (time)	Reveals the relationship between the operation and inactivity of systems, as well as the reliability
Unplanned system failure due to failures and malfunctions (time)	Shows how long the system can function properly without failures
MTBF (mean time between failures) of systems (time)	Reveals the reliability of systems
MTTR (mean time to repair) systems (time)	Reveals the significance of system failures and the ability of personnel to troubleshoot
Acquisition, improvement and maintenance of information systems: Management of system antivirus software
Computer workstations and servers without working antivirus software (pcs.)	Shows the number of workstations and servers unprotected by antivirus software (equipment may not be saved or disabled)
Computer workstations and servers without updated database lists of malicious anti-virus software code (pcs.)	Reveals the effectiveness of using antivirus software updates, preparing for threats of malicious software code
Acquisition, improvement and maintenance of information systems: Managing critical updates
Systems that have not received critical software updates (pcs.)	Shows the effectiveness of installing critical updates
Time required to install critical updates (time)	Shows the installation speed of critical updates
Delay in performing a critical security update (time)	Detects a lag in the implementation of critical updates from the planned schedule
Time allocated for testing critical updates (hours)	Shows how much time is spent testing critical updates

The field of operational security management includes several aspects [33]:

• Operations of the organization—ensuring that responsible persons properly carry out procedures;
• MPC—ensuring that the organization is prepared and aware of potential threats from the MPC;
• System backup—listing requirements related to system backup performance to prevent data loss;
• Logging and monitoring—allowing one to have documented evidence and a base for investigating security incidents;
• Ensuring the integrity of operating systems—ensuring the integrity of the software performing operations is carried out by managing the software recorded in the OS;
• Technical vulnerability management—ensuring that unauthorized persons do not exploit system vulnerabilities;
• Audit of information systems—aiming to minimize failures in auditing activities in the OS.

In order for the final aggregated metric to assess most aspects of the security zone of operations, an additional division into areas is carried out. The best one to two classical metrics are selected from each area by expert evaluation. To ensure operational security, the following areas are highlighted: the integrity of the PDA and OS, vulnerability management, backup and event monitoring.

The field of communication security management includes these aspects [37]:

• Network security management, aimed at ensuring the confidentiality, integrity and availability of information contained in networks;
• Security of the information transfer status.

In order for the resulting aggregated metric to evaluate most aspects of the communication security area, an additional division into areas is carried out. The best one or two classical metrics are selected from each area by expert evaluation. To ensure the security of communications, the following areas are highlighted: e-mail system, firewall management, session and traffic monitoring and network attacks.

It is worth noting that the task of compiling aggregated metrics requires the use of qualitative values. Consequently, AHP, WASPS and Fuzzy TOPSIS methods were selected from Table 5 as the research methodology. For this reason, two separate methods of solving the problem are used, as mentioned above.

For further study, it was decided to use the criteria that were defined in one of the scientific articles describing the quality of information security metrics [26]. The quality criteria of the most important metrics have been clarified and an expert assessment has already been applied (141 specialists). The most important classical metric criteria that are used in the study are correctness, ability to measure and significance [26].

The main purpose of the work is to obtain aggregated information security metrics, which consist of classical information security metrics with appropriate weighting coefficients. Often, at least two different solutions are used to solve problems using multi-criteria decision-making methods. The same principle is observed in this work. Two solutions are applied to solve this problem. The first application—the AHP method—results in weighting coefficients of the criteria and then these coefficients are applied to calculations using the MCDM method in the context of calculation using the MCDM WASPAS method. The second way to solve the MCDM problem is the Fuzzy TOPSIS.

3.2. TOPSIS Method for Obtaining Aggregated Metrics of Information Security

The solution to the problem, regardless of the MCDM method used, consists of four steps [38]. The idea of using the aggregated weighted sum assessment approach is based on the work of Turskis and Zavadskas [39].

First of all, a vector of the considered alternatives is formed, from which a rational alternative is selected [40]:

$$A=\left(A_1, A_2, \dots , A_i, \dots , A_m \right)$$

(1)

To compile aggregated information security metrics, experts selected 5 metrics out of 15 for 3 areas of information security management of the ISO/IEC 27001 standard. The selection of these metrics was carried out using a questionnaire among experts.

At the second stage, a vector of metrics is formed, according to which alternatives are evaluated:

$$X=\left(X_1, X_2, \dots , X_j, \dots , X_n \right)$$

(2)

The decision-making matrix X_[m×n] is formed in the form of a quantitative assessment of the i-th alternative by j-th metrics:

$$X_{\left[m\times n\right]}=\left(\begin{array}{c}\begin{array}{c}\begin{array}{cc}{x}_{11}& x_{12}\end{array} \begin{array}{cc}\cdots & x_{1n}\end{array}\\ \begin{array}{cc}{x}_{21}& x_{22}\end{array} \begin{array}{cc}\cdots & x_{2n}\end{array}\\ \begin{array}{cc}\cdots & \cdots \end{array} \begin{array}{cc}\cdots & \cdots \end{array}\end{array}\\ \begin{array}{cc}{x}_{m1}& x_{m2}\end{array} \begin{array}{cc}\cdots & x_{mn}\end{array}\end{array}\right)$$

(3)

Table 7 presents the selected classical information security metrics based on the results of an expert assessment of the three selected areas of information security management.

Table 7. Selected classical information security metrics based on the results of an expert assessment.

Operation Security Metrics	Communication Security Metrics	Acquisition, Improvement and Maintenance of Information Systems Metrics
Incidents related to malicious software code (pcs.)	Quantity of undetected spam (pcs.)	Quantity of configuration security tightening parameters for a specific system (pcs.)
Files of malicious software code found on the computers of employees of the organization (pcs.)	Changes to firewall rules (pcs.)	MTTR (mean time to repair) systems (time)
Time spent on fixing the vulnerability (time)	Logins (sessions) to online servers and services of the organization (pcs.)	Computer workstations and servers without working antivirus software (pcs.)
Quantity of failures in the backup system, including copying and restoring data (pcs.)	Quantity of network attacks (including successful and unsuccessful) (pcs.)	Systems that do not receive critical software updates (pcs.)
Response time to critical messages of logging and monitoring systems (time)	MTTR (mean time to repair) attacks (time)

In the third stage, the AHP method is applied to determine the weight criteria and the MCDM method for WASPAS.

In the last stage, the issue is solved by the Fuzzy TOPSIS method. The structure of the MCDM problem to be solved is defined in Table 8.

Table 8. Matrix of ranking solutions according to classical information security metrics.

	Criteria
	Correctness	Measurability	Meaningfulness
Alternatives	S1	S2	S3
1 metric	a11	a12	a13
2 metric	a21	a22	a23
3 metric	a31	a32	a33
4 metric	a41	a42	a43
5 metric	a51	a52	a53

The MCDM solution is explained by the hierarchical structure of the problem presented in Figure 1.

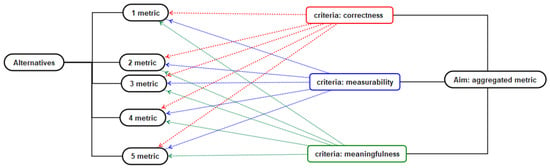
Figure 1. Compilation of aggregated metrics using MCDM. The hierarchical structure of the task.

3.3. Application of AHP to Determine the Weight of Criteria

Only some of the MCDM methods allow one to set criteria weights. One of them is the AHP method. This makes it possible to solve problems of various kinds by decomposing the problem into a hierarchical structure. AHP is used in various types of scientific work, from those aimed at choosing the best mobile phone [41] to scientific work that compares information security metrics used in companies [40]. The main calculations are performed by another MCDM method in the context of the current task, since the structure of the AHP method becomes too complex.

The solution to the problem of determining the weights of criteria by the AHP method consists of the following steps [38].

In the first stage, a vector of metrics is formed, from which alternatives are evaluated, as presented in Formula (2). Also, in this stage, we determine metrics that are used in the following research. Consequently, three abovementioned metrics are used [26].

In the second stage, we enter the values of metrics that are determined by specialists. Experts are asked to assess the significance of three qualitative criteria in the metric by assigning percentage values to criteria in accordance with the importance that determines the quality of the metric. This is carried out by applying the scale of evaluation of qualitative criteria proposed by the AHP method and creating a comparison matrix as presented in Table 9 [32].

Table 9. Matrix of paired comparison.

Criteria	K1	K2	K3	...	KN
K1	1	pp12	pp13	...	pp1N
K2	pp21	1	pp23	...	pp2N
K3	pp31	pp32	1	...	pp3N
...	...	...	...	...	...
KN	ppN1	ppN2	ppN3	...	1

Since qualitative criteria prevail in the problem under consideration, an expert assessment is applied. The expert evaluation is carried out using linguistic terms, which are then converted into numerical values based on Table 10 and Table 11. In the case of our problem that is being solved, this Table 9 reduces to Table 10.

Table 10. Matrix of paired comparison of qualitative, metrically characterizing criteria [32].

Criteria	Correctness	Measurability	Meaningfulness
Correctness	1	pp12	pp13
Measurability	pp21	1	pp23
Meaningfulness	pp31	pp32	1

Table 11. Scale of pairwise comparison of qualitative criteria of the AHP method [32].

Assessment (Rating)	Description of Assessment (Rating)	Explanation of the Assessment (Rating)
1	The importance of alternatives is equal	Both alternatives are the same for the criterion
3	Slightly superior to each other	According to the expert, the alternative is slightly superior to the other
5	An important advantage	According to the expert, the alternative is significantly superior to the other
7	A very important advantage	According to the expert, the alternative is very much superior to the other
9	An absolutely important advantage	According to the expert, the alternative is undoubtedly superior to the other
2, 4, 6, 8	Intermediate values	When compromise is needed
Assessment (rating)	Definition of assessment (rating)
1/2, 1/3, 1/4, 1/5 1/6, 1/7 1/8, 1/9	Reverse evaluation. If alternative i has been evaluated relative to alternative j using one of the above numbers n, the opposite alternative j will have a score of 1/n.

Thus, the expert solving the evaluation problem needs to determine the values of pp₁₂, pp₁₃ and pp₂₃ of the coefficients of paired comparison. The values of pp₂₁, pp₃₁ and pp₃₂ are reversed, so they are calculated pp₂₁ = 1/pp₁₂, pp₃₁ = 1/pp₁₃ and pp₃₂ = 1/pp₂₃. Table 11 shows a scale of pairwise comparison of the qualitative criteria of the AHP method.

Evaluation of pp₁₂, pp₁₃, pp₂₁, pp ₂₃, pp ₃₁ and pp₃₂ allows one to determine the weights for these criteria. This is performed with the help of special software [32]. Reference [42] uses the analytical hierarchy of SpiceLogic to process weak details. The obtained values of the criteria weights are used in further calculations performed by the WASPAS method.

Nevertheless, a new method MCDM WASPAS is considered to be quite accurate [43]. The WASPAS method consists of two methods: WSM and WPM.

Steps to configure the method WASPAS [43,44]:

• A decision-making matrix is formed, where the value of the i-th alternative is determined according to criterion j, m is the number of alternatives and n is the number of criteria. Since only qualitative criteria are used to evaluate information security metrics, an expert assessment is required. Linguistic descriptions are used for expert evaluation, which are converted into numerical values. The conversion is performed using Table 12. The weights of the criteria were obtained following the methodology described in the previous section (using the AHP method);
  Table 12. Conversion of linguistic characteristics of experts into numerical values, based on [43].

  Linguistic Term	The Numerical Value of the Criterion (Max)	The Numerical Value of the Criterion (Min)
  Very low (VL)	0	9
  Low (L)	1	7
  Below Average (BA)	2	5
  Average (A)	3	3
  Above Average (AA)	5	2
  High (H)	7	1
  Very high (VH)	9	0

• Normalization is performed using the following formulas [44]:
  Useful criterion:

  $${\overrightarrow{x}}_{ij}=\frac{x_{ij}}{ma{x}_{ij}{x}_{ij}}$$

  (4)
  Useless criterion:

  $${\overrightarrow{x}}_{ij}=\frac{mi{n}_{ij}{x}_{ij}}{x_{ij}}$$

  (5)

  Here, ${\overrightarrow{x}}_{ij}$ refers to the normalized value of $x_{ij}$;
• Calculation of the optimality criterion of the i-th alternative (the formula is based on the WSM method):

  $$Q_i^{\left(1\right)}={\displaystyle \sum }_{j=1}^n{\overrightarrow{X}}_{ij}{w}_j$$

  (6)

  where w_j is the weight of the j-th criterion;
• Calculation of the total relative importance (the formula is based on the WPM method):

  $$Q_i^{\left(2\right)}={\displaystyle \prod }_{j=1}^n{\left({\overrightarrow{X}}_{ij}\right)}^{w_j}$$

  (7)
• The combined generalized optimality criterion is calculated by the following formula:

  $$Q_i=0.5Q_i^{\left(1\right)}+0.5 Q_i^{\left(2\right)}$$

  (8)
• For a more generalized equation for calculating the optimality criterion, the value λ is entered. This allows one to achieve higher ranking accuracy [38]:

  $$Q_i=\lambda {\displaystyle \sum }_{j=1}^n{\overrightarrow{X}}_{ij}{w}_j+\left(1-\lambda \right){\displaystyle \prod }_{j=1}^n{\left({\overrightarrow{X}}_{ij}\right)}^{w_j}, \lambda =0, \dots , 1$$

  (9)
• Optimal values λ are calculated according to the following formula:

  $$\lambda =\frac{{\sigma }^2\left(Q_i^{\left(2\right)}\right)}{{\sigma }^2\left(Q_i^{\left(1\right)}\right)+{\sigma }^2\left(Q_i^{\left(2\right)}\right)}$$

  (10)
• Variations ${\sigma }^2\left(Q_i^{\left(1\right)}\right)$ or ${\sigma }^2\left(Q_i^{\left(2\right)}\right)$ are calculated by the following formula:

  $${\sigma }^2\left(Q_i^{\left(1\right)}\right)={\displaystyle \sum }_{j=1}^n{w}_j{}^2{\sigma }^2\left({\overrightarrow{X}}_{ij}\right){\overrightarrow{X}}_{ij}$$

  (11)

  $${\sigma }^2\left(Q_i^{\left(2\right)}\right)={\displaystyle \sum }_{j=1}^n{\left(\frac{{{\displaystyle \prod }}_{j=1}^n{\left({\overrightarrow{X}}_{ij}\right)}^{w_j}{w}_j}{{\left({\overrightarrow{X}}_{ij}\right)}^{w_j}{\left({\overrightarrow{X}}_{ij}\right)}^{\left(1-w_j\right)}}\right)}^2{\sigma }^2\left({\overrightarrow{X}}_{ij}\right)$$

  (12)
• Alternatives are sorted by priority row according to their utility values. From these values, an aggregated metric of information security is formed (according to Formula (1)). The resulting utility values are converted to a percentage expression and become weighting factors. The following formula is used for this:

  $$K_{a_i}=\frac{Q_i·100\%}{{{\displaystyle \sum }}_{i=1}^n{Q}_i}$$

  (13)

  where $K_{a_i}$ is the weighting factor for classical metrics in aggregated metrics; $Q_i$ is the optimality criterion of the i-th alternative; n is the number of alternatives.

The TOPSIS method is designed to solve problems in a certain environment when using quantitative quantities. To work in an uncertain environment, a method specifically designed by Fuzzy TOPSIS is usually used. The Fuzzy TOPSIS method is used to solve the problem in the following steps [45]:

1. The decision-making matrix is formed by X_{ij [m×n]}, where X_ij- is the value of the i-th alternative concerning criterion j, m is the number of alternatives and n is the number of criteria. Quantitative values are obtained using expert evaluation. Experts are asked to evaluate both quality criteria and alternatives to each criterion using linguistic terms. Linguistic terms are converted to numeric values using Table 13.

Table 13. Converting linguistic values to numeric values using the Fuzzy TOPSIS method (for ratings).

Linguistic Term	The Numeric Value Assigned to the Criteria	The Numeric Value Assigned to Alternatives
Very low (VL)	(0, 0, 0.1)	(0, 0, 1)
Low (L)	(0, 0.1, 0.3)	(0, 1, 3)
Below Average (BA)	(0.1, 0.3, 0.5)	(1, 3, 5)
Average (A)	(0.3, 0.5, 0.7)	(3, 5, 7)
Above Average (AA)	(0.5, 0.7, 0.9)	(5, 7, 9)
High (H)	(0.7, 0.9, 1.0)	(7, 9, 10)
Very high (VH)	(0.9, 1.0, 1.0)	(9, 10, 10)

2. Fuzzy decision matrix:

$$R={\left[r_{ij}\right]}_{m\times n}, i=1, 2, \dots , m;j=1, 2, \dots , n$$

(14)

Normalized values for useful and useless criteria are calculated using the following formulas:

Useful criterion:

$$r_{ij}=\left(\frac{a_{ij}}{c_j^{+}}, \frac{b_{ij}}{c_j^{+}},\frac{c_{ij}}{c_j^{+}}\right)$$

(15)

Useless criteria:

$$r_{ij}=\left(\frac{a_j}{c_{ij}}, \frac{a_j}{b_{ij}},\frac{a_j}{a_{ij}}\right)$$

(16)

Here, $c_j^{+}$ = max {c_ij} useful criteria or a_j = min {a_ij} useless criteria;

3. The constructed weighted normalized fuzzy decision-making matrix:

$$V={\left[v_{ij}\right]}_{m\times n}, i=1, 2, \dots , m;j=1, 2, \dots , n$$

(17)

Here, $v_{ij}=r_{ij}{w}_j$ and $w_j$= weight of j-th alternative;

4. Formulas for calculating positively ideal (FPIS, A+) and negatively ideal (FNIS, A−) solutions are determined:

$$A^{+}=\left(v_1^{+}, v_2^{+}, \dots , v_n^{+}\right)$$

(18)

$$A^{-}=\left(v_1^{-}, v_2^{-}, \dots , v_n^{-}\right)$$

(19)

Usually, scientific papers use two ways to determine the ideal:

In the first option, the ideal solution is defined as follows [45]:

Useful criteria: $A^{+}=\left(1,1,1,\dots , 1\right), A^{-}=\left(0, 0,0, \dots ,0\right)$;

Useless criteria: $A^{-}=\left(0,0,0,\dots , 0\right), A^{-}=\left(1, 1,1, \dots ,1\right)$.

In the second option, the ideal solution is defined as follows:

Useful criteria: $A^{+}=\left(ma{x}_j{v}_{ij}\left|j=1,2, \dots , m\right|\right),A^{-}=\left(mi{n}_j{v}_{ij}\left|j=1,2, \dots , m\right|\right)$.

In further calculations, the first option is used;

5. Calculating the distance between each alternative $A^{+}\left(d_i^{+}\right)$ and $A^{-}\left(d_i^{-}\right)$;

6. Distance calculation d (A, B):

$$d\left(A,B\right)=\sqrt{\frac{1}{3}({\left(a_1-a_2\right)}^2+{\left(b_1-b_2\right)}^2+{\left(c_1-c_2\right)}^2)}$$

(20)

7. The proximity coefficient of each alternative is calculated (CC_i):

$$C{C}_i=\frac{d_i^{-}}{d_i^{+}+d_i^{-}} , i=1,2, \dots , m$$

(21)

8. Alternatives are ranked using the resulting proximity coefficient values CC_i. The maximum value of the proximity coefficient means that the alternative is the most suitable;

9. Alternatives are sorted by priority row according to their utility values. From these values, an aggregated metric of information security is formed (according to Formula (1)). The resulting utility values are converted to a percentage expression and become weighting factors. The following formula is used for this:

$$K_{a_i}=\frac{C{C}_i·100\%}{{{\displaystyle \sum }}_{i=1}^{n}C{C}_i},$$

(22)

Here, K_ai is the weighting factor for classical metrics in aggregated metrics; CC_i is the proximity coefficient of the i-th alternative; n is the quantity of alternatives.

The full progress of the MCDM methods described above is described by the following diagram of the methodology for solving the problem, presented in Figure 2.

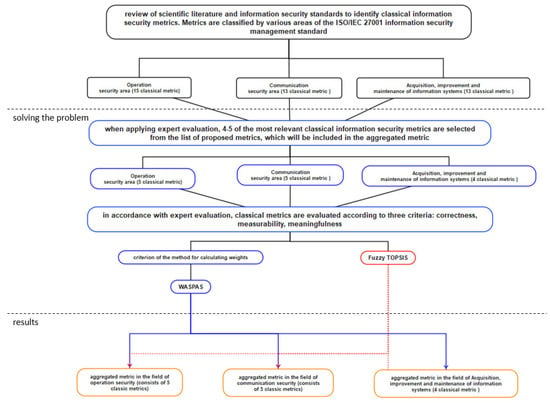
Figure 2. Methodology for solving the problem.

4. Application of MCDM and Expert Assessment on Aggregated Metrics of Information Security

4.1. Expert Assessment of Classical Metrics of Information Security

The accuracy of the expert assessment largely depends on the competence of the experts conducting the assessment. When solving multi-criteria tasks, the optimal group size is from 8 to 10 experts. According to [46], three expert quantities are allocated as the minimum recommended group size. In the current study, the expert group consists of 20 specialists working in the field of information security or engaged in scientific activities. Seven experts participate in the first round of the study and ten more experts participate in the second round. The remaining three experts carried out part of the verification of the metrics. The experts at the second and first stages are different. Equal weights are used for expert assessments.

The expert assessment is carried out according to the progress of the work described in Section 2 of this article. Each expert receives identical questions. The maximum number of possible answers in the questionnaire is eight and they are indicated by symbols from the letter a to h. It should be noted that in questions 1 and 8, experts need to choose two answers. Based on the results of the experts’ responses to the questionnaire, the most suitable four to five information security metrics are selected. These metrics are included in aggregated information security metrics. The results of the selection of classical information security metrics of experts are presented in Table 14.

Table 14. Expert answers to the questionnaire.

	Question Number
Experts	1	2	3	4	5	6	7	8	9	10	11	12
E1	e, f	c	b	a	b	a	a	b, d	c	b	a	a
E2	a, d	a	a	a	c	b	b	a, c	c	d	b	a
E3	b, f	d	a	b	b	a	a	a, e	b	b	a	a
E4	a, f	c	a	a	c	a	b	a, c	a	c	a	c
E5	a, d	c	b	b	b	a	a	c, d	a	d	b	a
E6	a, e	b	a	b	c	b	a	a, b	c	d	b	c
E7	a, g	b	a	b	c	a	a	a, c	b	d	a	a

Based on the expert responses presented in Table 14, classical information security metrics are compiled, which are included in the aggregated metrics. The selected classical information security metrics for three areas with assigned symbolic designations are presented in Table 15.

Table 15. Symbolic designations of classical metrics.

Area	Metrics	Designation
Operation security	1. Incidents related to the MPC (pcs.)	A1
	2. Files of malicious program code found on the computers of employees of the organization (pcs.)	A2
	3. Time spent fixing the vulnerability (time)	A3
	4. Quantity of failures in the backup system, including copying and restoring data (pcs.)	A4
	5. Response time to critical messages from logging and monitoring systems (time)	A5
Communication security	1. The amount of undetected spam (pcs.)	A1
	2. Firewall rule changes (pcs.)	A2
	3. Logins (sessions) to the organization’s online servers and services (pcs.)	A3
	4. Number of network attacks (including successful and unsuccessful) (pcs.)	A4
	5. MTTR (mean time to repair) attacks (time)	A5
System security	1. Number of configuration security tightening parameters for a specific system (pcs.)	A1
	2. MTTR (mean time to repair) system (time)	A2
	3. Computer workstations and servers without working antivirus software (pcs.)	A3
	4. Systems that do not receive critical software updates (pcs.)	A4

At the next stage, experts are invited to evaluate the criteria characterizing the indicators to determine the weighting factors of the criteria. Experts are invited to perform this task twice, using the AHP and Fuzzy TOPSIS methods. Consequently, Table 16 presents the results of the assessment of criteria by the AHP method. In Table 16, E is expert number x, C is correctness, M is measurability, S is significance and G is generalized assessment.

Table 16. Results of the assessment of criteria by the AHP method.

E 1	C	M	S	E 2	C	M	S	E 3	C	M	S
C	1	5	1/8	C	1	8	1/7	C	1	5	1
M	1/5	1	1/9	M	1/8	1	1/8	M	1/5	1	1/7
S	8	9	1	S	7	8	1	S	1	7	1
E 4	C	M	S	E 5	C	M	S	E 6	C	M	S
C	1	5	1	C	1	9	7	C	1	3	½
M	1/5	1	1	M	1/9	1	1/8	M	1/3	1	½
S	1	1	1	S	1/7	8	1	S	2	2	1
E 7	C	M	S	E 8	C	M	S	G	C	M	S
C	1	3	1/2	C	1	7	1/8	C	1	5.24	0.5
M	1/3	1	1/4	M	1/7	1	1/8	M	0.19	1	0.21
S	2	4	1	S	8	8	1	S	2	4.75	1

The calculations are performed using special software SpiceLogic Analytical Hierarchy Process Software and Excel [42]. Ten experts responded to the questionnaire, but the estimates submitted by two experts were rejected because their estimates were very contradictory. The selection of ratings is carried out by consistency ratio. When using the AHP method, it is stated that the compatibility rating of the assessments submitted by experts should not exceed 10% [47]. In the present case, the generalized compatibility rating was equal to 7.3% of what is considered a satisfactory size, so the assessment can be considered correct. Another size that is proposed to be calculated is the consensus rating, which, in the existing case, is 75.4%, which means that the consensus of experts when making this decision is “high” [42]. Thus, summing up the assessments of all experts, we obtain the weighting coefficients of the quality criteria of classical information security metrics correctness—35.9%; measurement capability—8.9%; significance—55.2%. The results of experts’ assessment of criteria by the AHP method are presented in Figure 3.

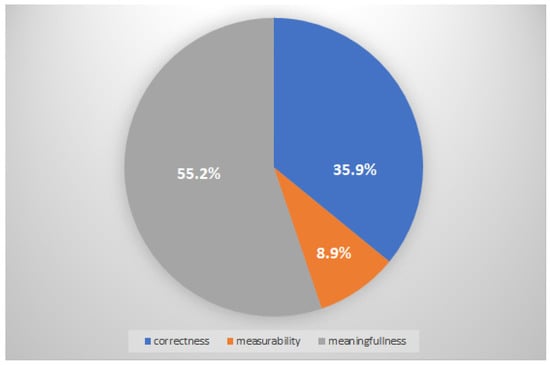
Figure 3. The results of experts’ assessment of criteria by the AHP method.

Further evaluation of the criteria was carried out using the Fuzzy TOPSIS method. Table 17 presents the results of an expert assessment of quality criteria by the Fuzzy TOPSIS method. In Table 17, E refers to expert number x, C is correctness, M is measurability and S is significance. Linguistic terms are used in the evaluation, the numerical values of which are presented in Table 14. The results of the expert evaluation presented in Table 16 and Table 17 are used in further calculations.

Table 17. The results of an expert assessment of quality criteria by the Fuzzy TOPSIS method.

	Experts
Criteria	E1	E2	E3	E4	E5	E6	E7	E8	E9	E10
C	H	VH	VH	VH	H	H	VH	H	H	AA
M	A	H	A	AA	AA	VH	VH	AA	AA	BA
S	VH	VH	VH	H	VH	H	H	VH	VH	H

In the third stage of the study, experts evaluate the selected classical indicators of information security in accordance with the specified quality criteria. Also, further calculations are carried out by the methods of WASPAS and Fuzzy TOPSIS.

4.1.1. WASPAS

Calculations are carried out by WASPAS using Formulas (4)–(13). Three decision-making matrices are formed, in which the average values of all estimates submitted by experts are calculated. The results of the calculations are presented in Table 18.

Table 18. Decision-making matrices (WASPAS).

Operation Security				Communication Security				Systems Security
	C	M	S		C	M	S		C	M	S
A1	5.3	6.2	5	A1	3.8	3.7	3.9	A1	5.6	6.1	6.8
A2	5.7	6.7	5.7	A2	5.2	6.5	4.9	A2	6.3	6	7.6
A3	5.9	5.3	4.8	A3	5.8	6	4.9	A3	6.8	8	6.6
A4	5.4	4.4	4.9	A4	5.5	6.2	7	A4	6.6	7	7
A5	6.3	6.9	6.8	A5	5.5	6.2	6.6	A5	-	-	-

Normalization of the matrix is performed according to Formulas (4)–(6). The normalization results are presented in Table 19.

Table 19. Normalized decision matrices (WASPAS).

Operation Security				Communication Security				Systems Security
	C	M	S		C	M	S		C	M	S
A1	0.84	0.90	0.74	A1	0.66	0.57	0.56	A1	0.82	0.76	0.89
A2	0.91	0.97	0.84	A2	0.90	1.00	0.70	A2	0.93	0.75	1.00
A3	0.94	0.77	0.71	A3	1.00	0.92	0.70	A3	1.00	1.00	0.87
A4	0.86	0.64	0.72	A4	0.95	0.95	1.00	A4	0.97	0.88	0.92
A5	1	1	1	A5	0.95	0.95	0.94	A5	-	-	-

The first optimality criterion is calculated using Formula (6). The values of the first optimality criterion are presented in Table 20.

Table 20. Values of the first optimality criterion (WASPAS).

	A1	A2	A3	A4	A5
Operation security Q(1)	0.79	0.87	0.79	0.76	1
Communication security Q(1)	0.59	0.80	0.83	0.98	0.95
System security Q(1)	0.86	0.95	0.93	0.93	-

The second optimality criterion is calculated using Formula (7). The values of the second optimality criterion are presented in Table 21.

Table 21. Values of the second optimality criterion (WASPAS).

	A1	A2	A3	A4	A5
Operation security Q(2)	0.79	0.87	0.79	0.76	1
Communication security Q(2)	0.59	0.79	0.82	0.98	0.95
System security Q(2)	0.86	0.95	0.93	0.93	-

Therefore, the calculation of the general optimality criterion using Formula (8), as well as using Formula (13), gives the weight of the classical metric in the aggregated metric. The value of the general optimality criterion and the weight of classical metrics in the aggregated metrics are presented in Table 22.

Table 22. The value of the general optimality criterion and the weight of classical metrics in the aggregated metric (WASPAS).

	Value	A1	A2	A3	A4	A5
Operation security	Qgeneral	0.79	0.87	0.79	0.76	1
	Ratio	4	2	3	5	1
	Kai	18.68	20.74	18.78	18.06	23.75
Communication security	Qgeneral	0.59	0.79	0.82	0.98	0.95
	Ratio	5	4	3	1	2
	Kai	14.35	19.21	19.89	23.66	22.90
System security	Qgeneral	0.86	0.95	0.93	0.94	-
	Ratio	4	1	3	2	-
	Kai	23.36	25.90	25.26	25.48	-

4.1.2. Fuzzy TOPSIS

When using the Fuzzy TOPSIS method, the initial decision-making matrices are also formed. The decision-making matrix for the Fuzzy TOPSIS method is presented in Table 23.

Table 23. The decision-making matrix for the Fuzzy TOPSIS method.

Operation Security				Communication Security				Systems Security
	C	M	S		C	M	S		C	M	S
A1	[1,7,10]	[1,7.8,10]	[1,6.6,10]	A1	[0,5.1,10]	[0,5.1,10]	[0,5.4,10]	A1	[0,6.9,10]	[0,7.5,10]	[3,8.5,10]
A2	[0,7.2,10]	[1,8.2,10]	[0,7.2,10]	A2	[0,6.4,10]	[1,8.1,10]	[0,6,10]	A2	[1,7.9,10]	[1,7.7,10]	[5,9.1,10]
A3	[1,7.6,10]	[0,6.6,10]	[3,6.7,10]	A3	[1,7.4,10]	[1,7.5,10]	[0,6.2,10]	A3	[3,8.3,10]	[5,9.4,10]	[1,7.9,10]
A4	[0,6.7,10]	[0,5.5,10]	[1,6.5,10]	A4	[1,7.1,10]	[3,7.9,10]	[0,8.2,10]	A4	[3,8.3,10]	[3,8.6,10]	[3,8.7,10]
A5	[1,7.9,10]	[1,8.3,10]	[5,8.5,10]	A5	[1,7.1,10]	[0,7.6,10]	[3,8.2,10]	A5	-	-	-

Normalization of the decision-making matrix using Formulas (15) and (16) is also carried out. The normalization results are presented in Table 24.

Table 24. The normalization of the decision-making matrix.

	Operation Security				Communication Security				Systems Security
	C	M	S		C	M	S		C	M	S
A1	[0.1,0.7,1]	[0.1,0.78,1]	[0.1,0.66,1]	A1	[0,0.51,1]	[0,0.51,1]	[0,0.54,1]	A1	[0,0.69,1]	[0,0.75,1]	[0.3,0.85,1]
A2	[0,0.72,1]	[0.1,0.82,1]	[0,0.72,1]	A2	[0,0.64,1]	[0.1,0.81,1]	[0,0.6,1]	A2	[0.1,0.79,1]	[0.1,0.77,1]	[0.5,0.91,1]
A3	[0.1,0.76,1]	[0,0.66,1]	[0.3,0.67,1]	A3	[0.1,0.74,1]	[0.1,0.75,1]	[0,0.62,1]	A3	[0.3,0.83,1]	[0.5,0.94,1]	[0.1,0.79,1]
A4	[0,0.67,1]	[0,0.55,1]	[0.1,0.65,1]	A4	[0.1,0.71,1]	[0.3,0.79,1]	[0,0.82,1]	A4	[0.3,0.83,1]	[0.3,0.86,1]	[0.3,0.87,1]
A5	[0.1,0.79,1]	[0.1,0.83,1]	[0.5,0.85,1]	A5	[0.1,0.71,1]	[0,0.76,1]	[0.3,0.82,1]	A5	-	-	-

The weighted normalized decision-making matrix is used by Formula (17). The results of the calculations are presented in Table 25.

Table 25. Weighted normalized decision-making matrix (Fuzzy TOPSIS).

Operation Security				Communication Security			Systems Security
	C	M	S	C	M	S	C	M	S
A1	[0.05,0.644,1]	[0.01,0.546,1]	[0.07,0.634,1]	[0,0.469,1]	[0,0.357,1]	[0,0.518,1]	[0,0.635,1]	[0,0.525,1]	[0.21,0.816,1]
A1	[0,0.663,1]	[0.01,0.574,1]	[0,0.691,1]	[0,0.588,1]	[0.01,0.567,1]	[0,0.576,1]	[0.050,0.727,1]	[0.01,0.539,1]	[0.35,0.874,1]
A3	[0.05,0.699,1]	[0,0.462,1]	[0.21,0.643,1]	[0.05,0.680,1]	[0.01,0.525,1]	[0,0.595,1]	[0.15,0.761,1]	[0.05,0.658,1]	[0.070,0.758,1]
A4	[0,0.616,1]	[0,0.385,1]	[0.07,0.624,1]	[0.05,0.653,1]	[0.03,0.553,1]	[0,0.787,1]	[0.15,0.764,1]	[0.03,0.602,1]	[0.21,0.835,1]
A5	[0.05,0.727,1]	[0.01,0.581,1]	[0.35,0.816,1]	[0.05,0.653,1]	[0,0.532,1]	[0.21,0.787,1]	-	-	-

Consequently, the positively ideal (FPIS, A+) and negatively ideal (FNIS, A−) values of alternatives are calculated according to Formulas (18) and (19). The calculation results are presented in Table 26.

Table 26. The positively ideal (FPIS, A+) and negatively ideal (FNIS, A−) values of alternatives (Fuzzy TOPSIS).

	Value	A1	A1	A3	A4	A5
Operation, communication and system security	A+	1	1	1	1	1
	A−	0	0	0	0	0

After carrying out all the procedures, the relative distances, the distances to the ideal alternative and the weights of the classical indicators in the aggregated indicators are calculated according to Formulas (20)–(24). Results of calculations performed are shown in Table 27.

Table 27. Relative distances, distances to the ideal alternative and weights of classical metrics in aggregated metrics (Fuzzy TOPSIS).

	Value	A1	A1	A3	A4	A5
Operation security	$d_i^{+}$	1.79	1.84	1.73	1.88	1.58
	$d_i^{-}$	2.03	2.06	2.04	1.98	2.16
	$C{C}_i$	0.53	0.53	0.54	0.51	0.58
	$K_{a_i}$	19.74	19.65	20.09	19.08	21.43
Communication security	$d_i^{+}$	1.98	1.88	1.84	1.79	1.69
	$d_i^{-}$	1.90	2.00	2.02	2.08	2.09
	$C{C}_i$	0.49	0.52	0.52	0.54	0.55
	$K_{a_i}$	18.69	19.70	20.01	20.53	21.08
System security	$d_i^{+}$	1.72	1.58	1.65	1.58	-
	$d_i^{-}$	2.09	2.16	2.15	2.17	-
	$C{C}_i$	0.55	0.58	0.57	0.58	-
	$K_{a_i}$	24.16	25.43	24.94	25.47	-

After the calculations by the methods of WASPAS and Fuzzy TOPSIS, the weight coefficients of the metrics are obtained. The weight coefficients obtained by different methods are presented in Table 28.

Table 28. Values of classical metrics obtained by various methods of solving the problem in aggregated metrics.

	Areas of Information Security Management
Classical Metrics	Operation Security		Communication Security		System Security
	WASPAS	Fuzzy TOPSIS	WASPAS	Fuzzy TOPSIS	WASPAS	Fuzzy TOPSIS
A1	18.68	19.74	14.35	18.69	23.36	24.16
A2	20.74	19.65	19.21	19.70	25.90	25.43
A3	18.78	20.09	19.89	20.01	25.26	24.94
A4	18.06	19.08	23.66	20.53	25.48	25.47
A5	23.75	21.43	22.90	21.08	-	-

Based on the results obtained by various methods of solving the problem, bar charts are constructed representing the weights of classical metrics in the aggregated metric. The weighting coefficients of the classical metrics of operations security in the aggregated metric are obtained by various methods of solving the problem are presented in Figure 4.

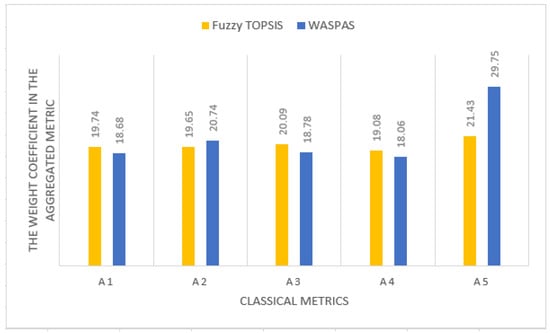
Figure 4. The weighting coefficients of the classical metrics of operations security in the aggregated metric, as obtained by various methods of solving the problem.

The weighting coefficients of the classical metrics of communication security in the aggregated metric are obtained by various methods of solving the problem, as presented in Figure 5.

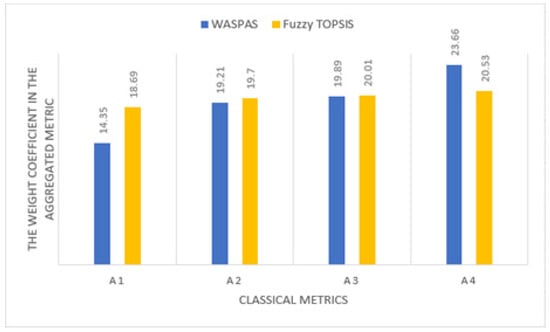
Figure 5. The weighting coefficients of the classical metrics of communication security in the aggregated metric, as obtained by various methods of solving the problem.

The weighting coefficients of the classical metrics of the security of the acquisition, development and maintenance of information systems in the aggregated metric are obtained by various methods of solving the problem, as presented in Figure 6.

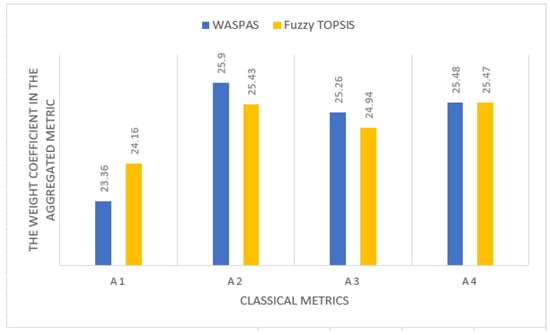
Figure 6. The weighting coefficients of the classical metrics of the security of the acquisition, development and maintenance of information systems in the aggregated metrics, as obtained by various methods of solving the problem.

The values of the weighting coefficients for the classical metrics obtained by two different ways of solving the problem were somewhat different. This was due to the differences between the WASPAS and Fuzzy TOPSIS methods and some computational features. The weight of the quality criteria differed in the calculation by different methods and the Fuzzy TOPSIS method was also used, which is considered not very suitable if there are large differences between the estimates of alternatives [35]. In the Fuzzy TOPSIS computational method, two variants of the ideal solution can be used; this choice can strongly affect the final answers. Based on the obtained coefficients of metrics and the convenience of the methods, it can be concluded that the MCDM WASPAS method is more suitable for solving the existing problem.

With the weight coefficients and average event numbers of classical metrics, we can calculate the aggregated metric. We do this by proposing a formula that can be used to calculate aggregated metrics:

$$f=\frac{{{\displaystyle \sum }}_{i=1}^n\left(\frac{a_i}{N_{a_i}}{K}_{a_i}\right)}{n}-\frac{1}{n}$$

(23)

Here, $f$ refers to an aggregated metric of real-time, $a_i$ is the number of events in the classical metric in real time, $N_{a_i}$ is the provision value (set tolerable number of events), $K_{a_i}$ is the i-th weight factor for each classical metric and n is the number of classical metrics forming multicriteria of aggregated metrics.

It should be noted that when applying this formula, the weight coefficients of classical metrics must be 100%:

$${\displaystyle \sum }_{i=1}^n\left(K_{a_i}\right)$$

(24)

With weight coefficients, three formulas for calculating aggregated information security metrics are formed, which we designate with symbols A_operations, A_{communications}, A_systems. Weight coefficients are used for calculations in the WASPAS method. Formulas are compiled using Formula (23):

$$A_{operation}=\frac{\frac{a_1}{N_{a_1}}·0.187+\frac{a_2}{N_{a_2}}·0.207+\frac{a_3}{N_{a_3}}·0.188+\frac{a_4}{N_{a_4}}·0.181+\frac{a_5}{N_{a_5}}·0.238}{5}-\frac{1}{5}$$

(25)

$$A_{communication}=\frac{\frac{b_1}{N_{b_1}}·0.144+\frac{b_2}{N_{b_2}}·0.192+\frac{b_3}{N_{b_3}}·0.199+\frac{b_4}{N_{b_4}}·0.237+\frac{b_5}{N_{b_5}}·0.229}{5}-\frac{1}{5}$$

(26)

$$A_{system}=\frac{\frac{c_1}{N_{c_1}}·0.234+\frac{c_2}{N_{c_2}}·0.259+\frac{c_3}{N_{c_3}}·0.253+\frac{c_4}{N_{c_4}}·0.255}{4}-\frac{1}{4}$$

(27)

The values $N_{x_1}, N_{x_2}, N_{x_3}, N_{x_4}, N_{x_5}$ are relevant to the average values of the metrics set by the organization. These values should be constantly reviewed and adjusted in accordance with the current state of the organization. The values a₁–a₅, b₁–b₅, c₁–c₄ rely on the values of the classical metrics (converted to a percentage expression).

It should be emphasized that the formulas for calculating these aggregated metrics are indicative. Therefore, when using aggregated indicators in practice, the formulas for calculating the final values should be adapted to individual needs. Aggregated metrics can make it possible to monitor the information security situation in the organization more effectively, to form a generalized picture. In comparison with classical information security metrics, aggregated metrics allow us to save resources spent on the process of monitoring the information security situation and the data can also serve to inform the management of the organization.

5. Discussion

In order to verify the compatibility of the criteria and alternatives presented by experts, we use the concordance coefficient, which characterizes whether the opinions of experts on the significance of the metrics are sufficiently coordinated [43]. The concordance factor is also known as Kendall’s concordance factor (W). Kendall’s compliance coefficient varies from 0 to 1. A value of 0 will mean complete incompatibility (estimates given by experts are random) and 1 means full compatibility (estimates given by experts are the same).

$${\chi }^2=\frac{12·S}{m·n·\left(n+1\right)}$$

(28)

Further, for all opinions submitted by experts, the significance values of the compliance coefficient are calculated (according to Formula (28)). The answers received are presented in Table 29.

Table 29. Expert assessment compatibility calculations.

	n	W	${\mathit{\chi }}^2$	${\mathit{\chi }}_{\mathit{k}\mathit{r}}^2$ (v = n − 1, α = 0.05)	The Opinion is Considered to Be in Agreement If  ${\mathit{\chi }}^2>{\mathit{\chi }}_{\mathit{k}\mathit{r}}^2$
Assessment of metric quality criteria for the method Fuzzy TOPSIS	3	0.360	7.20	5.991	Yes
Assessment of operational security metrics	15	0.182	25.52	23.685	Yes
Assessment of communication security metrics	15	0.282	39.44	23.685	Yes
Assessment of information system security metrics	12	0.307	33.80	19.675	Yes
Overall assessment of all responses	45	0.294	129.18	60.481	Yes

The values obtained are shown in the bar chart in Figure 7.

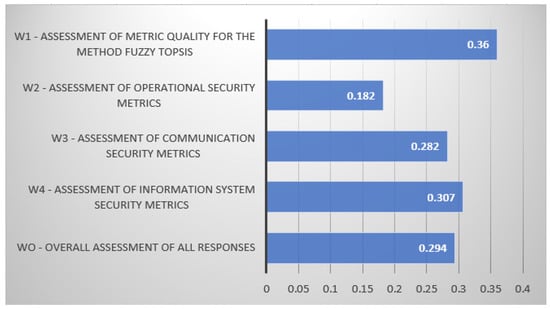
Figure 7. Kendall’s W compliance coefficients calculated for various areas of expert evaluation.

The calculated values of the compliance coefficient χ² confirm that the opinions of experts on all issues are agreed upon. The obtained values of the correspondence coefficient W should be interpreted based on the specifics of each problem. There are no established specific cracks that would state whether a certain coefficient value is acceptable or not. This coefficient can be applied to the rejection of certain expert opinions. This would allow for greater compatibility of opinions but, when solving the existing problem, this practice is decided to not be observed.

An experiment is also conducted to verify the obtained aggregated information security metrics. The essence of the verification experiment is to test the effectiveness of aggregated information security metrics when they are used in practice. The purpose of the experiment is to compare the advantages and disadvantages of classical and aggregated metrics in a situation when a monthly report on information security is being prepared.

The experiment simulates two scenarios:

• Preparation of a monthly information security report using only classical information security metrics;
• Preparation of a monthly report on information security using aggregated information security metrics.

A monthly report on information security will be presented to the management of the organization, which will be prepared by information security specialists. In this case, an expert assessment will be used to perform this task. The study involved three experts from the Corporate Security Department of «Kazakhstantemirzholy» JSC, who had to perform identical tasks: prepare reports on information security in two given scenarios. Later, the experts were asked to answer questions from the questionnaire. The initial data of the verification experiment for the preparation of the report (data from classical metrics) are presented in Figure 8.

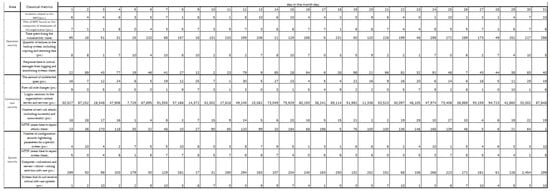
Figure 8. The initial data of the verification experiment for the preparation of the report (data from classical metrics).

The initial data of the verification experiment for the preparation of the report (data from aggregated metrics) are presented in Figure 9.

Figure 9. The initial data of the verification experiment for the preparation of the report (data from aggregated metrics).

The data are generated using the RANDBETWEEN function in Excel, indicating the minimum and maximum possible values (so that the possible value was logical).

The experiment is aimed at clarifying the results according to the main criteria for the preparation and presentation of the report:

• Report preparation time—shows how long it takes to prepare the report;
• Convenience of report preparation—quantifies quick or convenient report preparation;
• Readability of the results—shows to what extent the results obtained are easily understandable. It should also be borne in mind that the results can be presented to management without an engineering or technical education;
• Significance of the results—shows to what extent the results obtained are significant and allow one to rely on the organization’s decisions on information security;
• Quality of the report—shows how well the report describes the organization’s assistance in the field of security.

Based on these criteria, questions are compiled to compare the process of preparing a report using classical and aggregated metrics. The questionnaire consisted of five questions and the scale of answers ranged from −5 to 5. Here, −5 denotes the effectiveness of using classical metrics and 5 denotes the effectiveness of aggregated metrics. In turn, 0 is an equal value and −4, −3, −2, −1, 1, 2, 3 and 4 are intermediate values. Below are the answers given by experts to the questionnaire questions (Table 30).

Table 30. Expert responses to the questionnaire of the test experiment.

	Number of Questions
Expert	1	2	3	4	5
E1	5	5	0	0	0
E2	2	5	5	0	0
E3	4	4	0	−2	0

Consequently, the average values of these responses are calculated and the histogram shown in Figure 10 is constructed.

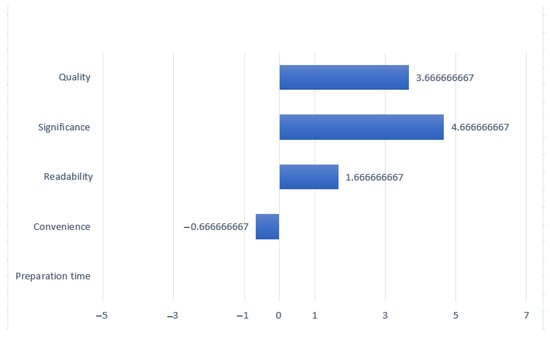
Figure 10. Results of comparison of the use of aggregated and classical metrics.

Three experts participated in the experiment, which was conducted to verify the obtained aggregated information security metrics. After the verification of the use of aggregated metrics was completed, a survey was conducted among experts regarding the effectiveness of the proposed aggregated metric. All three experts pointed out that the preparation of the report using aggregated metrics took less time and was convenient when preparing the report. Two experts pointed out that the results of the report using classical and aggregated metrics were understandable. Also, all experts indicated that the quality of the report from the use of different metrics had not changed.

According to the answers given by experts, it can be said that the preparation of a report using aggregated metrics is more convenient, faster and achieves higher intelligibility. The materiality of the report suffers somewhat and the quality of the aggregated metrics remains unchanged.

6. Conclusions

In the era of digitalization, ensuring the necessary level of information security for any organization depends on the proper choice of an assessment method, which ensures the sustainable functioning of information and communication infrastructure facilities. In turn, the sustainable functioning of information and communication infrastructure facilities of any country affects the sustainability of national security. However, the number of threats to national security has increased significantly due to the pandemic situation all over the world. In this regard, timely identification of threats to information security compromising national security will ensure the cyber sustainability of each country.

Therefore, after analyzing the literature, it was noticed that most scientific articles are aimed at evaluating information security metrics but not at improving them. The purpose of this article was to improve information security metrics. To achieve the goal, it was decided to propose aggregated information security metrics, which consisted of classical information security metrics, including weighting coefficients describing their importance.

In the course of the work, a methodology for constructing aggregated information security metrics was developed. The compilation of aggregated metrics was carried out based on the areas of the information security management standard ISO/IEC 27001. In the compiled methodology, two methods of solving the problem were applied. Based on the obtained metric coefficients and the convenience of the methods, it was concluded that the MCDM method was more suitable for solving the existing problem.

At the first stage of the study, 14 classical metrics of information security were selected for aggregated metrics. This stage of the study revealed the conclusion of the expert opinion—the most suitable 14 classical metrics. In the second stage of the study, 14 information security metrics were evaluated according to 3 quality criteria. Using two methods to solve the problem, the weights of classical metrics were calculated using various MCDM methods and aggregated metrics were proposed. The values of the weighting coefficients of classical metrics obtained by two different methods of solving the problem were somewhat different. This was due to differences in the methods of the WASPAS and Fuzzy TOPSIS methods, as well as some calculation features. The weights of the quality criteria were different in the calculation method and the Fuzzy TOPSIS method was used, which is considered not very suitable when there are significant differences between alternative estimates [31]. In the Fuzzy TOPSIS calculation method, two variants of the ideal solution can be used; however, this choice can greatly affect the final answers. Sensitivity analysis was not performed in this study. However, we relied on previously conducted sensitivity analyses in [48,49,50,51].

In order to confirm the fulfilment of the task of improving information security metrics, a verification experiment was conducted, during which aggregated and classical information security metrics were compared. The experiment showed that the use of aggregated metrics can be a more convenient and faster process and higher intelligibility is also achieved. The materiality of the results suffers somewhat and the quality when using aggregated metrics remains unchanged compared to the classical ones.