Machine Learning Supervisory Control of Grid-Forming Inverters in Islanded Mode
Abstract
1. Introduction
2. System Modelling and Configuration
2.1. Dynamic Model
2.2. Control Unit
2.2.1. Droop Control
2.2.2. Voltage Control
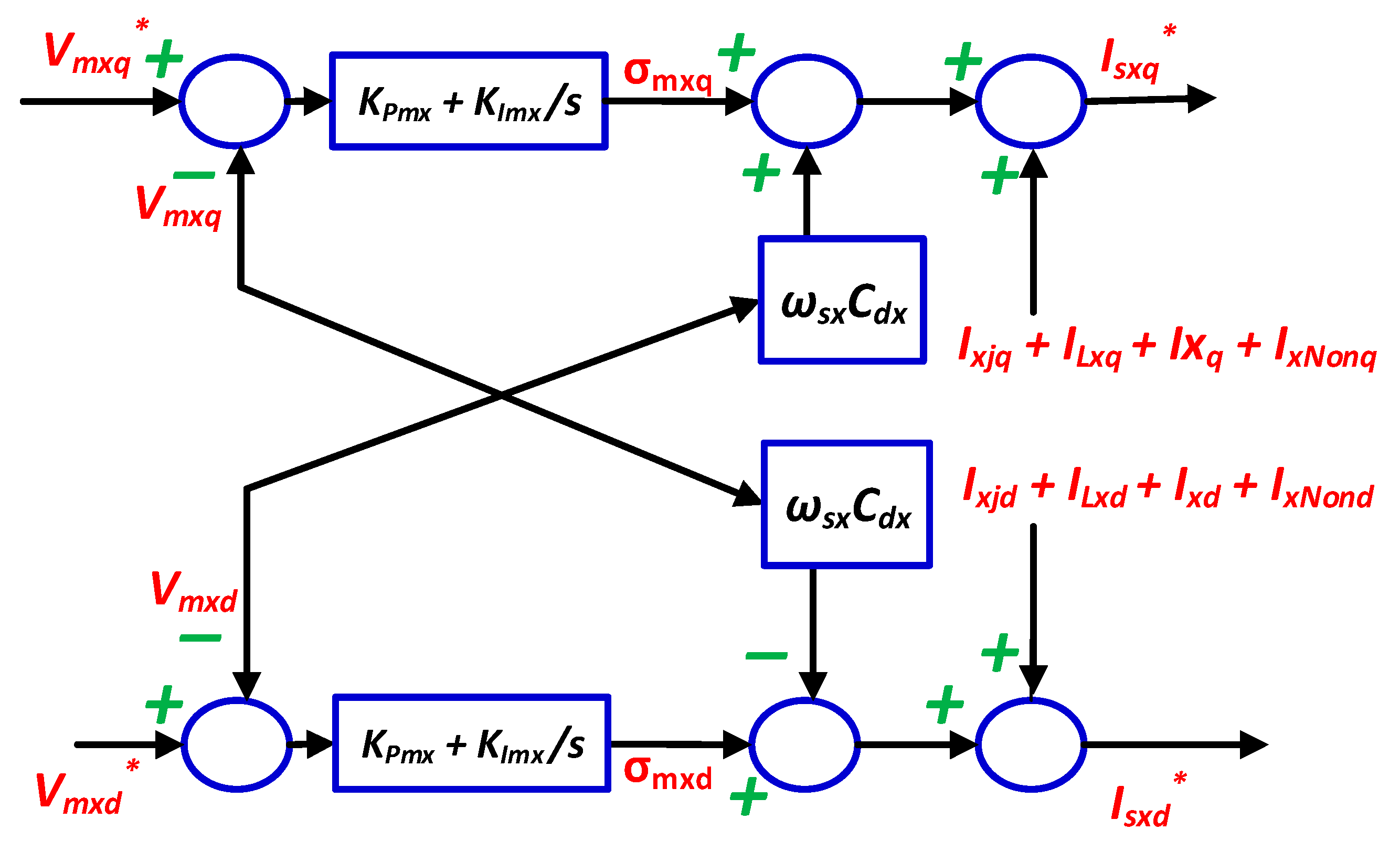
2.2.3. Current Control
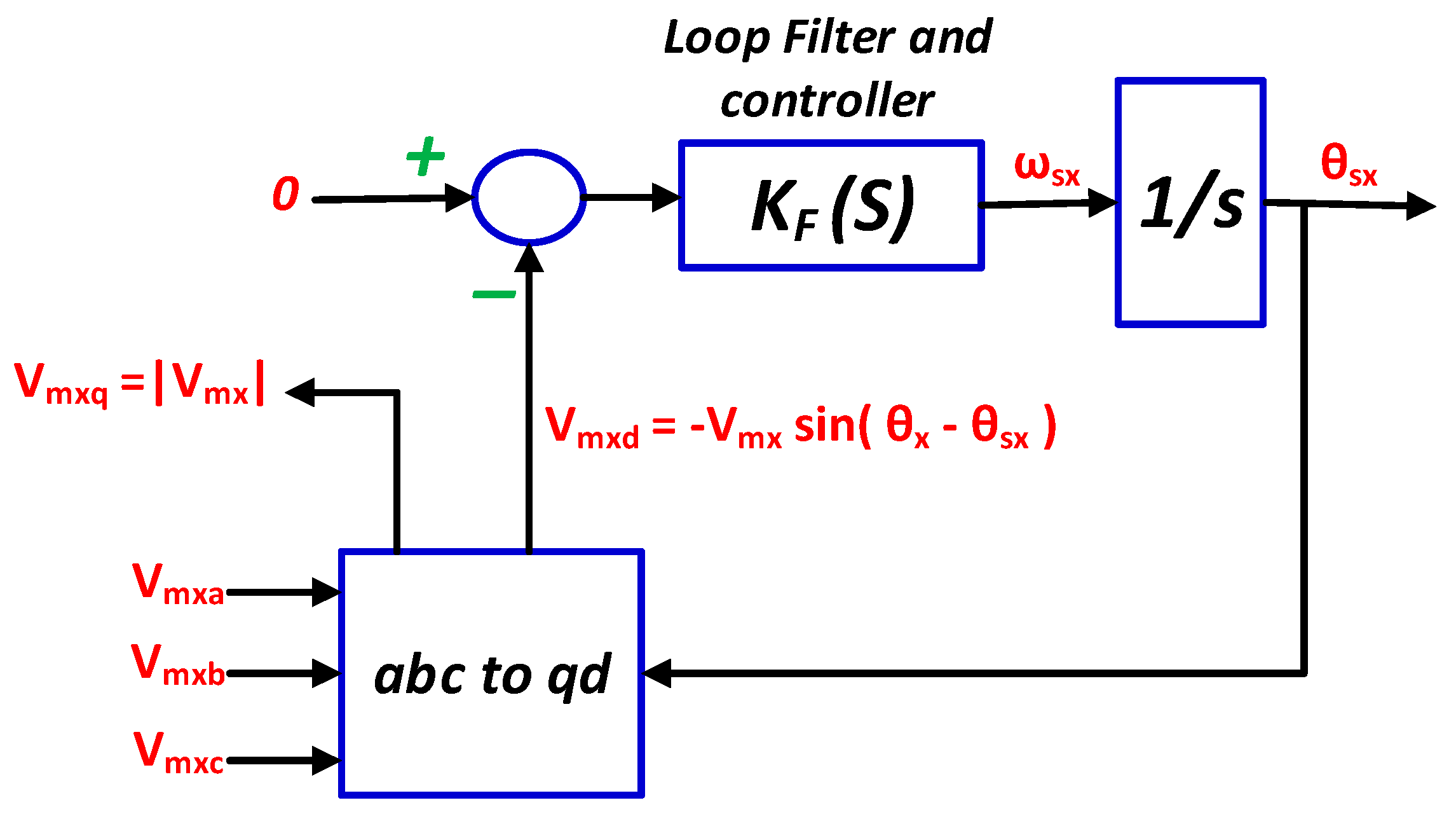
2.2.4. Phase Locked Loop
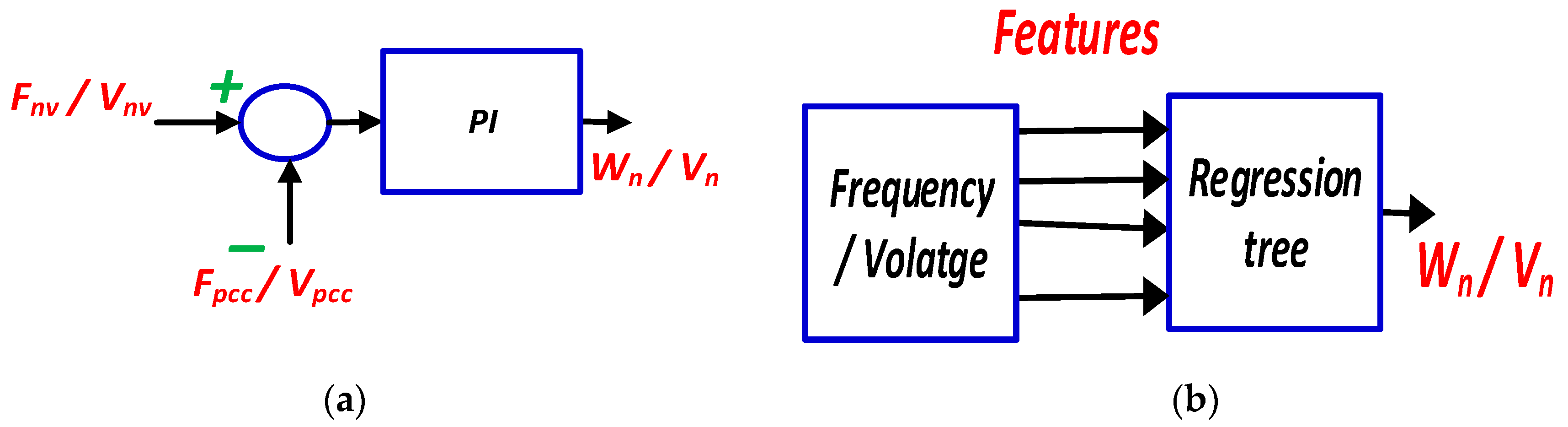
2.2.5. Supervisory Control
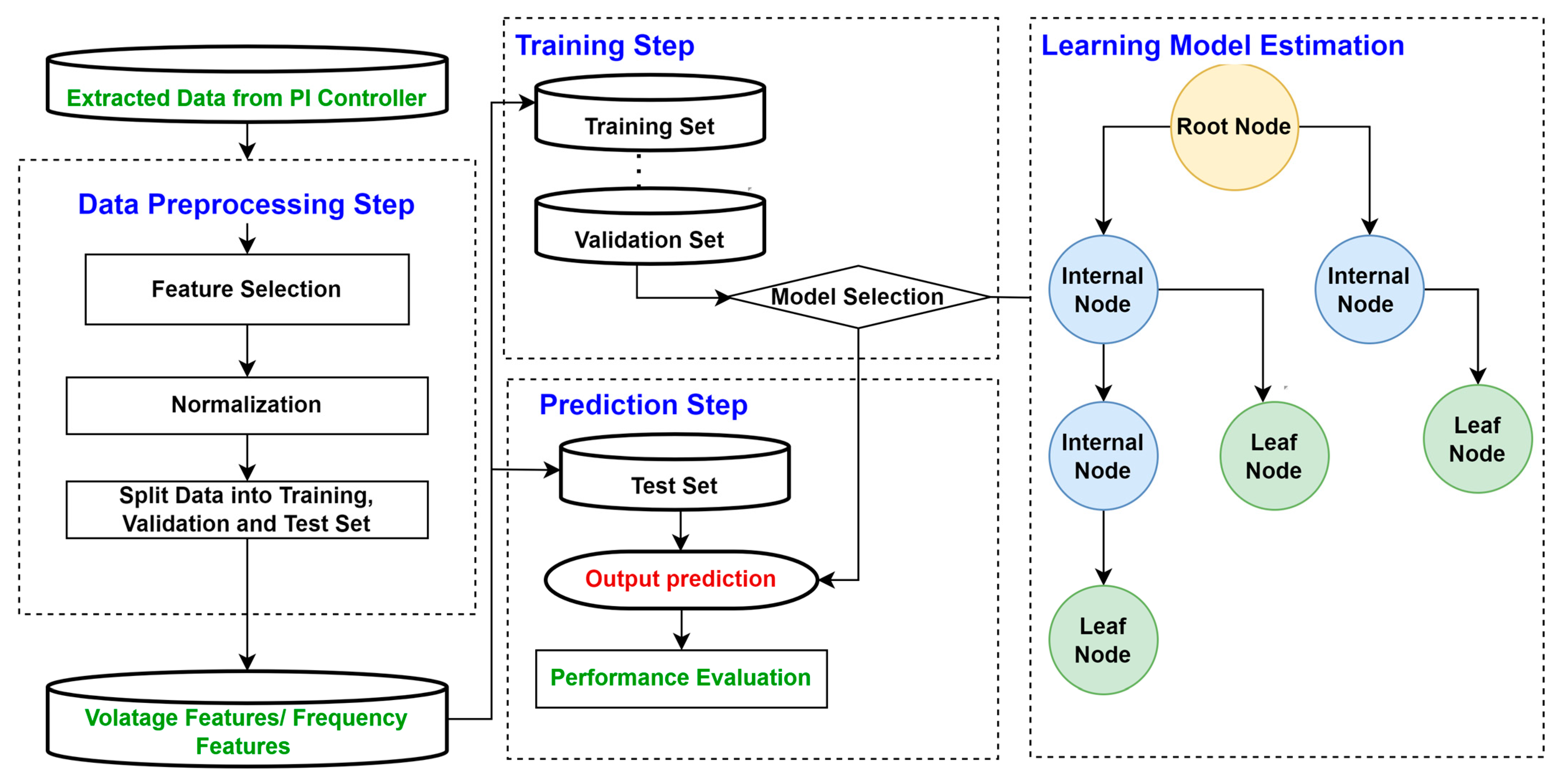
3. Regression Tree Algorithm
- Start with the entire dataset and calculate the MSE (or another chosen criterion) for the current group.
- Consider each possible split of the data based on the values of the predictor variables.
- For each split, calculate the MSE (or other chosen criterion) for each of the resulting subgroups.
- Choose the split that results in the lowest overall MSE (or another chosen criterion).
- Repeat steps 2–4 for each of the resulting subgroups until the tree is fully constructed.
- is the number of observations in the data.
- y is the actual value of the target variable for a given observation.
- is the predicted value of the target variable for a given observation.
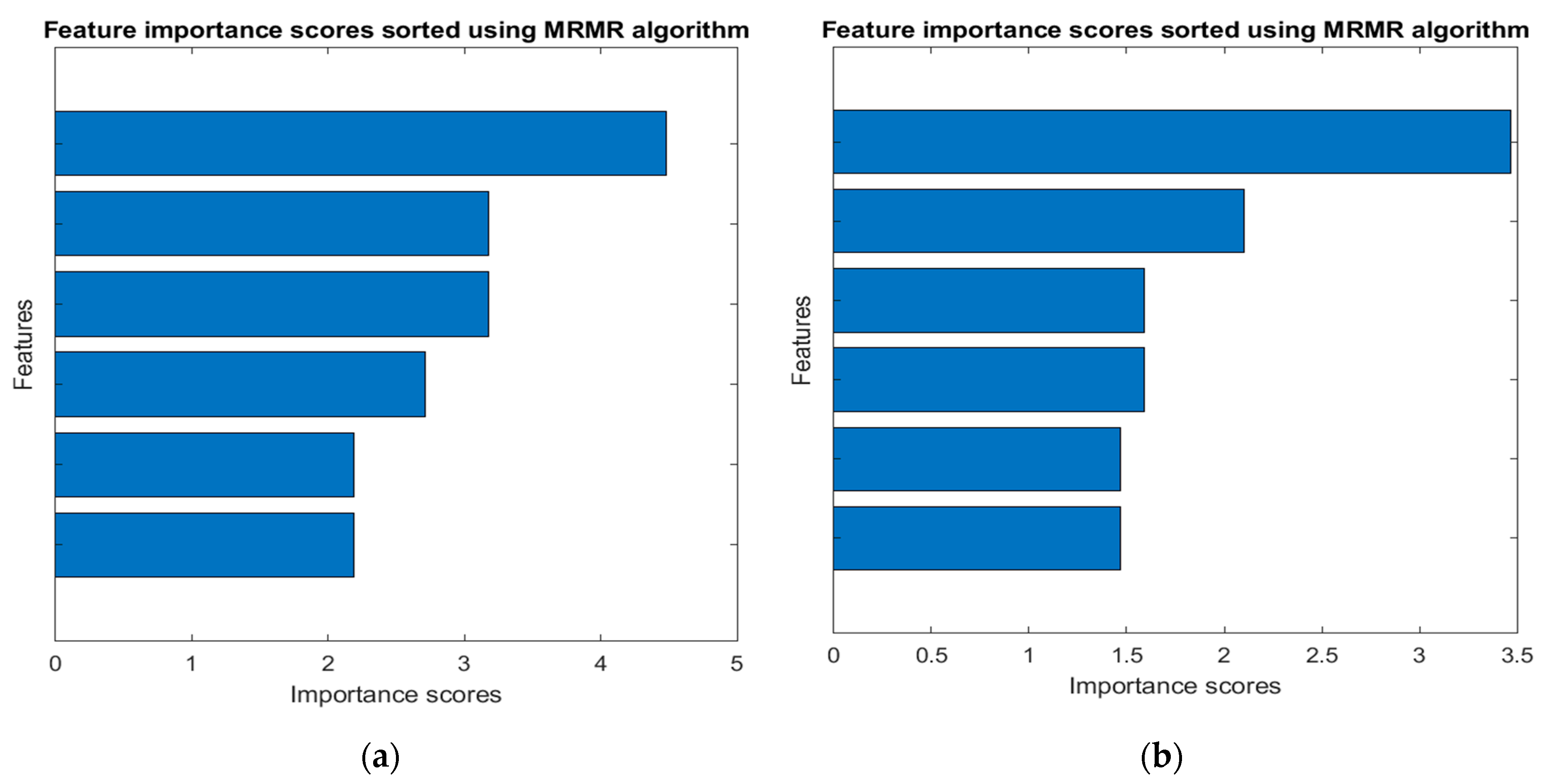
3.1. Dataset
3.2. Preprocessing
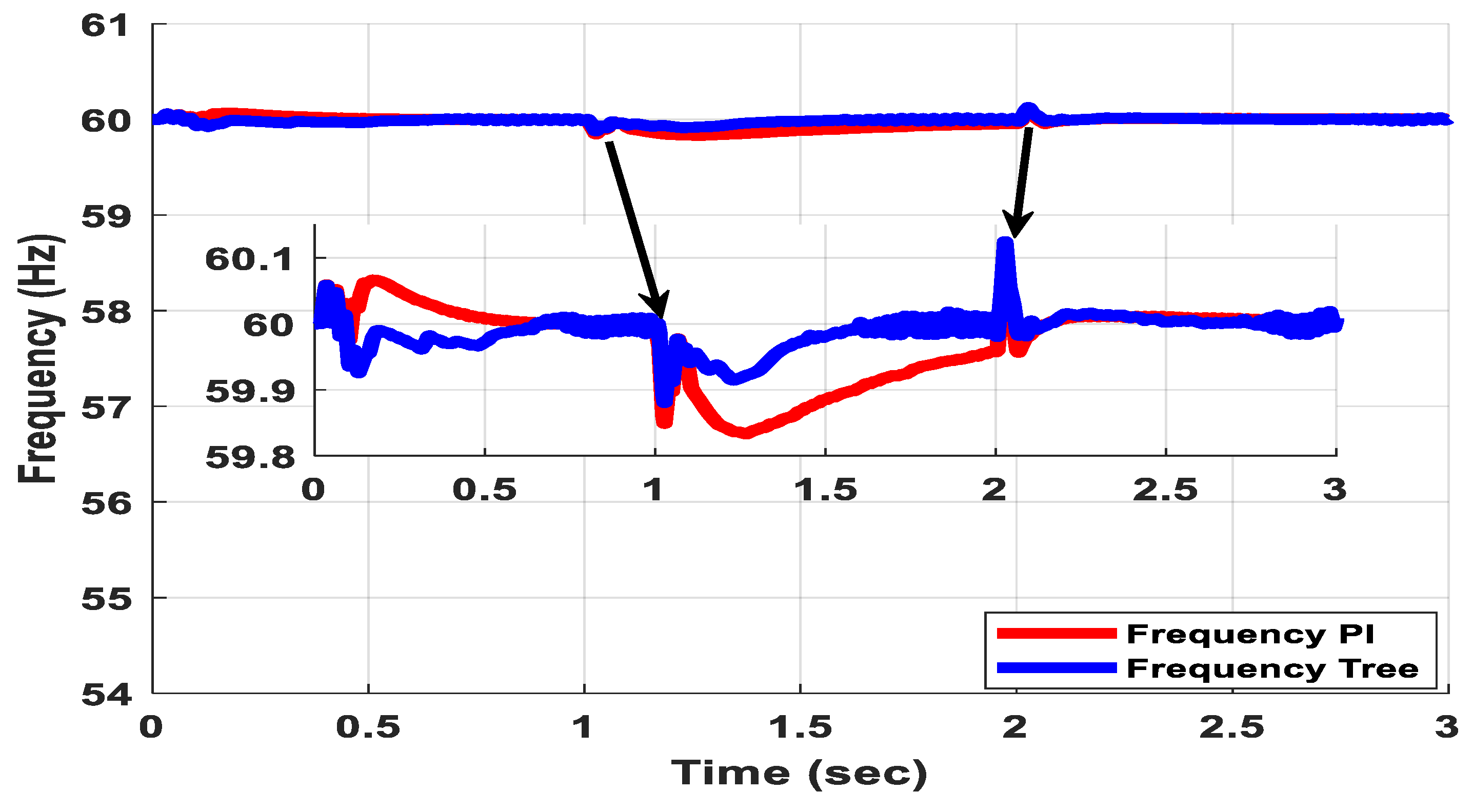
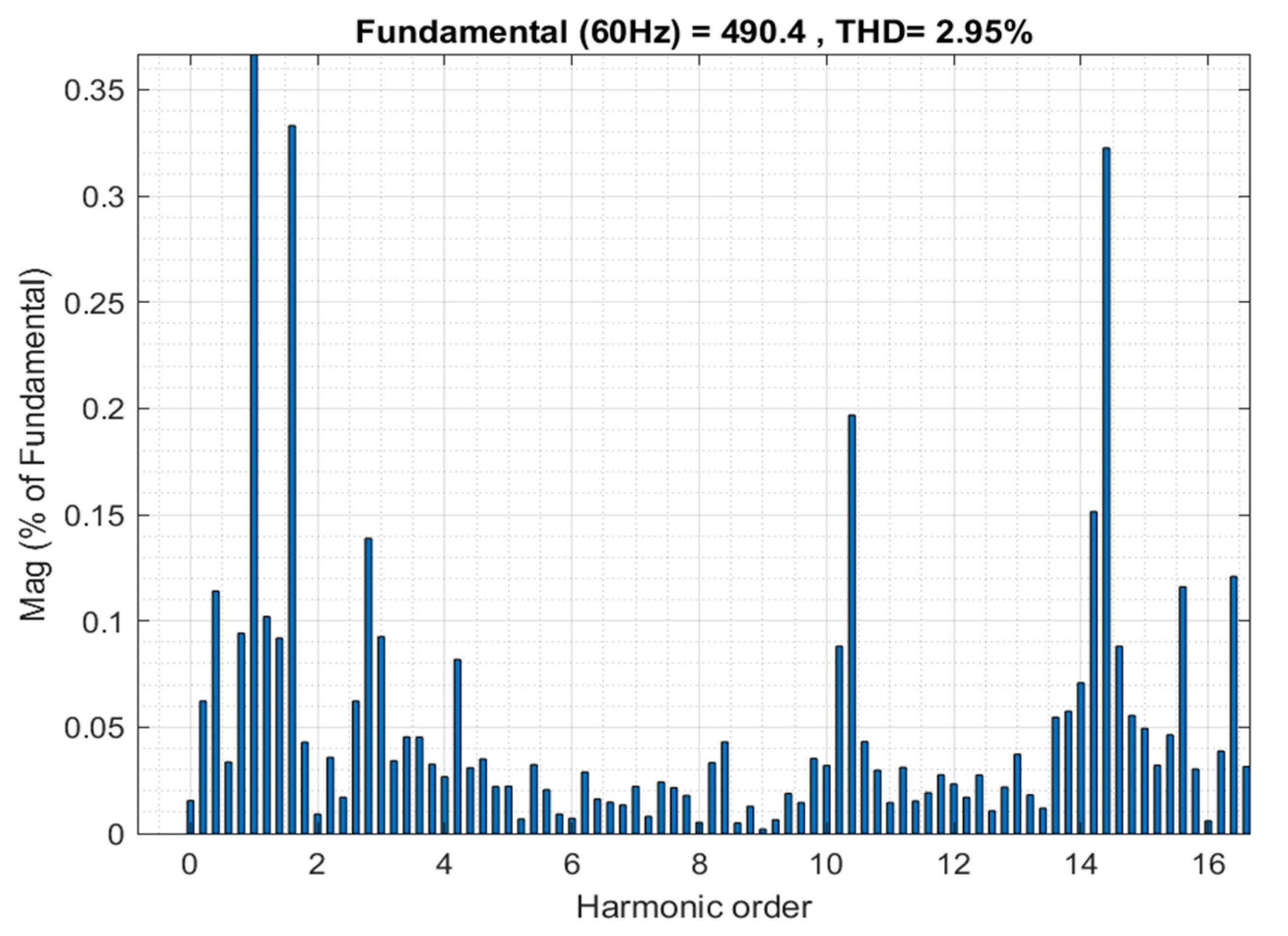
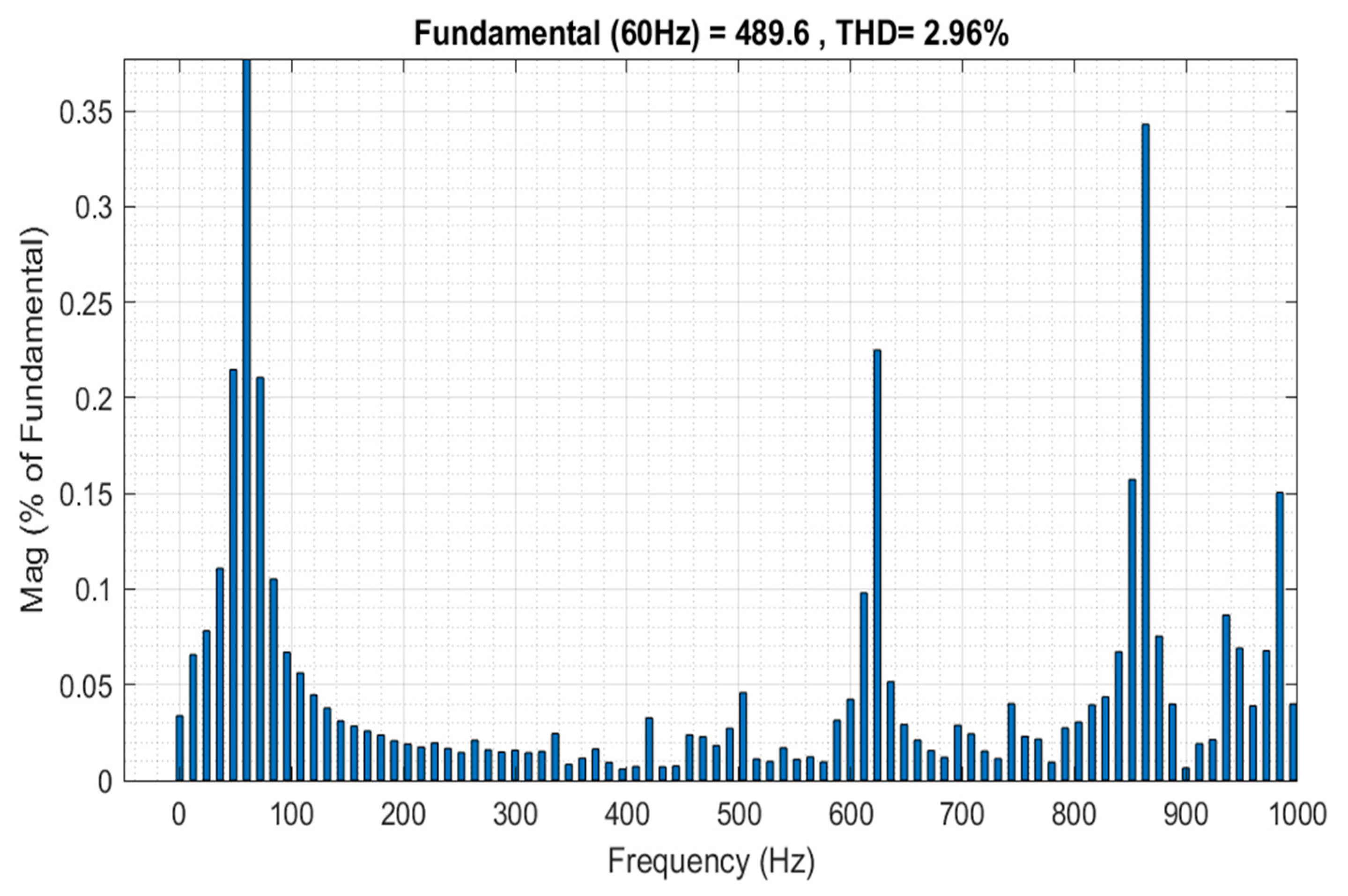
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, J.; Gong, C.; Chen, H.; Wang, Z. Secondary frequency regulation and stabilization method of islanded droop inverters based on integral leading compensator. Energy Rep. 2022, 8, 1718–1730. [Google Scholar] [CrossRef]
- Feng, C.-Y.; Yang, X.; Afshan, S.; Irfan, M. Can renewable energy technology innovation promote mineral resources’ green utilization efficiency? Novel insights from regional development inequality. Resour. Policy 2023, 82, 103449. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Gounder Ganapathy, V.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Alturki, F.A.; Omotoso, H.O.; Al-Shamma’a, A.A.; Farh, H.M.H.; Alsharabi, K. Novel Manta Rays Foraging Optimization Algorithm Based Optimal Control for Grid-Connected PV Energy System. IEEE Access 2020, 8, 187276–187290. [Google Scholar] [CrossRef]
- Al-Shamma’a, A.A.; Omotoso, H.O.; Noman, A.M.; Alkuhayli, A.A. Grey Wolf Optimizer Based Optimal Control for Grid-Connected PV System. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 20–21 October 2020; pp. 2863–2867. [Google Scholar] [CrossRef]
- Mohammed, N.; Ciobotaru, M. Adaptive Power Control Strategy for Smart Droop-based Grid-connected Inverters. IEEE Trans. Smart Grid 2022, 13, 2075–2085. [Google Scholar] [CrossRef]
- Safiullah, S.; Rahman, A.; Lone, S.A.; Hussain, S.M.S.; Ustun, T.S. Robust frequency–voltage stabilization scheme for multi-area power systems incorporated with EVs and renewable generations using AI based modified disturbance rejection controller. Energy Rep. 2022, 8, 12186–12202. [Google Scholar] [CrossRef]
- Cheng, C.; Xie, S.; Tu, L.; Tan, L.; Qian, Q.; Xu, J. Single Grid-Current Sensor-Controlled Weak-Grid-Following Inverters: A State-and-Disturbance-Observer-Based Robust Control Scheme Achieving Grid-Synchronization and Disturbance Rejection. IEEE Trans. Power Electron. 2022, 37, 13743–13754. [Google Scholar] [CrossRef]
- Kikusato, H.; Orihara, D.; Hashimoto, J.; Takamatsu, T.; Oozeki, T.; Matsuura, T.; Miyazaki, S.; Hamada, H.; Miyazaki, T. Performance evaluation of grid-following and grid-forming inverters on frequency stability in low-inertia power systems by power hardware-in-the-loop testing. Energy Rep. 2023, 9, 381–392. [Google Scholar] [CrossRef]
- Seguin, R.; Woyak, J.; Costyk, D.; Hambrick, J.C.; Mather, B.A. High-Penetration PV Integration Handbook for Distribution Engineers; National Renewable Energy Lab (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Hart, P.J.; Gong, M.; Liu, H.; Chen, Z.; Zhang, Y.; Wang, Y. Provably-Stable Overload Ride-Through Control for Grid-Forming Inverters Using System-Wide Lyapunov Function Analysis. IEEE Trans. Energy Convers. 2022, 37, 2761–2776. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Blaabjerg, F. Impedance-Based High-Frequency Resonance Analysis of DFIG System in Weak Grids. IEEE Trans. Power Electron. 2017, 32, 3536–3548. [Google Scholar] [CrossRef]
- Sun, Y.; Li, L.; Shi, G.; Hou, X.; Su, M. Power Factor Angle Droop Control—A General Decentralized Control of Cascaded Inverters. IEEE Trans. Power Deliv. 2021, 36, 465–468. [Google Scholar] [CrossRef]
- Mohammed, N.; Kerekes, T.; Ciobotaru, M. Communication-Free Equivalent Grid Impedance Estimation Technique for Multi-Inverter Systems. IEEE Trans. Ind. Electron. 2023, 70, 1542–1552. [Google Scholar] [CrossRef]
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.; Hannegan, B. Achieving a 100% Renewable Grid: Operating Electric Power Systems with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Mohammed, N.; Lashab, A.; Ciobotaru, M.; Guerrero, J.M. Accurate Reactive Power Sharing Strategy for Droop-Based Islanded AC Microgrids. IEEE Trans. Ind. Electron. 2023, 70, 2696–2707. [Google Scholar] [CrossRef]
- Hu, Q.; Han, R.; Quan, X.; Wu, Z.; Tang, C.; Li, W.; Wang, W. Grid-Forming Inverter Enabled Virtual Power Plants with Inertia Support Capability. IEEE Trans. Smart Grid 2022, 13, 4134–4143. [Google Scholar] [CrossRef]
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on Grid-Forming Inverter Control Methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Ko, H.-S.; Jang, M.-S.; Ryu, K.-S.; Kim, D.-J.; Kim, B.-K. Supervisory Power Quality Control Scheme for a Grid-Off Microgrid. IEEE Trans. Sustain. Energy 2018, 9, 1003–1010. [Google Scholar] [CrossRef]
- Lundberg, M.; Samuelsson, O.; Hillberg, E. Local voltage control in distribution networks using PI control of active and reactive power. Electr. Power Syst. Res. 2022, 212, 108475. [Google Scholar] [CrossRef]
- Sharma, D.; Sadeque, F.; Mirafzal, B. Synchronization of Inverters in Grid Forming Mode. IEEE Access 2022, 10, 41341–41351. [Google Scholar] [CrossRef]
- Al Badwawi, R.; Issa, W.R.; Mallick, T.K.; Abusara, M. Supervisory Control for Power Management of an Islanded AC Microgrid Using a Frequency Signalling-Based Fuzzy Logic Controller. IEEE Trans. Sustain. Energy 2019, 10, 94–104. [Google Scholar] [CrossRef]
- Tursini, M.; Parasiliti, F.; Zhang, D. Real-time gain tuning of PI controllers for high-performance PMSM drives. IEEE Trans. Ind. Appl. 2002, 38, 1018–1026. [Google Scholar] [CrossRef]
- Kalaam, R.; Muyeen, S.M.; Al-Durra, A.; Hasanien, H.; Al-Wahedi, K. Optimization of Controller Parameters for Grid-tied Photovoltaic System at Faulty Network using Artificial Neural Network based Cuckoo Search Algorithm. IET Renew. Power Gener. 2017, 11, 1517–1526. [Google Scholar] [CrossRef]
- Sanchis, R.; Peñarrocha-Alós, I. A new method for experimental tuning of PI controllers based on the step response. ISA Trans. 2022, 128, 329–342. [Google Scholar] [CrossRef] [PubMed]
- Ghalebani, P.; Niasati, M. A distributed control strategy based on droop control and low-bandwidth communication in DC microgrids with increased accuracy of load sharing. Sustain. Cities Soc. 2018, 40, 155–164. [Google Scholar] [CrossRef]
- Chen, G.; Li, Z.; Zhang, Z.; Li, S. An Improved ACO Algorithm Optimized Fuzzy PID Controller for Load Frequency Control in Multi Area Interconnected Power Systems. IEEE Access 2020, 8, 6429–6447. [Google Scholar] [CrossRef]
- Eslami, A.; Negnevitsky, M.; Franklin, E.; Lyden, S. Review of AI applications in harmonic analysis in power systems. Renew. Sustain. Energy Rev. 2022, 154, 111897. [Google Scholar] [CrossRef]
- Shalizi, C.R. Advanced Data Analysis from an Elementary Point of View; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- The Mathworks. Statistics and Machine Learning Toolbox. Available online: https://www.mathworks.com/help/releases/R2022a/pdf_doc/stats/stats.pdf (accessed on 1 March 2023).
- Chen, C.; Yan, X. Optimization of a Multilayer Neural Network by Using Minimal Redundancy Maximal Relevance-Partial Mutual Information Clustering With Least Square Regression. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1177–1187. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]




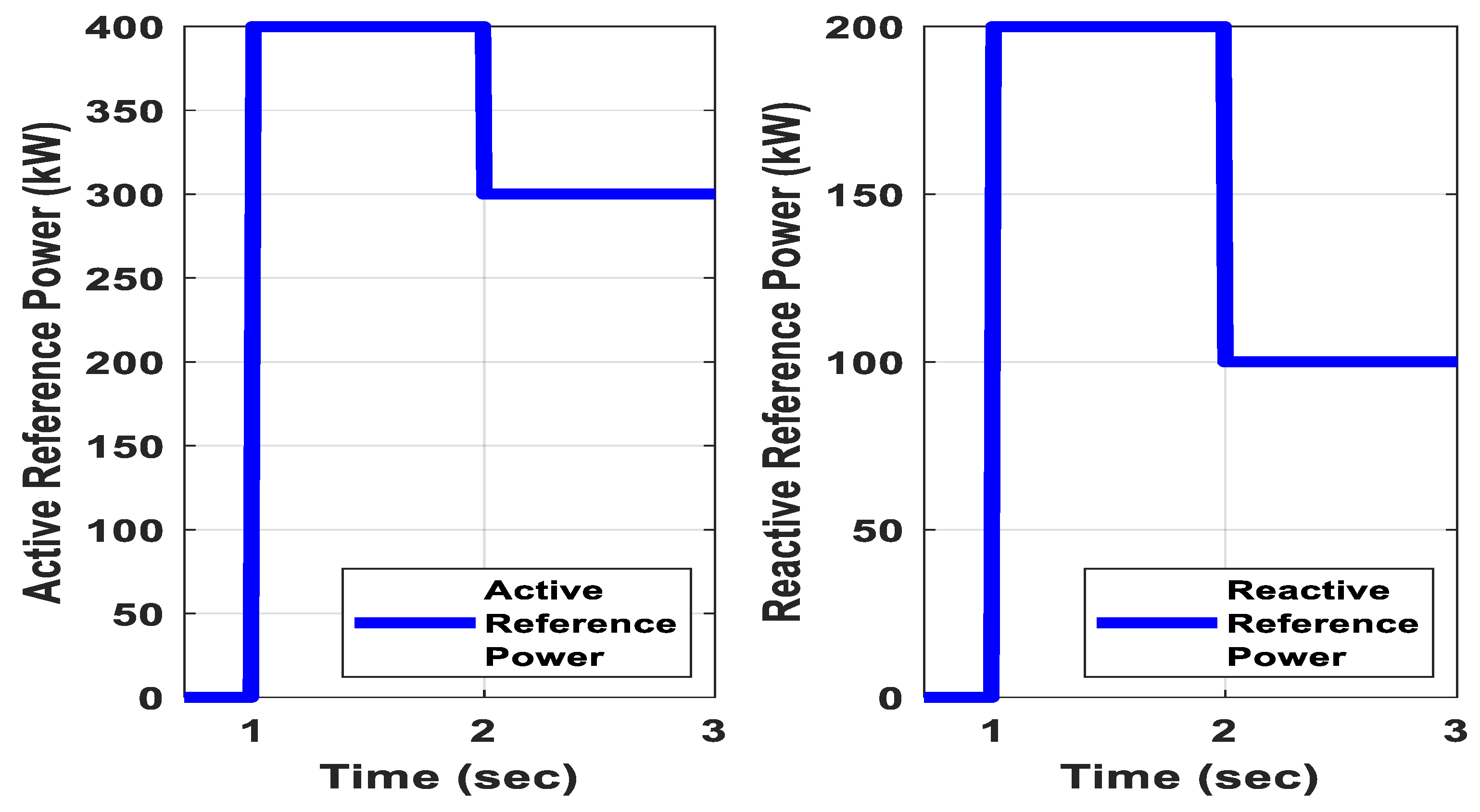


| Parameters | Values |
|---|---|
| 600 V | |
| 60 Hz | |
| P | 400 kW |
| Q | 100 kW |
| 2.7 kHz | |
| Mpx | 1% |
| Nqx | 4% |
| 1000 V | |
| , , | 500, 300, 200 kW |
| Frequency Features | Voltage Features |
|---|---|
| Measured active power at PCC | Measured reactive power at PCC |
| Measured frequency at PCC | Proportional parameter of PI controller |
| Derivative of PI controller | Derivative of PI controller |
| Integral of PI controller | Integral of PI controller |
| Response | PI | Tree |
|---|---|---|
| Settling minimum (V) | 59.8332 | 59.8808 |
| Settling maximum (V) | 60.0664 | 60.0586 |
| Overshoot (pu) | 0.1106 | 0.0976 |
| Peak (V) | 60.0664 | 60.0586 |
| Peak time (s) | 0.1701 | 0.0342 |
| Response | PI | Tree |
|---|---|---|
| Settling minimum (V) | 479.9 | 482 |
| Settling maximum (V) | 611.2616 | 606.623 |
| Overshoot (pu) | 1.8769 | 1.1038 |
| Peak (V) | 611.2616 | 606.623 |
| Peak Time (s) | 0.2314 | 0.9918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omotoso, H.O.; Al-Shamma’a, A.A.; Alharbi, M.; Farh, H.M.H.; Alkuhayli, A.; Abdurraqeeb, A.M.; Alsaif, F.; Bawah, U.; Addoweesh, K.E. Machine Learning Supervisory Control of Grid-Forming Inverters in Islanded Mode. Sustainability 2023, 15, 8018. https://doi.org/10.3390/su15108018
Omotoso HO, Al-Shamma’a AA, Alharbi M, Farh HMH, Alkuhayli A, Abdurraqeeb AM, Alsaif F, Bawah U, Addoweesh KE. Machine Learning Supervisory Control of Grid-Forming Inverters in Islanded Mode. Sustainability. 2023; 15(10):8018. https://doi.org/10.3390/su15108018
Chicago/Turabian StyleOmotoso, Hammed Olabisi, Abdullrahman A. Al-Shamma’a, Mohammed Alharbi, Hassan M. Hussein Farh, Abdulaziz Alkuhayli, Akram M. Abdurraqeeb, Faisal Alsaif, Umar Bawah, and Khaled E. Addoweesh. 2023. "Machine Learning Supervisory Control of Grid-Forming Inverters in Islanded Mode" Sustainability 15, no. 10: 8018. https://doi.org/10.3390/su15108018
APA StyleOmotoso, H. O., Al-Shamma’a, A. A., Alharbi, M., Farh, H. M. H., Alkuhayli, A., Abdurraqeeb, A. M., Alsaif, F., Bawah, U., & Addoweesh, K. E. (2023). Machine Learning Supervisory Control of Grid-Forming Inverters in Islanded Mode. Sustainability, 15(10), 8018. https://doi.org/10.3390/su15108018







