The authors would like to make the following corrections to a published paper [1]. The changes are as follows:
- The old “Abstract” section mentions terms such as well-definedness and the intendedness of the metrics, which can be understood by the reader as if some of the metrics of Westhofen et al. [2] analyzed by us in the manuscript are not well-defined and do not work as intended. This is not what we mean. What we mean is if these metrics can be used as rewards in Artificial Intelligence (AI) for training Reinforcement Learning (RL) agents. Furthermore, in the abstract section, it is mentioned that we discuss the possibility of applying these metrics in RL training and propose a way to apply some of the metrics in a simple car-following scenario. This can be understood as if we already applied some of the metrics to the training process of the RL in this simple car-following scenario, which we did not. However, in the updated version of the manuscript, all the above-mentioned aspects are solved by us, and there is no more room for confusion or possible misunderstandings.
A correction has been made to “Abstract”.
This paper presents an analysis of several criticality metrics used for evaluating the safety of Autonomous Vehicles (AVs) and also proposes environmentally friendly metrics with the scope of facilitating their selection by future researchers who want to evaluate both the safety and environmental impact of AVs. Regarding this, first, we investigate whether existing criticality metrics are applicable as a reward component in Reinforcement Learning (RL), which is a popular learning framework for training autonomous systems. Second, we propose environmentally friendly metrics that take into consideration the environmental impact by measuring the CO2 emissions of traditional vehicles as well as measuring the motor power used by electric vehicles. Third, we discuss the usefulness of using criticality metrics for Artificial Intelligence (AI) training. Finally, we apply a selected number of criticality metrics as RL reward component in a simple simulated car-following scenario. More exactly, we applied them together in an RL task, with the objective of learning a policy for following a lead vehicle that suddenly stops at two different opportunities. As demonstrated by our experimental results, this work serves as an example for the research community of applying metrics both as reward components in RL and as measures of the safety and environmental impact of AVs.
- 2.
- The old “Introduction” section only shortly mentions the existent criticality metrics found in the literature and does not clearly explain to the reader how such criticality metrics can be used for AI training. However, in the updated version of the manuscript, all the above-mentioned aspects are solved by us, and there is no more room for confusion or possible misunderstandings.
A correction has been made to “Introduction”.
The research interest in the domain of AVs, especially regarding their safety, has grown exponentially in the last few years. This is mainly due to recent advancements in the field of AI, especially regarding deep RL algorithms, which are showing promising results when implemented in AI components found in AVs, especially when combined with prior knowledge [1].
Concerning traffic scenarios, the safety of all traffic participants is considered to be the most important aspect on which the researchers should focus, this being especially reflected by projects such as VVM—Verification and Validation Methods for Automated Vehicles Level 4 and 5 [2], SET Level—Simulation-Based Development and Testing of Automated Driving [3], as well as KI Wissen—Automotive AI Powered by Knowledge [4], all three projects being funded by the German Federal Ministry for Economic Affairs and Climate Action. In addition to these, many other projects of the VDA Leitinitiative autonomous and connected driving [5] bring together various research partners from the industry and academia to solve challenging and contemporary research problems related to the AV domain, emphasizing the relevance of criticality and safety in traffic.
With regards to the meaning of criticality, despite the existent ambiguity regarding its definition in both industry and academia, for an easier understanding of its meaning in the context of this paper, we follow the definition given by the work in [6] (Def. I), namely: “the combined risk of the involved actors when the traffic situation is continued”.
Regarding this, to assess how critical a traffic situation is, literature focuses on the use of so-called criticality metrics for automated driving [7,8]. However, because AVs are operating in a complex traffic environment where a high number of actors are present, such as AVs, non-AVs, and pedestrians, to name only a few, it is imperative to not only identify the suitable criticality metrics that can mitigate dangerous situations as it is currently done in the literature [7,8] but also to implement and evaluate them efficiently regarding their environmental impact as well.
This is of high importance, especially when the transportation sector is known to be a key contributor to climate change, accounting for more than 35% of carbon dioxide emissions in the United States alone [9]. It is therefore imperative that existent and future researchers do not only use existent metrics that can evaluate critical situations in traffic, but also make efforts in proposing novel environmentally friendly criticality metrics that can be used to evaluate the AV’s impact on the environment and economy as well. A recent effort in this direction is made by a new global initiative that tries to catalyze impactful research work at the intersection of climate change and machine learning such as the work of the Climate Change AI [10] organization as well as in recent works that try to encourage researchers to power and evaluate their deep learning-based systems using green energy [11,12].
Autonomous systems can be rule-based, i.e., there is a pre-defined deterministic policy that decides which action the AV should take in which situation (e.g., regarding distances to other vehicles and relative velocities), but the growing potential of deep learning leads to AVs trained with AI or even a combination of rule- and AI-based components as intended by the KIWissen project [4]. The AI-based training of AVs is usually based on RL. As the criticality metrics evaluate the safety of the AV, it is hence a logical step to respect those metrics already in the training process which, for RL, can be done by reward shaping, i.e., integrating additional (criticality-related) terms into the reward function that acts as target function during training.
Therefore, in this paper, we present an analysis of several criticality metrics, mainly the ones already collected in [7,8], in order to determine whether they can be applied as reward components in AI training by RL to easily facilitate their selection for criticality assessment in the context of AV safety evaluation. To this end, the used criticality metrics must satisfy the property that the desired behaviour, represented by an optimal policy, is flagged as optimal by the respective metrics. It is important to mention that our analysis is a special case of the proposed application, as per the “Objective function” in [7] (Section 3.1.1). This is done, first, on the base of the formula and secondly, via an evaluation of selected criticality metrics. Additionally, we propose to combine these metrics with what we call “environmentally friendly metrics” in order to take the CO2 footprint explicitly into account. Furthermore, due to recent emergent paradigms, such as Green AI [13], which encourage researchers to move towards more sustainable methods that are environmentally friendly and inclusive, we also propose several environmentally friendly metrics that are used to create an environmentally friendly criticality metric, which is suitable for evaluating a critical scenario not only regarding safety but also regarding the environmental impact in a car-following scenario.
Our main contributions are as follows: (i) an analysis of the existing criticality metrics in terms of applicability as a reward component and how they can be used to learn towards safe and desired behavior; (ii) the integration of existing criticality metrics as reward components in RL and of emission estimations into the criticality metrics framework; (iii) an investigation of the suitability of the criticality metrics for AI training; (iv) illustrative simulations of the metrics applied in a car-following scenario.
The paper is organized as follows. In Section 2, we present the related work. Section 3 details the analysis of several criticality metrics, as well as adaptions allowing for their possible applicability as a reward component. Section 4 presents the proposed environmentally friendly criticality metrics. Section 5 presents our contribution regarding the usage of criticality metrics for AI training. In Section 6 we present the application of the metrics. Finally, in Section 7, we present the conclusions, limitations and future work of this paper.
- 3.
- The old “Related Work” section mentions that the use of criticality metrics is not restricted to the evaluation of traffic scenarios but can be extended to the training of autonomous driving agents by integrating suitable metrics into the reward function. However, the reader can misunderstand this and think that such an application has not been proposed already and that we are the first ones who do it. We solved this problem in the updated version of the manuscript by stating and citing that such an application has already been proposed and we analyze in more depth the general requirements of such metrics for the use case of RL.
A correction has been made to “Related Work”.
An extensive overview of criticality metrics in autonomous driving has been given by Westhofen et al. in [7,8]. The usage of criticality metrics is not restricted to the evaluation of traffic scenarios, but can be extended to the training of autonomous driving agents by integrating suitable metrics into the reward function, whereas such an application has already been proposed in [7] and is analyzed here in depth regarding general requirements of such metrics for the use case of RL. This technique is called reward shaping and allows for prior knowledge to be included in the training, as seen in [14]. Three of these criticality metrics, namely Headway (HW), Time Headway (THW), and Deceleration to Safety Time (DST), were implemented and tested in an Adaptive Cruise Control (ACC) use case, as detailed by the authors of [1]. In their work, the authors have shown that different RL models can be evaluated for the ACC use case using these metrics; however, the DST metric, at the very least, does not coincide with the supposed objective of this function.
The ecological impact of autonomous driving has been discussed in many works, such as the ones in [15–19]. These works do not only consider fuel consumption or emissions but also analyze the socio-ecological aspects, like a higher driving demand if AVs are available, or indirect implications, like reduced land use due to optimized parking. Moreover, the work in [20] proposes a model for estimating the emissions and evaluating it in different scenarios with respect to, for example, the relative part of AVs in the traffic. The authors of [21] propose a model for CO2 emission estimation. The power consumption of electric vehicles was also measured by [22–24].
The cited references generally consider fuel consumption and emissions for evaluation. These measures can be seen as environmentally friendly metrics, which have already been used for AI training. For example, the authors of [25] train a deep RL model that is encouraged to minimize emissions, and the authors of [26] proposed a deep RL controller based on a partially observed Markov Decision Problem for connected vehicles so that eco-driving is encouraged where battery state-of-charge and safety aspects (e.g., speed limits or safety distances) are integrated into the model. Additionally, the work in [27] presents an extensive overview of eco-driving RL papers where the reward function is nearly always state-of-charge or fuel consumption. The authors of [28] propose a hybrid RL strategy where conflicting goals such as saving energy and accelerating are captured by a long-short-term reward (LSTR). To not let energy-saving jeopardize safety, the acceleration energy is only penalized for accelerations, not for decelerations. The reward function also consists of a green-pass reward term, which essentially encourages reaching the stopping line of an intersection when the traffic light is green (i.e., driving forward-looking). Some of these references not only focus on carbon dioxide emissions but also consider, for example, carbon monoxide, methane, or nitrogen oxides. Besides training AVs, ecological aspects are also taken into consideration regarding traffic system controls [29].
- 4.
- The old “Mathematical Analysis of Criticality Metrics” section presents definitions of the criticality metrics that can make the reader think it is our own definition of the metrics because it is not clearly mentioned and cited by us which parts of the definition is from the original paper source and which is from the Westhofen et al. paper. Furthermore, as mentioned earlier regarding the “Abstract” section, the terms well-definedness, intendedness, and optimality do not clearly portray the scope and purpose of our paper. In the new version of the manuscript, we solve all the mentioned aspects and clearly marked the sources, verbatim quotations, and necessary adaptations.While Westhofen et al. put a lot of emphasis on an abstract, unifying presentation of the metrics, in our old paper, the necessary concretization for the case of a car-following scenario read, in parts, as unjustified criticism of Westhofen et al. We have removed this erroneous impression in the new version.
A correction has been made to “Mathematical Analysis of Criticality Metrics”.
- (1)
- Replacing the title on page 3:
Mathematical Analysis of Criticality Metrics
with
Applicability Analysis of Criticality Metrics
- (2)
- Replacing the paragraph spanning pages 3, 4, and 5:
In the following, we present the mathematical analysis of … absorption of a bump shock absorber in the work presented in [26].
with
In the following, we present an analysis of several existing criticality metrics. We have mostly made use of the excellent overview and detailed presentation in Westhofen et al. [7] and the supplementary material [8]. While Westhofen et al. put a lot of emphasis on an abstract, unifying representation of the metrics, we concretized most of the metrics to the case of a track-/car-following scenario. In particular, this means that we generally view an actor’s position as a one-dimensional quantity, pi, that measures the progress of actor i from an arbitrary reference point relative to a given route. All actor positions refer to the same reference point, so, for every two actors, i and j, it can be effectively decided whether actor i is in front of actor j (pi > pj), the other way around (pi < pj), or whether both actors are in the same position (pi = pj), which usually indicates the presence of a collision. Only in a few cases do we consider the position of the actor i as a vector quantity, pi, in the two-dimensional plane.
As for the notation in the subsequent parts, please see the Abbreviations and Nomenclature sections where the most frequent abbreviations and symbols used in this paper are presented. Note that state variables like position (pi(t)), velocity (vi(t)) and acceleration (ai(t)), specific to actor i, are functions over time. The current time of a scene is denoted by t0, and if we refer to a state variable at time t0, we often omit the time parameter; i.e., we briefly write pi instead of pi(t0).
In general, criticality metrics refer to an underlying prediction model (PM) to predict the future evolution of the actual traffic scene. While in the standard literature such predictive models are fixed in the definition of the metrics, we benefit from the preliminary work by Westhofen et al. [7], who have freed many metrics from the fixed predictive models and made them a flexible component of the metrics. Often, a prediction model can be obtained from a dynamic motion model (DMM) that approximates the agent’s future position. If, for example, in the definition of a metric, the position function pi(t) is applied to future time points, then it is mandatory to specify a DMM for an in-situ computation. Typical DMMs arise from the assumption of constant velocity (pi(t0 + t) = pi + vit) or constant acceleration ().
In AI training, criticality metrics can be used as penalty terms, for example, as negative reward components in RL. More precisely, RL training corresponds to (approximately) solving a so-called Markov decision process (MDP), represented by a tuple (S, A, T, r, γ) (e.g., [30]) for the state space , the action space ; and a transition model where is the transition probability from state s to state if action a has been selected by the ego agent. The ego agent’s behaviour is described by a policy where describes the probability that the ego agent selects action a in state s. is a discount factor and is a reward function which returns a real-valued feedback for the ego agent’s decision. This reward function can consist of different reward components that aim to encourage or discourage certain behaviours. RL training is an iterative process where one starts with some initial policy. For given states, actions are selected by this policy and some time steps are played out using the given transition model, up to some finite horizon. Then, the resulting trajectories are evaluated by the reward function so that the policy is updated accordingly in the sense that actions that were appropriate for the given states, therefore leading to high rewards, are encouraged in the future by modifying the current policy.
The agent, therefore, successively learns to select appropriate actions, resulting in maneuvers that are not critical or in which criticality is sufficiently low, evaluating the selected metrics. As an action usually only considers acceleration/deceleration and changing the heading angle, parameters that cannot be influenced by the agent like payloads; the length of the vehicle; or, generally, its structure, could only implicitly be considered when computing the rewards; e.g., higher payloads can be integrated into the computation of the braking distance. These parameters often correspond to passive safety and optimizing them is part of the manufacturing process [31], but it does not correspond to the scope of this work. Note that, due to the playout of the trajectories in RL training, one has to be careful considering metrics like TTC where one searches for a particular timestep in the future where the vehicles would collide. If a collision did not happen in the played-out trajectories, one could empirically set TTC at least to ∞, but that would not fully reflect its definition. Overall, the relationship between the prediction models of the metrics and the policy/transition model remains an interesting object of investigation. While a prediction model usually specifies the behavior of all agents deterministically, the policy of the agent under training is learned during RL, and the behavior of the remaining agents is specified by a transition model often as a probability distribution over possible actions. So, on the one hand, one could consider whether and to what extent it makes sense to merge prediction models and policy/transition models. However, this connection is not examined further in this paper as we treat the prediction models strictly separated from the policy/transition models. In the following analysis, we use the same classification of metrics according to their scales such as time, distance, velocity, acceleration, jerk, index, probability, and potential as in Westhofen et al. [7]. First, we introduce each metric, generally following the presentation of Westhofen et al. and note important features as needed. In some cases we also draw on the original sources. Overall, the collection of Westhofen et al. is further extended by the Time to Arrival of Second Actor (T2) metric of Laureshyn et al. [32], several potential-scale metrics taken from [33–35], and by the self-developed criticality metric CollI.
Second, we evaluate the metric if it is applicable as a reward component for RL. For each metric, it is first necessary to assess whether and how they can be integrated into the RL algorithm. Not all metrics can or should be used for RL. For example, scenario-based metrics require knowledge of agent states over the entire course of the scenario and therefore cannot be readily used for an in-situ assessment of the reward function, and other metrics (such as TTM) inherently constrain the action space of the agent by predefined evasive maneuvers and thus conflict with RL’s goal to learn such evasive maneuvers. Besides finding such inadequacies, the focus of the analysis is to assess the metric’s impact on the learned behavior of the agent if it is used as a reward component.
- (3)
- Replacing the paragraph on page 5:
The ET metric was proposed in [27]. It is supposed to measure the time … if the conflict area is an occluded intersection, which A1 evidently should not pass with high speed.
with
Crit. Metric 1 (Encroachment Time (ET), verbatim quote of [7]; see also [8,36])
The ET metric … measures the time that an actor A1 takes to encroach a designated conflict area CA, i.e.,
Applicability as a Reward Component in RL
ET is a scenario-level metric [8] that allows for an effective evaluation as long as the requested time points texit and tentry exist, are uniquely determined, and methods to evaluate texit and tentry are provided. According to [8], there is no prediction model for ET, and, hence, cannot be used for an in-situ assignment.
Generally, it seems desirable to have the ET and, therefore, the time in the critical area be as short as possible. Using the ET values as a penalty term in the reward function could yield a training towards high velocities, which might be undesirable in a conflict area. Therefore, it would be interesting to have a speed-relative version that additionally takes an a priori estimate of a reasonable encroachment time of the scenario-specific CA into account.
In order to use ET as a reward component, a scene-level variant would have to be defined, and individual target values would have to be known for each scenario. Hence, the ET metric is not directly applicable as a reward component.
- (4)
- Replacing the paragraph on pages 5 and 6:
The PET metric [27] intends to calculate the time gap between … for the future trajectories of A1 until A1 exits the conflict area.
with
Crit. Metric 2 (Post-Encroachment Time (PET); verbatim quote of [7] with agents’ identifiers swapped; see also [8,36])
The PET calculates the time gap between one actor leaving and another actor entering a designated conflict area CA on scenario level. Assuming A2 passes CA before A1, the formula is
Applicability as a Reward Component in RL
PET is a scenario-level metric that allows for an effective evaluation as long as the requested time points texit and tentry exist, are uniquely determined, and methods to evaluate texit and tentry are provided. According to [8] there is no prediction model for PET, and, hence, it cannot be used for an in-situ assignment.
High values of the PET indicate a long time gap between the actors leaving and entering the conflict area. In general, it seems to be desirable to avoid low values, especially values below zero. Therefore, using PET as a reward term of a reward function could yield training towards low velocities of the following agent.
In order to use PET as a reward component, a scene-level variant would have to be defined. Hence, the PET metric is not directly applicable as a reward component.
- (5)
- Replacing the paragraph on page 6:
The work in [7] does not give an explanation for the metric, only the formula, … while driving with the same velocity v.
with
Crit. Metric 3 (Predictive Encroachment Time (PrET); see also [6–8])
The PrET calculates the smallest time difference at which two vehicles reach the same position, i.e.,
Applicability as a Reward Component in RL
PrET is a scene-level metric that refers to an unbound prediction model [8]. Provided an appropriate prediction model, it can be used for in-situ reinforcement learning.
Low values of PrET indicate a short velocity-relative safety distance between both actors and should be avoided in general. On the other hand, high values indicate a larger velocity-relative distance between both actors and should also be avoided in a car-following scenario. Therefore, it seems to be desirable to use the absolute distance of the PrET metric towards a reasonable target value as a penalty term of the reward function. As a reasonable target value, we propose to use 2s. Further target values can be found in [8].
To sum up, the absolute deviation from a target value seems to be an interesting candidate for a reward component in reinforcement learning.
- (6)
- Replacing the paragraph on page 6:
The THW metric intends to calculate the time … so that the target value for THW is attained.
with
Crit. Metric 4 (Time Headway (THW), verbatim quote of [7] with the alignment of variable names; see also [8,37])
The THW metric calculates the time until actor A1 reaches the position of a lead vehicle A2, i.e.,
Applicability as a Reward Component in RL
THW is a scene-level metric that refers to an unbound prediction model [8]. Provided an appropriate prediction model, it hence can be used for in-situ reinforcement learning.
Low values of THW indicate a short velocity-relative safety distance between both actors and should be avoided in general. On the other hand, high values indicate a larger velocity-relative distance between both actors and should also be avoided in a car-following scenario. Therefore, it seems to be desirable to use the absolute distance of the THW metric towards a reasonable target value as a penalty term of the reward function. As a reasonable target value we propose to use 2s. Further target values can be found in [8].
To sum up, the absolute deviation from a target value seems to be an interesting candidate for a reward component in reinforcement learning.
- (7)
- Replacing the paragraph on pages 6 and 7:
The TTC metric intends to return the minimal time … if it could not brake even more efficiently than the leading agent.
with
Crit. Metric 5 (Time to Collision (TTC), verbatim quote of [7] with formula adjustment to a car-following scenario and alignment of variable names; see also [8,38])
[T]he TTC metric returns the minimal time until A1 and A2 collide …, or infinity if the predicted trajectories do not intersect …. It is defined by
Applicability as a Reward Component in RL
TTC is a scene-level metric that refers to an unbound prediction model [8]. Provided an appropriate prediction model, it could, in principle, be used for in-situ reinforcement learning.
The TTC metric is, however, rather conflictive with other criticality metrics, as it does not guide the following agent. From the perspective of criticality metrics like THW, it would be desirable to keep an appropriate velocity-dependent distance from the leading agent. Of course, if the leading agent brakes, the TTC becomes finite due to the reaction time of the following agent. Although one can compare different braking maneuvers, the TTC values depend mostly on the braking behavior of the leading agent. From the pure TTC perspective, however, a high TTC value would be desirable, although there are different target values for this metric. The implication to the rear agent would be to keep a sufficiently large distance from the leading agent. In other words, assuming an infinite TTC to be optimal, all maneuvers of the agent that correspond to a finite TTC value would be discouraged while all other actions would not be distinguishable through the lens of TTC, potentially prohibiting RL training convergence. The only case where TTC may be interesting as a reward component would be very challenging situations, where the TTC is finite for all maneuvers, so an agent should learn to avoid collisions by the sole mean of braking.
- (8)
- Replacing the paragraph on page 7:
The TET metric [28,29] intends to measure the amount of time … shares the disadvantages of TTC.
with
Crit. Metric 6 (Time Exposed TTC (TET), verbatim quote of [7] with the alignment of variable names; see also [8,39,40])
TET measures the amount of time for which the TTC is below a given target value τ[, i.e.,]
where1denotes the indicator function.
Applicability as a Reward Component in RL
As a scenario-level metric, TET would be hardly applicable as reward component in reinforcement learning.
TET measures the amount of time for which the TTC is below a given threshold . Therefore, high values of the TET should be avoided. In order to ensure the comparability of target values over different scenarios, it is worth considering dividing the TET by the total duration of the scenario.
In summary the TET metric is not directly applicable as a reward component in reinforcement learning.
- (9)
- Replacing the paragraph on pages 7 and 8:
TIT is supposed to aggregate the difference … so our analysis for TET remains valid for TIT.
with
Crit. Metric 7 (Time Integrated TTC (TIT), verbatim quote of [7] with alignment of variable names; see also [8])
[TIT] aggregates the difference between the TTC and a target value τ in a time interval [ts, te][, i.e.,]
Applicability as a Reward Component in RL
As a scenario-level metric, TIT would hardly be applicable as a reward component in reinforcement learning.
Whenever the TTC falls below the given target value, τ, its deviation from the target value contributes to TIT. Hence, low values of the TIT metric seem to be desirable. Similar to our previous consideration of the TET, it could be worthwhile to consider a variant where the TIT value is divided by the duration of the scenario.
In summary the TIT metric is not directly applicable as a reward component in reinforcement learning.
- (10)
- Adding one new paragraph on page 8 explaining the Time to Arrival of Second Actor (T2) metric and how it can be used for RL.
- (11)
- Replacing the paragraph on pages 8 and 9:
The PTTC metric has been proposed by [30]. However, it is important … As PTTC is just a special case of TTC, our analysis for TTC remains valid for PTTC.
with
Crit. Metric 9 (Potential Time to Collision (PTTC) [7]; see also [8,41])
According to [7], “[t]he PTTC metric … constraints the TTC metric by assuming constant velocity of A1 and constant deceleration of A2 in a car following scenario, where A1 is following A2.” The PTTC is defined as follows:
where s0 = p2 − p1, v0 = v2 − v1, and d2 is the deceleration of A2.
Notes
Westhofen et al. [7] refer to [41] as the original source, in which the PTTC is only implicitly given as the root of a quadratic equation. Interestingly, when we solved the quadratic equation, we arrived at a slightly different result than Westhofen et al., which is even unambiguous: As depicted in Figure 1, the distance between the following vehicle, A1, and the leading vehicle, A2, describes a downward opening parabola: . In a car-following scenario the distance is clearly greater or equal to zero at time t0. This guarantees the existence of a collision point where the distance is zero. Moreover, as we are interested in a collision at a time greater or equal to t0, the PTTC is given as the greater of the two roots. With d2 > 0, we, therefore, obtain the Formula (9).
Applicability as a Reward Component in RL
As PTTC is a special case of TTC, the issues that TTC implies for RL training remain valid for PTTC.
- (12)
- Adding a new figure (Figure 1) on page 9:
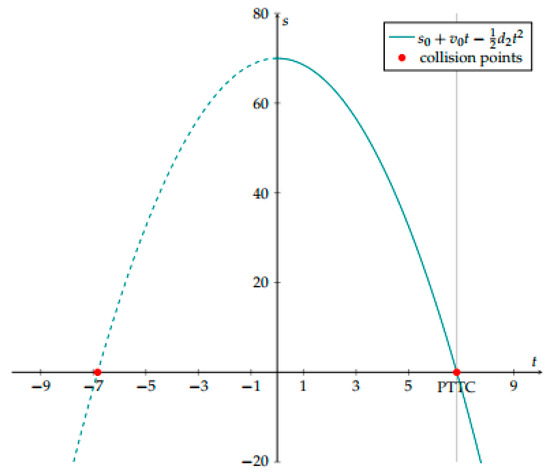
Figure 1.
Distance of A1 and A2 in PTTC.
- (13)
- Replacing the paragraph on page 9:
The WTTC metric intends to extend the usual … It is not clear how to obtain the traces of the actors.
with
Crit. Metric 10 (Worst Time to Collision (WTTC); verbatim quote of [7] with formula adjustment to a car-following scenario and alignment of variable names; see also [8])
[T]he WTTC metric extends the usual TTC by considering multiple traces of actors, i.e.[,]
Applicability as a Reward Component in RL
As RL aims at training an agent, Tr1(t) is to be learned; therefore, one would have to consider only different traces for A2. The issues that TTC implies remain valid. In the already suggested challenging situations, one could think of training with respect to WTTC as some kind of robust RL training method, where several adversarial actions of A2 are taken into account instead of restricting training to one (realized) maneuver of A2.
- (14)
- Replacing the paragraph on page 9:
The definition of the TTM metric in the original source found in [31] is different … should be executed as quickly as possible.
with
Crit. Metric 11 (Time to Maneuver (TTM) [7]; see also [8,42])
According to [7], the TTM metric “returns the latest possible time in the interval [0, TTC] such that a considered maneuver performed by a distinguished actor A1 leads to collision avoidance or −∞ if a collision cannot be avoided.” The following definition of TTM is also from [7] and has been adapted to a car-following scenario:
where p1,m(t0 + t, t0 + s) denotes the predicted position of A1 at time t0 + t if A1 started performing the maneuver m at time t0 + s.
Applicability as a Reward Component in RL
This metric is conflictive with the idea of RL since pre-defining the maneuver already manually reduces the effective action space of the agent. Moreover, reporting the latest time point where a collision could be avoided strongly contradicts forward-looking maneuver planning.
- (15)
- Replacing the paragraph on page 10:
The TTR metric aims to approximate the latest time … See the TTM metric.
with
Crit. Metric 12 (Time to React (TTR), verbatim quote of [7], with the alignment of variable names; see also [8,42])
The TTR metric … approximates the latest time until a reaction is required by aggregating the maximum TTM metric over a predefined set of maneuvers M, i.e.,
Applicability as a Reward Component in RL
TTR can be regarded as the extension of TTM to a whole set of maneuvers. If the action space considered in RL is fully covered, the problem we described for the applicability of TTM as a reward term is alleviated; however, the contradiction to the goal of forward-looking maneuver planning is still valid. Hence, TTR is also conflictive with RL.
- (16)
- Replacing the paragraph on page 10:
The TTZ metric intends to measure the time … as the agent has to attain and even cross it eventually.
with
Crit. Metric 13 (Time to Zebra (TTZ), verbatim quote of [7] with formula adjustment to a car-following scenario and alignment of variable names; see also [8,43])
[T]he TTZ measures the time until actor A1reaches a zebra crossing CA, hence
Applicability as a Reward Component in RL
The metric is a scene metric and is potentially applicable as in-situ reward component if a prediction model is available. However, as the TTZ metric solely measures the time needed until the zebra crossing is reached, it is unsuitable for agent training as the agent has to attain and even cross it eventually.
- (17)
- Replacing the paragraph on page 10:
The TTCE is supposed to measure the time … is even more critical than attaining it at some other time step.
with
Crit. Metric 14 (Time to Closest Encounter (TTCE) [7]; see also [8,44])
According to [7], “the TTCE returns the time … which minimizes the distance to another actor in the future.” Compared with [7], we have prefixed our definition of TTCE with an additional min-operator that resolves possible ambiguities of the set-valued arg min-function, yielding
The proposed definition thus returns the earliest future time, at which point, the distance becomes minimal.
Applicability as a Reward Component in RL
Not applicable, as TTCE solely reports the future time step where both vehicles have the smallest distance without taking the distance itself into account.
- (18)
- Replacing the paragraph on page 11:
The HW metric is supposed to measure the distance … The HW metric has the run-time capability.
with
Crit. Metric 15 (Headway (HW); verbatim quote of [7] with the alignment of variable names; see also [8,37])
[T]he Headway (HW) metric … [is defined] as the distance to a lead vehicle, i.e.,
Applicability as a Reward Component in RL
HW is a scene metric and, therefore, applicable to RL in the sense that, if there is a suitable target value for the given conditions, one can penalize the distance of HW to this target value.
The metric only evaluates the instantaneous situation. The calculation does not require a prediction model to be used and is instantaneous. However, the metric does not take the velocity into account. Therefore, the target value should be selected depending on the speed. For passenger cars, we suggest following the well-known rule of thumb “distance equals half speed (in km/h)”; i.e., τ = 1.8v1 for velocities measured in m/s. Note that a velocity-dependent penalty term in the form (1.8v1 − HW) is equivalent to the term v1(1.8 − THW) using the THW metric with constant velocity assumption for actor A1.
- (19)
- Replacing the paragraph on page 11:
The AGS metric intends to quantify the gap … so there are no implications for the agent.
with
Crit. Metric 16 (Accepted Gap Size (AGS), verbatim quote of [7] with the alignment of variable names; see also [8])
[F]or an actor A1 at time t, the AGS … is the spatial distance that is predicted for A1to act, i.e.,
where a model action(A1, t0, s) predicts […] whether A1 decides to act given the gap size s.
Applicability as a Reward Component in RL
Let be a deterministic ego-policy mapping from state space to action space . The term can be re-written as for the considered action, a, where we can assume that the gap size s, is part of the states . Obviously, AGS is not applicable to RL as the evaluation of AGS already requires an ego-policy which should be computed during RL training.
- (20)
- Replacing the paragraph on page 11:
The section on the criticality metrics paper [7] is just a reference to the TTCE metric (which we already covered in this paper).
with
Crit. Metric 17 (Distance to Closest Encounter (DCE) [7]; see also [8,44])
The DCE is the minimal distance of two actors during a whole scenario and given by
Note the relation to TTCE, which defines the (earliest) time step of the closest encounter.
Applicability as a Reward Component in RL
DCE only takes the closest encounter into account, making it very uninformative as it ignores all other states in the scenario. For example, DCE would even prefer a car-following scenario where both vehicles drive at very high speed and a rather large distance that, due to the high velocities, corresponds to a rather low THW, over a traffic jam scenario where the vehicles are crowded, i.e., the DCE is very low, but barely moves.
- (21)
- Replacing the paragraph on pages 11 and 12:
The PSD metric is defined as the distance to … should be avoided or if it is inevitable.
with
Crit. Metric 18 (Proportion of Stopping Distance (PSD), verbatim quote of [7] with formula adjustment to a car-following scenario and alignment of variable names; see also [8,36])
The PSD metric … is defined as the distance to a conflict area CA divided by the Minimum Stopping Distance (MSD) …. Therefore,
where d1,max is the maximal deceleration available for actor A1.
Applicability as a Reward Component in RL
PSD is, as a scene-level metric, applicable to RL as, an in-situ reward component. As smaller values of PSD indicate a higher criticality, one can indeed use PSD directly as a reward component. Values smaller than one indicate that entering the conflict area is unavoidable. However, it is unsuitable for agent training if the agent has to attain and even cross the conflict area eventually, e.g., if CA is a zebra crossing.
- (22)
- Replacing the paragraph on page 12:
The CS metric intends to estimate the severity of a potential … or the acceleration it took at that point in time as part of its evasive maneuver.
with
Crit. Metric 20 (Conflict Severity (CS) [7]; see also [8,32,46])
The CS metric estimates “the severity of a potential collision in a scenario” and extends the Delta-v metric by additionally accounting for the decrease in the predicted impact speed due to an evasive braking maneuver. While CS was originally proposed by [46], we present here the extended Delta-v metric proposed by [32]; which is based on the same idea.
Let be the remaining time for an evasive maneuver; then, the final speed, , of actor is computed as follows:
where is the maximal deceleration available to actor i. Then,
where α is the approach angle and can be computed as the difference in the angles of the driving directions of A1 and A2. As an estimate for tevasive, Laureshyn et al. [32] proposed using the T2 indicator, i.e., tevasive = T2(A1, A2, t0).
Applicability as a Reward Component in RL
As CS generalizes ∆v by additionally taking braking maneuvers before the collision into account, the above assessment regarding the applicability of ∆v in RL remains valid for CS.
- (23)
- Replacing the paragraph on page 12:
The ∆v metric is defined as the change in speed over collision duration, … The intention of the Equation (18a) is not given
with
Crit. Metric 19 (Delta-v (∆v) [7,32]; see also [8,45])
According to [7], the ∆v metric is defined as “the change in speed over collision duration … to estimate the probability of a severe injury or fatality”. Moreover, “it is it is typically calculated from post-collision measurements”. We refer to a simplified approach presented in [32] that calculates ∆v as if it was given by an ideal inelastic collision
where α is the approach angle and can be computed as the difference in the angles of the driving directions of A1 and A2.
Applicability as a Reward Component in RL
As presented, the ∆v and hence the severity of an impact is determined based only on the actual velocities. Thus, other metrics, such as CollI, AM, or RSS-DS, must be used to assess whether a collision actually occurred. In general, ∆v can be used to weigh the penalty terms due to near collisions: The larger ∆v, the more severe the potential accident. In this way, severity-reducing driving behavior could be trained.
- (24)
- Replacing the paragraph on page 13:
For an actor A1 following another actor A2, the DST metric intends … required acceleration is always comfortable for the person in the vehicle.
with
Crit. Metric 21 (Deceleration to Safety Time (DST), verbatim quote of [7] with formula adjustment to a car-following scenario and alignment of variable names; see also [8,47–49])
[T]he DST metric calculates the deceleration (i.e., negative acceleration) required by A1 in order to maintain a safety time of ts ≥ 0 s under the assumption of constant velocity v2of actor A2… The corresponding formula can be written as
here s0= p2− p1.
Applicability as a Reward Component in RL
The presented version of the DST should only be used under the restrictive conditions of case (a), i.e., v1 > v2 and v2ts < s0, as under these conditions the formula provides correct values for the required deceleration in order to maintain a safety time. Large positive values should be avoided; positive values close to zero indicate that the Safety Time Distance has almost been reached.
Alas, given this restriction, however, one loses those highly critical cases (b) and (d) in which the distance falls below the safety time.
In order to use DST for RL over more general scenarios, the metric would need to be redefined to provide reasonable criticality values over all cases considered. For the special case ts = 0, this is possible, as shown in the following section on along,req.
- (25)
- Adding one new paragraph on pages 13 and 15 about the DST metric and the limitations of its use for RL.
- (26)
- Adding a new figure (Figure 2) on page 14:
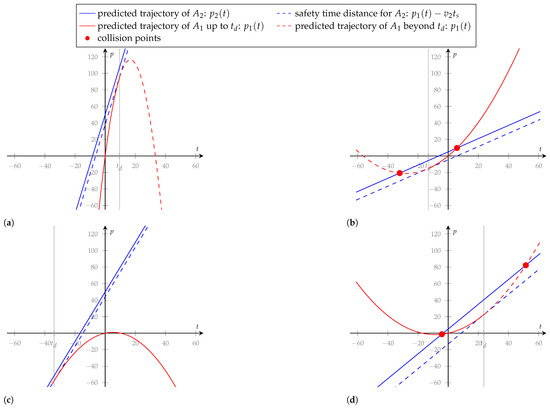 Figure 2. Behavior of DST in cases (a–d). (a) approaches with a high relative velocity. The safety time distance has not yet been established. The computed DST is positive and is a future time point.; (b) approaches with a high relative velocity. The safety time distance has already been undershot. The computed DST is negative and is a past time point; (c) drives slower then . The safety time distance has not yet been established. The computed DST is positive and is a past time point; (d) drives slower then . The safety time distance has already been undershot. The computed DST is negative and is a future time point.
Figure 2. Behavior of DST in cases (a–d). (a) approaches with a high relative velocity. The safety time distance has not yet been established. The computed DST is positive and is a future time point.; (b) approaches with a high relative velocity. The safety time distance has already been undershot. The computed DST is negative and is a past time point; (c) drives slower then . The safety time distance has not yet been established. The computed DST is positive and is a past time point; (d) drives slower then . The safety time distance has already been undershot. The computed DST is negative and is a future time point.
- (27)
- Replacing one paragraph on pages 15 and 16:
Required Longitudinal Acceleration (along,req) For two actors A1, A2 at time t, along,req is supposed to measure … Similarly, as for DST, this required acceleration should be comfortable.
with
Crit. Metric 22 (Required Longitudinal Acceleration (along,req) [7]; see also [8])
According to [7], “along,req measures the maximum longitudinal backward acceleration required … by actor A1 to avoid a collision [with A2] in the future.” We propose using the following modification of the definition in [7], where we assume that the maximal backward acceleration is constant over time.
Applicability as a Reward Component in RL
along,req is an interesting metric that indicates the magnitude of deceleration required so that the following vehicle does not rear-end.
Because of its close relationship to DST, it is worth comparing the two metrics. First of all, it is noticeable that the along,req metric does not take into account any safety time, so in relation to the DST this means ts = 0. The DST with ts = 0 is then a variant of the metric (with swapped sign) for the case where the leading car drives with constant speed. Because ts = 0, cases (b) and (d) discussed for the DST do not apply.
The inadequacy described for the DST in case (c), i.e., the case that the vehicle in front is traveling faster than the vehicle behind, is not an issue for the along,req metric thanks to its abstract definition: in this particular case, the following vehicle may still accelerate (at least for a short moment), and the inequality has a positive solution a1 > 0. However, since only non-positive values for a1 are considered, the metric would return the value zero. Hence, we propose using the following definition for along,req under a constant speed assumption for the leading vehicle:
where s0 = p2 − p1.
In general, the along,req can be used as a reward term that penalizes large negative values, especially values that indicate a required deceleration that is larger than the maximal possible deceleration of the agent. For a version of this metric that takes the maximal deceleration into account, see the BTN.
- (28)
- Replacing the paragraph on page 16:
Required Lateral Acceleration (alat,req) The metric is intended to provide the minimal absolute lateral acceleration in either direction that is required … Similarly, as for DST, this required acceleration should be comfortable
with
Crit. Metric 23 (Required Lateral Acceleration (alat,req), see [7] and [8,37])
According to [7], “the alat,req [metric] is defined as the minimal absolute lateral acceleration in either direction that is required for a steering maneuver to evade collision.” Under the assumption of a constant acceleration model, the required lateral acceleration can be computed as follows [37]:
where the py,i and vy,i denote the lateral components of the position and velocity vectors, respectively, of actor Ai, and sy is the minimal lateral distance of the actors that is required to evade the collision. It can be calculated from the respective widths w1 and w2 of actors A1 and A2 as .
Applicability as a Reward Component in RL
In general, it seems plausible to keep the value of the metric below a target value in order to avoid excessively strong lateral evasive maneuvers. A possible consequence could be that the following vehicle stabilizes in a parallel movement to the vehicle in front with a sufficient lateral distance. If this behavior is undesired, suitable further metrics for lateral guidance should be used.
- (29)
- Replacing the paragraph on page 16:
The metric is defined as follows … See the required lateral and longitudinal acceleration metric.
with
Crit. Metric 24 (Required Acceleration (areq) [7]; see also [8,37])
The required acceleration metric areq is in general an aggregate of the along,req and alat,req. We follow [7] and adopt the proposed definition of the metric “by taking the norm of the required acceleration of both directions”, verbatim with alignment of variable names as
Applicability as a Reward Component in RL
In general, it seems desirable to keep the value of the metric below a reasonable target value to avoid excessively strong evasive maneuvers. Since the value of the lateral metric alat,req is also included in this metric, criticality-reducing parallel movements to the vehicle in front cannot be excluded here without further countermeasures.
- (30)
- Replacing the paragraph on pages 16 and 17:
This section refers to the longitudinal jerk metric, which will be evaluated … The LongJ metric has a run-time capability.
with
Crit. Metric 25 (Lateral Jerk (LatJ); Longitudinal Jerk (LongJ) [7]; see also [8])
In [7], the jerk is introduced as “the rate of change in acceleration”. The following metric definitions refer to j1,long(t) or j1,lat(t), the longitudinal or lateral jerks of actor 1 at time t, and are taken verbatim from [7] with the alignment of variable names:
Applicability as a Reward Component in RL
Both jerk-scale metrics are clearly applicable as reward components. Provided that a bound for the comfortability of the jerks is provided, one could use the negative absolute difference between an uncomfortably high jerk and the bound in order to penalize such jerks.
- (31)
- Replacing the paragraph on page 17:
The AM metric intends to evaluate whether an accident happened … Having no accident is optimal.
with
Crit. Metric 26 (Accident Metric (AM), verbatim quote of [7]; see also [8])
AM evaluates whether an accident happened in a scenario [Sc]:
Applicability as a Reward Component in RL
Although having no accident should be the aim in the reinforcement learning of safe behavior, the AM metric is not directly applicable as a reward term in reinforcement learning, as it is a scenario-level metric and cannot be used for in-situ computations.
- (32)
- Adding one new paragraph on page 17 regarding the Collision Indicator (CollI) metric and its use for RL.
- (33)
- Replacing the paragraph on pages 17 and 18:
For actor A1, the BTN metric is defined as … so BTN has to be always smaller than 1.
with
Crit. Metric 28 (Brake Threat Number (BTN); verbatim quote of [7] with the alignment of variable names; see also [8])
[T]he BTN metric ... is defined as the required longitudinal acceleration imposed on actor by actor at time , divided by the [minimal] longitudinal acceleration that is ... available to in that scene, i.e.,
Applicability as a Reward Component in RL
If the value of the metric is at least one, it is not possible to avoid a collision by braking under the given assumptions of the prediction model, so BTN has to be always smaller than one. Hence, BTN, in a negated version, can be used as a penalty term. Using BTN as the sole reward term in a car-following scenario is problematic because the metric cannot be used to distinguish whether the vehicle behind it is maintaining the speed of the vehicle in front or is falling behind. Therefore, BTN should only be used in combination with reward terms that ensure that the vehicle in the rear is moving forward. For example, let V be a term that rewards the rear vehicle’s high speeds. Then, V(1 − BTN) represents an interesting combination of terms that rewards high values of V and takes its optimum (for a given V) if the rear vehicle is slower or exactly maintains the velocity of the leading car.
- (34)
- Replacing the paragraph on page 18:
The STN metric is defined as … Similarly, as for BTN, a value of at least 1 indicates that the agent cannot avoid a collision by steering.
with
Crit. Metric 29 (Steer Threat Number (STN); verbatim quote of [7] with the alignment of variable names; see also [8,37])
[T]he STN … is defined as the required lateral acceleration divided by the lateral acceleration at most available to A1in that direction:
Applicability as a Reward Component in RL
Similarly, as for BTN, if the STN is at least one, it is not possible to avoid a collision by steering, so a negated version of STN can enter the reward term. Note that, as lateral movements are essentially only executed for lane change, turning etc., a combination with a velocity-scale metric as with BTN is not necessary for STN.
- (35)
- Replacing the paragraph on page 18:
The CI metric intends to enhance the PET metric … which would by definition work as intended assuming everything is well-defined
with
Crit. Metric 30 (Conflict Index (CI); verbatim quote of [7]; see also [8,50])
The conflict index enhances the PET metric with a collision probability estimation as well as a severity factor …:
with β being a calibration factor dependent on [scenario properties] e.g., country, road geometry, or visibility, and … α∈ [0, 1] is again a calibration factor for the proportion of energy that is transferred from the vehicle’s body to its passengers and∆Ke is the predicted absolute change in kinetic energy acting on the vehicle’s body before and after the predicted collision.
Applicability as a Reward Component in RL
In principle, this metric is applicable as a reward component, provided that its evaluation as a scenario-level metric is possible.
As this metric measures how likely a crash is weighted by the severity of the eventual crash, it would be desirable to minimize both aspects to find a tradeoff in the sense that if a collision is unavoidable, maneuvers (such as emergency braking) that minimize the causalities have to be preferred.
- (36)
- Replacing the paragraph on page 18:
The CPI metric intends to calculate the average probability … The metric works as intended by definition.
with
Crit. Metric 31 (Crash Potential Index (CPI), verbatim quote of [7] with the alignment of variable names; see also [8,51])
The CPI is a scenario level metric and calculates the average probability that a vehicle cannot avoid a collision by deceleration. … [T]he CPI can be defined in continuous time as:
Applicability as a Reward Component in RL
In principle, this metric is applicable as a reward component, provided that its evaluation as a scenario-level metric is possible. One should however be aware of the restriction to the collision probabilities themselves, where the severity of the potential crashes is not taken into account, in contrast to the Conflict Index.
- (37)
- Replacing the paragraph on pages 18 and 19:
The ACI metric intends to measure the collision … adds up to the total probability of a crash, so it works as intended.
with
Crit. Metric 32 (Aggregated Crash Index (ACI) [7]; see also [8,52])
According to [7], “[t]he ACI [metric] measures the collision risk for car following scenarios”. It is defined as follows [7]:
The idea is to define n different conflict types, represented as leaf nodes Lj in a tree where the parent nodes represent the corresponding conditions. Given a probabilistic causal model, let P(Lj, t0) be the probability to reach Lj, starting from the state in t0 and let CLj be the indicator, whether Lj includes a collision (CLj = 1) or not (CLj = 0), so that the collision risk at S at t0 is CRLj(S, t0) = P(Lj, t0) · CLj.
Applicability as a Reward Component in RL
This metric is applicable as a reward component, provided that a probabilistic causal model is provided. As low values of ACI correspond to a lower collision risk, it is desirable to keep ACI as small as possible; hence, a negated version of ACI can enter RL as a reward component.
- (38)
- Replacing the paragraph on page 19:
The PRI metric intends to estimate the conflict probability and severity for pedestrian crossing scenarios, … to derive why the agent failed to avoid this situation.
with
Crit. Metric 33 (Pedestrian Risk Index (PRI); verbatim quote of [7] with the alignment of variable names; see also [8])
The PRI [metric] estimates the conflict probability and severity for pedestrian crossing scenario ... . The scenario shall include a unique and coherent conflict period where . Here, is the time needs to come to a full stop at time t, including its reaction time, leading to
where is the predicted speed at the time of contact with the pedestrian crossing.
Applicability as a Reward Component in RL
In principle, this metric is applicable as a reward component, provided that it, as a scenario-level metric, can be evaluated. Obviously, the performance of an agent in a scenario would be better in terms of PRI the smaller the PRI value is; hence, it can enter the RL reward as a negated version. Note that, although including the severity of the impact—in contrast to a metric such as AM – PRI, in the given notion, is restricted to zebra crossings. One should consider replacing the zebra crossing with the position of a lane-crossing pedestrian in order to also respect pedestrians that cross the road without using a zebra crossing. One should further note that, although CS already incorporates the severity of a collision, due to ethical reasons, pedestrians should indeed be respected individually, so even using CS and PRI in combination, there would be essentially no redundancy.
- (39)
- Replacing the paragraph on pages 19 and 20:
The RSS-DS metric is intended for the identification of a dangerous … coordinate their maneuvers to achieve the optimal value 0 of RSS-DS
with
Crit. Metric 34 (Responsibility Sensitive Safety Dangerous Situation (RSS-DS); verbatim quote of [7]; see also [8,53]):
[T]he safe lateral and longitudinal distances and are formalized, depending on the current road geometry. The metric RSS-DS for the identification of a dangerous situation is [...] defined as
Applicability as a Reward Component in RL
Usually, one trains the ego agent in RL training, so one only would inspect the RSS-DS metric for the ego agent; however, one can also perform joint training in the sense of training multiple agents simultaneously, so that one has to use the sum or the maximum of the individual RSS-DS values in RL. Besides being a scenario-level metric and, therefore, hardly applicable to in-situ RL, the whole metric is questionable in light of other metrics, as it only outputs whether the safety distances are violated, but not to what extent or how long, making the RSS-DS values quite non-informative. Hence, we suggest not including RSS-DS in RL training.
- (40)
- Replacing the paragraph on page 20:
For a given scenario in the time … Same as mentioned before for the RSS-DS metric.
with
Crit. Metric 35 (Space Occupancy Index (SOI) [7]; see also [8,54])
According to [7], “[t]he SOI defines a personal space for a given actor … and counts violations by other participants while setting them in relation to the analyzed period of time” [ts, te]. The SOI is defined as
where counts the conflicting overlaps of the personal spaces, , of actor with the personal space, , any other actor , , at time t:
Applicability as a Reward Component in RL
In a similar argumentation to RSS-DS, apart from SOI being a scenario-level metric and therefore hardly applicable to in-situ RL, SOI again only outputs whether the personal spaces overlapped, which can be interpreted as a more flexible extension of RSS-DS where the personal spaces are defined solely by longitudinal and lateral distances. The only difference is that SOI takes the number of time steps with a violation into account but not the extent of the violation, i.e., whether one agent deeply infiltrated the personal space of some other actor with high velocity and nearly provoked a collision or whether one agent constantly drives in a way such that its personal space slightly overlaps the personal space of some other agent. Note that the second example, which is unarguably less critical, could easily lead to a higher SOI value; hence, we discourage the usage of SOI in RL.
- (41)
- Replacing the paragraph on pages 20 and 21:
The TCI metric intends to find a minimum difficulty value … it is desirable to have low difficulty values where the concrete values depend on the concrete situation.
with
Crit. Metric 36 (Trajectory Criticality Index (TCI); verbatim quote of [7] with the alignment of variable names; see also [8,55])
The task [of the TCI metric] is to find a minimum difficulty value, i.e., how demanding even the easiest option for the vehicle will be under a set of physical and regulatory constraints. ... Assuming the vehicle behaves according to Kamm’s circle, TCI for a scene S ... reads as
where is the prediction horizon, and the longitudinal and lateral accelerations, the maximum coefficient of friction, g the gravitational constant, w weights, and and the longitudinal and lateral margins for angle corrections:
Here, , is the position, the discrete time step size, the maximum velocity, the reference for a following distance (set to ), the position with the maximum lateral distance to all obstacles in S, , the maximum longitudinal and lateral deviations from , .
Applicability as a Reward Component in RL
The usage of TCI would contradict the idea of RL. Although TCI is interesting for scenario evaluation, agent training should not be biased towards simple maneuvers (where the term “simple” is defined by low TCI values) but encourage safe driving at all costs. Hence, taking the difficulty of maneuvers into account may have the potential to decide on a simple but less safe maneuver if the reward terms are unsuitably weighted. Hence, in order not to even risk having such a situation, we discourage the use of TCI for RL.
- (42)
- Replacing the paragraph on page 21:
The P-MC metric intends to produce a collision probability … it is not clear how to compute P(C|U) or solve the integral
with
Crit. Metric 37 (Collision Probability via Monte Carlo (P-MC); see also [7,8,56])
The P-MC metric intends to produce a collision probability estimation based on future evolutions from a Monte Carlo path-planning prediction and is defined [7] as follows:
where
is the collision probability of actor in S under concrete control inputs and where the are priority weights.
Applicability as a Reward Component in RL
Provided that all necessary components for the computation of P-MC are available, P-MC could be used for RL training for discrete action spaces. Given such an action space where , one would replace the formula for with the current policy . Hence, for each state S, can be computed with respect to the current policy and the assumed transition model. Thus, deciding for some action, , in time step and rolling the scenario out for the subsequent time steps will provide information about how likely a collision will be, indeed allowing for a retrospective decision for the best action in the current time step in the spirit of RL; therefore, using P-MC (in a negated version as small values are better than large values) as a reward component is reasonable. One has to be careful in the situation of continuous action spaces as one would have to integrate over the full continuous action space instead of a finite selection of control inputs.
- (43)
- Replacing the paragraph on pages 21 and 22:
The P-SMH metric intends to assign … and neither is a way of getting the probabilities of each trajectory.
with
Crit. Metric 38 (Collision Probability via Scoring Multiple Hypotheses (P-SMH) [7]; see also [8,57])
The P-SMH metric assigns probabilities to predicted trajectories and accumulates them into a collision probability. We follow [7] where the metric is presented verbatim with alignment of variable names as
where—again from [7]—“ equals one if and only if the i-th trajectory of and the j-th trajectory of the actors in lead to a collision, and resp. are the probabilities of the trajectories being realized.”
Applicability as a Reward Component in RL
P-SMH can be interpreted as a cumulative compromise between RSS-DS and AM in the sense that one not only checks whether a collision or whether a near-collision between the ego agent and another agent occurred but how often the ego agent collides with any other actor, summed up in a weighted manner over all considered trajectories. Hence, it shares the same disadvantage as RSS-DS and AM, namely the non-informativity, but, thanks to the integrated prediction module, different ego-actions should be easier to distinguish; they should not lead to exactly the same collision probabilities in contrast to RSS-DS or AM. Hence, P-SMH is applicable as a reward component, again, in a negated version, provided that all components are available.
- (44)
- Replacing the paragraph on page 22:
The P-SRS metric intends to estimate a collision probability … making it hard to apply in practice.
with
Crit. Metric 39 (Collision Probability via Stochastic Reachable Sets (P-SRS) [7]; see also [8,58])
According to [7], the P-SRS metric “estimate[s] a collision probability using stochastic reachable sets” and originates from [58]. Assuming a discretized controller input space and state space, let ph(tk) denote the probability vector of the states reached in time step tk for input partition h. These probability vectors are updated by a Markov chain model. The goal is to approximate the probability of a crash.
First, ref. [58] (Section V.B) shows how to compute the probability vectors with respect to time intervals given for all input partitions, h. By respecting vehicle dynamics, road information, speed limits, and the interactions of the agents, they eventually compute the probability for a path segment, e, being attained in some interval , denoted by . As the vehicles may not exactly follow the paths, the authors of [58] additionally model the lateral deviations from the paths, denoted by , indicating the probability that the deviation from the path lands in some interval, , where they assume that the probability is constant for intervals in which the whole deviation range is discretized. Assuming that the path and deviation probabilities are independent, the actual position can be computed for each time interval and agent, enabling us to compute the probability of crashes by summing up all the probabilities for cases where the vehicle bodies overlap.
Applicability as a Reward Component in RL
P-SRS could be interpreted as a counterpart of P-MC, which differs from it by the underlying model and computation but which is not (necessarily) restricted to discrete action spaces. Hence, P-SRS can be used (again, in a negated version) as a reward component for RL.
- (45)
- Adding new paragraphs on pages 22 and 23 regarding the Lane Potential, Road Potential, Car Potential, and Velocity Potential, as well as their use for RL.
- (46)
- Replacing the paragraph on pages 23 and 24:
The SP metric intends to measure how unsafe … The metric is not well-defined since it is not clear how to compute tstop(Ai) or tint.
with
Crit. Metric 44 (Safety Potential (SP) [7]; see also [8,59])
The SP metric measures how unsafe, with regards to collision avoidance, a situation is. We reproduce the definition of [7] verbatim with the alignment of variable names as
where and where is the earliest intersection time predicted by a short-time prediction model of the trajectories and refers to the first time step of an intersection while denotes the time where actor i has achieved a full stop.
Applicability as a Reward Component in RL
As the SP metric quantifies a time distance, large values are desirable. Hence, SP can enter as reward component as it is.
- (47)
- Adding new paragraphs on page 24 regarding the Off-Road Loss and Yaw Loss and their use for RL.
- 5.
- The old “Proposed Green-Based Criticality Metrics” chapter presents metrics that can give the reader the impression that they can be used on their own as reward components when training RL agents. However, this is not the case, and, therefore, in the new version of the manuscript, we present new, environmentally friendly metrics and explain their applicability as a reward component in RL.
A correction has been made to “Proposed Green-Based Criticality Metrics”.
- (1)
- Replacing the title on page 24:
Proposed Green-Based Criticality Metrics
with
Proposed Environmentally Friendly Criticality Metrics
- (2)
- Replacing one paragraph on pages 24 and 25:
Considering the importance of climate change … but also the safety in a car-following scenario.
with
Considering the importance of climate change and recent efforts in the literature to propose methods that can reduce the number of CO2 emissions, in this section, we both collect corresponding metrics from the literature and propose an environmentally friendly criticality metric that combines not only the environmental impact but also the safety in a car-following scenario.
- (3)
- Replacing one paragraph on page 25:
4.1. Average Car CO2 Emissions Per KM According to the European Environment Agency [34], the average CO2 emissions per km of a diesel-powered car … where d is the distance travelled by the vehicle in the drive in kilometers.
with
Crit. Metric 47 (Dynamic-based Car CO2 Emissions (DCCO2E))
The DCCO2E metric approximates, based on the car’s dynamics, the number of grams of CO2 emitted by the car on a given drive.
In [21], Zeng et al. consider the vehicle dynamics of vehicles with combustion engines, including rolling resistance force, aerodynamic drag force and gravitational force. They derived a formula where they took the rolling resistance, the air drag force, and the inclination of the road into account; however, they emphasize that their formula contains some parameters that are hard to estimate in practice. Hence, in a linear regression approach, they derive the following simplified formula describing the instant petrol consumption in grams per second of a vehicle with a combustion engine:
where θ is the angle of road inclination. The parameters, β, summarize different environment or vehicle-specific quantities such as the mass density of air and the mass of the car. Zeng et al. report a parameter estimation and validation against other CO emission models and propose the following parameter values for an average petrol-powered vehicle , , , , , and .
To determine the fuel consumption of an average diesel-powered car note that the parameters (except ) are inversely proportional to the fuel energy constant of the particular fuel. That is, while keeping all other specifics of the vehicle at their average value, for a diesel-powered vehicle one has to set the parameters as follows , , as the fuel energy constants are ca. 41.0 MJ/kg for petrol and 43.0 MJ/kg for diesel (Source: https://de.wikipedia.org/wiki/Motorenbenzin and https://de.wikipedia.org/wiki/Dieselkraftstoff (accessed on 7 December 2022)).
One key issue with Zeng et al. is that it is unclear whether they consider petrol or diesel-powered cars.
Nonetheless, the CO emission can be approximated linear to fuel consumption, where the emission for a petrol-powered vehicle is and for a diesel-powered vehicle kilogram per second (Source for emission per liter https://www.helmholtz.de/newsroom/artikel/wie-viel-co2-steckt-in-einem-liter-benzin/, source for density of petrol https://de.wikipedia.org/wiki/Motorenbenzin (accessed on 7 December 2022) and diesel https://de.wikipedia.org/wiki/Dieselkraftstoff (accessed on 7 December 2022)).
Hence, we define the DCCO2E metric as follows:
where v is the velocity at time t, a is the acceleration at time t, and θ the inclination of the road. A scenario-level variant of this metric can be obtained by integrating over time:
Applicability as a Reward Component in RL
This metric is, on its own not applicable as a reward component as it would encourage the agent not to move at all. However, it is clearly applicable as an auxiliary reward component in RL provided that the reward term consists of at least one reward component that encourages the liveness of the agent.
- (4)
- Replacing one paragraph on page 26:
4.1.2. Green Energy CO2 Emissions Saved (GECO2ES) The GECO2ES metric measures how much CO2 is saved in an electric vehicle … where d is the distance travelled by the vehicle in the drive in kilometers.
with
Crit. Metric 48 (Dynamic-based CO2 Emissions Weighted Vehicle Performance (DCO2-EWVP))
This metric will combine the DCCO2E metric with a performance indicator from 0 to 1, 0 being the worst performance and 1 being the best performance (the method of quantifying the vehicle performance depends on the scenario and the particular interest of the experiment and may be quantified using a normalized version of one or a combination of criticality metrics). It returns a similar performance indicator (ranging from 0 to 1) that also accounts for the CO2 emissions of the vehicle. We define it as follows:
where S is the scenario, A is the vehicle to evaluate, p is the performance indicator of the vehicle, and α a parameter controlling the impact of the in the calculation.
A few possible options for p would be the percentage of travels that do not result in accidents, the percentage of scenarios that were completed by the vehicle, the accuracy with which the vehicle followed a route, etc.
Applicability as a Reward Component in RL
This metric is a vehicle metric and cannot be used as a reward component since the agent cannot learn to change vehicle type and does not take into account the driving behavior. However, it can be applied to a scenario as a measure of how many CO2 emissions are produced on average by different types of vehicles (powered by diesel, petrol, electricity from the grid, or by green energy) in the scenario.
- (5)
- Replacing one paragraph on pages 26 and 27:
4.1.3. CO2 Emissions Weighted Safety Distance (CO2EWSD) With the previous metrics defined in this chapter, we now create a novel green-based criticality … is the ratio of time spent driving at a safe distance of the total time.
with
Crit. Metric 49 (Electric vehicle’s power consumption (EVP))
The formulae for the fuel consumption and the CO2 emissions of petrol and diesel cars cannot be applied to electric vehicles, however, they also use power and are, therefore, not emission-free. As the amount of petrol or diesel can be expressed in terms of energy, it would be desirable to also compute the amount of energy used for electric vehicles. We use the approach of [22] here in order to compute the necessary motor power of an electric vehicle, being aware that there are very similar approaches in other works such as [24] or [23].
Combining [22] (Section 2.2.7) and [23] (Equation (1)), the required motor power is provided by
with the vehicle’s mass, m, the gravitational acceleration, g; the inclination angle, θ, of the road; rolling resistance coefficients, , and ([23]), the density, ρ, of the air; the vehicle’s front surface, , the aerodynamic drag coefficient, ([23]); the wind speed, ; the rotary inertia coefficient, ([22]); and the transmission efficiency, , from the motor to the wheels ([22]). Note that we do not take battery efficiency or regenerative braking energy into account here.
Applicability as a Reward Component in RL
This metric is, on its own, not applicable as a reward component, as it would encourage the agent not to move at all. However, it is clearly applicable as an auxiliary reward component in RL, provided that the reward term consists of at least one reward component that encourages the liveness of the agent.
- 6.
- The old “Usage of Criticality Metrics for AI Training” section presents a noncomplete theoretical discussion about the usefulness of the metrics for AI training. However, in the new version of the manuscript, we extended the discussion and provide the reader with a better understanding of the metrics and better explain how some metrics can be more interesting than others when selecting them for AI training.
A correction has been made to “Usage of Criticality Metrics for AI Training” to reflect the previous changes.
- 7.
- The old “Application of the Metrics” chapter presents only a way to apply the metrics in a simple scenario, which, despite proving that certain metrics can be used for evaluating a critical situation in a scenario, are not actually applied as reward components in AI training. This is another major minus in the old version of the paper because it proves to the reader that the existing work lacks in quality and is incomplete without this aspect being covered. In the new version of the manuscript, we much better explained the scope and purpose of our experiments and described the entire scenario and the considered metrics used as reward components in RL training by also presenting the mathematical equations regarding the reward functions. We also compared all the trained metrics in order to provide the reader with a better understanding of which agent performed better by which metric. On top of that, we also evaluated how many CO2 emissions were produced by different types of vehicles on the trained metrics.
A correction has been made to “Application of the Metrics”.
- (1)
- Replacing the title on page 28:
Application of the Metrics
with
Application of the Criticality Metrics as Reward Component in RL
- (2)
- Adding new paragraphs on pages 28–39 describing the implementation of the metrics as a reward function in RL as well as describing the simulation setup and the training results, followed by a comparison of the trained metrics results and an evaluation regarding their environmental impact, also including all relevant figures and tables.
- 8.
- The old “Conclusions and Future Work” section mentions that the paper investigates if the existent criticality metrics are well defined and work as intended. This can be misunderstood by the reader, as mentioned earlier, as meaning that some of the metrics of Westhofen et al. are not well defined or do not work as intended. In the new version of the manuscript, we clearly stated the scope and intention of the performed metrics analysis as being their applicability as a reward component in RL, as well as that the metrics were applied in AI training, providing the reader with valuable information regarding the reward choice.
A correction has been made to “Conclusions and Future Work”.
In this paper, we analyzed several criticality metrics in terms of their applicability as a reward component in RL training and proposed environmentally friendly metrics as well as an environmentally friendly criticality metric that combines performance and environmental impact, a metric for measuring the CO2 emissions of traditional vehicles and a metric to measure the motor power used by electric vehicles, with the goal being the facilitation of their selection by future researchers who want to evaluate both the safety and environmental impact of AVs. Regarding the application of the metrics, we applied some of the metrics in a simple car-following scenario and showed in a simulation that our proposed environmentally friendly criticality metric, called DCO2EWVP, can be successfully used to evaluate AVs from the performance and environmental points of view. We also showed that AVs powered by diesel emitted the most carbon emissions (447 g of CO2), followed closely by petrol-powered AVs (379 g of CO2). Similar results are found using the EVP metric, and we find a correlation between the DCCO2E metric and the EVP metric. Considering that in our evaluation regarding the training of criticality metrics as reward components in RL, all models were trained for the same amount of training iterations, the fact that these results were so different, shows the importance of the reward choice. In conclusion, our work encourages future researchers and the industry to develop more actively sustainable methods and metrics that can be used to power AVs and evaluate them regarding both safety and environmental impact. Regarding the limitations of this work, we are aware that safety and sustainability are just two facets of autonomous driving and that their acceptance also depends on other aspects such as performance-to-price value, travel time, or symbolic value, as seen in the work presented in [61]. As this work considers the training of an autonomous agent where safety, sustainability, and travel time can be optimized, the price or social values cannot be affected by AI training itself, therefore, this work is restricted to the former aspects. In future work, we plan to make use of these criticality metrics when training an AI in selected real use cases such as an overtaking scenario.
- 9.
- The old “Abbreviations” section gives the reader the impression that we entirely used our own abbreviations, which is not correct. In the new version of the manuscript, we clearly mention the original source of the abbreviations and extended them by including Collision Indicator, Time to Arrival of Second Actor, Lane Potential, Road Potential, Car Potential, Velocity Potential, Off-Road Loss, Yaw Loss, Dynamic-Based Car CO2 Emissions, Dynamic-Based CO2 Emissions, Weighted Vehicle Performance, and Electric Vehicle’s Power Consumption.
- 10.
- The old “Nomenclature” section did not separate the symbols between Scenario/Scene and actor-specific symbols or short and general notations. In the new version of the manuscript, this problem is solved, thus providing the reader with a better understanding of the symbols presented in the manuscript. We also added scenario/scene and actor-specific symbols as well as short notations and general notations.
- 11.
- Other questions
The authors and the Editorial Office would like to apologize for any inconvenience caused to the readers and state that the scientific conclusions are unaffected. The original article has been updated.
References
- Jurj, S.L.; Werner, T.; Grundt, D.; Hagemann, W.; Möhlmann, E. Towards safe and sustainable autonomous vehicles using environmentally-friendly criticality metrics. Sustainability 2022, 14, 6988. [Google Scholar] [CrossRef]
- Westhofen, L.; Neurohr, C.; Koopmann, T.; Butz, M.; Schütt, B.; Utesch, F.; Kramer, B.; Gutenkunst, C.; Böde, E. Criticality metrics for automated driving: A review and suitability analysis of the state of the art. Arch. Comput. Methods Eng. 2023, 30, 1–35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).