Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrologic and Hydraulic Models
2.1.1. EPA-SWMM
2.1.2. MOHID Land
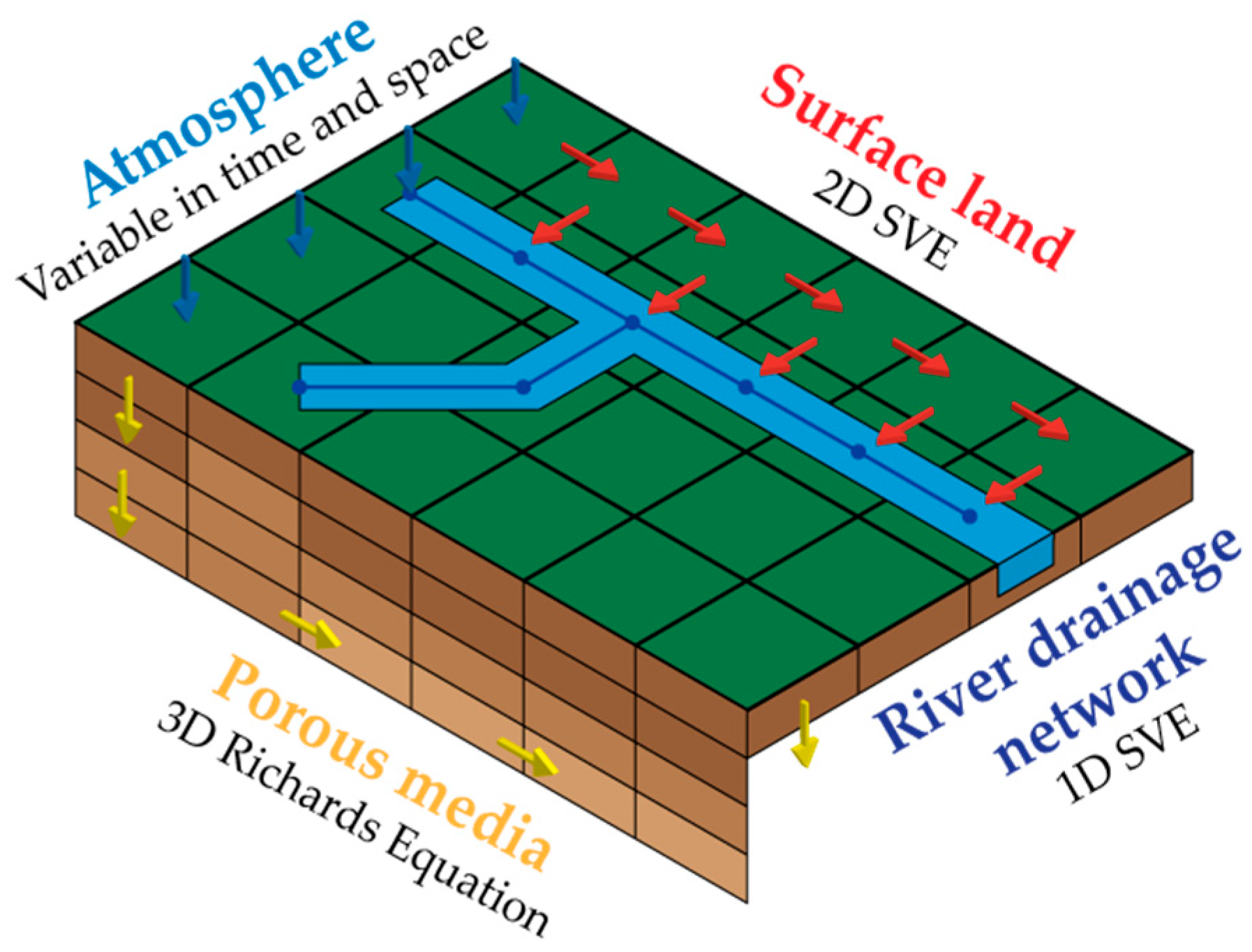
2.2. SWMM/Land Coupling Methodology
2.2.1. Coupling Rationale
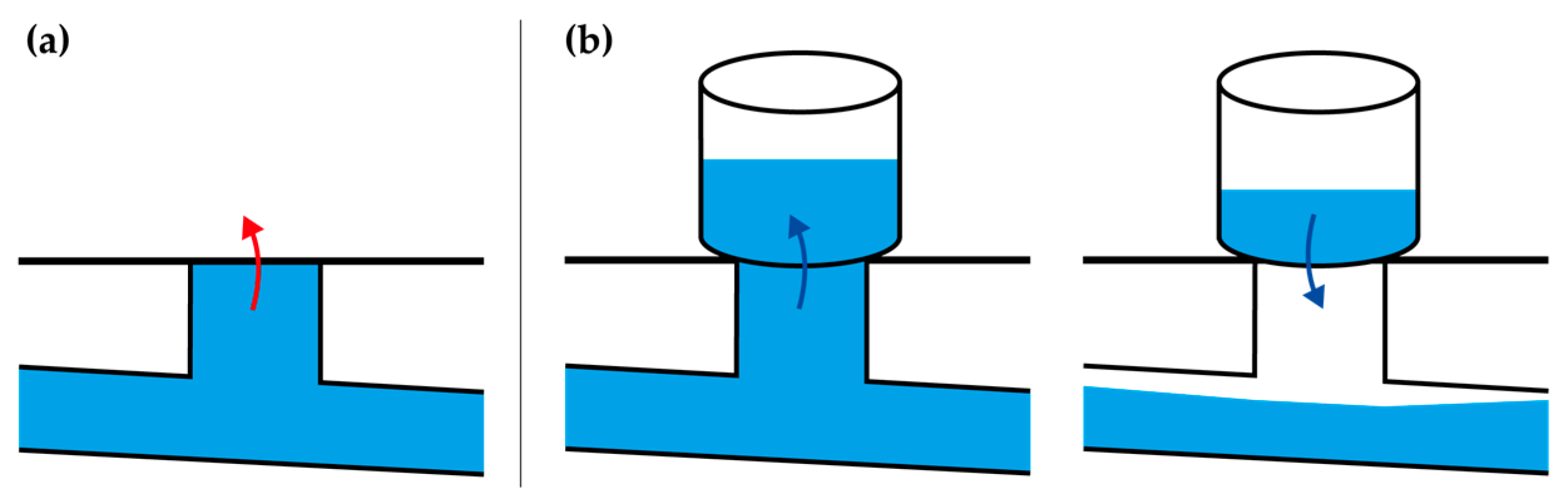
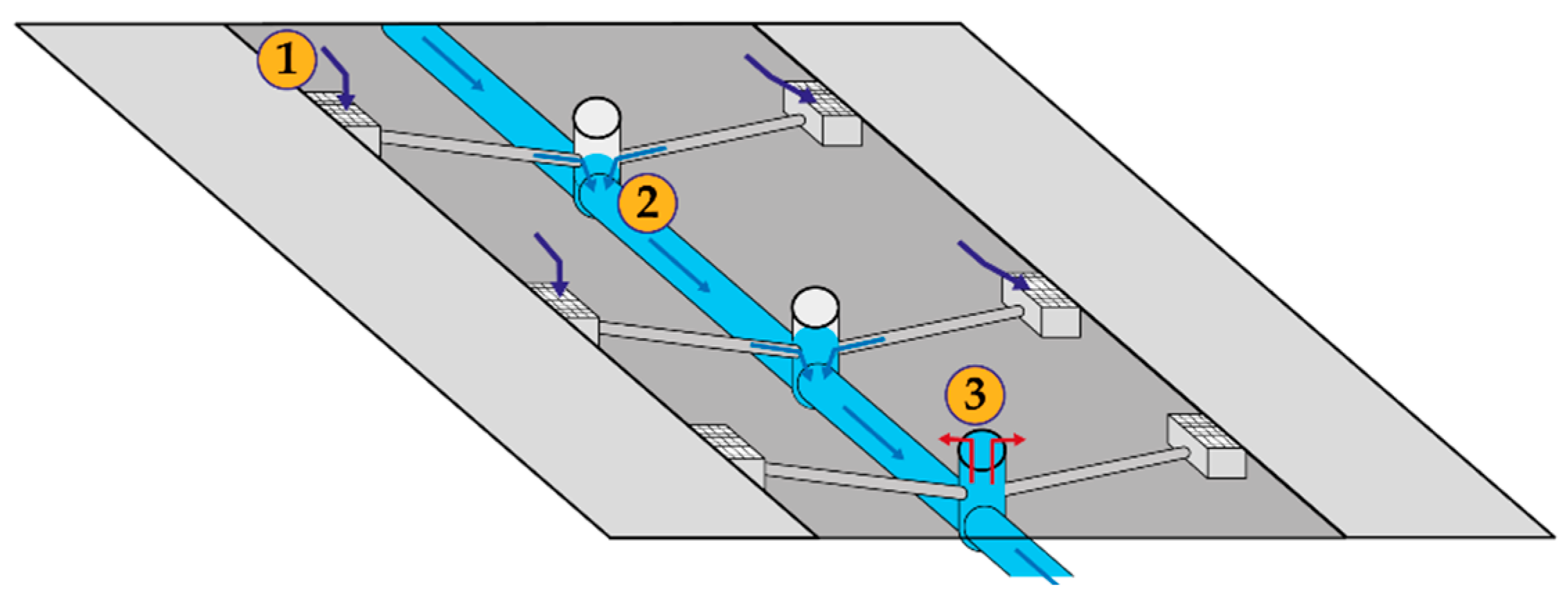
- Stormwater inlets capture surface runoff (on MOHID Land) and route it to the urban drainage network. The captured water will decrease the water level at the surface, i.e., the water column in the corresponding cell of the 2D surface grid. In abnormal conditions, flooding occurs if the stormwater inlets are insufficient in number and/or have insufficient capacity, leading to water accumulation at the surface.
- Water captured by the stormwater inlets is conveyed by the urban drainage network and discharged at the outfall (on SWMM), often a river or sea.
- When the captured flow surpasses the carrying capacity of the urban drainage infrastructures, such that the water depth inside the network reaches the surface level, part of the captured water can return to the surface through manhole overflow. If a given manhole is overflowing, the intake capacity of the connected inlet devices is set to zero.
2.2.2. Data Requirements
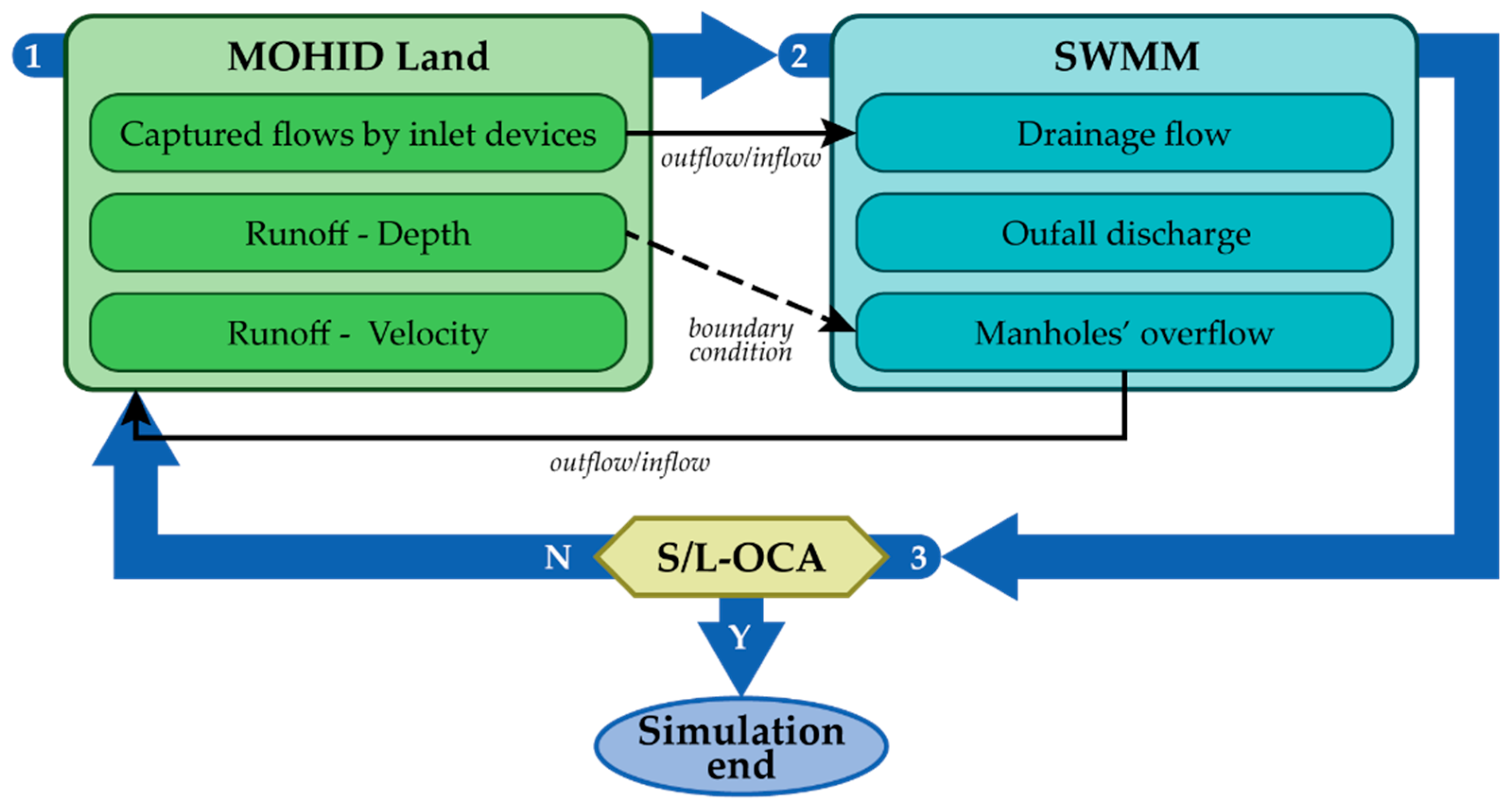
2.2.3. Coupling Procedure
- Manhole overflow occurrence: if there is any manhole overflow during the simulation time, another simulation cycle is required to model such inflows at the surface.
- Water depth convergence between cycles: from the second cycle onwards, the water depth results in a set of user-defined 2D probe cells that are compared, and a new simulation cycle is required if the convergence is smaller than a given user-defined threshold.
3. Application to Case Study and Results
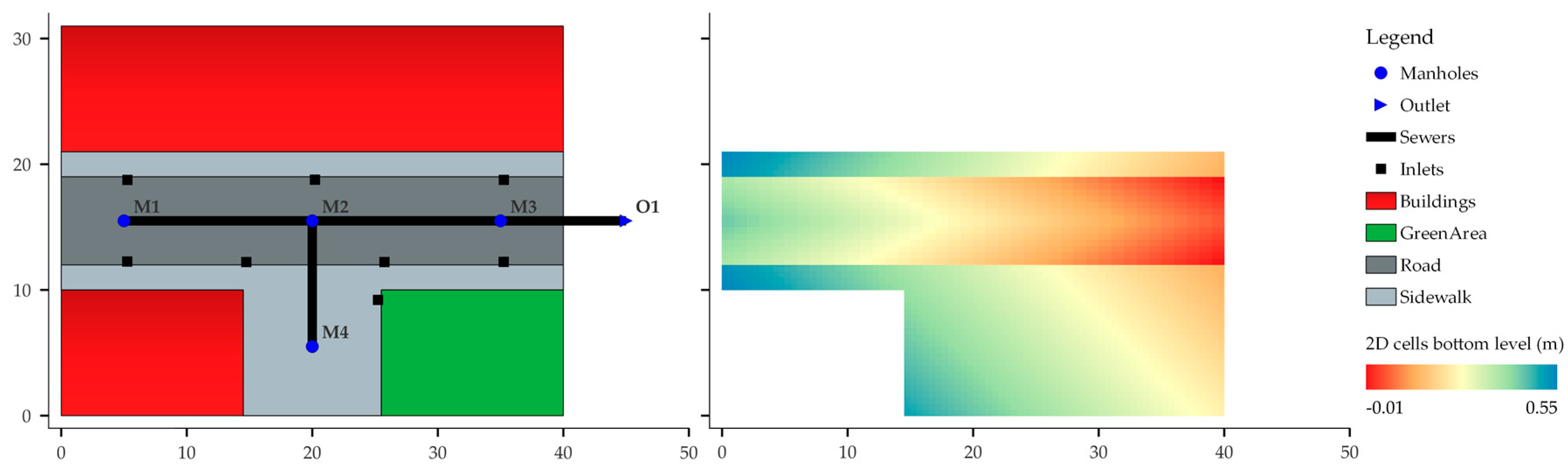
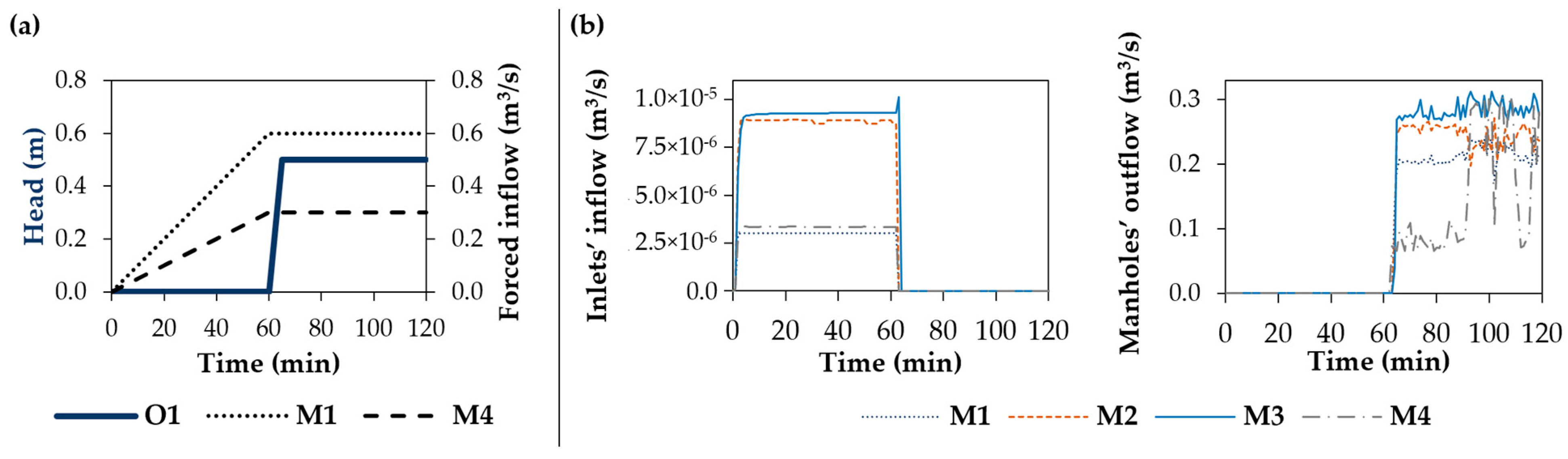
3.1. Synthetic Case Study: Simplified Street
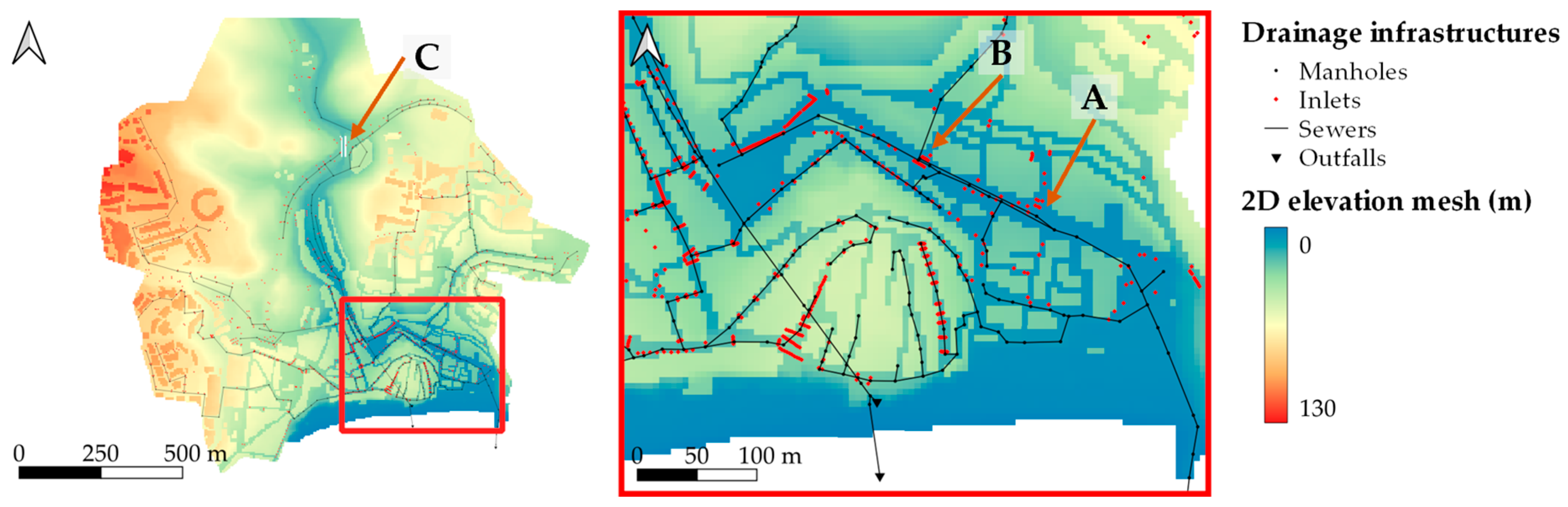
3.2. Real Case Study: Downtown Albufeira
3.2.1. Real Case Study Description
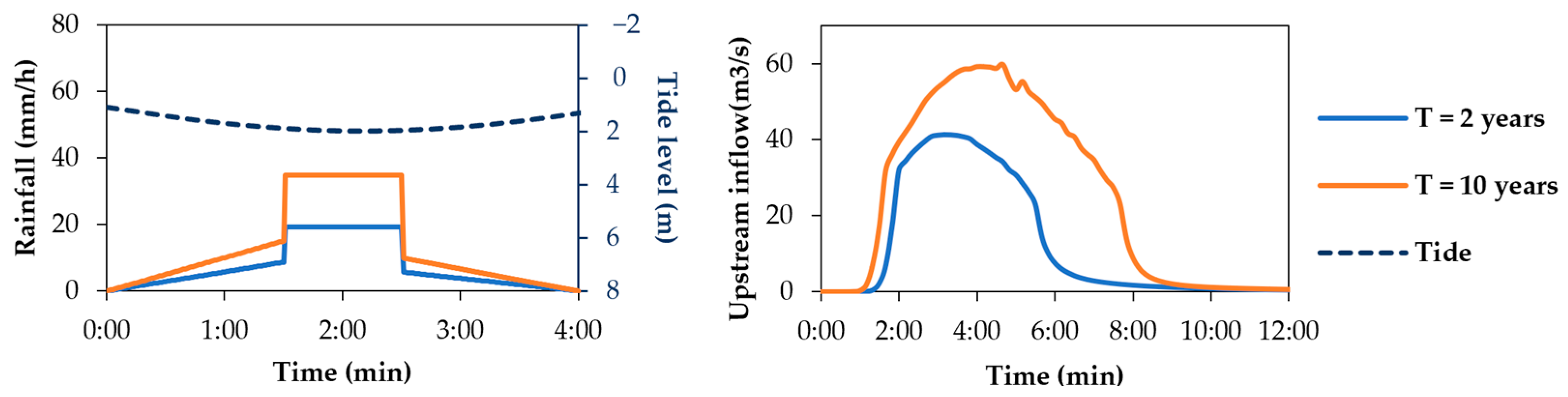
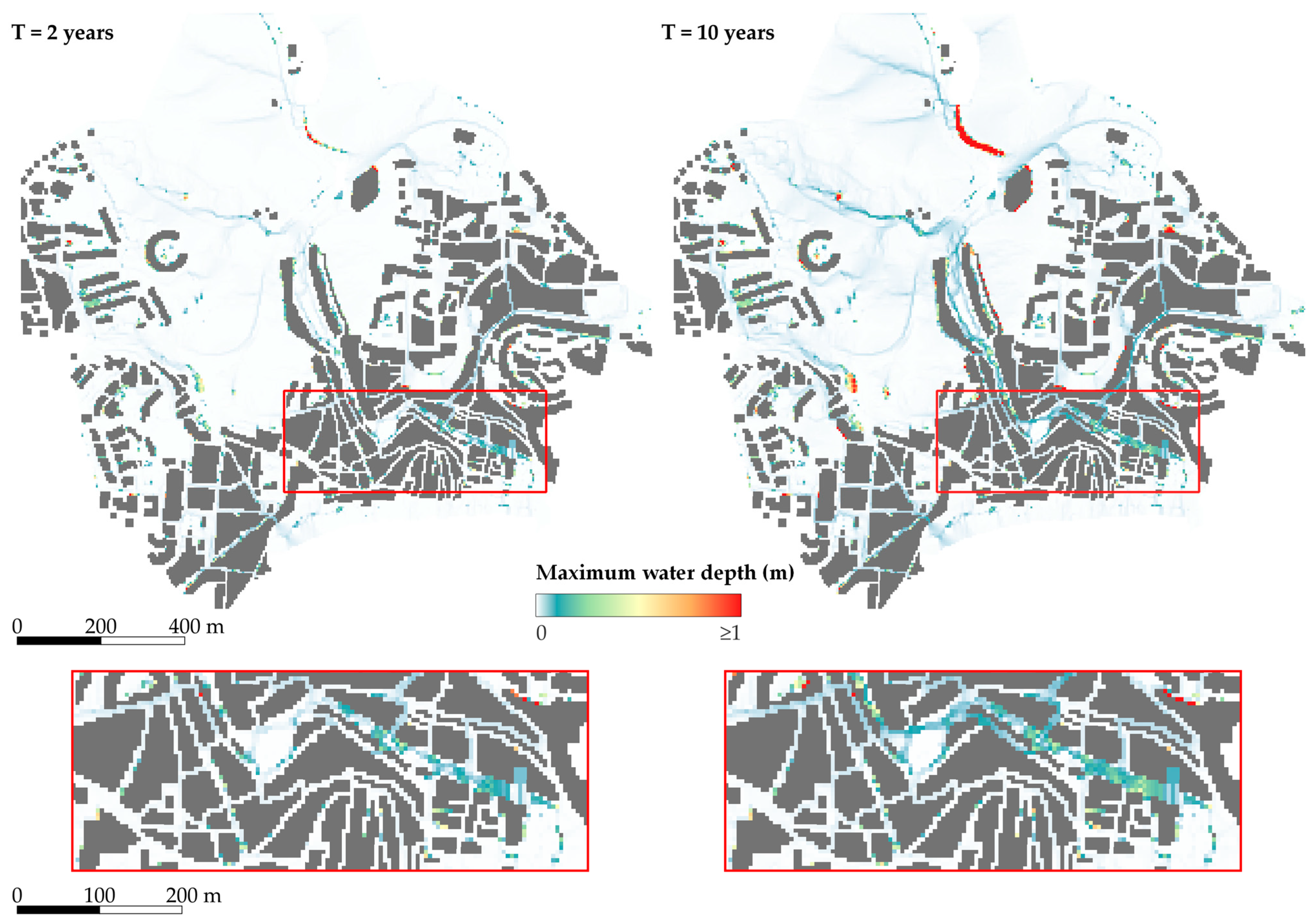
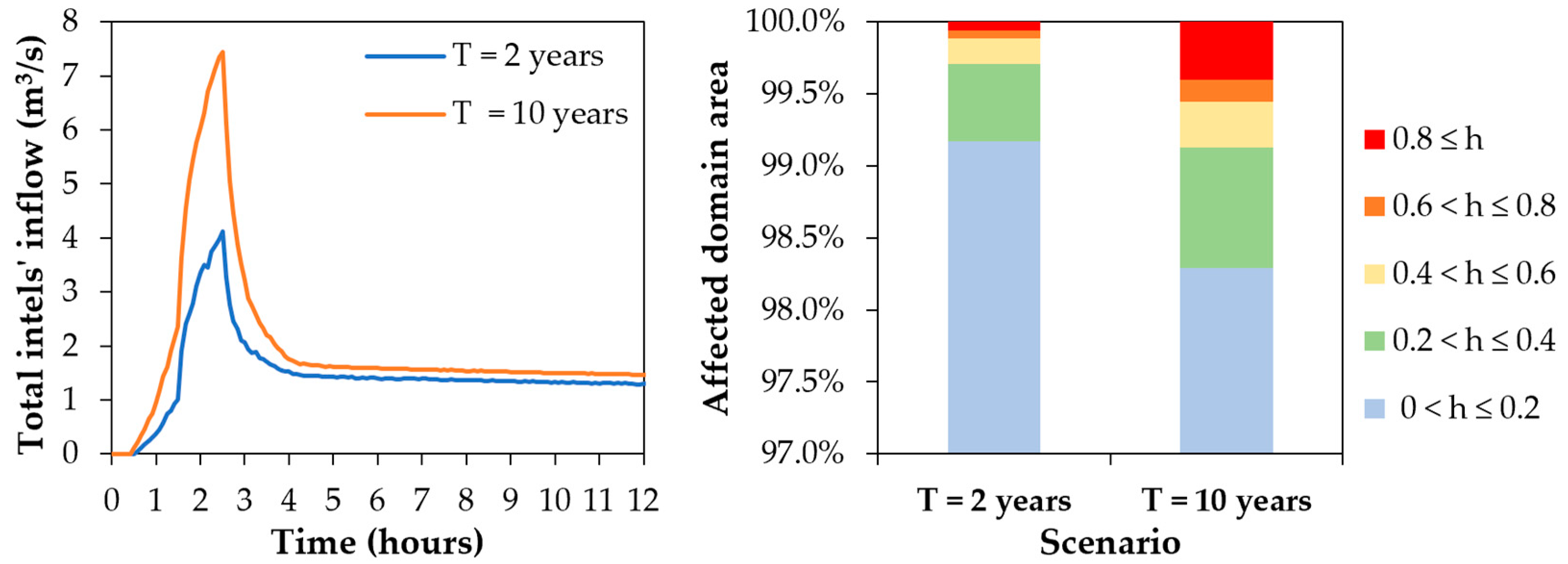
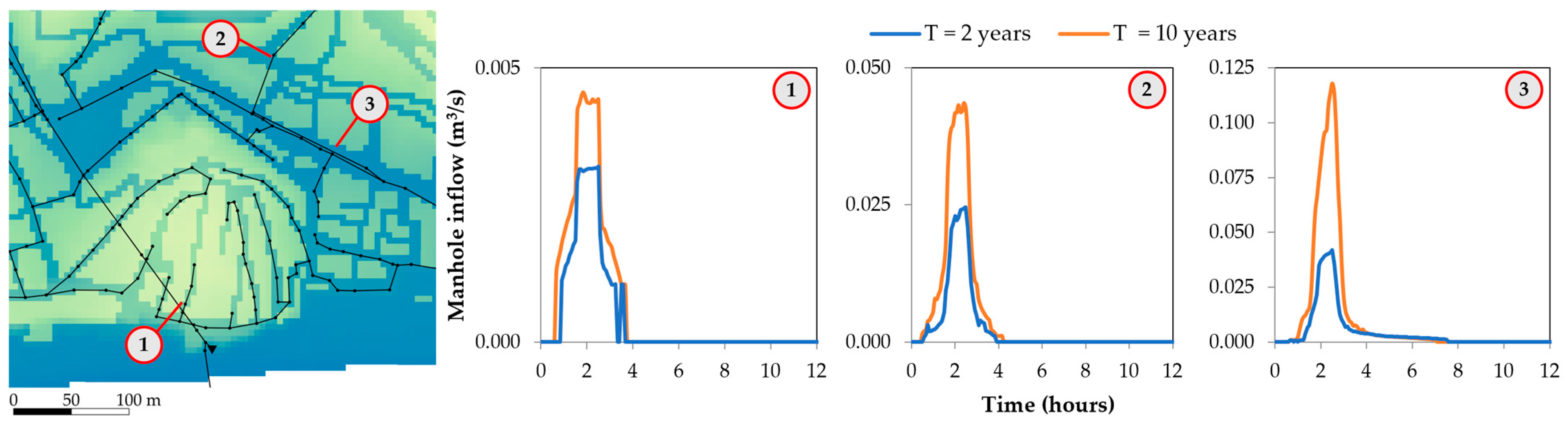
3.2.2. Real Case Study Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramos, C. Perigos naturais devidos a causas meteorológicas: O caso das cheias e inundações. e-LP Eng. Technol. J. 2013, 4, 11–16. [Google Scholar]
- World Meteorological Organization. Selecting Measures and Designing Strategies for Integrated Flood Management: A Guidance Document; Global Water Partnership: Stockholm, Sweden, 2017. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2022: Impacts, Adaptation and Vulnerability; Pörtner, H.-O., Roberts, D., Poloczanska, E., Mintenbeck, K., Tignor, M., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; pp. 3–33. ISBN 978-1-00-932584-4. [Google Scholar]
- Howard, G.; Bartram, J. The Resilience of Water Supply and Sanitation in the Face of Climate Change; Vision 2030; World Health Organization: Geneva, Switzerland, 2010. [Google Scholar]
- United Nations. World Urbanization Prospects: The 2018 Revision (ST/ESA/SER.A/420); United Nations: New York, USA, 2019. [Google Scholar]
- Paul, M.J.; Meyer, J.L. Streams in the Urban Landscape. Annu. Rev. Ecol. Syst. 2001, 3, 333–365. [Google Scholar] [CrossRef]
- Sousa, V.; Ferreira, F.M.; Meireles, I.; Almeida, N.; Saldanha Matos, J. Comparison of the Inspector and Rating Protocol Uncertainty Influence in the Condition Rating of Sewers. Water Sci. Technol. 2014, 69, 862–867. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tscheikner-Gratl, F.; Caradot, N.; Cherqui, F.; Leitão, J.P.; Ahmadi, M.; Langeveld, J.G.; Le Gat, Y.; Scholten, L.; Roghani, B.; Rodríguez, J.P.; et al. Sewer Asset Management—State of the Art and Research Needs. Urban Water J. 2019, 16, 662–675. [Google Scholar] [CrossRef]
- Matos, J.S. Ambiente e Saneamento—Sistemas de Drenagem Urbana; IST Press: Lisbon, Portugal, 2006. [Google Scholar]
- Lhomme, S.; Serre, D.; Diab, Y.; Laganier, R. GIS Development for Urban Flood Resilienc. In Proceedings of the WIT Transactions on Ecology and the Environment; WIT Press: La Coruna, Spain, 2010; Volume 129, pp. 661–671. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Series in Water Resources and Environmental Engineering; McGraw-Hill: New York, NY, USA, 1988; ISBN 978-0-07-010810-3. [Google Scholar]
- Rossman, L.A. Storm Water Management Model Reference Manual, Volume II—Hydraulics; USEPA: Cincinnati, OH, USA, 2017. [Google Scholar]
- Djordjević, S.; Prodanović, D.; Maksimović, Č. An Approach to Simulation of Dual Drainage. Water Sci. Technol. 1999, 39, 95–103. [Google Scholar] [CrossRef]
- Leandro, J. Advanced Modelling of Flooding in Urban Areas Integrated 1D/1D and 1D/2D Models. Ph.D. Thesis, University of Exeter, Exter, UK, 2008. [Google Scholar]
- Nanía, L.S.; León, A.S.; García, M.H. Hydrologic-Hydraulic Model for Simulating Dual Drainage and Flooding in Urban Areas: Application to a Catchment in the Metropolitan Area of Chicago. J. Hydrol. Eng. 2015, 20, 04014071. [Google Scholar] [CrossRef]
- Leitão, J.P.; Almeida, M.d.C.; Simões, N.E.; Martins, A. Methodology for Qualitative Urban Flooding Risk Assessment. Water Sci. Technol. 2013, 68, 829–838. [Google Scholar] [CrossRef] [PubMed]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-Time Urban Flood Forecasting and Modelling—A State of the Art. J. Hydroinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- DHI MIKE URBAN. Available online: https://www.mikepoweredbydhi.com/products/mike-urban (accessed on 5 May 2019).
- Innovyze Infoworks ICM. Available online: https://www.innovyze.com/en-us/products/infoworks-icm (accessed on 4 May 2019).
- Bentley. OpenFlows FLOOD Modeling Software. Available online: https://www.bentley.com/en/products/product-line/hydraulics-and-hydrology-software/openflows-flood (accessed on 25 February 2021).
- Leandro, J.; Martins, R. A Methodology for Linking 2D Overland Flow Models with the Sewer Network Model SWMM 5.1 Based on Dynamic Link Libraries. Water Sci. Technol. 2016, 73, 3017–3026. [Google Scholar] [CrossRef]
- Hsu, M.; Chen, S.; Chang, T. Dynamic Inundation Simulation of Storm Water Interaction between Sewer System and Overland Flows. J. Chin. Inst. Eng. 2002, 25, 171–177. [Google Scholar] [CrossRef]
- Chen, W.; Huang, G.; Zhang, H. Urban Stormwater Inundation Simulation Based on SWMM and Diffusive Overland-Flow Model. Water Sci. Technol. 2017, 76, 3392–3403. [Google Scholar] [CrossRef] [PubMed]
- Gómez, M.; Russo, B. Methodology to Estimate Hydraulic Efficiency of Drain Inlets. Proc. Inst. Civ. Eng. Water Manag. 2011, 164, 81–90. [Google Scholar] [CrossRef]
- Russo, B.; Valentín, M.G.; Tellez-Álvarez, J. The Relevance of Grated Inlets within Surface Drainage Systems in the Field of Urban Flood Resilience. A Review of Several Experimental and Numerical Simulation Approaches. Sustainability 2021, 13, 7189. [Google Scholar] [CrossRef]
- Russo, B.; Sunyer, D.; Velasco, M.; Djordjević, S. Analysis of Extreme Flooding Events through a Calibrated 1D/2D Coupled Model: The Case of Barcelona (Spain). J. Hydroinform. 2015, 17, 473–491. [Google Scholar] [CrossRef]
- Martins, R. Development of a Fully Coupled 1D/2D Urban Flood Model. Ph.D. Thesis, Tese de Doutoramento em Engenharia Civil, no ramo de Hidráulica, Recursos Hídricos e Ambiente, Faculdade de Ciências e Tecnologia da Universidade de Coimbra, Coimbra, Portugal, 2016. [Google Scholar]
- Courty, L. Integrated Modelling of Overland Flows and Drainage Networks in a Urban Environment. Ph.D. Thesis, Doutoramento em Engenharia, Universidade Nacional Autónoma do México, Mexico City, Mexico, 2018. [Google Scholar]
- Jang, J.-H.; Chang, T.-H.; Chen, W.-B. Effect of Inlet Modelling on Surface Drainage in Coupled Urban Flood Simulation. J. Hydrol. 2018, 562, 168–180. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Guo, S.; Lai, C.; Chen, X. A Simplified Approach for Flood Modeling in Urban Environments. Hydrol. Res. 2018, 49, 1804–1816. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; García-Navarro, P. Development of a New Simulation Tool Coupling a 2D Finite Volume Overland Flow Model and a Drainage Network Model. Geosciences 2018, 8, 288. [Google Scholar] [CrossRef]
- Sañudo, E.; Cea, L.; Puertas, J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water 2020, 12, 2647. [Google Scholar] [CrossRef]
- Gómez, M.; Russo, B.; Tellez-Alvarez, J. Experimental Investigation to Estimate the Discharge Coefficient of a Grate Inlet under Surcharge Conditions. Urban Water J. 2019, 16, 85–91. [Google Scholar] [CrossRef]
- Rubinato, M.; Martins, R.; Kesserwani, G.; Leandro, J.; Djordjević, S.; Shucksmith, J. Experimental Calibration and Validation of Sewer/Surface Flow Exchange Equations in Steady and Unsteady Flow Conditions. J. Hydrol. 2017, 552, 421–432. [Google Scholar] [CrossRef]
- Jahanbazi, M.; Egger, U. Application and Comparison of Two Different Dual Drainage Models to Assess Urban Flooding. Urban Water J. 2014, 11, 584–595. [Google Scholar] [CrossRef]
- EPA. Volume I—Final Report: Storm Water Management Model; Environmental Protection Agency: Washington, DC, USA, 1971. [Google Scholar]
- Huber, W.C.; Dickinson, R.E. Storm Water Management Model, Version 4.0: User’s Manual; USEPA: Athens, GA, USA, 1988. [Google Scholar]
- Rossman, L. Storm Water Management Model User’s Manual Version 5.1; USEPA: Cincinnati, OH, USA, 2015. [Google Scholar]
- Rossman, L.; Simon, M. Storm Water Management Model User’s Manual Version 5.2; USEPA: Cincinnati, OH, USA, 2022. [Google Scholar]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual, Volume I—Hydrology; USEPA: Cincinnati, OH, USA, 2016. [Google Scholar]
- Brito, D.; Campuzano, F.J.; Sobrinho, J.; Fernandes, R.; Neves, R. Integrating Operational Watershed and Coastal Models for the Iberian Coast: Watershed Model Implementation—A First Approach. Estuar. Coast. Shelf Sci. 2015, 167, 138–146. [Google Scholar] [CrossRef]
- MARETEC MOHID Land. Available online: http://www.mohid.com/pages/models/mohidland/mohid_land_home.shtml (accessed on 1 June 2022).
- Matos, J.S.; Ferreira, F.S.; Lopes, R.; Leboeuf, Y.; Oliveira, R.; Simões, J.; Santos, A.; Matos, M.E.; Estudante, M. Plano Geral de Drenagem de Albufeira: Fase B—Avaliação de Soluções Alternativas e Escolha da Solução Recomendada; Câmara Municipal de Albufeira: Albufeira, Portugal, 2016. [Google Scholar]
- © European Union, Copernicus Land Monitoring Service Imperviousness Density. Available online: https://land.copernicus.eu/pan-european/high-resolution-layers/imperviousness/status-maps/imperviousness-density-2018 (accessed on 1 October 2022).
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; ISBN 0-07-085906-X. [Google Scholar]
- Ballabio, C.; Panagos, P.; Monatanarella, L. Mapping Topsoil Physical Properties at European Scale Using the LUCAS Database. Geoderma 2016, 261, 110–123. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Matos, R. Métodos de Análise e de Cálculo de Caudais Pluviais Em Sistemas de Drenagem Urbana, Estudo Referenciado Em Dados Experimentais de Bacias Urbanas Portuguesas. Tese Apresentada a Concurso Para Obtenção do Grau de Especialista e Acesso à Categoria de Investigador Auxiliar do Laboratório Nacional de Engenharia Civil; LNEC: Lisboa, Portugal, 1987. [Google Scholar]
- Brandão, C.; Rodrigues, R.; da Costa, J.P. Análise de Fenómenos Extremos: Precipitações Intensas Em Portugal Continental; Direção dos Serviços de Recursos Hídricos: Lisboa, Portugal, 2001. [Google Scholar]







| Data Required | Typical Formats | Relevant Grid | Main Process |
|---|---|---|---|
| Contour lines/DEM | Vectorial/raster | Surface grid | Runoff |
| Buildings and urban obstacles | Vectorial | Surface grid | Runoff |
| Land use | Vectorial/raster | Manning’s coefficient grid | Runoff |
| Imperviousness factor | Raster | Imperviousness grid | Infiltration |
| Soil properties | Vectorial/raster | Soil properties 1 | Infiltration |
| Infrastructure | Main Data Required |
|---|---|
| Manholes | Invert elevation; depth from invert to ground |
| Sewer/channel | Cross-section shape; length; roughness |
| Storm tank | Invert elevation; depth of the storage unit; storage curve (surface area as function of water depth) |
| Pump | Pump type and curve; startup and shutoff depths |
| Outfall | Invert elevation; discharge boundary condition |
| Element | Dimension (m) | Slopes (%) | Manning Coefficient (s/m1/3) |
|---|---|---|---|
| Road | L = 40, W = 7 | ST = 2, SL = 1 | 0.016 |
| Sidewalk | L = 40, W = 2 | ST = 1, SL = 1 | 0.016 |
| Green area | L = 14.5, W = 10 | ST = 1, SL = 1 | 0.032 |
| Buildings 1 | L = 40, W = 10 L = 14.5, W = 10 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barreiro, J.; Santos, F.; Ferreira, F.; Neves, R.; Matos, J.S. Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land. Sustainability 2023, 15, 707. https://doi.org/10.3390/su15010707
Barreiro J, Santos F, Ferreira F, Neves R, Matos JS. Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land. Sustainability. 2023; 15(1):707. https://doi.org/10.3390/su15010707
Chicago/Turabian StyleBarreiro, João, Flávio Santos, Filipa Ferreira, Ramiro Neves, and José S. Matos. 2023. "Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land" Sustainability 15, no. 1: 707. https://doi.org/10.3390/su15010707
APA StyleBarreiro, J., Santos, F., Ferreira, F., Neves, R., & Matos, J. S. (2023). Development of a 1D/2D Urban Flood Model Using the Open-Source Models SWMM and MOHID Land. Sustainability, 15(1), 707. https://doi.org/10.3390/su15010707










