Abstract
In recent years, the shortage of water resources and the deterioration of water ecological environment have led to the increasing contradiction between supply and demand of water resources in river basins. How to realize the balanced allocation and scientific regulation of water resources in river basins is a serious challenge for China to face water resources problems. In this paper, the dynamic process and allocation scheme of water resources and water benefit allocation under different cooperative scenarios are simulated by constructing the water resources equilibrium allocation model of water benefit sharing. The influencing factors of water benefit sharing mechanism and the process of allocation compensation are studied, and the benefit relationship in regional coordinated utilization of water resources is revealed. The upstream, midstream and downstream water users of the Yellow River Basin are formed into alliances, respectively. Based on the principle of master–slave game theory, a basin system optimization problem with multi-level hierarchical structure is established. The initial allocation of water resources is carried out with the maximum overall benefit of water resources allocation, and the incremental benefits of the system optimization compared with the current individual and overall benefits are analyzed. The fuzzy cooperative alliance is used to allocate incremental benefits, improve the stability of cooperation among alliances, realize the cooperation and interaction of water resources in distribution, and finally achieve a dynamic equilibrium state. This paper focuses on the allocation mechanism of water resources competition and cooperation under water benefit sharing, which can provide a scientific basis for improving water resources security in water shortage basins and adapt to new problems and challenges brought by changing environments.
1. Introduction
Under the background of global environmental change, serious water crisis problems such as water shortage, frequent floods and droughts, and deterioration of water environment are becoming more and more serious. At the same time, the coordinated development of society, economy and ecology puts forward higher requirements for the study of optimal allocation of water resources. The balanced allocation of water resources, while considering economic, social and ecological benefits, is an important measure to solve the resource-based water shortage. Therefore, its related scientific issues have attracted wide attention of domestic and foreign scholars, and fruitful theoretical research results have been achieved in recent years.
At present, domestic and foreign research mainly focuses on the water allocation and optimization model for optimal water resources allocation [1,2], with little consideration of the coordination and cooperation among stakeholders. However, the study of these problems is a useful supplement to the deep analysis of the contradiction between supply and demand in water shortage basins, and it is of great significance to solve the conflict of interest in regional coordinated utilization of water resources. The existing distribution model has certain limitations. The water allocation between provinces (regions) in the basin is easy to cause unequal transactions between provinces and regions and increase the risk of ecosystem degradation [3,4,5].Therefore, water benefit sharing, which focuses on the use and distribution of benefits arising from water resources, can better facilitate cooperation between basin parties. Compared with water allocation, benefit sharing considers economic, policy and environmental issues, and it is the basic principle of water resources cooperation. The concept of benefit sharing instead of water allocation will focus on how to improve the overall interests of the whole basin and find a fair and effective benefit sharing mechanism, which is conducive to giving full play to the benefits of water resources and reducing regional conflicts.
Water benefit sharing is the embodiment of the idea of benefit sharing in the field of water resources utilization. At present there are few studies on benefit sharing, with most of the existing studies focusing on water resource sharing and distribution [6,7] and fewer considering the benefits brought by water resource transfer and the sharing allocation among water users. Water benefit sharing is the progress of water resource sharing, which fully considers the overall characteristics of the basin and the coordination of the interests of water users; it also improves the utilization efficiency of water resources from the perspective of the whole basin [8]. From the perspective of development, water resource utilization has experienced a process from gaming to sharing, and simple water resource sharing has been unable to meet the needs of human beings to cope with global changes [9,10,11]. Benefit sharing has been studied in transboundary rivers as a form of regional cooperation [12,13,14], where, for example, the interest sharing of the Mekong River achieves regional cooperation by optimizing economic, social, environmental and political achievements in the use of transboundary water resources; Zhang et al. [15] analyze benefit sharing based on cost proportionality, using the Columbia River as an example, and this collaboration can lead to incremental benefits or cost reduction. Because cooperation can bring more benefits to the players, cooperative game is often used to study the rational allocation of water resources. Gold et al. [16] used the coordination mechanism of water resources transfer and regional demand management to improve the robustness of water supply systems through regional cooperation among water supply companies; Fu et al. [17] constructed the water allocation model of Yongding River Basin by calculating the Shapley value of the cooperative game; Fu et al. [18] used the cooperative game method to establish a cooperative game model for water users, and the results show that the total benefit of the cooperative game allocation method is greater than the total benefit of the non-cooperative game allocation method; Yang et al. [19] used Choquet integral to define the τ-value and coalition value of coalition cooperative games; Su et al. [20] provided suggestions for the future cooperative game stability of water resources and the sustainable development of the system in Beijing by analyzing different water supply scenarios and game weight combination schemes. Although the water benefit sharing mechanism is not perfect at present, the reasonable application of this theory has achieved good results both in theory and in practice of transboundary water resources utilization, and it is an effective way to realize the reasonable utilization of water resources [21].
The challenge is how to take into account the competitive and coordinated development of water use efficiency and ecology under the sharing of water benefits, to reveal the competition and cooperation relationship between society, economy, ecology and environment for water resources, to propose a balanced and dynamic allocation scheme of water resources to adapt to environmental changes, and to find the obstacles to its healthy development and sustainable development mode. These studies have important scientific research value and practical significance for improving the balanced allocation of water resources, enhancing the coordination of economic and social development and ecological environment, and implementing the national water-saving policy. Therefore, this paper takes the Yellow River Basin as the research object, and studies the balanced allocation of water resources in the Yellow River Basin based on water benefit sharing, which will provide theoretical and technical support for alleviating the contradiction between water supply and demand and optimizing national water resources allocation.
2. Overview of the Study Area
The water distribution scheme of the Yellow River is the first basin water distribution scheme for large rivers in China. It balances and distributes the ecological environment water inside and outside the river channel and the economic and social water in each administrative region. Since 1997, the Yellow River has suffered an exceptionally dry period, and it is proposed that the water supply of the Yellow River in dry years should be determined by the same proportion reduction method. However, in the dry year or the peak season of water use, the water diversion projects along the Yellow River are competing for water diversion, resulting in water diversion out of control. Therefore, under the premise of total water consumption control in the Yellow River Basin, the key problems to be solved in practice are how to embody the principle of maximizing the overall interests of the basin, while benefiting all parties to the water area and formulating a balanced allocation scheme of water resources among provinces in the Yellow River Basin with shared water interests.
This paper takes the Yellow River Basin as the research object, in which the Yellow River Basin is a complex water resources system with multi-sources, multi-levels, multi-users, and multi-variables. The balanced allocation model of water resources in the Yellow River Basin takes the provincial allocation as the research scale. The provinces, main sections and main water use nodes are generalized, including the ecological water outside the river and the water and soil conservation nodes of the river and lake wetlands. At the same time, the ecological water demand of the Lijin section is taken as the ecological water demand of the whole river, and the ecological water use nodes in the river are set up.
The Yellow River Basin off-channel area is generalized into 182 calculation units, and each calculation unit considers seven types of water demand: urban life, rural life, tertiary industry, industry, agriculture, urban ecology and rural ecology. Through hydraulic connections such as natural rivers and artificial channels, the calculation unit, reservoir hub (34), inflow nodes (199 surface water and 181 groundwater) are organically connected to form a water resource allocation network in the basin, as shown in Figure 1.
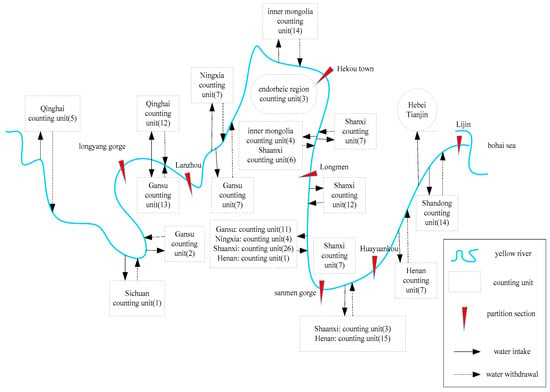
Figure 1.
Water Resources Allocation Network in the Yellow River Basin.
3. Research Methods
Constrained by limited water resources, it is inevitable to make the competitive water use contradiction between social economy and ecology more prominent. The balanced allocation of basin water resources based on environmental changes involves multi-level, multi-objective and multi-process decision problems such as water resources, society, economy and ecological environment. Taking the water resources system, economic and social system and ecological environment system as an organic whole, on the basis of ensuring the threshold of ecological water use, taking the maximum benefit of water resources utilization in the basin as the goal, the utilization efficiency of water resources is fully improved, and the distribution pattern of ecological water and economic and social water is determined at the same time of reducing the contradiction and conflict of regional water use, so as to promote resources, social economy and ecological environment into a virtuous circle and realize the win-win situation of economic development and ecological protection.
Due to the incomplete consistency of the objectives of various stakeholders, water conflicts between regions and industries often occur in the process of basin water resources allocation. In the process of basin water resources allocation, the optimal allocation of water resources based on the cooperation of water resources among water use sectors can make each department obtain as much benefit as possible fairly. While maximizing the benefit of limited water resources in the region, fair, reasonable and balanced allocation of water resources is an urgent problem to be solved. The balanced and optimized allocation of water resources is carried out in the way of regional water resources cooperation. Water interests should be shared among the alliances, and the incremental benefits of water use in the alliance should be fairly distributed so as to obtain higher water use benefits than when water resources are used alone, and the overall water use benefits in the region are higher than when water resources are used alone by various departments. The overall optimization and benefit sharing model framework of water resources balanced allocation is shown in Figure 2.
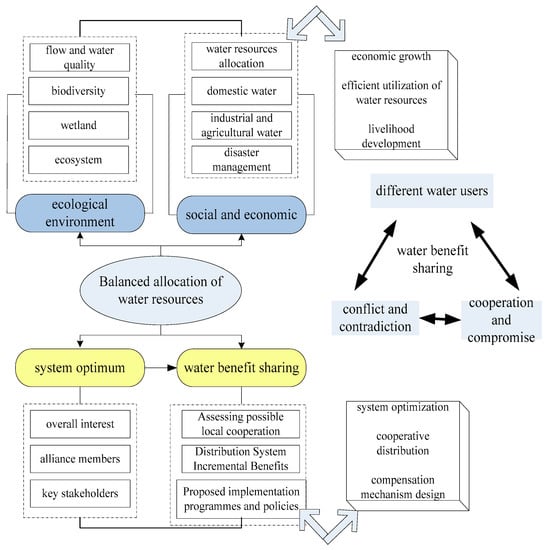
Figure 2.
Framework of System Optimality and Benefit Sharing Model for Balanced Allocation of Water Resources.
4. Water Benefit Sharing Model Based on System Optimality
4.1. Cooperative Relationship of Systematic Optimal Water Resource Allocation
Water use efficiency is the total output that can be obtained by unit allocation of water, including water use in economic and social aspects. If a socio-economic system can effectively allocate and use resources, it can be considered that the socio-economic system is efficient. In view of the complexity, dynamics and uncertainty of water supply and benefit relationship between upstream, middle and downstream provinces in the balanced allocation of water resources in the basin, in order to improve the utilization efficiency of water resources and maintain the stability of the whole basin ecosystem the initial allocation of water resources is carried out with the maximum overall benefit of water resources allocation, and the incremental benefits generated by the optimal system compared with the current individual and overall benefits are calculated. Different development levels will lead to different water resource utilization rates in different regions and different water use sectors. Accurate assessment of the comprehensive value of unit water use in different regions, such as life, industry, agriculture and ecology, is of great significance for in-depth understanding of water resource utilization efficiency. Taking maximum benefit of water resources utilization as objective function:
where J is the calculation unit for the number of provinces or alliances in the basin; Vk1 is the domestic water use benefit; Vk2 is the industrial water use benefit; Vk3 is the agricultural water use benefit; and Vk4 is the ecological water use benefit.
Constraint conditions:
(1) Basin water balance constraints:
where fu is upstream inflow; fR is interval inflow; fd is the downstream water intake; fl is lost water such as evaporation.
(2) Water consumption constraint:
where Cj,k is the water consumption of the k industry of the j calculation unit; k is the industry number, k = 1,2,3,4 are, respectively, life, industry, agriculture and ecology; Gj is the upper limit of water consumption of the j calculation unit.
(3) Reservoir constraints:
Water balance constraint:
where is the initial and final storage capacity of reservoir in period; is the natural inflow of reservoir in period ; is the water supply of reservoir in period ; is the water loss of reservoir in period .
Reservoir storage constraint:
where are the maximum and minimum allowable storage capacity of reservoir in period. is generally dead storage, is the maximum allowable storage capacity; in non-flood season, it is generally the storage capacity under normal storage level; in flood season, it is the storage capacity under flood control limited water level.
Water supply capacity constraint:
where , are the maximum and minimum water supply capacity of reservoir in period.
(4) Minimum ecological flow constraint:
where Ep,t, Rp,t are the minimum ecological flow and actual flow in the period of the p ecological control section.
4.2. Master–Slave Relationship between Water Resources Allocation Alliances
The Yellow River Basin passes through multiple provinces and regions which are called water users; these water users may form alliances with their upstream or downstream water users; domestic, industrial, agricultural and ecological water use in each alliance are called the water use sectors. The profit of alliance is determined by competition among water users. Limited by the flow direction, there are upstream, midstream and downstream relationships among water users, which is a master–slave game relationship dominated by upstream water users. Therefore, the water use strategy of the upstream water user will affect the decision of the midstream and downstream of the water user, and the water use strategy of the midstream and downstream also limits the upstream water use. In view of the complexity, dynamics and uncertainty of the upstream, midstream and downstream water supply and benefits of the balanced allocation of water resources in the basin, a basin system optimization problem with multi-layer hierarchical structure is established by applying the principle of master–slave game theory. The upstream, midstream and downstream water users form alliances, respectively, among which the upstream includes Qinghai, Sichuan, Gansu, Ningxia and Inner Mongolia; the midstream includes Shaanxi, Shanxi and Henan; and the downstream includes Shandong, Hebei and Tianjin. The locations and sections of the upstream, midstream and downstream of the Yellow River Basin are shown in Figure 3.
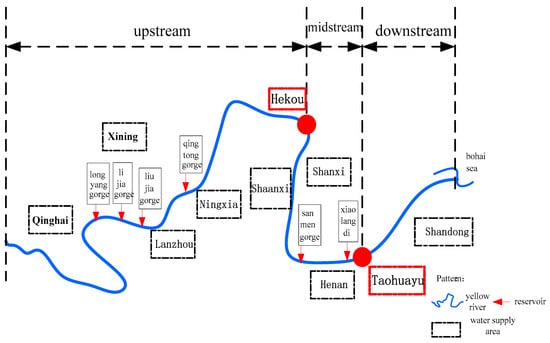
Figure 3.
Diagram of the upstream, middle and downstream sections of the Yellow River Basin.
In the allocation of water resources in public rivers, the alliance makes decisions in order. At this time, the alliance formed by the upstream water users first acts, and then the alliance formed by the midstream and downstream water users acts separately until all the decisions of the alliance are completed and the decision ends. However, each alliance has its own objective function and constraint conditions. The high-level objective function is not only related to the decision variables of this level, but also depends on the optimal solution of other low-level problems. The optimal solution of the low-level problem is affected by the high-level decision variables. If the structure of the alliance is {1}, {2}, {3}, that is, the upstream, middle and downstream compete with each other, then considering the upstream, middle and downstream of the three-level planning problem, a three-level master–slave game model of the upstream, middle and downstream is established to reveal the master–slave hierarchical relationship and dynamic correlation between the upstream, middle and downstream of the basin. The general form of the model is:
where x ∈ Rn1, y∈ Rn2, z∈ Rn3, x, y and z are the decision variables in the upper, middle, and lower levels, respectively; n1, n2 and n3 are the numbers of research objects in each level; Bi(x,y,z) (i = 1,2,3) is the objective function of upstream, midstream and downstream, indicating the benefit of the i participant when choosing strategy (x,y,z); ψi (x,y,z) (i = 1,2,3) is the constraint condition of each level. The upstream determines the water resources allocation strategy according to the effective water demand of the water user and transmits it to the midstream model. The midstream water user decision reacts to the upstream decision to determine its optimal water resources allocation decision . Finally, the downstream reacts to the upstream decision and the midstream decision to determine its optimal water resources allocation decision . After the above process is completed, the upstream decision is then adjusted according to the midstream and downstream decisions, and the midstream and downstream are adjusted according to the upstream, through the cycle of this process to finally achieve the optimal water allocation decision for the whole system. The balance solution of this multi-stage dynamic game problem can be obtained, and then the balance water resource allocation scheme obtained by the master–slave relationship between the alliances can be determined. If the structure of the alliance is {1,2}, {3}, that is, the upstream and midstream alliances cooperate and compete with the downstream, then consider the upstream–midstream and downstream two-level planning problem and establish the upstream–midstream and downstream two-level master–slave game model. Then the objective function is:
The constraint conditions are the same as Formula (8). Formula (9) shows that the upstream and midstream alliance {1,2} as a water user first makes decisions, and the downstream alliance {3} will make its own decisions according to the decision of alliance {1,2}.
If the structure of the alliance is {1}, {2,3}, that is, the competition between the upstream alliance and the alliance formed in the midstream and downstream, similarly consider the two-level planning problem of the upstream and midstream–downstream and establish the master–slave game model of the upstream and midstream–downstream. The objective function is:
The constraint conditions are the same as Formula (8). Formula (11) shows that the upstream {1} as an alliance first decision, the middle and downstream {2,3} as an alliance will make their own alliance decisions according to the alliance {1} decision.
If the alliance structure is {1,2,3}, that is, the upstream, midstream and downstream form a large alliance, the whole basin cooperation, pay attention to the interests of the whole basin. The objective function is:
The constraint conditions are the same as Formula (8). The Formula (13) shows that the upstream, middle and downstream water users form an alliance {1,2,3}, and stakeholders pay more attention to the maximization of their own interests, while watershed managers pay more attention to the maximum interests of the whole basin.
4.3. Incremental Benefit Allocation Based on Fuzzy Cooperative Game
Social and economic interests, environmental interests or the benefits brought by the basin itself can be managed in various regions and departments to promote regional cooperation and assess possible local cooperation. Different cooperation scenarios between the alliances allocate the benefits of water use for the alliance, which directly affects the stability of the alliance. The larger the core size, the greater the benefits, indicating that cooperation can bring some benefits. The difference between the benefits generated by alliance cooperation and the allocation of basic water resources is called incremental benefit ΔB.
Cooperative game means that the interests of both sides of the game have increased, or at least one party’s interests have increased and the interests of the other party are not damaged, so the interests of the whole society have increased. At the same time, the cooperative game studies how to allocate the benefits of cooperation, that is, income distribution. The Shapley value method of cooperative game is a game analysis method used to solve the cooperative countermeasures of multiple subjects. The contribution degree of each cooperative subject to its cooperative alliance reflects the importance of each member in the cooperation, and the contribution degree of each cooperative subject is used to allocate the cooperative benefits, which is an effective method to solve the distribution of cooperative benefits. In the conventional alliance (upstream, midstream and downstream alliance) it is required that the players (provinces) of the alliance carry all their resources to participate in a certain alliance, and the benefits of a player in the alliance depend on its contribution to the alliance. In the fuzzy alliance (Aubin, 1974), the player only needs to carry part of the resources (domestic, industry, agriculture, ecological water resources) to participate in each alliance, and the income is equal to the sum of the income obtained by participating in each alliance. Fuzzy alliance does not require the players to carry all the resources they own to participate in a certain alliance, but it allows them to carry some resources to participate in different alliances; that is, fuzzy alliance is to participate in different alliances with different participation rates. In this paper, the fuzzy cooperative alliance is used to allocate incremental benefits. The water use sector can participate in multiple cooperative alliances at the same time, and the water resources obtained in the initial allocation are dispersed in all the cooperative alliances that it participates in. Each water user carries a certain amount of water resources to participate in different fuzzy alliances, and the water resources of each water user will be redistributed among different fuzzy alliances, forming a fuzzy alliance of water resources cooperation in the region. The research on the distribution of the increase in revenue ΔB among the players improves the stability of cooperation among the alliances, realizes the cooperation and interaction of water resources in the distribution, and finally reaches a dynamic balance state.
In this paper, upstream alliance, midstream alliance and downstream alliance are represented by A, B and C; industrial, agricultural and ecological sectors are represented by water use sectors 1, 2 and 3, then water use sectors of different alliances are represented by , , . Assuming that the amount of water resources transfer is w, the amount of water resources transfer in each water use sector is: ; ; , and satisfy:
Then the benefit functions in the transfer-out area A and the transfer-in area B or C are expressed as; , respectively.
Because the water use benefit of the upstream, middle and downstream of the Yellow River is different, the total benefit of all participants in the transfer of water resources is set to , namely:
Each player can participate in multiple water resources cooperation coalitions at the same time, and the members of the coalition share water resources cooperation and distribute water benefits. Let denote a fuzzy alliance of water resources cooperation in the basin, where denotes the participation rate of the i water user in alliance s, ; V(s) is the benefit of alliance s. In order to make the target T optimal, that is, to maximize the overall benefit of the basin, the objective function is:
The constraint condition is:
where Vi(s) is the benefit of the i water user acting alone to participate in the water resources of alliance s; b(i) is the benefit of the unit water volume of the i water user; wi is the amount of water initially allocated by the i water user in the alliance.
where V(s) is the benefit of the alliance s; B(s) is the benefit generated by unit of water in the alliance s; W(s) is the amount of water resources carried by the water users participating in the alliance s; Q(s) is the maximum demand of alliance s for water resources; other symbols are the same as above.
Each water user carries a certain amount of water resources to participate in different fuzzy alliances, the goal is to maximize the benefits of the whole basin system, and then the incremental benefits ΔB generated by the alliance cooperation to maximize the benefits are distributed among the players, and the fairness and efficiency of water use are integrated to achieve the balanced allocation of water resources in the basin. Therefore, the benefits distribution method based on fuzzy Shapley value is a fair and just distribution method. The application of fuzzy Shapley value method to benefit distribution of trans-regional shared water resources needs to meet at least two conditions:
The cooperation benefits obtained by the combination of subsets is more than that obtained by the action of each subset alone, namely:
where n represents the number of participants in the cooperative game, and is the set of n participants. For any coalition s of N, it corresponds to a real value function V(s), and V(s) denotes the benefits obtained by coalition s when there is cooperation among participants.
The benefits of each participant from cooperation are greater than those from their individual actions.
where is the income of the ith water user participating in the alliance S.
When each participant participates in cooperation, Shapley value can be obtained by the following formula:
where represents the benefits brought to the cooperative alliance due to the participation of participant i; is a weighting factor as the weight assigned under different combinations. represents the number of alliance S elements.
Since the cooperative game satisfies superadditivity, the total fuzzy benefit of each water user is equal to the sum of the benefits obtained from each alliance, namely:
where L(s) is the set of fuzzy coalitions of water resources cooperation, and other formulas have the same meaning as above.
5. Results and Analysis
Based on the development needs and supply and demand pattern of each province in the Yellow River Basin, this paper analyzes the allocation and compensation methods of water benefit sharing and makes a balanced allocation of water resources in the Yellow River Basin. In general, domestic water belongs to basic water and does not transfer in the basin. In this paper, it is assumed that the water use sectors for water transfer include industrial water, agricultural water and ecological water. Table 1 shows the water consumption and unit water value of each water use sector in the upstream, middle and downstream of the Yellow River Basin.

Table 1.
The water consumption and unit water value of each water use sector in the upstream, middle and downstream of the Yellow River Basin.
Due to the limitation of water flow direction, there is a relationship between upstream, middle and downstream water users. Therefore, the water use strategy of upstream water users will affect the decision of middle and downstream water users, and the water use strategy of middle and downstream also plays a restrictive role in upstream water use. In view of the complexity, dynamics and uncertainty of the upstream, midstream and downstream water supply and benefits of the balanced allocation of water resources in the basin, a basin system optimization problem with multi-layer hierarchical structure is established by applying the principle of master–slave game theory. The upstream, middle and downstream water users form alliances, respectively. Due to the upstream–downstream relationship between alliance cooperation, the cooperation modes among different alliances in the upstream, middle and downstream of the Yellow River Basin are as follows: Scheme 1 is the mutual independence of the upstream, midstream and downstream; Scheme 2 is the cooperation between the upstream and midstream; Scheme 3 is the cooperation between the midstream and downstream; Scheme 4 is the cooperation of the whole basin of the upstream, midstream and downstream. The upstream, midstream, downstream and total benefits under different cooperation modes in different water years are calculated.
Table 2 shows that the average unit water value of industry and agriculture in the midstream and downstream is higher than that of industry and agriculture in the upstream. The cooperation potential of Scheme 2 and Scheme 3 is relatively large. The basic benefit Vn of Scheme 1 is relatively small, which is 40.47 billion USD. The benefits of Scheme 2 and Scheme 3 are 45.23 billion USD and 42.91 billion USD, respectively. The benefit V’n of the whole basin cooperation in Scheme 4 is the largest, which is 48.13 billion USD, and the incremental benefit ΔB = V’n − Vn is 7.66 billion USD.

Table 2.
Benefits of different cooperation scenarios in the upstream, midstream and downstream of the Yellow River Basin Unit: billion USD.
Taking the whole basin cooperation of Scheme 4 as an example, the incremental benefit ΔB is allocated according to the overall optimal water allocation, the contribution of each alliance and the participation rate of water use sector. See Table 3, Table 4 and Table 5 below.

Table 3.
The situation of upstream forming alliances Unit: billion USD.

Table 4.
The situation of midstream forming alliances Unit: billion USD.

Table 5.
The situation of downstream forming alliances Unit: billion USD.
The above table shows that the basic benefits of upstream, midstream and downstream are V(1) = 13.47 billion USD, V(2) = 19.03 billion USD, V(3) = 7.98 billion USD, the cooperation benefits of upstream and midstream are 37.25 billion USD, the cooperation benefits of midstream and downstream are 29.44 billion USD, and the cooperation benefits of upstream, midstream and downstream are 48.13 billion USD. After the water benefits are shared, the upstream, midstream and downstream benefits will be 16.00 billion USD, 22.78 billion USD and 9.35 billion USD, respectively. In the whole basin cooperation, the water distribution in the upstream has changed from 11.569 billion m3 to 9.255 billion m3; the water distribution in the midstream has changed from 9.131 billion m3 to 7.305 billion m3; the water distribution in the downstream has changed from 4.904 billion m3 to 9.044 billion m3.
The incremental benefit distribution of basin water benefit sharing is shown in Table 6.

Table 6.
Incremental benefit distribution results of basin water benefit sharing Unit: billion USD.
It can be seen from Table 6 and Figure 4 that cooperation brings incremental benefits. Compared with the basic benefits, the incremental benefit of water benefit sharing is 7.66 billion USD, and the cooperative game brings about an increase in benefits. However, the cooperation benefit of upstream and midstream alliance is less than that of non-cooperation, and it is necessary to provide benefit compensation for an upstream and midstream alliance to avoid its deviation from cooperation; The benefit of its downstream alliance under the cooperative game is also higher than that of non-cooperative game, and only in this way can a stable alliance and cooperative relationship be formed. The upstream benefit increased by 2.53 billion USD, and the benefit after water benefit sharing was 16.00 billion USD; the benefit of the midstream increased by 3.75 billion USD, and the benefit after water benefit sharing was 22.78 billion USD; the downstream benefit increased by 1.38 billion USD, and the benefit after water benefit sharing was 9.35 billion USD; the total benefit increased from 40.47 billion USD to 48.13 billion USD. In the water benefit sharing, the economic benefits of the upstream and midstream increase because the upstream and midstream contribute to the improvement in the total benefit of the whole basin. Therefore, in the allocation of incremental benefit, the interests of the upstream and midstream should be considered, reflecting the principles of water benefit sharing and incremental benefit allocation.
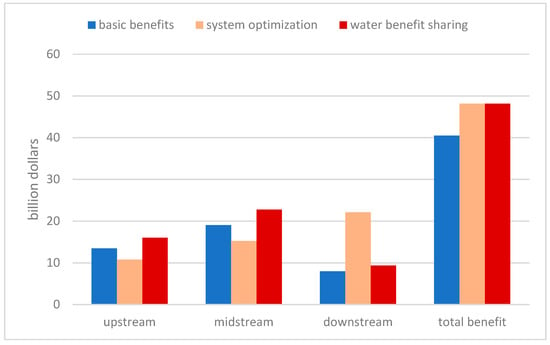
Figure 4.
Benefit comparison diagram of different cooperation scenarios in upstream, midstream and downstream.
In the case study, the microeconomic principle and game theory are used to connect the traditional water resources system model with the game theory method, and a balanced allocation model of water resources combining system optimization and water benefit sharing is constructed to simulate the dynamic process and allocation scheme of water resources and water benefit allocation under different competition and cooperation scenarios. The benefit distribution and benefit compensation of stakeholders participating in water resources transfer cooperation are quantified, which maximizes the water use benefit of the Yellow River Basin and provides theoretical support for alleviating the contradiction between supply and demand of water resources and high-quality development in the Yellow River Basin. However, based on the current management and operation mode of the Yellow River Basin, the application of the research content of this paper to the water resources allocation of the Yellow River Basin needs to be tried in practice, which has certain limitations. In future research, the balanced allocation of water resources in different regions and different seasons and different inflow years will be more refined.
6. Conclusions
The benefit distribution and benefit compensation of stakeholders participating in water resources transfer cooperation are quantified, which maximizes the water use benefit of the Yellow River Basin and provides theoretical support for alleviating the contradiction between supply and demand of water resources and high-quality development in the Yellow River Basin.
This paper focuses on the allocation mechanism of water resources competition and cooperation under water benefit sharing. On the basis of overall consideration of system optimization, the cooperative relationship and master–slave relationship of basin water resources allocation are fully considered. The Shapley value method and cooperative game theory are used to analyze the incremental benefit distribution generated by water resources transfer in different situations and quantify the benefit distribution and benefit compensation of stakeholders involved in water resources transfer cooperation. The effectiveness and reliability of the method are proved by an example of the Yellow River Basin, which realizes the maximization of water use efficiency of limited water resources in the region. At the same time, the equitable and reasonable allocation of water resources provides theoretical and technical support for alleviating the contradiction between supply and demand of regional water resources and the optimization of national water resources allocation. In this paper, the preliminary exploration and theoretical research on the allocation of water resources in the Yellow River Basin is based on water benefit sharing, and there are many ways of cooperation and alliance. The upstream alliance, midstream alliance and downstream alliance in this paper are exemplary and representative. In future studies, various forms of cooperation will be analyzed to lay a theoretical foundation for the balanced allocation of water resources and high-quality development of the Yellow River Basin under the new situation.
Author Contributions
All authors contributed to the study conception and design. F.W. and Y.W. performed material preparation, data collection, and modeling. X.Z. (Xiangnan Zhou) and X.Z. (Xiaokang Zheng) performed result analysis and discussion. J.W. edited the manuscript. L.X. Reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by The National Key Research and Development Program of China(2022YFC3202300), Major Science and Technology Special Projects in Henan Province (201300311400), General Science Foundation Program of Henan Province (222300420491). Key Research and Development and Extension Project (Soft Science) of Henan Province in 2022 (No. 87).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to data privacy.
Conflicts of Interest
The author declares no conflict of interest.
References
- Ahmad, I.; Zhang, F.; Liu, J. A linear bi-level multi-objective program for optimal allocation of water resources. PLoS ONE 2018, 13, e0192294. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Li, Y.P.; Zhuang, X.W.; Jin, S.W.; Huang, G.H.; Feng, R.F.; Dixon, R. Identifying water resources management strategies in adaptation to climate change under uncertainty. Mitig. Adapt. Strateg. Glob. Change 2018, 23, 553–578. [Google Scholar] [CrossRef]
- Acquah, S.; Ward, F.A. Optimizing adjustments to trans-boundary water sharing plans: A multi-basin approach. Water Resour. Manag. 2017, 31, 5019–5042. [Google Scholar] [CrossRef]
- Degefu, D.M.; He, W.; Liang, Y.; An, M.; Qi, Z. Bankruptcy to Surplus: Sharing Transboundary River Basin’s Water under Scarcity. Water Resour. Manag. 2018, 32, 2735–2751. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Z.; Sun, Z.; Wang, G.; Jin, J.; Wang GBao, Z.; Liu, C.; He, R. Multi-objective Water Resources Allocation in Trans-boundary Rivers Based on the Concept of Water Benefit-sharing: A Case in the Lancang-Mekong River. Sci. Geogr. Sinica 2019, 39, 387–393. [Google Scholar]
- Mcintyre. Benefit-sharingand upstream/downstream cooperation for ecological protection of transboundrary waters: Opportunities for China as an upstream state. Water Int. 2015, 40, 48–70. [Google Scholar] [CrossRef]
- Aguilar-Barajas, I.; Garrick, D.E. Water reallocation, benefit sharing, and compensation in northeastern Mexico: A retrospective assessment of El Cuchillo Dam. Water Secur. 2019, 8, 100036. [Google Scholar] [CrossRef]
- Ilkhom, S.; Kai, W.; Jusipbek, K. The Costs of Benefit Sharing: Historical and Institutional Analysis of Shared Water Development in the Ferghana Valley, the Syr Darya Basin. Water 2015, 7, 2728–2752. [Google Scholar]
- Mccracken, M.; Meyer, C. Monitoring of transboundary water cooperation: Review of sustainable development goal indicator methodology. J Hydrol. 2018, 563, 1–12. [Google Scholar] [CrossRef]
- Kuang, Y.; Li, H.; Xia, J.; Yang, Z.C. Impacts of climate change on transboundary water resources and adaptation management framework. Clim. Chang. Res. 2018, 14, 67–76. [Google Scholar]
- Kang, L.Y.; Sun, Z.L.; Liu, Y.L.; Liu, Y.; Guan, T.S.; Liu, C.S.; Wang, G.Q.; Jin, J.L. Overview of Water Benefit Sharing Theory and Its Application. Yellow River 2021, 43, 77–81. [Google Scholar]
- Lee, L. Benefit sharing in the Mekong River basin. Water Int. 2015, 40, 139–152. [Google Scholar] [CrossRef]
- Malik, T. Pak-Afghan Water Issue: A Case for Benefit-Sharing. Policy Perspect. 2019, 16, 77–98. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Guo, H.; An, X. Benefit Allocation in Shared Water-Saving Management Contract Projects Based on Modified Expected Shapley Value. Water Resour. Manag. 2021, 35, 39–62. [Google Scholar] [CrossRef]
- Zhang, C.; Fan, Y.; Hu, W. Benefit sharing on transboundary rivers: Case study and theoretical exploration. J. Resour. Ecol. 2019, 10, 1–8. [Google Scholar]
- Gold, D.F.; Reed, P.M.; Trindade, B.C.; Characklis, G.W. Identifying actionable compromises: Navigating multi-city robustness conflicts to discover cooperativesafe operating spaces for regional water supply portfolios. Water Resour. Res. 2019, 55, 9024–9050. [Google Scholar] [CrossRef]
- Fu, Y.C.; Wu, W.Q.; Ruan, B.Q. Discussion on eco-compensation standard of water quantity in Yongding River watershed. J. Hydraul. Eng. 2014, 45, 142–149. [Google Scholar]
- Fu, X.; Lu, F.; Hu, T.S. Game theory in water resources allocation for stakeholders. J. Hydraul. Eng. 2016, 47, 38–43. [Google Scholar]
- Yang, D.Q.; Li, D.F. τ-values for fuzzy graph cooperative games. Control. Decis. 2017, 32, 1653–1658. [Google Scholar]
- Su, X.Y.; Yu, Y.; Zhao, J.S.; Li, T.J. Game Analysis of Trans-Regional Water Resources Allocation in Beijing. J. Basic. Sci. Eng. 2019, 27, 239–251. [Google Scholar]
- Tan, J.Y.; Jiang, D.K. Optimal allocation of water resources in water-stressed regions based on water resources cooperation among water using sectors. J. Syst. Manag. 2020, 29, 377–388. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).