Abstract
The ability to assess the risks of the functional safety of railway tracks allows harmonizing characteristics of track elements under certain operating conditions under certain maintenance for the efficient use of the track structure throughout its life cycle. The concept of detailing conditions of the interaction of the rolling stock and railway track was used for the productive solution of tasks of infrastructure functional safety assessment. The paper formed an approach to the analytical solution of determination problems of deformability parameters over time using the elastic waves theory. The formation method of interconnections between the technical and economic aspects of the operation of railway infrastructure was proposed. The criteria of deformability work and intensity of use were utilized for the effective use of the track structure through its life cycle. The results of calculations are presented to assess changes in the deformability behaviour of the track elements and structure when the force and speed parameters of the operating conditions change, as well as the algorithm of the method for estimating the operation deformability of the railway track. Thus, the proposed approach can be adapted to optimize objects by railway functional safety assessment at the stage of object operation simulation.
1. Introduction
The technological development of humanity is faced with the need to provide an innovative and effective tool for productively solving the issues of ensuring the reliability, availability [1], maintainability [2,3,4,5], and safety of railway systems [6,7].
In the future, the way in which people inform themselves, choose, and purchase goods and services online is expected to change continuously:
- -
- Increased connections with mobile devices through high-capacity telecommunication networks (5G, etc.) [8,9,10];
- -
- Increased use of multimodal integration platforms in mobility-as-a-service mode [11,12];
- -
- Growth of online commerce, with consequent stress on the logistics system and an increase in the number of delivery vehicles in cities [13,14,15].
In the face of these important transformations, a strategy of change must be adopted to revitalize and develop various countries [16,17,18]. Rail transport, in particular, can make a major contribution.
By improving sustainable [19,20,21] rail-based mobility, the share of travel with high environmental performance [22,23,24], such as rail transport, collective road transport [25,26], or shared systems, can make a significant contribution to reducing the many negative impacts [27,28,29,30], such as pollutant emissions [31] and climate impacts [32,33,34,35].
Energy efficiency, renewable energies, redesign of production cycles, and a modal shift towards environmentally friendly [36] means of transport are necessary measures for the transport sector [37,38,39,40,41]. In terms of energy and emissions, rail transport is among the most energy-efficient and lowest-emission transport systems.
The risk assessment of the functional safety [42,43,44,45,46] of any engineering object is associated with the definition of reliability [47,48,49], availability, maintainability, and safety (RAMS) [50,51]. It determines the suitability of objects to perform their functions safely (with defined risk levels at all stages of the life cycle) [25,52,53] and efficiently (with a certain level of costs) under specific operating conditions [54,55,56,57]. This state is assessed by deformability.
However, modern tools used to determine the state of an object are based on principles developed to determine the first limit state, which determines the general suitability of an object to work in certain conditions [58,59,60]. The strength [61,62,63] and stability [64,65,66,67] indicators used to evaluate this state are obtained by numerical modeling to simulate quasi-dynamic deformation processes [68,69,70,71] occurring inside the elements under the influence of external [72,73,74] and climatic impulses [75,76,77].
In the numerical simulation [78,79], the conditions are simulated to obtain a relevant result. However, to assess risks, it is necessary to employ analytical methods, using time-space dependencies [80,81,82,83] to model the processes both within elements of the structure and in the track structure as a whole.
Existing engineering approaches only solve 3% of the tasks by analytical methods, and the remaining 97% are solved by choosing individual solutions based on experimental data obtained for certain operating conditions [84,85]. The following time characteristics are not taken into account for existing computing systems:
- -
- Change of force impulses over time;
- -
- Changes in the deformability process over time.
The lack of time parameters in the calculations makes it impossible to link the original causes with the symptoms identified as the result.
The solution to this issue is, firstly, the formation of an approach to analytical problem solving of determining the parameters of deformability in time using the elastic waves theory [50]. Secondly, the formation of relationships between the technical and economic aspects of the operation of railway infrastructure facilities.
This paper aims to demonstrate that the concept of detailing the conditions for the interaction of rolling stock and the railway track makes it possible to expand the possibilities of simulating and diagnosing natural phenomena necessary for productively solving the issues of railway functional safety assessment.
2. Research Methods
Determining the conditions for reliable operation of the crew-railway system involves identifying in the mechanism of the system operation all intermediate events (components) in the chain of cause-and-effect relationships that will lead from immediate causes to final consequences. The disclosure of the mechanisms of the physical essence of the destruction of the railway track, firstly, allows determining the necessary control criteria for the railway track, evaluating the state of the track according to reliability criteria, predicting the operation of the track for different periods, and determining the optimal work for its restoration. Secondly, to ensure that the reliable operation of the crew system is the way to establish the criteria for monitoring this system, classify its state of reliability and predict its behaviour.
Modeling the life cycle of the deformability work of the railway track involves considering the problem in a stochastic formulation because the use of numerical methods does not allow describing the change in rail deformations under the influence of rolling stock wheels over time. However, the basis of the modeling used in the work is the presence of wave processes caused by both external and internal vibrations of the track structure elements [50,80]. Thus, the variability of the problem statement is reduced by establishing a pattern between the magnitude of the impact and the processes of vibration of the track structure over time for specific operating conditions. To apply this method, a mathematical model of the operation of the railway track structure has been developed, taking into account the spatial propagation of elastic waves during the interaction of the track and rolling stock. This model combines three blocks: the mechanism of the rolling stock impact on the track, the propagation of a force wave in the elements of the track structure, and the transition of a force wave from one element to another. The calculation algorithm for the developed model is as follows:
where are the trajectory of the wheels, the length and width of the contact area, and the gap between the wheel and the rail at the moment of contact, respectively;
are the loads, speeds of movement, load impulse parameters, time, track elements, force waves by direction, reaction waves by direction, and deformation states of the model, respectively;
are the assembly of track elements, connections between elements, element of the set of geometric dimensions and physical and mechanical properties of the element , , element of the set of parameters of propagation of longitudinal and transverse waves by direction, and element of deformation states element , respectively.
The principle of assembling geometric models for the proposed simulation is similar to the assembly of geometric models when applying the finite element method. Geometric models can be built in any software. The geometry of the parts complies with current regulations and design.
According to the physical characteristics of the materials of the elements, the propagation velocities of the longitudinal and transverse waves in each element along the directions of propagation are determined.
On the geometric model of the track structure, the coordinates of the trajectory of the wheels of the rolling stock are determined. These coordinates are decisive for the construction of local coordinate systems, in which the propagation of impulses applied along the rail at a certain point in time is considered as an excitation factor. The geometric arrangement of local coordinates is determined by the direction of the force acting at a certain point from the rolling stock on the rail, while maintaining the perpendicularity of the angles of application of the force to the outline of the rail head. The magnitude of the forces acting on the path is determined by existing methods [86]. The time of action of the force is determined by the ratio of the length of the contact area of the wheel with the rail to the speed of the rolling stock. For the proposed model, the geometric parameters that describe the physical process of force wave propagation in the elements of the track structure are the main ones, as their superposition in time characterizes the vibration process. The vibrational process itself is a superposition of spherical and quasi-spherical waves of incidence-reflection-refraction in time at each point of the object. Wave propagation is represented as vectors propagating from the wheel/rail contact, taking into account the direction of wave propagation and the direction of displacements relative to the direction of propagation. Therefore, the displacements caused by the impulse and carried by longitudinal waves are realized in the direction of propagation, and by the transverse wave in the direction perpendicular to the direction of propagation in time. In addition to the direction of the displacement caused by the impulse, the wave propagation velocity is taken into account because the propagation velocity of longitudinal waves is higher than the propagation velocity of transverse waves.
The existing track infrastructure maintenance systems are based on the geometric and elastic characteristics to determine the technical states of both the elements and the track structure for various operating conditions [59,81,85]. Therefore, they can be used to determine such criteria of deformability as deformability work (work to move an object under the action of a force impulse in time) and intensity of use (the ratio of the amount of work to the time of the force action)
where is the force that affects the element, and is the shift caused by the force during the action .
where is the force exposure time.
Questions on the assessment of functional safety during the life cycle are effectively relevant [87,88]. However, in solving them, the time indicator is used as the interval of time during which the process under consideration takes place. Using the elastic wave theory allows describing cyclic dynamic processes by two types of frequencies: frequency of impulse, characterized by the time of direct action, and frequency of repetition, characterized by the time between impulses. Such divisions do not exist when solving problems using the theory of elasticity. Hence, when studying the influence of both the impulse itself [89,90,91,92,93] and its repetition [94,95,96,97], as well as in modeling and validation [98,99,100], it is considered as a formed oscillation process. The theory of propagation of elastic waves allows directly forming this process, using the property of all types of waves to transfer momentum without change to all points in space, taking into account both the time the force field reaches each element of the railway structure and the absorption of each element of the force impact during the collision of waves. This allows studying the influence of both the impulse itself and its repetition separately and makes it possible to establish the relationships between the technical conditions of the elements and the structure of the railway track, the operating conditions, and the maintenance system during the life cycle.
3. Research Results
For a productive solution to the problems of the railway functional safety assessment, the concept of detailing the interaction process of rolling stock/railway track was used. Detailing was carried out in two directions.
In the first direction, the process of describing the dynamics of the deformability of the elements and the structure of the railway track under the influence of the rolling stock was detailed in two blocks: (1) impact, (2) transfer and transformation of impact.
The second direction of detailing is the introduction of deformability criteria for the formation of relationships between the techno-economic aspects of the operation of railway infrastructure facilities.
3.1. The First Direction of Detailing
Detailing the “impact” block led to the following results:
- 1.
- Since energy exchange occurs during the impact, one of its characteristics is the law of change of the acting physical quantity over time. This value characterizes the intensity of the impact of the force impulse and allows describing such characteristics of the impact as “legato” and “staccato” in music or “soft” and “hard/sharp” in mechanical systems.
The speed of transfer of the external impulse inside the elements remains constant because it depends on the characteristics of the materials, which means that the speed of propagation of the internal force is constant. Changing the speed of the rolling stock leads to a change in the contact time of the wheels and rails in one cross section, which leads to a change in the rate of deformability at each point of the elements. Therefore, at the same speed of propagation of force fields inside any element of the track structure, a change in the speed of the rolling stock leads to a change in the intensity of the impact on each point of the track structure element. Thus, an increase in the speed of the train leads to the effect “staccato” in music or “hard/sharp” impact in mechanical systems. The lower the speed of movement, the greater the effect of “legato” in music or “soft” impact in mechanical systems.
- 2.
- The action of a constant force per unit time on an object, regardless of the time of its impact, is characterized by the same value of the amount of motion per unit time, which serves as a potential for performing the same amount of work of the object per unit time. This means that it transfers the same amount of energy per unit time during the action of the force. If the force has a variable value in time, then the impulses of the variable forces cause the exchange of a variable amount of energy per unit time during the duration of the force.
The detailing of the “transfer and transformation of impact” block made it possible to assess the probability of fatigue and defects under certain operating conditions, depending on the design and material characteristics of the rail structure elements. The collision of waves of incidence and reflection results in a concentration of deformation within the elements, as well as heat production in proportion to the amount of deformation not realized in each direction.
Using the elastic waves theory allows establishing: (a) the deformability of elements over time; (b) the time ratio of the impulse impact and its propagation along the length and depth of the track structure; (c) the change in the amount of energy in any point of the structure in time. The above-mentioned parameters allow changing the deformability processes. The following are the results of calculations that allow determining and comparing the processes of deformability within the elements and track structure when exposed to rolling stock with different speeds and loads.
The investigation is carried out for the track structure model consisting of the following elements: rails R65, concrete sleepers SB3, fastenings KPP-5-K, ballast stone of 0.4 m thick, subgrade. Their characteristics are given in Table 1.

Table 1.
The properties of track structure elements.
The rolling stock influence on the track was considered with respect to the central position of the wheel set. As a result of the investigation, Figure 1 demonstrates the dependence of oscillation amplitudes of the track structure section over time with a motion speed of 80 km/h under the single force impact of the section’s different loads. Table 2 and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show the ratios demonstrating the change in the values of the impact force and the speed of movement on the work of deformability and the intensity of the use of track and structure elements relative to the values when exposed to a load of F = 225 kN and V = 80 km/h.
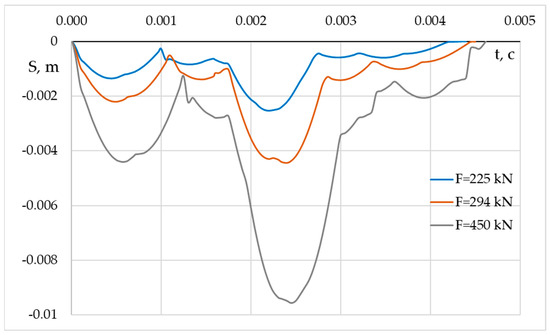
Figure 1.
The dependence of oscillation amplitudes of the track structure section over time with a motion speed of 80 km/h under the single force impact of the section’s different loads.

Table 2.
Force and deformability behaviour ratios at various motion speeds.
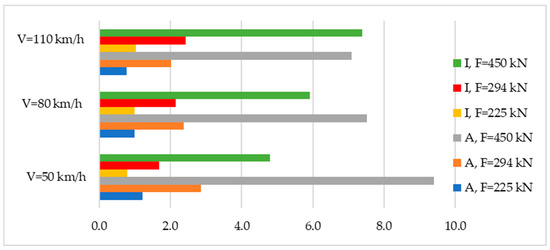
Figure 2.
Ratio of deformability work and intensity of use for section of track construction under different axle loads and speed of rolling stock.
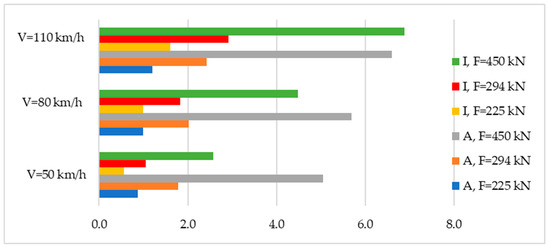
Figure 3.
Ratio of deformability work and intensity of use for pad under different axle loads and speed of rolling stock.
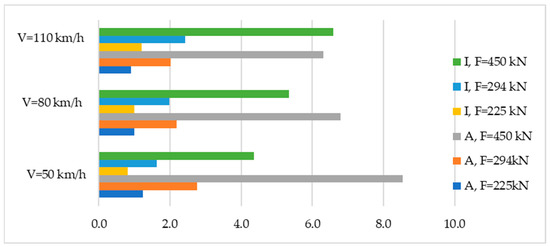
Figure 4.
Ratio of deformability work and intensity of use for sleeper under different axle loads and speed of rolling stock.
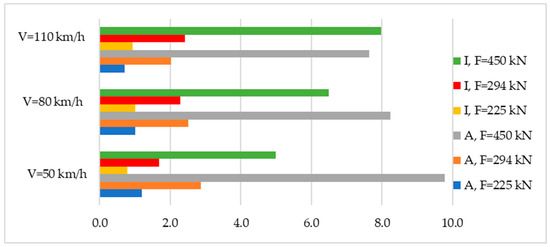
Figure 5.
Ratio of deformability work and intensity of use for ballast under different axle loads and speed of rolling stock.
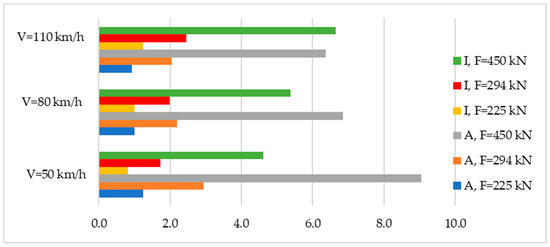
Figure 6.
Ratio of deformability work and intensity of use for ground base under different axle loads and speed of rolling stock.
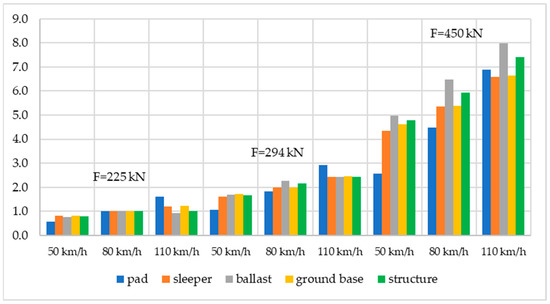
Figure 7.
Ratio of intensity of use for railway track structure and its elements under different axle loads and speed of rolling stock.
The complex dependence of the oscillation amplitudes, shown in Figure 1, demonstrates a non-uniform change in both the amplitudes and frequencies of the oscillations in the deformability process of the track structure section under the action of a force load. This is the result of the superposition of waves as they propagate along the track structure.
Figure 2 shows an increase in both the work that the track structure performs in the process of deformability and the intensity of use of the structure with an increase in axial load. At the same time, an increase in the speed of the rolling stock causes an increase in the intensity of the use of the track structure, but there is a decrease in the amount of work to accomplish the deformability process. This is explained by the fact that an increase in the speed of the rolling stock reduces the contact time of the wheel with the rail during their interaction, which increases the frequency of both the impact of the rolling stock and the vibration of the track structure. However, the speed gradient exceeds the force pressure gradient, which leads to an increase in the length of the track section, perceiving rolling stock loads.
The ratios presented in Figure 3 show that both an increase in axial loads and an increase in travel speeds lead to an intensification in the operating mode of the pad.
Figure 4 shows that an increase in axial loads and speed of the rolling stock increases the intensity of the use of sleepers, but at a lower cost of work of the sleepers for deformability.
The ratios presented in Figure 5 show that an increase in axial loads and speed of the rolling stock increases the intensity of the use of ballast, but at a lower cost of amount of work of the ballast for deformability.
Figure 6 shows that an increase in axial loads and speed of the rolling stock increases the intensity of the use of ground base, but at a lower cost of work of the ground base for deformability.
The ratios shown in Figure 7 help to determine the general trends in the change in the intensity of the use of elements and the railway track structure under the influence of rolling stock with various speeds and axial load, as well as the particular conditions that distinguish elements that perceive the load more intensively. For example, at a speed of 110 km/h, the pads wear out more intensively, regardless of the axle load. This is due to the fact that the behaviour of the pad with the accepted geometric, physical, and mechanical characteristics resonates with the frequency of the load application, that is, when the rolling stock passes at the specified speed. The above ratios also demonstrate the involvement of the ballast in the intensive vibration process, with the accepted geometric and physical-mechanical characteristics, with an increase in the axial load.
The proposed detailing allows establishing the interdependences of the rolling stock dynamics and the intensity of using the railway track elements. The use of the proposed evaluation parameters of deformability behaviour will further allow defining the effect of the aggregate change in the states of elements on the track structure operation and, in compliance with the current requirements for the track structure and its maintenance, to form the set of evaluation data of the track state in terms of acceptable deviations in the track elements.
3.2. The Second Direction of Detailing
One of the main factors in the impossibility of ensuring the relationship between the technical and economic aspects of the work of railway transport facilities is the lack of knowledge about the relationship between the technical conditions of the elements and the structure of the railway track, operating conditions, and the system of periodicity maintenance at the operational stage of its life cycle. This factor requires the introduction of new approaches to the criteria and methods for its assessment.
Therefore, based on the introduced criteria of deformability work and intensity of use, a method for evaluating the operation deformability of a railway track is proposed, the algorithm of which is shown in Figure 8. The method involves the use of the existing system of standards that characterize the state of both the elements and the track structure. These standards make it possible to determine under what geometric or rigid deviations from the norms the track elements and structures refer to the following different technical states: railway track good state, faulty state, up state, partial up state, disabled state, damage, defect, partial failure, complete failure. These states characterize the functional state of the track during the life cycle of the track operation. In turn, the functional states determine such characteristics as reliability, availability, maintainability, and safety (RAMS) of both the element and the track structure. The existing regulatory systems for the maintenance of the track, developed on the basis of experience with its operation, determine the scope and procedure for its restoration from one technical state to another. Modeling of the processes of interaction of a path and rolling stock using the theory of elastic waves allows establishing the dependence of the influence of the technical condition of each element and their aggregate on a technical condition of a track structure. Thus, the relationship between the techno-economic aspects of exploitation can be investigated.
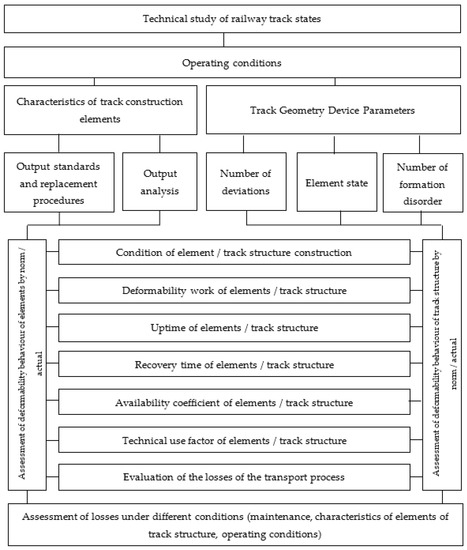
Figure 8.
Algorithm of the Method of Estimating the Operation Deformability of a Railway Track.
The combination of using the proposed modeling method and systems of normative evaluation of the track allows assessing the influence of both the geometry of the structure of each element and the state of the material of each element of the track structure on the operation of the track structure itself according to the norm and the current actual state. Thus, the above algorithm for a certain section of the track allows for determining the efficiency of the relationship, in terms of technical use of the track, between track operating conditions, periodicity of track maintenance, and track structure by estimating losses in their various variations.
4. Discussion, Conclusions and Future Recommendation
Since the proposed approach allows you to correctly describe the physical processes that occur inside both the track elements and the structure over time, this allows evaluating and managing the infrastructure’s functional safety at the stage of object operation simulation by:
- -
- Modeling of time-space processes occurring both inside each element of the structure and in the track structure as a whole under the influence of both external and internal influences;
- -
- Modifying of models by changing the geometric and physical-mechanical characteristics of structural elements for certain operating conditions;
- -
- Optimizing the risks associated with unsuccessful trials;
- -
- Controlling deformability parameters in dynamic processes;
- -
- Expanding existing methods for diagnosing dynamic systems;
- -
- Optimizing costs for the manufacture and operation of simulation objects, as well as damage prediction during continued operation.
This allows optimizing objects by modifying their design, the properties of materials of objects, and the technology of maintenance under specific operating conditions. All this contributes to increasing the competitiveness of infrastructure facilities in general.
Improving the railway infrastructure can bring about improvements in terms of both geometry and safety. A careful analysis of the materials used in its construction will make it possible to make more sustainable modal choices with respect to the environment and the objectives of the 2030 Agenda (UN), also correlating them with the development of rail-road intermodality, thereby also reducing the environmental impact.
Author Contributions
Conceptualization, I.B., T.C., G.T. and L.N.; methodology, I.B., T.C., G.T. and L.N.; software, I.B., T.C., G.T. and L.N.; validation, I.B., T.C., G.T. and L.N.; formal analysis, I.B., T.C., G.T. and L.N.; resources, I.B., T.C., G.T. and L.N.; data curation, I.B., T.C., G.T. and L.N.; writing—original draft preparation, I.B., T.C., G.T. and L.N.; writing—review and editing, I.B., T.C., G.T. and L.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Coelho, B.Z.; Varandas, J.N.; Hijma, M.P.; Zoeteman, A. Towards network assessment of permanent railway track deformation. Transp. Geotech. 2021, 29, 100578. [Google Scholar] [CrossRef]
- Neuhold, J.; Landgraf, M.; Marschnig, S.; Veit, P. Measurement Data-Driven Life-Cycle Management of Railway Track. Transp. Res. Rec. 2020, 2674, 685–696. [Google Scholar] [CrossRef]
- Söderholm, P.; Nilsen, T. Systematic risk-Analysis to support a living maintenance programme for railway infrastructure. J. Qual. Maint. Eng. 2017, 23, 326–340. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, P.; Yang, G.; Chen, L.; Li, J. BIC-Based Data-Driven Rail Track Deterioration Adaptive Piecewise Modeling Framework. Front. Mater. 2021, 8, 620484. [Google Scholar] [CrossRef]
- Goodarzi, S.; Kashani, H.F.; Oke, J.; Ho, C.L. Data-driven methods to predict track degradation: A case study. Constr. Build. Mater. 2022, 344, 128166. [Google Scholar] [CrossRef]
- Bondarenko, I. Modeling for establishment of evaluation conditions of functional safety of the railway track. East.-Eur. J. Enterp. Technol. 2016, 1, 79. [Google Scholar] [CrossRef][Green Version]
- Kostovasilis, D.; Ntotsios, E.; Hussein, M.F.M.; Thompson, D.J.; Squicciarini, G. A holistic approach for the design and assessment of railway tracks. In Proceedings of the IX International Conference on Structural Dynamics (EURODYN 2014), Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Lipecki, T.; Jamińska-Gadomska, P.; Sumorek, A.; Błazik-Borowa, E.; Bęc, J. A system for measuring environmental data in full-scale. J. Phys. Conf. Ser. 2018, 1101, 012019. [Google Scholar] [CrossRef]
- Sol-Sánchez, M.; Castillo-Mingorance, J.M.; Moreno-Navarro, F.; Mattinzioli, T.; Rubio-Gámez, M.C. Piezoelectric-sensored sustainable pads for smart railway traffic and track state monitoring: Full-scale laboratory tests. Constr. Build. Mater. 2021, 301, 124324. [Google Scholar] [CrossRef]
- Kulupa, M.; Magda, P.; Mrówczyńska, M. Accuracy Characteristics of the Selected Diagnostics Methods and the Adjustment of Geodetic Observations. Civ. Environ. Eng. Rep. 2021, 31, 167–183. [Google Scholar] [CrossRef]
- Borghetti, F.; Petrenj, B.; Trucco, P.; Marchionni, G.; Ponti, M.; Calabrese, V. Multi-level approach to assessing the resilience of road network infrastructure. Int. J. Crit. Infrastruct. 2021, 17, 97. [Google Scholar] [CrossRef]
- Bibik, S.; Strelko, O.; Nesterenko, H.; Muzykin, M.; Kuzmenko, A. Formulation of the mathematical model for the planning system in the carriage of dangerous goods by rail. IOP Conf. Ser. Mater. Sci. Eng. 2020, 985, 012024. [Google Scholar] [CrossRef]
- Babyak, M.; Neduzha, L. Transportation Optimization of Homogeneous Freight in the Transport Systems. In Proceedings of the 26th International Conference Transport Means, Kaunas, Lithuania, 5–7 October 2022; pp. 755–760. [Google Scholar]
- Yan, H.; Gao, C.; Elzarka, H.; Mostafa, K.; Tang, W. Risk assessment for construction of urban rail transit projects. Saf. Sci. 2019, 118, 583–594. [Google Scholar] [CrossRef]
- He, C.; Zhou, S.; Di, H.; Zhang, X. An efficient prediction model for vibrations induced by underground railway traffic and experimental validation. Transp. Geotech. 2021, 31, 100646. [Google Scholar] [CrossRef]
- Zlatov, N.; Sattar, T. The development of a lifelong learning framework for mechatronics engineering. In Proceedings of the 15th International Workshop on Research and Education in Mechatronics (REM), El Gouna, Egypt, 9–11 September 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Papathanasiou, N.; Adey, B.T. Identifying the Input Uncertainties to Quantify When Prioritizing Railway Assets for Risk-Reducing Interventions. CivilEng 2020, 1, 8. [Google Scholar] [CrossRef]
- Eickhoff, B.; Mazzola, L.; Bezin, Y.; Tucker, G.; Stradtmann, H.; Stradtmann, H.; Haigermoser, A.; Chollet, H.; Landais, J. Track loading limits and cross-acceptance of vehicle approvals. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 229, 710–728. [Google Scholar] [CrossRef]
- Dong, B.X.; Shan, M.; Hwang, B.G. Simulation of transportation infrastructures resilience: A comprehensive review. Environ. Sci. Pollut. Res. 2022, 29, 12965–12983. [Google Scholar] [CrossRef]
- Guo, D.; Shan, M.; Owusu, E.K. Resilience Assessment Frameworks of Critical Infrastructures: State-of-the-Art Review. Buildings 2021, 11, 464. [Google Scholar] [CrossRef]
- Pons, J.J.; Sanchis, I.V.; Franco, R.I.; Yepes, V. Life cycle assessment of a railway tracks substructures: Comparison of ballast and ballastless rail tracks. Environ. Impact Assess. Rev. 2020, 85, 106444. [Google Scholar] [CrossRef]
- Hedel, R.; Boustras, G.; Gkotsis, I.; Vasiliadou, I.; Rathke, P. Assessment of the European Programme for Critical Infrastructure Protection in the surface transport sector. Int. J. Crit. Infrastruct. 2018, 14, 311–335. [Google Scholar] [CrossRef]
- Ribeiro, F.B.; Nascimento, F.A.C.; Silva, M.A.V. Environmental performance analysis of railway infrastructure using life cycle assessment: Selecting pavement projects based on global warming potential impacts. J. Clean. Prod. 2022, 365, 132558. [Google Scholar] [CrossRef]
- Pîrvan, A.I.; Pătru, G.C.; Trancă, D.C.; Contaşel, C.; Rosner, D. Infrastructure independent rail quality diagnosis and monitoring system. In Proceedings of the 2019 18th RoEduNet Conference: Networking in Education and Research (RoEduNet), Galati, Romania, 10–12 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Charoenwong, C.; Connolly, D.P.; Odolinski, K.; Costa, P.A.; Galvín, C.P.; Smith, A. The effect of rolling stock characteristics on differential railway track settlement: An engineering-economic model. Transp. Geotech. 2022, 37, 100845. [Google Scholar] [CrossRef]
- Czarnuch, A.; Stembalski, M.; Szydłowski, T.; Batory, D. Method of reconstructing dynamic load characteristics for durability test Indexed by: Of heavy semitrailer under different road conditions. Eksploat. I Niezawodn. 2021, 23, 548–558. [Google Scholar] [CrossRef]
- Goolak, S.; Riabov, I.; Gorobchenko, O.; Yurchenko, V.; Nezlina, O. Improvement of the model of an asynchronous traction motor of an electric locomotive by taking into account power losses. Prz. Elektrotechniczny 2022, 98, 1–10. [Google Scholar] [CrossRef]
- Indraratna, B.; Singh, M.; Nguyen, T.T.; Rujikiatkamjorn, C.; Malisetty, R.S.; Arivalagan, J.; Nair, L. Internal Instability and Fluidisation of Subgrade Soil under Cyclic Loading. Indian Geotech. J. 2022, 52, 1226–1243. [Google Scholar] [CrossRef]
- Villalba, I.; Ricardo, S.; Franco, I.; Martínez, P.; Zuriaga, F.P.S.P. Experimental and numerical investigations of dual gauge railway track behaviour. Constr. Build. Mater. 2021, 299, 123943. [Google Scholar] [CrossRef]
- Urbancová, Z.; Sventeková, E. Assessing vulnerability of key elements of railway infrastructure. Transp. Res. Procedia 2019, 40, 1597–1603. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Feng, B.; Tutumluer, E.; Hashash, Y.M.A.; Kaewunruen, S. Evaluation of lateral stability of railway tracks due to ballast degradation. Constr. Build. Mater. 2021, 278, 122342. [Google Scholar] [CrossRef]
- Brzeżański, M.; Noga, M.; Szalek, A. Operation of the Fuel Cell Electric Vehicle in Moderate and Low-Temperature Ambient Conditions; SAE Technical Paper; SAE Technical Paper 2022-01-1129; SAE International: Warrendale, PA, USA, 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Kaewunruen, S.; Baniotopoulos, C. Nonlinear buckling instabilities of interspersed railway tracks. Comput. Struct. 2021, 249, 106516. [Google Scholar] [CrossRef]
- Hodás, S.; Pultznerová, A. Modelling of Railway Track Temperature Regime with Real Heat-Technical Values for Different Climatic Characteristics. Civ. Environ. Eng. 2017, 13, 134–142. [Google Scholar] [CrossRef]
- Bosomworth, C.; Spiryagin, M.; Alahakoon, S.; Cole, C.; Sneath, B.; Makin, B. Rail temperature variation under heavy haul operations. Railw. Eng. Sci. 2022, 30, 148–161. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Lv, Q.; Jiao, H.; Xiao, X. Measuring, modelling and optimising an embedded rail track. Appl. Acoust. 2017, 116, 70–81. [Google Scholar] [CrossRef]
- Sañudo, R.; Jardí, I.; Martínez, J.-C.; Sánchez, F.-J.; Miranda, M.; Alonso, B.; dell’Olio, L.; Moura, J.-L. Monitoring Track Transition Zones in Railways. Sensors 2022, 22, 76. [Google Scholar] [CrossRef]
- Ramos, A.; Correia, A.G.; Indraratna, B.; Ngo, T.; Calçada, R.; Costa, P.A. Mechanistic-empirical permanent deformation models: Laboratory testing, modelling and ranking. Transp. Geotech. 2020, 23, 100326. [Google Scholar] [CrossRef]
- Belding, M.; Enshaeian, A.; Rizzo, P. Vibration-Based Approach to Measure Rail Stress: Modeling and First Field Test. Sensors 2022, 22, 7447. [Google Scholar] [CrossRef]
- Moliner, E.; Martínez-Rodrigo, M.D.; Galvín, P.; Chordà-Monsonís, J.; Romero, A. On the vertical coupling effect of ballasted tracks in multi–span simply–supported railway bridges under operating conditions. Struct. Infrastruct. Eng. 2022. [Google Scholar] [CrossRef]
- Jarillo, J.M.; Moreno, J.; Alfi, S.; Barcet, S.; Bouvet, P.; Bruni, S.; Cervello, S.; Costa, B.; Licciardello, R. Novel technology concepts and architecture for on-board condition-based monitoring of railway running gear: The RUN2Rail vision. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 616–630. [Google Scholar] [CrossRef]
- Arena, M.; Foiadelli, F.; Acquaro, G.; Gentile, M. Functional safety of railway systems. In Proceedings of the 2015 AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015. [Google Scholar] [CrossRef]
- Hendrix, B.; Lewis, T.; Emery, M.; Rachele, B. Model Based Functional Safety—How Functional Is It? J. Syst. Saf. 2022, 57, 32–38. [Google Scholar] [CrossRef]
- Liu, J.; Dai, X.; Guo, Z.; Wang, Y. Quantitative safety assessment method based on risk in railway system. China Railw. Sci. 2009, 29, 60–63. [Google Scholar]
- Sasidharan, M.; Torbaghan, M.E. Risk-informed sustainable asset management of railway tracks. Infrastruct. Asset Manag. 2021, 8, 25–35. [Google Scholar] [CrossRef]
- Eidsvig, U.; Santamaría, M.; Galvão, N.; Tanasic, N.; Piciullo, L.; Hajdin, R.; Nadim, F.; Sousa, H.S.; Matos, J. Risk Assessment of Terrestrial Transportation Infrastructures Exposed to Extreme Events. Infrastructures 2021, 6, 163. [Google Scholar] [CrossRef]
- Shtompel, A.M.; Kondratenko, O.P.; Bratchenko, O.V.; Pashchenko, V.V.; Baulin, D.S. Dynamic impact on the construction of the railway track and on the deformability of the basement. IOP Conf. Ser. Mater. Sci. Eng. 2019, 708, 012029. [Google Scholar] [CrossRef]
- Jin, Q.; Thompson, D.J.; Lurcock, D.E.J.; Toward, M.G.R.; Ntotsios, E. A 2.5D finite element and boundary element model for the ground vibration from trains in tunnels and validation using measurement data. J. Sound Vib. 2017, 422, 373–389. [Google Scholar] [CrossRef]
- Litherland, J.; Andrews, J. A reliability study of railway switch and crossing components. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 1–13. [Google Scholar] [CrossRef]
- Bondarenko, I.; Severino, A.; Olayode, I.O.; Campisi, T.; Neduzha, L. Dynamic Sustainable Processes Simulation to Study Transport Object Efficiency. Infrastructures 2022, 7, 124. [Google Scholar] [CrossRef]
- Sasidharan, M.; Burrow, M.P.N.; Ghataora, G.S.; Marathu, R. A risk-informed decision support tool for the strategic asset management of railway track infrastructure. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 236, 183–197. [Google Scholar] [CrossRef]
- Kumar, N.; Kossmann, C.; Scheriau, S.; Six, K. An efficient physical-based method for predicting the long-term evolution of vertical railway track geometries. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 447–465. [Google Scholar] [CrossRef]
- Jang, S.Y. Analysis of Life Cycle Costs of Railway Track: A Case Study for Ballasted and Concrete Track for High-Speed Railway. J. Korea Inst. Struct. Maint. Insp. 2016, 20, 110–121. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, S.; Zhai, W. An advanced train-slab track spatially coupled dynamics model: Theoretical methodologies and numerical applications. J. Sound Vib. 2021, 501, 116059. [Google Scholar] [CrossRef]
- Garmabaki, A.H.S.; Thaduri, A.; Famurewa, S.; Kumar, U. Adapting Railway Maintenance to Climate Change. Sustainability 2021, 13, 13856. [Google Scholar] [CrossRef]
- Blackwood, L.; Renaud, F.G.; Gillespie, S. Nature-based solutions as climate change adaptation measures for rail infrastructure. Nat.-Based Solut. 2022, 2, 100013. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Z.; Yang, C.; Zhang, W.; Liu, X. Reduced-order modeling of train-curved-slab-track dynamics with the effects of fastening failures. Acta Mech. Sin. 2022, 38, 522039. [Google Scholar] [CrossRef]
- Erhova, N.; Bondarenko, I.; Shibko, O.; Velmagina, N. Development of the procedure for verifying the feasibility of designing an active suspension system for transport carriages. East.-Eur. J. Enterp. Technol. 2018, 3, 53–63. [Google Scholar] [CrossRef]
- Bondarenko, I.; Keršys, R.; Neduzha, L. Analysis of problem related to experimental data processing in the study of the crew’s influence on the track. In Proceedings of the 26th International Conference Transport Means, Kaunas, Lithuania, 5–7 October 2022; pp. 663–668. [Google Scholar]
- El-sayed, H.M.; Fayed, M.N.; Riad, H.S.; Zohny, H.N. A review of the structural performance of prestressed monoblock concrete sleepers in ballasted railway tracks. Eng. Fail. Anal. 2022, 140, 106522. [Google Scholar] [CrossRef]
- Izvolt, L.; Kardos, J. Influence of Parameters of Railway Track Construction on Vertical Dynamic Interaction Vehicle/Track. Komunikacie 2011, 13, 63–70. [Google Scholar] [CrossRef]
- Zeng, Z.; Hu, J.; Guo, W.; Huang, X.; Li, P.; Wang, W.; Tian, C.; Shuaibu, A. Indoor simulation test research on cumulative longitudinal displacement of rail based on force and displacement sensors data collection. Sci. Prog. 2021, 104, 368504211023287. [Google Scholar] [CrossRef]
- Blanco, B.; Alonso, A.; Kari, L.; Gil-Negrete, N.; Giménez, J.G. Distributed support modelling for vertical track dynamic analysis. Veh. Syst. Dyn. 2018, 56, 529–552. [Google Scholar] [CrossRef]
- Han, S.H.; Hwang, S.H.; Kim, H.J.; Cho, S.J.; Lim, N.H. Numerical study on the characteristics of temperature distribution in continuous welded rail by solar radiation and rail orientation. J. Mater. Sci. Technol. 2020, 34, 4819–4829. [Google Scholar] [CrossRef]
- Sanchis, I.V.; Franco, R.I.; Zuriaga, P.S.; Fernández, P.M. Risk of increasing temperature due to climate change on high-speed rail network in Spain. Transp. Res. Procedia 2020, 45, 5–12. [Google Scholar] [CrossRef]
- Hong, S.U.; Kim, H.U.; Lim, N.H.; Kim, K.H.; Kim, H.; Cho, S.J. A Rail-Temperature-Prediction Model Considering Meteorological Conditions and the Position of the Sun. Int. J. Precis. Eng. Manuf. 2019, 20, 337–346. [Google Scholar] [CrossRef]
- Mulholland, E.; Feyen, L. Increased risk of extreme heat to European roads and railways with global warming. Clim. Risk Manag. 2021, 34, 100365. [Google Scholar] [CrossRef]
- Aggestam, E.; Nielsen, J.C.O.; Bolmsvik, R. Simulation of vertical dynamic vehicle–track interaction using a two-dimensional slab track model. Veh. Syst. Dyn. 2018, 56, 1633–1657. [Google Scholar] [CrossRef]
- Shen, C.; Deng, X.; Wei, Z.; Dollevoet, R.; Li, Z. Comparisons between beam and continuum models for modelling wheel-rail impact at a singular rail surface defect. Int. J. Mech. Sci. 2021, 198, 106400. [Google Scholar] [CrossRef]
- Kalivoda, J.; Neduzha, L. Running Dynamics of Rail Vehicles. Energies 2022, 15, 5843. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Bruzek, R.; Sussmann, T.R.; Thompson, H.B.; Mishra, D. A study of vertical tie reaction forces in ballasted railroad tracks through field instrumentation and numerical modeling. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022. [Google Scholar] [CrossRef]
- Chen, M.; Sun, Y.; Zhu, S. Dynamic performance comparison of different types of ballastless tracks using vehicle-track-subgrade coupled dynamics model. Eng. Struct. 2021, 249, 113390. [Google Scholar] [CrossRef]
- Bragança, C.; Neto, J.; Pinto, N.; Montenegro, P.A.; Ribeiro, D.; Carvalho, H.; Calçada, R. Calibration and validation of a freight wagon dynamic model in operating conditions based on limited experimental data. Veh. Syst. Dyn. 2022, 60, 3024–3050. [Google Scholar] [CrossRef]
- Matsumoto, A.; Sato, Y.; Ohno, H.; Shimizu, M.; Kurihara, J.; Tomeoka, M.; Saitou, T.; Michitsuji, Y.; Tanimoto, M.; Sato, Y.; et al. Continuous observation of wheel/rail contact forces in curved track and theoretical considerations. Veh. Syst. Dyn. 2012, 50 (Suppl. 1), 349–364. [Google Scholar] [CrossRef]
- Piloto, P.A.; Frigeri, A.V.; Minhoto, M.; Silva, D.A. Validation of a rail temperature model with experimental measurements. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 1104–1113. [Google Scholar] [CrossRef]
- Hong, S.; Park, C.; Cho, S. A Rail-Temperature-Prediction Model Based on Machine Learning: Warning of Train-Speed Restrictions Using Weather Forecasting. Sensors 2021, 21, 4606. [Google Scholar] [CrossRef]
- Magalhães, K.M.M.; Brasil, R.M.L.R.F.; Wahrhaftig, A.M.; Siqueira, G.H.; Bondarenko, I.; Neduzha, L. Influence of Atmospheric Humidity on the Critical Buckling Load of Reinforced Concrete Columns. Int. J. Struct. Stab. Dyn. 2022, 22, 2250011. [Google Scholar] [CrossRef]
- Hall, L. Simulations and analyses of train-induced ground vibrations in finite element models. Soil Dyn. Earthq. Eng. 2003, 23, 403–413. [Google Scholar] [CrossRef]
- Connolly, D.; Giannopoulos, A.; Forde, M.C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments. Soil Dyn. Earthq. Eng. 2013, 46, 13–19. [Google Scholar] [CrossRef]
- Bondarenko, I. Development of algorithm for calculating dynamic processes of railroad track deformability work. East.-Eur. J. Enterp. Technol. 2016, 6–7, 28–36. [Google Scholar] [CrossRef][Green Version]
- Bondarenko, I.; Lunys, O.; Neduzha, L.; Keršys, R. Dynamic Track Irregularities Modeling when Studying Rolling Stock Dynamics. In Proceedings of the 23rd International Conference Transport Means, Palanga, Lithuania, 2–4 October 2019; pp. 1014–1019. [Google Scholar]
- Celiński, I.; Burdzik, R.; Młyńczak, J.; Kłaczyński, M. Research on the Applicability of Vibration Signals for Real-Time Train and Track Condition Monitoring. Sensors 2022, 22, 2368. [Google Scholar] [CrossRef]
- Ulianov, C.; Hyde, P.; Shaltout, R. Railway Applications for Monitoring and Tracking Systems. In Sustainable Rail Transport. Lecture Notes in Mobility; Marinov, M., Ed.; Springer: Cham, Switzerland, 2018; pp. 77–91. [Google Scholar] [CrossRef]
- Bondarenko, I.; Keršys, R.; Neduzha, L. Studying of Dynamic Parameters Impulse Impact of the Vehicle Taking into Account the Track Stiffness Variations. In Proceedings of the 25th International Conference Transport Means, Kaunas, Lithuania, 6–8 October 2021; pp. 684–689. [Google Scholar]
- Bondarenko, I.; Keršys, A.; Neduzha, L. Assessment of the Railway Track Deformability Behaviour as the Parameter of Operational Availability Function. In Proceedings of the 25th International Conference Transport Means, Kaunas, Lithuania, 6–8 October 2021; pp. 644–648. [Google Scholar]
- Rules for Calculating the Railway Track for Strength and Stability; No. 960-Ц3; Ukrainian Railways: Kyiv, Ukraine, 2004; 170p.
- Praticò, F.; Giunta, M. Proposal of a Key Performance Indicator for Railway Track Based on LCC and RAMS Analyses. J. Constr. Eng. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Djordjević, B.; Mane, A.S.; Krmac, E. Analysis of dependency and importance of key indicators for railway sustainability monitoring: A new integrated approach with DEA and Pearson correlation. Res. Transp. Bus. Manag. 2021, 41, 100650. [Google Scholar] [CrossRef]
- Xin, X.; Ren, Z. The Effect of Interface Damage between Slab and Mortar Layer on the Dynamic Performances of Vehicle and Track Systems under the High Frequency Train Loads. Appl. Sci. 2022, 12, 4555. [Google Scholar] [CrossRef]
- El Moueddeb, M.; Louf, F.; Boucard, P.-A.; Dadié, F.; Saussine, G.; Sorrentino, D. An Efficient Numerical Model to Predict the Mechanical Response of a Railway Track in the Low-Frequency Range. Vibration 2022, 5, 19. [Google Scholar] [CrossRef]
- Punetha, P.; Nimbalkar, S.; Khabbaz, H. Simplified geotechnical rheological model for simulating viscoelasto-plastic response of ballasted railway substructure. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 2019–2047. [Google Scholar] [CrossRef]
- Zhang, Q.; Leng, W.; Dong, J.; Xu, F. Dynamic Response Characteristics of Railway Subgrade Using a Newly-Developed Prestressed Reinforcement Structure: Case Study of a Model Test. Materials 2022, 15, 6651. [Google Scholar] [CrossRef]
- Hurtado-Hurtado, G.; Morales-Velazquez, L.; Valtierra-Rodríguez, M.; Otremba, F.; Jáuregui-Correa, J.C. Frequency Analysis of the Railway Track under Loads Caused by the Hunting Phenomenon. Mathematics 2022, 10, 2286. [Google Scholar] [CrossRef]
- Liu, J.; Liu, G.; Gao, T.; Wang, P.; Xiao, J.; Hu, C. Settlement and Stress Distribution Characteristics of a Railway Ballast Layer under a Dynamic Load. In Proceedings of the Transportation Research Board 100th Annual Meeting 2021, Washington, DC, USA, 5–9 January 2021; Available online: http://worldcat.org/issn/03611981 (accessed on 7 November 2022).
- Germonpré, M.; Degrande, G.; Lombaert, G. Periodic track model for the prediction of railway induced vibration due to parametric excitation. Transp. Geotech. 2018, 17, 98–108. [Google Scholar] [CrossRef]
- Wang, H.; Markine, V.; Liu, X. Experimental analysis of railway track settlement in transition zones. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1774–1789. [Google Scholar] [CrossRef] [PubMed]
- Trinh, H.; Haas, N.; Li, Y.; Otto, C.; Pankanti, S. Enhanced rail component detection and consolidation for rail track inspection. In Proceedings of the 2012 IEEE Workshop on the Applications of Computer Vision (WACV), Breckenridge, CO, USA, 9–11 January 2012; pp. 289–295. [Google Scholar] [CrossRef]
- Kouroussis, G.; Verlinden, O.; Conti, C. Free field vibrations caused by high-speed lines: Measurement and time domain simulation. Soil Dyn. Earthq. Eng. 2011, 31, 692–707. [Google Scholar] [CrossRef]
- Li, T.; Su, Q.; Kaewunruen, S. Influences of piles on the ground vibration considering the train-track-soil dynamic interactions. Comput. Geotech. 2020, 120, 103455. [Google Scholar] [CrossRef]
- Wang, L.; Wang, P.; Wei, K.; Dollevoet, R.; Li, Z. Ground vibration induced by high speed trains on an embankment with pile-board foundation: Modelling and validation with in situ tests. Transp. Geotech. 2022, 34, 100734. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).