The Sustainability Evaluation of Masks Based on the Integrated Rank Sum Ratio and Entropy Weight Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sustainable Evaluation Materials
2.2. Sustainable Evaluation Principles
2.3. Rank-Sum Ratio–Entropy Method Evaluation Model
- Put raw evaluation data into a matrix. Suppose that there are m kinds of masks as evaluation objects and n evaluation indexes, then obtain the raw data matrix of m rows and n columns , where denotes the score of the j-th index of the i-th mask.
- Forward standardized scores for each index. For benefit indexes (the higher, the better principle), their standardization process is expressed in Equation (1); For cost indexes (the lower, the better principle), their standardization process is expressed in Equation (2).
- Calculate the rank value for each index. In order to overcome the drawback that RSR tends to lose the quantitative information of the original index value when performing ranking, this work does not directly compare the index scores but adopts a method similar to linear interpolation. There exists a quantitative linear correspondence between the compiled rank and the original index value, which is calculated by:
- The weights of each index are calculated by EWM, and the calculation procedure contains the following three steps:
- Step 1.
- Work out the weight of the i-th evaluation object under the j-th index . is regarded as the probability used in the relative entropy calculation process, and its formula is presented in Equation (4).
- Step 2.
- Calculate the information entropy of each index ; the information entropy calculation formula is shown in Equation (5).
- Step 3.
- Normalize the information entropy to determine the entropy weight of each indicator , as presented in Equation (6).
- Calculate the weighted RSR values and rank them. The weighted rank-sum ratio is calculated by Equation (7):
- Determine the distribution of (transformed into probability units). The distribution of is the cumulative frequency of the value specific expressed in probability units Probit. The Probit model is a generalized linear model that obeys a normal distribution, and its transformation process consists of the following five steps:
- Step 1.
- Arrange the values of in ascending order.
- Step 2.
- List the frequency of each group , and calculate the cumulative frequency of each group .
- Step 3.
- Determine the average rank of each . For values whose frequency equals 1, the value of is the rank of . The higher the rank is, the better the evaluation object is. For values whose frequency is not 1, the value of is the average value of each rank.
- Step 4.
- Calculate the downward cumulative frequency and correct the last item with .
- Step 5.
- Convert the downward cumulative frequencies to probability units Probit. Probit is the standard normal deviation μ plus 5 corresponding to the cumulative frequencies. Refer to reference [30] for the “comparison table of percentages and probability units”.
- Take the probability unit Probit corresponding to the cumulative frequency as the independent variable and as the dependent variable, calculate the linear regression equation shown in Equation (8), and test this regression equation.
- The binning process is performed according to the probability unit Probity and the correct rank-sum-ratio value .
3. Results and Discussion
3.1. Mask Sustainability Evaluation Results
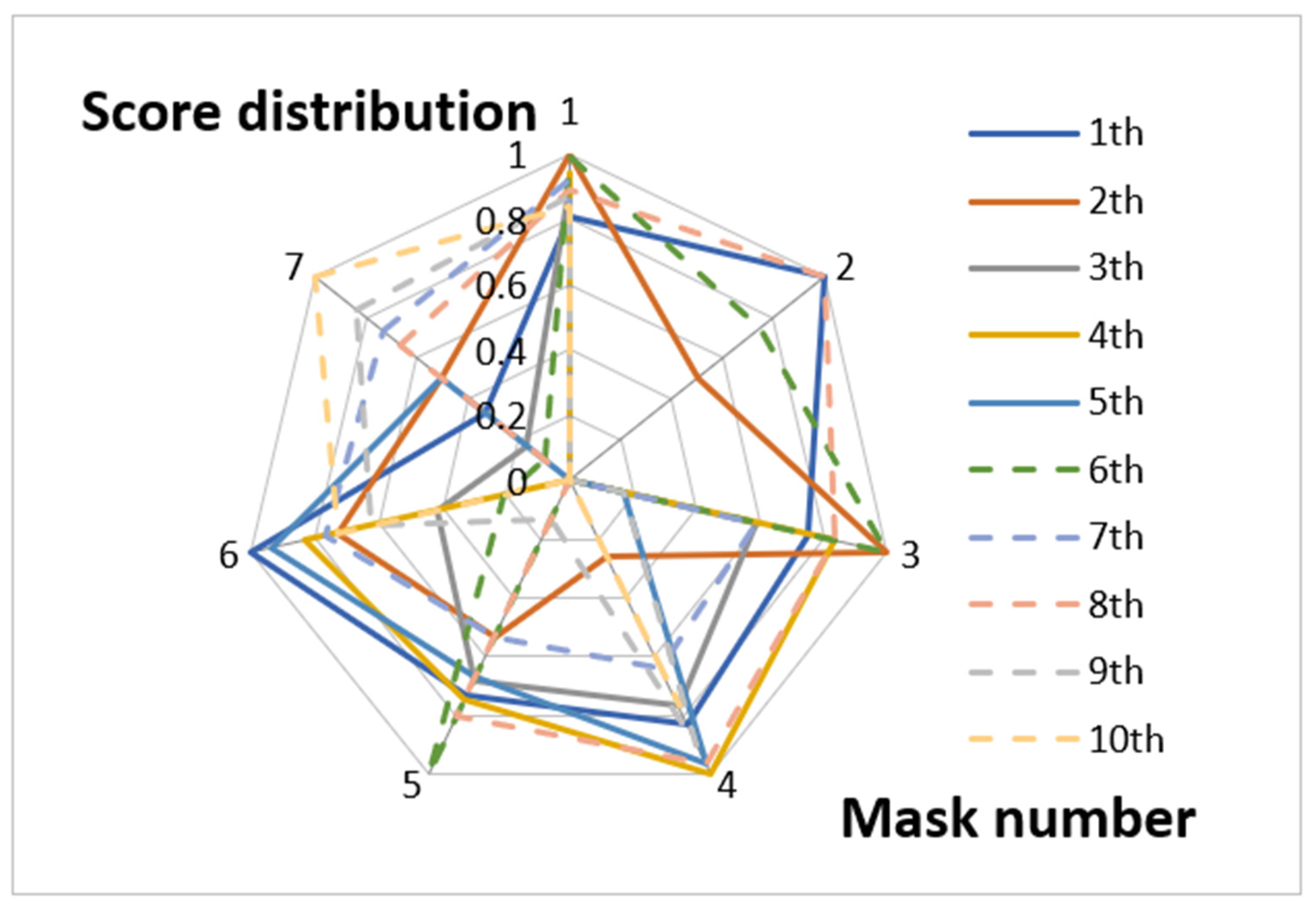
- Based on the scores of the seven indicators of the ten masks presented in Table 2 and step “1” of the rank-sum ratio comprehensive evaluation method, an original evaluation matrix is constructed and presented as follows:
- Positive standardization on masks sustainability evaluation indexes. Scores of the indexes are standardized by Equations (1) and (2), and the obtained results are as follows:
- Calculate the rank of each index for the sustainability evaluation of masks . Indexes 1 and 3 are cost indicators, while the other indexes are benefit indicators, which are calculated by Equation (3). The calculation results are as follows:
- Calculate weights by EWM. According to Equation (4), the information entropy and entropy weight of the seven evaluation indexes can be obtained, and the results are shown in Table 3. It can be seen from Table 3 that the information entropy of index 2 is obviously lower than other indexes, indicating that index 2 has the biggest weight. Meanwhile, it can also be found that various types of masks have the greatest difference in terms of material environmental friendliness and are most likely to attract more people’s attention.
- Determine the value of the weighted rank-sum ratio WRSR. Calculate the weighted rank-sum ratio for the ten masks by Equation (7) in step (5), and experimental results are shown below. It can be figured out that the values of the weighted rank-sum ratio of masks numbered 1 and 8 are significantly better than other masks.
- Statistics on the distribution of WRSR. According to step “6”, the frequency, cumulative frequency, average rank, downward cumulative rating, and probability unit are listed in Table 4. As Table 4 demonstrates, the two masks with a WRSR value of 0.52 jointly occupy the second and third place in the ranking; thus, the average rank is 2.5. The probability unit is obtained from the “Comparison table of percentages and probability units”. It should be emphasized that in terms of the rank-sum-ratio evaluation method used in this work, a higher ranking indicates a better evaluation object.
- Linear regression calculation and test. Calculation results are obtained by IBM SPSS Statistics 26 software, and they are reported in Table 5 since SPSS Statistics 26 can provide more scientific support for data processing [31]. It can be seen that Sig ≤ 0.05 in Table 5, and thus the regression results pass the confidence test. The regression equation is formulated in Equation (9).
3.2. Discussion of Sustainable Evaluation of Masks
3.3. Verification
4. Conclusions
- The environmental, economic, and social sustainability of the masks are evaluated simultaneously, and it is found that some disposable masks show better sustainability than reusable masks.
- The integrated rank-sum ratio and entropy weight method can effectively realize the sustainability evaluation of masks, and its reliability is also tested and verified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Chang, J.; Wang, M. Mask Design for Life in The Midst of COVID-19. Sustainability 2021, 13, 8011. [Google Scholar] [CrossRef]
- Ippolito, M.; Vitale, F.; Accurso, G.; Iozzo, P.; Gregoretti, C.; Giarratano, A.; Cortegiani, A. Medical masks and Respirators for the Protection of Healthcare Workers from SARS-CoV-2 and other viruses. Pulmonology 2020, 26, 204–212. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization Rational Use of Personal Protective Equipment for COVID-19 and Considerations during Severe Shortages. 2020, p. 1. Available online: https://apps.who.int/iris/bitstream/handle/10665/338033/WHO-2019-nCoV-IPC_PPE_use-2020.4-eng (accessed on 30 March 2022).
- Clark, G.; Kosoris, J.; Hong, L.; Crul, M. Design for Sustainability: Current Trends in Sustainable Product Design and Development. Sustainability 2009, 1, 409–424. [Google Scholar] [CrossRef]
- Ertz, M.; Patrick, K. The Future of Sustainable Healthcare: Extending Product Lifecycles. Resour. Conserv. Recycl. 2020, 153, 104589. [Google Scholar] [CrossRef]
- Feng, S.; Shen, C.; Xia, N.; Song, W.; Fan, M.; Cowling, B.J. Rational Use of Face Masks in the COVID-19 Pandemic. Lancet Respir. Med. 2020, 8, 434–436. [Google Scholar] [CrossRef]
- Schmutz, M.; Hischier, R.; Batt, T.; Wick, P.; Nowack, B.; Wäger, P.; Som, C. Cotton and Surgical Masks-What Ecological Factors Are Relevant for Their Sustainability? Sustainability 2020, 12, 10245. [Google Scholar] [CrossRef]
- Furukawa, K.; Sato, K.; Okachi, S.; Kawashima, H.; Fujishiro, M. Surgical Mask Designed for Endoscopic Procedures to Prevent the Diffusion of Droplets. Acta Gastro Enterol. Belg. 2021, 84, 517–519. [Google Scholar] [CrossRef]
- Chao, F.L. Face Mask Designs Following Novel Coronavirus. J. Public Health Res. 2020, 9, 31–35. [Google Scholar] [CrossRef]
- Allison, A.L.; Ambrose-Dempster, E.; Domenech Aparsi, T.; Bawn, M.; Casas Arredondo, M.; Chau, C.; Chandler, K.; Dobrijevic, D.; Hailes, H.; Lettieri, P.; et al. The Environmental Dangers of Employing Single-Use Face Masks as Part of a COVID-19 Exit Strategy. UCL Open Environ. 2020. [Google Scholar] [CrossRef]
- Phan, T.L.; Ching, C.T.S. A Reusable Mask for Coronavirus Disease 2019 (COVID-19). Arch. Med. Res. 2020, 51, 455–457. [Google Scholar] [CrossRef]
- Boix Rodríguez, N.; Formentini, G.; Favi, C.; Marconi, M. Engineering Design Process of Face Masks Based on Circularity and Life Cycle Assessment in the Constraint of the COVID-19 Pandemic. Sustainability 2021, 13, 4948. [Google Scholar] [CrossRef]
- Monzamodeth, R.S.; Román-Roldán, N.I.; Hernández-Morales, B.; Puente, I.; Flores, O.; Castillo, F.; Campillo, B. The Feasibility of Masks and Face Shields Designed by 3D Printing Makers; Some Considerations of Their Use against The COVID-19. Mater. Today Proc. 2021. [Google Scholar] [CrossRef] [PubMed]
- Muñoz López, N.; Valero Martín, J.I.; Biedermann, A.; Santolaya Sáenz, J.L.; Fernández-Vazquez, A. Projecting More Sustainable Product and Service Designs. Sustainability 2021, 13, 11872. [Google Scholar] [CrossRef]
- WCED (World Commission on Environment and Development). Our Common Future; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Morone, P.; Yilan, G.; Imbert, E.; Becchetti, L. Reconciling Human Health with The Environment While Struggling Against The COVID-19 Pandemic Through Improved Face Maskeco-Design. Sci. Rep. 2022, 12, 2445. [Google Scholar] [CrossRef]
- Hong, Y.; Xue, Z.; Liu, C.; Dai, X. Development of Mask Design Knowledge Base Based on Sensory Evaluation and Fuzzy Logic. Autex Res. J. 2021, 21, 224–230. [Google Scholar] [CrossRef]
- An, B.Y.; Porcher, S.; Tang, S.Y.; Kim, E.E. Policy Design for COVID-19: Policy Design for COVID-19: Worldwide Evidence on the Efficacies of Early Mask Mandates and Other Policy Interventions. Public Admin. Rev. 2021, 81, 1157–1182. [Google Scholar] [CrossRef]
- Shin, H.D.; Bull, R. Three Dimensions of Design for Sustainable Behaviour. Sustainability 2019, 11, 4610. [Google Scholar] [CrossRef] [Green Version]
- Liao, T.; MacDonald, E.F. Priming on Sustainable Design Idea Creation and Evaluation. Sustainability 2021, 13, 5227. [Google Scholar] [CrossRef]
- He, B.; Yu, Q. Product Sustainable Design for Carbon Footprint during Product Life Cycle. J. Eng Design. 2021, 32, 478–495. [Google Scholar] [CrossRef]
- Ingabire, J.; McKenney, H.; Sebesta, C.; Badhiwala, K.; Kemere, C.; Kapur, S.; Robinson, J.T. Evaluation of Aerosol Particle Leak and Standard Surgical Mask Fit With 3 Elastomeric Harness Designs. J. AMA Network Open. 2022, 5, e2145811. [Google Scholar] [CrossRef]
- Littig, B.; Griessler, E. Social Sustainability: A Catchword between Political Pragmatism and Social Theory. Int. J. Sustain. Dev. 2005, 8, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Lepelletier, D.; Grandbastien, B.; Romano-Bertrand, S.; Aho, S.; Chidiac, C.; Géhanno, J.F.; Chauvin, F. What face mask for what use in the context of the COVID-19 pandemic? The French guidelines. J. Hosp. Infect. 2020, 105, 414–418. [Google Scholar] [CrossRef] [PubMed]
- National Medical Products Administration. Available online: https://udi.nmpa.gov.cn/showListXXCX.html (accessed on 16 March 2022).
- Mao, S.S.; Cheng, Y.M.; Pu, X.L. Probability and Mathematical Statistics Tutorial, 2nd ed.; Education Press: Beijing, China, 2011. [Google Scholar]
- Fan, H.; Ji, H.P.; Du, X.M.; You, H.; Lu, H. Comprehensive evaluation of medical service quality in A City from 2008 to 2010 By Applying Comprehensive Index Method and Rank Sum Ratio Method. Health Soft Sci. 2012, 26, 201–203. [Google Scholar]
- Wei, Y.Y.; Yan, Y.; Hu, Y.F.; Guo, Y.F.; Zhang, L. Combining TOPSIS and rank sum ratio method to evaluate the quality of survival of urban elderly. Chin. J. Gerontol. 2006, 26, 440–442. [Google Scholar]
- Lin, L.Q.; Sun, F.M. Research on the internal control evaluation system of enterprise mergers and acquisitions based on entropy value assignment method. Technol. Ind. 2013, 13, 119–136. [Google Scholar]
- Wang, S.G.; Zhang, Z.Z.; Cheng, W.H.; Gao, L.D. Probability Theory and Mathematical Statistics; Science Press: Beijing, China, 2006. [Google Scholar]
- Wu, W.W.; Ao, X.Q.; Li, F. On curriculum relevance of the information management and information system major in the age of big data. J. Phys. Conf. Ser. 2020, 1550, 032147. [Google Scholar] [CrossRef]

| Items | Content | ||||
|---|---|---|---|---|---|
| Number | 1 | 2 | 3 | 4 | 5 |
| Image |  |  |  |  |  |
| Materials | Filter: pp Mask strap: None Nose joint: EVA Breathing valve: None | Filter: PP Mask strap: PP Nose joint: None Breathing valve: None | Filter: PS Mask strap: ABS Nose joint: ABS Breathing valve: None | Filter: PP Mask strap: PP Nose joint: None Breathing valve: ABS | Filter: PP Mask strap: PE Nose joint: aluminum Breathing valve: PU |
| Number | 6 | 7 | 8 | 9 | 10 |
| Image |  |  |  |  |  |
| Materials | Filter: PP Mask strap: PE Nose joint: PP Breathing valve: ABS | Filter: PP Mask strap: PP Nose joint: None Breathing valve: None | Filter: PP Mask strap: PE Nose joint: None Breathing valve: PU | Filter: PP Mask strap: PE Nose joint: NR Breathing valve: PU | Filter: PP Mask strap: PE Nose joint: None Breathing valve: None |
| Sustainability Evaluation Principles | Economic Competitiveness | Environmental Friendliness | Social Desirability | ||||
|---|---|---|---|---|---|---|---|
| Evaluation Indicators | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Whole Lifecycle Costs | Material Environmental Friendliness | Waste Production | Recyclable Value | Use of Man-Machine Sex | Aesthetics | Functionality | |
| (Yuan/Day) | (Percentage) | (Percentage) | (Percentage) | (Percentage) | (Percentage) | (Percentage) | |
| No. 1 | 12 | 100 | 3 | 85 | 75 | 98 | 80 |
| No. 2 | 0.4 | 90 | 0 | 40 | 60 | 85 | 85 |
| No. 3 | 6 | 80 | 5 | 80 | 71 | 70 | 75 |
| No. 4 | 4 | 80 | 2 | 98 | 76 | 90 | 70 |
| No. 5 | 60 | 80 | 10 | 95 | 70 | 95 | 85 |
| No. 6 | 1 | 95 | 0 | 20 | 95 | 60 | 73 |
| No. 7 | 5 | 80 | 5 | 70 | 60 | 87 | 92 |
| No. 8 | 7 | 100 | 2 | 95 | 80 | 50 | 90 |
| No. 9 | 8 | 80 | 10 | 90 | 30 | 80 | 95 |
| No. 10 | 10 | 80 | 10 | 80 | 20 | 85 | 100 |
| Index 1 | Index 2 | Index 3 | Index 4 | Index 5 | Index 6 | Index 7 | |
|---|---|---|---|---|---|---|---|
| Information entropy | 0.95 | 0.59 | 0.90 | 0.93 | 0.92 | 0.93 | 0.89 |
| Weights | 0.05 | 0.46 | 0.11 | 0.08 | 0.09 | 0.08 | 0.13 |
| Mask Number | WRSR | f | ∑f | Ranking | Probit | ||
|---|---|---|---|---|---|---|---|
| 3 | 0.051 | 1 | 1 | 1 | 1 | 10% | 3.71 |
| 5, 10 | 0.052 | 2 | 3 | 2, 3 | 2.5 | 25% | 4.33 |
| 9 | 0.054 | 1 | 4 | 4 | 4 | 40% | 4.75 |
| 4 | 0.060 | 1 | 5 | 5 | 5 | 50% | 5 |
| 7 | 0.062 | 1 | 6 | 6 | 6 | 60% | 5.25 |
| 2 | 0.090 | 1 | 7 | 7 | 7 | 70% | 5.52 |
| 6 | 0.095 | 1 | 8 | 8 | 8 | 80% | 5.84 |
| 8 | 0.121 | 1 | 9 | 9 | 9 | 90% | 6.28 |
| 1 | 0.123 | 1 | 10 | 10 | 10 | 97.5% | 6.96 |
| Non-Standardized Coefficient | Standard Coefficient | Sig | ||
|---|---|---|---|---|
| B | Standard Error | β | ||
| Constants | −0.066 | 0.022 | 0.928 | 0.021 |
| Probit | 0.027 | 0.004 | 0.000 | |
| Grade | Probit | Mask Number | |
|---|---|---|---|
| Excellent | ≥6 | ≥0.121 | 1, 8 |
| Moderate | 4~6 | 0.052~0.095 | 2, 4, 5, 6, 7, 9, 10 |
| Poor | <4 | <0.051 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Zhu, C.; Cao, X.; Hsu, Y. The Sustainability Evaluation of Masks Based on the Integrated Rank Sum Ratio and Entropy Weight Method. Sustainability 2022, 14, 5706. https://doi.org/10.3390/su14095706
Lu H, Zhu C, Cao X, Hsu Y. The Sustainability Evaluation of Masks Based on the Integrated Rank Sum Ratio and Entropy Weight Method. Sustainability. 2022; 14(9):5706. https://doi.org/10.3390/su14095706
Chicago/Turabian StyleLu, Honglei, Chunxiao Zhu, Xin Cao, and Yen Hsu. 2022. "The Sustainability Evaluation of Masks Based on the Integrated Rank Sum Ratio and Entropy Weight Method" Sustainability 14, no. 9: 5706. https://doi.org/10.3390/su14095706
APA StyleLu, H., Zhu, C., Cao, X., & Hsu, Y. (2022). The Sustainability Evaluation of Masks Based on the Integrated Rank Sum Ratio and Entropy Weight Method. Sustainability, 14(9), 5706. https://doi.org/10.3390/su14095706







