Energy Consumption of the Urban Transport Fleet in UNESCO World Heritage Sites: A Case Study of Ávila (Spain)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phase I: Route Data Collection
2.2. Phase II: Data Processing

2.2.1. Kinematic Characteristics
- The bus must be stopped at all bus stops (velocity v = 0 km/h).
- The bus shall not exceed 50 km/h (maximum velocity allowed within the urban area).
- The bus increases its velocity with constant acceleration a corresponding to going from 0 to 50 km/h in 10 s (a = 1.39 m/s2). The same acceleration value will be used for braking.
2.2.2. Dynamic Characteristics
2.2.3. Energetic Characteristics
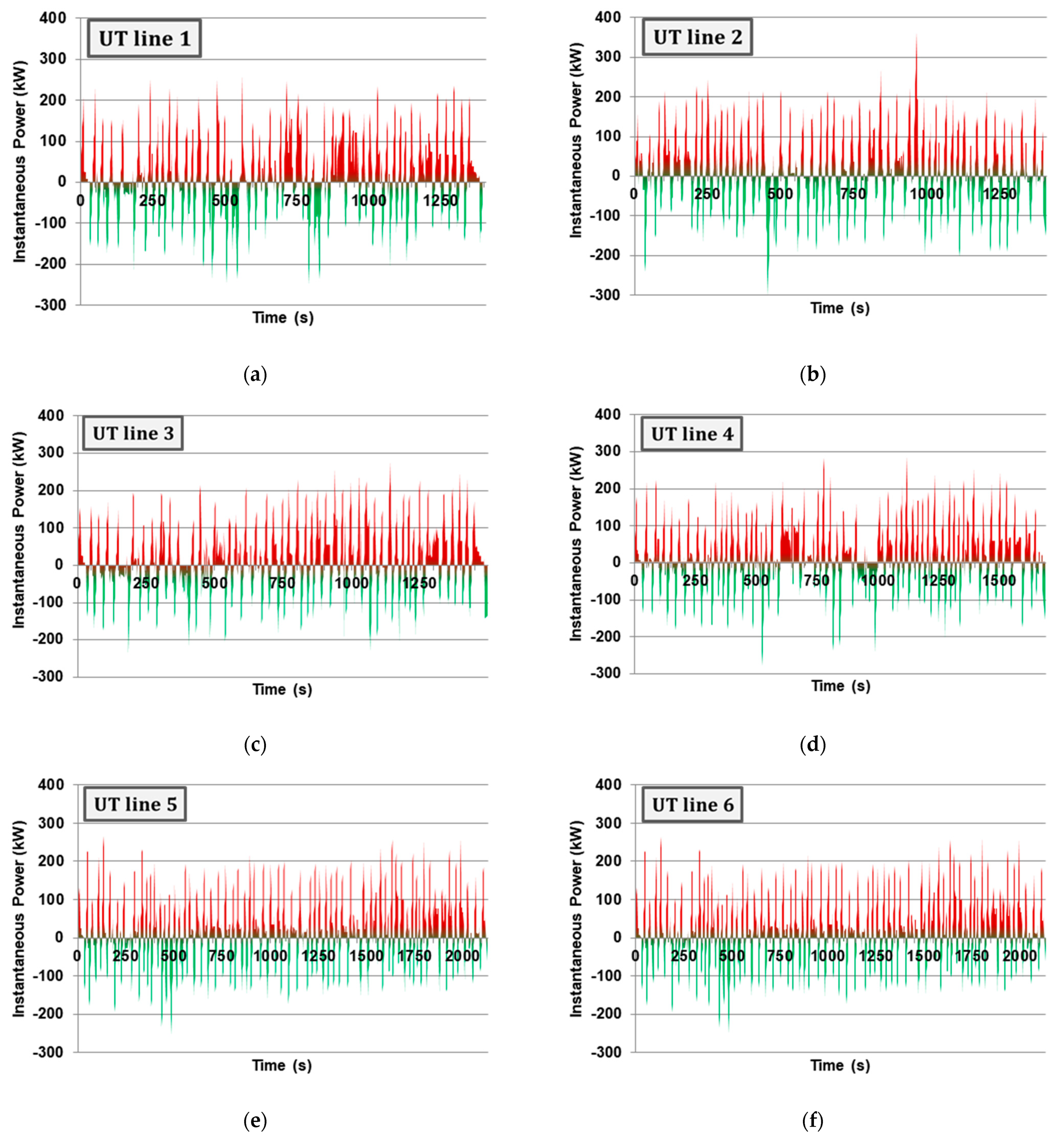
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| Symbol | Variable Description |
| Aerodynamic power | |
| Aerodynamic drag | |
| Cx | Aerodynamic drag coefficient |
| ρ | Air density |
| X2 | Cumulative elevation gains per km |
| d | Distance |
| g | Earth gravity acceleration |
| r | Earth radius |
| Estimated supplied energy | |
| Estimated recoverable energy | |
| Af | Frontal area |
| Grading power | |
| Grading drags | |
| H | Height |
| Increased kinetic energy | |
| IP | Instantaneous power |
| Latitude of point 1 and latitude of point 2 | |
| Longitude of point 1 and longitude of point 2 | |
| MRO | Mass in running order |
| MAM | Maximum authorized mass |
| pax | Number of passengers |
| X1 | Number of bus stops per km |
| Supplied power | |
| Recoverable power | |
| Rolling power | |
| Rolling drag | |
| Rolling drag coefficient | |
| S | Separation between two points |
| Slope angle | |
| Supplied energy | |
| m | Vehicle mass |
| v | Velocity |
| W | Width |
| vw | Wind velocity |
References
- Gkoumas, K.; Marques, F.L.; Stepniak, M.; Pekár, F. Research and Innovation Supporting the European Sustainable and Smart Mobility Strategy: A Technology Perspective from Recent European Union Projects. Appl. Sci. 2021, 11, 11981. [Google Scholar] [CrossRef]
- Von Homeyer, I.; Oberthür, S.; Jordan, A.J. EU climate and energy governance in times of crisis: Towards a new agenda. J. Eur. Public Policy 2021, 28, 959–979. [Google Scholar] [CrossRef]
- Ossewaarde, M.; Ossewaarde-Lowtoo, R. The EU’s Green Deal: A Third Alternative to Green Growth and Degrowth? Sustainability 2020, 12, 9825. [Google Scholar] [CrossRef]
- Rhodes, C.J. The 2015 Paris Climate Change Conference: COP21. Sci. Prog. 2016, 99, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Pietrzak, M.B.; Olczyk, M.; Kuc-Czarnecka, M.E. Assessment of the Feasibility of Energy Transformation Processes in European Union Member States. Energies 2022, 15, 661. [Google Scholar] [CrossRef]
- Tian, J.; Yu, L.; Xue, R.; Zhuang, S.; Shan, Y. Global low-carbon energy transition in the post-COVID-19 era. Appl. Energy 2022, 307, 118205. [Google Scholar] [CrossRef]
- Pakulska, T. Green Energy in Central and Eastern European (CEE) Countries: New Challenges on the Path to Sustainable Development. Energies 2021, 14, 884. [Google Scholar] [CrossRef]
- Quintana-Rojo, C.; Callejas-Albiñana, F.-E.; Tarancón, M.-Á.; Martínez-Rodríguez, I. Econometric Studies on the Development of Renewable Energy Sources to Support the European Union 2020–2030 Climate and Energy Framework: A Critical Appraisal. Sustainability 2020, 12, 4828. [Google Scholar] [CrossRef]
- Kulovesi, K.; Oberthür, S. Assessing the EU’s 2030 Climate and Energy Policy Framework: Incremental Change toward Radical Transformation? Rev. Eur. Comp. Int. Environ. Law 2020, 29, 151–166. [Google Scholar] [CrossRef]
- Wójcik-Jurkiewicz, M.; Czarnecka, M.; Kinelski, G.; Sadowska, B.; Bilińska-Reformat, K. Determinants of Decarbonisation in the Transformation of the Energy Sector: The Case of Poland. Energies 2021, 14, 1217. [Google Scholar] [CrossRef]
- Calise, F.; Fabozzi, S.; Vanoli, L.; Vicidomini, M. A sustainable mobility strategy based on electric vehicles and photovoltaic panels for shopping centers. Sustain. Cities Soc. 2021, 70, 102891. [Google Scholar] [CrossRef]
- Gössling, S.; Cohen, S. Why sustainable transport policies will fail: EU climate policy in the light of transport taboos. J. Transp. Geogr. 2014, 39, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Pamuła, T.; Pamuła, W. Estimation of the Energy Consumption of Battery Electric Buses for Public Transport Networks Using Real-World Data and Deep Learning. Energies 2020, 13, 2340. [Google Scholar] [CrossRef]
- Kim, J.; Song, I.; Choi, W. An Electric Bus with a Battery Exchange System. Energies 2015, 8, 6806–6819. [Google Scholar] [CrossRef] [Green Version]
- Abdelaty, H.; Mohamed, M. A Prediction Model for Battery Electric Bus Energy Consumption in Transit. Energies 2021, 14, 2824. [Google Scholar] [CrossRef]
- Bottiglione, F.; Contursi, T.; Gentile, A.; Mantriota, G. The Fuel Economy of Hybrid Buses: The Role of Ancillaries in Real Urban Driving. Energies 2014, 7, 4202–4220. [Google Scholar] [CrossRef] [Green Version]
- Pojani, D.; Stead, D. Sustainable Urban Transport in the Developing World: Beyond Megacities. Sustainability 2015, 7, 7784–7805. [Google Scholar] [CrossRef] [Green Version]
- Goldman, T.; Gorham, R. Sustainable urban transport: Four innovative directions. Technol. Soc. 2006, 28, 261–273. [Google Scholar] [CrossRef]
- Sánchez-Chóliz, J.; Duarte, R. CO2 emissions embodied in international trade: Evidence for Spain. Energy Policy 2004, 32, 1999–2005. [Google Scholar] [CrossRef]
- Alcántara, V.; Roca, J. Energy and CO2 emissions in Spain: Methodology of analysis and some results for 1980–1990. Energy Econ. 1995, 17, 221–230. [Google Scholar] [CrossRef]
- Ministry for Ecological Transition and the Demographic Challenge. Transport Sector. Available online: https://www.miteco.gob.es/es/cambio-climatico/temas/mitigacion-politicas-y-medidas/transporte.aspx (accessed on 11 January 2022).
- Navas-Anguita, Z.; García-Gusano, D.; Iribarren, D. Long-term production technology mix of alternative fuels for road transport: A focus on Spain. Energy Convers. Manag. 2020, 226, 113498. [Google Scholar] [CrossRef] [PubMed]
- Junta de Castilla y León. Regional Strategy against Climate Change in Castilla and León 2009–2012–2020. Available online: https://medioambiente.jcyl.es/web/jcyl/MedioAmbiente/es/Plantilla100Detalle/1246988359553/Programa/1284497829991/Comunicacion (accessed on 14 January 2022).
- Martín-Viso, I. Commons and the construction of power in the early Middle Ages: Tenth-century León and Castile. J. Mediev. Hist. 2020, 46, 1–23. [Google Scholar] [CrossRef]
- United Nations Educational, Scientific and Cultural Organization. World Heritage List. Available online: https://whc.unesco.org/en/list/ (accessed on 4 January 2022).
- Bigio, A.G.; Ochoa, M.C.; Amirtahmasebi, R. Climate-Resilient, Climate-Friendly World Heritage Cities; Urban Development Series; The World Bank Group: Washington, DC, USA, 2014. [Google Scholar]
- Gullino, P.; Beccaro, G.L.; Larcher, F. Assessing and Monitoring the Sustainability in Rural World Heritage Sites. Sustainability 2015, 7, 14186–14210. [Google Scholar] [CrossRef] [Green Version]
- Ramos-Soler, I.; Martínez-Sala, A.-M.; Campillo-Alhama, C. ICT and the Sustainability of World Heritage Sites. Analysis of Senior Citizens’ Use of Tourism Apps. Sustainability 2019, 11, 3203. [Google Scholar] [CrossRef] [Green Version]
- May, A.D. Urban Transport and Sustainability: The Key Challenges. Int. J. Sustain. Transp. 2013, 7, 170–185. [Google Scholar] [CrossRef]
- Lin, C.-L.; Hung, H.-C.; Li, J.-C. Active Control of Regenerative Brake for Electric Vehicles. Actuators 2018, 7, 84. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Li, L.; Wang, X.; Mei, M.; Liu, C.; Song, J. Braking force decoupling control without pressure sensor for a novel series regenerative brake system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 1750–1766. [Google Scholar] [CrossRef]
- Cai, J.W.; Chu, L.; Fu, Z.C.; Ren, L.P. Regenerative Braking System for a Pure Electric Bus. Appl. Mech. Mater. 2014, 543–547, 1405–1408. [Google Scholar] [CrossRef]
- Han, T.; Zeng, B.; Tong, Y. Theoretical study on energy recovery rate of regenerative braking for hybrid mining trucks with different parameters. J. Energy Storage 2021, 42, 103127. [Google Scholar] [CrossRef]
- Yadav, D.; Kumar, R.; Kulshrestha, U.; Jain, A.; Rani, S. Enhancement of fuel efficiency in heavy duty vehicles through integrated module of TEG, piezoelectric and regenerative braking solutions. Mater. Today Proc. 2021, in press. [CrossRef]
- Ghafouryan, M.M.; Ataee, S.; Dastjerd, F.T. A novel method for the design of regenerative brake system in an urban automotive. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 945–953. [Google Scholar] [CrossRef]
- Ma, Z. Parameters design for a parallel hybrid electric bus using regenerative brake model. Adv. Mech. Eng. 2014, 6, 760815. [Google Scholar] [CrossRef]
- Xiao, B.; Lu, H.; Wang, H.; Ruan, J.; Zhang, N. Enhanced Regenerative Braking Strategies for Electric Vehicles: Dynamic Performance and Potential Analysis. Energies 2017, 10, 1875. [Google Scholar] [CrossRef] [Green Version]
- Avanza Spain, S.L.U. Plano de las Líneas de la Ciudad de Ávila. Available online: https://avila.avanzagrupo.com/lineas-y-horarios/plano-de-las-lineas (accessed on 11 March 2022).
- Zhao, P.; Haitao, H.; Li, A.; Mansourian, A. Impact of data processing on deriving micro-mobility patterns from vehicle availability data. Transp. Res. Part D Trans. Environ. 2021, 97, 102913. [Google Scholar] [CrossRef]
- Whang, F.; Chen, C. On data processing required to derive mobility patterns from passively-generated mobile phone data. Transp. Res. Part C Emerg. Tech. 2018, 87, 58–74. [Google Scholar] [CrossRef]
- Dauni, P.; Firdaus, M.D.; Asfariani, R.; Saputra, M.I.N.; Hidayat, A.A.; Zulfikar, W.B. Implementation of Haversine formula for school location tracking. J. Phys. Conf. Ser. 2019, 1402, 077028. [Google Scholar] [CrossRef]
- Baure, G.; Dubarry, M. Synthetic vs. Real driving cycles: Baure, G.; Dubarry, M. Synthetic vs. Real Driving Cycles: A Comparison of Electric Vehicle Battery Degradation. Batteries 2019, 5, 42. [Google Scholar] [CrossRef] [Green Version]
- Huzayyin, O.A.; Salem, H.; Hassan, M.A. A representative urban driving cycle for passenger vehicles to estimate fuel consumption and emission rates under real-world driving conditions. Urban Clim. 2021, 36, 100810. [Google Scholar] [CrossRef]
- Cui, Y.; Xu, H.; Zou, F.; Chen, Z.; Gong, K. Optimization based method to develop representative driving cycle for real-world fuel consumption estimation. Energy 2021, 235, 121434. [Google Scholar] [CrossRef]
- Mercedes Benz Bus. Available online: https://www.mercedes-benz-bus.com/es_ES/models/citaro/facts/technical-data.html (accessed on 14 February 2022).
- Humanetics. Available online: https://humanetics.humaneticsgroup.com/products/anthropomorphic-test-devices/frontal-impact/hybrid-iii-50th-male/hybrid-iii-50th-male (accessed on 14 February 2022).
- Ehsani, M.; Gao, Y.; Gay, S.E.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2005; pp. 21–29. [Google Scholar]
- Greenwood, J.A.; Minshall, H.; Tabor, D. Hysteresis losses in rolling and sliding friction. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1961, 259, 480–507. [Google Scholar] [CrossRef]
- Komandi, G. An evaluation of the concept of rolling drag. J. Terramechanics 1999, 36, 159–166. [Google Scholar] [CrossRef]
- Rill, G. Road Vehicle Dynamics. Fundamentals and modeling; CRC Press: Boca Raton, FL, USA, 2012; pp. 225–227. [Google Scholar]
- Guiggiani, M. The Science of Vehicle Dynamics. Handling, Braking, and Ride of Road and Race Cars; Springer: Dordrecht, The Netherlands; Heidelberg, Germany; New York, NY, USA, 2014; pp. 59–61. [Google Scholar]
- Lin, N.; Zong, C.; Shi, S. The method of mass estimation considering system error in vehicle longitudinal dynamics. Energies 2019, 12, 52. [Google Scholar] [CrossRef] [Green Version]
- Koreny, M.; Simonik, P.; Klein, T.; Mrovec, T.; Ligori, J.J. Hybrid research platform for fundamental and empirical modeling and analysis of energy management of shared electric vehicles. Energies 2022, 15, 1300. [Google Scholar] [CrossRef]
- Guerrero, A.; Castilla, R.; Eid, G. A Numerical aerodynamic analysis on the effect of rear underbody diffusers on road cars. Appl. Sci. 2022, 12, 3763. [Google Scholar] [CrossRef]
- Luján, J.M.; Piqueras, P.; de la Morena, J.; Redondo, F. experimental characterization of real driving cycles in a light-duty diesel engine under different dynamic conditions. Appl. Sci. 2022, 12, 2472. [Google Scholar] [CrossRef]
- Kaluva, S.T.; Pathak, A.; Ongel, A. Aerodynamic drag analysis of autonomous electric vehicle Platoons. Energies 2020, 13, 4028. [Google Scholar] [CrossRef]



| H (m) | W (m) | MRO (kg) | MAM (kg) | pax | Cx |
|---|---|---|---|---|---|
| 3.10 | 2.55 | 10,000 | 18,000 | 86 | 0.65 |
| UT Line | Total Distance in Each Line (km) | Number of Bus Stops | Cumulative Elevation Gain (m) |
|---|---|---|---|
| 1 | 13.286 | 45 | 231.96 |
| 2 | 13.030 | 48 | 189.09 |
| 3 | 14.390 | 47 | 190.85 |
| 4 | 16.641 | 50 | 234.53 |
| 5 | 14.683 | 46 | 192.26 |
| 6 | 20.729 | 65 | 200.38 |
| UT Line | ||
|---|---|---|
| 1 | 264.55 | 73.29 |
| 2 | 305.37 | 71.59 |
| 3 | 321.84 | 67.81 |
| 4 | 278.28 | 68.74 |
| 5 | 263.50 | 71.59 |
| 6 | 254.93 | 75.29 |
| UT Line | ||
|---|---|---|
| 1 | 63.50 | 44.48 |
| 2 | 63.43 | 44.95 |
| 3 | 65.87 | 45.23 |
| 4 | 73.19 | 49.08 |
| 5 | 66.65 | 45.46 |
| 6 | 90.14 | 60.24 |
| UT Line | Total Distance in Each Line (km) | Relative Results | Relative Energy Results | Percentage of Recoverable Energy (%) | ||
|---|---|---|---|---|---|---|
| Number of Stop per km (n°/km) X1 | Cumulative Elevation Gains per km (m/km) X2 | Erec per km (MJ/km) | ||||
| 2 | 13.0305 | 3.68 | 14.51 | 4.87 | 3.45 | 70.84 |
| 1 | 13.2861 | 3.39 | 17.46 | 4.78 | 3.35 | 70.08 |
| 6 | 20.7292 | 3.14 | 9.67 | 4.35 | 2.91 | 66.90 |
| 3 | 14.3902 | 3.27 | 13.26 | 4.58 | 3.14 | 68.56 |
| 5 | 14.6833 | 3.13 | 13.09 | 4.54 | 3.10 | 68.28 |
| 4 | 16.6416 | 3.00 | 14.09 | 4.40 | 2.95 | 67.05 |
| UT Line | X1 | X2 | ||
|---|---|---|---|---|
| 1 | 3.39 | 17.46 | 4.93 d | 3.36 d |
| 2 | 3.68 | 14.51 | 5.22 d | 3.50 d |
| 3 | 3.27 | 13.26 | 4.65 d | 3.13 d |
| 4 | 3.00 | 14.09 | 4.32 d | 2.93 d |
| 5 | 3.13 | 13.09 | 4.46 d | 3.00 d |
| 6 | 3.14 | 9.67 | 4.37 d | 2.90 d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos-Iglesia, C.; Fernández-Arias, P.; Antón-Sancho, Á.; Vergara, D. Energy Consumption of the Urban Transport Fleet in UNESCO World Heritage Sites: A Case Study of Ávila (Spain). Sustainability 2022, 14, 5641. https://doi.org/10.3390/su14095641
Santos-Iglesia C, Fernández-Arias P, Antón-Sancho Á, Vergara D. Energy Consumption of the Urban Transport Fleet in UNESCO World Heritage Sites: A Case Study of Ávila (Spain). Sustainability. 2022; 14(9):5641. https://doi.org/10.3390/su14095641
Chicago/Turabian StyleSantos-Iglesia, Carlos, Pablo Fernández-Arias, Álvaro Antón-Sancho, and Diego Vergara. 2022. "Energy Consumption of the Urban Transport Fleet in UNESCO World Heritage Sites: A Case Study of Ávila (Spain)" Sustainability 14, no. 9: 5641. https://doi.org/10.3390/su14095641
APA StyleSantos-Iglesia, C., Fernández-Arias, P., Antón-Sancho, Á., & Vergara, D. (2022). Energy Consumption of the Urban Transport Fleet in UNESCO World Heritage Sites: A Case Study of Ávila (Spain). Sustainability, 14(9), 5641. https://doi.org/10.3390/su14095641









