Development and Comparison of Prediction Models for Sanitary Sewer Pipes Condition Assessment Using Multinomial Logistic Regression and Artificial Neural Network
Abstract
:1. Introduction
2. Literature Review
2.1. Sewer Pipe Classification
2.2. Physical Factors
2.3. Environmental Factors
2.4. Sewer Pipe Condition Prediction Models
2.5. Statistical Methods
- β0 is the intercept
- β1 is the parameter associated with x1,
- β2 is the parameter associated with x2, and so on
- is the parameters that cannot be included and are collectively contained in u
- Y = dependent variable
- a = intercept parameter
- βp = regression coefficients associated with p independent variables.
- Probability of (y = 1) determined using exponential transformation.
- π =
- i = 1, 2, …, k − 1 correspond to categories of the dependent variable,
- xs are independent variables,
- n is the number of independent variables,
- is the intercept for category i,
- are the regression coefficients of independent variables defined for each category i.
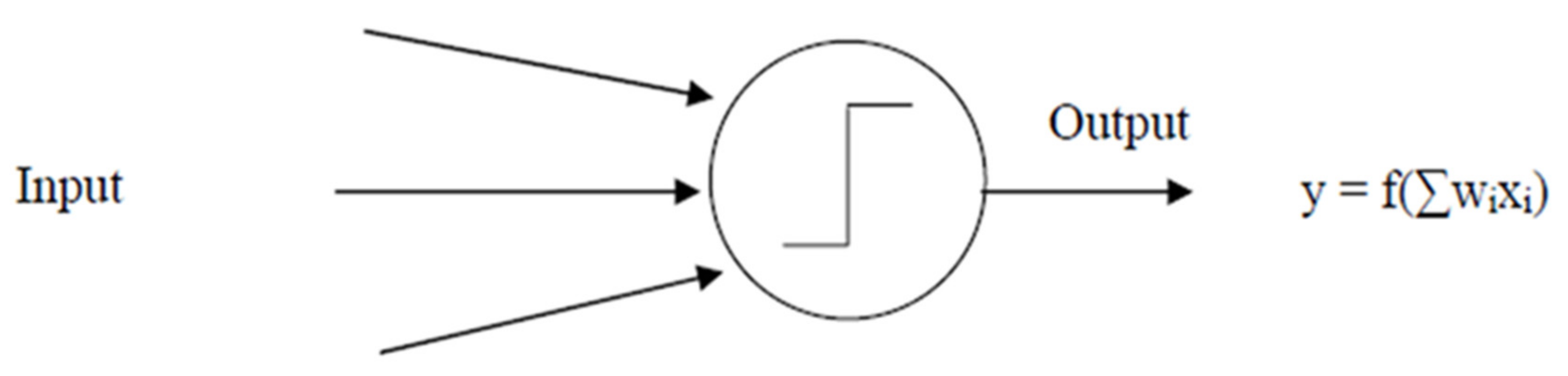
2.6. Artificial Intelligence System
2.7. Problem Statement and Objectives
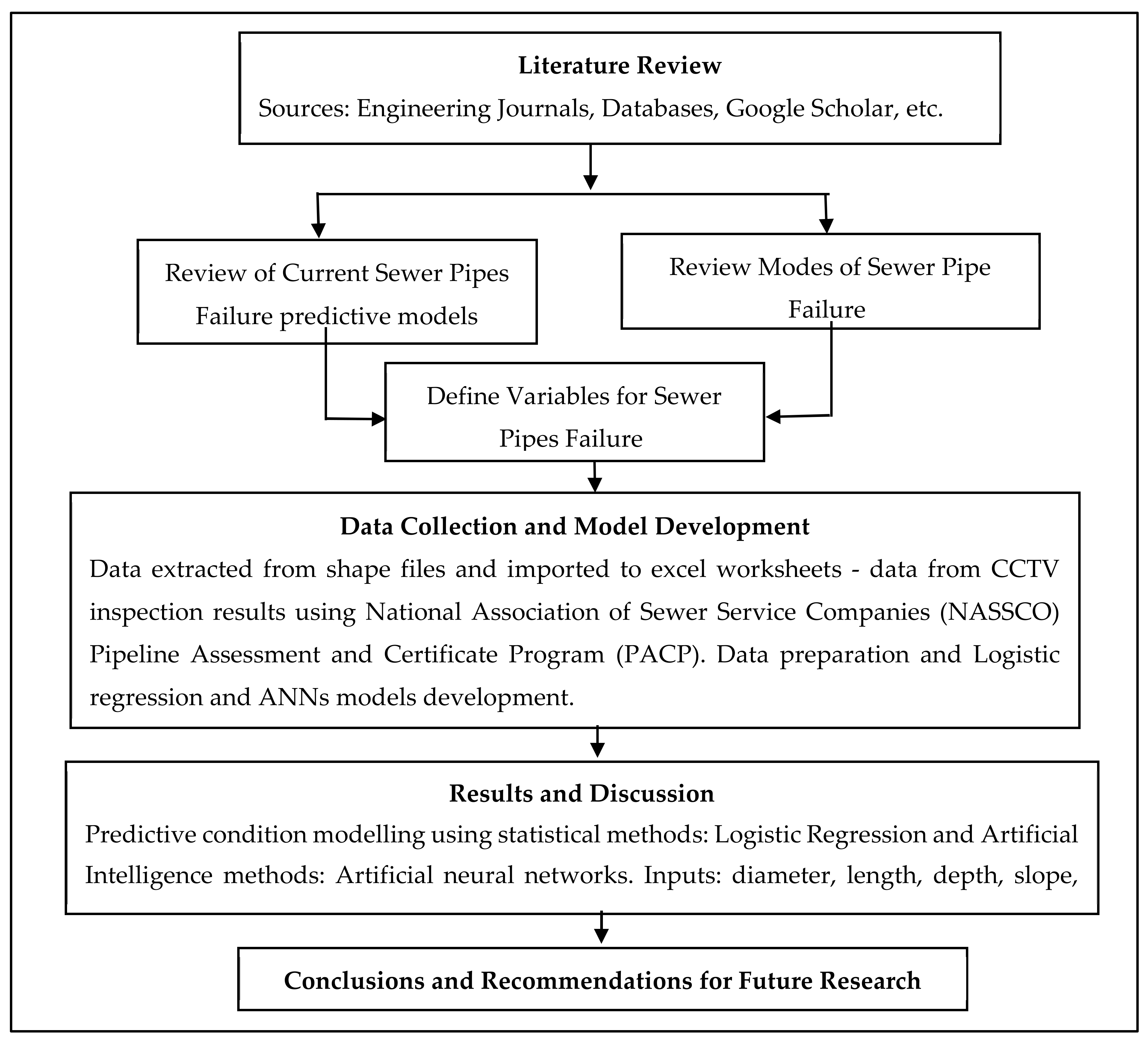
3. Methodology
4. Model Development
4.1. Multinomial Logistic Regression Model
4.1.1. Model Parameters Estimation
4.1.2. Validation of Multinomial Logistic Model
- Pr (C = 1) is the probability of sanitary sewer pipe condition dependent variable being condition 1 relative to condition 5.
- Pr (C = 5) is the probability of reference category condition 5.
- Pr (C = 2) is the probability of sanitary sewer pipe condition dependent variable, condition 2 being relative to condition 5.
- Pr (C = 5) is the probability of reference category condition 5.
- Pr (C =3) is the probability of sanitary sewer pipe condition dependent variable, condition 3 being relative to condition 5.
- Pr (C = 5) is the probability of reference category condition 5.
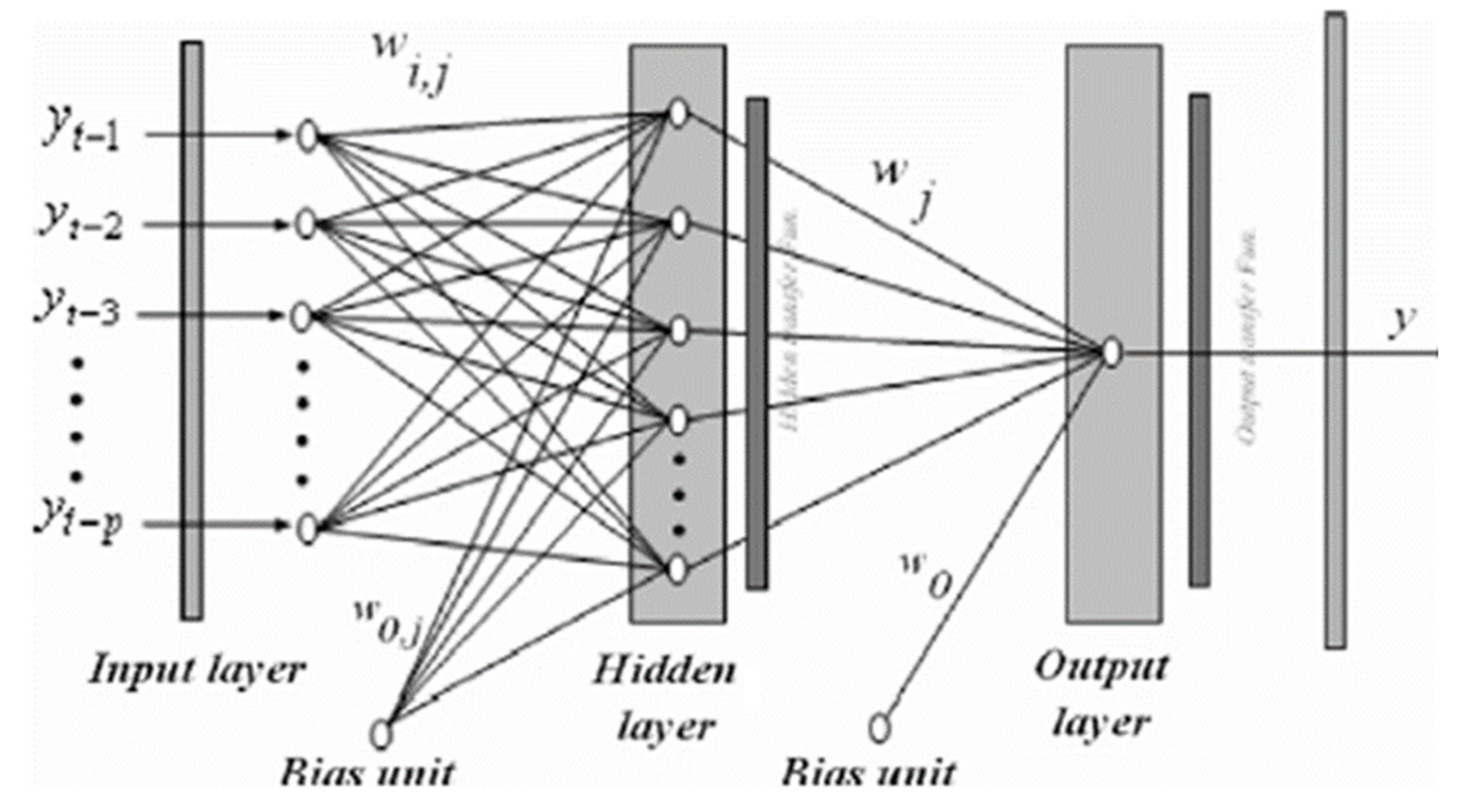
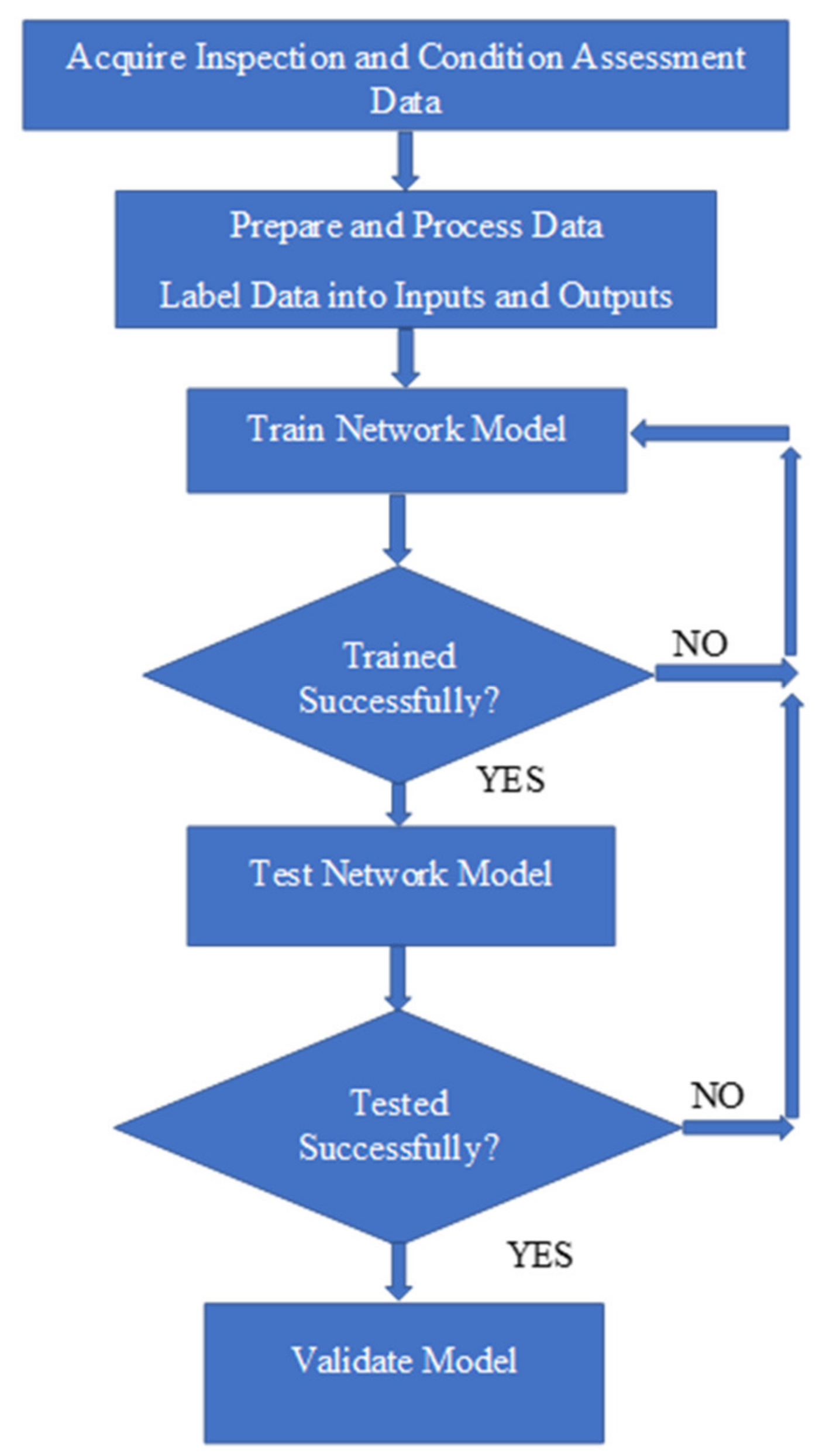
4.1.3. Artificial Neural Networks Model
4.1.4. Neural Networks Data Processing Software Selection
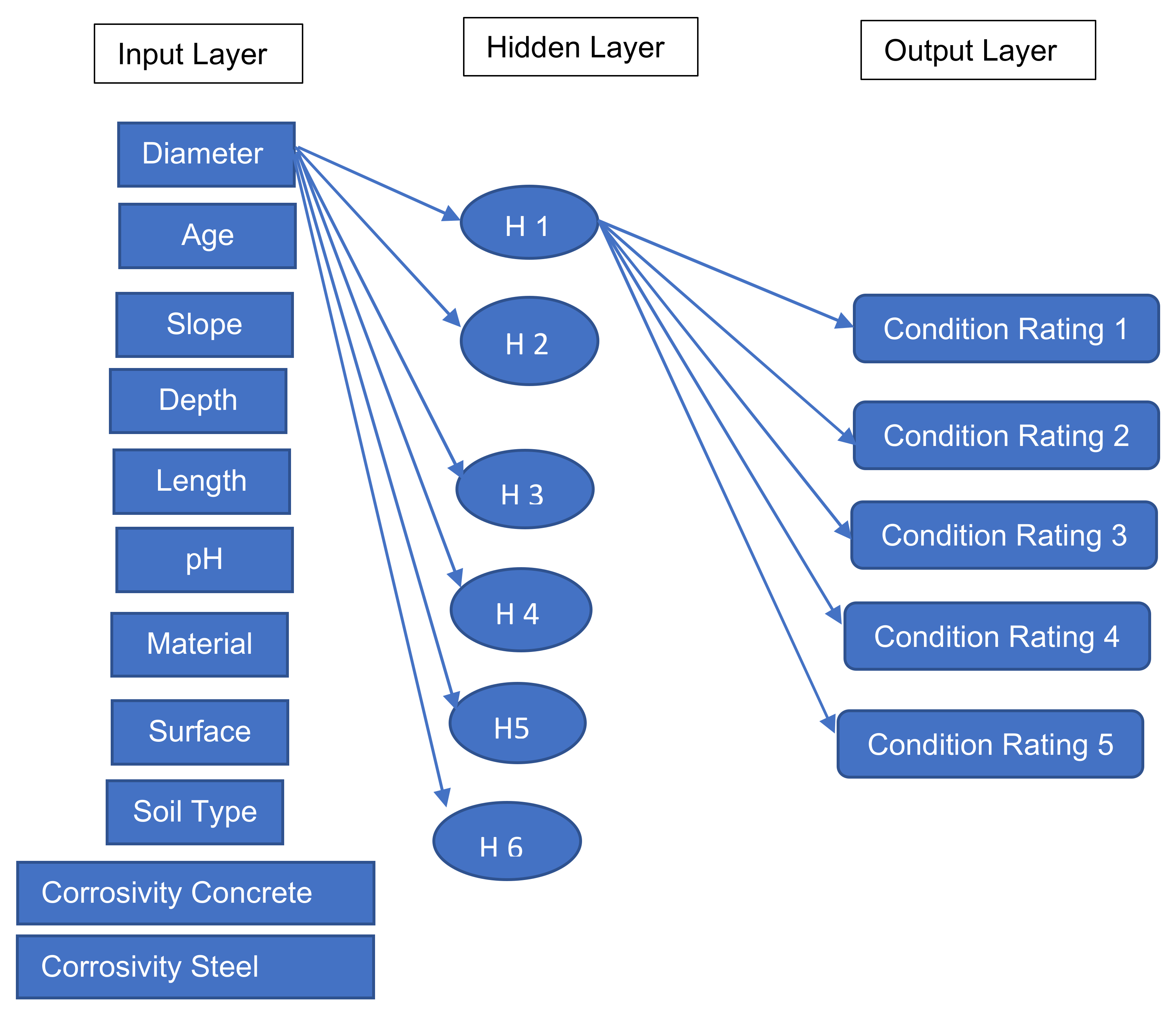
4.1.5. Neural Networks Architecture
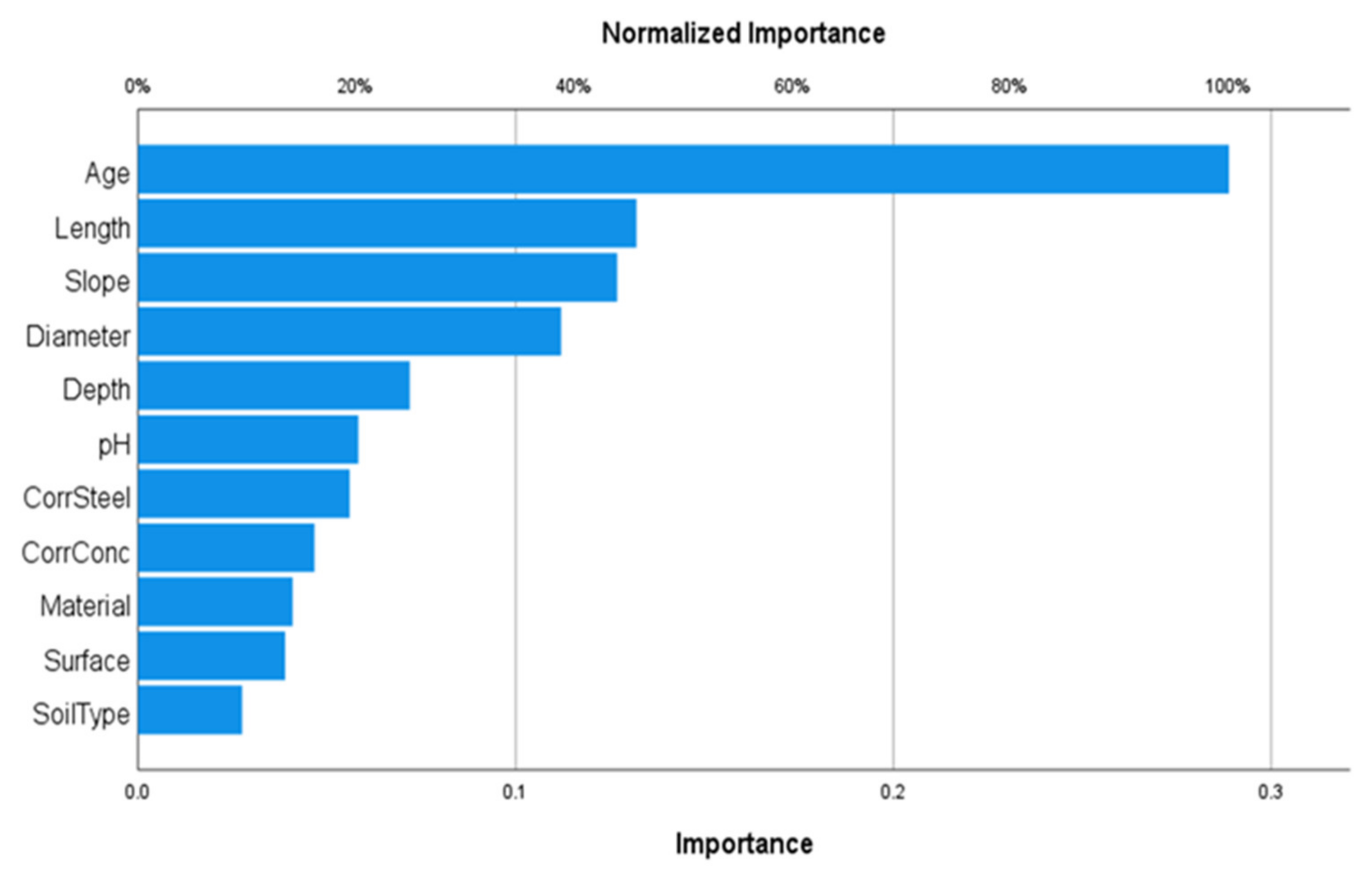
4.2. Neural Networks Model Development
5. Results and Discussion
5.1. Performance of the Models
5.1.1. Multinomial Logistic Regression Model
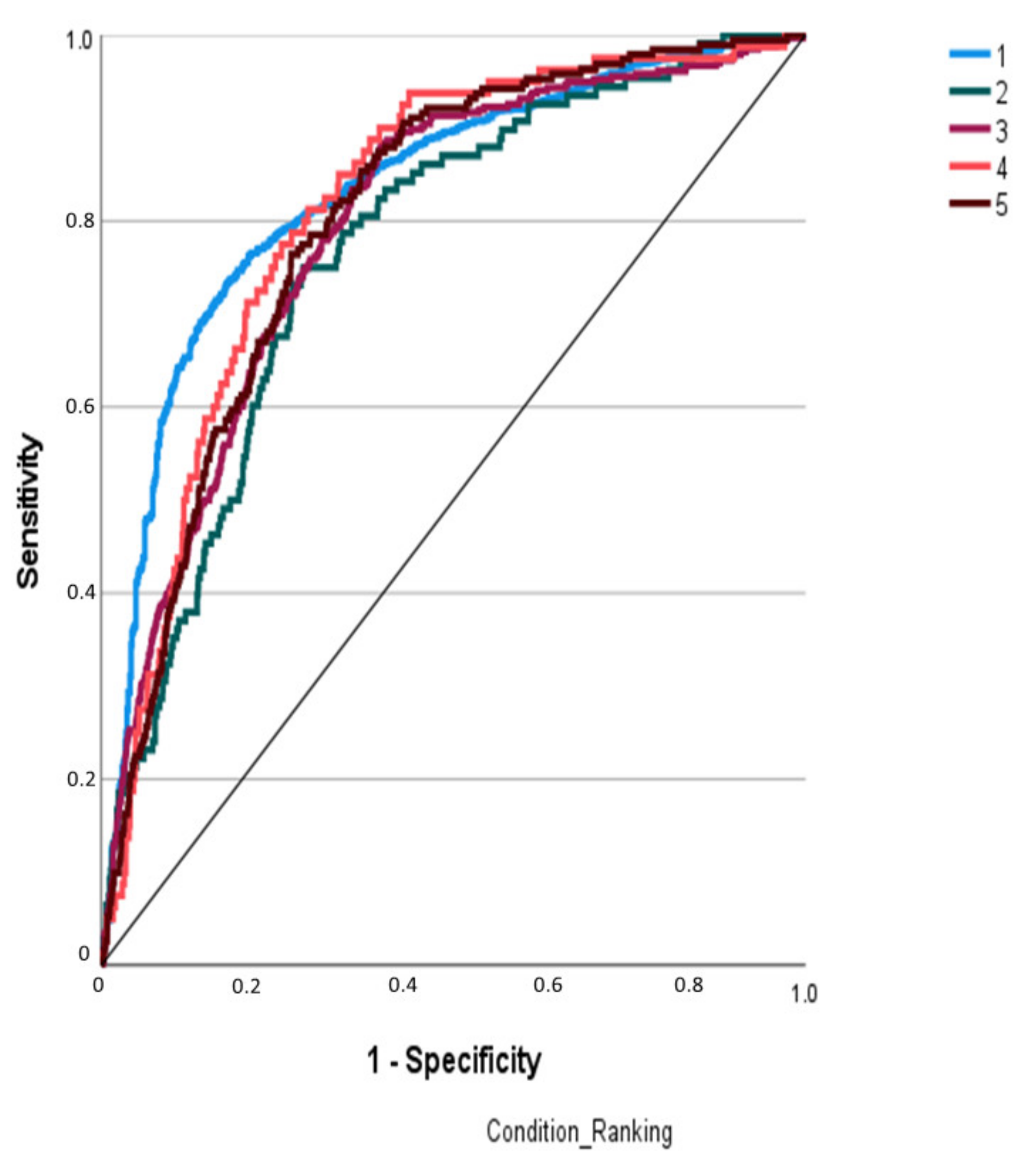
5.1.2. Neural Networks Model Performance
5.2. Discussion
5.3. Justification of Results
Comparison of MLR and ANN Models and Conclusions
6. Recommendations for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammadi, M.M.; Najafi, M.; Kaushal, V.; Serajiantehrani, R.; Salehabadi, N.; Ashoori, T. Sewer Pipes Condition Prediction Models: A State-of-the-Art Review. Infrastructures 2019, 4, 64. [Google Scholar] [CrossRef] [Green Version]
- Kaushal, V.; Najafi, M.; Serajiantehrani, R. Environmental Impacts of Conventional Open-Cut Pipeline Installation and Trenchless Technology Methods: State-of-the-Art Review. J. Pipeline Syst. Eng. Pr. 2020, 11, 03120001. [Google Scholar] [CrossRef]
- Hawari, A.; Alkadour, F.; Elmasry, M.; Zayed, T. A state of the art review on condition assessment models developed for sewer pipelines. Eng. Appl. Artif. Intell. 2020, 93, 103721. [Google Scholar] [CrossRef]
- American Society of Civil Engineers (ASCE). 2021 Report Card for America’s Infrastructure; ASCE: Washington, DC, USA, 2017. [Google Scholar]
- Serajiantehrani, R.; Najafi, M.; Mohammadi, M.M.; Kaushal, V. Framework for Life-Cycle Cost Analysis of Trenchless Renewal Methods for Large Diameter Culverts. In Pipelines 2020; American Society of Civil Engineers: Reston, VI, USA, 2020; pp. 309–320. [Google Scholar]
- Wirahadikusumah, R.; Abraham, D.M.; Castello, J. Markov decision process for sewer rehabilitation. Eng. Constr. Arch. Manag. 1999, 6, 358–370. [Google Scholar] [CrossRef]
- Alegre, H. Is strategic asset management applicable to small and medium utilities? Water Sci. Technol. 2010, 62, 2051–2058. [Google Scholar] [CrossRef] [PubMed]
- Bruaset, S.; Rygg, H.; Sægrov, S. Reviewing the Long-Term Sustainability of Urban Water System Rehabilitation Strategies with an Alternative Approach. Sustainability 2018, 10, 1987. [Google Scholar] [CrossRef] [Green Version]
- Najafi, M. Pipeline Infrastructure Renewal and Asset Management; Mc-Graw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Khan, Z.; Zayed, T.; Moselhi, O. Structural Condition Assessment of Sewer Pipelines. J. Perform. Constr. Facil. 2010, 24, 170–179. [Google Scholar] [CrossRef]
- Malek Mohammadi, M.; Najafi, M.; Kermanshachi, S.; Kaushal, V.; Serajiantehrani, R. Factors Influencing the Condition of Sewer Pipes: State-of-the-Art Review. J. Pipeline Syst. Eng. Pract. 2020, 11, 03120002. [Google Scholar] [CrossRef]
- Lubini, A.T.; Fuamba, M. Modeling of the deterioration timeline of sewer systems. Can. J. Civ. Eng. 2011, 38, 1381–1390. [Google Scholar]
- Khudair, H.B.; Khalid, K.G.; Jbbar, K.R. Condition Prediction Model of Deteriorated Trunk Sewer using Mul-tinomial Logistic Regression and Artificial Neural Network. Int. J. Civ. Eng. Technol. 2019, 10, 93–104. [Google Scholar]
- Muhlbauer, K. Pipeline Risk Management Manual Ideas, Techniques, and Resources, 3rd ed.; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Hou, P.; Yi, X.; Dong, H. A Spatial Statistic Based Risk Assessment Approach to Prioritize the Pipeline Inspection of the Pipeline Network. Energies 2020, 13, 685. [Google Scholar] [CrossRef] [Green Version]
- Caradot, N.; Riechel, M.; Fesneau, M.; Hernandez, N.; Torres, A.; Sonnenberg, H.; Eckert, E.; Lengemann, N.; Waschnewski, J.; Rouault, P. Practical benchmarking of statistical and machine learning models for predicting the condition of sewer pipes in Berlin, Germany. J. Hydroinformatics 2018, 20, 1131–1147. [Google Scholar] [CrossRef] [Green Version]
- Syachrani, S.; Jeong, H.D.; Chung, C.S. Advanced criticality assessment method for sewer pipeline assets. Water Sci. Technol. 2013, 67, 1302–1309. [Google Scholar] [CrossRef]
- Laakso, T.; Kokkonen, T.; Mellin, I.; Vahala, R. Sewer Condition Prediction and Analysis of Explanatory Factors. Water 2018, 10, 1239. [Google Scholar] [CrossRef] [Green Version]
- Najafi, M.; Gokhale, S. Trenchless Technology Pipeline and Utility Design, Construction, and Renewal; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Burn, S.; Marlow, D.; Tran, D. Modelling asset lifetimes and their role in asset management. J. Water Supply Res. Technol. 2010, 59, 362–377. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons. Inc.: Columbus, OH, USA, 2013. [Google Scholar]
- Khashei, M.; Bijari, M. An artificial neural network (p,d,q) model for timeseries forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Elmasry, M.; Hawari, A.; Zayed, T. Defect based deterioration model for sewer pipelines using Bayesian belief networks. Can. J. Civ. Eng. 2017, 44, 675–690. [Google Scholar] [CrossRef]
- Ward, B.; Savić, D.A. A multi-objective optimization model for sewer rehabilitation considering critical risk of failure. Water Sci. Technol. 2012, 66, 2410–2417. [Google Scholar] [CrossRef] [Green Version]
- Peponi, A.; Morgado, P.; Trindade, J. Combining Artificial Neural Networks and GIS Fundamentals for Coastal Erosion Prediction Modeling. Sustainability 2019, 11, 975. [Google Scholar] [CrossRef] [Green Version]
- Rokstad, M.M.; Ugarelli, R.M. Evaluating the role of deterioration models for condition assessment of sewers. J. Hydroinformatics 2015, 17, 789–804. [Google Scholar] [CrossRef] [Green Version]
- Chughtai, F.M.; Zayed, T. Infrastructure Condition Prediction Models for Sustainable Sewer Pipelines. J. Perform. Constr. Facil. 2008, 5, 333–341. [Google Scholar] [CrossRef]
- Kulandaivel, G. Sewer Pipeline Condition Prediction Using Neural Network Models. Master’s Thesis, Michigan State University, East Lansing, MI, USA, 2004. [Google Scholar]
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, W01528. [Google Scholar] [CrossRef]
- Chakraverty, S.; Mall, S. Artificial Neural Networks for Engineers and Scientists: Solving Ordinary Differential Equations; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Salman, B. Infrastructure Management and Deterioration Risk Assessment of Wastewater Collection Systems. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2010. [Google Scholar]
- Syachrani, S. Advanced Sewer Asset Management Using Dynamic Deterioration Models. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 2010. [Google Scholar]
- Vahidi, E.; Jin, E.; Das, M.; Singh, M.; Zhao, F. Environmental life cycle analysis of pipe materials for sewer systems. Sustain. Cities Soc. 2016, 27, 167–174. [Google Scholar] [CrossRef]
- Yin, X.; Chen, Y.; Bouferguene, A.; Al-Hussein, M.; Russell, R.; Kurach, L. A neural network-based approach to predict the condition for sewer pipes. In Proceedings of the Construction Research Congress 2020: Infrastructure Systems and Sustainability—Selected Papers from the Construction Research Congress 2020, Tempe, AZ, USA, 8–10 March 2020. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Mikovits, C.; Rauch, W.; Kleidorfer, M. Adaptation of sewer networks using integrated rehabilitation management. Water Sci. Technol. 2014, 70, 1847–1856. [Google Scholar] [CrossRef] [PubMed]
- Geem, Z.W.; Tseng, C.-L.; Kim, J.; Bae, C. Trenchless Water Pipe Condition Assessment Using Artificial Neural Network. In Pipelines 2007; American Society of Civil Engineers: Reston, VI, USA, 2007; pp. 1–9. [Google Scholar]
- Sousa, V.; Matos, J.P.; Almeida, N.; Matos, J.S. Risk assessment of sewer condition using artificial intelligence tools: Application to the SANEST sewer system. Water Sci. Technol. 2014, 69, 622–627. [Google Scholar] [CrossRef] [PubMed]
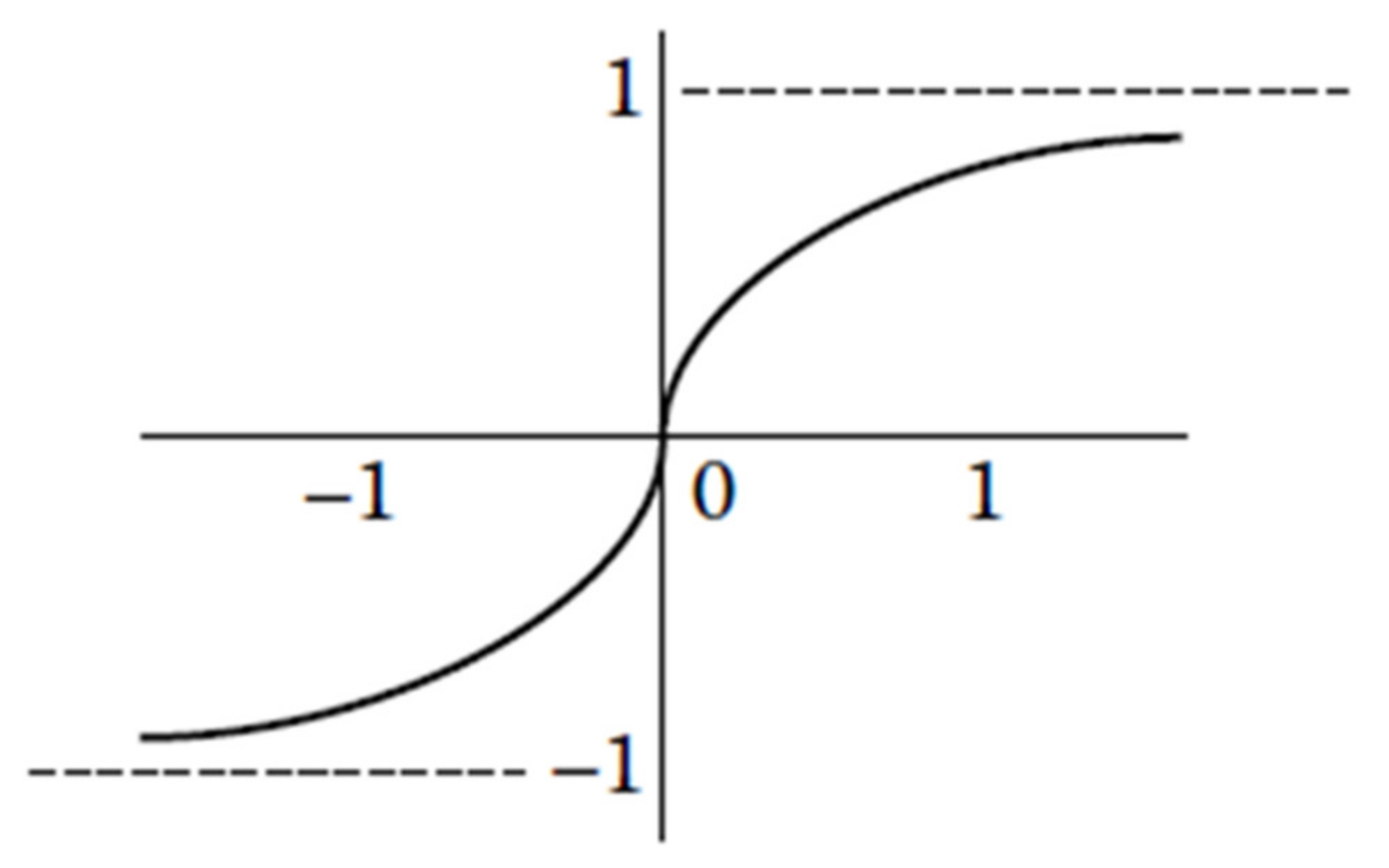
| ID | Diameter | Age | Pipe Material | Slope | Surface Condition | Depth | Length | pH | Soil Type | Corrosion Concrete | Corrosion Steel | Condition Rating |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2472 | 12 | 43 | PVC | 0.24 | Street | 15 | 480.157 | 6.7 | Sand | Low | Moderate | 1 |
| 1814 | 10 | 50 | VCP | 0.1 | Easement | 15 | 421.0372 | 6.7 | Sand | Low | Moderate | 1 |
| 843 | 6 | 97 | VCP | 0.8 | Alley | 15 | 263.5681 | 6.7 | Sand | Low | Moderate | 1 |
| 2343 | 8 | 23 | PVC | 0.3 | Street | 15 | 235.9731 | 6.7 | Sand | Low | Moderate | 1 |
| 2795 | 18 | 50 | VCP | 0.08 | Alley | 15 | 80.58689 | 6.7 | Sand | Low | Moderate | 1 |
| 65 | 8 | 50 | VCP | 0.3 | Street | 11 | 535.9586 | 6.7 | Sand | Low | Moderate | 1 |
| 623 | 12 | 71 | CONC | 0.6 | Highway | 10 | 472.1441 | 6.7 | Sand | Low | Moderate | 1 |
| 624 | 24 | 64 | CONC | 0.12 | Street | 10 | 465.4685 | 6.7 | Sand | Low | Moderate | 1 |
| 2366 | 12 | 51 | VCP | 0.3 | Alley | 10 | 401.3963 | 6.7 | Sand | Low | Moderate | 1 |
| 3215 | 8 | 22 | PVC | 0.33 | Street | 10 | 384.402 | 6.7 | Sand | Low | Moderate | 1 |
| 3097 | 12 | 51 | VCP | 0.3 | Street | 10 | 325.2434 | 6.7 | Sand | Low | Moderate | 1 |
| 1365 | 8 | 24 | PVC | 0.4 | Alley | 10 | 283.7502 | 6.7 | Sand | Low | Moderate | 1 |
| 3327 | 48 | 29 | PVC | 0.14 | Street | 10 | 278.4683 | 6.7 | Sand | Low | Moderate | 1 |
| 2146 | 12 | 39 | PVC | 2.1 | Street | 10 | 159.0316 | 6.7 | Sand | Low | Moderate | 1 |
| 2295 | 15 | 66 | VCP | 0.32 | Street | 10 | 156.1034 | 6.7 | Sand | Low | Moderate | 1 |
| 285 | 8 | 35 | PVC | 0.8 | Easement | 10 | 99.28742 | 6.7 | Sand | Low | Moderate | 1 |
| 181 | 10 | 48 | VCP | 0.8 | Alley | 10 | 70.07311 | 6.7 | Sand | Low | Moderate | 1 |
| 47 | 8 | 16 | PVC | 0.4 | Street | 10 | 24.48685 | 6.7 | Sand | Low | Moderate | 1 |
| 2428 | 12 | 9 | PVC | 0.2 | Street | 8 | 479.9761 | 6.7 | Sand | Low | Moderate | 1 |
| Model # | Architecture | RMS Training | RMS Testing |
|---|---|---|---|
| 1 | 22–4-1 | 0.3089 | 0.2745 |
| 2 | 22–5-1 | 0.3165 | 0.2857 |
| 3 | 22–6-1 | 0.2860 | 0.2620 |
| 4 | 22–7-1 | 0.3001 | 0.2647 |
| 5 | 22–8-1 | 0.3048 | 0.2720 |
| 6 | 22–9-1 | 0.3009 | 0.2662 |
| 7 | 22–10-1 | 0.3010 | 0.2751 |
| 8 | 22–11-1 | 0.3021 | 0.2716 |
| 9 | 22–12-1 | 0.3001 | 0.2730 |
| 10 | 22–13-1 | 0.3001 | 0.2695 |
| 11 | 22–14-1 | 0.3002 | 0.2712 |
| 12 | 22–15-1 | 0.3001 | 0.2700 |
| Total Factors | Good | Bad | Tolerance | Average Error | RMS Error |
|---|---|---|---|---|---|
| Training Configuration | |||||
| 2224 | 1599 (72%) | 625 (28%) | 0.3 | 0.2519 | 0.3048 |
| Testing Configuration | |||||
| 392 | 334 (85%) | 58 (15%) | 0.3 | 0.227 | 0.2823 |
| Condition | Area Under Curve |
|---|---|
| 1 | 0.833 |
| 2 | 0.768 |
| 3 | 0.794 |
| 4 | 0.815 |
| 5 | 0.802 |
| Factors | Sewer Pipe Condition | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Diameter | 0.001 | 0.000 | 0.199 | 0.008 |
| Age | 0.000 | 0.001 | 0.000 | 0.807 |
| Length | 0.000 | 0.228 | 0.113 | 0.980 |
| Material | 0.503 | 0.025 | 0.001 | 0.280 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atambo, D.O.; Najafi, M.; Kaushal, V. Development and Comparison of Prediction Models for Sanitary Sewer Pipes Condition Assessment Using Multinomial Logistic Regression and Artificial Neural Network. Sustainability 2022, 14, 5549. https://doi.org/10.3390/su14095549
Atambo DO, Najafi M, Kaushal V. Development and Comparison of Prediction Models for Sanitary Sewer Pipes Condition Assessment Using Multinomial Logistic Regression and Artificial Neural Network. Sustainability. 2022; 14(9):5549. https://doi.org/10.3390/su14095549
Chicago/Turabian StyleAtambo, Daniel Ogaro, Mohammad Najafi, and Vinayak Kaushal. 2022. "Development and Comparison of Prediction Models for Sanitary Sewer Pipes Condition Assessment Using Multinomial Logistic Regression and Artificial Neural Network" Sustainability 14, no. 9: 5549. https://doi.org/10.3390/su14095549
APA StyleAtambo, D. O., Najafi, M., & Kaushal, V. (2022). Development and Comparison of Prediction Models for Sanitary Sewer Pipes Condition Assessment Using Multinomial Logistic Regression and Artificial Neural Network. Sustainability, 14(9), 5549. https://doi.org/10.3390/su14095549