1. Introduction
The global demand for energy is ever-increasing in order to meet the needs of an emergent human population, with fossil fuels being the most prominent source. The use of fossil fuels leads to environmental emissions of “greenhouse gases (GHGs)” and pollutants, which contribute to global warming [
1,
2]. Over the last few decades, many international organizations and governments have collectively pledged to slow global warming [
3]. In the recent past, the fast development of the urban areas has led to a rising demand for public transportation. The transportation industry produces a major fraction of all energy-related emissions, which accounts for approximately one-fifth of global CO
2 emissions. This transportation fuel is mainly based on the combustion of fossil fuels, making it one of the key sources of air pollution in both the urban and regional areas [
4,
5].
Sustainable transportation is an essential solution to have a substantial reduction in fuel economy, the amount of air pollutants, and GHG footprints, which could create sustainable development in the transport sector. Hybrid “electric vehicles (EVs)”, hydrogen vehicles, plug-in hybrid EVs, battery EVs, electrically-chargeable vehicles, biofuels, and natural gas vehicles are technologies that could offer solutions to decrease our reliance on fossil fuel-based energy and reduce GHG emissions [
2]. The emergence of cleaner vehicles is a real opportunity to embrace healthier and safer transport networks. Because of energy and transport policies aiming to incorporate more options and “renewable energy sources (RESs)”, the latest technologies are increasingly incorporated into the vehicle fleet [
6].
As the world shifts towards low-carbon emission sources, the “alternative fuel vehicles (AFVs)” have received more consideration as a way to decrease GHG emissions in sustainable transportation [
7]. They provide a prospect to lower fuel costs, as well as to decrease our ecological footprint.
The importance of sustainable transport for countries is also widely recognized by the international community, such as in the Agenda 2030 for Sustainable Development. This is an action program for the population, the planet, and prosperity signed in September 2015 by the governments of the 193 UN countries. Agenda 2030 concerns 17 sustainable development goals, or SDGs, included in a large action for a total of 169 ‘targets’. The UN Member States recognize that ending poverty must be accompanied with strategies that build economic growth and address a range of social needs including education, health, equality, and job opportunities, while tackling climate change and working to preserve the ecosystem. Transport is fueled by energy and is, therefore, directly linked to SDG 7, which focuses on affordable and clean energy. However, sustainable transport is also mainstreamed across several SDGs and targets, especially those related to economic growth, climate change, infrastructure, and sustainable cities and communities. The transport sector will play a crucial role in the achievement of the Paris Agreement, considering that near a quarter of energy-related global greenhouse gas emissions come from transport. Due to increasing demands for mobility, the energy intensity and environmental impact of transport may, unfortunately, grow substantially. Thus, to increase the share of sustainable transport may be crucial. The possible use of alternative fuels has become an urgent issue, and a large number of researchers are studying the development of alternative fuel vehicles (AFVs). The evaluation of AFVs should consider not only their effect on air pollution, but also on the sustainability pillars [
8]. Some studies highlighted the strong relationship between sustainability and AFVs. In particular, Ghosh [
9] offered a review about using electric vehicles to reduce the carbon footprint in the transport industry. Kene et al. [
10] analyzed the current state of research and development of electric vehicles. Offer et al. [
11] compares battery electric vehicles (BEVs) to hydrogen fuel cell electric vehicles (FCEVs) and hydrogen fuel cell plug-in hybrid vehicles (FCHEVs) for sustainable transport. Faria et al. [
12] proposed a study of the life-cycle assessment (LCA) for both conventional and electric vehicles, focusing mainly on their greenhouse gas (GHG) emissions. Krishnan et al. [
13] proposed a model to evaluate hydrogen as a sustainable alternative fuel for vehicles. Wu et al. [
14] suggested some models of light-duty plug-in electric vehicle (PEV) fleets for conducting national-level planning studies of the energy and transportation sectors. Liu et al. [
15] compared alternative fuel vehicles and conventional gasoline vehicles (and hybrid vehicles) using sensor data from global positioning system devices. Mesut and Ismail [
16] introduced a vehicle routing problem, considering alternative fuel vehicle (AFV) adoption into a service fleet. Mizik [
17] provided an overview of alternative fuels by describing their advantages and disadvantages with respect to fossil fuels. Onat [
18] provided an integrated sustainability framework to analyze environmental, social, and economic impacts, and to rank alternative fuel vehicles. Loo et al. [
19] analyzed the characteristics of different biodiesel blends that can be used in vehicle’s engines. Peksen [
20] reviewed the potential of new energy vehicles and hydrogen technology. Betancourt-Torcat et al. [
21] proposed a system of integrated electric vehicle network planning. Sinha-Brophy [
22] applied the life-cycle assessment to renewable hydrogen for fuel cell passenger vehicles. Furthermore, Antonini et al. [
23] investigated the environmental footprint of technologies for hydrogen production as a transport fuel.
At today’s industrial and market development level, the assessment and selection of the most suitable AFV is a challenging problem for fleet operators. Due to the involvement of the human mind and several aspects of sustainability factors, the AFV evaluation procedure can be treated as an uncertain “multi-attribute decision analysis (MADA)” problem [
5,
24]. In this regard, MADA approaches can be used to investigate this concern in a systematic way.
Uncertainty is an inherent feature of information. In several scientific and industrial applications, we make decisions in an environment with diverse kinds of uncertainty. The “fuzzy set theory (FST)” invented by Zadeh [
25] has successfully been employed in varied areas and has demonstrated its powerful ability to deal with vague and uncertain information. In the literature, several doctrines and principles have been studied on FST [
26,
27,
28]. Furthermore, Atanassov [
29] extended the FST to an “intuitionistic fuzzy set (IFS)”, which deals with uncertain and ambiguous information more accurately. In IFSs, each object is defined with a “membership function (MF)”, a “non-membership function (NF, and an “indeterminacy function (IF)”. Research works on IFS theory and its applications in different settings are developing speedily, and several significant outcomes have been obtained [
30,
31,
32].
The theory of IFS is one of the most powerful and suitable tools to cope with the vagueness presented in numerous realistic decision-making applications. Taking the flexibility and efficacy of IFSs, the aim of the paper is to develop a hybrid method for assessing the MADA problem in IFSs. Due to their flexibility and efficacy, this study considers the context of IFSs. In this line, the weight-determining methods are separated into the following two categories:
objective weights, and subjective weights. In the literature, several objective and subjective weight methods have been introduced [
33,
34,
35]. Recently, Keshavarz-Ghorabaee et al. [
36] provided an innovative objective-weighting tool for assessing the criteria weights, called “method based on the removal effects of criteria (MEREC)”. It utilizes each attribute’s removal effect on the assessment of an alternative to obtain the attribute’s weights. Assuming the deviations, the assessment of an option with the removal of an attribute is a latest idea for estimating the attribute weights [
37]. For a subjective weighting model, a procedure of the “ranking sum (RS)” weighting method was given by Stillwell et al. [
38] to assist the “decision experts (DEs)” to give their preference ratings for considered criteria. Until now, no one has developed an integrated MEREC-RS weighting method, or used “double normalization-based multiple aggregation (DNMA)”-based method under IFSs setting for the assessment of AFVs.
For the first time, we introduce a hybridized MADA methodology by combining the MEREC [
20], RS method [
38], and the DNMA approach [
39] with IFSs, named as the “intuitionistic fuzzy-MEREC-RS-DNMA (IF-MEREC-RS-DNMA)” approach. In this method, new “intuitionistic fuzzy generalized Dombi weighted averaging (IFGDWA)” and “intuitionistic fuzzy generalized Dombi weighted geometric (IFGDWG)” operators are utilized to aggregate the individual’s decision opinions. The MEREC process is used to compute the objective weights of the attributes. The RS tool is utilized to obtain the subjective weights of the attributes. The DNMA approach on IFSs is developed for multi-criteria assessment, which takes the benefits of different normalization methods and aggregation functions and combines them in an appropriate way. The final assessment value of the DNMA model widely reflects the subordinate utility degrees and the ranks of options, and, thus, the overall priority outcome has a high dependability. Furthermore, we implement the proposed IF-MEREC-RS-DNMA framework for the evaluation and selection of AFVs for sustainable road transportation.
The primary outcomes of the present work are listed as:
We identify the parameters for selecting AFVs for sustainable road transportation, using a survey approach based on the literature and interviews with the experts.
We present a comprehensive procedure to evaluate and analyze the related parameters of AFV selection for sustainable road transportation with a hybrid decision support method.
We propose a weighting procedure called the intuitionistic fuzzy subjective objective integrated approach, using the IF-MEREC and RS method to obtain the parameters weights of selecting AFVs for sustainable road transportation.
The IF-DNMA method on IFSs is discussed using the IF-generalized Dombi operator and the IF-MEREC-RS method, with the aim of ranking AFVs for sustainable road transportation.
We present sensitivity and comparison analyses to validate the integrated IF-MEREC-RS-DNMA approach.
The remaining sections are prepared in the following way. In
Section 2, we present a comprehensive literature review about the study. In
Section 3, the basic concepts and proposed “aggregation operators (AOs)” are presented. In
Section 4, the developed IF-MEREC-RS-DNMA method is discussed. In
Section 5, a case study of AFV assessment is presented to validate the efficiency and usefulness of the introduced approach. In addition, comparison and sensitivity analysis are shown to certify the outcomes. Finally,
Section 6 discusses the conclusions and recommendations for future work.
4. Proposed IF-MEREC-RS-DNMA Method
This section introduces a hybrid IF-MEREC-RS-DNMA method. The DNMA framework takes the benefits of different normalization methods and aggregation functions and combines them in an appropriate way. The procedure of the IF-MEREC-RS-DNMA methodology is displayed in the following steps (
Figure 1):
Step 1: Form an “intuitionistic fuzzy-decision matrix (IF-DM)”.
In a MADA procedure, the purpose is to decide an ideal candidate from a set of m options over the attribute set . Form a committee of experts to elect the best option(s). Let us assume that is the “linguistic decision-matrix (LDM)” articulated by DEs, in which implies the linguistic performance rating of an option Gi over attribute Cj given by kth expert, and further, converted into IF-DM.
Step 2: Evaluate the DEs’ weights.
In order to estimate the weights of DEs, initially the significance degrees of the DEs are supposed as “linguistic variables (LVs)” and then articulated by IFNs. Let us suppose
be an IFN, then the procedure for evaluating
kth DE weight is as follows:
Step 3: Determine the “aggregated IF-DM (AIF-DM)”.
In this step, all individual decision matrices are required to be combined into an AIF-DM. For this perspective, an IFGDWA (or IFGDWG) operator is employed, and then the AIF-DM is
where:
Step 4: Proposed IF-MEREC-RS to the computation of attribute weight.
All the attributes are not assumed to be of the same importance. Consider to be the attribute weight with and Here, the criteria weight is computed by the combination of objective and subjective weights.
Case I: Determination of objective weights by the method of IF-MEREC.
Now, to obtain the objective weights, the classic MEREC [
20] is expanded within the IFSs setting. The computational procedure of MEREC is given as follows:
Step 4.1: Normalize the AIF-DM.
To create the normalized AIF-DM
we utilize the linear normalization process, which is
where
Cb and
Cn represent the benefit and cost-type attributes, respectively.
Step 4.2: Obtain the score-matrix.
By means of Formula (20), the score matrix
of each IFN
is estimated
Step 4.3: Compute the overall performance of alternatives.
In this step, a logarithmic mapping with equivalent weights is used to determine the options’ overall performances [
36]. Along with the normalized values attained in the last step, we can confirm that the lesser values of
yield the better ratings of the performances. In the following, we present the formula for computing the overall performance of the options:
Step 4.4: Estimate the performance of alternatives by removing each attribute.
In this following step, the options’ performances are computed by means of removing each attribute separately:
Consequently, n sets of performances are obtained with respect to n criteria.
Step 4.5: Compute the summation of absolute deviations.
In this step, we calculate the removal effect of the
jth criterion based on the values obtained from Steps 4.3 and 4.4. Let
represents the effect of removing the
jth attribute. We estimate the values of
with the expression as follows:
Step 4.6: Obtain the final weights of attribute.
The final weight
of the
jth attribute is determined by
Case II: Determine the subjective weights by the IF-ranking sum (RS) weighting method.
The subjective weight-determining method permits us to reveal in the opinions and intrinsic ratings of the DEs. In this study, the RS method [
38,
63] is utilized to derive the subjective weights of attributes under IFS context. The procedural step is given by:
where
determines the subjective weight of
jth attribute and
n signifies the number of attributes, and
rj symbolizes the rank of each attribute, where
Case III: Integrated weights using the IF-MEREC-RS method.
To obtain the combined weight, the DEs want to employ the subjective and objective weights in order to derive the more accurate attributes’ weights. An integrated weight-determining formula is as follows:
where
is a precision objective factor of the decision strategy. In this expression,
and
represent the objective and subjective weights of the
jth attribute, respectively.
Step 5: Assessment of the normalized AIF-DM.
Here, we discuss both the linear and vector normalization formulae. The linear normalization removes the dimensions of attributes using the principle with the interval maximum-minimum. It is utilized in the VIKOR [
54] and TOPSIS [
53] models. A linear normalization procedure is defined by
Here is an improved score function of IFNs.
The vector normalization has been used in the MULTIMOORA [
55] and conventional TOPSIS [
64]. We utilize it to normalize the AIF-DM
with
into
where
such that
Due to the fact that both the target-based vector and linear normalization hold some benefits and restrictions simultaneously [
39], they are combined in this method using various AOs in a way to achieve various utility degrees of alternatives.
Step 6: Using the subordinate aggregation models.
Here, different types of aggregation models are developed using the following normalization procedures.
Step 6.1: The “complete compensatory method (CCM)”.
The CCM can be defined based on IFGDWA operator as follows:
where
represents the attribute weight and
shows the target-based linear normalization value. The alternatives can be ordered by arranging
in a decreasing manner, and we obtain the ranking outcomes
Step 6.2: The “un-compensatory method (UCM)”.
For the avoidance of a situation in which the chosen solution has a very improper performance in the case of a certain criterion, the weighted maximum operator is used for the purpose of composing the second aggregation function, as shown below:
The options can be prioritized by arranging in a decreasing way, and we obtain the ranking outcomes
Step 6.3: The “incomplete compensatory method (ICM)”.
We utilize the vector normalization of the third aggregation procedure by the IFGDWG operator:
where
signifies the attribute weight and
denotes the target-based vector normalized value. The alternatives can be arranged by listing
in a descending manner, and we obtain the ranking outcomes
Step 7: Combination of subordinate “utility degrees (UDs)” and priority orders.
The last phase necessitates the achievement of all-inclusive ranking by combining the outcomes of the given three models. These are considered as the following three parameters or attributes: CCM UCM and ICM Each option has two kinds of degrees, the “utility degree (UD)” , and the preference order over each attribute . Evidently, we generate two “decision matrices (DMs)”, which are the UD-DM and the ranking-DM
To preserve the inventive assessment of the subordinate UDs
the normalized versions are given by
Step 8: Compute the “overall utility degree (OUD)” of each option.
A parameter is taken to show the subordinate UDs and the subordinate preferences of options. Here, we take .
The OUD of each option is presented by
where
and
are the weight of the CCM, UCM, and ICM, respectively, such that
. Here, the weights
and
are obtained using the developed IF-RS method, or provide equal weights. The ultimate preference set
is obtained in decreasing order of
Step 9: End.
5. Case Study: Assessment of Alternative Fuel Vehicles (AFVs)
Due to rising oil import bills and a diminishing stock of fossil-based fuels, the search for cleaner and safer alternative fuels is now the leading challenge being faced by scientists and decision makers in India. Recent years have seen a noticeable shift towards the use of renewable and alternative fuels, moving away from conventional fossil-based fuels. In recent times, the progress of AFVs has become gradually more important worldwide. One of the most significant causes for this increase is that AFVs are seen as a valuable way of dealing with climate change, shifting energy consumption to produce less carbon and less pollution, and because they offer more energy diversity.
To display the effectiveness and applicability of the proposed approach, a case study related to the AFV selection problem for a private home healthcare service provider (XYZ), situated in Chandigarh, India, is presented. In this region, the selected healthcare service provider serves the patients within a 45 miles radius of Chandigarh. The healthcare service provider requires a passenger car to carry the patients from their home. In the current section, we have concentrated on the development and implementation of a new model that will help the service provider to assess and choose a suitable AFV option.
In real-life situations, it is very difficult to evaluate the exact criteria for AFV evaluation problems, due to lack of precise knowledge/information, increasing complexity, and time-limitations. To evaluate the criteria and alternatives, we created a panel of four DEs, who are experts in sustainable development, internal combustion engines and, the automotive industry in India. Two of them are from the automotive industry, one expert is from the internal combustion engine sector, and the other is from the field of sustainable development. The qualifications of three experts are Ph.D. and the other is a master’s degree holder working at Autonomous Intelligence Motors Private Limited, India. The DEs collaborated with the authors during the entire study.
Furthermore, the panel of decision experts participated in an online questionnaire in order to determine the importance of criteria in the selection of AFV alternatives. The significant goal of this questionnaire is to discuss the potential factors/criteria influencing the AFV selection. The criteria that may affect the AFV selection were collected by reviewing the literature. Based on the literature review, online questionnaire and open interviews, a set of sustainability perspectives, and indicators were collected to choose the best AFVs. After that, five main dimensions of criteria were considered, namely the environmental, technical, economic, social, and political dimensions [
5,
46].
In the meantime, based on the accessibility of vehicle models suitable for this fleet operation and the availability of fuel, a panel of experts considered five AFVs, namely hybrid electric vehicles (
G1), electric vehicles (
G2), hydrogen vehicles (
G3), natural gas vehicles (
G4), and biofuel vehicles (
G5). In addition, open interviews and literature reviews facilitated us to recognize global AFVs. On account of the initial analysis, extant literature, and discussion with experts, 15 attributes have been recognized, as shown in
Table 1. Afterward, DEs are invited to give their opinions and experiences, both to weigh the evaluation criteria and to score the candidate AFVs by means of each criterion. As per their domain knowledge, DEs express their preferences in the form of LVs.
Steps 1–3:
Table 2 and
Table 3 adopted from Kumari and Mishra [
81], to present the importance of the DEs and criteria to estimate the significance ratings of the DEs and the assessment criteria for AFVs, which were then articulated in terms of IFNs. Using
Table 2 and Equation (17), the DEs’ weights are calculated and portrayed in
Table 4.
Table 5 represents the LDM by DEs for each option AFV
Gi over the different attributes. From Equation (18) and
Table 5, the AIF-DM is computed (taking
p = 1 and
q = 1) and shown in
Table 6.
Step 4: To compute the objective weights of criteria by MEREC, firstly the normalized AIF-DM is computed with the use of Equation (19). Next, the overall performances of the options based on Equation (20) are determined and presented as
S1 = 0.370,
S2 = 0.353,
S3 = 0.404,
S4 = 0.358 and
S5 = 0.389. By means of Equation (21), the overall performance of each option by removing each attribute is computed and shown in
Table 7. Next, we derive the removal effect of each attribute on the overall performance of the options using Equation (22). Furthermore, we calculate the final attributes’ weights for AFV selection by utilizing Equations (23) and (24), and given in last column of
Table 7. The resultant values are in depicted in
Figure 2.
From Equation (25), we have calculated the subjective weights using the IF-RS weighting method of each criterion for AFVs selection. The required results are shown in
Table 8, and depicted in
Figure 2.
To derive the combined weights of attributes, we have combined the results obtained by the IF-MEREC for objective weighting and the IF-RS method for subjective weighting by means of Equation (26). The final weight for
is shown in
Figure 2 and given as follows:
wj = (0.0473, 0.0670, 0.0570, 0.0669, 0.0500, 0.0949, 0.0576, 0.0530, 0.0610, 0.0876, 0.0520, 0.0702, 0.0770, 0.0755, 0.0830).
Here,
Figure 2 displays the significance value or weights of different criteria of AFV selection for sustainable road transportation with respect to the goal. The parameter social benefits (
C6), with a weight value of 0.0949, have been determined to be the most important parameter in AFV selection. Fueling/charging infrastructure (
C11), with a weight value of 0.0876, is the second most important parameter in AFV selection. Financial incentives (
C15), with a significance value of 0.0830, is the third most significant parameter in AFV selection, and others are considered as crucial parameters in AFV selection for sustainable road transportation.
Step 5: According to the Equations (27)–(29) and
Table 6, the linear and vector normalization values for AFV selection are estimated and given in
Table 9 and
Table 10.
Step 6: The subordinate utility degrees of the CCM, UCM and ICM are estimated by Equations (30)–(32), and portrayed in
Table 11.
Step 7: Corresponding to Equation (33), the normalized degrees of the subordinate UDs of CCM, UCM, and ICM are estimated, and their preferences are also obtained and are shown in
Table 12. Next, the normalized subordinate UDs and the weights of subordinate UDs are calculated and mentioned in
Table 10.
Step 8: From Equation (34), the subordinate normalized UDs and ranks, the OUDs and the final preference orders of options are obtained and depicted in
Table 12. Regardless of assuming
the weights can be chosen as per the preferences of DEs on the basis of the comprehensive accomplishment by the alternatives or of their poor performances. CCM is preferred if the attention of the alternatives’ comprehensive abilities can be drawn from DEs. If the DEs are not interested in taking risks, then a large weight can be attached to the UCM. It is pertinent to mention that ICM can be endowed by a large weight in cases when the DEs focus solely upon comprehensive performance as well as decision risks. Hence, the preference order of options is
, and the option
G2 is with a highest UD of appropriateness of options.
5.1. Comparative Study
In the current part of the study, a comparison is made between the outcomes obtained from the IF-MEREC-RS-DNMA method and those from other MCDM models. To demonstrate the efficiency and show the unique advantages of the IF-MEREC-RS-DNMA framework, we compare the present approach with the previously developed approaches, which are the “intuitionistic fuzzy complex proportional assessment (IF-COPRAS)” [
82] and the “intuitionistic fuzzy weighted aggregated
sum product assessment (IF-WASPAS)” method [
83].
5.1.1. IF-COPRAS Method
To show the comparison, we choose the IF-COPRAS model given by Gitinavard and Shirazi [
82] with the analysis of decision-making problem given in above section.
Steps 1–4: Same as earlier method.
Step 5: Add the values of attributes for benefit and cost.
In this step, to calculate the values of
and
for benefit and cost-type criteria, we implement the following procedure:
In these formulae, is number of benefit-type attributes, while n is the whole criteria.
Step 6: Calculate the “relative degree (RD)” of each option.
The RD
of the
ith option is computed by
Here, and denote the score degrees of and respectively.
Step 7: Compute the “utility degree (UD)” of each option.
The formula for the computation of the utility degree
of each option is
Step 8: End.
Now, the whole outcomes of IF-COPRAS [
82] model are shown in
Table 13. From
Table 6 and Equations (35)–(38), the priority order of options and the UDs of options are evaluated. According to utility degrees (see
Table 13),
G2 is obtained to be the most appropriate AFV, as it has the highest relative weight value (0.2933).
5.1.2. IF-WASPAS Method
The IF-WASPAS method [
83] consists of the following steps:
Steps 1–5: These steps are similar to those of the previous method.
Step 6: Calculate the degrees of the weighted sum model (WSM)
and weighted product model (WPM)
of each option by means of the following formulae:
Step 7: Define the aggregated degree or the total significance, i.e., the WASPAS measure of each option, which is presented as the following formula:
where
signifies the aggregating coefficient of the accuracy of the decision (when
and
the WASPAS is changed to the WPM and WSM methods). The aggregating methods have been proved to be more accurate compared with single ones.
Step 8: Rank the current option(s) by minimizing the crisp score values of
Next, the entire computational results of the IF-WASPAS approach are presented in
Table 14.
Therefore, the ranking of treatment choice is and the option G2 is with higher degree of appropriateness of the selection AFVs.
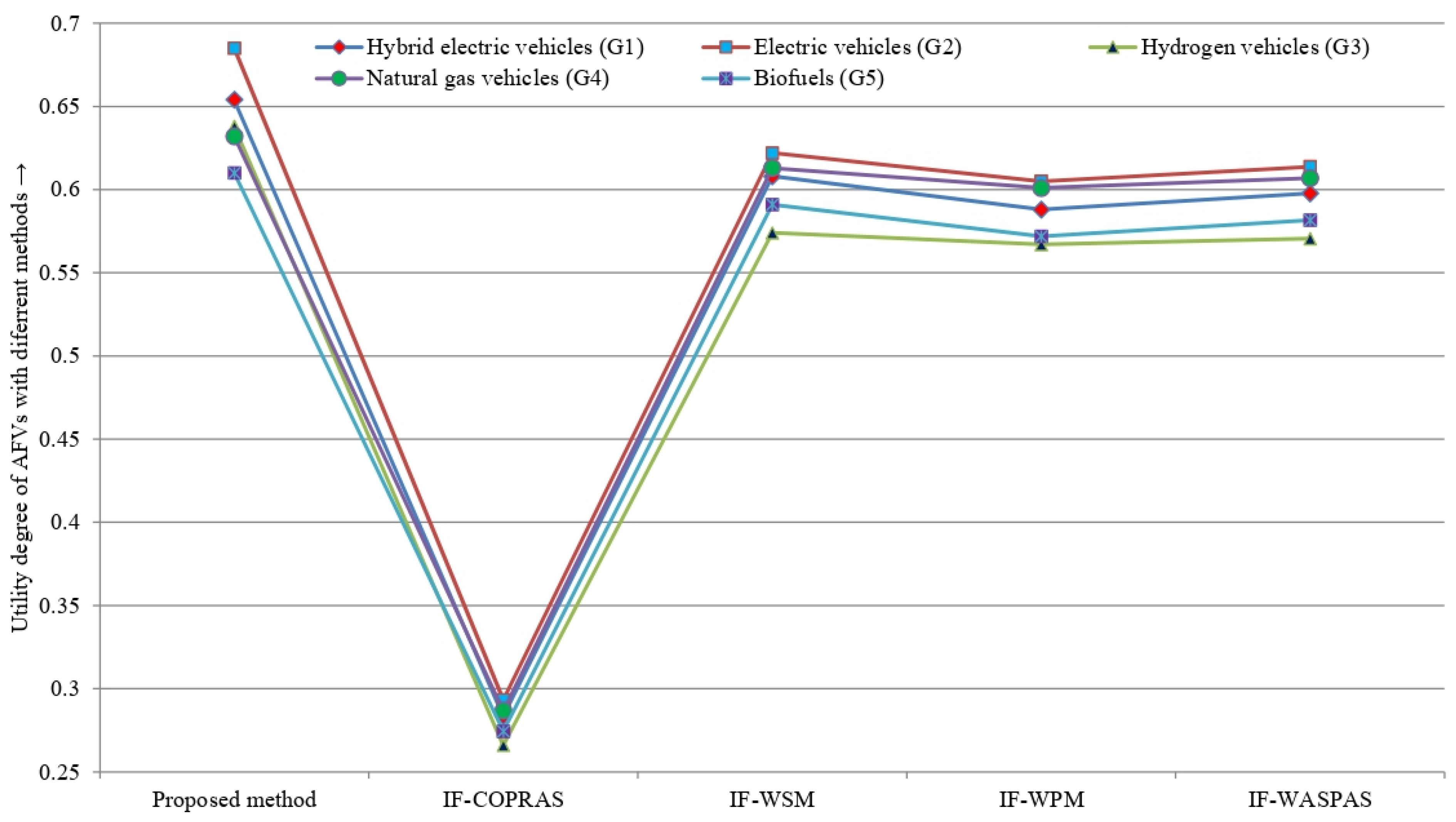
In comparison with existing methods, the benefits of the presented method are discussed as follows (see
Figure 3):
The presented methodology estimates the attribute weights with the use of a combined IF-MEREC-RS process, which achieves more accurate attributes’ weights, while in IF-WASPAS, only the objective weight of criteria is estimated with the use of a similarity measure, and in IF-COPRAS, the weight of criteria is assumed by experts.
According to the computation procedures of the three methods, we can find the subordinate utility degrees and rank the options by using the IF-DNMA method, which can not only ensure that the selected alternative performs excellently in total, but also avoids the bad performance under each criterion. To this point, the IF-MEREC-RS-DNMA can provide experts with a more robust reference compared with the IF-WASPAS method and IF-COPRAS.
Aggregation functions used in the IF-MEREC-RS-DNMA model have both the linear and vector normalizations, while the IF-COPRAS model uses vector normalization, and the IF-WASPAS model utilizes the linear normalization. So, the IF-MEREC-RS-DNMA method is more reliable and flexible than extant methods.
The proposed methodology is applied in the IF-DNMA method to increase the robustness of the fuzzy-DNMA model. Compared to the extant utility based ranking method (namely MULTIMOORA [
84], VIKOR [
85], TOPSIS [
86], ELECTRE [
87], COPRAS [
81], WASPAS [
83], CoCoSo [
88], and others), the key benefit of the DNMA approach is that it is considered by two normalization procedures (namely target-based linear and vector normalization). Moreover, DNMA approach gives the DEs to adjust the weight of subordinate models (namely CCM, UCM, and ICM) to reveal their preferences on the “group utility” values and the “individual regret” values of options. Thus, the proposed hybrid DNMA approach is fulfilling the existing gap in the study of AFV assessment.
5.2. Sensitivity Investigation
In this section, we have been changing and investigating the importance of objective and subjective weights for chosen attributes in the presented weighting tool and changing the parameter ϑ of the DNMA method to show the performance of subordinate UDs to the preferences of AFVs. The analyses are carried out by making two cases.
Case I: When utilizing the DNMA method. This subsection shows sensitivity investigation associated with the parameter
ϑ. The variation of
ϑ is a useful issue helping to evaluate the sensitivity level of the approach, changing from subordinate UDs to the subordinate preferences. In addition, changing the values of
ϑ is applied for the sensitivity investigation of the proposed method to the eminence of criteria weights.
Table 15 and
Figure 4 represent the sensitivity analysis of the AFVs for diverse values of the utility parameter
ϑ. Based on the assessments, we obtain the similar preferences
for
ϑ = 0.0 to
ϑ = 0.8,
for
ϑ = 0.9 and
for
ϑ = 1.0, which implies
G2 is at the top of the ranking, while the
G5 has the last rank for
ϑ = 0.0 to
ϑ = 0.8 and the
G3 is at the top of the ranking and
G5 has the last rank for
ϑ = 0.9 to
ϑ = 1.0. Therefore, it is observable that the developed method possesses adequate stability with numerous parameter values. As shown clearly in
Table 15, the developed IF-MEREC-RS-DNMA methodology is capable of generating stable and, at the same time, flexible preference results in a variety of utility parameter. This property is of high importance for MCDM procedures and decision-making reality.
Case II: When introducing a weight-determining approach, the presented weighting tool is registered to offer appropriate weights for considered attributes. Initially, the criteria weights are computed with objective weights using MEREC in the place of combined weights. Thus, the prioritization has been obtained by the objective weighting in place of IF-MEREC-RS weight and presented in
Table 16 and
Figure 5. Using IF-MEREC, the OUD of AFVs:
G1 = 0.604,
G2 = 0.704,
G3 = 0.631,
G4 = 0.655, and
G5 = 0.631, and the prioritization of the following AFVs:
Applying the RS method, the OUD of the AFVs is as follows:
G1 = 0.618,
G2 = 0.675,
G3 = 0.638,
G4 = 0.690 and
G5 = 0.582 and the prioritization of AFVs as follows:
In the aforementioned discussion, we observe that the diverse parameter values will recover the steadiness of the IF-MEREC-RS-DNMA method.
6. Conclusions
The aim of the study is to propose an innovative MADA methodology with a combination of IF-MEREC-RS and IF-DNMA models for the assessment of candidate AFVs for private fleets. The developed MADA framework offers a better assessment approach to make an effective decision in selecting the most suitable AFV for sustainable transportation. The developed model has been implemented on an illustrative study of an AFV selection problem for a private home healthcare service provider in Chandigarh, India, which confirms its applicability, as well as the effectiveness of the IF-MEREC-RS-DNMA approach. From the sustainable viewpoints, a comprehensive evaluation index system has been made for this case study, which consists of the following five main attributes: economic, social, environmental, technological, and political. In this context, globally existing AFVs for sustainable transportation sector are identified and then prioritized against fifteen different criteria relevant to environmental, economic, technological, social, and political aspects of sustainability. This study contributes to the promotion of sustainable transport and the development of green transport. The proposed model is used to evaluate five alternative fuel vehicles in Chandigarh, India. It is distinguished that electric vehicles (G2), with an overall utility degree of 0.685, hybrid electric vehicles (G1), with an overall utility degree of 0.654, and hydrogen vehicles (G3), with an overall utility degree of 0.638 achieve higher overall performance compared to the other technologies in India. The assessment outcomes prove that electric vehicles can serve as a valuable alternative for decreasing carbon emissions and negative effects on the environment for India. This technology contributes to transportation sector development in less developed areas of the country. The EVs make an important impact on environmental issues since they generate less carbon dioxide than traditional vehicles (gasoline/diesel). The EVs reduce CO, NOx, and SOx gas emissions by 98–100%, 88–100%, and 100%, respectively [
5,
89]. In another study, Moro and Lonza [
90] highlighted that EVs demonstrate average GHG savings of around 50%.
Here, we observe the three main contributions of this study: (1) the development of new intuitionistic fuzzy generalized Dombi aggregation operators that provide the combined information on IFSs; (2) the proposal of a new combination of weighting procedures that enables objective weights using the MEREC and subjective weights using the RS method, and (3) the proposal of a framework which provides a flexible MADA approach for choosing the most sustainable AFV candidate.
It is important to be aware of certain limitations in the developed framework. A practical difficulty is that DEs must be trained with the preference style to properly utilize the flexibility and potential of IFNs. In the following, we present the limitations of the introduced MCDM methodology: (1) In this study, the evaluation index system should include more sustainability criteria, for instance, specific energy consumption, refueling/recharging time, emissions using usage, combustion duration, safety, resale value etc., (2) In realistic circumstances, there is requirement to consider the large number of DEs for assessment of AFV selection, however, we have taken only a set of four DEs, and (3) This work has limitations in dealing with more uncertain decision-making problems because of the constraint condition of the intuitionistic fuzzy set.
Future research studies will try to handle the limitations of this work. Further development of this study is suggested to incorporate other MADM methods such as MARCOS, “operational competitiveness rating (OCRA)” and “multi-attribute ideal real comparative analysis (MAIRCA)” with Archimedean Copula and Aczel–Alsina aggregation operators. Apart from that, other weight-determining methods such as “Level Based Weight Assessment (LBWA)” and FUCOM may be incorporated with DNMA method to improve the MADA process. Moreover, the model presented in this study may be applied to other MADM problems, namely sustainable plastic recycling processes, site selection for electric vehicle charging stations, facility location selection for automotive lithium-ion batteries, and others under different uncertain contexts.