Permanent Deformation and Breakage Response of Recycled Concrete Aggregates under Cyclic Loading Subject to Moisture Change
Abstract
1. Introduction
2. Materials and Methods
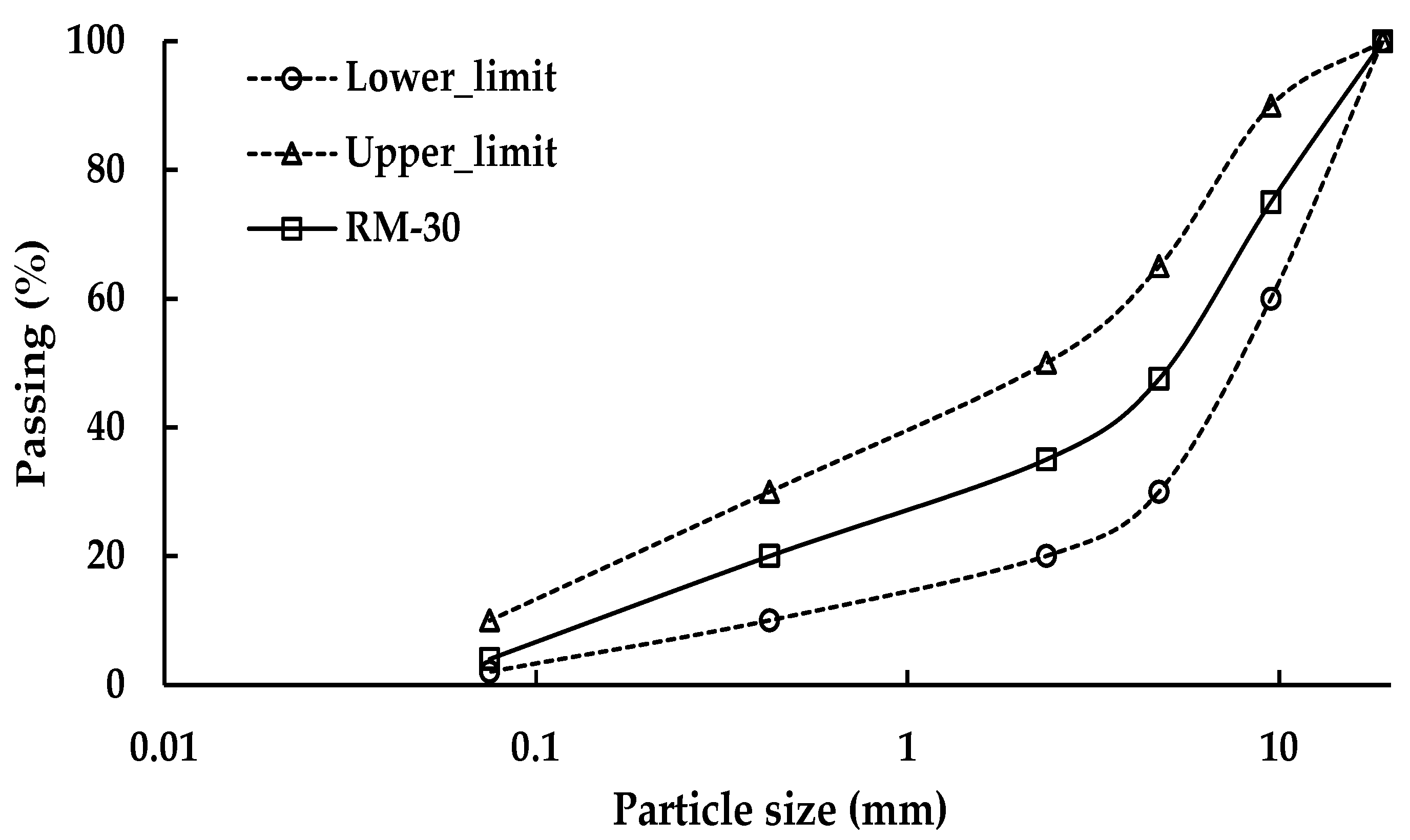
2.1. Material
2.2. Testing Methods
2.2.1. Preparation of Samples
2.2.2. Compaction Test
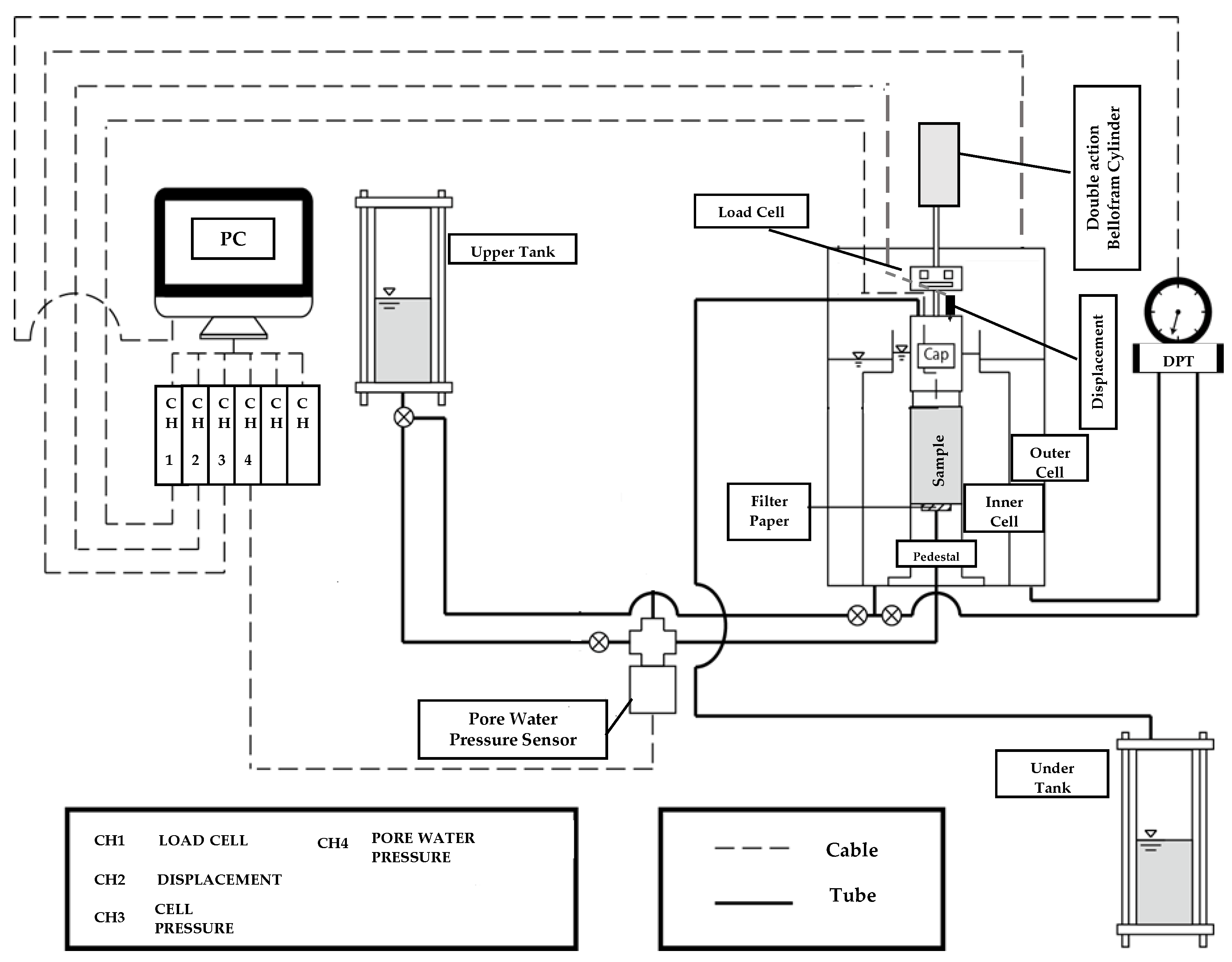
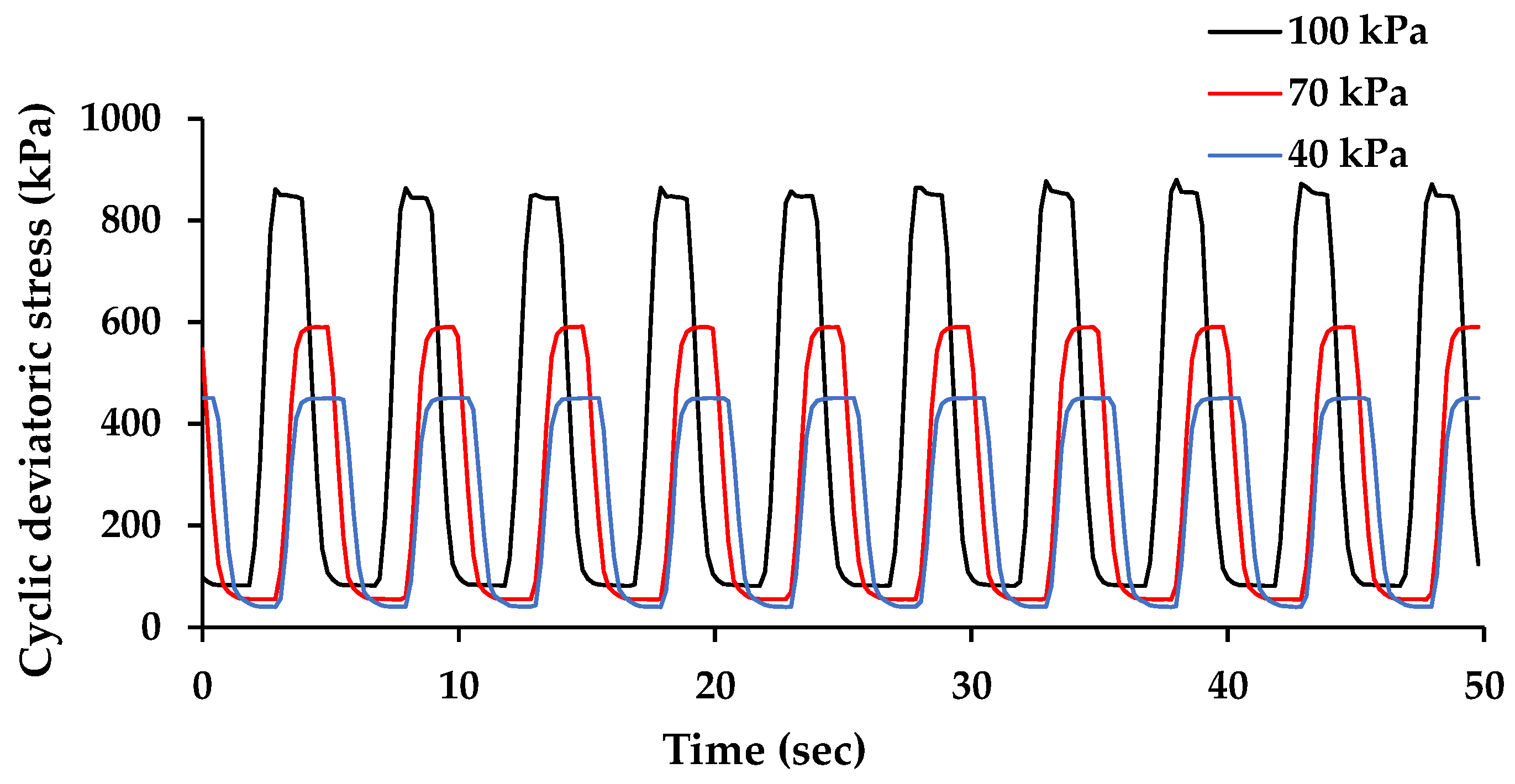
2.2.3. Static and Cyclic Triaxial Tests
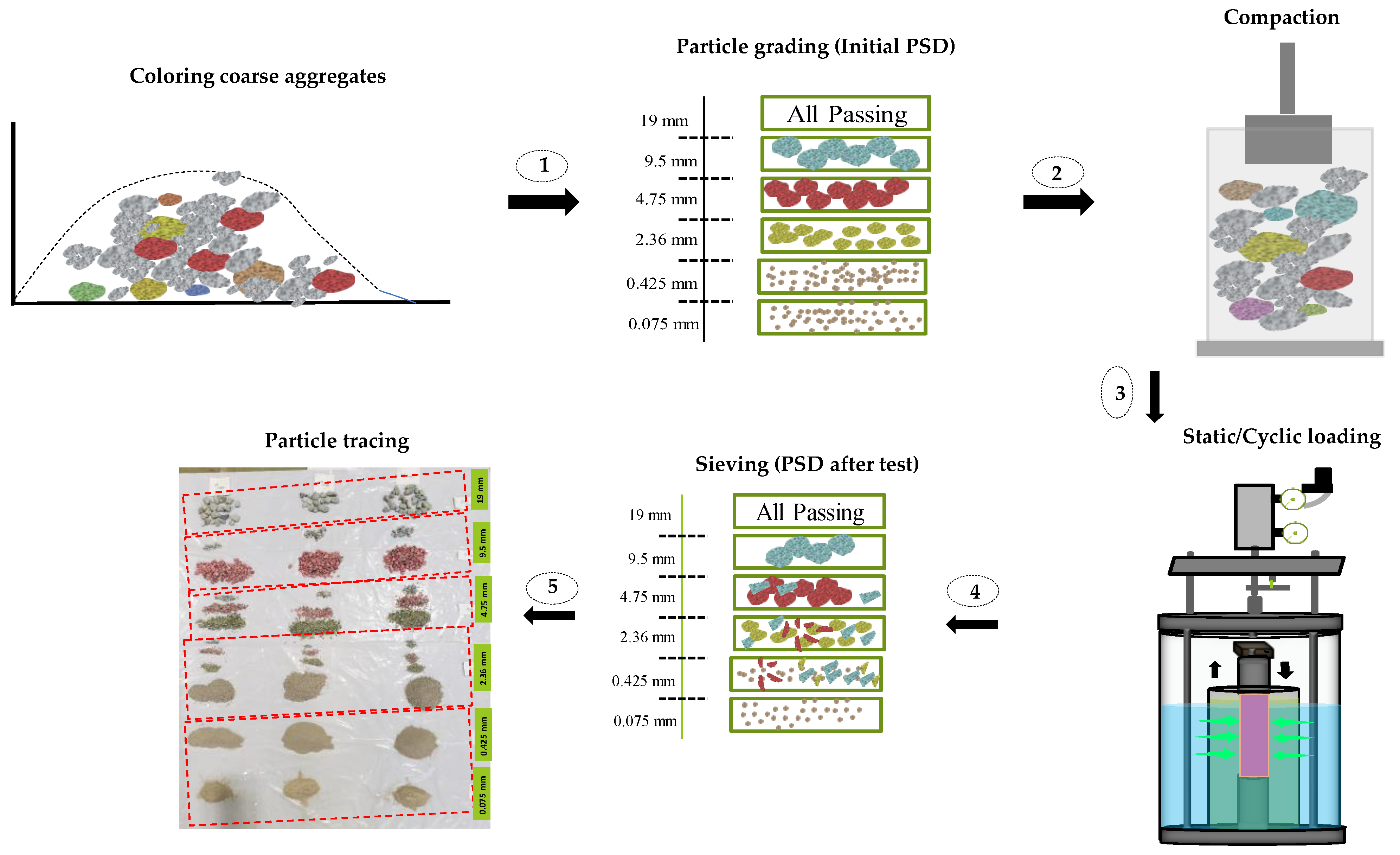
2.2.4. Coloring Technique to Characterize Particle Breakage
3. Results and Discussion
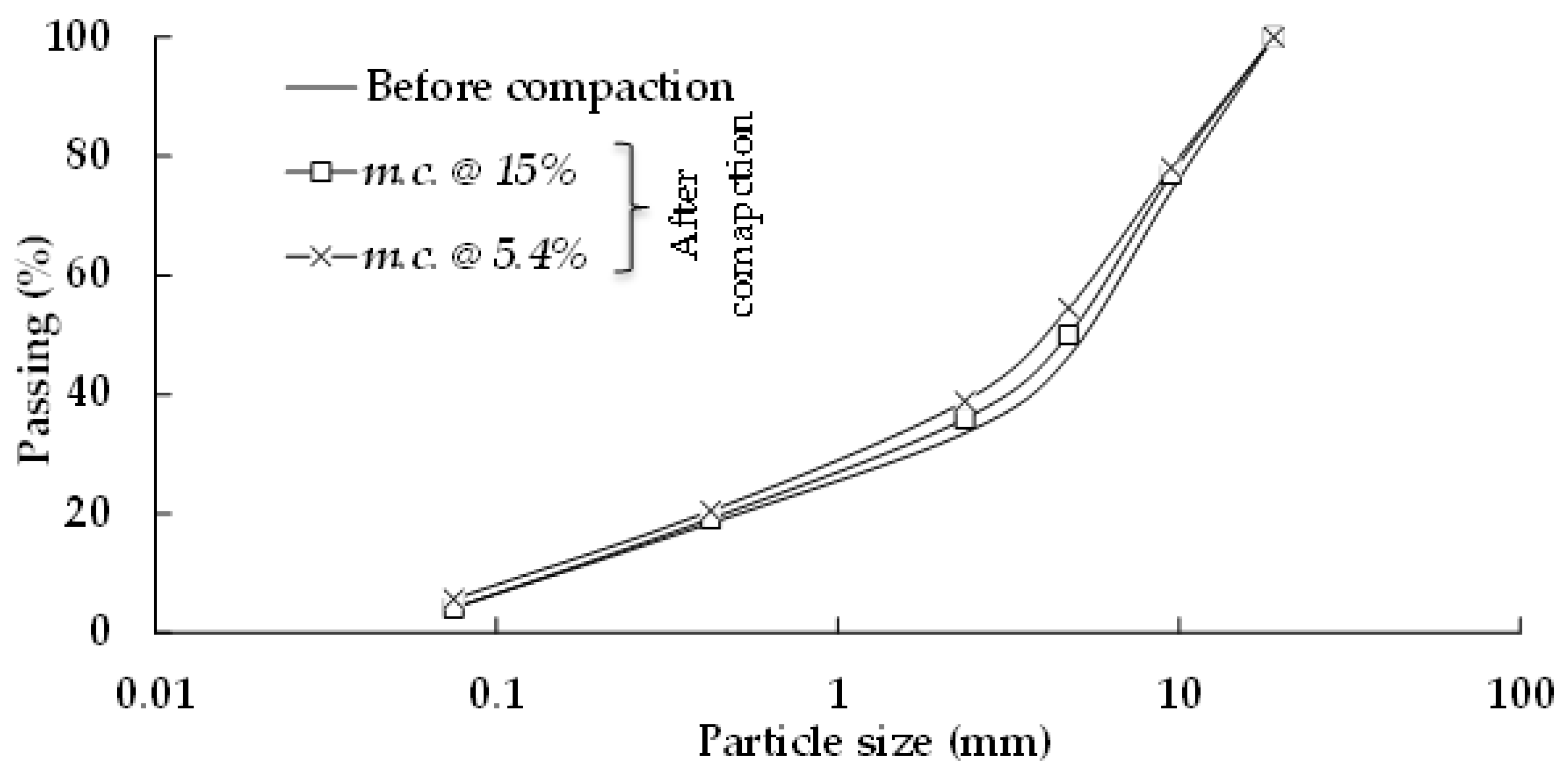
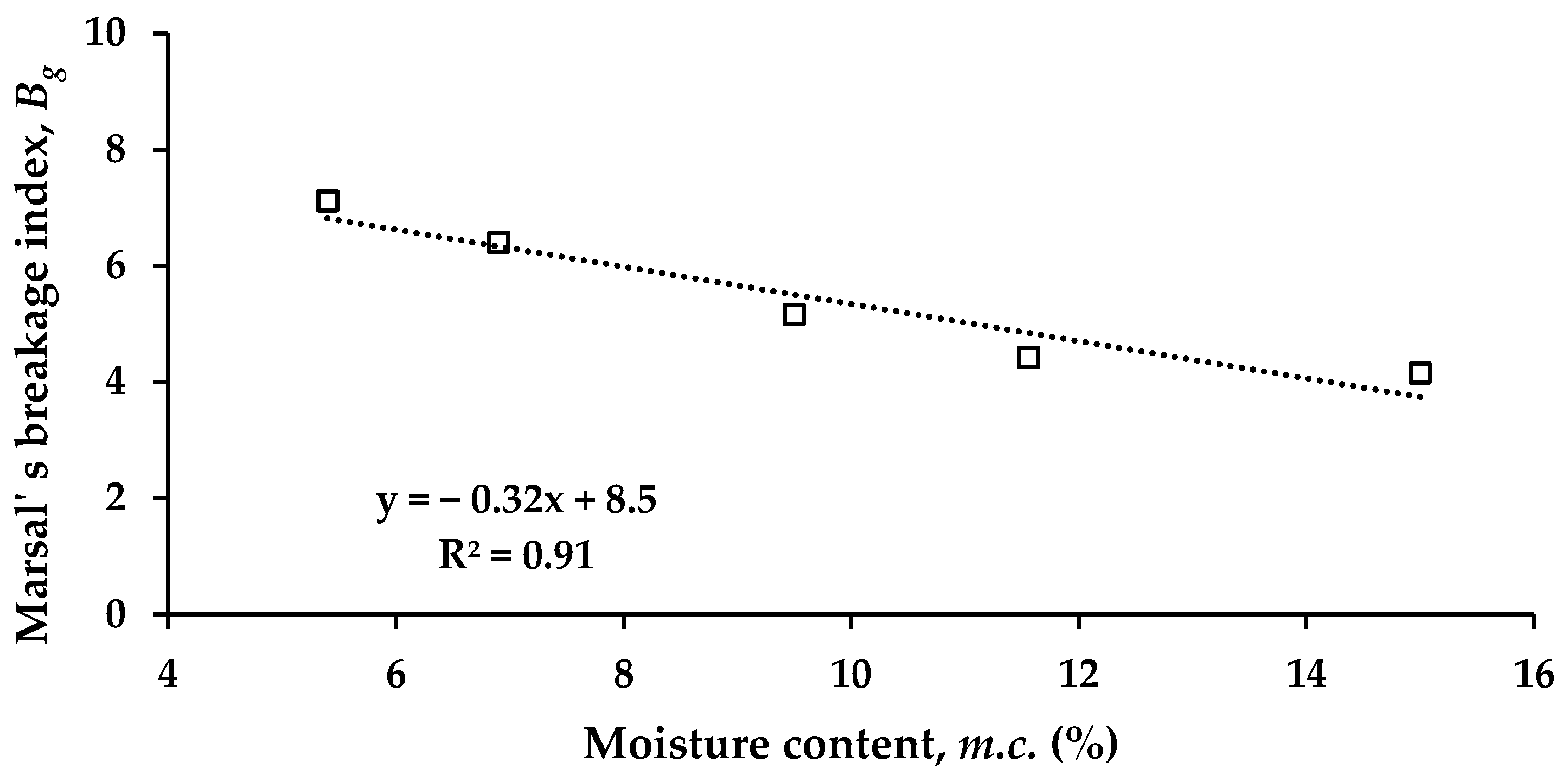
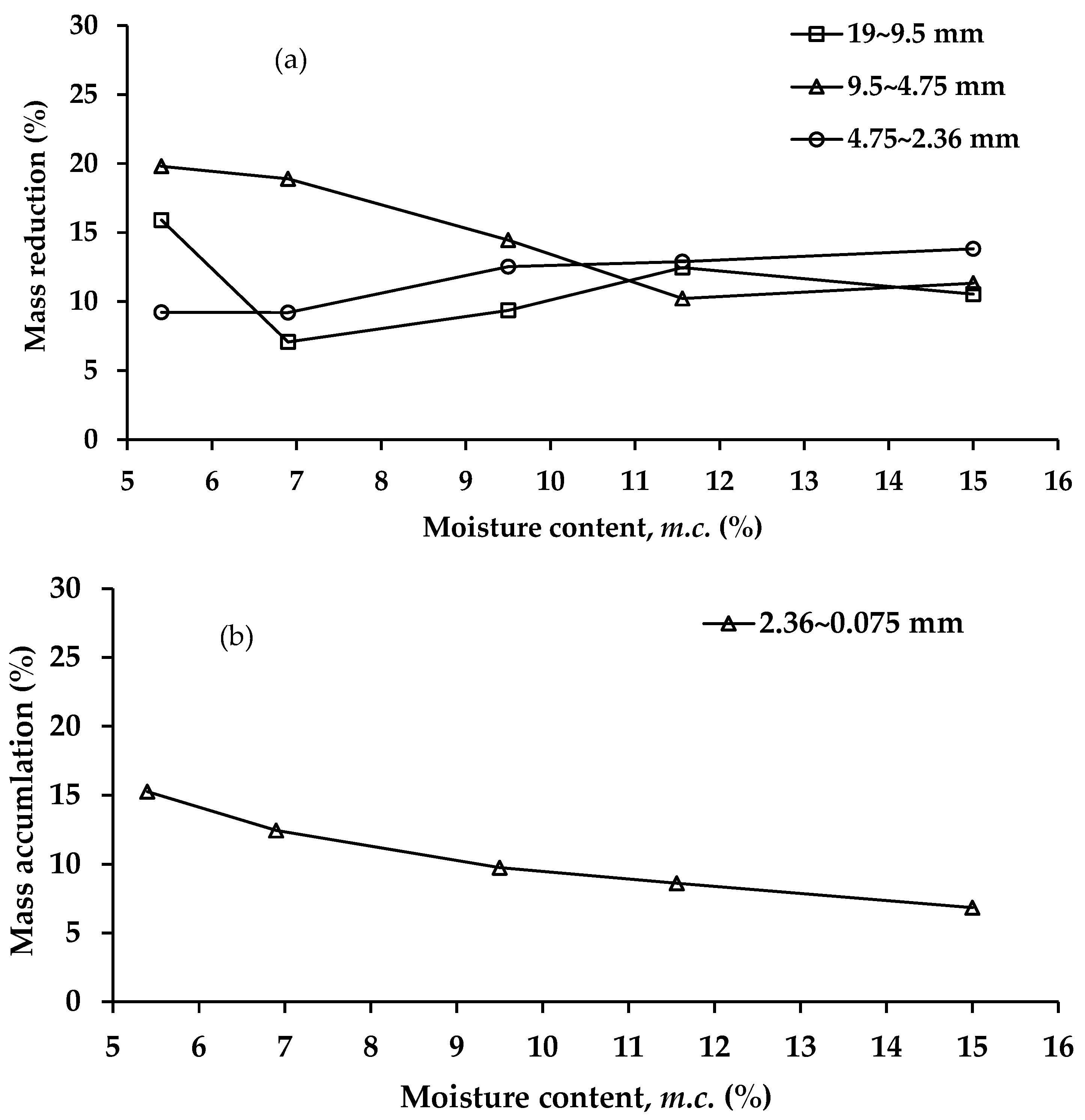
3.1. Particle Breakage after Compaction
3.2. Static Triaxial Test
3.3. Cyclic Triaxial Test
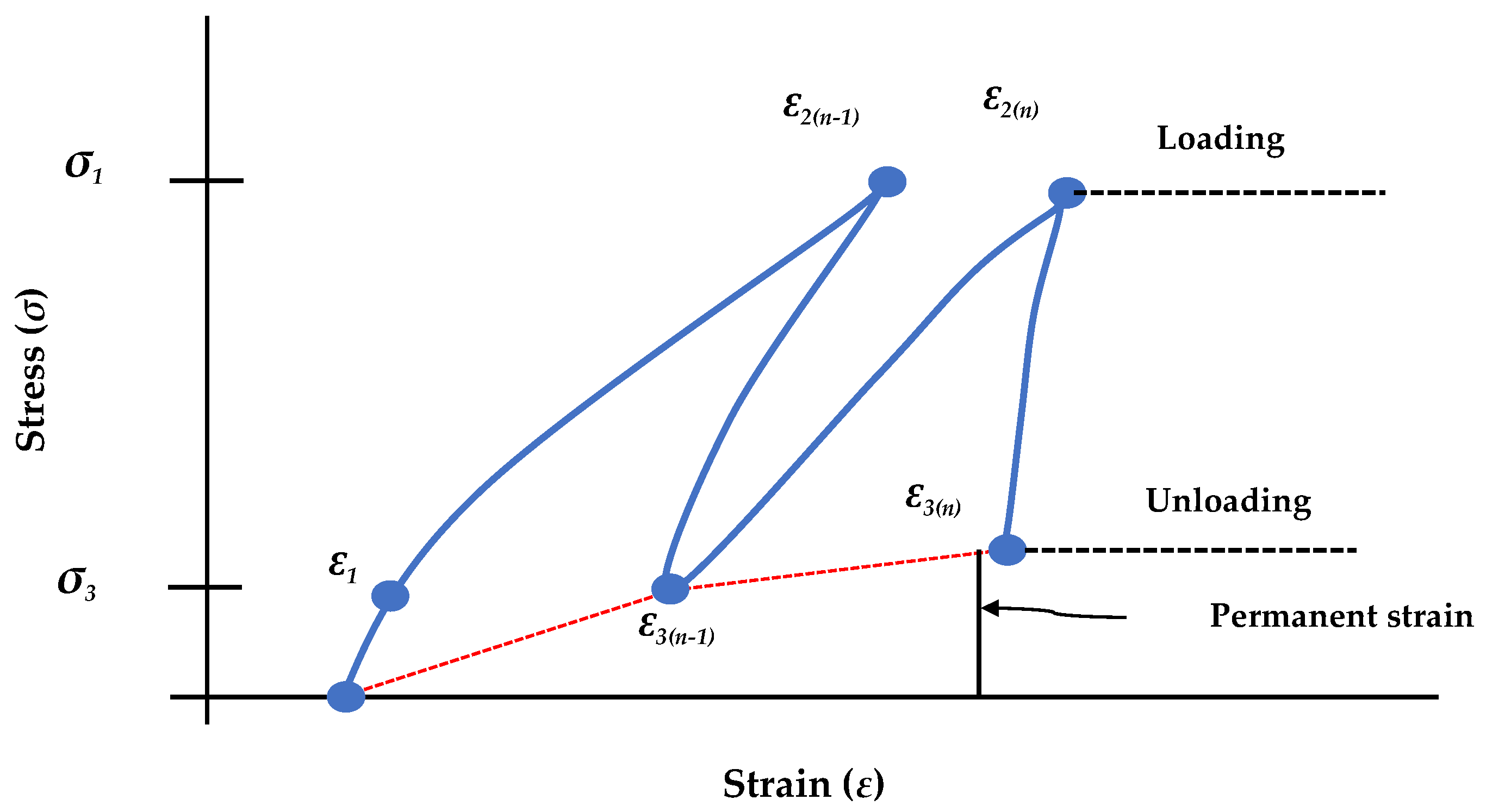
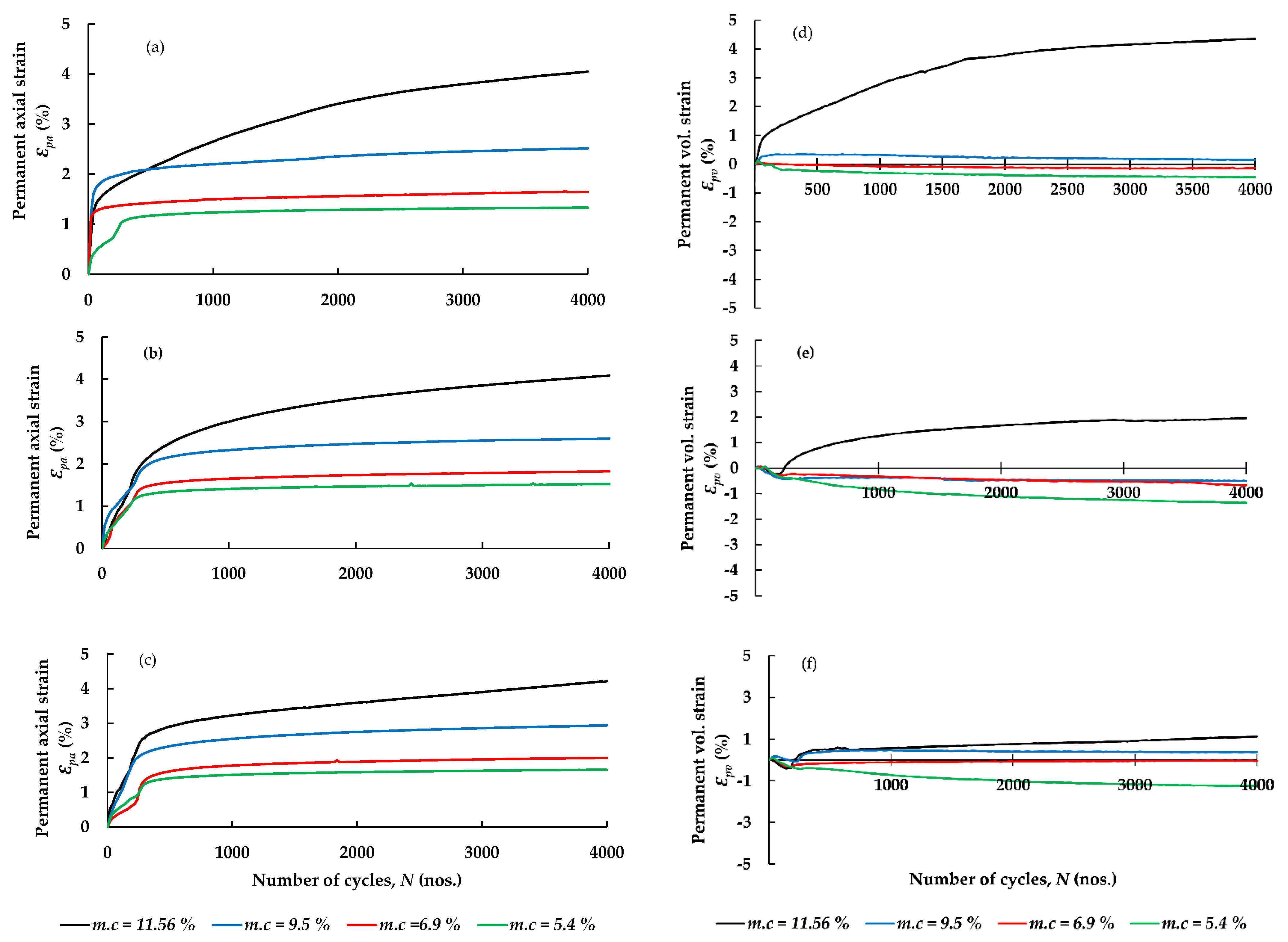
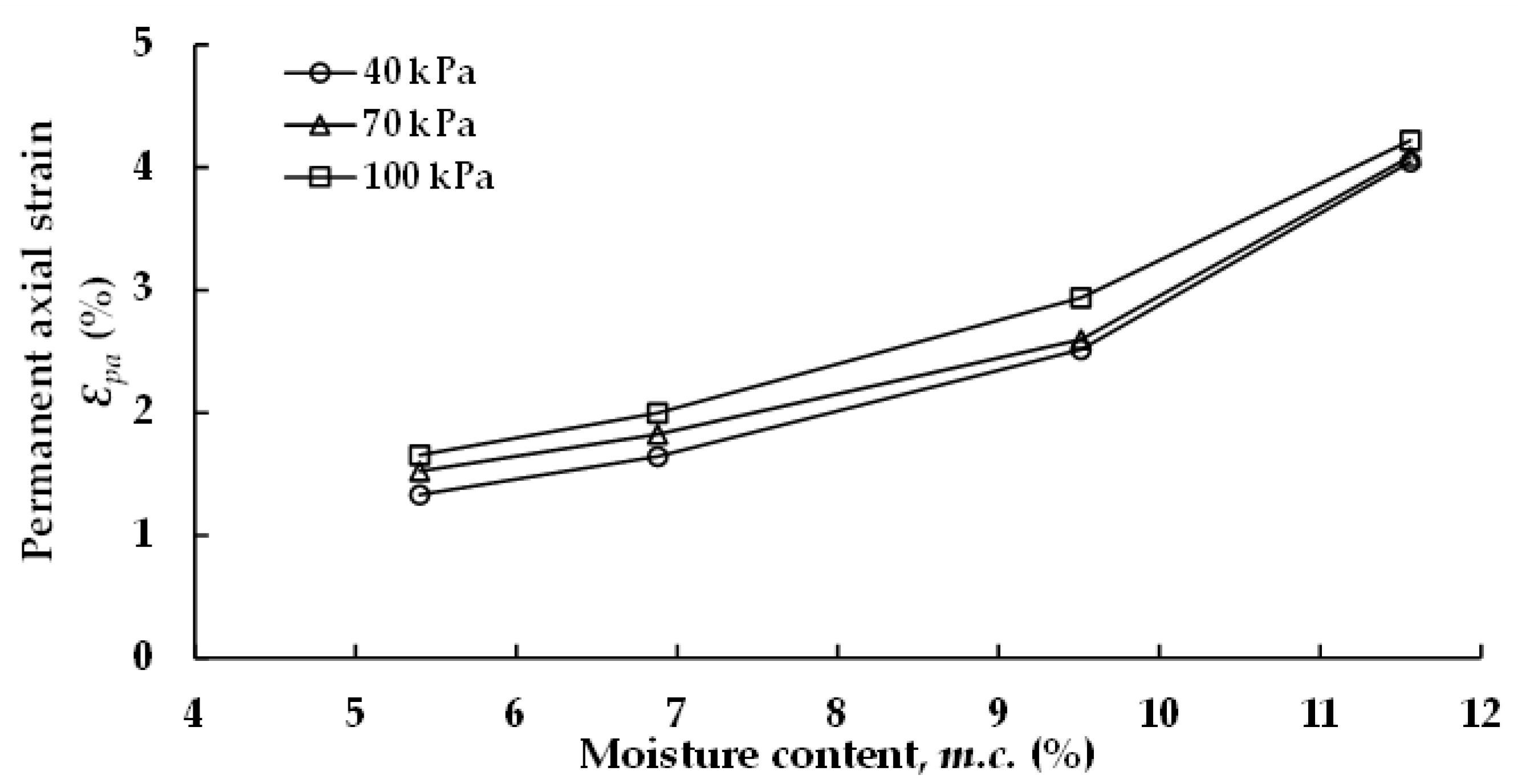
3.3.1. Permanent and Volumetric Axial Strains
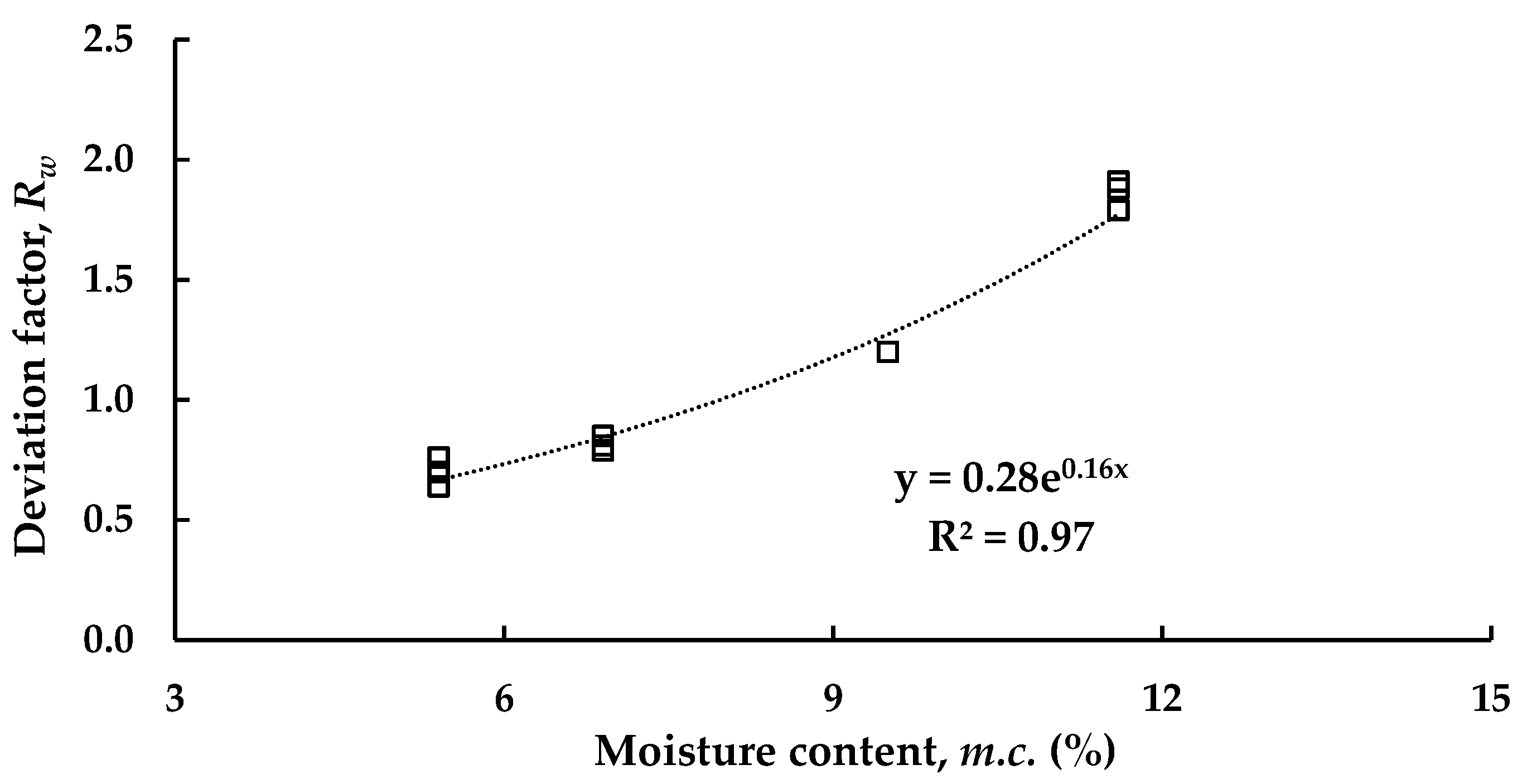
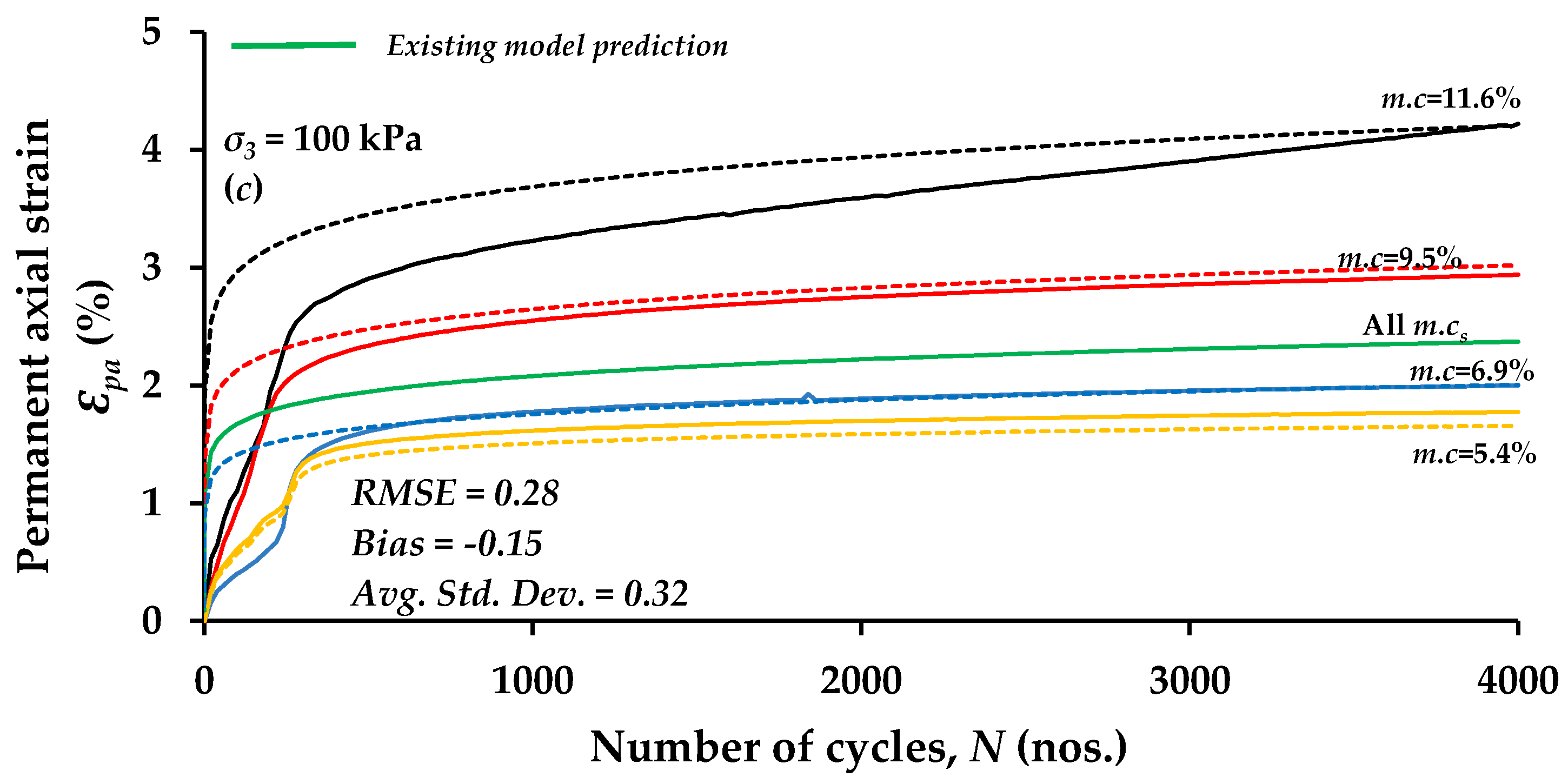
3.3.2. Permanent Deformation Model
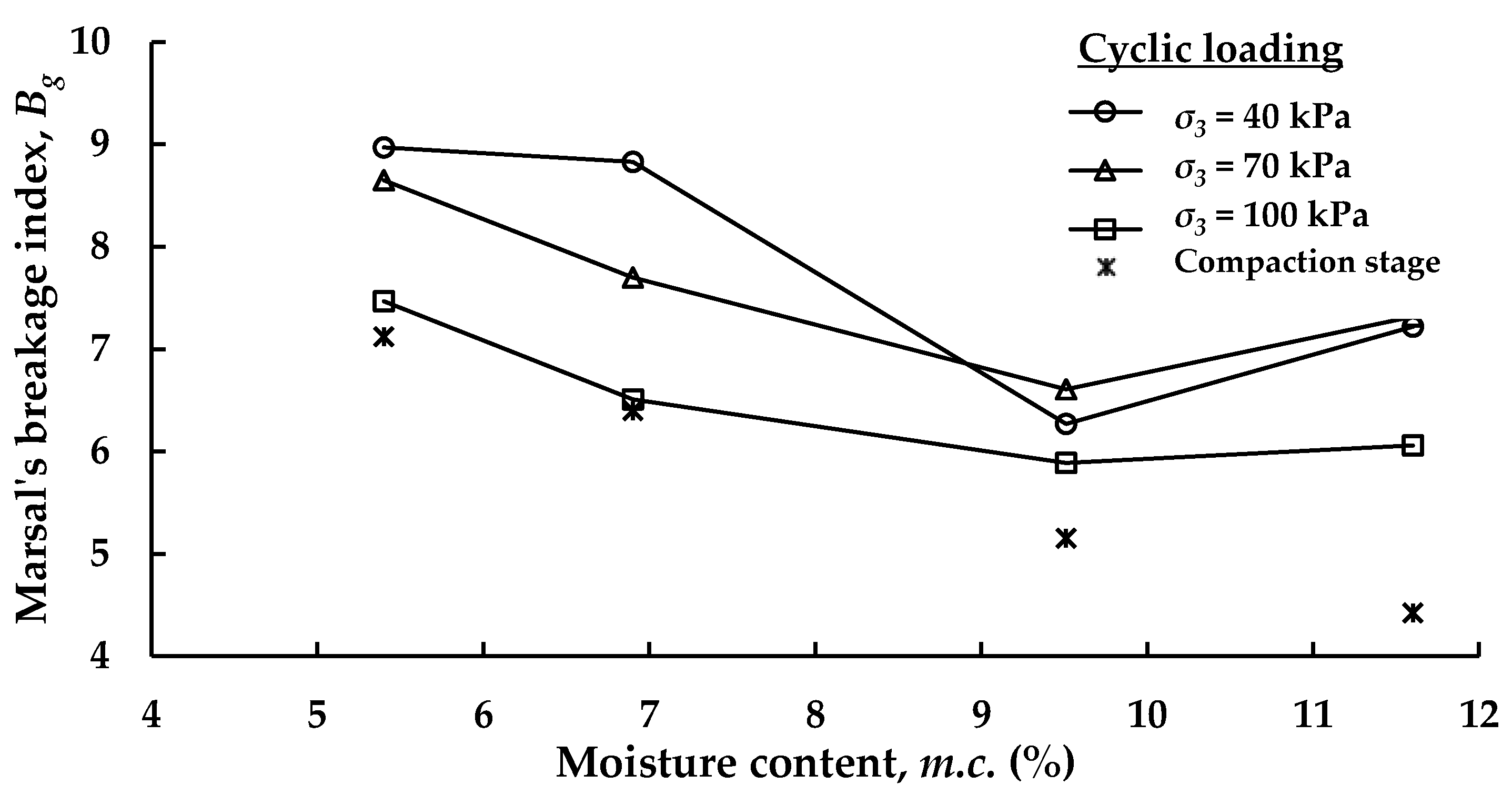
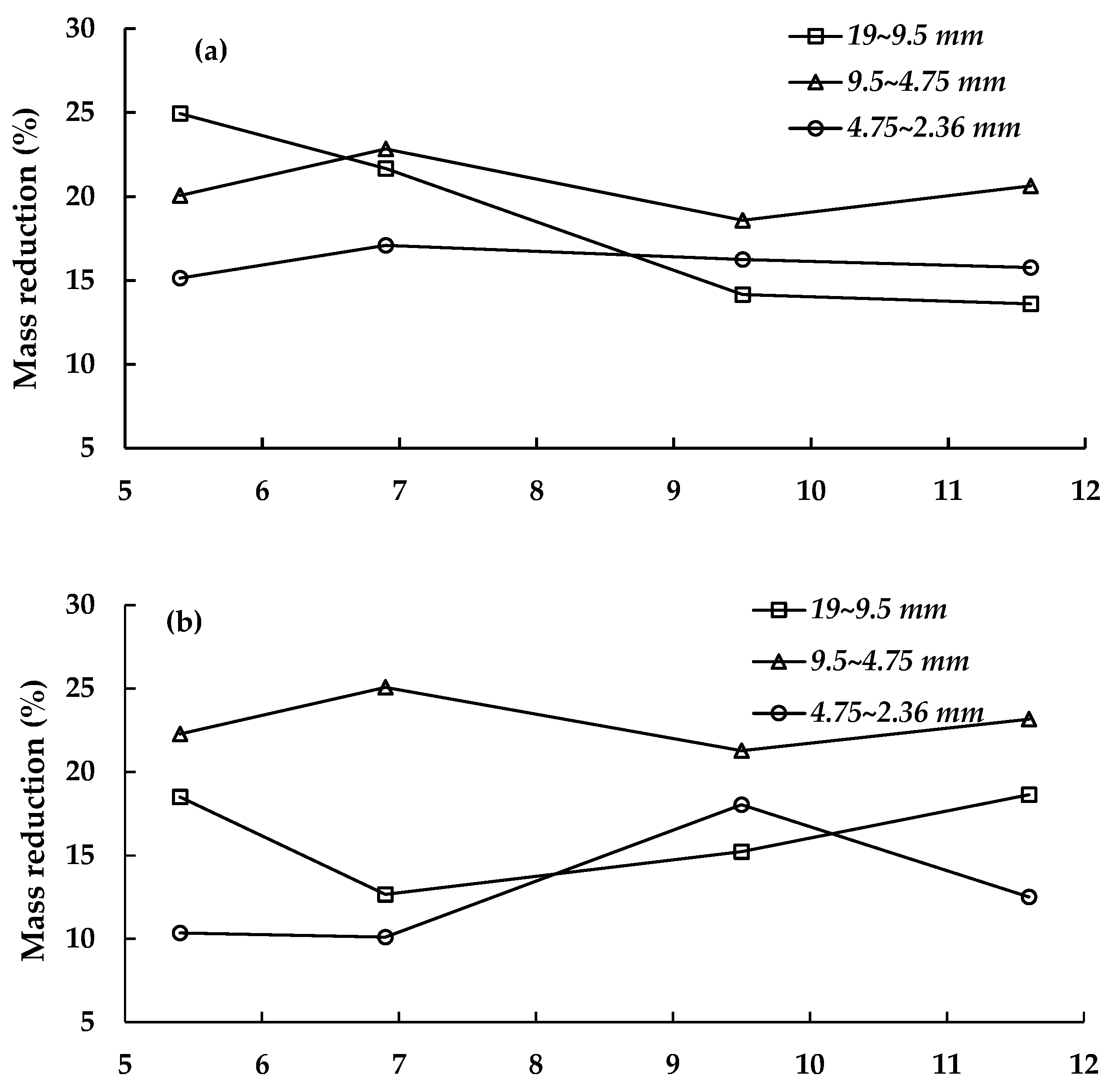
3.3.3. Particle Breakage after Cyclic Loading
4. Conclusions
- (1)
- The compaction moisture content has a significant effect on particle breakage. The results of both Marsal’s breakage ratio and mass reduction/accumulation showed that the particle breakage of RCA decreased with increasing moisture content.
- (2)
- The coloring technique introduced in this study showed that a coarse fraction of 9.5~4.75 mm was more breakable than the other fractions, mainly resulting in mass accumulations of fine fractions, suggesting a weak link in the particle size range, which needs to be adjusted.
- (3)
- The results from cyclic loading tests indicated that the moisture content of tested specimens had a considerable effect on the accumulation of permanent strain, and the increase in moisture content of tested specimens caused a decrease in stiffness, and consequently, an increase in permanent deformation in pavements.
- (4)
- Overall, the breakage and permanent deformation show opposite trends to each other.
- (5)
- Based on the experimental results, a model for evaluating a permanent axial strain was amended by newly incorporating it into a deviation factor induced by moisture content. The model fitted the experimental data well, suggesting that it would be useful to have a quantitative estimation of the permanent axial strain of RCA under cyclic loading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| εa | Axial strain [%] |
| σ3 | Confining pressure [kPa] |
| σd | Deviatoric stress [kPa] |
| σdmax | Maximum deviatoric stress [kPa] |
| σdmin | Minimum deviatoric stress [kPa] |
| εpa | Permanent axial strain [%] |
| εpv | Permanent volumetric strain [%] |
| εv | Volumetric strain [%] |
| ΔWk | Change in weight retained [g] |
| Wkf | Final weight retained [g] |
| Wki | Initial weight retained [g] |
| Br | Marsal’s breakage index (no.) |
| m.c. | Moisture content [%] |
| po | Normalizing stress [kPa] |
| N | Number of cycles (no.) |
| PSD | Particle size distribution |
| RCA | Recycled concrete aggregate |
References
- Jayakody, S.; Gallage, C.; Kumar, A. Assessment of recycled concrete aggregates as a pavement material. Geomech. Eng. 2014, 6, 235–248. [Google Scholar] [CrossRef]
- Cardoso, R.; Silva, R.V.; de Brito, J.; Dhir, R. Use of recycled aggregates from construction and demolition waste in geotechnical applications: A literature review. Waste Manag. 2016, 49, 131–145. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, K.; Shi, C.; Chu, H.; Guo, H.; Song, B.; Ding, Y.; Guan, X.; Zhu, J.; Zhang, H.; Wang, Y.; et al. An overview on the efficiency of different pretreatment techniques for recycled concrete aggregate. J. Clean. Prod. 2016, 263, 121264. [Google Scholar] [CrossRef]
- Tawk, M.; Qi, Y.; Indraratna, B.; Rujikiatkamjorn, C.; Heitor, A. Behavior of a Mixture of Coal Wash and Rubber Crumbs under Cyclic Loading. J. Mater. Civ. Eng. 2021, 33, 21–54. [Google Scholar] [CrossRef]
- Abukhettala, M. Use of recycled materials in road construction. In Proceedings of the 2nd International Conference on Civil, Structural and Transportation Engineering, ICCSTE’16, Ottawa, ON, Canada, 5–6 May 2016; p. 138. [Google Scholar]
- Teijón-López-Zuazo, E.; Vega-Zamanillo, Á.; Calzada-Pérez, M.Á.; Robles-Miguel, Á. Use of Recycled Aggregates Made from Construction and Demolition Waste in Sustainable Road Base Layers. Sustainability 2020, 12, 6663. [Google Scholar] [CrossRef]
- Shi, C.; Li, Y.; Zhang, J.; Li, W.; Chong, L.; Xie, Z. Performance enhancement of recycled concrete aggregate–a review. J. Clean. Prod. 2016, 112, 466–472. [Google Scholar] [CrossRef]
- Gu, F.; Zhang, Y.; Luo, X.; Sahin, H.; Lytton, R.L. Characterization and Prediction of Permanent Deformation Properties of Unbound Granular Materials for Pavement ME Design. Constr. Build. Mater. 2017, 155, 584–592. [Google Scholar] [CrossRef]
- Alnedawi, A.; Rehman, M.A. Recycled Concrete Aggregate as Alternative Pavement Materials: Experimental and Parametric Study. J. Transp. Eng. Part B Pavements 2021, 147. [Google Scholar] [CrossRef]
- Alnedawi, A.; Nepal, K.P.; Al-Ameri, R.; Alabdullah, M. Effect of vertical stress rest period on deformation behavior of unbound granular materials: Experimental and numerical investigations. J. Rock Mech. Geotech. Eng. 2018, 11, 172–180. [Google Scholar] [CrossRef]
- Xiao, Y.; Zheng, K.; Chen, L.; Mao, J. Shakedown analysis of cyclic plastic deformation characteristics of unbound granular materials under moving wheel loads. Constr. Build. Mater. 2018, 167, 457–472. [Google Scholar] [CrossRef]
- Piratheepan, J.; Gnanendran, C.T. Back-calculation of resilient modulus of lightly stabilized granular base materials from cyclic load testing facility. J. Mater. Civ. Eng. 2012, 25, 1068–1076. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Gabryś, K.; Soból, E.; Szymański, A. Deformation behavior of recycled concrete aggregate during cyclic and dynamic loading laboratory tests. Materials 2016, 9, 780. [Google Scholar] [CrossRef] [PubMed]
- El-Ashwah, A.S.; Awed, A.M.; El-Badawy, S.M.; Gabr, A.R. A new approach for developing resilient modulus master surface to characterize granular pavement materials and subgrade soils. Constr. Build. Mater. 2019, 194, 372–385. [Google Scholar] [CrossRef]
- Zeghal, M. The impact of grain crushing on road performance. Geotech. Geol. Eng. 2009, 27, 549–558. [Google Scholar] [CrossRef][Green Version]
- Arulrajah, A.; Piratheepan, J.; Ali MM, Y.; Bo, M.W. Geotechnical properties of recycled concrete aggregate in pavement sub-base applications. Geotech. Test. J. 2012, 35, 743–751. [Google Scholar] [CrossRef]
- Arulrajah, A.; Piratheepan, J.; Disfani, M.M.; Bo, M.W. Geotechnical and geo-environmental properties of recycled construction and demolition materials in pavement subbase applications. J. Mater. Civ. Eng. 2013, 25, 1077–1088. [Google Scholar] [CrossRef]
- Arulrajah, A.; Piratheepan, J.; Disfani, M.M. Reclaimed asphalt pavement and recycled concrete aggregate blends in pavement subbases: Laboratory and field evaluation. J. Mater. Civ. Eng. 2014, 26, 349–357. [Google Scholar] [CrossRef]
- Aqil, U.; Tatsuoka, F.; Uchimura, T.; Lohani, T.N.; Tomita, Y.; Matsushima, K. Strength and deformation characteristics of recycled concrete aggregate as a backfill material. Soils Found. 2005, 45, 53–72. [Google Scholar] [CrossRef]
- Gobieanandh, V.; Jayakody, S. Evaluate the strength of cement treated recycled construction and demolition aggregates as a pavement material. In Proceedings of the 7th International Conference on Sustainable Built Environment, Kandy, Sri Lanka, 16–18 December 2016. [Google Scholar]
- JRA-RM-30; Gradation Standard for Recycled Materials. Japan Road Association (JRA): Tokyo, Japan, 2010. (In Japanese)
- ASTM D 1557; Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort. American Society for Testing and Materials: West Conshohocken, PA, USA, 2007.
- JIS A 1210; Soil Compaction Test Method by Compaction: Test Method for Soil Compaction Using a Rammer. Japanese Standards Association: Tokyo, Japan, 2020. (In Japanese)
- Frost, M.W.; Fleming, P.R.; Rogers, C.D.F. Threshold stress and asymptotic stiffness of UK clays in the repeated load triaxial test. In Proceedings of the 6th International Conference on the Bearing Capacity of Roads and Airfields, Lisbon, Portugal, 24–26 June 2002; pp. 1099–1108. [Google Scholar]
- Marsal, R.J. Large scale testing of rockfill materials. J. Soil Mech. Found. Div. ASCE 1967, 93, 27–43. [Google Scholar] [CrossRef]
- Tawk, M.; Indraratna, B.; Rujikiatkamjorn, C.; Heitor, A. Review on compaction and shearing induced breakage of granular material. Geotech. Transp. Infrastruct. 2019, 2, 259–270. [Google Scholar]
- Sun, Y.; Nimbalkar, S.; Chen, C. Particle breakage of granular materials during sample preparation. J. Rock Mech. Geotech. Eng. 2019, 11, 417–422. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Tomita, Y.; Iguchi, Y.; Harikawa, D. Strength and stiffness of compacted crushed concrete aggregate. Soils Found. 2013, 53, 835–852. [Google Scholar] [CrossRef]
- Kayani, J.Q. Feasibility for Use of Recycled Graded Concrete Aggregate and Crushed Autoclaved Lightweight Concrete (ALC) in Permeable Pavement System. Master’s Thesis, Saitama University, Saitama, Japan, 2018. [Google Scholar]
- Cerni, G.; Cardone, F.; Virgili, A.; Camilli, S. Characterization of permanent deformation behavior of unbound granular materials under repeated triaxial loading. Constr. Build. Mater. 2012, 28, 79–87. [Google Scholar] [CrossRef]
- Lekarp, F.; Richardson, I.R.; Dawson, A. Influences on permanent deformation behavior of unbound granular materials. Transp. Res. Record. 1996, 1547, 68–75. [Google Scholar] [CrossRef]
- Ullidtz, P. Modelling of granular materials using discrete element method. In Proceedings of the 8th International Conference on Asphalt Pavements, Seattle, WA, USA, 10–14 August 1997; pp. 757–769. [Google Scholar]
- Tutumluer, E. NCHRP Synthesis of Highway Practice 445: Practices for Unbound in Aggregate Pavement Layers; Transportation Research Board of the National Academies: Washington, DC, USA, 2013. [Google Scholar]
- Indraratna, B.; Lackenby, J.; Christie, D. Effect of confining pressure on the degradation of ballast under cyclic loading. Geotechnique 2005, 55, 325–328. [Google Scholar] [CrossRef]





| Mold | Rammer | ||
|---|---|---|---|
| Height (cm) | 15 | Drop height (cm) | 45 |
| Diameter (cm) | 7.5 | Weight (kg) | 4.5 |
| Test Conditions | |
|---|---|
| Compaction energy [kJ/m3] | 2700 |
| Moisture content [%] | 5.4, 6.9, 9.5, 11.56, 15 (15% for compaction only) |
| Frequency [Hz] | 0.2 |
| Number of cycles [Nos.] | 4000 |
| Confining pressure [kPa] | 40, 70, 100 |
| Max. cyclic deviatoric stress [kPa] | 450, 580, 850 |
| Min. cyclic deviatoric stress [kPa] | 45, 58, 85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.K.H.; Uchimura, T.; Kawamoto, K. Permanent Deformation and Breakage Response of Recycled Concrete Aggregates under Cyclic Loading Subject to Moisture Change. Sustainability 2022, 14, 5427. https://doi.org/10.3390/su14095427
Shah SKH, Uchimura T, Kawamoto K. Permanent Deformation and Breakage Response of Recycled Concrete Aggregates under Cyclic Loading Subject to Moisture Change. Sustainability. 2022; 14(9):5427. https://doi.org/10.3390/su14095427
Chicago/Turabian StyleShah, Syed Kamran Hussain, Taro Uchimura, and Ken Kawamoto. 2022. "Permanent Deformation and Breakage Response of Recycled Concrete Aggregates under Cyclic Loading Subject to Moisture Change" Sustainability 14, no. 9: 5427. https://doi.org/10.3390/su14095427
APA StyleShah, S. K. H., Uchimura, T., & Kawamoto, K. (2022). Permanent Deformation and Breakage Response of Recycled Concrete Aggregates under Cyclic Loading Subject to Moisture Change. Sustainability, 14(9), 5427. https://doi.org/10.3390/su14095427







