Vision Robot Path Control Based on Artificial Intelligence Image Classification and Sustainable Ultrasonic Signal Transformation Technology
Abstract
:1. Introduction
2. Sustainable Artificial Intelligence (SAI) Controller Design
2.1. ART Controller Design
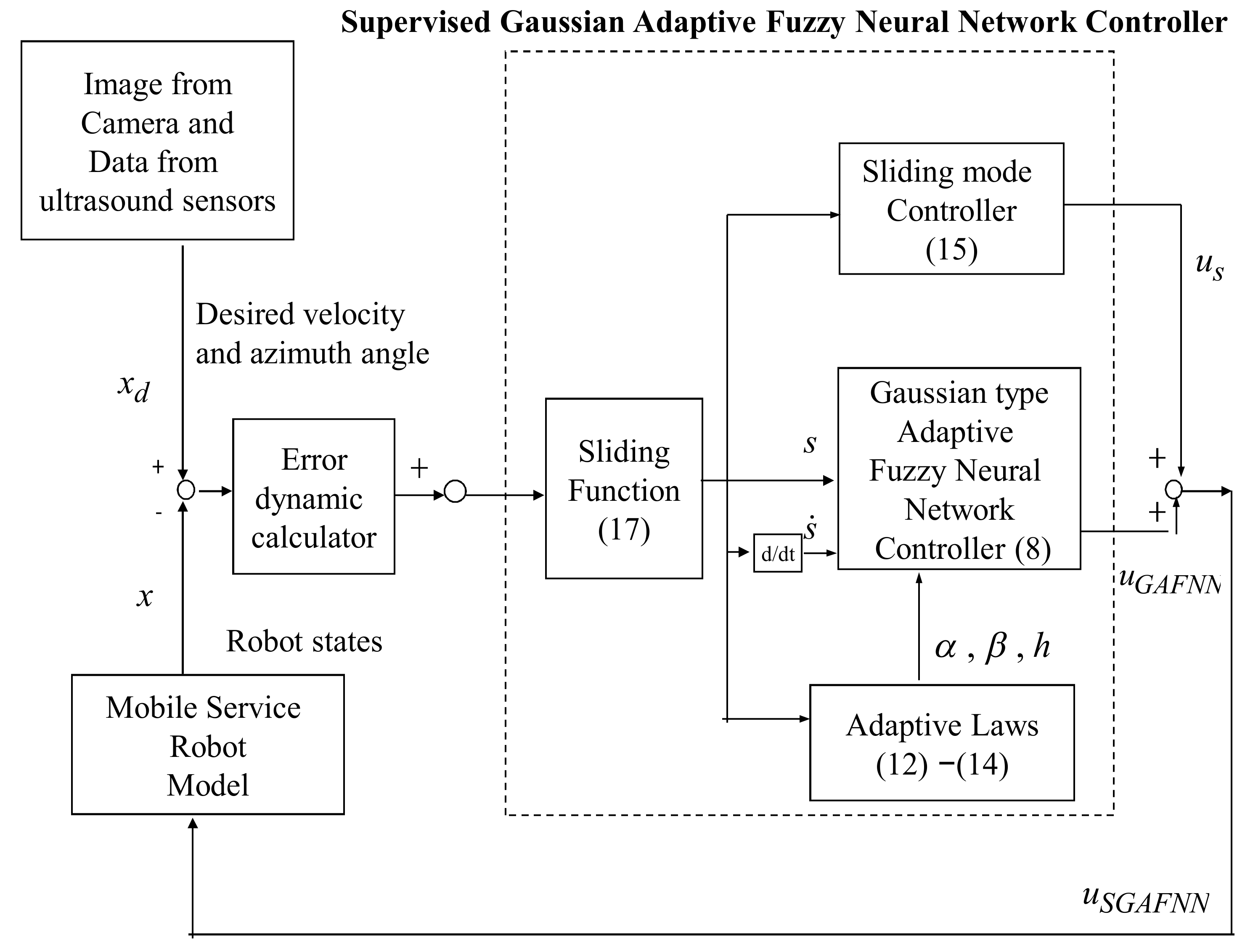
2.2. Supervised Gaussian Adaptive Fuzzy Neural Network (SGAFNN) Controller Design
2.3. Sliding Mode Controller Design
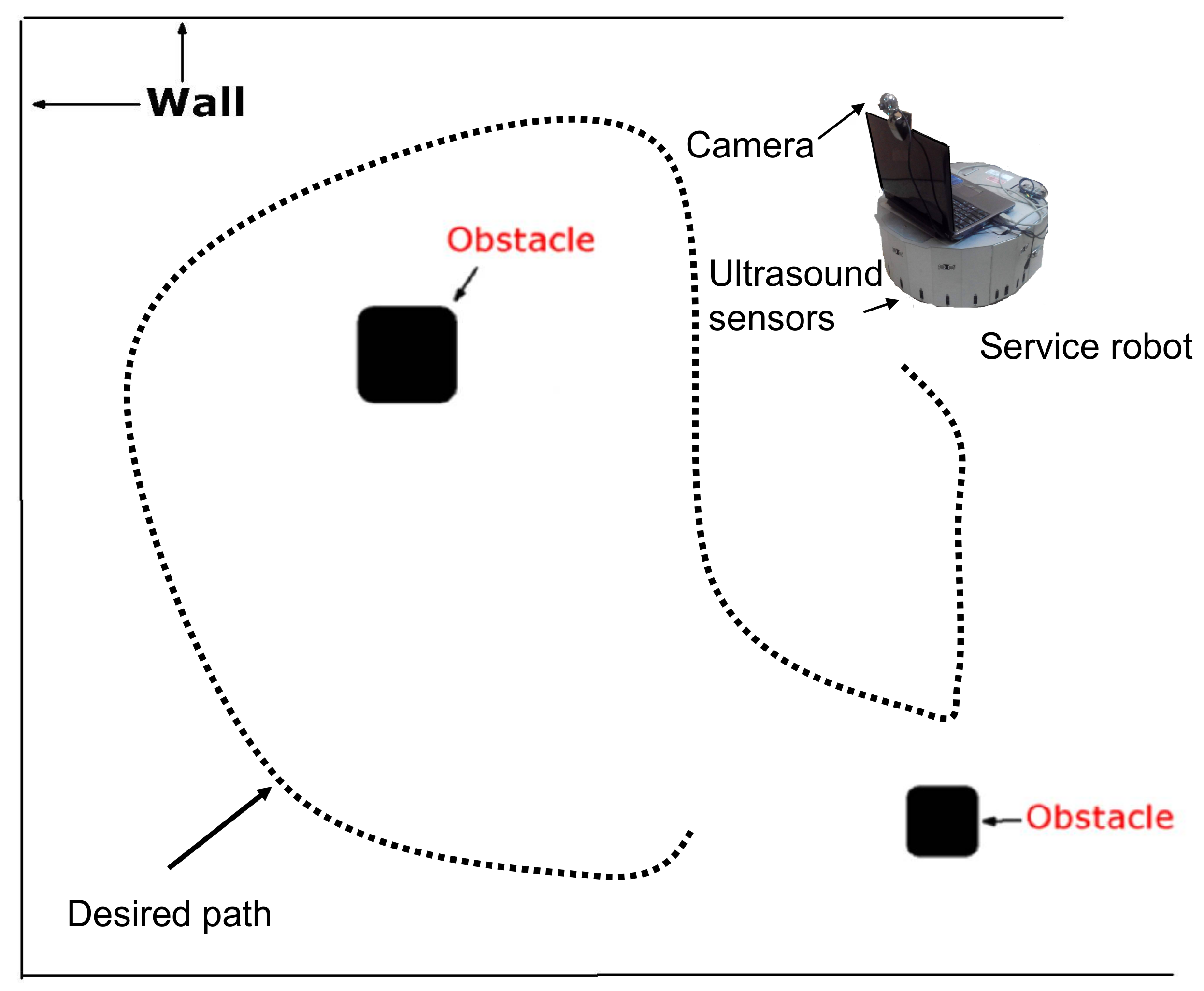
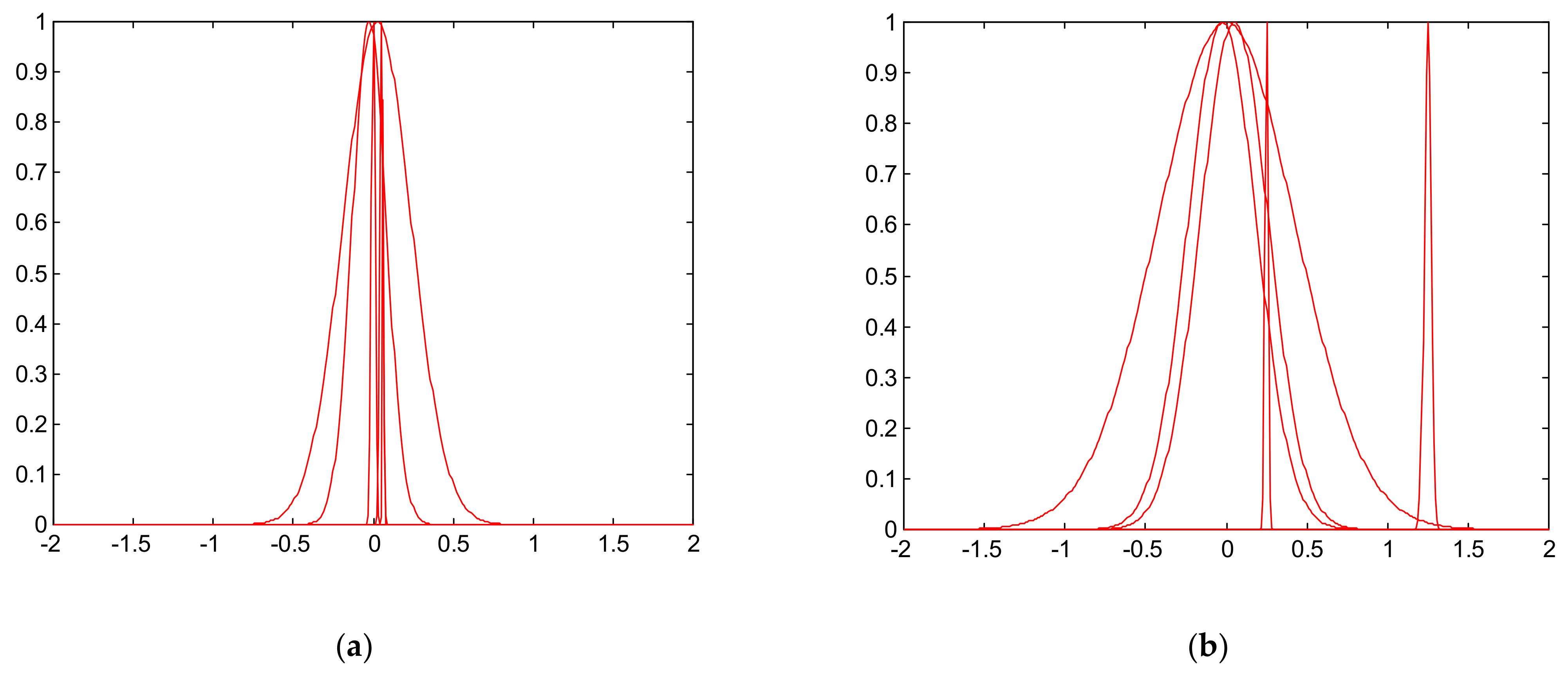
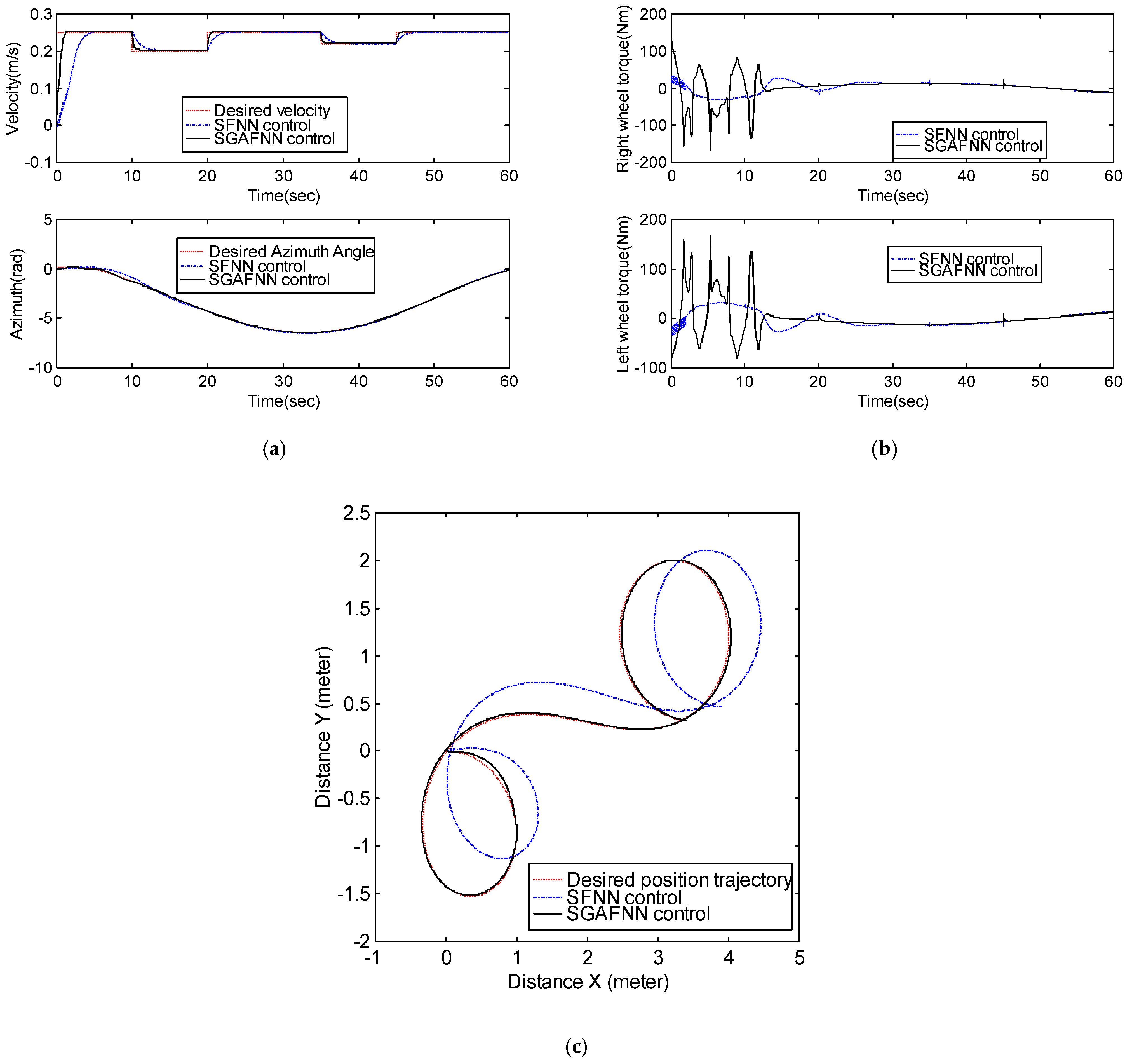
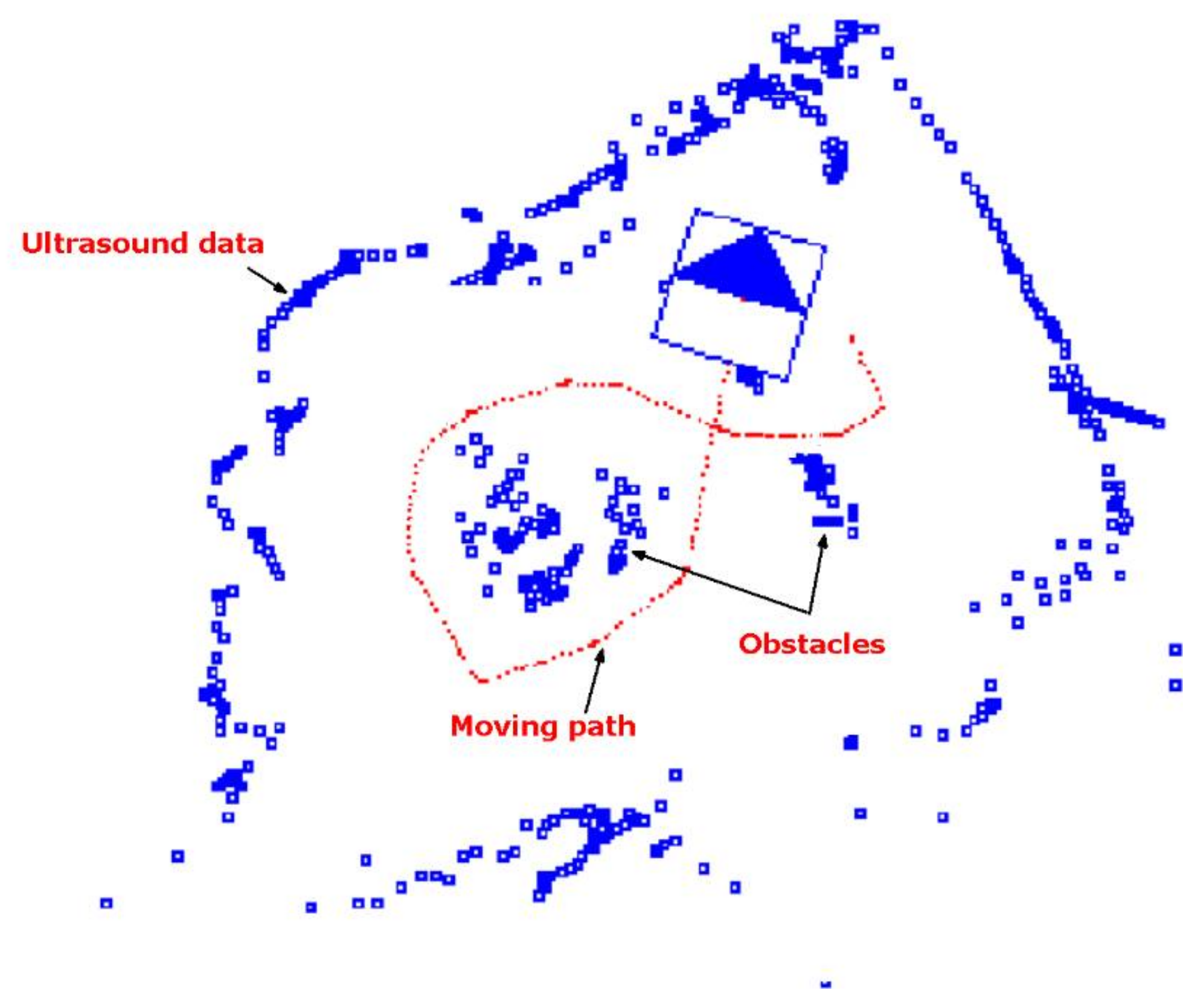
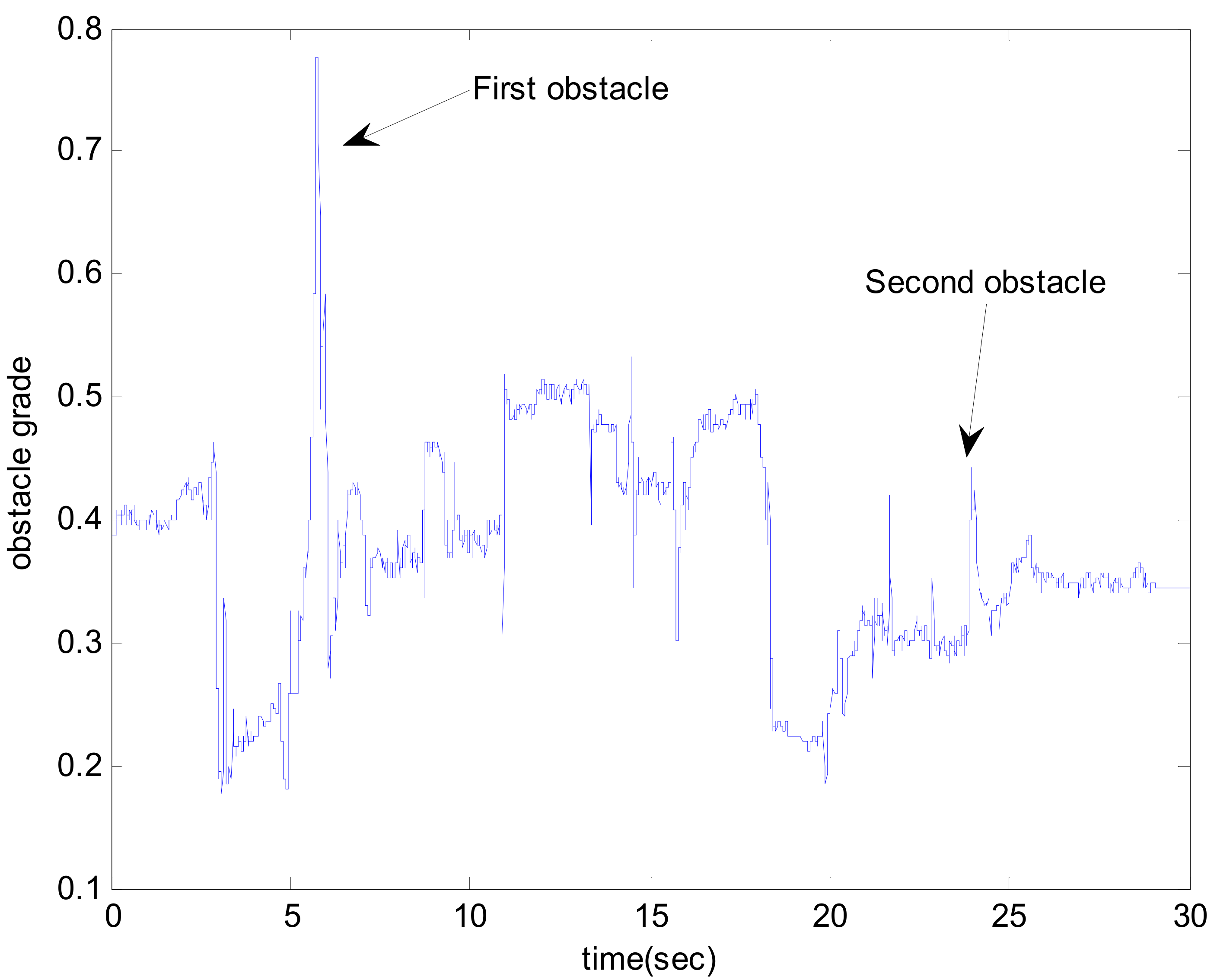
3. Simulation Result
4. Practical Evaluations
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full text meaning |
| ART | Adaptive Resonance Theory |
| CNN | Convolution neural network |
| PSO | Particle swarm optimization |
| SGAFNN | Supervised Gaussian adaptive fuzzy neural network |
| AFNN | Adaptive Fuzzy neural network |
| FNN | Fuzzy neural network |
| SC | Sliding mode controller |
| SAI | Sustainable artificial intelligence |
| SFNN | Sliding mode fuzzy neural network |
References
- Carpenter, G.A.; Grossberg, S. ART 2: Self-organization of stable category recognition codes for analog input patterns. Appl. Opt. 1987, 26, 4919–4930. [Google Scholar] [CrossRef] [PubMed]
- Petridis, V.; Kaburlasos, V. Fuzzy Lattice Neural Network (FLNN): A hybrid model for learning. IEEE Trans. Neural Netw. 1998, 9, 877–890. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, G.A.; Grossberg, S.; Markuzon, N.; Reynolds, J.H.; Rosen, D.B. Fuzzy ARTMAP: A neural network architecture for incremental supervised learning of analog multidimensional maps. IEEE Trans. Neural Netw. 1992, 3, 698–713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massey, L. Soft-clustering and improved stability for adaptive resonance theory neural networks. Soft Comput. 2008, 12, 657–665. [Google Scholar] [CrossRef]
- Heins, L.G.; Tauritz, D.R. Adaptive Resonance Theory (ART): An Introduction. 1995. Available online: https://www.researchgate.net/publication/247749347_Adaptive_Resonance_Theory_ART_An_Introduction (accessed on 7 April 2022).
- Parham, N.; Loo, C.K.; Manjeevan, S. Semi-supervised topo-Bayesian ARTMAP for noisy data. Appl. Soft Comput. 2018, 62, 134–147. [Google Scholar] [CrossRef]
- Amutha, A.L.; Annie Uthra, R.; Preetha Roselyn, J.; Golda Brunet, R. Classification of Anomalies in Multivariate Streaming Phasor Measurement Unit Data Using Supervised and Clustering Ensemble Techniques. In Proceedings of the 2021 5th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 2–4 December 2021; pp. 1460–1466. [Google Scholar]
- Rashid, M.; Khan, M.A.; Alhaisoni, M.; Wang, S.-H.; Naqvi, S.R.; Rehman, A.; Saba, T. A Sustainable Deep Learning Framework for Object Recognition Using Multi-Layers Deep Features Fusion and Selection. Sustainability 2020, 12, 5037. [Google Scholar] [CrossRef]
- Nalpantidis, L.; Gasteratos, A. Stereovision-based fuzzy obstacle avoidance method. Int. J. Humanoid Robot. 2011, 8, 169–183. [Google Scholar] [CrossRef]
- Mon, Y.J. WSN-based indoor location identification system (LIS) applied to vision robot designed by fuzzy neural network. J. Digit. Inf. Manag. 2015, 13, 39–44. [Google Scholar]
- Wang, H.; Ren, Y.; Meng, Z. A Farm Management Information System for Semi-Supervised Path Planning and Autonomous Vehicle Control. Sustainability 2021, 13, 7497. [Google Scholar] [CrossRef]
- Das Sharma, K.; Chatterjee, A.; Rakshit, A. A PSO—Lyapunov Hybrid Stable Adaptive Fuzzy Tracking Control Approach for Vision-Based Robot Navigation. IEEE Trans. Instrum. Meas. 2012, 61, 1908–1914. [Google Scholar] [CrossRef]
- Mon, Y.J. Machine vision based sliding fuzzy-PDC control for obstacle avoidance and object recognition of service robot platform. J. Intell. Fuzzy Syst. 2015, 28, 1119–1126. [Google Scholar] [CrossRef]
- DeSouza, G.; Kak, A. Vision for mobile robot navigation: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 237–267. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, K.; Tang, J.; Nakamura, M.; Koga, S.; Fukuda, T. A fuzzy-Gaussian neural network and its application to mobile robot control. IEEE Trans. Control Syst. Technol. 1996, 4, 193–199. [Google Scholar] [CrossRef]
- Mon, Y.J.; Lin, C.M. Supervisory fuzzy Gaussian neural network design for mobile robot path control. Int. J. Fuzzy Syst. 2013, 15, 142–148. [Google Scholar]
- Hmoud Al-Adhaileh, M.; Waselallah Alsaade, F. Modelling and Prediction of Water Quality by Using Artificial Intelligence. Sustainability 2021, 13, 4259. [Google Scholar] [CrossRef]
- Li, Z. Tension control system design of a filament winding structure based on fuzzy neural network. Eng. Rev. 2015, 35, 9–17. [Google Scholar]
- David, J.; Brom, P.; Starý, F.; Bradáč, J.; Dynybyl, V. Application of Artificial Neural Networks to Streamline the Process of Adaptive Cruise Control. Sustainability 2021, 13, 4572. [Google Scholar] [CrossRef]
- Nguyen, T.-B.-T.; Liao, T.-L.; Yan, J.-J. Adaptive Sliding Mode Control of Chaos in Permanent Magnet Synchronous Motor via Fuzzy Neural Networks. Math. Probl. Eng. 2014, 2014, 868415. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zhou, Q.; Yang, X.; Karimi, H.R. Robust Decentralized Adaptive Neural Control for a Class of Nonaffine Nonlinear Large-Scale Systems with Unknown Dead Zones. Math. Probl. Eng. 2014, 2014, 841306. [Google Scholar] [CrossRef] [Green Version]
- Seshagiri, S.; Khalil, H.K. Output feedback control of nonlinear systems using RBF neural networks. IEEE Trans. Neural Netw. 2000, 11, 69–79. [Google Scholar] [CrossRef] [Green Version]
- Owens, D.H. Iterative Learning Control: An Optimization Paradigm; Springer: Cham, Switzerland, 2015; ISBN 978-1-4471-6772-3. [Google Scholar]
- Wang, L.X. Adaptive Fuzzy Systems and Control: Design and Stability Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994; pp. 140–154. [Google Scholar]
- Slotine, J.-J.E.; Li, W.P. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Wu, L.; Su, X.; Shi, P. Sliding mode control with bounded L2 gain performance of Markovian jump singular time-delay systems. Automatica 2012, 48, 1929–1933. [Google Scholar] [CrossRef]
- Li, F.; Wu, L.; Shi, P.; Lim, C.-C. State estimation and sliding mode control for semi-Markovian jump systems with mismatched uncertainties. Automatica 2015, 51, 385–393. [Google Scholar] [CrossRef]
- Delavari, H. A novel fractional adaptive active sliding mode controller for synchronization of non-identical chaotic systems with disturbance and uncertainty. Int. J. Dyn. Control 2017, 5, 102–114. [Google Scholar] [CrossRef]
- Li, H.-R.; Jiang, Z.-B.; Kang, N. Sliding Mode Disturbance Observer-Based Fractional Second-Order Nonsingular Terminal Sliding Mode Control for PMSM Position Regulation System. Math. Probl. Eng. 2015, 2015, 370904. [Google Scholar] [CrossRef] [Green Version]
- Rahman, N.; Lee, M.C. Actual reaction force separation method of surgical tool by fuzzy logic based SMCSPO. Int. J. Control. Autom. Syst. 2015, 13, 379–389. [Google Scholar] [CrossRef]
- Bajrami, X.; Pajaziti, A.; Likaj, R.; Shala, A.; Berisha, R.; Bruqi, M. Control Theory Application for Swing Up and Stabilisation of Rotating Inverted Pendulum. Symmetry 2021, 13, 1491. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Jin, Z. The Approximation of the Nonlinear Singular System with Impulses and Sliding Mode Control via a Singular Polynomial Fuzzy Model Approach. Symmetry 2021, 13, 1409. [Google Scholar] [CrossRef]




| Step 1 | Set the initial network weightings. |
| Step 2 | Enter the vector values of the training data. |
| Step 3 | Calculate the match values for all categories of existing classifications. |
| Step 4 | Find the one with the largest matching value and calculate its similarity value with this category. |
| Step 5 | If it exceeds the similarity value, it belongs to this category, otherwise, it is a new generated category. |
| Step 6 | Return to step 2, repeat the calculation of all input data until they are finished and stop the calculation of the program. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mon, Y.-J. Vision Robot Path Control Based on Artificial Intelligence Image Classification and Sustainable Ultrasonic Signal Transformation Technology. Sustainability 2022, 14, 5335. https://doi.org/10.3390/su14095335
Mon Y-J. Vision Robot Path Control Based on Artificial Intelligence Image Classification and Sustainable Ultrasonic Signal Transformation Technology. Sustainability. 2022; 14(9):5335. https://doi.org/10.3390/su14095335
Chicago/Turabian StyleMon, Yi-Jen. 2022. "Vision Robot Path Control Based on Artificial Intelligence Image Classification and Sustainable Ultrasonic Signal Transformation Technology" Sustainability 14, no. 9: 5335. https://doi.org/10.3390/su14095335
APA StyleMon, Y.-J. (2022). Vision Robot Path Control Based on Artificial Intelligence Image Classification and Sustainable Ultrasonic Signal Transformation Technology. Sustainability, 14(9), 5335. https://doi.org/10.3390/su14095335






