Application of the Choquet Integral: A Case Study on a Personnel Selection Problem
Abstract
1. Introduction
2. Problem Description and Descriptive Statistics of Input Data
- Strongly Disagree,
- Disagree,
- Undecided,
- Agree,
- Strongly Agree.
3. Rankings Obtained Using Some Standard Methods
3.1. Ranking Employees Using TOPSIS Method
3.2. Ranking Employees Using the PROMETHEE Method
4. The Main Results
4.1. Discrete Choquet Integral
- ;
- for all
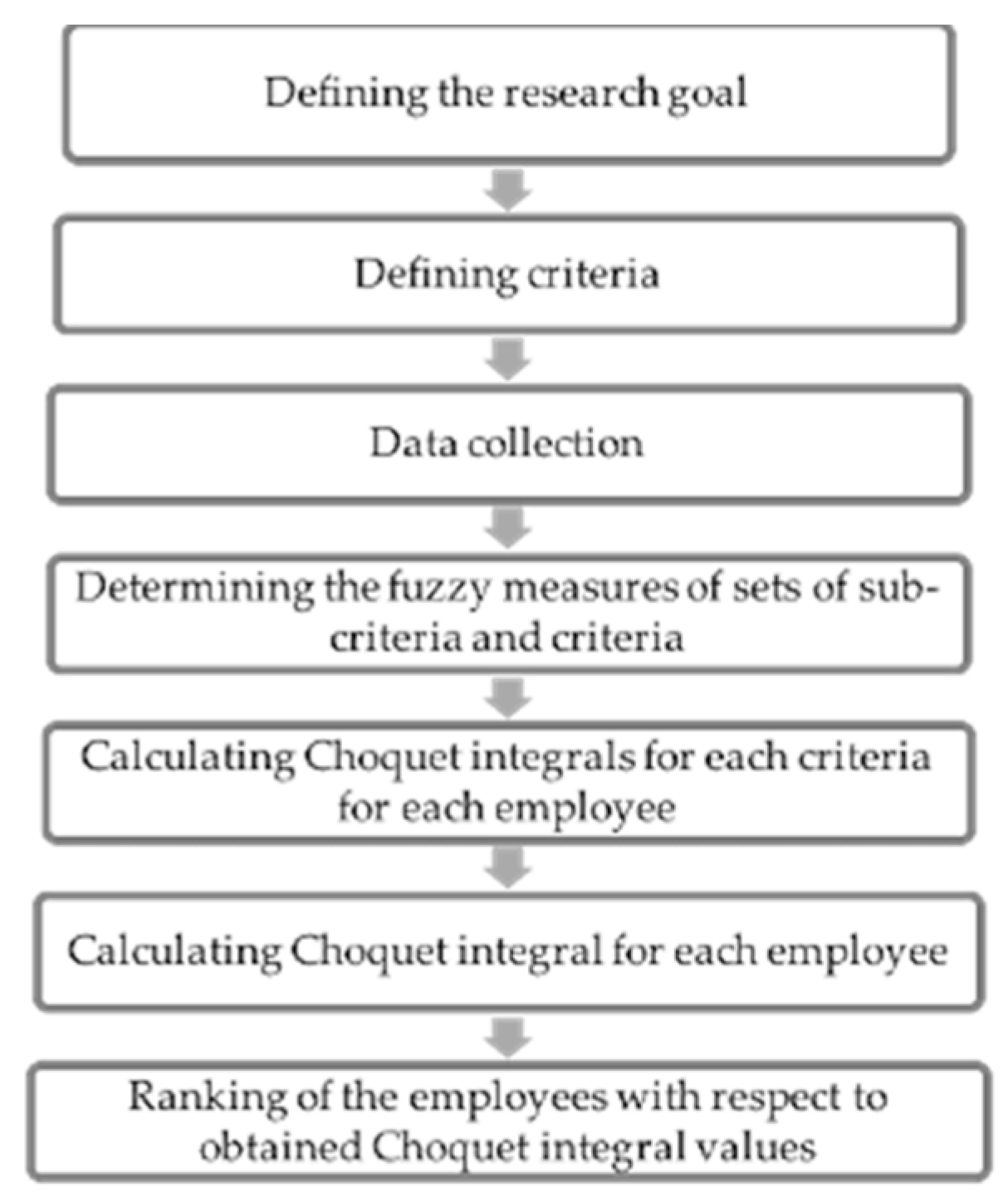
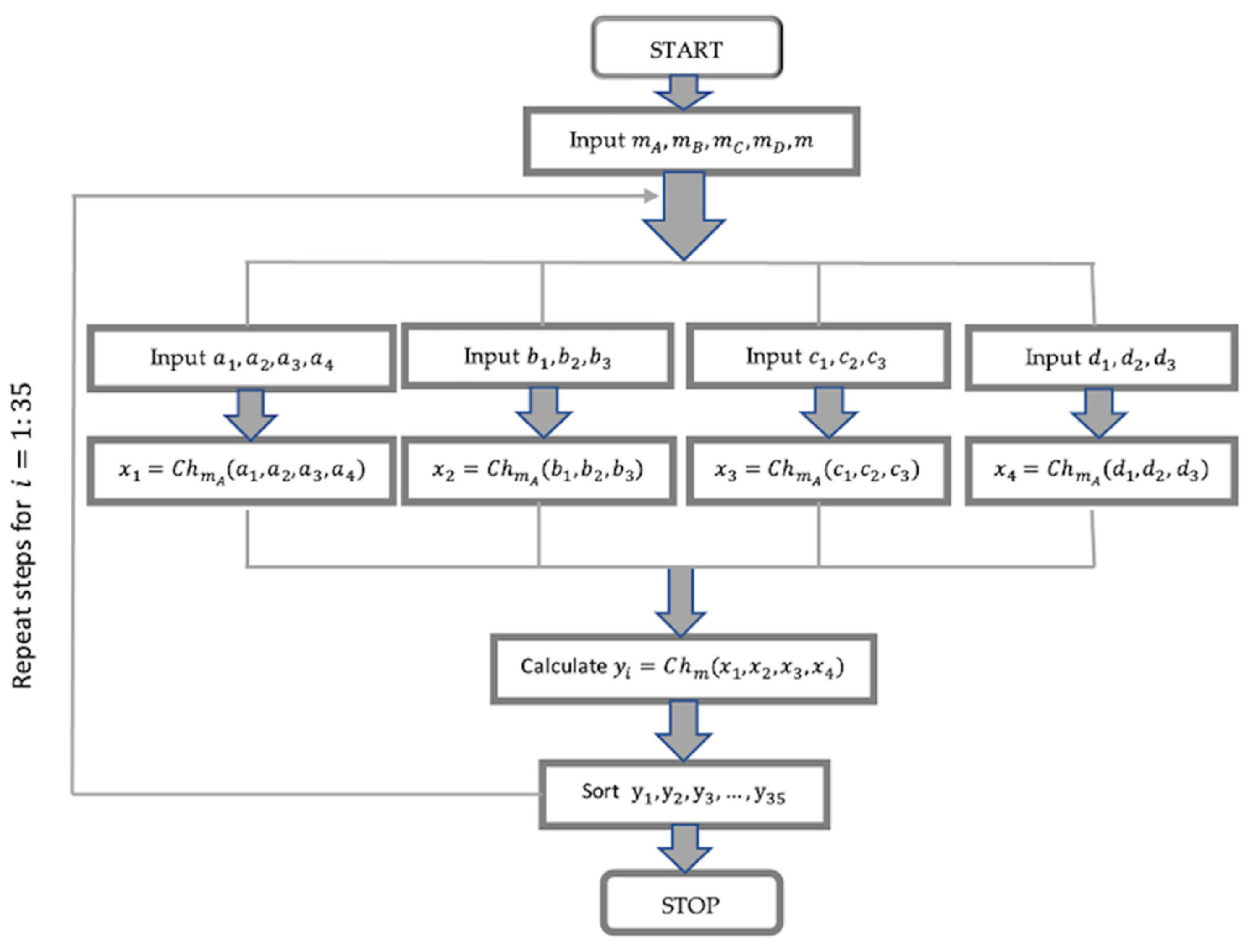
4.2. Methodology of Research
- are fuzzy measures
- are grades for sub-criteria , respectively
- are grades for sub-criteria , respectively
- are grades for sub-criteria , respectively
- are grades for sub-criteria , respectively
- is the value of the Choquet integral of w.r.t. fuzzy measure
- is the value of the Choquet integral of w.r.t. fuzzy measure
- is the value of the Choquet integral of w.r.t. fuzzy measure
- is the value of the Choquet integral of w.r.t. fuzzy measure
- is the value of the Choquet integral of w.r.t. fuzzy measure m for the i-th employee, .
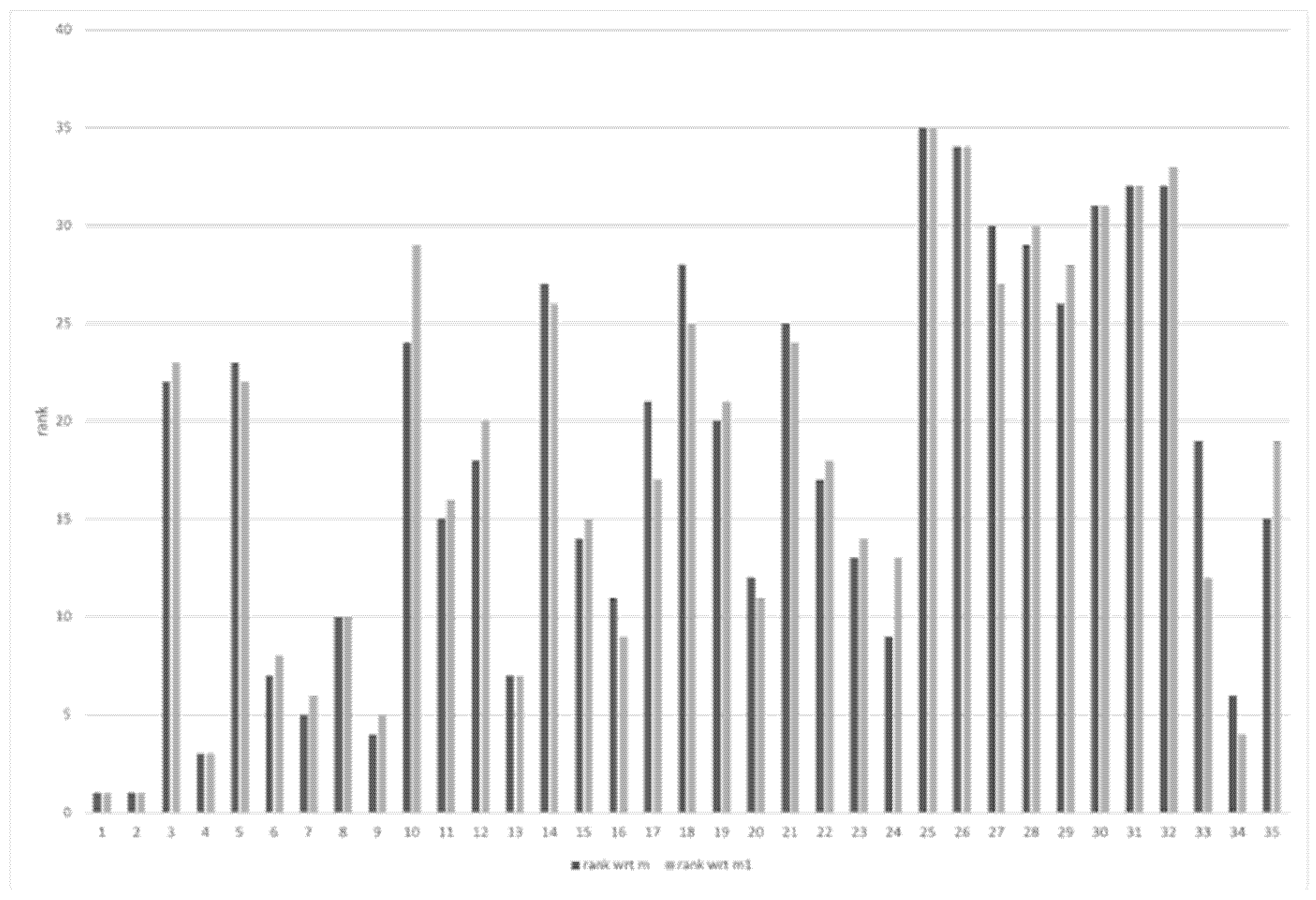
4.3. Application of the Discrete Choquet Integral for Personnel Selection
- The personal characteristics of employee,
- Task performance,
- Employee employee relationship approaches,
- Effectiveness of communication.
- (A)
- The personal characteristics of employee
- (B)
- Task performance
- (C)
- Employee–employee relationship approaches
- (D)
- Effectiveness of communication
- (E)
- Employee ranking
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Employee | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 5 | 3 | 4 | 3 | 4 | 4 | 3 | 3 | 4 | 2 | 4 | 4 | 2 | |
| 5 | 5 | 5 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 2 | 3 | 3 | 3 | 4 | 4 | 4 | 3 | 2 | 3 | 4 | 4 | 4 | |
| 5 | 5 | 5 | 4 | 5 | 4 | 4 | 5 | 5 | 3 | 5 | 4 | 4 | |
| 5 | 5 | 5 | 4 | 5 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 4 | |
| 5 | 5 | 5 | 3 | 5 | 2 | 4 | 4 | 4 | 4 | 4 | 5 | 4 | |
| 5 | 5 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | |
| 5 | 3 | 2 | 2 | 4 | 4 | 3 | 2 | 3 | 2 | 4 | 4 | 2 | |
| 5 | 4 | 4 | 3 | 4 | 2 | 2 | 4 | 4 | 4 | 5 | 5 | 3 | |
| 5 | 4 | 4 | 3 | 5 | 2 | 3 | 4 | 3 | 3 | 4 | 4 | 2 | |
| 5 | 4 | 4 | 4 | 4 | 5 | 4 | 4 | 5 | 5 | 5 | 5 | 4 | |
| 5 | 2 | 2 | 1 | 4 | 4 | 3 | 3 | 5 | 5 | 5 | 4 | 1 | |
| 5 | 4 | 4 | 3 | 4 | 4 | 2 | 4 | 5 | 5 | 5 | 5 | 2 | |
| 5 | 4 | 4 | 4 | 4 | 2 | 2 | 4 | 4 | 5 | 5 | 5 | 4 | |
| 4 | 4 | 4 | 2 | 4 | 2 | 2 | 4 | 5 | 3 | 5 | 5 | 3 | |
| 3 | 2 | 2 | 2 | 4 | 4 | 2 | 3 | 4 | 2 | 5 | 5 | 2 | |
| 5 | 3 | 4 | 2 | 4 | 3 | 4 | 3 | 5 | 2 | 5 | 5 | 2 | |
| 3 | 4 | 4 | 4 | 4 | 2 | 2 | 4 | 5 | 4 | 5 | 5 | 4 | |
| 5 | 2 | 2 | 2 | 4 | 4 | 3 | 3 | 5 | 3 | 4 | 4 | 1 | |
| 5 | 2 | 2 | 2 | 4 | 4 | 4 | 3 | 5 | 3 | 5 | 5 | 1 | |
| 5 | 4 | 4 | 2 | 4 | 4 | 4 | 4 | 5 | 4 | 5 | 4 | 2 | |
| 5 | 4 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 3 | 5 | 5 | 3 | |
| 2 | 1 | 1 | 1 | 2 | 4 | 1 | 2 | 1 | 1 | 2 | 3 | 1 | |
| 5 | 3 | 3 | 1 | 4 | 4 | 1 | 3 | 5 | 3 | 5 | 5 | 1 | |
| 4 | 4 | 2 | 1 | 4 | 4 | 2 | 4 | 5 | 2 | 5 | 4 | 1 | |
| 4 | 3 | 3 | 1 | 4 | 4 | 2 | 3 | 5 | 2 | 5 | 4 | 1 | |
| 5 | 4 | 4 | 2 | 4 | 4 | 4 | 4 | 5 | 3 | 5 | 5 | 2 | |
| 5 | 2 | 2 | 1 | 4 | 4 | 1 | 3 | 5 | 4 | 5 | 5 | 1 | |
| 2 | 2 | 2 | 2 | 3 | 4 | 1 | 3 | 4 | 1 | 4 | 4 | 1 | |
| 2 | 2 | 1 | 1 | 4 | 4 | 2 | 2 | 3 | 1 | 4 | 3 | 1 | |
| 5 | 3 | 2 | 2 | 4 | 4 | 3 | 4 | 4 | 2 | 4 | 4 | 1 | |
| 5 | 5 | 5 | 5 | 5 | 2 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| 5 | 4 | 3 | 4 | 4 | 2 | 3 | 3 | 4 | 1 | 5 | 5 | 2 |
| Rank | Employee | Relative Closeness |
|---|---|---|
| 1 | 2.362994 | |
| 2 | 2.362992 | |
| 3 | 2.133280 | |
| 4 | 2.098566 | |
| 5 | 2.043925 | |
| 6 | 2.031870 | |
| 7 | 2.015559 | |
| 8 | 2.012834 | |
| 9 | 1.997021 | |
| 10 | 1.982772 | |
| 11 | 1.959623 | |
| 12 | 1.913884 | |
| 13 | 1.911120 | |
| 14 | 1.868947 | |
| 15 | 1.839883 | |
| 16 | 1.822605 | |
| 17 | 1.821991 | |
| 18 | 1.784999 | |
| 19 | 1.761233 | |
| 20 | 1.746783 | |
| 21 | 1.613952 | |
| 22 | 1.592135 | |
| 23 | 1.581164 | |
| 24 | 1.573219 | |
| 25 | 1.565685 | |
| 26 | 1.468762 | |
| 27 | 1.400000 | |
| 28 | 1.358742 | |
| 29 | 1.358090 | |
| 30 | 1.316060 | |
| 31 | 1.172919 | |
| 32 | 1.172919 | |
| 33 | 1.136000 | |
| 34 | 1.000000 | |
| 35 | 1.000000 |
| Employee | ||||||
|---|---|---|---|---|---|---|
5 5 5 5 | 0 5 5 5 5 | 0 5 0 0 0 | - - - | 1 - - - | 5.0 | |
5 5 5 5 | 0 5 5 5 5 | 5 0 0 0 | - - - | 1 - - - | 5.0 | |
5 3 4 3 | 0 3 3 4 5 | 3 0 1 1 | A - | 1 - 0.4 0.2 | 3.6 | |
5 5 5 5 | 0 5 5 5 5 | 5 0 0 0 | - - - | 1 - - - | 5.0 | |
2 3 3 3 | 0 2 3 3 3 | 2 1 0 0 | - - | 1 0.6 - - | 2.6 | |
5 5 5 4 | 0 4 5 5 5 | 4 1 0 0 | - - | 1 0.5 - - | 4.5 | |
5 5 5 4 | 0 4 5 5 5 | 4 1 0 0 | - - | 1 0.5 - - | 4.5 | |
5 5 5 3 | 0 3 5 5 5 | 3 2 0 0 | - - | 1 0.5 - - | 4.0 | |
5 5 5 4 | 0 4 5 5 5 | 4 1 0 0 | - - | 1 0.5 - - | 4.5 | |
5 3 2 2 | 0 2 2 3 5 | 2 0 1 2 | - | 1 - 0.4 0.2 | 2.8 | |
5 4 4 3 | 0 3 4 4 5 | 3 1 0 1 | - | 1 0.5 - 0.2 | 3.7 | |
5 4 4 3 | 0 3 4 4 5 | 0 3 1 0 1 | - | 1 0.5 - 0.2 | 3.7 | |
5 4 4 4 | 0 4 4 4 5 | 4 0 0 1 | - - | 1 - - 0.2 | 4.2 | |
5 2 2 1 | 0 1 2 2 5 | 1 1 0 3 | - | 1 0.5 - 0.2 | 2.1 | |
5 4 4 3 | 0 3 4 4 5 | 3 1 0 1 | - | 1 0.5 - 0.2 | 3.7 | |
5 4 4 4 | 0 4 4 4 5 | 4 0 0 1 | - - | 1 - - 0.2 | 4.2 | |
4 4 4 2 | 0 2 4 4 4 | 2 2 0 0 | - - | 1 0.5 - - | 3.0 | |
3 2 2 2 | 0 2 2 2 3 | 2 0 0 1 | - - | 1 - - 0.2 | 2.2 | |
5 3 4 2 | 0 2 3 4 5 | 2 1 1 1 | 1 0.5 0.4 0.2 | 3.1 | ||
3 4 4 4 | 0 3 4 4 4 | 3 1 0 0 | - - | 1 0.6 - - | 3.6 | |
5 2 2 2 | 0 2 2 2 5 | 2 0 0 3 | - - | 1 - - 0.2 | 2.6 | |
5 2 2 2 | 0 2 2 2 5 | 2 0 0 3 | - - | 1 - - 0.2 | 2.6 | |
5 4 4 2 | 0 2 4 4 5 | 2 2 0 1 | - | 1 0.5 - 0.2 | 3.2 | |
5 4 3 3 | 0 3 3 4 5 | 3 0 1 1 | - | 1 - 0.4 0.2 | 3.6 | |
2 1 1 1 | 0 1 1 1 2 | 1 0 0 1 | - - | 1 - - 0.2 | 1.2 | |
5 3 3 1 | 0 1 3 3 5 | 1 2 0 2 | - | 1 0.5 - 0.2 | 2.4 | |
4 4 2 1 | 0 1 2 4 4 | 1 1 2 0 | - | 1 0.5 0.4 - | 2.3 | |
4 3 3 1 | 0 1 3 3 4 | 1 2 0 1 | - | 1 0.5 - 0.2 | 2.2 | |
5 4 4 2 | 0 2 4 4 5 | 2 2 0 1 | - | 1 0.5 - 0.2 | 3.2 | |
5 2 2 1 | 0 1 2 2 5 | 1 1 0 3 | - | 1 0.5 - 0.2 | 2.1 | |
2 2 2 2 | 0 2 2 2 2 | 2 0 0 0 | - - - | 1 - - - | 2.0 | |
2 2 1 1 | 0 1 1 2 2 | 1 0 1 0 | - - | 1 - 0.4 - | 1.4 | |
5 3 2 2 | 0 2 2 3 5 | 2 0 1 2 | - | 1 - 0.4 0.2 | 2.8 | |
5 5 5 5 | 0 5 5 5 5 | 5 0 0 0 | - - - | 1 - - - | 5 | |
5 4 3 4 | 0 3 4 4 5 | 3 1 0 1 | - | 1 0.7 - 0.2 | 3.9 |
| Employee | ||||||
|---|---|---|---|---|---|---|
5 5 5 | 0 5 5 5 | 5 0 0 | - - | 1 - - | 5.0 | |
5 5 5 | 0 5 5 5 | 5 0 0 | - - | 1 - - | 5.0 | |
4 4 3 | 0 3 4 4 | 3 1 0 | - | 1 0.6 - | 3.6 | |
5 5 4 | 0 4 5 5 | 4 1 0 | - | 1 0.6 - | 4.6 | |
4 4 4 | 0 4 4 4 | 4 0 9 | - - | 1 0.6 - | 4.0 | |
5 4 4 | 0 4 4 5 | 4 0 1 | - | 1 - 0.4 | 4.4 | |
5 4 5 | 0 4 5 5 | 4 1 0 | - | 1 0.5 - | 4.5 | |
5 2 4 | 0 2 4 5 | 2 2 1 | 1 0.5 0.4 | 3.4 | ||
5 5 4 | 0 4 5 5 | 4 1 0 | - | 1 0.6 - | 4.6 | |
4 4 3 | 0 3 4 4 | 3 1 0 | - | 1 0.6 - | 3.6 | |
4 2 2 | 0 2 2 4 | 2 0 2 | - | 1 - 0.4 | 2.8 | |
5 2 3 | 0 2 3 5 | 2 1 2 | 1 0.6 0.4 | 3.4 | ||
4 5 4 | 0 4 4 5 | 4 0 1 | - | 1 - 0.5 | 4.5 | |
4 4 3 | 0 3 4 4 | 3 1 0 | - | 1 0.6 - | 3.6 | |
4 4 2 | 0 2 4 4 | 2 2 0 | - | 1 0.6 | 3.2 | |
4 2 2 | 0 2 2 4 | 2 0 2 | - | 1 - 0.4 | 2.8 | |
4 2 2 | 0 2 2 4 | 2 0 2 | - | 1 - 0.4 | 2.8 | |
4 4 2 | 0 2 4 4 | 2 2 - | - | 1 0.6 - | 3.2 | |
4 3 4 | 0 3 4 4 | 3 1 0 | - | 1 0.5 - | 3.5 | |
4 2 2 | 0 2 2 4 | 2 0 2 | - | 1 - 0.4 | 2.8 | |
4 4 3 | 0 3 4 4 | 3 1 0 | - | 1 0.6 - | 3.6 | |
4 4 4 | 0 4 4 4 | 4 0 0 | - - | 1 - - | 4.0 | |
4 4 4 | 0 4 4 4 | 4 0 0 | - - | 1 - - | 4.0 | |
4 4 4 | 0 4 4 4 | 4 0 0 | - - | 1 - - | 4.0 | |
2 4 1 | 0 1 2 4 | 1 1 2 | 1 0.6 0.5 | 2.6 | ||
2 4 1 | 0 1 2 4 | 1 1 2 | 1 0.6 0.5 | 2.6 | ||
4 4 1 | 0 1 4 4 | 1 3 0 | - | 1 0.6 - | 2.8 | |
4 4 2 | 0 2 4 4 | 2 2 0 | - | 1 0.6 - | 3.2 | |
4 4 2 | 0 2 4 4 | 2 2 0 | - | 1 0.6 - | 3.2 | |
4 4 1 | 0 1 4 4 | 1 3 0 | - | 1 0.6 - | 2.8 | |
3 4 1 | 0 1 3 4 | 1 2 1 | 1 0.6 0.5 | 2.7 | ||
4 4 2 | 0 2 4 4 | 2 2 0 | - | 1 0.6 - | 3.2 | |
4 4 3 | 0 3 4 4 | 3 1 0 | - | 1 0.6 - | 3.6 | |
5 2 5 | 0 2 5 5 | 2 3 0 | - | 1 0.5 - | 3.5 | |
4 2 3 | 0 2 3 4 | 2 1 1 | 1 0.5 0.4 | 2.9 |
| Employee | ||||||
|---|---|---|---|---|---|---|
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 2.9 | |||||
| 3 | 2 | 2 | 1 | |||
| 4 | 3 | 1 | 0.6 | |||
| 2 | 4 | 1 | 0.3 | |||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 2.2 | |||||
| 3 | 2 | 2 | 1 | |||
| 2 | 3 | 1 | 0.2 | |||
| 3 | 3 | 0 | - | - | ||
| 0 | 4.2 | |||||
| 5 | 3 | 3 | 1 | |||
| 5 | 5 | 2 | 0.6 | |||
| 3 | 5 | 0 | - | - | ||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 4 | |||||
| 4 | 4 | 4 | 1 | |||
| 4 | 4 | 0 | - | - | ||
| 4 | 4 | 0 | - | - | ||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 2.3 | |||||
| 2 | 2 | 2 | 1 | |||
| 3 | 2 | 0 | - | - | ||
| 2 | 3 | 1 | 0.3 | |||
| 0 | 4 | |||||
| 4 | 4 | 4 | 1 | |||
| 4 | 4 | 0 | - | - | ||
| 4 | 4 | 0 | - | - | ||
| 0 | 3.4 | |||||
| 4 | 3 | 3 | 1 | |||
| 3 | 3 | 0 | - | - | ||
| 3 | 4 | 1 | 0.4 | |||
| 0 | 4.2 | |||||
| 4 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.2 | |||
| 5 | 5 | 0 | - | - | ||
| 0 | 3.4 | |||||
| 3 | 3 | 3 | 1 | |||
| 5 | 5 | 2 | 0.2 | |||
| 5 | 5 | 0 | - | - | ||
| 0 | 4.2 | |||||
| 4 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.2 | |||
| 5 | 5 | 0 | - | - | ||
| 0 | 4.2 | |||||
| 4 | 4 | 4 | 1 | |||
| 4 | 4 | 0 | - | - | ||
| 5 | 5 | 1 | 0.2 | |||
| 0 | 3.9 | |||||
| 4 | 3 | 3 | 1 | |||
| 5 | 4 | 1 | 0.6 | |||
| 3 | 5 | 1 | 0.3 | |||
| 0 | 2.9 | |||||
| 3 | 2 | 2 | 1 | |||
| 4 | 3 | 1 | 0.6 | |||
| 2 | 4 | 1 | 0.3 | |||
| 0 | 3.2 | |||||
| 3 | 2 | 2 | 1 | |||
| 5 | 3 | 1 | 0.6 | |||
| 2 | 5 | 2 | 0.3 | |||
| 0 | 4.3 | |||||
| 4 | 4 | 4 | 1 | |||
| 5 | 4 | 0 | - | - | ||
| 4 | 5 | 1 | 0.3 | |||
| 0 | 3.6 | |||||
| 3 | 3 | 3 | 1 | |||
| 5 | 3 | 0 | - | - | ||
| 3 | 5 | 2 | 0.3 | |||
| 0 | 3.6 | |||||
| 3 | 3 | 3 | 1 | |||
| 5 | 3 | 0 | - | - | ||
| 3 | 5 | 2 | 0.3 | |||
| 0 | 4.3 | |||||
| 4 | 4 | 4 | 1 | |||
| 5 | 4 | 0 | - | - | ||
| 4 | 5 | 1 | 0.3 | |||
| 0 | 3.9 | |||||
| 4 | 3 | 3 | 1 | |||
| 5 | 4 | 1 | 0.6 | |||
| 3 | 5 | 1 | 0.3 | |||
| 0 | 1.4 | |||||
| 2 | 1 | 1 | 1 | |||
| 1 | 1 | 0 | - | - | ||
| 1 | 2 | 1 | 0.4 | |||
| 0 | 1.4 | |||||
| 2 | 1 | 1 | 1 | |||
| 1 | 1 | 0 | - | - | ||
| 1 | 2 | 1 | 0.4 | |||
| 0 | 3.6 | |||||
| 3 | 3 | 3 | 1 | |||
| 5 | 3 | 0 | - | - | ||
| 3 | 5 | 2 | 0.3 | |||
| 0 | 3.5 | |||||
| 4 | 2 | 2 | 1 | |||
| 5 | 4 | 2 | 0.6 | |||
| 2 | 5 | 1 | 0.3 | |||
| 0 | 3.2 | |||||
| 3 | 2 | 2 | 1 | |||
| 5 | 3 | 1 | 0.6 | |||
| 2 | 5 | 2 | 0.3 | |||
| 0 | 3.5 | |||||
| 3 | 3 | 3 | 1 | |||
| 5 | 4 | 1 | 0.2 | |||
| 4 | 5 | 1 | 0.3 | |||
| 0 | 2.5 | |||||
| 3 | 1 | 1 | 1 | |||
| 4 | 3 | 2 | 0.6 | |||
| 1 | 4 | 1 | 0.3 | |||
| 0 | 1.9 | |||||
| 2 | 1 | 1 | 1 | |||
| 3 | 2 | 1 | 0.6 | |||
| 1 | 3 | 1 | 0.3 | |||
| 0 | 5 | |||||
| 4 | 5 | 5 | 1 | |||
| 4 | 5 | 0 | - | - | ||
| 2 | 5 | 0 | - | - | ||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 2.5 | |||||
| 3 | 1 | 1 | 1 | |||
| 4 | 3 | 2 | 0.6 | |||
| 1 | 4 | 1 | 0.3 |
| Employee | ||||||
|---|---|---|---|---|---|---|
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 3.2 | |||||
| 4 | 2 | 2 | 1 | |||
| 4 | 4 | 2 | 0.6 | |||
| 2 | 4 | 0 | - | - | ||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 4 | |||||
| 4 | 4 | 4 | 1 | |||
| 4 | 4 | 0 | - | - | ||
| 4 | 4 | 0 | - | - | ||
| 0 | 4.3 | |||||
| 5 | 4 | 4 | 1 | |||
| 4 | 4 | 0 | - | - | ||
| 4 | 5 | 1 | 0.3 | |||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 4.4 | |||||
| 4 | 4 | 4 | 1 | |||
| 5 | 4 | 0 | - | - | ||
| 4 | 5 | 1 | 0.4 | |||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 3.2 | |||||
| 4 | 2 | 2 | 1 | |||
| 4 | 4 | 2 | 0.6 | |||
| 2 | 4 | 0 | - | - | ||
| 0 | 4.2 | |||||
| 5 | 3 | 3 | 1 | |||
| 5 | 5 | 2 | 0.6 | |||
| 3 | 5 | 0 | - | - | ||
| 0 | 3.2 | |||||
| 4 | 2 | 2 | 1 | |||
| 4 | 4 | 2 | 0.6 | |||
| 2 | 4 | 0 | - | - | ||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 3.1 | |||||
| 5 | 1 | 1 | 1 | |||
| 4 | 4 | 3 | 0.6 | |||
| 1 | 5 | 1 | 0.3 | |||
| 0 | 3.8 | |||||
| 5 | 2 | 2 | 1 | |||
| 5 | 5 | 3 | 0.6 | |||
| 2 | 5 | 0 | - | - | ||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 4.2 | |||||
| 5 | 3 | 3 | 1 | |||
| 5 | 5 | 2 | 0.6 | |||
| 3 | 5 | 0 | - | - | ||
| 0 | 3.8 | |||||
| 5 | 2 | 2 | 1 | |||
| 5 | 5 | 3 | 0.6 | |||
| 2 | 5 | 0 | - | - | ||
| 0 | 3.8 | |||||
| 5 | 2 | 2 | 1 | |||
| 5 | 5 | 3 | 0.6 | |||
| 2 | 5 | 0 | - | - | ||
| 0 | 4.6 | |||||
| 5 | 4 | 4 | 1 | |||
| 5 | 5 | 1 | 0.6 | |||
| 4 | 5 | 0 | - | - | ||
| 0 | 2.8 | |||||
| 4 | 1 | 1 | 1 | |||
| 4 | 4 | 3 | 0.6 | |||
| 1 | 4 | 0 | - | - | ||
| 0 | 3.4 | |||||
| 5 | 1 | 1 | 1 | |||
| 5 | 5 | 4 | 0.6 | |||
| 1 | 5 | 0 | - | - | ||
| 0 | 3.5 | |||||
| 5 | 2 | 2 | 1 | |||
| 4 | 4 | 2 | 0.6 | |||
| 2 | 5 | 1 | 0.3 | |||
| 0 | 4.2 | |||||
| 5 | 3 | 3 | 1 | |||
| 5 | 5 | 2 | 0.6 | |||
| 3 | 5 | 0 | - | - | ||
| 0 | 2 | |||||
| 2 | 1 | 1 | 1 | |||
| 3 | 2 | 1 | 0.6 | |||
| 1 | 3 | 1 | 0.4 | |||
| 0 | 2 | |||||
| 2 | 1 | 1 | 1 | |||
| 3 | 2 | 1 | 0.6 | |||
| 1 | 3 | 1 | 0.4 | |||
| 0 | 3.4 | |||||
| 5 | 1 | 1 | 1 | |||
| 5 | 5 | 4 | 0.6 | |||
| 1 | 5 | 0 | - | - | ||
| 0 | 3.1 | |||||
| 5 | 1 | 1 | 1 | |||
| 4 | 4 | 3 | 0.6 | |||
| 1 | 5 | 1 | 0.3 | |||
| 0 | 3.1 | |||||
| 5 | 1 | 1 | 1 | |||
| 4 | 4 | 3 | 0.6 | |||
| 1 | 5 | 1 | 0.3 | |||
| 0 | 3.4 | |||||
| 5 | 1 | 1 | 1 | |||
| 5 | 5 | 4 | 0.6 | |||
| 1 | 5 | 0 | - | - | ||
| 0 | 2.8 | |||||
| 4 | 1 | 1 | 1 | |||
| 4 | 4 | 3 | 0.6 | |||
| 1 | 4 | 0 | - | - | ||
| 0 | 2.5 | |||||
| 4 | 1 | 1 | 1 | |||
| 3 | 3 | 2 | 0.6 | |||
| 1 | 4 | 1 | 0.3 | |||
| 0 | 2.8 | |||||
| 4 | 1 | 1 | 1 | |||
| 4 | 4 | 3 | 0.6 | |||
| 1 | 4 | 0 | - | - | ||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 3.8 | |||||
| 5 | 2 | 2 | 1 | |||
| 5 | 5 | 3 | 0.6 | |||
| 2 | 5 | 0 | - | - |
| Employee | ||||||
|---|---|---|---|---|---|---|
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 5 | |||||
| 5 | 5 | 5 | 1 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 3.45 | |||||
| 3.6 | 2.9 | 2.9 | 1 | |||
| 3.6 | 3.2 | 0.3 | 0.9 | |||
| 2.9 | 3.6 | 0.4 | } | 0.7 | ||
| 3.2 | 3.6 | 0 | - | - | ||
| 0 | 4.65 | |||||
| 5 | 4 | 4 | 1 | |||
| 4.6 | 5 | 1 | 0.65 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | - | ||
| 0 | 3.23 | |||||
| 2.6 | 2.2 | 2.2 | 1 | |||
| 4 | 2.6 | 0.4 | 0.65 | |||
| 2.2 | 4 | 1.4 | 0.55 | |||
| 4 | 4 | 0 | - | - | ||
| 0 | 4.41 | |||||
| 4.5 | 4.2 | 4.2 | 1 | |||
| 4.4 | 4.3 | 0.1 | 0.9 | |||
| 4.2 | 4.4 | 0.1 | 0.7 | |||
| 4.3 | 4.5 | 0.1 | 0.5 | |||
| 0 | 4.55 | |||||
| 4.5 | 4.5 | 4.5 | 1 | |||
| 4.5 | 4.5 | 0 | - | - | ||
| 4.6 | 4.6 | 0.1 | 0.45 | |||
| 4.6 | 4.6 | 0 | - | - | ||
| 0 | 3.95 | |||||
| 4 | 3.4 | 3.4 | 1 | |||
| 3.4 | 4 | 0.6 | 0.65 | |||
| 4 | 4 | 0 | - | - | ||
| 4.4 | 4.4 | 0.4 | 0.4 | |||
| 0 | 4.58 | |||||
| 4.5 | 4.5 | 4.5 | 1 | |||
| 4.6 | 4.6 | 0.1 | 0.8 | |||
| 4.6 | 4.6 | 0 | - | - | ||
| 4.6 | 4.6 | 0 | - | - | ||
| 0 | 3.21 | |||||
| 2.8 | 2.3 | 2.3 | 1 | |||
| 3.6 | 2.8 | 0.5 | 0.9 | |||
| 2.3 | 3.2 | 0.4 | 0.55 | |||
| 3.2 | 3.6 | 0.4 | 0.6 | |||
| 0 | 3.6 | |||||
| 3.7 | 2.8 | 2.8 | 1 | |||
| 2.8 | 3.7 | 0.9 | 0.65 | |||
| 4 | 4 | 0.3 | 0.45 | |||
| 4.2 | 4.2 | 0.2 | 0.4 | |||
| 0 | 3.52 | |||||
| 3.7 | 3.2 | 3.2 | 1 | |||
| 3.4 | 3.4 | 0.2 | 0.85 | |||
| 3.4 | 3.4 | 0 | - | 0.7 | ||
| 3.2 | 3.7 | 0.2 | 0.5 | |||
| 0 | 4.41 | |||||
| 4.2 | 4.2 | 4.2 | 1 | |||
| 4.5 | 4.2 | 0 | - | - | ||
| 4.2 | 4.5 | 0.3 | 0.55 | |||
| 4.6 | 4.6 | 0.1 | 0.4 | |||
| 0 | 3.17 | |||||
| 2.1 | 2.1 | 2.1 | 1 | |||
| 3.6 | 3.1 | 1 | 0.8 | |||
| 3.4 | 3.4 | 0.3 | 0.5 | |||
| 3.1 | 3.6 | 0.2 | 0.6 | |||
| 0 | 3.65 | |||||
| 3.7 | 3.2 | 3.2 | 1 | |||
| 3.2 | 3.7 | 0.5 | 0.65 | |||
| 4.2 | 3.8 | 0.1 | 0.45 | |||
| 3.8 | 4.2 | 0.4 | 0.2 | |||
| 0 | 3.87 | |||||
| 4.2 | 2.8 | 2.8 | 1 | |||
| 2.8 | 4.2 | 1.4 | 0.65 | |||
| 4.2 | 4.2 | 0 | - | - | ||
| 4.6 | 4.6 | 0.4 | 0.4 | |||
| 0 | 3.46 | |||||
| 3 | 2.8 | 2.8 | 1 | |||
| 2.8 | 3 | 0.2 | 0.65 | |||
| 3.9 | 3.9 | 0.9 | 0.45 | |||
| 4.2 | 4.2 | 0.3 | 0.4 | |||
| 0 | 3.17 | |||||
| 2.2 | 2.2 | 2.2 | 1 | |||
| 3.2 | 2.9 | 0.7 | 0.8 | |||
| 2.9 | 3.2 | 0.3 | 0.55 | |||
| 3.8 | 3.8 | 0.6 | 0.4 | |||
| 0 | 3.47 | |||||
| 3.1 | 3.1 | 3.1 | 1 | |||
| 3.5 | 3.2 | 0.1 | 0.8 | |||
| 3.2 | 3.5 | 0.3 | 0.55 | |||
| 3.8 | 3.8 | 0.3 | 0.4 | |||
| 0 | 3.76 | |||||
| 3.6 | 2.8 | 2.8 | 1 | |||
| 2.8 | 3.6 | 0.8 | 0.65 | |||
| 4.3 | 4.3 | 0.7 | 0.45 | |||
| 4.6 | 4.6 | 0.3 | 0.4 | |||
| 0 | 3.2 | |||||
| 2.6 | 2.6 | 2.6 | 1 | |||
| 3.6 | 2.8 | 0.2 | 0.8 | |||
| 3.6 | 3.6 | 0.8 | 0.55 | |||
| 2.8 | 3.6 | 0 | - | - | ||
| 0 | 3.58 | |||||
| 2.6 | 2.6 | 2.6 | 1 | |||
| 4 | 3.4 | 0.8 | 0.8 | |||
| 3.6 | 3.6 | 0.2 | 0.5 | |||
| 3.4 | 4 | 0.4 | 0.6 | |||
| 0 | 3.75 | |||||
| 3.2 | 3.2 | 3.2 | 1 | |||
| 4 | 3.5 | 0.3 | 0.8 | |||
| 4.3 | 4 | 0.5 | 0.5 | |||
| 3.5 | 4.3 | 0.3 | 0.2 | |||
| 0 | 3.98 | |||||
| 3.6 | 3.6 | 3.6 | 1 | |||
| 4 | 3.9 | 0.3 | 0.8 | |||
| 3.9 | 4 | 0.1 | 0.55 | |||
| 4.2 | 4.2 | 0.2 | 0.4 | |||
| 0 | 2.05 | |||||
| 1.2 | 1.2 | 1.2 | 1 | |||
| 2.6 | 1.4 | 0.2 | 0.8 | |||
| 1.4 | 2 | 0.6 | 0.55 | |||
| 2 | 2.6 | 0.6 | 0.6 | |||
| 0 | 2.34 | |||||
| 2.4 | 1.4 | 1.4 | 1 | |||
| 2.6 | 2 | 0.6 | 0.9 | |||
| 1.4 | 2.4 | 0.4 | 0.7 | |||
| 2 | 2.6 | 0.2 | 0.6 | |||
| 0 | 3.01 | |||||
| 2.3 | 2.3 | 2.3 | 1 | |||
| 2.8 | 2.8 | 0.5 | 0.8 | |||
| 3.6 | 3.4 | 0.6 | 0.45 | |||
| 3.4 | 3.6 | 0.2 | 0.2 | |||
| 0 | 3.04 | |||||
| 2.2 | 2.2 | 2.2 | 1 | |||
| 3.2 | 3.1 | 0.9 | 0.8 | |||
| 3.5 | 3.2 | 0.1 | 0.55 | |||
| 3.1 | 3.5 | 0.3 | 0.2 | |||
| 0 | 3.19 | |||||
| 3.2 | 3.1 | 3.1 | 1 | |||
| 3.2 | 3.2 | 0.1 | 0.85 | |||
| 3.2 | 3.2 | 0 | - | - | ||
| 3.1 | 3.2 | 0 | - | - | ||
| 0 | 2.95 | |||||
| 2.1 | 2.1 | 2.1 | 1 | |||
| 2.8 | 2.8 | 0.7 | 0.8 | |||
| 3.5 | 3.4 | 0.6 | 0.45 | |||
| 3.4 | 3.5 | 0.1 | 0.2 | |||
| 0 | 2.55 | |||||
| 2 | 2 | 2 | 1 | |||
| 2.7 | 2.5 | 0.5 | 0.8 | |||
| 2.5 | 2.7 | 0.2 | 0.55 | |||
| 2.8 | 2.8 | 0.1 | 0.4 | |||
| 0 | 2.55 | |||||
| 1.4 | 1.4 | 1.4 | 1 | |||
| 3.2 | 1.9 | 0.5 | 0.8 | |||
| 1.9 | 2.5 | 0.6 | 0.55 | |||
| 2.5 | 3.2 | 0.7 | 0.6 | |||
| 0 | 3.48 | |||||
| 2.8 | 2.8 | 2.8 | 1 | |||
| 3.6 | 2.8 | 0 | - | - | ||
| 5 | 3.6 | 0.8 | 0.5 | |||
| 2.8 | 5 | 1.4 | 0.2 | |||
| 0 | 4.48 | |||||
| 5 | 3.5 | 3.5 | 1 | |||
| 3.5 | 5 | 1.5 | 0.65 | |||
| 5 | 5 | 0 | - | - | ||
| 5 | 5 | 0 | - | 0 | ||
| 0 | 3.6 | |||||
| 3.9 | 2.5 | 2.5 | 1 | |||
| 2.9 | 2.9 | 0.4 | 0.9 | |||
| 2.5 | 3.8 | 0.9 | 0.65 | |||
| 3.8 | 4.1 | 0.3 | 0.5 |
References
- Transforming Our World: The 2030 Agenda for Sustainable Development|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/publications/transforming-our-world-2030-agenda-sustainable-development-17981 (accessed on 28 March 2022).
- Allen, C.; Metternicht, G.; Wiedmann, T. Prioritising SDG targets: Assessing baselines, gaps and interlinkages. Sustain. Sci. 2019, 14, 421–438. [Google Scholar] [CrossRef]
- Le Roux, C.; Pretorius, M. Navigating Sustainability Embeddedness in Management Decision-Making. Sustainability 2016, 8, 444. [Google Scholar] [CrossRef]
- Bastons, M.; Armengou, J. Realism and Impartiality: Making Sustainability Effective in Decision-Making. Sci. Eng. Ethics 2016, 23, 969–987. [Google Scholar] [CrossRef] [PubMed]
- Cohen, S.; Taylor, E.; Muller-Camen, M. HRM’s Role in Corporate Social and Environmental Sustainability; SHRM Foundation: Alexandria, VA, USA, 2012; Available online: https://www.shrm.org/hr-today/trends-and-forecasting/special-reports-and-expert-views/Documents/Corporate-Social-Environmental-Sustainability.pdf (accessed on 28 March 2022).
- Stankevičiūtė, Ž.; Savanevičienė, A. Designing Sustainable HRM: The Core Characteristics of Emerging Field. Sustainability 2018, 10, 4798. [Google Scholar] [CrossRef]
- Mikulić, I.; Lisjak, D.; Štefanić, N. A Rule-Based System for Human Performance Evaluation: A Case Study. Appl. Sci. 2021, 11, 2904. [Google Scholar] [CrossRef]
- Yalçın, N.; Pehlivan, N.Y. Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem. Symmetry 2019, 11, 493. [Google Scholar] [CrossRef]
- Mc Loughlin, E.; Priyadarshini, A. Adaptability in the workplace: Investigating the adaptive performance job requirements for a project manager. Proj. Leadersh. Soc. 2021, 2, 100012. [Google Scholar] [CrossRef]
- Pulakos, E.D.; Arad, S.; Donovan, M.A.; Plamondon, K.E. Adaptability in the workplace: Development of a taxonomy of adaptive performance. J. Appl. Psychol. 2000, 85, 612–624. [Google Scholar] [CrossRef]
- Decision Support System Best Employee Assessments with Technique for Order of Preference by Similarity to Ideal Solution. Spéc. Issue 2017, 3, 6–17. [CrossRef]
- Ulutaş, A.; Popovic, G.; Stanujkic, D.; Karabasevic, D.; Zavadskas, E.K.; Turskis, Z. A New Hybrid MCDM Model for Personnel Selection Based on a Novel Grey PIPRECIA and Grey OCRA Methods. Mathematics 2020, 8, 1698. [Google Scholar] [CrossRef]
- Chen, C.-T.; Hung, W.-Z. A Two-Phase Model for Personnel Selection Based on Multi-Type Fuzzy Information. Mathematics 2020, 8, 1703. [Google Scholar] [CrossRef]
- Baležentis, A.; Baležentis, T.; Brauers, W.K. Personnel selection based on computing with words and fuzzy multimoora. Expert Syst. Appl. 2012, 39, 7961–7967. [Google Scholar] [CrossRef]
- Luo, S.-Z.; Xing, L.-N. A Hybrid Decision Making Framework for Personnel Selection Using bwm, mabac and promethee. Int. J. Fuzzy Syst. 2019, 21, 2421–2434. [Google Scholar] [CrossRef]
- Canós, L.; Casasús, T.; Crespo, E.; Lara, T.; Pérez, J.C. Personnel selection based on fuzzy methods. Rev. Matemática Teoría Apl. 2011, 18, 177–192. [Google Scholar] [CrossRef][Green Version]
- Afshari, A.R.; Nikolić, M.; Akbari, Z. Personnel selection using group fuzzy AHP and SAW methods. J. Eng. Manag. Compet. 2017, 7, 3–10. [Google Scholar]
- Decision Support System of Performance Appraisal Policy Continuity in the Logistic Staff of Indonesian Armed Force Using Discrepancy Evaluation Model And Analytical Hierarchy Process. Int. J. Recent Technol. Eng. 2019, 8, 5372–5380. [CrossRef]
- Sicilia, M.-Á.; Barriocanal, G.E.; Calvo, T. An inquiry-based method for Choquet integral-based aggregation of interface usability parameters. Kibernetika 2003, 39, 601–614. [Google Scholar]
- Abdullah, L.; Awang, N.A.; Othman, M. Application of Choquet Integral-Fuzzy Measures for Aggregating Customers’ Satisfaction. Adv. Fuzzy Syst. 2021, 2021, 2319004. [Google Scholar] [CrossRef]
- Jullien, S.; Mauris, G.; Valet, L.; Bolon, P.; Teyssier, S. Identification of Choquet integral’s parameters based on relative entropy and applied to classification of tomographic images. Proc. IPMU 2008, 8, 1360–1367. [Google Scholar]
- Pasrija, V.; Srivastava, P.R. Evaluation of Software Quality using Choquet Integral Approach. Int. J. Fuzzy Syst. Appl. 2013, 3, 51–81. [Google Scholar] [CrossRef][Green Version]
- Heilpern, S. Using Choquet integral in economics. Stat. Pap. 2002, 43, 53–73. [Google Scholar] [CrossRef]
- Akasaka, Y.; Onisawa, T. Pedestrian Navigation System Reflecting Users Subjectivity and Taste. 2003. Available online: https://www.koreascience.kr/article/CFKO200333239336696.view (accessed on 2 March 2022).
- Peters, J.; Ramanna, S. Application of the Choquet integral in software cost estimation. In Proceedings of the IEEE 5th International Fuzzy Systems, New Orleans, LA, USA, 11 September 1996; Volume 2, pp. 862–866. [Google Scholar]
- Grabisch, M.; Labreuche, C. A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid. 4OR 2007, 6, 1–44. [Google Scholar] [CrossRef]
- Sakulin, S.; Alfimtsev, A. Problems of Choquet Integral Practical Applications. Indones. J. Electr. Eng. Inform. (IJEEI) 2013, 1, 43–48. [Google Scholar] [CrossRef][Green Version]
- Mondal, A.; Roy, S.K. Application of Choquet integral in interval type-2 Pythagorean fuzzy sustainable supply chain management under risk. Int. J. Intell. Syst. 2021, 37, 217–263. [Google Scholar] [CrossRef]
- Bonetti, A.; Bortot, S.; Fedrizzi, M.; Pereira, R.A.M.; Molinari, A. Modelling group processes and effort estimation in project management using the Choquet integral: An MCDM approach. Expert Syst. Appl. 2012, 39, 13366–13375. [Google Scholar] [CrossRef]
- Bhutia, P.W.; Phipon, R. Application of ahp and topsis method for supplier selection problem. IOSR J. Eng. 2012, 2, 43–50. [Google Scholar] [CrossRef]
- Monjezi, M.; Dehghani, H.; Singh, T.N.; Sayadi, A.R.; Gholinejad, A. Application of TOPSIS method for selecting the most appropriate blast design. Arab. J. Geosci. 2010, 5, 95–101. [Google Scholar] [CrossRef]
- Rahim, R.; Supiyandi, S.; Siahaan, A.P.U.; Listyorini, T.; Utomo, A.P.; Triyanto, W.A.; Irawan, Y.; Aisyah, S.; Khairani, M.; Sundari, S.; et al. TOPSIS Method Application for Decision Support System in Internal Control for Selecting Best Employees. J. Phys. Conf. Ser. 2018, 1028, 012052. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Saeed, M.; Ahmad, N.; Dayan, F.; Ahmad, B. Application of TOPSIS Method for Decision Making. Int. J. Sci. Res. Math. Stat. Sci. 2020, 7, 76–81. [Google Scholar]
- Dimitrijević, B. Višeatributivno Odlučivanje–Primene u Saobraćaju i Transportu; Univerzitet u Beogradu–Saobraćajni fakultet, Vojvode Stepe 305: Beograd, Srbija, 2017. [Google Scholar]
- Lakićević, M.; Srđević, B. Multiplicative version of Promethee method in assesment of parks in Novi Sad. Matice Srp. Prir. Nauk. 2017, 132, 79–86. [Google Scholar] [CrossRef]
- Kangas, A.; Kurttila, M.; Hujala, T.; Eyvindson, K.; Kangas, J. Decision Support for Forest Management; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Grabisch, M. The application of fuzzy integrals in multicriteria decision making. Eur. J. Oper. Res. 1996, 89, 445–456. [Google Scholar] [CrossRef]
- Gérard, R.; Kaci, S.; Prade, H. Ranking alternatives on the basis of generic constraints and examples—A possibilistic approach. In Proceedings of the 12th International Joint Conference on Artificial Intelligence (IJCAI 2007), Hyderabad, India, 6–12 January 2007; pp. 393–398. [Google Scholar]



| A—The Personal Characteristics of Employee |
| —The employee maintains personal discipline |
| —The employee could modify knowledge and skills |
| —The employee easily learns new tasks, technologies, and procedures |
| —The employee gives suggestions for improving the work processes |
| B—Task performance |
| —The employee follows the rules and procedures of the organization |
| —Employee’s mistakes were not critical in terms of safety and work quality |
| —The employee almost never breaks rules |
| C—Employee employee relationship approaches |
| —The employee is willing to devote time, energy, and effort to adapts to the changing work environment and new employees in the team |
| —The employee willingly adjusting on-the-job behavior and shows respect for others’ values and customs |
| —The employee active participates in joint activities with other employees. |
| D—Effectiveness of communication |
| —The employee has good verbal skills in the interaction between members of the working team |
| —The communication between the employee and manager is careful and effective |
| —The employee has good verbal skills to organize work in small groups |
| n | Minimum | Maximum | Mean | Std. Deviation | |
|---|---|---|---|---|---|
| 35 | 2.00 | 5.00 | 4.4571 | 1.03875 | |
| 35 | 1.00 | 5.00 | 3.5429 | 1.14642 | |
| 35 | 1.00 | 5.00 | 3.4000 | 1.26491 | |
| 35 | 1.00 | 5.00 | 2.7429 | 1.31379 | |
| 35 | 2.00 | 5.00 | 4.1714 | 0.61767 | |
| 35 | 2.00 | 5.00 | 3.6571 | 0.99832 | |
| 35 | 1.00 | 5.00 | 3.0571 | 1.23533 | |
| 35 | 2.00 | 5.00 | 3.6857 | 0.90005 | |
| 35 | 1.00 | 5.00 | 4.4000 | 0.97619 | |
| 35 | 1.00 | 5.00 | 3.2286 | 1.33032 | |
| 35 | 2.00 | 5.00 | 4.6571 | 0.63906 | |
| 35 | 3.00 | 5.00 | 4.5429 | 0.61083 | |
| 35 | 1.00 | 5.00 | 2.5714 | 1.44070 |
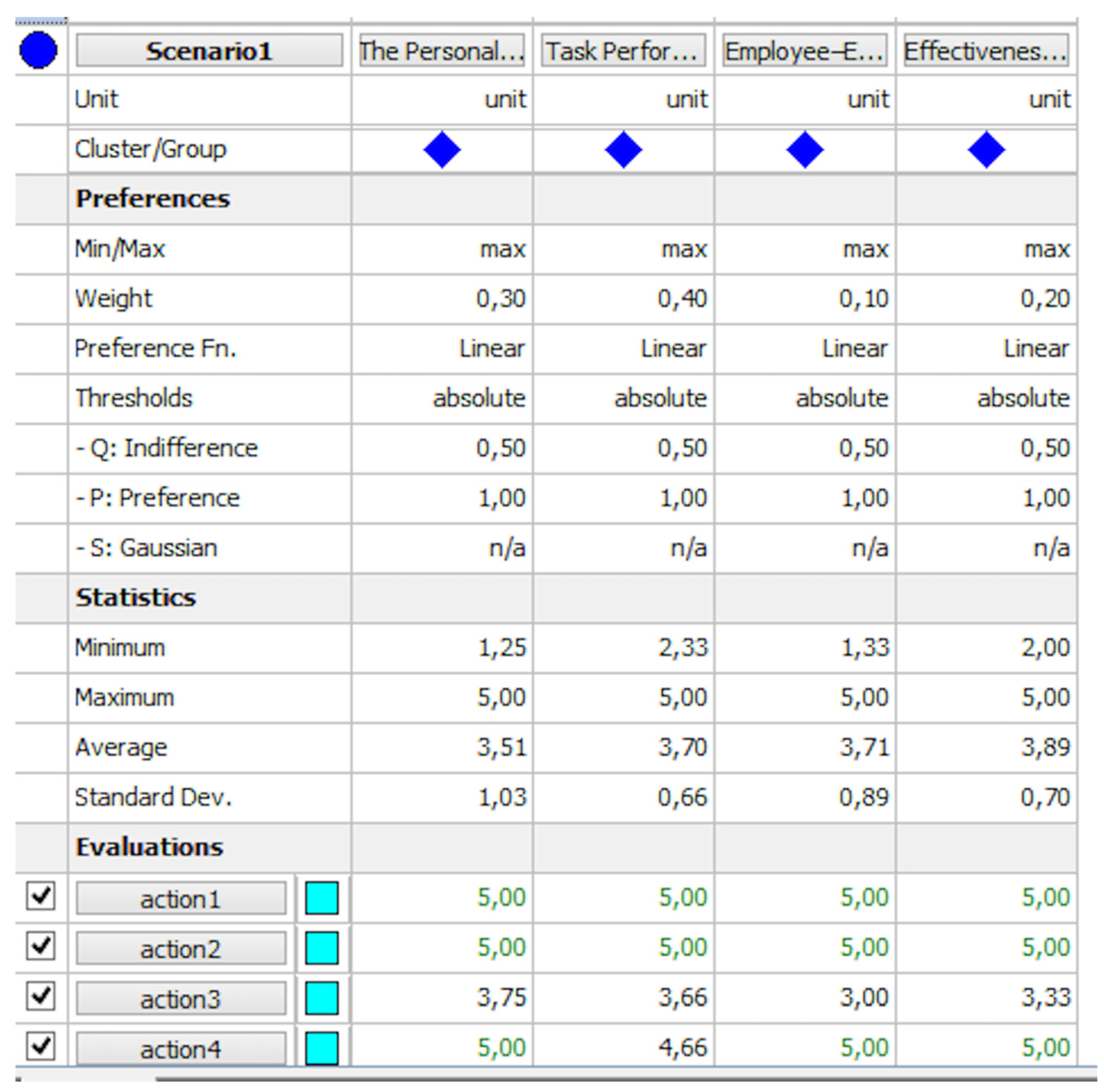
| The Personal Characteristics of Employee | Task Performance | Employee–Employee Relationship Approaches | Effectiveness of Communication | |
|---|---|---|---|---|
| 0.3 | 0.4 | 0.1 | 0.2 |
| Employee | ||||||||||||
| 5.0 | 5.0 | 3.6 | 5.0 | 2.6 | 4.5 | 4.5 | 4.0 | 4.5 | 2.8 | 3.7 | 3.7 | |
| Employee | ||||||||||||
| 4.2 | 2.1 | 3.7 | 4.2 | 3.0 | 2.2 | 3.1 | 3.6 | 2.6 | 2.6 | 3.2 | 3.6 | |
| Employee | ||||||||||||
| 1.2 | 2.4 | 2.3 | 2.2 | 3.2 | 2.1 | 2.0 | 1.4 | 2.8 | 5.0 | 3.9 |
| Employee | ||||||||||||
| 5.0 | 5.0 | 3.6 | 4.6 | 4.0 | 4.4 | 4.5 | 3.4 | 4.6 | 3.6 | 2.8 | 3.4 | |
| Employee | ||||||||||||
| 4.5 | 3.6 | 3.2 | 2.8 | 2.8 | 3.2 | 3.5 | 2.8 | 3.6 | 4.0 | 4.0 | 4.0 | |
| Employee | ||||||||||||
| 2.6 | 2.6 | 2.8 | 3.2 | 3.2 | 2.8 | 2.7 | 3.2 | 3.6 | 3.5 | 2.9 |
| Employee | ||||||||||||
| 5.0 | 5.0 | 2.9 | 5.0 | 2.2 | 4.2 | 4.6 | 4.0 | 4.6 | 2.3 | 4.0 | 3.4 | |
| Employee | ||||||||||||
| 4.2 | 3.4 | 4.2 | 4.2 | 3.9 | 2.9 | 3.2 | 4.3 | 3.6 | 3.6 | 4.3 | 3.9 | |
| Employee | ||||||||||||
| 1.4 | 1.4 | 3.6 | 3.5 | 3.2 | 3.5 | 2.5 | 1.9 | 5.0 | 5.0 | 2.5 |
| Employee | ||||||||||||
| 5.0 | 5.0 | 3.2 | 5.0 | 4.0 | 4.3 | 4.6 | 4.4 | 4.6 | 4.6 | 3.2 | 4.2 | |
| Employee | ||||||||||||
| 4.6 | 3.1 | 3.8 | 4.6 | 4.2 | 3.8 | 3.8 | 4.6 | 2.8 | 3.4 | 3.5 | 4.2 | |
| Employee | ||||||||||||
| 2.0 | 2.0 | 3.4 | 3.1 | 3.1 | 3.4 | 2.8 | 2.5 | 2.8 | 5.0 | 3.8 |
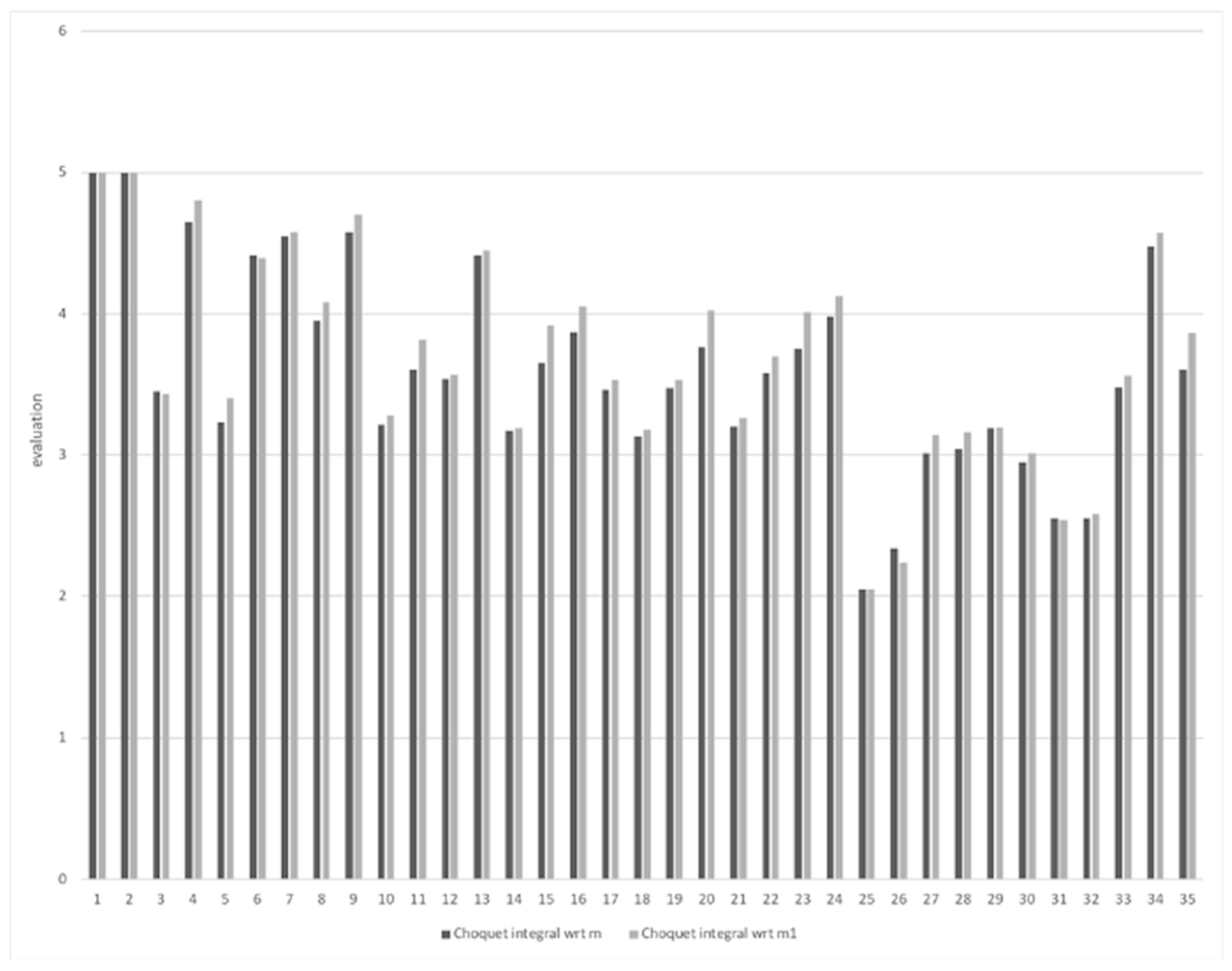
| Employee | ||||||||||||
| 5.00 | 5.00 | 3.45 | 4.65 | 3.23 | 4.41 | 4.55 | 3.95 | 4.58 | 3.21 | 3.60 | 3.52 | |
| Employee | ||||||||||||
| 4.41 | 3.17 | 3.65 | 3.87 | 3.46 | 3.17 | 3.47 | 3.76 | 3.20 | 3.58 | 3.75 | 3.98 | |
| Employee | ||||||||||||
| 2.05 | 2.34 | 3.01 | 3.04 | 3.19 | 2.95 | 2.55 | 2.55 | 3.48 | 4.48 | 3.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumnić, S.; Mostarac, K.; Ninović, M.; Jovanović, B.; Buhmiler, S. Application of the Choquet Integral: A Case Study on a Personnel Selection Problem. Sustainability 2022, 14, 5120. https://doi.org/10.3390/su14095120
Dumnić S, Mostarac K, Ninović M, Jovanović B, Buhmiler S. Application of the Choquet Integral: A Case Study on a Personnel Selection Problem. Sustainability. 2022; 14(9):5120. https://doi.org/10.3390/su14095120
Chicago/Turabian StyleDumnić, Slaviša, Katarina Mostarac, Milena Ninović, Bojan Jovanović, and Sandra Buhmiler. 2022. "Application of the Choquet Integral: A Case Study on a Personnel Selection Problem" Sustainability 14, no. 9: 5120. https://doi.org/10.3390/su14095120
APA StyleDumnić, S., Mostarac, K., Ninović, M., Jovanović, B., & Buhmiler, S. (2022). Application of the Choquet Integral: A Case Study on a Personnel Selection Problem. Sustainability, 14(9), 5120. https://doi.org/10.3390/su14095120






