3.2. Objective Function
This study aims to appropriately size PV, WT, and EVCS for stable system operation. The following
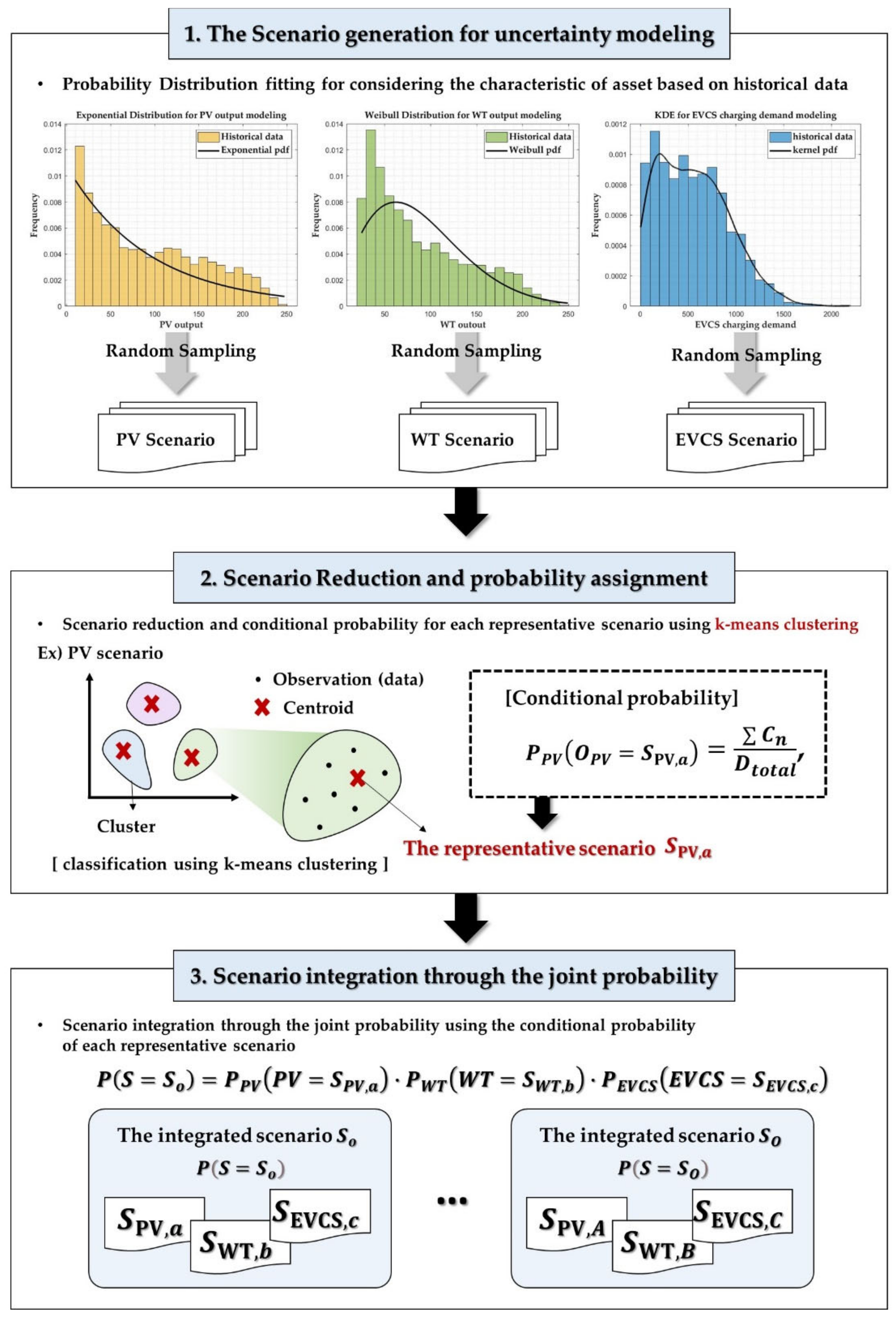
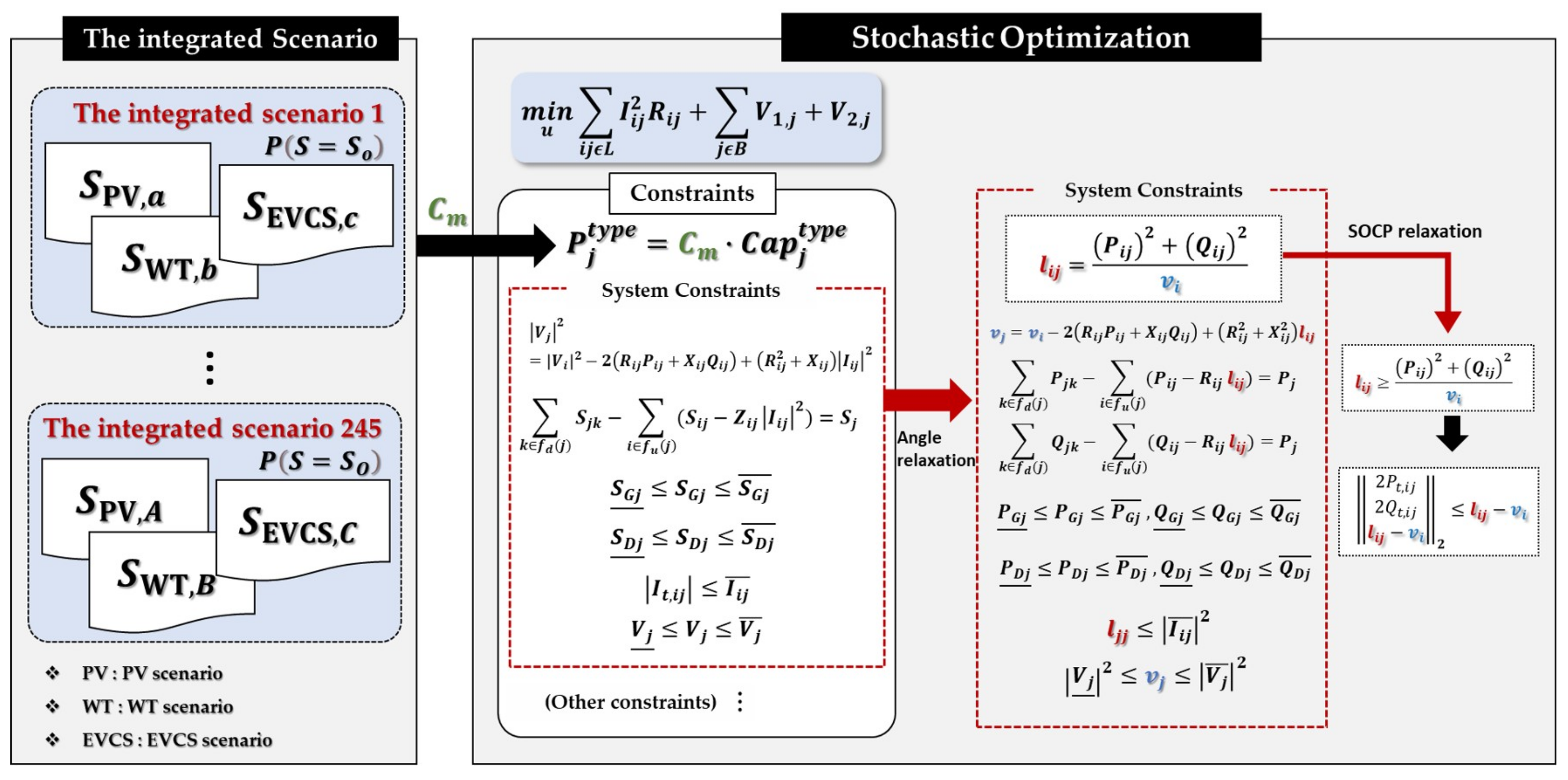
Figure 3 shows the proposed framework for stochastic programming, and
Table 2 lists the nomenclature of the proposed optimization problem.
The objective function of the optimization model was to minimize the voltage deviation and line loss using a multi-objective function. This function was formulated as follows:
Here,
and
denote the sets of lines and buses in the power system, respectively.
represents the line connecting the
-th and
-th bus.
and
represent the current and resistance, respectively, of the line
.
is the nominal voltage and
is the complex bus voltage at
-th bus. That is,
is the line loss of line
and
is the voltage deviation.
is the set of control variables, which is described in detail in the constraint explanation. However, the objective function is nonlinear owing to the absolute value of the function’s second term. To convexify the objective function, Equation (10) can be rewritten with auxiliary variables as follows:
Here,
and
are auxiliary variables for convexification and positive values. These variables have no physical meaning in the power system, just for linearization. According to the convexification of Equation (11), related constraints were added to ensure equivalence to Equation (10), as follows:
3.3. Constraints
In general, the AC power flow is nonlinear and non-convex in nature; therefore, DC power flows are extensively applied in practice, and these flows are formulated as linearized power flow equations. DC power flow is convex and makes simulation faster. However, the optimal solution of the DC power flow is incorrect because errors from linearization are inevitable. In this study, the AC power flow was applied to the optimization model and relaxed in the SOCP model with a branch flow model and the remaining AC power flow.
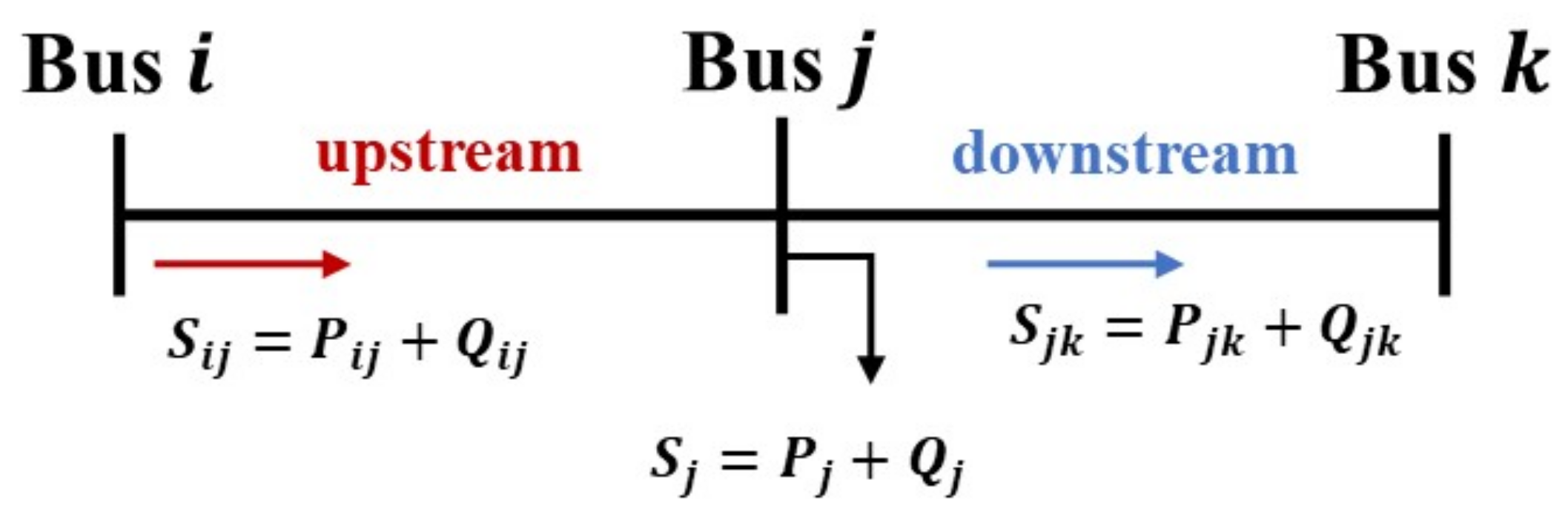
Figure 4 presents a summary of the notations used in the branch flow model employed in this study.
and
denote the complex powers in branches
and
, respectively.
, and
are the active and reactive powers in each branch, respectively.
,
, and
are the injected complex, active, and reactive powers, respectively, of bus
. The equations below represent Ohm’s law and the definition of branch power flow, respectively:
where
denotes complex conjugate of
. Based on the above definition, the power balance at each bus was expressed as follows:
and
are the sets of downstream and upstream buses connected to bus
. The complex power at the upstream bus is the active power loss attributable to the line impedance. Furthermore, substituting Equation (15) into Equation (14) produces
; then, by taking the squared magnitude, we obtain
However, the equations above are nonconvex because
S is a complex number reflecting the angle difference between the real and reactive power, and the bus voltage and branch flow equations include the magnitude squared forms of
and
. To convexify these equations, auxiliary variables were introduced as
and
, and these notations were substituted into
and
. Let
, and
. Thus, these constraints should be separated as real variables and relaxed using auxiliary variables, as follows:
Here,
and
denote the subtraction of the consumption and generation power at bus
and can be expressed as
and
, respectively. Indexes
and
denote the amount of generation and consumption at bus
. The constraint-related auxiliary variables
were rewritten as follows:
Equations (18) and (19) represent the real and reactive power, respectively, separated from the complex power. Then, the constraint due to the auxiliary variable was formulated to represent the relation between the auxiliary variables, real power, and reactive power:
In the power system, the
,
of each bus have limited real and reactive powers of generation or demand under conditions of system:
In this study, the power-consuming system assets were the EVCS and generic load, and the power-generating assets were the DG units and substation (slack bus). The
of the power-generating connected bus and the
of the power-consuming connected bus were zero.
and
can be classified into five types according to the connected assets: slack, PV, WT, EVCS, and generic load. The capacity of each asset also limits the maximum active power at the connected bus and should always be positive. This can be expressed as
where
and
represent the capacities of the power-consuming and power-generating assets, respectively, and
and
denote the maximum active power at the asset-connected bus. Furthermore, the EVCS should be able to supply the minimum power for charging, to ensure driver’s convenience; this depends on the EV penetration
, which is expressed as
where
denotes the minimum power of the EVCS. The output of the assets should be lower than the capacity and should always have a positive value:
and are the asset output and capacity, respectively.
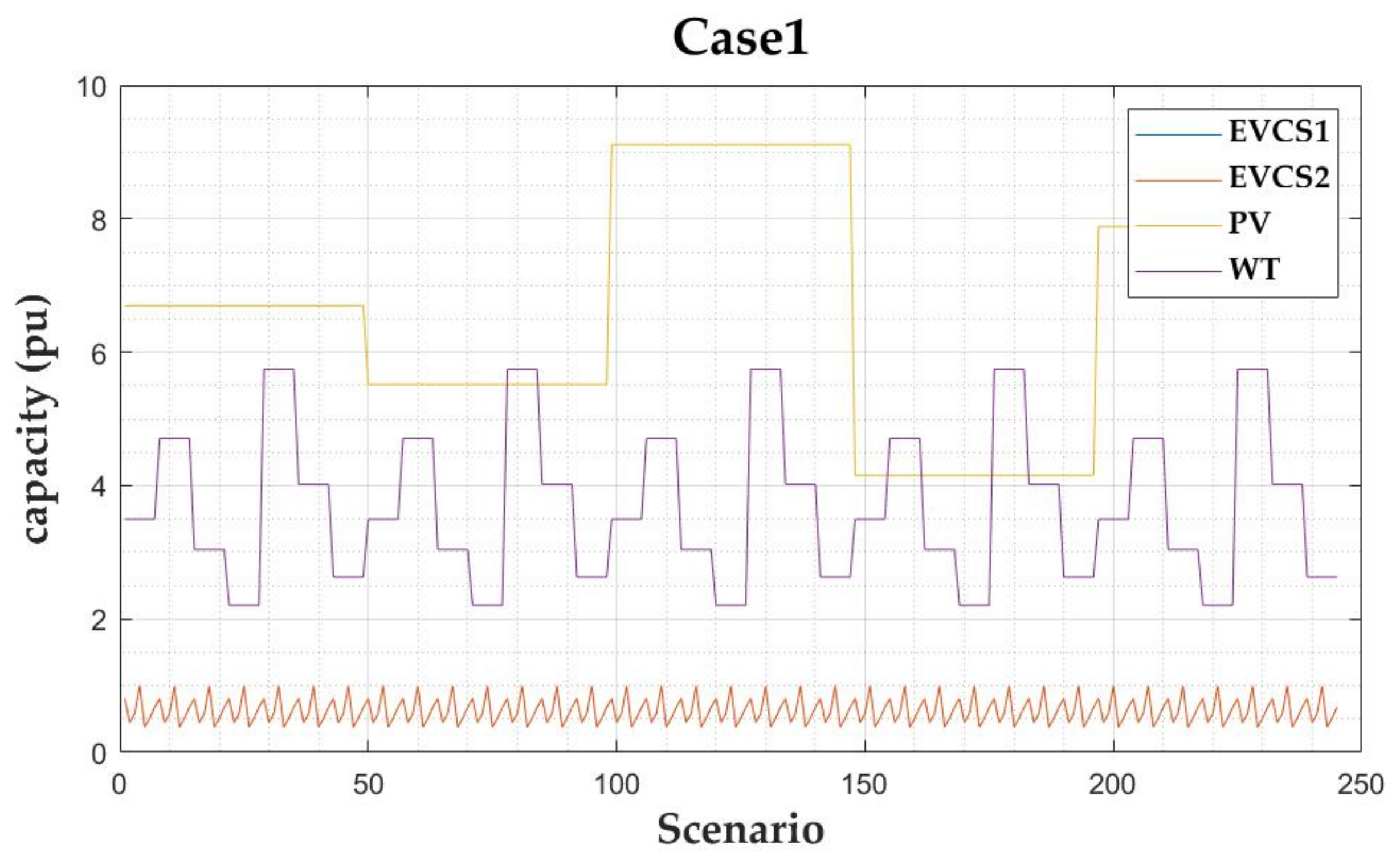
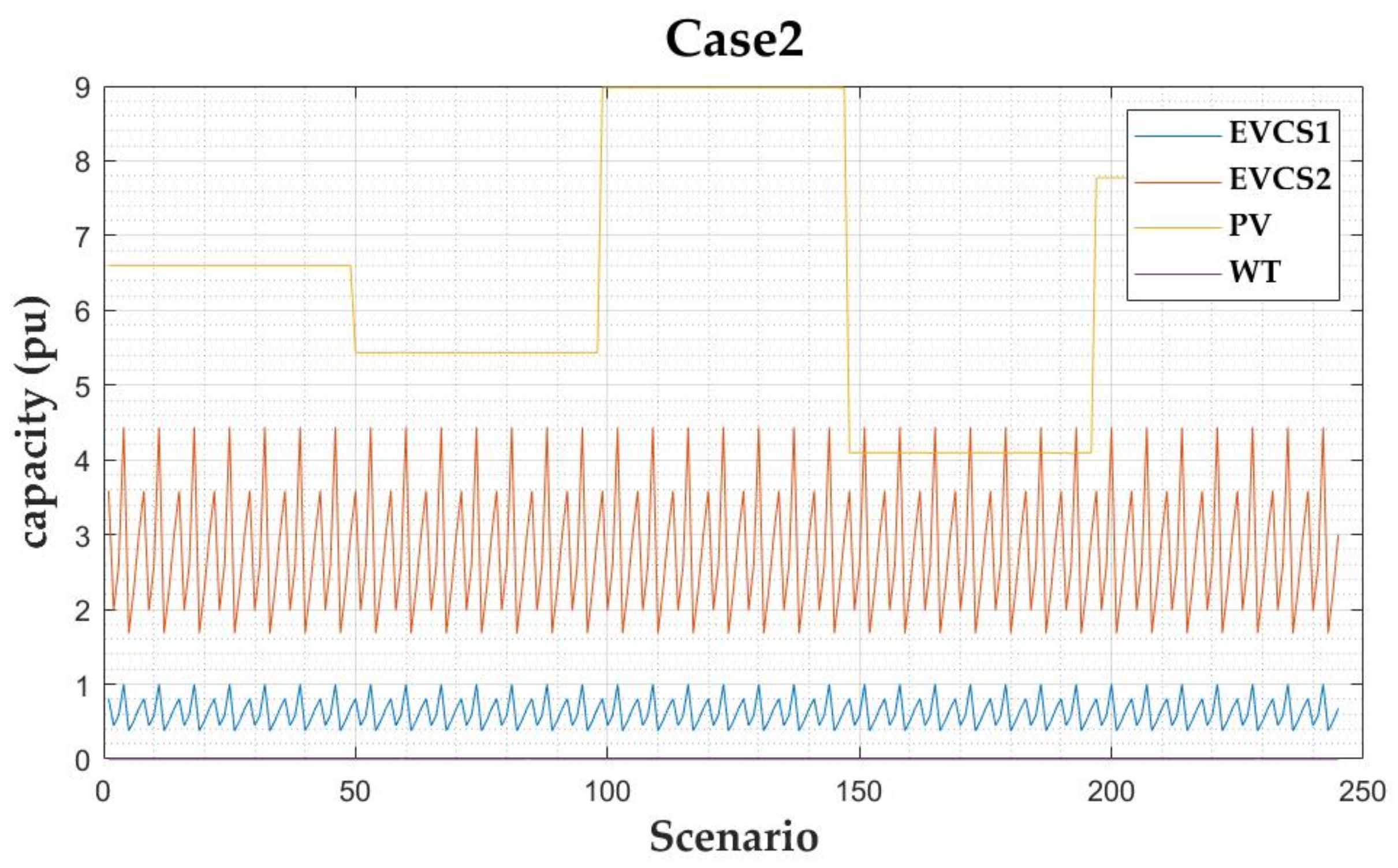
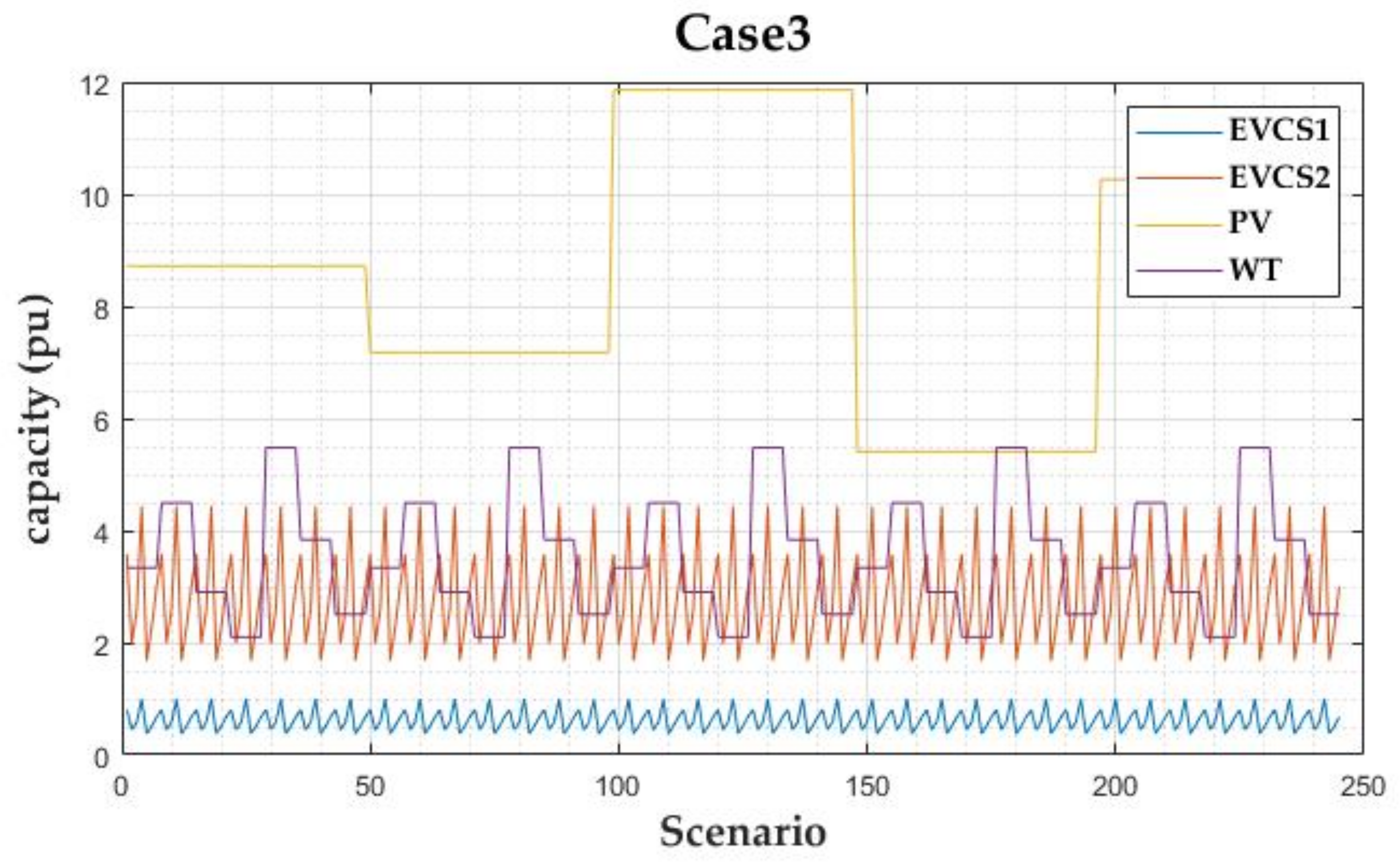
For stochastic programming, the integrated scenario described in
Section 2 and the asset output coefficient
were applied as follows:
Here,
denotes the normalization coefficient of the
scenario. This can be used to reflect the output uncertainty. The reactive power was determined by the active power, because it is assumed that the system assets are operated at a fixed power factor:
Here,
is the power factor of each asset and differs for each one. The line current was limited to the permitted current, to prevent thermal overload:
In addition, the voltage magnitude should be maintained between the allowable lower and upper limits, and the slack bus voltage should be fixed at 1.0 pu:
However, this problem is still nonconvex, owing to the quadratic equalities in Equation (22). To convexify this problem, conic relaxation was applied to transform the problem into an SOCP. Finally, this constraint was relaxed to inequalities:
This inequality constraint is equivalent to the standard form of the SOCP:
Because the objective function is linear, this optimization problem is a SOCP optimization. In a spanning-tree radial distribution system, the AC power flow relaxation is always exact; the exactness and validation of the SOCP relaxation in AC power flow are proven and comprehensively described in [
27,
28].
Finally, the proposed optimization problem for the optimal sizing of system assets was reformulated as follows:
In the above constraints, the constraints for AC power flow are Equations (18–20), (23), (24), (32), (33) and (35). Equations (12) and (13) are for linearization of the objective function, and other equations are for optimal sizing of each asset.