Fuzzy Hysteresis Current Controller for Power Quality Enhancement in Renewable Energy Integrated Clusters
Abstract
:1. Introduction
- ▪
- Proposes the idea of interoperating many adjacent microgrids in an urban energy community to form a renewable-energy-based microgrid cluster. This increases the energy availability, thereby improving the power supply reliability by allowing the cluster to manage its own energy requirement rather than relying on the utility grid;
- ▪
- Proposes a new inverter control mechanism, namely “Fuzzy Hysteresis Current Controller-based Pulse Width Modulation (FHCC-PWM)”, which improves the power supply quality. The proposed fuzzy logic improves the control loop ability to regulate the system under variety of operating conditions.
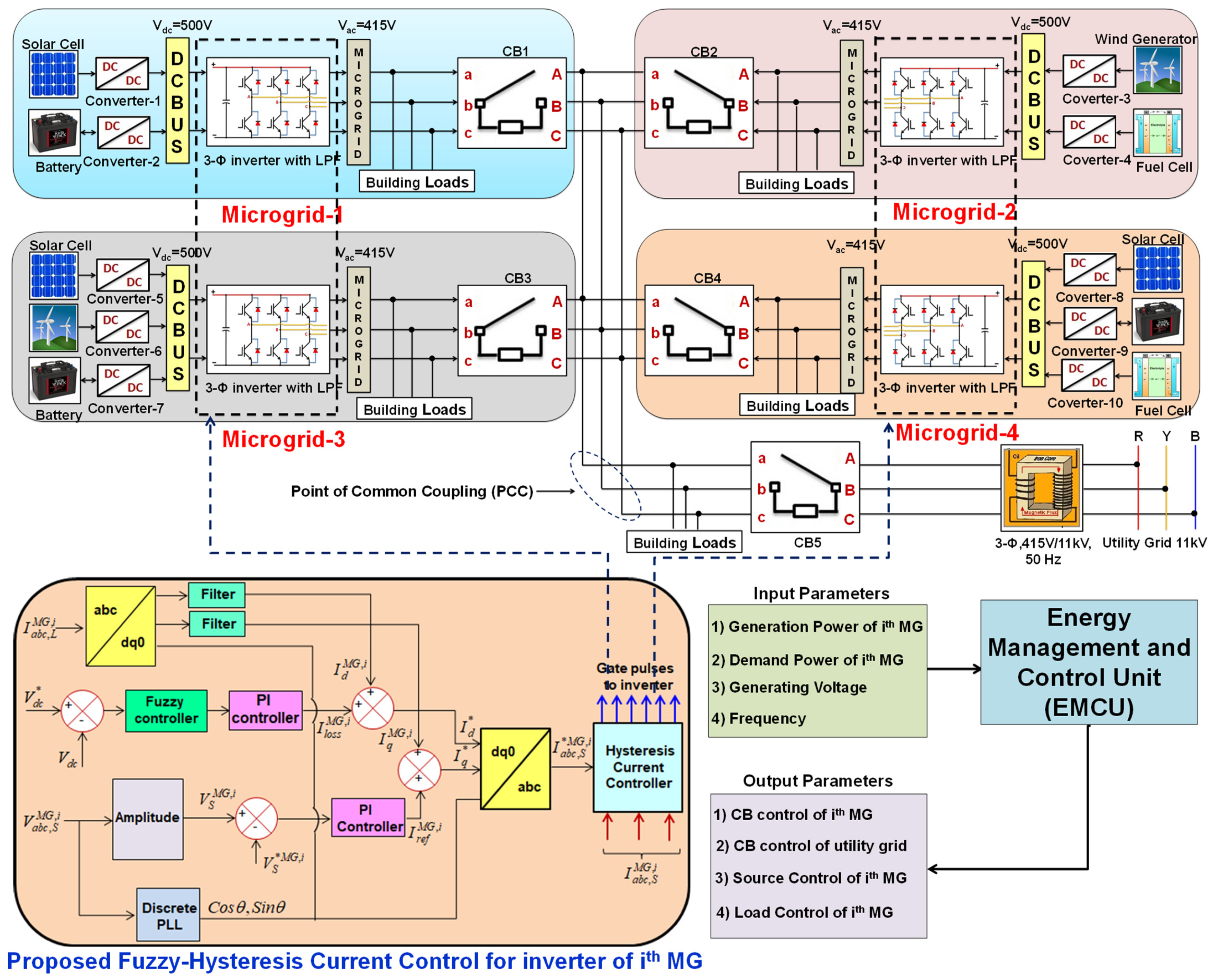
2. Description of the Components Present in Cluster Microgrids
2.1. Description of ST-PWM Based Multilevel Inverter
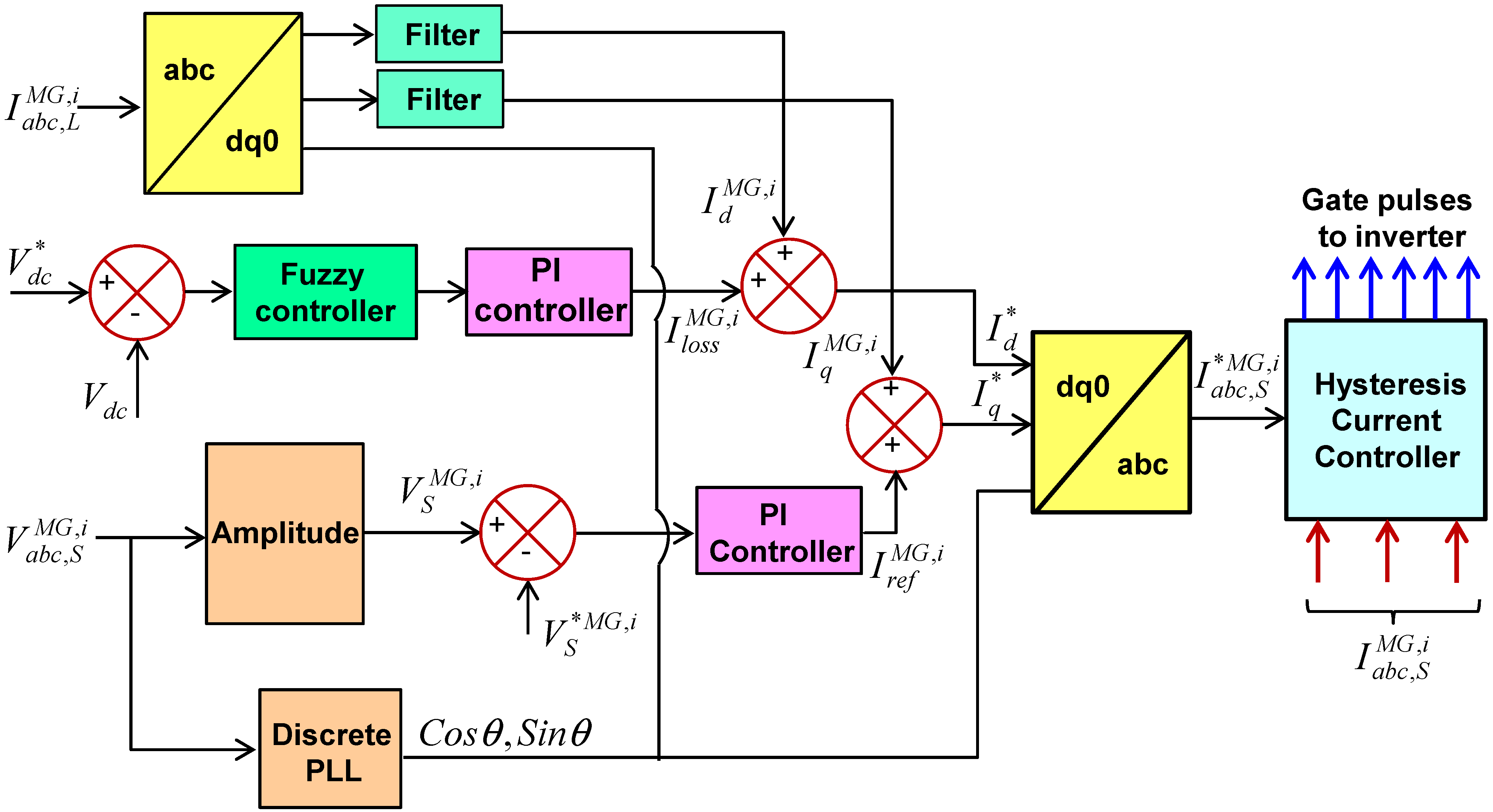
2.2. Description of Proposed FHCC Based Inverter
2.3. Description of Energy Management Control Unit (EMCU)
2.4. Performance Issues and Measures
- ▪
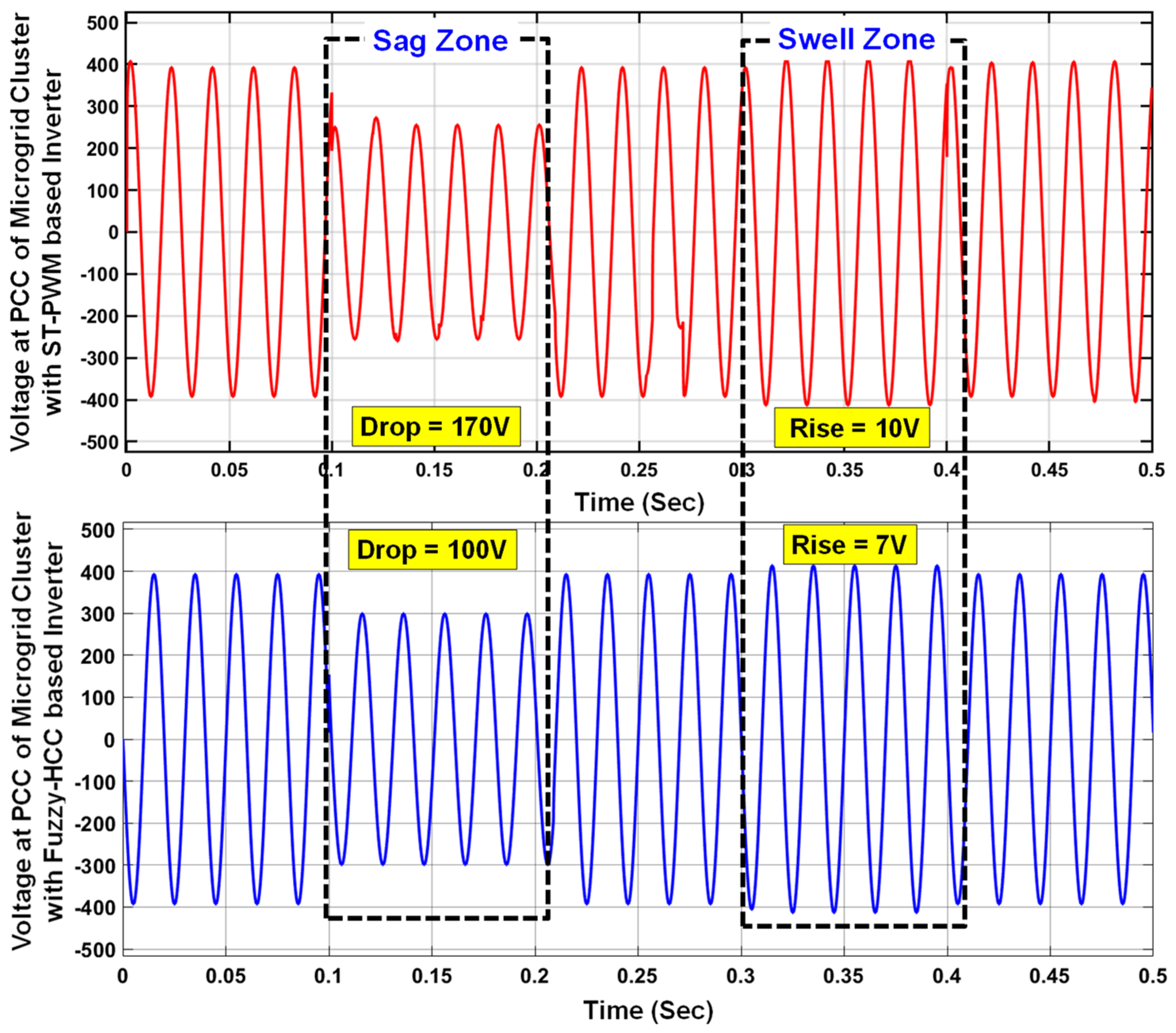
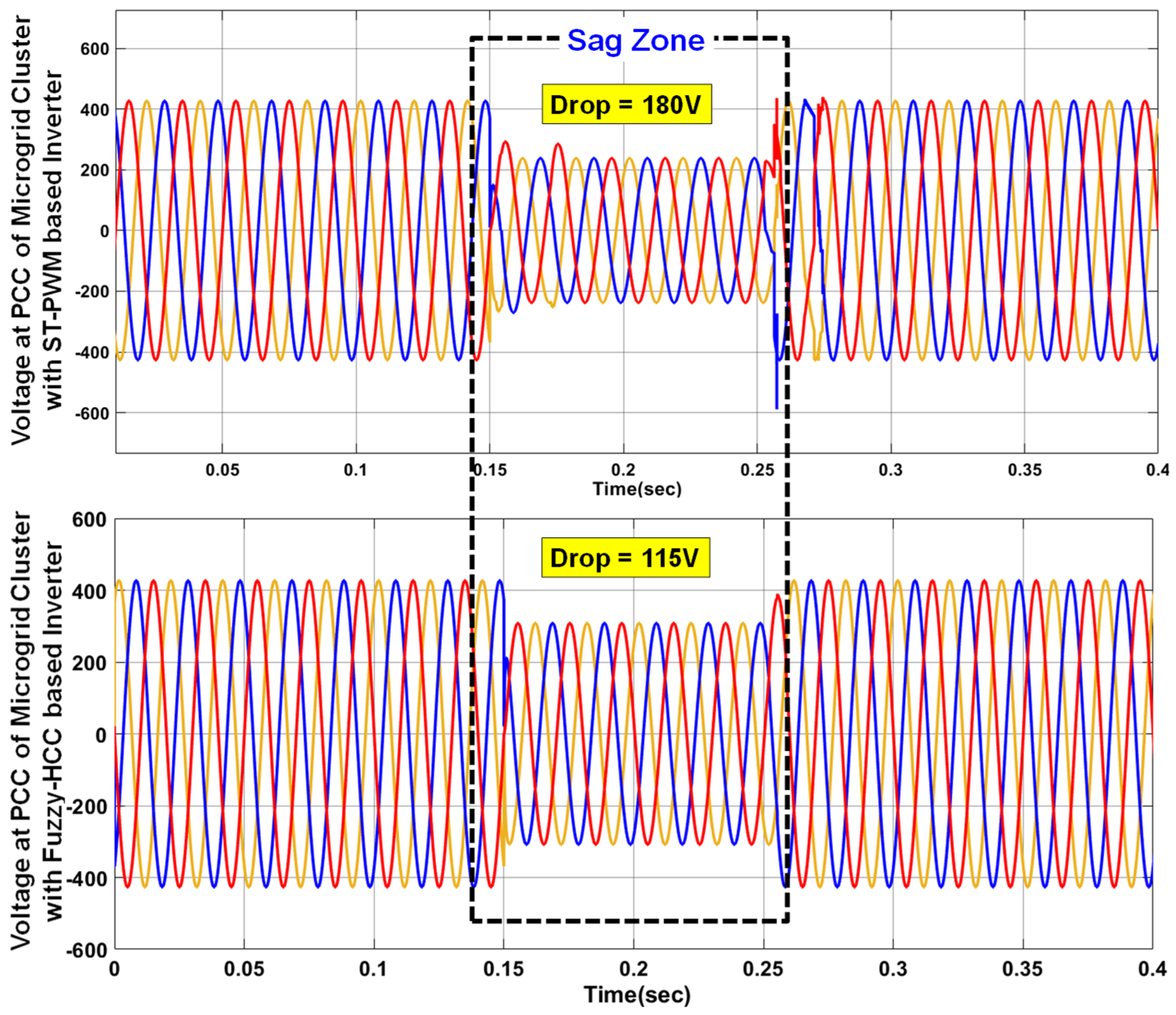
- Voltage sag/swell: Root mean square (RMS) value of voltage () is calculated by squaring all the sampled voltages and is averaged over a window with a duration of one cycle at the sampling instant x given in Equation (1). Voltage sag and swell are the drop and rise that are observed in the RMS value of the voltage that occurs due to sudden rise and fall of the load, respectively.
- ▪
- Voltage imbalance: It is defined as the ratio of negative sequence voltage to positive sequence voltage expressed in terms of the percentage given in Equation (2).
- ▪
- Frequency variations: The load frequency is to be continuously monitored and maintained close to 50 Hz with the penetration of DG sources in microgrids and is given in Equation (3).
- ▪
- Total harmonic distortion (THD): THD is the measure for the level of distortion (harmonic) present in a three-phase power system. It is calculated by measuring the ratio between the amplitudes (RMS value) of a set of total higher-frequency components with respect to harmonics and the value at fundamental frequency components given in Equations (4) and (5).
3. Proposed Fuzzy Hysteresis Current Controller (FHCC)
3.1. Reference (Source) Current Generation
- ▪
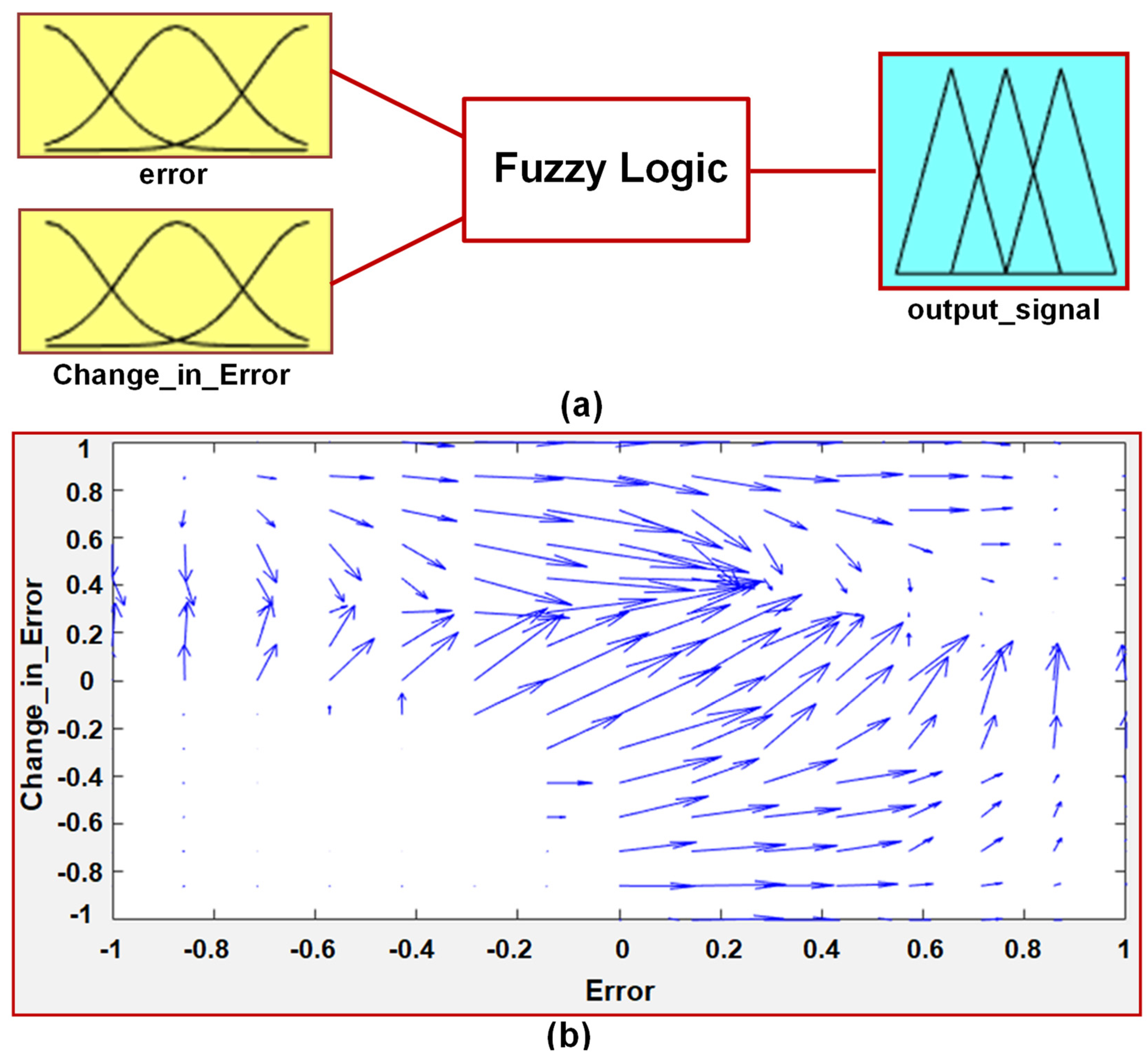
- Scheme of fuzzy logic: In this scheme, the fuzzy controller of the proposed inverter is implemented by considering and evaluating some linguistic rules. The internal process of fuzzy controller is explained as follows. The input error value is calculated by taking the difference between the reference voltage (V*dc) and sensed voltage (Vdc). Here, both input signals, i.e., and , are numerical variables and are transformed to linguistic variables by considering the following fuzzy sets as given. The characterization of fuzzy logic is as follows:
- Consists of seven fuzzy sets (N-3, N-2, N-1, E0, P1, P2, and P3);
- For simplicity, the triangular membership function is considered;
- Mamdani fuzzy inference mechanism is used;
- “Centroid method” is used for defuzzification.
- ▪
- Fuzzification: In this process, instead of numerical values, fuzzy uses linguistic variables. In the system, the error signal can be assigned to negative large (N-3), negative medium (N-2), negative small (N-1), extreme zero (E0), positive small (P1), positive medium (P2), and positive large (P3). This process converts numerical variables to linguistic variables (fuzzy numbers), and the surface plot of the fuzzy logic controller is shown in Figure 4.
- ▪
- Rule elevation: Basic operations of fuzzy logic are needed to evaluate fuzzy set rules shown in Figure 5, which are obtained by considering “union”, “intersection”, and “complement” functions. Considering two fuzzy sets ( and ), the universe and the following Equations (16)–(18) are the basic relations performed on fuzzy sets.
- ▪
- Process of getting defuzzified output: With the process of defuzzification, a fuzzy set is converted to its crispest version. The mathematical expression for obtaining defuzzified output is as given in Equation (19).
- ▪
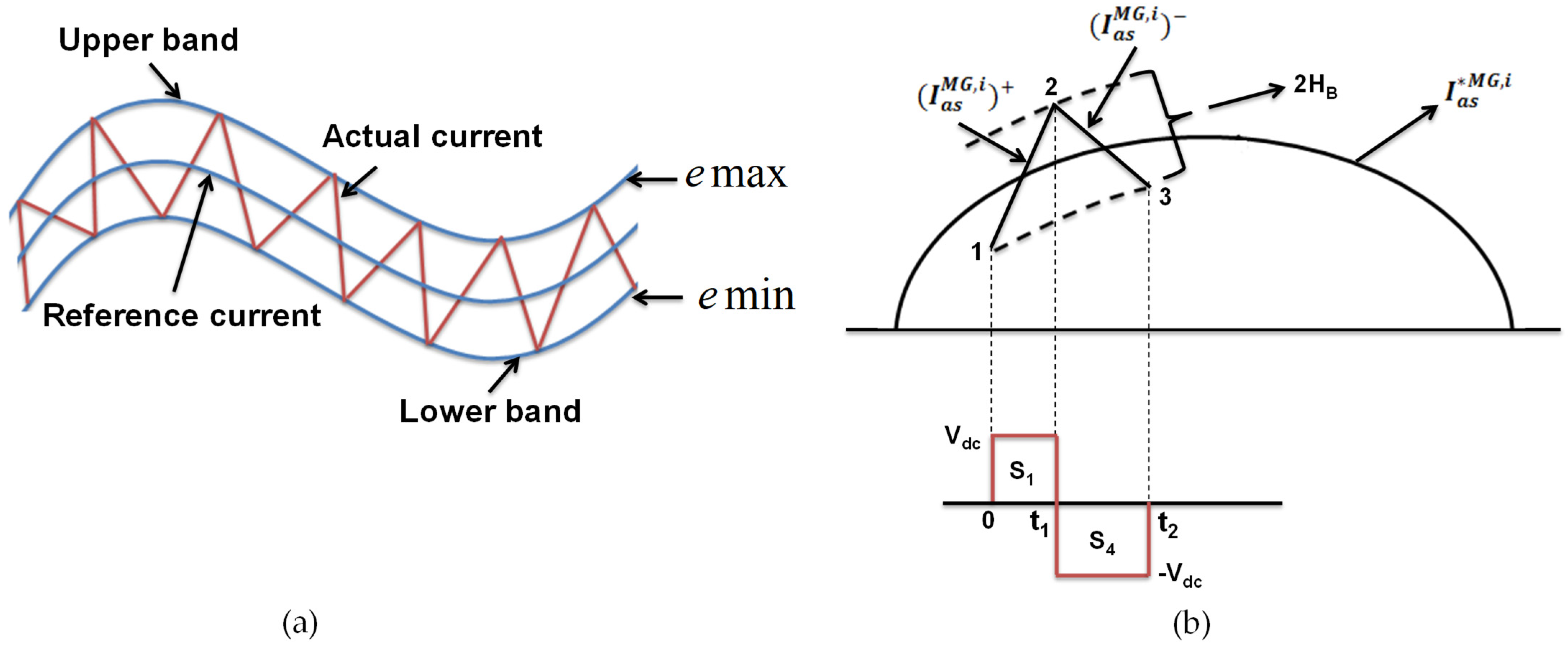
3.2. Gate Pulses Generation from Hysteresis Current Controller
- (1)
- If , then inverter upper switch is OFF, and lower switch is ON for leg corresponding to phase A of the ith microgrid;
- (2)
- If , then inverter upper switch is ON, and lower switch is OFF for leg corresponding to phase A of the ith microgrid.
4. Results and Discussion
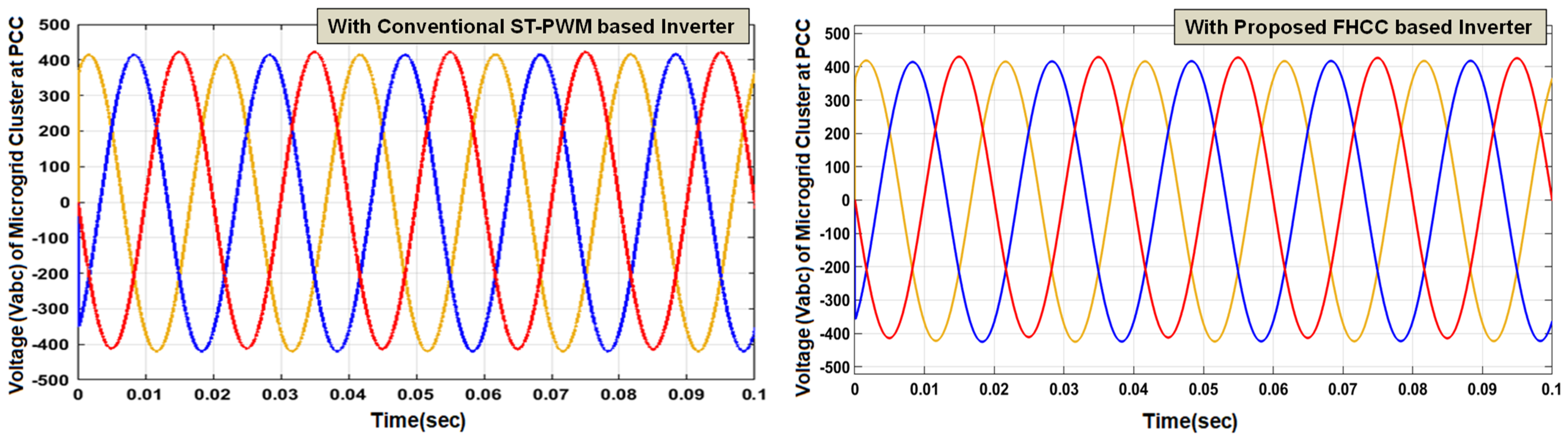
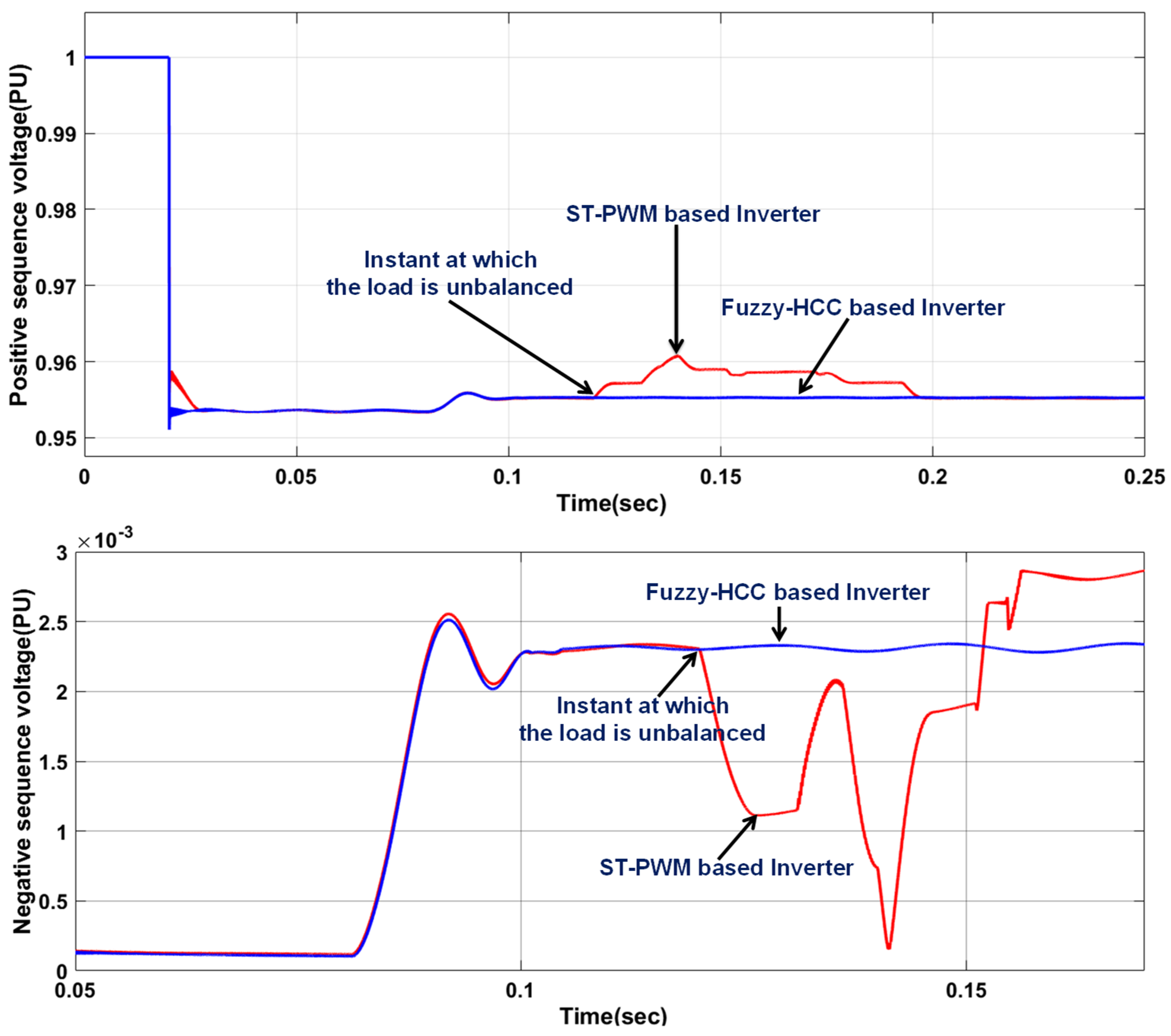
4.1. Analysis of Voltage Characteristics
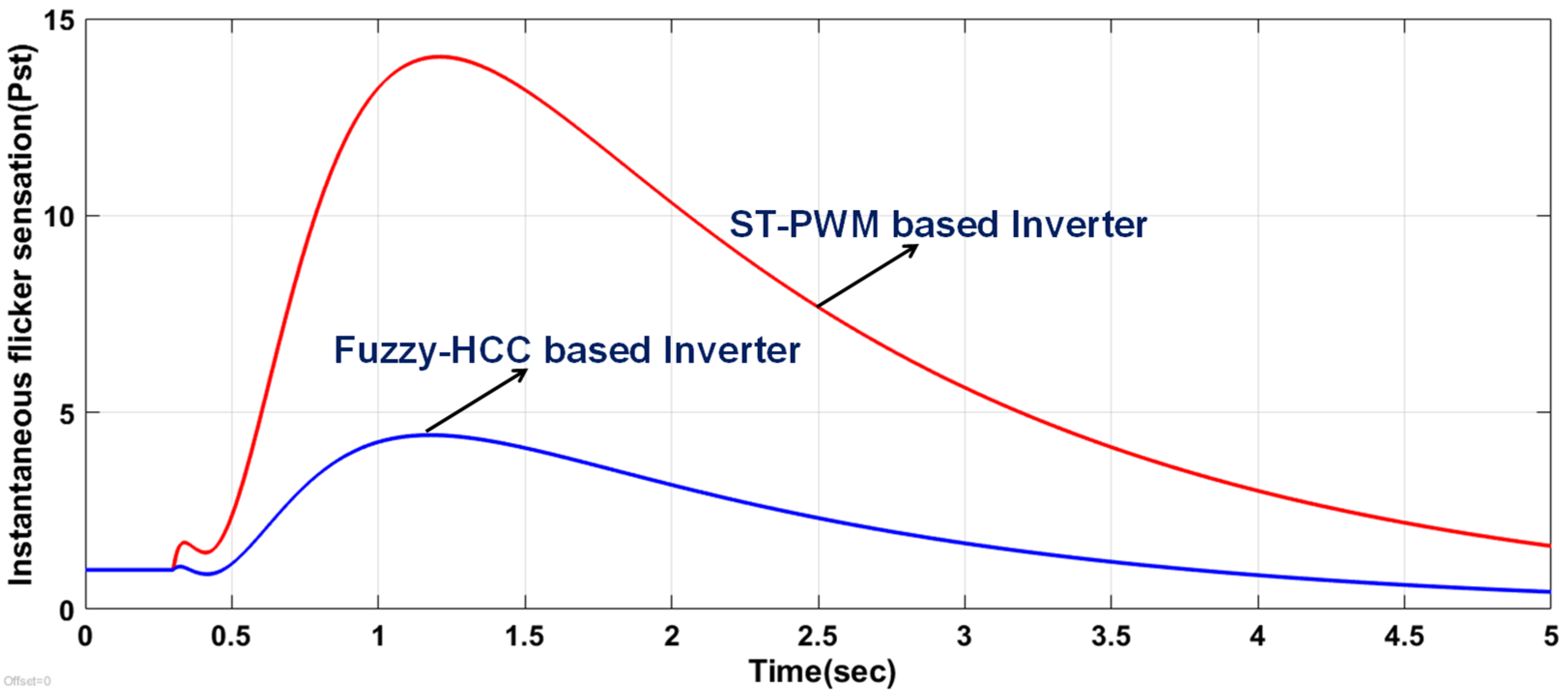
4.2. Analysis of Frequency Characteristics
- Switch the inductive load ON at 0.5 s and OFF at 0.8 s;
- Switch the capacitive load ON at 1.3 s and OFF at 1.6 s:
- Observe deviation in case of dynamic loading.
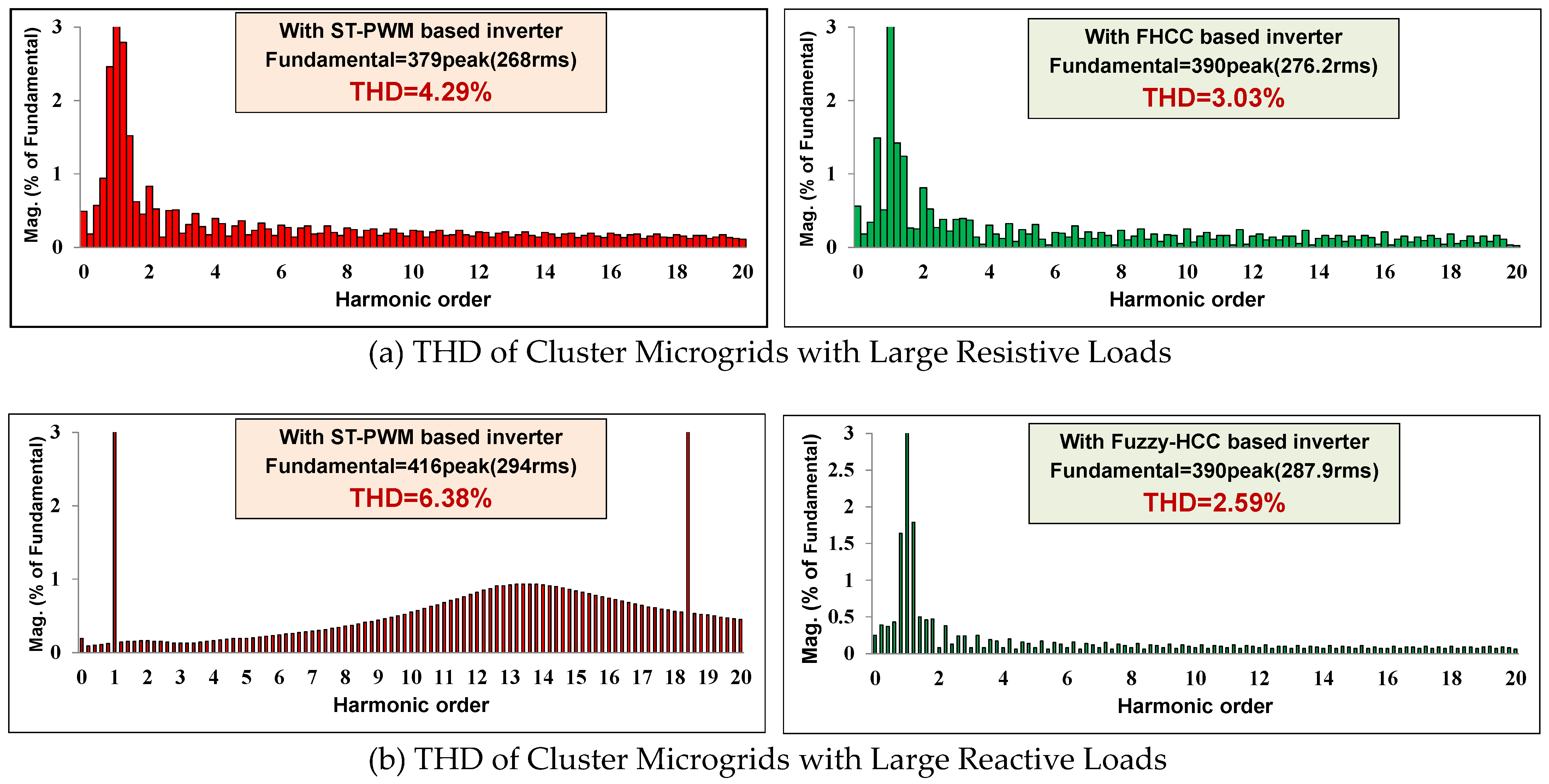
4.3. Analysis of THD
5. Conclusions
- ▪
- The proposed FHCC-based inverter is easy to build, as it does not require any clamping diodes and capacitors when compared to conventional configurations. This further reduces the switching losses.
- ▪
- The proposed inverter employs fuzzy logic, which reduces the complexity in mathematical formulation.
- ▪
- From results, the FHCC-based inverter:
- -
- Reduces the voltage sag to 25% when compared with conventional ST-PWM-based inverter (42.5%) and recent FSV-PWM-based inverter (29.5%) when the system is subjected to single line-to-ground fault. Similarly, it reduces the voltage sag to 27.7% when compared with conventional ST-PWM-based inverter (43.37%) and recent FSV-PWM-based inverter (38.6%) when subjected to arcing loads;
- -
- Reduces the voltage swell to 2.5% when compared with conventional ST-PWM-based inverter (4.76%) and recent FSV-PWM-based inverter (2.73%) when subjected to sudden disconnection of major part (75%) of the system load;
- -
- Reduces the voltage unbalance to 2.46% when compared with conventional ST-PWM-based inverter (3.08%) and recent FSV-PWM-based inverter (2.87%) when subjected to large reactive loads injected into the system;
- -
- Reduces the settling time of the system to 0.35 s when compared with conventional ST-PWM-based inverter (0.55 s) and recent FSV-PWM-based inverter (0.42 s);
- -
- Reduces the frequency deviation of the system to 0.3% when compared with conventional ST-PWM-based inverter (1%) and recent FSV-PWM-based inverter (0.45%);
- -
- Reduces the total harmonic distortion of the system to 3.03% when compared with conventional ST-PWM-based inverter (4.29%) and recent FSV-PWM-based inverter (3.85%) when subjected to large resistive loading. Similarly, it reduces the total harmonic distortion of the system to 2.59% when compared with conventional ST-PWM-based inverter (6.38%) and recent FSV-PWM-based inverter (4.73%) for large reactive loading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| MG | Microgrid | Direct axis current of ith MG in amps | |
| THD | Total Harmonic Distortion | Quadrature axis current of ith MG in amps | |
| DG | Distributed Generation | Loss component of current in ith MG in amps | |
| PQ | Power quality | Reference source current of d-axis in d-q frame in amps | |
| Frequency Droop coefficient | Reference source current of q-axis in d-q frame in amps | ||
| ∆f | Change in frequency in Hz | Three-phase source current of ith MG in a-b-c frame in amps | |
| Voltage (RMS) at a sampling instant x in volts | Three-phase source current of ith MG in α-β-ο frame in amps | ||
| Voltage (RMS) at ith MG at nth harmonic in volts | Three-phase source reference current of ith MG in a-b-c frame in amps | ||
| Current (RMS) at ith MG at nth harmonic in amps | Three-phase source reference current of ith MG in α-β-ο frame in amps | ||
| Voltage (RMS) at ith MG at fundamental frequency in volts | Actual current of ith MG in amps | ||
| Current (RMS) at ith MG at fundamental frequency in amps | Reference current of ith MG in amps | ||
| Three-phase load current of ith MG in amps | HB | Hysteresis band | |
| Three-phase voltage at PCC of ith MG in volts | Raising segment of current in phase A in amps | ||
| Reference DC voltage in volts | Falling segment of current in phase A in amps | ||
| Sensed DC voltage in volts | fc | Modulation frequency in Hz |
Appendix A
| Parameter | Typical Ratings |
| Irradiance of PV cell | (150–1000) kW/m2 |
| Temperature of PV cell | (20–45) °C |
| Electric charge (Q) | 1.6 × 10−19 Coulombs |
| Boltzmann’s constant | 1.3805 × 10−23 J/K |
| Base power of wind turbine | 1.1 kVA |
| Speed of wind | 10 m/s |
| Nominal voltage of Ni-cd battery | 88 Volts |
| Rated capacity of Ni-cd battery | 6.5 Ah |
| Gas constant of fuel cell | 8314.7 |
| No of cells in stack of fuel cell | 80 |
| Duty cycle of the boost converter | 0.76 |
| Switching frequency of the converter | 100 kHz |
| Cutoff frequency of low pass filter | 500 Hz |
| Transmission line length | 10 Km |
| Power of transformer | 300 kVA |
| Voltage | 415 Volts |
| DC capacitor voltage | 680 Volts |
| 0.19 | |
| 6.25 | |
| 0.19 | |
| 7.5 | |
| NB-3: (−1.333 −0.7 −0.3) |
| NM-2: (−0.726 −0.354 −0.1372) | |
| NM-1: (−0.277 −0.147 0) | |
| EZ0: (−0.1 0 0.1) | |
| PS + 1: (0 0.18 0.38) | |
| PM + 2: (0.18 0.38 0.75) | |
| PB + 3: (0.38 0.75 1.33) |
References
- Razmjoo, A.; Nezhad, M.M.; Kaigutha, L.G.; Marzband, M.; Mirjalili, S.; Pazhoohesh, M.; Memon, S.; Ehyaei, M.A.; Piras, G. Investigating Smart City Development Based on Green Buildings, Electrical Vehicles and Feasible Indicators. Sustainability 2021, 13, 7808. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Li, Z.; Ganji, M. Smart cities for a sustainable urbanization: Illuminating the need for establishing smart urban infrastructures. IEEE Electrif. Mag. 2018, 6, 16–33. [Google Scholar] [CrossRef]
- Warneryd, M.; Håkansson, M.; Karltorp, K. Unpacking the complexity of community microgrids: A review of institutions’ roles for development of microgrids. Renew. Sustain. Energy Rev. 2020, 121, 109690. [Google Scholar] [CrossRef]
- Rao, S.N.V.B.; Padma, K. A Review on Schemes for Interconnecting Microgrids of Urban Buildings. In Microelectronics, Electromagnetics and Telecommunications; Book chapter; Springer: Berlin/Heidelberg, Germany, 2020; pp. 431–438. [Google Scholar] [CrossRef]
- Kakran, S.; Chanana, S. Smart operations of smart grids integrated with distributed generation: A review. Int. J. Renew. Sustain. Energy Rev. 2018, 81, 524–534. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Vazquez, S.; Gil-de-Castro, A.; Roncero-Sanchez, P.; Moreno-Munoz, A. Microgrids Power Quality Enhancement Using Model Predictive Control. Electronics 2021, 10, 328. [Google Scholar] [CrossRef]
- Alshehri, J.; Khalid, M. Power Quality Improvement in Microgrids Under Critical Disturbances Using an Intelligent Decoupled Control Strategy Based on Battery Energy Storage System. IEEE Access 2019, 7, 147314–147326. [Google Scholar] [CrossRef]
- Lavanya, V.; Kumar, N.S. A Review: Control strategies for power quality improvement in microgrid. Int. J. Renew. Res. 2018, 8, 150–162. [Google Scholar]
- Amoozegar, D. DSTATCOM modelling for voltage stability with fuzzy logic PI current controller. Int. J. Electr. Power Energy Syst. 2016, 76, 129–135. [Google Scholar] [CrossRef]
- Gandoman, H.F.; Ahmadi, A.; Sharaf, A.M.; Siano, P.; Pou, J.; Hredzak, B.; Agelidis, V.G. Review of FACTS technologies and applications for power quality in smart grids with renewable energy systems. Int. J. Renew. Sustain. Energy Rev. 2018, 82, 502–514. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Ramadan, H.S. Power quality enhancement of grid connected fuel cell using evolutionary computing techniques. Int. J. Hydrog. Energy 2018, 43, 11568–11582. [Google Scholar] [CrossRef]
- Kaushal, J.; Basak, P. Power quality control based on voltage sag/swell, unbalancing, frequency, THD and power factor using artificial neural network in PV integrated AC microgrid. Sustain. Energy Grids Netw. 2020, 23, 100365. [Google Scholar] [CrossRef]
- Naderi, Y.; Hosseini, S.H.; Zadeh, S.G.; Mohammadi-Ivatloo, B.; Vasquez, J.C.; Guerrero, J.M. An overview of power quality enhancement techniques applied to distribute generation in electrical distribution networks. Int. J. Renew. Sustain. Energy Rev. 2018, 93, 201–214. [Google Scholar] [CrossRef] [Green Version]
- Kumar, Y.P.; Ravikumar, B.A. A simple modular multilevel inverter topology for the power quality improvement in renewable energy based green building microgrids. Electr. Power Syst. Res. 2016, 140, 147–161. [Google Scholar] [CrossRef]
- Barik, P.K.; Shankar, G.; Sahoo, P.K. Power quality assessment of microgrid using fuzzy controller aided modified SRF based designed SAPF. Int. Trans. Electr. Energy Syst. 2019, 30, e12289. [Google Scholar] [CrossRef]
- Esmaeili, M.; Shayeghi, H.; Valipour, K.; Safari, A.; Sedaghati, F. Power quality improvement of multimicrogrid using improved custom power device called as distributed power condition controller. Int. Trans. Electr. Energy Syst. 2019, 30, e12259. [Google Scholar] [CrossRef]
- Salem, A.E.-S.; Salim, O.M.; Arafa, S.I. New triple-action controller for inverter power quality improvement. Comput. Electr. Eng. 2019, 81, 106543. [Google Scholar] [CrossRef]
- Yazdi, F.; Hosseinian, S. A novel “Smart Branch” for power quality improvement in microgrids. Int. J. Electr. Power Energy Syst. 2019, 110, 161–170. [Google Scholar] [CrossRef]
- Nolasco, D.H.; Costa, F.B.; Palmeira, E.S.; Alves, D.K.; Bedregal, B.R.; Rocha, T.O.; Ribeiro, R.L.; Silva, J.C. Wavelet-fuzzy power quality diagnosis system with inference method based on overlap functions: Case study in an AC microgrid. Eng. Appl. Artif. Intell. 2019, 85, 284–294. [Google Scholar] [CrossRef]
- Naderi, Y.; Hosseini, S.H.; Zadeh, S.G.; Mohammadi-Ivatloo, B.; Savaghebi, M.; Guerrero, J.M. An optimized direct control method applied to multilevel inverter for microgrid power quality enhancement. Int. J. Electr. Power Energy Syst. 2018, 107, 496–506. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.; Ray, P.K. Power Quality Improvement Using Photovoltaic Fed DSTATCOM Based on JAYA Optimization. IEEE Trans. Sustain. Energy 2016, 7, 1672–1680. [Google Scholar] [CrossRef]
- Vantuch, T.; Misak, S.; Jezowicz, T.; Burianek, T.; Snasel, V. The Power Quality Forecasting Model for Off-Grid System Supported by Multiobjective Optimization. IEEE Trans. Ind. Electron. 2017, 64, 9507–9516. [Google Scholar] [CrossRef]
- Rao, S.B.; Padma, K. Control of Grid Frequency under Unscheduled Load Variations: A Two Layer Energy Management Controller in Urban Green Buildings. Int. J. Renew. Energy Res. 2020, 10, 1951–1961. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Xiao, S.; Balog, R.S. Hybrid hysteresis current control and low-frequency current harmonics mitigation based on proportional resonant in dc/ac inverter. IET Power Electron. 2018, 11, 2093–2101. [Google Scholar] [CrossRef]
- Karuppanan, P.; Mahapatra, K.K. PI and fuzzy logic controllers for shunt active power filter—A report. Int. J. Electr. Power Energy Syst. 2012, 51, 163–169. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Chang, G.W.; Lin, S.C. A digital implementation of IEC 61000-4-15 flicker meter. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Kumar, Y.V.P.; Bhimasingu, R. Electrical machines based DC/AC energy conversion schemes for the improvement of power quality and resiliency in renewable energy microgrids. Int. J. Electr. Power Energy Syst. 2017, 90, 10–26. [Google Scholar] [CrossRef]
- IEEE Std. 141-1993(Revision of ANSI/IEEE Std 141-1986); IEEE Recommended Practice for Electric Power Distribution for Industrial Plants. IEEE: Piscataway, NJ, USA, 1994; pp. 1–768.
- Electromagnetic Compatibility (EMC)—Part 4–34: Electromagnetic Compatibility (EMC)-Part 4-11: Testing and Measurement techniques-Voltage Dips, Short Interruptions and Voltage Variations Immunity Tests for Equipment with Input Current up to 16 A Per Phase. 2020. Available online: https://webstore.iec.ch/publication/60729 (accessed on 18 March 2022).
- IEEE Std. 1159.3-2019 (Revision of IEEE Std. 1159.3-2003); IEEE Recommended Practice for Power Quality Data Interchange Format (PQDIF). IEEE: Piscataway, NJ, USA, 2019; pp. 1–185. [CrossRef]
- Voltage Characteristics of Electricity Supplied by Public Electricity Networks. 2019. Available online: http://www.leonardo-energy.org (accessed on 18 March 2022).
- 2004 Standard–Photovoltaic (PV) Systems–Characteristics of the Utility Interface. International Electrotechnical Commission: London, UK, 2004. Available online: https://webstore.iec.ch/publication/5736 (accessed on 18 March 2022).
- Electromagnetic Compatibility (EMC)–Part 2-2: Environment-Compatibility Levels for Low-Frequency Conducted Disturbances and Signaling in Public Low-voltage Power Supply Systems. International Electrotechnical Commission: London, UK, 2002. Available online: https://webstore.iec.ch/publication/4133 (accessed on 18 March 2022).
- IEEE Std. 1547.1-2020; IEEE Standard Conformance Test Procedures for Equipment Interconnecting Distributed Energy Resources with Electric Power Systems and Associated Interfaces. IEEE: New York, NY, USA, 2020; pp. 1–282. [CrossRef]
- IEEE Std. 519-2014 (Revision of IEEE Std. 519-1992); IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2014; pp. 1–29. [CrossRef]
- Rao, S.N.V.B.; Kumar, Y.V.P.; Pradeep, D.J.; Reddy, C.P.; Flah, A.; Kraiem, H.; Al-Asad, J.F. Power Quality Improvement in Renewable-Energy-Based Microgrid Clusters Using Fuzzy Space Vector PWM Controlled Inverter. Sustainability 2022, 14, 4663. [Google Scholar] [CrossRef]
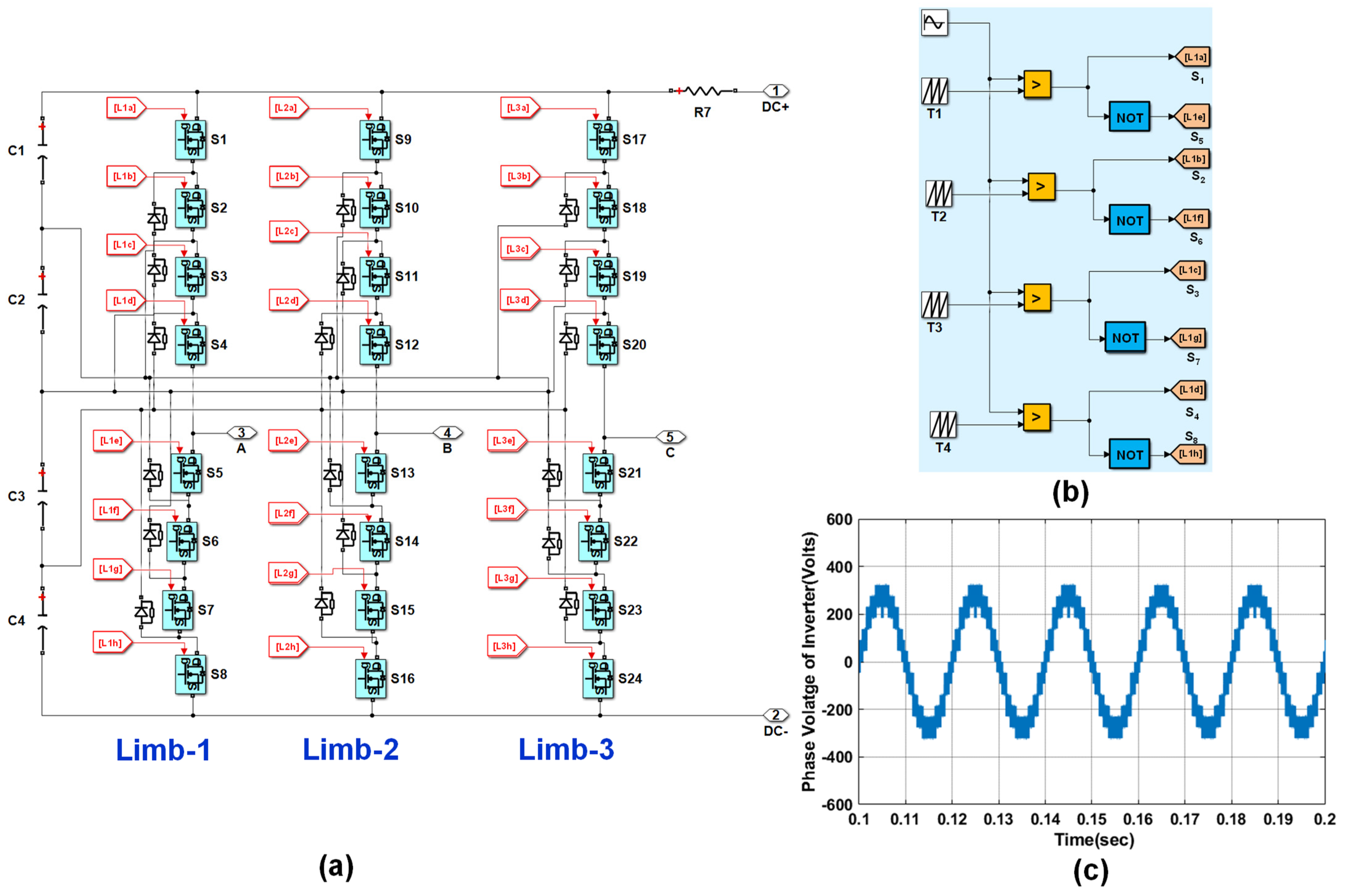




| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | VAO | VAN |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | Vdc | Vdc/2 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 3Vdc/4 | Vdc/4 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | Vdc/2 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | Vdc/4 | −Vdc/4 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | −Vdc/2 |
| ∆e(n) | N-3 | N-2 | N-1 | E0 | P1 | P2 | P3 | |
|---|---|---|---|---|---|---|---|---|
| e(n) | ||||||||
| N-3 | N-3 | N-3 | N-3 | N-3 | N-2 | N-1 | N-3 | |
| N-2 | N-2 | N-3 | N-3 | N-2 | N-1 | E0 | N-2 | |
| N-1 | N-3 | N-3 | N-2. | N-1 | E0 | P1 | N-1 | |
| E0 | N-3 | N-2 | N-1 | E0 | P1 | P2 | E0 | |
| P1 | N-2 | N-1 | E0 | P1 | P2 | P3 | P1 | |
| P2 | N-1 | E0 | P1 | P2 | P3 | P3 | P2 | |
| P3 | E0 | P1 | P2 | P3 | P3 | P3 | P3 | |
| Power Quality Indices | Cluster Microgrids with Conventional ST-PWM-Based Inverter [14] | Cluster Microgrids with Conventional FSV-PWM-Based Inverter [36] | Cluster Microgrids with Proposed FHCC-Based Inverter | Standard Requirements | |
|---|---|---|---|---|---|
| Voltage Characteristics | Signal shape | Distorted sinewave | Pure sinewave | Pure sinewave | Pure Sinewave |
| Sag | 42.5% (violated) | 29.5% | 25% | 40% (IEC 61000-4-11 [28,29]) | |
| 43.37% (violated) | 38.6% | 27.7% | |||
| Swell | 4.76% | 2.73% | 2.5% | ||
| Unbalance | 3.08% (violated) | 2.87% | 2.46% | 3% (IEEE 1159.3 [30], EN 50160 [31]) | |
| Frequency Characteristics | Settling time | 0.55 s | 0.42 s | 0.35 s | 2% (IEC 61727 [32], IEC 61000-2-2 [33]) |
| Deviation (Dynamic load) | 1 | 0.45 | 0.3 | ||
| Total Harmonic Distortion (THD) | 4.29% | 3.85% | 3.03% | 5% (IEEE 1547.1 [34], IEEE 519 [35]) | |
| 6.38% (violated) | 4.73% | 2.59% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, Y.V.P.; Rao, S.N.V.B.; Padma, K.; Reddy, C.P.; Pradeep, D.J.; Flah, A.; Kraiem, H.; Jasiński, M.; Nikolovski, S. Fuzzy Hysteresis Current Controller for Power Quality Enhancement in Renewable Energy Integrated Clusters. Sustainability 2022, 14, 4851. https://doi.org/10.3390/su14084851
Kumar YVP, Rao SNVB, Padma K, Reddy CP, Pradeep DJ, Flah A, Kraiem H, Jasiński M, Nikolovski S. Fuzzy Hysteresis Current Controller for Power Quality Enhancement in Renewable Energy Integrated Clusters. Sustainability. 2022; 14(8):4851. https://doi.org/10.3390/su14084851
Chicago/Turabian StyleKumar, Yellapragada Venkata Pavan, Sivakavi Naga Venkata Bramareswara Rao, Kottala Padma, Challa Pradeep Reddy, Darsy John Pradeep, Aymen Flah, Habib Kraiem, Michał Jasiński, and Srete Nikolovski. 2022. "Fuzzy Hysteresis Current Controller for Power Quality Enhancement in Renewable Energy Integrated Clusters" Sustainability 14, no. 8: 4851. https://doi.org/10.3390/su14084851
APA StyleKumar, Y. V. P., Rao, S. N. V. B., Padma, K., Reddy, C. P., Pradeep, D. J., Flah, A., Kraiem, H., Jasiński, M., & Nikolovski, S. (2022). Fuzzy Hysteresis Current Controller for Power Quality Enhancement in Renewable Energy Integrated Clusters. Sustainability, 14(8), 4851. https://doi.org/10.3390/su14084851













