Population Prediction of Chinese Prefecture-Level Cities Based on Multiple Models

Abstract

In recent years, the population growth rate has been gradually declining in China. As the population problem becomes increasingly significant, the accurate prediction of population development trends has become a top priority, used to facilitate national scientific planning and effective decision making. Based on historical data spanning a period of 20 years (1999–2018), this article presents predictions of the populations of 210 prefecture-level cities using the Malthusian model, Unary linear regression model, Logistic model, and Gray prediction model. Furthermore, because the gray prediction model exhibited the highest degree of accuracy in formulating predictions, this study uses the model to predict and analyze future population development trends. The results reveal that the population gap between cities is gradually widening, and the total urban population shows a pattern of rising in middle-tier cities (second-tier cities and third-tier cities) and declining in high-tier cities (first-tier cities and new first-tier cities) and low-tier cities (fourth-tier cities and fifth-tier cities). From the viewpoint of geographical distribution, the population growth rate is basically balanced between the northern part and the southern part of China. In addition, the population growth of the high-tier cities is gradually slowing while the low-tier cities are experiencing a negative growth of population, but middle-tier cities are experiencing skyrocketing population growth. From the viewpoint of regional development, although the development of regional integration has been strengthened over the years, the radiative driving effect of large urban agglomerations and metropolitan areas is relatively limited.

1. Introduction

As the world’s most populous country, population has always been an important issue in the social development of China. The latest statistics from China’s National Bureau of Statistics, calculated at of the end of 2019, revealed that China is facing the lowest birth rate and natural growth rate among its population (10.48‰ and 3.34‰) since the years 1949 and 1961, respectively. The total population of Mainland China is 1.405 billion, and the population growth rate has increased by 0.33% year on year. The labor force participation rate dropped to a historical low (68%) in 2019, indicating that the demographic dividend may soon be exhausted. In terms of demographic structure, as the proportion of the aged population continues to increase, China has already begun to suffer from the rapid aging problem [1]. The urbanization rate and aging rate exhibit similar growth patterns [2], while the fertility rate has been decreasing year on year [3]. China has been an aging society since 2000, requiring continuous improvements in healthcare and provisions for ensuring the welfare of aged people, and the proportion of the aged population will continue to rise. Furthermore, the fertility level and fertility pattern of young women of childbearing age, as well as the proportion of the total population who are classed as women of childbearing age, are decreasing at significant rates [4]. The number of children per woman of childbearing age is only 1.047; thus, China may now be approaching the peak of its population size. In terms of migration, due to a high degree of difference in the opportunities and welfare offered by top-tier cities, the inflow of migrants from low-tier cities into high-tier cities continues.

As the driver of social development, population is closely related to development-related issues such as economic development, resource consumption, and ecological environmental protection. Apart from being the reflection of the fundamental status of the country, as well as its regions and cities, population is also a core element for further research on microenvironmental development [5]. Social problems, such as the overall slowdown of the population growth rate in China, the increasingly serious problems of sub-replacement fertility and an aging population, the year-on-year decrease in the fertility rate [6], and the large quantities of people who have travelled from rural areas and into cities, have brought heavy pressure upon and presented severe challenges to social care and welfare systems. These issues may also bring with them risks that are yet unforeseen and may threaten the operation of the country’s entire socioeconomic system.

Recently, the competition among the regions and cities has shifted from attracting highly educated and talented people to their areas to vying for young labor instead. The competition to attract a young labor force has intensified, which indicates that the economically developed regions are attracting more people who do not yet possess a household registration for that region (China’s household registration system is a state-implemented population management policy by which the state collects, confirms, and registers citizens’ births, deaths, familial relationships, legal addresses, and other basic information as part of population management. It informs policy decisions in areas such as employment, education, and social welfare provision) [7]. Most developed cities have been able to maintain their economic growth by absorbing young laborers, whose migration has left rural areas with an ever-greater proportion of aged inhabitants [8]. Therefore, there is an urgent need to formulate urban economic and social development plans and regional population development policies that are efficient and reasonable. To formulate relevant plans and policies scientifically, it is particularly important to accurately analyze and predict the development trends of the urban population.

Through a literature review, it is found that the mainstream population theories include Malthus’ population theory, sociological population theory, biological population theory, moderate population theory, population transition theory, population explosion theory, zero population growth theory, and so on [9,10]. Does China’s current population growth conform to the previous population theories? Based on the population agglomeration effect, economic siphon effect, the dialectical materialism of the whole and the part, mean regression, and other theories, this paper proposes a hypothesis about population theory: the future population growth of prefecture-level cities in China generally conforms to the zero population growth theory.

In the following, four models are used to predict the population development trend of 210 prefecture-level cities in China, the most accurate model data is used for further analysis, and some suggestions are put forward for future development.

2. Methodology

The prediction of population involves estimations of the scale, level, and trends of population development at a certain time in the future, using scientific methods based on the current population status and factors that may influence population development. Population prediction provides information that aids decision making. Numerous methods and models have been proposed for population prediction. Seven widely used types of population prediction methods are listed in

Table 1. Summary of mainstream population prediction methods.

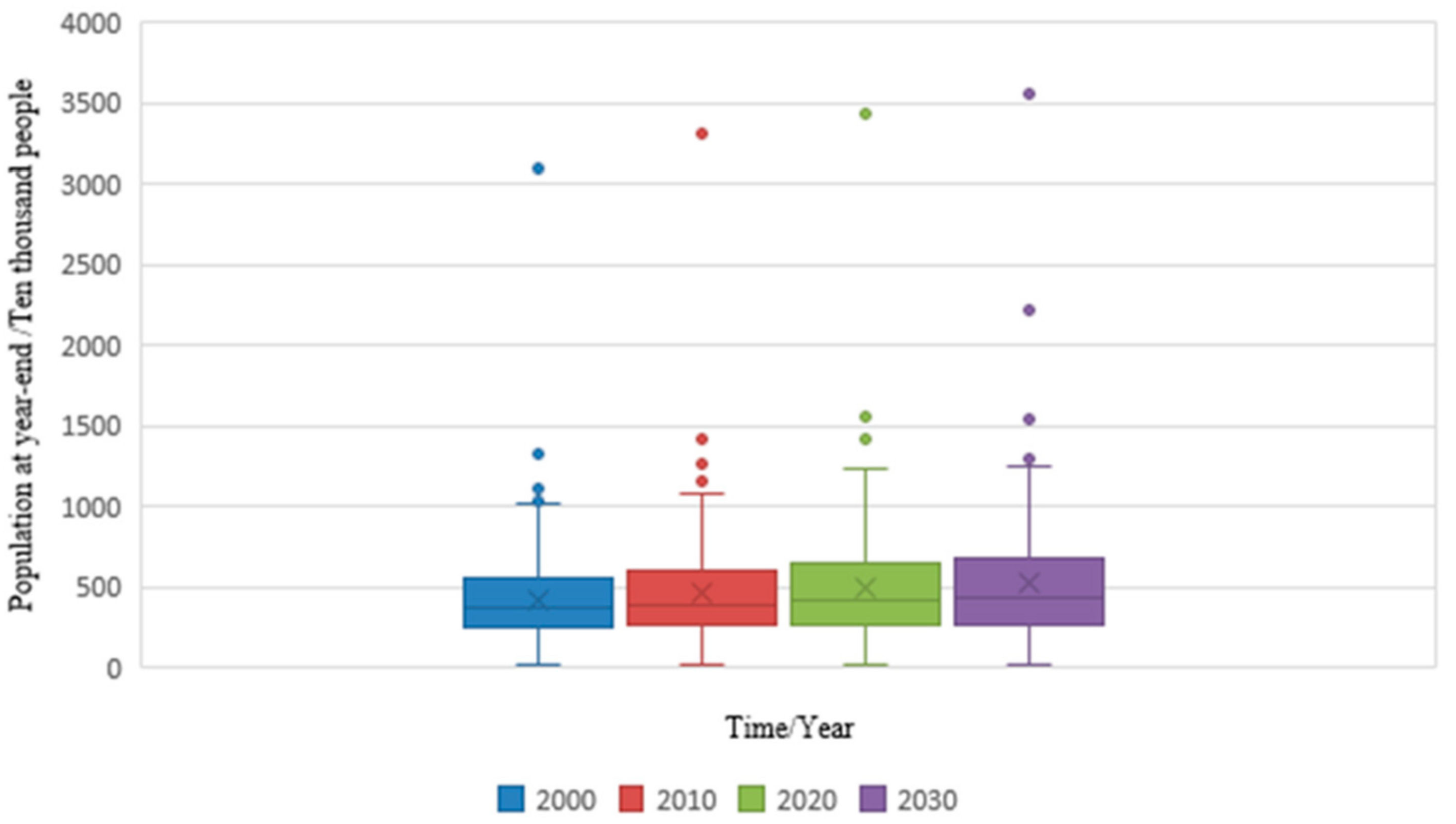
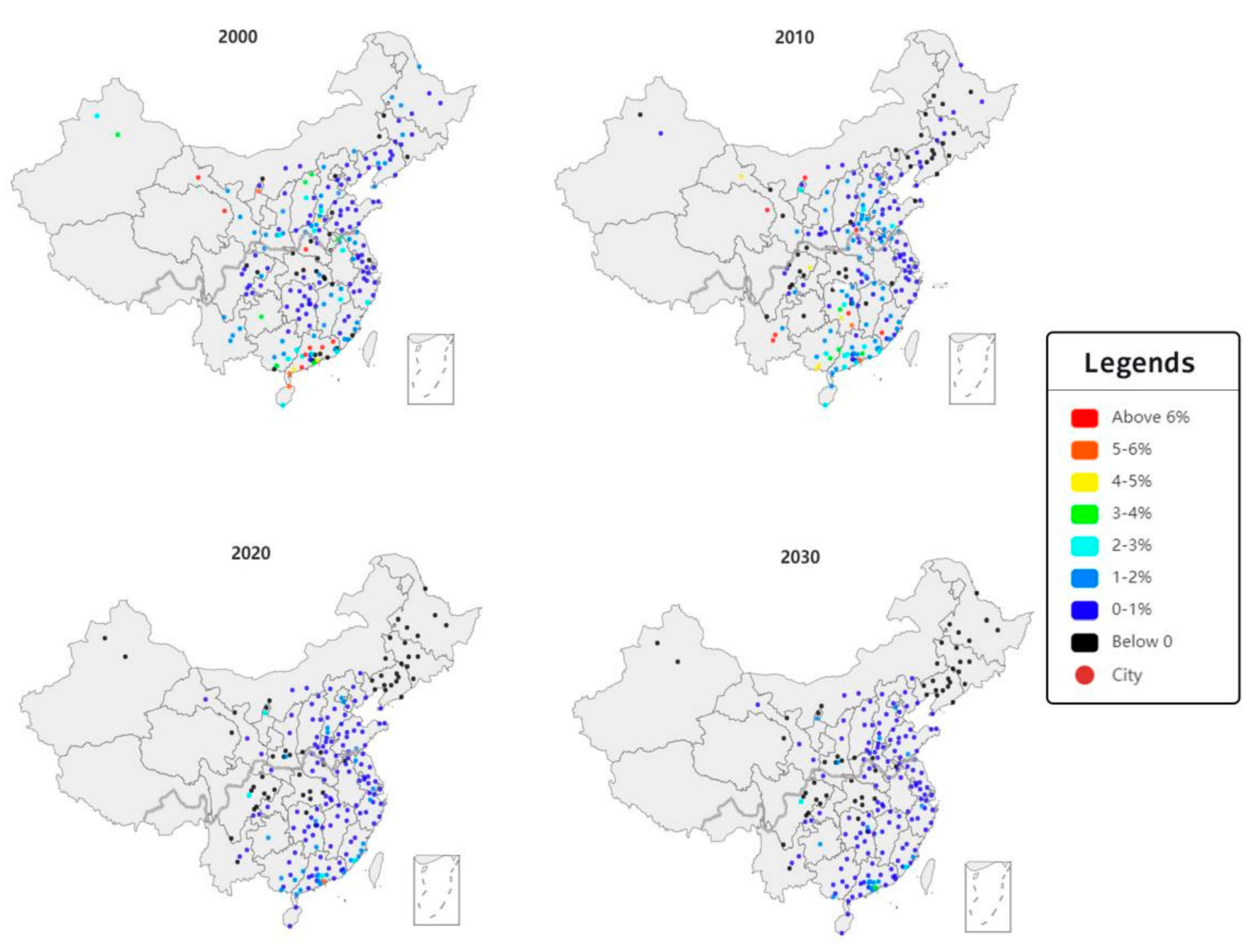
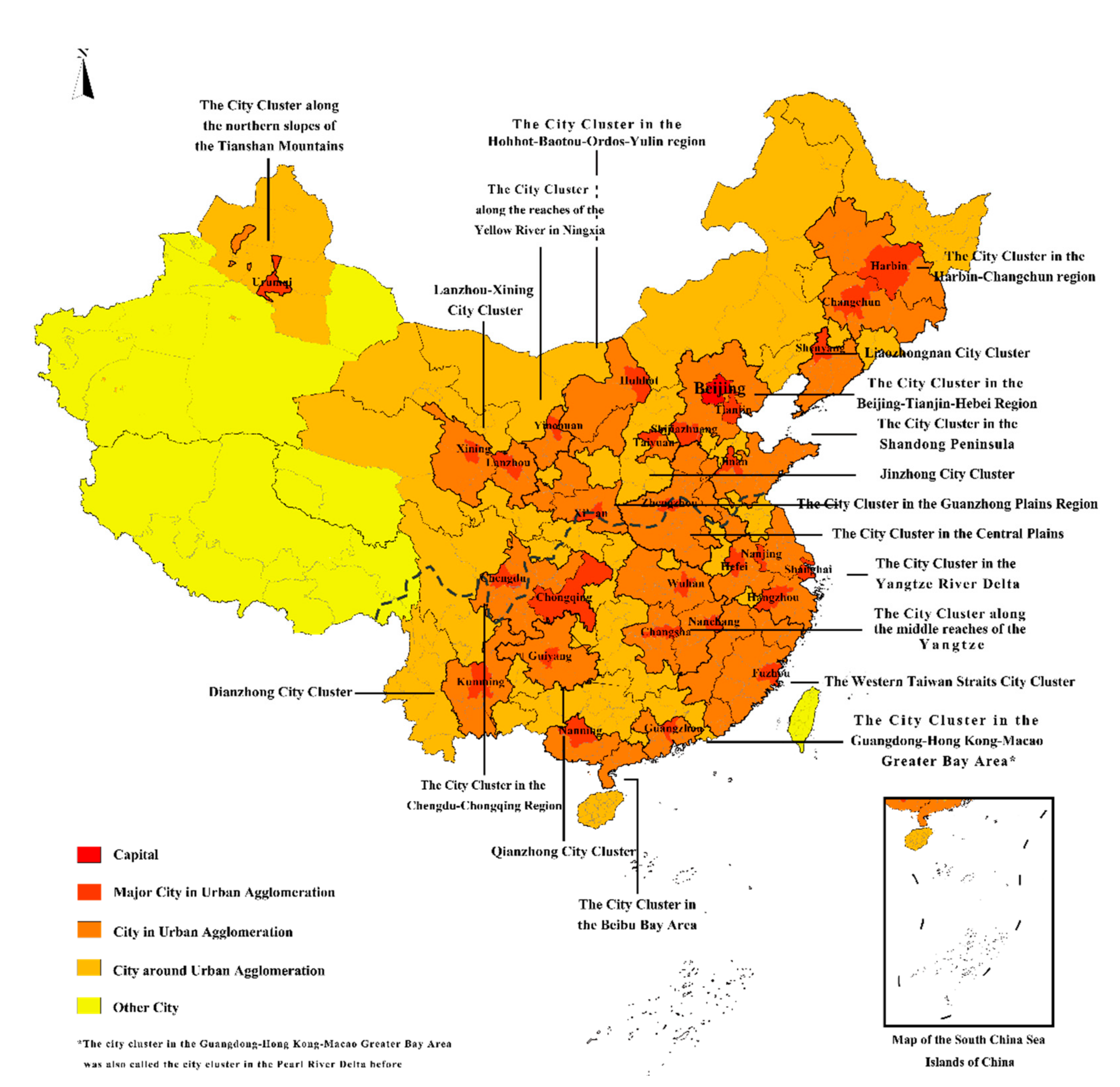
Method	Core Content	Hypothesis	Pros	Cons
Historical trend method	Historical growth trends, demographic characteristics, inertial measurement of population, Malthus model	Future population would show the same pattern as population in the past	The method is classical and widely used	Long-term prediction accuracy will decline
Classical population analysis	Life table technology, hypothetical cohort analysis, population prediction technology and total fertility rate	Accounting for birth and death of people, the measure of population is not the only factor	High prediction accuracy	The demand for data is high and requires long-term accumulation
Regression model	Logistic model, ARIMA model, Leslie matrix, unitary and multiple linear regression model	Sociology investors believe that population growth may have linear or quasi-linear relationship on certain factors	Less data is required and the method is simple	Long-term prediction error fluctuation is relatively large
Gray system prediction model	GM (1, 1) model	The trend of population is a fuzzy system, which means the status in the past cannot be used to predict the accurate population growth, only the probability of the status in the future	Less required data, high accuracy of prediction	Only for short- and medium-term forecasts
Population prediction model	Gravity model, radiation model, Song Jian population equation model, population flow model, etc.	Spatial interaction among cities reflects the growth pattern of population	The model form is more intuitive and explicable	The data requirements are strict and the model is complex
BP neural network, artificial intelligence	Nonlinear dynamics systems, mathematical equations, etc.	High-order statistical rule reflections from big data might be suitable for population prediction, which cannot be calculated by small amounts of data	Strong ability of nonlinear mapping and generalization	The convergence rate of the algorithm is slow, the interpretability is poor
System dynamics	Differential dynamical equations and nonlinear stochastic processes	Population is embedded into the whole system of the society, and might be correlated with a number of factors	Can find the root cause from the internal structure of the system	The subjective color is heavy

[11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Among them, the most common used methods are historical trend analysis, classic population analysis, the regression model, and the gray prediction model.

China’s unique national conditions include extensive geographical coverage (land area of 9.6 million square kilometers, ranking third in the world) [28], large number of cities (34 provincial-level administrative regions and 333 prefecture-level city administrative regions) [29], and a large population base (1.443 billion people, ranking first in the world) [30]. By organically combining China’s national conditions with the advantages and disadvantages of the model (see Table 1 for details), the model was filtered.

With the continuous improvement of science and technology, the timeliness and accuracy of statistical data are getting higher and higher. Therefore, using data close to the current year (short- and medium-term data) for prediction can avoid data prediction errors to a certain extent and the analysis results will be more accurate. The classical population analysis and population prediction models are not suitable for this study due to their high requirements for data and longtime accumulation; the BP neural network and the system dynamics approach meet these difficulties in implementation. However, the former requires extensive data for the training procedure [31], and the latter has a higher degree of subjectivity in its parameter-setting process and is prone to problems such as the omission of important variables [32].

However, the Malthusian model, the unary linear regression model, the logistic competitive biological model (or logistic model), and the gray prediction model are suitable for China’s national conditions and the analysis requirements of this study due to the characteristics of requiring small amounts of data, appropriate suitability for short- and medium-term prediction, and strong explanatory ability.

Therefore, this paper proposes a hypothesis about the model: by assuming that these four models can achieve decent results in population prediction, among them, gray prediction model has the highest prediction accuracy. Next, prediction and analysis will be carried out through these four methods. The following is an introduction to these four models.

2.1. Malthusian Model

This model was proposed by British demographer Thomas Malthus in 1798 and is based on the principle that, under normal circumstances, the population growth rate within a certain period can be approximately regarded as a certain value, and the population is predicted by an exponential growth function. The model is as follows:

$$P_t=P_0{\left(1+r\right)}^n,$$

(1)

where $P_t$ is set as the population size at the end of the prediction target year, $P_0$ is set as the population size of the prediction base year, $r$ is set as the average annual population growth rate, and $n$ is set as the prediction period.

2.2. Unary Linear Regression Model

The unary linear regression model is as follows:

$$Y=a+bX,$$

(2)

Among the terms above, the estimated values of the parameters are:

$$\hat{a}=\overline{Y}-\hat{b}\overline{X},$$

(3)

$$\hat{b}=\frac{\sum \left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)}{\sum {\left(X_i-\overline{X}\right)}^2}=\frac{\sum X_i{Y}_i-n\overline{X}\overline{Y}}{\sum {\left(X_i-\overline{X}\right)}^2},$$

(4)

where time $X$ is set as the control variable and the population $Y$ is set as the state variable. The parameters $a$ and $b$ can be calculated by Equations (3) and (4) using historical data or by utilizing the ordinary least squares (OLS) method.

In the processing of population growth, unary linear regression can be used for population estimation when the population development rates of each period are relatively close; in other words, when the slopes of the tangent lines at all points on the population development curve are the same and approximate a linear growth. Subject to the limitations of the estimation conditions, this model is more suitable for short-term predictions. When used for long-term predictions, the errors caused by population changes would be gradually amplified thus affecting the accuracy of the prediction results.

2.3. Logistic Model

The logistic competitive biological model considers the limitations of population growth and proposes a law of population growth, which says that as the total population grows, the population growth rate will gradually decrease.

Let $p\left(t\right)$ be the population size at time $t$. When the population is large, $p\left(t\right)$ can be considered continuous or even differentiable. Let $b\left(t,p\right)$ represent the birth rate of a single living being in the population per unit of time at time $t$, while $d\left(t,p\right)$ represents the death rate in the population per unit of time at time $t$. Consequently, $r\left(t,p\right)=b\left(t,p\right)-d\left(t,p\right)$ represents the natality rate of a single individual at time $t$. The model is as follows:

$$\Delta P=P_t+\Delta \left(t-P_t\right)=r\left(t,P\right)\ast P_t\Delta t,$$

(5)

Let $\Delta t\to 0,$ then we have:

$$\frac{dp}{dt}=r\left(t,p\right)\ast P,$$

(6)

When $r\left(t,p\right)=a,$ then:

$$P^{\prime }=aP-b{P}^2,P\left(t_0\right)=P_0,$$

(7)

This is the idea behind the Malthusian model.

Owing to environmental constraints, competition between individuals results in a decrease in $r\left(t,P\right)$. Therefore, the Dutch biologist Verhulst proposed to add the competition term $-b{p}^2(b>0)$. Thus, we get:

$$P^{\prime }=aP-b{p}^2,P\left(t\right)=P,$$

(8)

The above equation is the logistic competitive biological model.

2.4. Gray Prediction Model

Due to certain conditions that are particular to some cities (such as a unique culture, special policies, etc.), the development of the population in some urban areas will be a more complicated, versatile, and nonstationary random process. Thus, static models such as linear regression models and exponential growth models, cannot guarantee accurate prediction results. On certain occasions, the confidence interval of the prediction result is extremely large due to errors in the model; thus, the results are of no practical significance. The gray prediction model generates a dynamic or nondynamic white module from a known data sequence according to a certain rule, explores the inner law from the noisy raw data, and builds a gray model according to certain changes and solutions to start the prediction. Characteristics including a low modeling information requirement, high operation, and high accuracy, make the model significantly better than the others in improving the randomness of data and accuracy of prediction.

With reference to Wang [33], Camelia [34,35], and Gao et al. [36], the GM (1, 1) model, which is a method of the gray prediction model, is suitable for population prediction. The prediction steps taken by this study are as shown below.

• Set the original sequence $\left\{X_t\right\}=\left\{X_1,X_2,X_3,\dots ,X_n\right\},\left(t=1,2,3,\dots ,n\right)$ and conduct accumulative generation on $\left\{X_t\right\}$ to obtain the new sequence $\left\{Y_t\right\}$ and the mean-value sequence $\left\{Z_t\right\}$:

  $$Y_t={\displaystyle \sum }_{i=1}^t{X}_i,Z_t=\frac{\left(Y_t+Y_{t-1}\right)}{2},$$

  (9)
• Establish a first-order differential equation:

  $$\frac{d{Y}_t}{dt}+a{Y}_t=u,$$

  (10)

  where $a$ is the gray developmental coefficient and $u$ is the gray action quantity.
• Conduct parameter estimation using OLS:

  $$\hat{a}={\left(B^{T}B\right)}^{-1}{B}^T{\lambda }_t,$$

  (11)

  $$B={\left[\begin{array}{cccc}-Z_2& -Z_3& \dots & -Z_n\\ 1& 1& \dots & 1\end{array}\right]}^T,$$

  (12)
• Obtain the time function:

  $${\widehat{Y}}_t\left(t+1\right)=\left(X_t-\mu \right)ex\left(-at\right)+\frac{u}{a},$$

  (13)

  and then calculate the estimated value of $X_t$:

  $${\hat{X}}_t={\hat{Y}}_t-{\hat{Y}}_{t-1}\left(t=1,2,3,\dots ,n\right),$$

  (14)
• Test the fitting effect using the after-test rule.

3. Results

The vast majority of previous studies predicted China’s total population on the national level and/or the provincial level, while a small minority of studies focused on the prediction of city populations using large samples. While the prefecture-level city unit is not only the smallest administrative division in China (smaller units include county and district levels), prefecture-level cities are important driving forces behind China’s economic development and policy decisions made at the city level, having a large effect upon wider regional development. Therefore, it is necessary to analyze the data of prefecture-level cities.

This study focuses on the analysis of urban population data at the level of cities using data from the China City Statistical Yearbook from 1999 to 2018. First, the population data of cities with missing values or abnormal population structure changes from year to year were identified and eliminated from this study. Next, cities that have been merged, split, or renamed during the selected years were eliminated. Finally, the population data of 210 prefecture-level cities from 1999 to 2018 were screened from 333 prefecture-level cities. Predictions were conducted using the four above mentioned models and methods, while the data with the highest degree of accuracy were chosen from the prediction results as the result for subsequent analysis. Owing to the large number of cities involved in this research, it is impossible to list the prediction data of all 210 cities. Therefore, only the prediction results of four first-tier cities are listed: Beijing, Shanghai, Guangzhou, and Shenzhen. (The city classification system adopted in this paper mirrors China’s new city classification list. The list evaluates prefecture-level cities according to five dimensions: business resource concentration, urban hub, urban activity, lifestyle diversity, and future plasticity. These dimensions decide the city’s tier: first-tier, new first-tier, second-tier, third-tier, fourth-tier, or fifth-tier. It is sometimes useful to groups these city tiers into the following groupings: the high-tier group includes first- and new first-tier cities, the middle-tier group includes second- and third-tier cities, and the low-tier group includes fourth- and fifth-tier cities.).

3.1. Population Prediction Results

3.1.1. Malthusian Model

According to the population development pattern of the four first-tier cities, based on population data on these cities from 1999 to 2018, three scenarios that utilize high, middle, and low natural population growth rates for prediction were selected.

With reference to the model used by Zhang et al. [5] for population prediction, the specific settings of growth rates for the high-, low- and middle-value scenarios are as follows. The high-value scenario uses the maximum natural population growth rate in 1999–2018, and the low-value scenario uses the minimum natural population growth rate in 1999–2018. The middle-value scenario uses the mean value of the growth rates of the high- and low-value scenarios as the annual population growth rate. According to the Malthusian population model, with 2010 as the base period, the predicted values of each city’s total population from 2011 to 2030 can be obtained from the high-, middle- and low-value scenarios. The prediction results are shown in

Table 2. Population prediction results of cities based on the Malthusian model.

The Results of Population Prediction of Beijing
Year	High Scheme	Middle Scheme	Low Scheme	Year	High Scheme	Middle Scheme	Low Scheme
2011	1268.53	1259.52	1250.52	2021	1380.98	1276.89	1179.97
2012	1279.35	1261.25	1243.28	2022	1392.76	1278.63	1173.14
2013	1290.26	1262.98	1236.08	2023	1404.64	1280.39	1166.35
2014	1301.27	1264.71	1228.92	2024	1416.63	1282.14	1159.59
2015	1312.37	1266.44	1221.81	2025	1428.71	1283.90	1152.88
2016	1323.56	1268.17	1214.73	2026	1440.90	1285.66	1146.20
2017	1334.85	1269.91	1207.70	2027	1453.19	1287.42	1139.57
2018	1346.24	1271.65	1200.71	2028	1465.58	1289.18	1132.97
2019	1357.72	1273.39	1193.75	2029	1478.08	1290.95	1126.41
2020	1369.30	1275.14	1186.84	2030	1490.69	1292.72	1119.89
The Results of Population Prediction of Shanghai
Year	High Scheme	Middle Scheme	Low Scheme	Year	High Scheme	Middle Scheme	Low Scheme
2011	1413.01	1410.36	1407.72	2021	1419.95	1390.95	1362.49
2012	1413.70	1408.41	1403.13	2022	1420.65	1389.03	1358.05
2013	1414.40	1406.46	1398.55	2023	1421.34	1387.10	1353.62
2014	1415.09	1404.51	1393.99	2024	1422.04	1385.18	1349.21
2015	1415.78	1402.57	1389.45	2025	1422.74	1383.26	1344.81
2016	1416.48	1400.62	1384.92	2026	1423.43	1381.35	1340.43
2017	1417.17	1398.68	1380.40	2027	1424.13	1379.43	1336.06
2018	1417.87	1396.75	1375.90	2028	1424.83	1377.52	1331.70
2019	1418.56	1394.81	1371.42	2029	1425.53	1375.61	1327.36
2020	1419.26	1392.88	1366.95	2030	1426.23	1373.71	1323.03
The Results of Population Prediction of Guangzhou
Year	High Scheme	Middle Scheme	Low Scheme	Year	High Scheme	Middle Scheme	Low Scheme
2011	818.71	813.33	807.95	2021	955.68	888.81	826.23
2012	831.47	820.58	809.76	2022	970.58	896.74	828.08
2013	844.43	827.89	811.57	2023	985.71	904.73	829.93
2014	857.60	835.27	813.39	2024	1001.08	912.80	831.79
2015	870.97	842.72	815.21	2025	1016.69	920.94	833.66
2016	884.55	850.23	817.04	2026	1032.54	929.15	835.52
2017	898.34	857.81	818.87	2027	1048.63	937.43	837.39
2018	912.34	865.46	820.70	2028	1064.98	945.79	839.27
2019	926.57	873.18	822.54	2029	1081.58	954.22	841.15
2020	941.01	880.96	824.38	2030	1098.45	962.72	843.03
The Results of Population Prediction of Shenzhen
Year	High Scheme	Middle Scheme	Low Scheme	Year	High Scheme	Middle Scheme	Low Scheme
2011	266.41	264.37	262.32	2021	341.63	313.85	288.13
2012	273.12	268.94	264.79	2022	350.23	319.28	290.85
2013	280.00	273.60	267.29	2023	359.05	324.80	293.59
2014	287.05	278.33	269.81	2024	368.09	330.42	296.36
2015	294.28	283.15	272.36	2025	377.36	336.14	299.16
2016	301.69	288.05	274.92	2026	386.86	341.96	301.98
2017	309.28	293.03	277.52	2027	396.61	347.88	304.83
2018	317.07	298.10	280.13	2028	406.59	353.90	307.70
2019	325.06	303.26	282.78	2029	416.83	360.02	310.60
2020	333.24	308.51	285.44	2030	427.33	366.25	313.53

Note: unit is ten thousand people.

below.

3.1.2. Unary Linear Regression Model

With reference to the approach of Jia et al. [37], the population data from 1999 to 2018 are divided into two data sequences of 2009–2018 (10-year sample) and 1999–2018 (20-year sample) according to different sample sizes. The final prediction results are as shown in

Table 3. Population prediction results of first-tier cities based on the unary linear regression model.

The Results of Population Prediction of Beijing
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	1279.83	1282.84	2021	1429.27	1415.97
2012	1294.78	1296.15	2022	1444.21	1429.29
2013	1309.72	1309.46	2023	1459.15	1442.60
2014	1324.66	1322.78	2024	1474.10	1455.91
2015	1339.61	1336.09	2025	1489.04	1469.23
2016	1354.55	1349.40	2026	1503.98	1482.54
2017	1369.49	1362.72	2027	1518.93	1495.85
2018	1384.44	1376.03	2028	1533.87	1509.17
2019	1399.38	1389.35	2029	1548.81	1522.48
2020	1414.32	1402.66	2030	1563.76	1535.79
The Results of Population Prediction of Shanghai
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	1418.00	1412.06	2021	1482.12	1494.55
2012	1424.41	1420.31	2022	1488.54	1502.80
2013	1430.82	1428.56	2023	1494.95	1511.05
2014	1437.24	1436.81	2024	1501.36	1519.30
2015	1443.65	1445.06	2025	1507.77	1527.55
2016	1450.06	1453.31	2026	1514.19	1535.80
2017	1456.47	1461.56	2027	1520.60	1544.05
2018	1462.89	1469.81	2028	1527.01	1552.29
2019	1469.30	1478.05	2029	1533.42	1560.54
2020	1475.71	1486.30	2030	1539.84	1568.79
The Results of Population Prediction of Guangzhou
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	812.52	819.02	2021	947.45	932.48
2012	826.02	830.37	2022	960.94	943.83
2013	839.51	841.72	2023	974.43	955.17
2014	853.00	853.06	2024	987.92	966.52
2015	866.49	864.41	2025	1001.42	977.87
2016	879.99	875.75	2026	1014.91	989.21
2017	893.48	887.10	2027	1028.40	1000.56
2018	906.97	898.44	2028	1041.89	1011.90
2019	920.46	909.79	2029	1055.38	1023.25
2020	933.95	921.14	2030	1068.88	1034.59
The Results of Population Prediction of Shenzhen
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	274.06	292.12	2021	511.43	463.50
2012	297.80	309.26	2022	535.17	480.64
2013	321.53	326.40	2023	558.91	497.78
2014	345.27	343.54	2024	582.64	514.91
2015	369.01	360.67	2025	606.38	532.05
2016	392.75	377.81	2026	630.12	549.19
2017	416.48	394.95	2027	653.85	566.33
2018	440.22	412.09	2028	677.59	583.47
2019	463.96	429.22	2029	701.33	600.60
2020	487.69	446.36	2030	725.07	617.74

Note: unit is ten thousand people.

.

3.1.3. Logistic Model

Differentiation and separation of variables are conducted in Equation (6). Subsequently, a logistic population prediction model for the 210 cities is established. We again use two data sequences: the 10-year sample from 2009–2018 and the 20-year sample from 1999–2018. The prediction results are shown in

Table 4. Population prediction results of first-tier cities based on the logistic competitive biological model.

The Results of Population Prediction of Beijing
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	1299.63	1294.98	2021	1411.37	1333.79
2012	1315.16	1298.81	2022	1418.24	1337.73
2013	1329.57	1302.65	2023	1424.52	1341.69
2014	1342.92	1306.50	2024	1430.27	1345.65
2015	1355.26	1310.37	2025	1435.52	1349.63
2016	1366.66	1314.24	2026	1440.32	1353.62
2017	1377.16	1318.13	2027	1444.70	1357.63
2018	1386.83	1322.02	2028	1448.70	1361.64
2019	1395.72	1325.93	2029	1452.35	1365.67
2020	1403.88	1329.85	2030	1455.67	1369.71
The Results of Population Prediction of Shanghai
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	1425.82	1413.47	2021	1474.00	1487.02
2012	1432.83	1421.25	2022	1476.80	1493.86
2013	1439.25	1428.93	2023	1479.33	1500.61
2014	1445.11	1436.52	2024	1481.64	1507.26
2015	1450.46	1444.02	2025	1483.74	1513.82
2016	1455.35	1451.42	2026	1485.65	1520.28
2017	1459.80	1458.73	2027	1487.38	1526.65
2018	1463.87	1465.94	2028	1488.95	1532.93
2019	1467.57	1473.06	2029	1490.38	1539.12
2020	1470.94	1480.09	2030	1491.67	1545.22
The Results of Population Prediction of Guangzhou
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	824.27	814.38	2021	931.32	912.58
2012	834.40	824.69	2022	942.76	921.73
2013	844.65	834.90	2023	954.34	930.76
2014	855.02	845.01	2024	966.07	939.64
2015	865.53	855.01	2025	977.94	948.39
2016	876.16	864.91	2026	989.95	957.00
2017	886.93	874.68	2027	1002.12	965.47
2018	897.82	884.34	2028	1014.43	973.79
2019	908.85	893.88	2029	1026.89	981.97
2020	920.02	903.29	2030	1039.51	990.01
The Results of Population Prediction of Shenzhen
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	299.93	274.81	2021	581.05	548.75
2012	320.44	294.49	2022	620.77	588.04
2013	342.34	315.58	2023	663.21	630.15
2014	365.74	338.17	2024	708.54	675.27
2015	390.75	362.39	2025	756.98	723.62
2016	417.46	388.34	2026	808.73	775.43
2017	446.00	416.14	2027	864.02	830.95
2018	476.49	445.94	2028	923.09	890.45
2019	509.06	477.87	2029	986.19	954.21
2020	543.87	512.08	2030	1053.61	1022.53

Note: unit is ten thousand people.

.

3.1.4. Gray Prediction Model

Following the step 1 to step 5 listed in Section 2.4, the prediction results of the GM (1, 1) model are shown in

Table 5. Population prediction results of first-tier cities based on the GM (1, 1) model.

The Results of Population Prediction of Beijing
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	1281.70	1277.93	2021	1430.31	1446.31
2012	1295.84	1293.85	2022	1446.09	1464.32
2013	1310.13	1309.96	2023	1462.04	1482.55
2014	1324.58	1326.28	2024	1478.16	1501.02
2015	1339.19	1342.79	2025	1494.47	1519.71
2016	1353.97	1359.52	2026	1510.95	1538.64
2017	1368.90	1376.45	2027	1527.62	1557.80
2018	1384.00	1393.59	2028	1544.47	1577.20
2019	1399.27	1410.94	2029	1561.51	1596.84
2020	1414.70	1428.52	2030	1578.73	1616.73
The Results of Population Prediction of Shanghai
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	1419.65	1411.38	2021	1480.54	1497.13
2012	1425.62	1419.73	2022	1486.77	1505.98
2013	1431.62	1428.13	2023	1493.03	1514.89
2014	1437.65	1436.58	2024	1499.31	1523.85
2015	1443.70	1445.08	2025	1505.62	1532.87
2016	1449.77	1453.62	2026	1511.96	1541.94
2017	1455.87	1462.22	2027	1518.32	1551.06
2018	1462.00	1470.87	2028	1524.71	1560.23
2019	1468.15	1479.57	2029	1531.13	1569.46
2020	1474.33	1488.33	2030	1537.57	1578.74
The Results of Population Prediction of Guangzhou
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	809.11	816.87	2021	957.91	943.15
2012	822.89	828.70	2022	974.22	956.80
2013	836.90	840.69	2023	990.81	970.66
2014	851.15	852.87	2024	1007.68	984.71
2015	865.64	865.21	2025	1024.83	998.97
2016	880.37	877.74	2026	1042.28	1013.43
2017	895.36	890.45	2027	1060.03	1028.10
2018	910.61	903.34	2028	1078.07	1042.99
2019	926.11	916.42	2029	1096.43	1058.09
2020	941.88	929.69	2030	1115.09	1073.41
The Results of Population Prediction of Shenzhen
Year	Population (10 Years)	Population (20 Years)	Year	Population (10 Years)	Population (20 Years)
2011	268.32	273.74	2021	569.60	558.38
2012	289.29	293.97	2022	614.14	599.63
2013	311.91	315.69	2023	662.15	643.94
2014	336.30	339.02	2024	713.92	691.52
2015	362.59	364.06	2025	769.74	742.61
2016	390.94	390.96	2026	829.92	797.48
2017	421.50	419.85	2027	894.80	856.40
2018	454.46	450.87	2028	964.76	919.68
2019	489.99	484.18	2029	1040.19	987.63
2020	528.30	519.96	2030	1121.52	1060.60

Note: unit is ten thousand people.

.

3.2. Error Tests and Analysis

3.2.1. Malthusian Model

To get as accurate a forecast as possible, based on the previous prediction results of the Malthusian model, the predicted values of the high-, middle- and low-value scenarios for each of the cities were compared with the existing population data from 2011 to 2018. Thus, the results of the error tests on the three scenarios were obtained (

Table 6. Error test of high-, middle- and low-value scenarios.

Error Test of Each Scheme in Beijing
Year	High Scheme		Middle Scheme		Low Scheme
	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	−9.37	−0.73%	−18.38	−1.44%	−27.38	−2.14%
2012	−18.15	−1.40%	−36.25	−2.79%	−54.22	−4.18%
2013	−26.04	−1.98%	−53.32	−4.05%	−80.22	−6.09%
2014	−32.13	−2.41%	−68.69	−5.15%	−104.48	−7.84%
2015	−32.83	−2.44%	−78.76	−5.85%	−123.39	−9.17%
2016	−39.44	−2.89%	−94.83	−6.96%	−148.27	−10.88%
2017	−24.15	−1.78%	−89.09	−6.56%	−151.30	−11.13%
2018	−29.76	−2.16%	−104.35	−7.58%	−175.29	−12.74%
Error Test of Each Scheme in Shanghai
Year	High Scheme		Middle Scheme		Low Scheme
	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	−6.39	−0.45%	−9.04	−0.64%	−11.68	−0.82%
2012	−13.20	−0.92%	−18.49	−1.30%	−23.77	−1.67%
2013	−17.90	−1.25%	−25.84	−1.80%	−33.75	−2.36%
2014	−23.61	−1.64%	−34.19	−2.38%	−44.71	−3.11%
2015	−27.19	−1.88%	−40.40	−2.80%	−53.52	−3.71%
2016	−33.52	−2.31%	−49.38	−3.41%	−65.08	−4.49%
2017	−37.83	−2.60%	−56.32	−3.87%	−74.60	−5.13%
2018	−44.13	−3.02%	−65.25	−4.46%	−86.10	−5.89%
Error Test of Each Scheme in Guangzhou
Year	High Scheme		Middle Scheme		Low Scheme
	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	4.11	0.50%	−1.27	−0.16%	−6.65	−0.82%
2012	9.17	1.12%	−1.72	−0.21%	−12.54	−1.53%
2013	12.13	1.46%	−4.41	−0.53%	−20.73	−2.49%
2014	15.20	1.80%	−7.13	−0.85%	−29.01	−3.44%
2015	16.78	1.96%	−11.47	−1.34%	−38.98	−4.56%
2016	14.55	1.67%	−19.77	−2.27%	−52.96	−6.09%
2017	0.34	0.04%	−40.19	−4.48%	−79.13	−8.81%
2018	−15.66	−1.69%	−62.54	−6.74%	−107.30	−11.56%
Error Test of Each Scheme in Shenzhen
Year	High Scheme		Middle Scheme		Low Scheme
	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	−1.49	−0.55%	−3.53	−1.32%	−5.58	−2.08%
2012	−14.48	−5.03%	−18.66	−6.49%	−22.81	−7.93%
2013	−30.50	−9.82%	−36.90	−11.89%	−43.21	−13.92%
2014	−45.15	−13.59%	−53.87	−16.22%	−62.39	−18.78%
2015	−60.71	−17.10%	−71.84	−20.24%	−82.63	−23.28%
2016	−83.31	−21.64%	−96.95	−25.18%	−110.08	−28.59%
2017	−125.72	−28.90%	−141.97	−32.64%	−157.48	−36.20%
2018	−137.93	−30.31%	−156.90	−34.48%	−174.87	−38.43%

Note: unit is ten thousand people.

).

The comparison result reveals that all the population prediction results of the listed first-tier cities in the high-value scenario are more accurate. However, when the sample size expanded to 210 cities, the average relative errors of the predictions for the 210 cities in the high-, middle- and low-value scenarios are 3.88%, 0.82%, and −2.12%, respectively. Therefore, considering the overall prediction results, the predicted value of the middle-value scenario is slightly lower than the actual populations and has the smallest overall error. Under this model method, the middle scheme is the most reliable.

3.2.2. Unary Linear Regression Model

With the prediction steps introduced in Section 3.1, the prediction results of the unary regression model are as follows (

Table 7. Error test of prediction results of the unary regression model.

Error Test of Each Scheme in Beijing					Error Test of Each Scheme in Shanghai
year	10 Years Sample		20 Years Sample		10 Years Sample		20 Years Sample
	Error	Relative Error	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	1.93	0.15%	4.94	0.39%	−1.40	−0.10%	−7.34	−0.52%
2012	−2.72	−0.21%	−1.35	−0.10%	−2.49	−0.17%	−6.59	−0.46%
2013	−6.58	−0.50%	−6.84	−0.52%	−1.48	−0.10%	−3.74	−0.26%
2014	−8.74	−0.66%	−10.62	−0.80%	−1.46	−0.10%	−1.89	−0.13%
2015	−5.59	−0.42%	−9.11	−0.68%	0.68	0.05%	2.09	0.14%
2016	−8.45	−0.62%	−13.60	−1.00%	0.06	0.00%	3.31	0.23%
2017	10.49	0.77%	3.72	0.27%	1.47	0.10%	6.56	0.45%
2018	8.44	0.61%	0.03	0.00%	0.89	0.06%	7.81	0.53%
Error Test of Each Scheme in Guangzhou					Error Test of Each Scheme in Shenzhen
Year	10 Years Sample		20 Years Sample		10 Years Sample		20 Years Sample
	Error	Relative Error	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	−2.08	−0.25%	4.42	0.54%	6.16	2.30%	24.22	9.04%
2012	3.72	0.45%	8.07	0.98%	10.20	3.55%	21.66	7.53%
2013	7.21	0.87%	9.42	1.13%	11.03	3.55%	15.90	5.12%
2014	10.60	1.26%	10.66	1.27%	13.07	3.93%	11.34	3.41%
2015	12.30	1.44%	10.22	1.20%	14.02	3.95%	5.68	1.60%
2016	9.99	1.15%	5.75	0.66%	7.75	2.01%	−7.19	−1.87%
2017	−4.52	−0.50%	−10.90	−1.21%	−18.52	−4.26%	−40.05	−9.21%
2018	−21.03	−2.27%	−29.56	−3.18%	−14.78	−3.25%	−42.91	−9.43%

Note: unit is ten thousand people.

).

The results of the error tests in Table 7 reveal that the prediction model of the 10-year sample has a smaller error (both error and relative error) than that of the 20-year sample, possibly owing to irregularities caused by a longer data sequence. It also shows that such a model is better suited to short-term population prediction, as the accuracy of the prediction results may decline along with the prediction term of the model.

3.2.3. Logistic Model

The following prediction results are obtained from the logistic biological competition model (

Table 8. Error test of prediction results of logistic biological competition model.

Error Test of Each Scheme in Beijing					Error Test of Each Scheme in Shanghai
Year	10 Years Sample		20 Years Sample		10 Years Sample		20 Years Sample
	Error	Relative Error	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	21.73	1.70%	17.08	1.34%	6.42	0.45%	−5.93	−0.42%
2012	17.66	1.36%	1.31	0.10%	5.93	0.42%	−5.65	−0.40%
2013	13.27	1.01%	−13.65	−1.04%	6.95	0.48%	−3.37	−0.24%
2014	9.52	0.71%	−26.90	−2.02%	6.41	0.45%	−2.18	−0.15%
2015	10.06	0.75%	−34.83	−2.59%	7.49	0.52%	1.05	0.07%
2016	3.66	0.27%	−48.76	−3.58%	5.35	0.37%	1.42	0.10%
2017	18.16	1.34%	−40.87	−3.01%	4.80	0.33%	3.73	0.26%
2018	10.83	0.79%	−53.98	−3.92%	1.87	0.13%	3.94	0.27%
Error Test of Each Scheme in Guangzhou					Error Test of Each Scheme in Shenzhen
Year	10 Years Sample		20 Years Sample		10 Years Sample		20 Years Sample
	Error	Relative Error	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	9.67	1.19%	−0.22	−0.03%	32.03	11.96%	6.91	2.58%
2012	12.10	1.47%	2.39	0.29%	32.84	11.42%	6.89	2.40%
2013	12.35	1.48%	2.60	0.31%	31.84	10.25%	5.08	1.64%
2014	12.62	1.50%	2.61	0.31%	33.54	10.10%	5.97	1.80%
2015	11.34	1.33%	0.82	0.10%	35.76	10.07%	7.40	2.08%
2016	6.16	0.71%	−5.09	−0.59%	32.46	8.43%	3.34	0.87%
2017	−11.07	−1.23%	−23.32	−2.60%	11.00	2.53%	−18.86	−4.34%
2018	−30.18	−3.25%	−43.66	−4.70%	21.49	4.72%	−9.06	−1.99%

Note: unit is ten thousand people.

).

Table 8 shows that the prediction results of the four first-tier cities fit better with the populations in reality. The average relative errors of the 10-year sample size and the 20-year sample size are 0.371% and −0.303%, respectively. The overall prediction accuracy of the logistic competitive biological model is high, but the accuracy of the 20-year sample size is much higher. This shows that the characteristics of the data cannot be fully reflected when a shorter time series is used, and the use of a longer time series will improve the model’s accuracy.

3.2.4. Gray Prediction Model

The average prediction error of the GM (1, 1) model is shown in

Table 9. Error test of the GM (1, 1) model prediction results.

Error Test of Each Scheme in Beijing					Error Test of Each Scheme in Shanghai
Year	10 Years Sample		20 Years Sample		10 Years Sample		20 Years Sample
	Error	Relative Error	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	3.80	0.30%	0.03	0.00%	0.25	0.02%	−8.02	−0.56%
2012	−1.66	−0.13%	−3.65	−0.28%	−1.28	−0.09%	−7.17	−0.50%
2013	−6.17	−0.47%	−6.34	−0.48%	−0.68	−0.05%	−4.17	−0.29%
2014	−8.82	−0.66%	−7.12	−0.53%	−1.05	−0.07%	−2.12	−0.15%
2015	−6.01	−0.45%	−2.41	−0.18%	0.73	0.05%	2.11	0.15%
2016	−9.03	−0.66%	−3.48	−0.26%	−0.23	−0.02%	3.62	0.25%
2017	9.90	0.73%	17.45	1.28%	0.87	0.06%	7.22	0.50%
2018	8.00	0.58%	17.59	1.28%	0.00	0.00%	8.87	0.61%
Error Test of Each Scheme in Guangzhou					Error Test of Each Scheme in Shenzhen
Year	10 Years Sample		20 Years Sample		10 Years Sample		20 Years Sample
	Error	Relative Error	Error	Relative Error	Error	Relative Error	Error	Relative Error
2011	−5.49	−0.67%	2.27	0.28%	0.42	0.16%	5.84	2.18%
2012	0.59	0.07%	6.40	0.78%	1.69	0.59%	6.37	2.21%
2013	4.60	0.55%	8.39	1.01%	1.41	0.45%	5.19	1.67%
2014	8.75	1.04%	10.47	1.24%	4.10	1.23%	6.82	2.05%
2015	11.45	1.34%	11.02	1.29%	7.60	2.14%	9.07	2.56%
2016	10.37	1.19%	7.74	0.89%	5.94	1.54%	5.96	1.55%
2017	−2.64	−0.29%	−7.55	−0.84%	−13.50	−3.10%	−15.15	−3.48%
2018	−17.39	−1.87%	−24.66	−2.66%	−0.54	−0.12%	−4.13	−0.91%

Note: unit is ten thousand people.

below.

The results in Table 9 show that, compared to the three models and methods above, the average relative error of the gray prediction method is the lowest of the four. For the first-tier cities, being popular immigration destinations, the errors increased slightly with time over the last few years. This is probably caused by increasing population flow into first-tier cities. Through error testing and numerical prediction, the prediction results of the 10-year sample size prove to be more accurate, with an average relative error of only 0.005%, which confirms that the GM (1, 1) model has high accuracy while requiring less data.

As shown in

Table 10. Comparison of precision of urban population prediction in 210 prefecture-level cities.

Model	Malthusian Model (High Growth Rate)	Malthusian Model (Middle Growth Rate)	Malthusian Model (Low Growth Rate)	Unary Linear Regression Model (10 Years)	Unary Linear Regression Model (20 Years)
Average relative error rate (%)	3.885%	0.825%	−2.122%	−0.018%	0.166%
Model	Logistic biological competition model (10 years)	Logistic biological competition model (20 years)	GM (1, 1) model (10 years)	GM (1, 1) model (20 years)	Multi-model average
Average relative error rate (%)	0.371%	−0.303%	0.005%	1.327%	0.460%

Note: all models take year 2010 as the base year for prediction, the prediction duration is 20 years, and the error test period is 2011–2018.

, by comprehensively comparing the errors of the four prediction models mentioned above, it is found that the 10-year sample size of the GM (1, 1) model has the smallest error: only 0.005%. Among the hypotheses about the model mentioned above, the four models can basically make appropriate predictions, and GM (1, 1) has the highest accuracy. Thus, the GM (1, 1) model passes the hypothesis.

Therefore, the prediction data of the GM (1, 1) model were selected for analysis of the future development trends in the remainder of this article.

4. Discussion

The calculations in this section refer to the data analysis methods of Langford [38] and Koenker and Bassett [39]. Based on the quartile analysis method, the box plots of the four sets of data for the years 2000, 2010, 2020, and 2030 are shown to facilitate intuitive analysis, as well as the comparison of the average levels and degrees of variation among multiple data sets. The box plots are shown in Figure 1 below.

The analysis shows that in the selected four years (2000, 2010, 2020, and 2030), among the 210 cities selected, Chongqing has the largest population (3091.09, 3303.45, 3432.93, and 3552.76, respectively), while Jiayuguan has the smallest population (15.96, 21.8, 21.34, and 22.02, respectively). The median of the urban population was 425.06, 465.71, 491.16, and 522.56, respectively. The data dispersion in each year is relatively high, while all population values are right-skewed, and all of them contain extreme values. This is because, in different years, the population values of the cities of Chongqing, Shanghai, Chengdu, and Nanyang are extremely large in their respective groups and are judged to be outliers, which increased the average population of each year thus leading to the right skewness of data. The population growth pattern in each city exhibits spatial difference over the years, while the degree of population dispersion in each city maintains an increasing momentum, resulting in enormous numerical gaps between cities in terms of their populations.

The growth in populations has accelerated the speed at which cities change their spatial layout, adopt different development models, and adapt in other ways to accommodate this growth. Cities are also profiting due to the economic benefits of population growth, which drives up demand for goods and services while providing additional labor. Consequently, there is an interaction between population growth and city expansion. As the public calls for regional development, the role of metropolitan areas in delivering development have become increasingly important [22,40].

For a clearer and more intuitive analysis of the development trends of the cities’ populations, the latitude and longitude coordinates of the above mentioned 210 prefecture-level cities were imported to the geo module of pyecharts (v1.9.0) in Python (v3.7). The highly accurate population prediction results from the GM (1, 1) model mentioned above were matched with the imported cities to draw the spatial distribution of the cities’ populations in 2000, 2010, 2020, and 2030.

As shown in Figure 2 and Figure 3, the populations of the sample cities have grown steadily in general but the population growth rates have slowed down significantly. In terms of specific cities, the total populations of the first-tier cities and new first-tier cities are stabilizing, while the growth rates of these cities all show a downward trend. The population growth rates of all cities fell below 1%, except for Guangzhou, Shenzhen, Chengdu, Hangzhou, Xi’an, Changsha, and Dongguan. Among them, the population growth rate of Zhengzhou City was −1.05%. For some cities, including Beijing, due to the implementation of population regulations, as well as factors such as housing prices and living costs, there is a noticeable growth in reverse migration.

As for total population, most first-tier and new first-tier cities have populations between 5–10 million. It is expected that the population of Xi’an and Guangzhou will exceed 10 million in 2023 and 2025, respectively. In addition, China has 19 first-tier and new first-tier cities, and it is expected that the population of seven of these cities will exceed 10 million by 2030.

The population growth rates of second- and third-tier cities are increasing steadily, and those of most cities fluctuate around 0.5%. Among them, the population growth rates of Zhuhai, Foshan, Huizhou, Zhongshan, Guiyang, Handan, Langfang, Putian, Linyi, and Yinchuan are relatively higher than other second- and third-tier cities.

As for population growth, only three second- or third-tier cities (Baoding, Linyi, Nanyang) had a population exceeding 10 million in 2000. Owing to the rapid development of middle-tier cities (second-tier cities and third-tier cities), it is expected that there will be nine second- or third-tier cities (Shijiazhuang, Xuzhou, Handan, Baoding, Fuyang, Ganzhou, Linyi, Nanyang, and Shangqiu) with a population exceeding 10 million in 2030. Many cities have a population that exceeds 1 million; the only city with less than 1 million people is Sanya (643,600 people). The population sizes of the fourth- and fifth-tier cities are significantly smaller, but there are numerous low-tier cities that have a population in the range of 2–5 million. In recent years, population growth has slowed down, and the population growth rates of most cities have been negative. It is expected that in 2030, Yichun (969,000 people), Tongchuan (763,000 people), Shizuishan (739,200 people), Jinchang (431,500 people), Wuhai (316,300 people), Jiayuguan (217,800 people), and Karamay (169,600 people) will still each have a population under 1 million.

Owing to the ever-expanding economic advantages and talent introduction policies of core cities, their agglomeration effects have been continuously enhanced [40]. To further analyze the trend of inter-regional population development in the future, Figure 4 and Figure 5 are drawn by overlaying the original urban agglomeration distribution data upon a map with latitude and longitude coordinates for each city, sourced from Google Maps, to show the distribution of urban agglomerations in China.

The analysis of cities shows that the overall population development of the north and south of the country is relatively stable, but the city disparity is obvious. (The geographical boundary between north and south China is the Qinling-Huai River line, along the southeast side of the Qinghai-Tibet Plateau, which coincides with the 800 mm isothermal precipitation line and the January zero isothermal line. The area north of this line is called Northern China, and the area south of this line is called Southern China.) In the sample data of 210 cities, the sample range from 1999 to 2018 show that the average annual population growth of southern cities (totaling 106) was 3.862 million people, and that of northern cities (totaling 104) was 2.652 million people. The development characteristic can be described as fast in the southern cities and slow in the northern cities. In the prediction data of 2021–2030, the average annual population growth in the southern and northern cities is expected to be 2.0451 million and 1.9081 million, respectively, indicating a population growth trend that is roughly equal in the southern cities and the northern cities.

As for the urban agglomerations, as shown in Figure 4 and Figure 5, the overall population growth rate of the sample city data is steady while slowing down. The population growth rates of the northern cities have gradually surpassed those of the southern cities. The ratio of the population growth in the northern urban agglomerations to that of the southern urban agglomerations is expected to increase from 0.73 from 1999–2018 to 0.79 from 2021–2030. Among them, the population growth of the urban agglomeration in the middle reaches of the Yangtze River Delta has a significantly slowing growth rate. The population growth rates of Yichang, Jingmen, Xiaogan, Huanggang, Jingzhou, Xiangtan, and Changde are all negative, and the average annual population growth is expected to be 259,600 from 2021 to 2030. The population growth of the Central Plains urban agglomeration and the Yangtze River Delta urban agglomeration has been progressing steadily. The growth rates are stable at around 1% and 0.5% in the long term, and it is expected that the average annual population growth in the next 10 years will reach 774,900 and 420,500, respectively.

Regarding the metropolitan areas, the core metropolitan areas, including the Yangtze River Delta interlocking the metropolitan areas, Guangdong–Hong Kong–Macao Greater Bay Area, and the capital, Beijing, have attracted talent from across the nation to migrate there due to these areas offering a solid economic base, being well-located, and presenting policy advantages. Consequently, the population has grown especially rapidly in these areas. It is expected that the average annual population growth in 2021–2030 will exceed 400,000. Among these areas, the average annual population growth of the Guangdong–Hong Kong–Macao Greater Bay Area is expected to exceed 600,000. For the city circles represented by Shenyang, Changchun, Xi’an, and Chengdu, the population growth rates are negative. In particular, the city population growth rates in the northeastern regions have decreased rapidly due to economic depression and the harsh climate there, and there is a serious outflow of population.

Generally speaking, the future population growth of prefecture-level cities in China generally meets the theory of zero population growth, and the hypothesis of population theory above is basically valid. This study finds that population growth exhibits inconsistent patterns between different city tiers. The population growth of high-tier cities (first-tier cities and new first-tier cities) is shrinking, the populations of low-tier cities (fourth-tier cities and fifth-tier cities) are experiencing negative growth, and the populations of middle-tier cities are exploding. With the continuous enhancement of the regional integration of large urban agglomerations and metropolitan areas, the layout with scattered groups has been replaced by a large landscape with a uniform pace. However, the promotional effect of core urban agglomerations and metropolitan areas on the surrounding areas is still not significant.

5. Conclusions

Population growth is a source of economic and social vitality, the foundation of innovation and entrepreneurship, and a core element in encouraging urban development. China is now facing population problems such as the overall slowdown of the population growth rate, the intensifying of sub-replacement fertility and an aging population, the decrease in the fertility rate, and the overly rapid mobilization of the population. Furthermore, the competition to attract labor has turned into a competition to retain labor as migration becomes ever easier.

Based on the data from the cities’ statistics bureaus, statistical yearbooks over the years, and population censuses, this study utilized the Malthusian model, unary linear regression model, logistic model, and gray prediction model to perform population predictions on 210 prefecture-level cities and analyzed the characteristics of urban population distribution and development. This study has found that the total urban population has changed from fast growth in developed cities and slow growth in underdeveloped cities to slow growth in high- and low-tier cities, and fast growth in middle-tier cities. The growth rates of city populations have changed from a fast pattern in the southern cities and a slow pattern in the northern cities to being basically balanced between the northern and southern cities. Comparing the populations of cities at different tiers, the high-tier cities had once dominated the top rankings, but the middle- and low-tier cities are gradually catching up and weakening the dominance of high-tier cities. The target of the urban agglomerations and the metropolitan areas is gradually shifting from integration to urban cohesion, although the population gaps between cities tend to widen; as the growth rate of the population declines, China’s total population is likely to be relatively stable in the future. In addition to the population aggregation effect, economic siphon effect, and other reasons, fertility decline may also be an important reason for this phenomenon. Cities with faster economic development attract highly educated people [40], and their high expectations for potential marriage partners coupled with the huge marriage costs of China’s skyrocketing housing prices may hinder the willingness of highly educated people to marry [41]. Those who are married, especially highly educated married women, often choose to have only one child or give up work because it is difficult to balance work and family [42], also leading to slow urban population growth.

In the future, the state should accelerate the reform of the household registration system and optimize the employment promotion mechanism. It should conform to the pattern of urbanization development and guide the population to migrate to small- and medium-sized cities surrounding the densely populated urban agglomerations and metropolitan areas. The purpose of this is to coordinate the populations of the regions and to connect different parts of the nation. The state must also proactively intensify the leading effect of core cities and regions while at the same time facilitate the harmonious development of regional economies. It must determine the largest scope of common interests, target the highest common factors that affect mutual benefit, promote industrial development, upgrade and renew the regional populations, and move high-quality talents to the core regions. Further, the state should focus on building a policy system and social environment conducive to elderly care and filial piety, and cancel all policy constraints on childbirth. This should encourage people to get married and reproduce at an appropriate age, let families control their own reproduction, and further accelerate the construction of a support system for accelerating reproduction.

This study used microdata on the population of prefecture-level cities in China to make population predictions and used visualization software to more intuitively show the development and change of the future population, and combines prefecture-level cities and urban agglomerations to provide suggestions for the government to help cities develop better. This study certainly has reference value to the research of urban population development, urban agglomeration, and urban agglomeration development. Due to the limitation of population data system construction, the data granularity in this study can only reach prefecture-level cities. After obtaining more detailed data, its practical and theoretical significance will be more prominent.