Machine Learning and Deep Learning in Energy Systems: A Review
Abstract
1. Introduction
2. The Main Applications of ML and DL in Energy Systems
2.1. Energy Consumption and Demand Forecast
2.2. Predicting the Output Power of Solar Systems
2.3. Predicting the Output Power of Wind Systems
2.4. Optimization
2.5. Fault and Defect Detection
2.6. Other Applications and Algorithms Comparison
3. Machine Learning (ML)
3.1. Types of ML
3.1.1. Supervised Learning (SL)
3.1.2. Unsupervised Learning (USL)
3.1.3. Reinforcement Learning (RL)
3.1.4. Semi-Supervised Learning (SSL)
3.2. ML Algorithms
3.2.1. Linear Regression (LR)
Simple Linear Regression (SLR)
Multiple Linear Regression (MLR)
3.2.2. Logistic Regression (LOR)
3.2.3. k Nearest Neighbor (kNN)
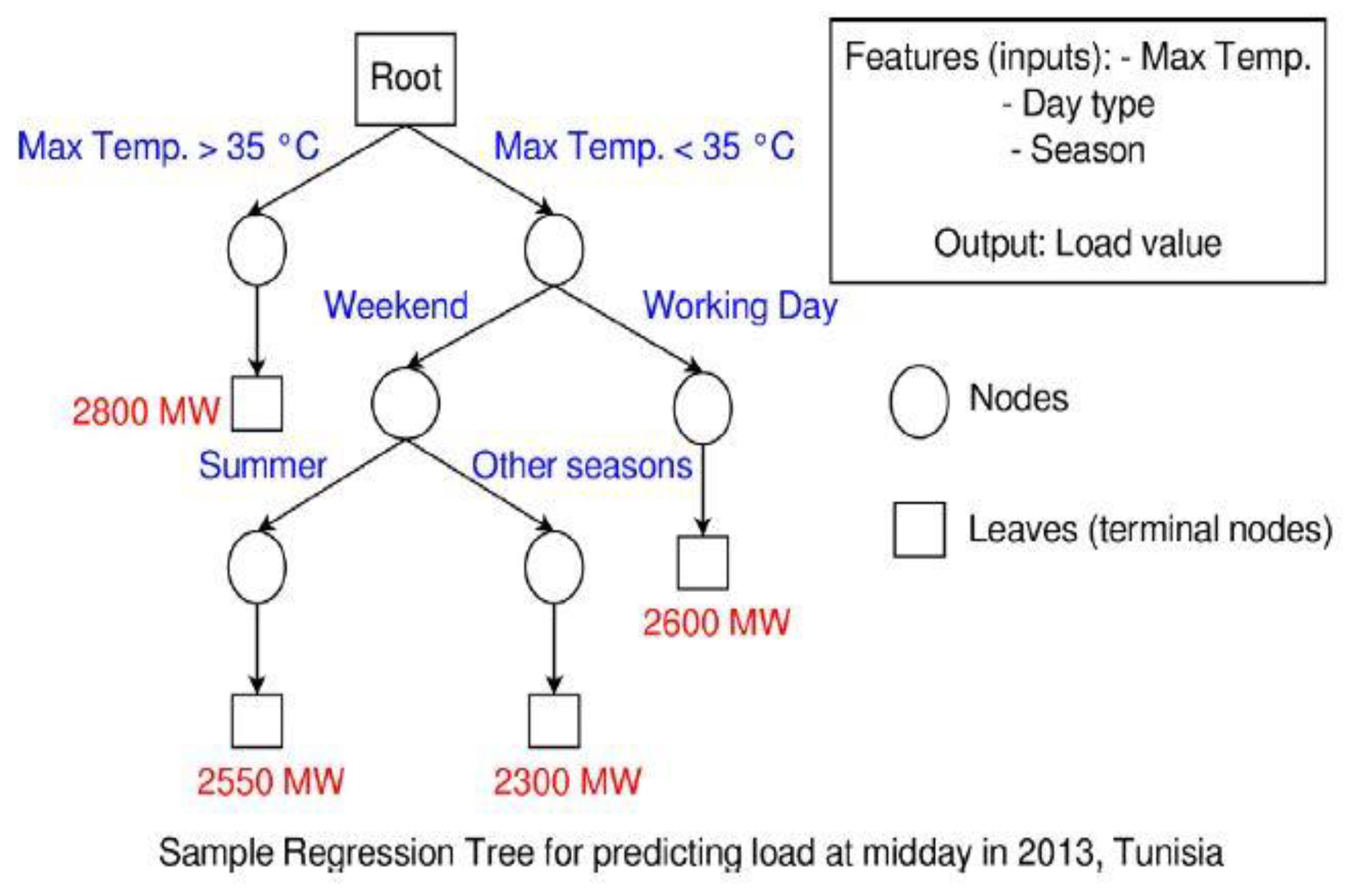
3.2.4. Decision Tree (DT)
3.2.5. Random Forest (RF)
3.2.6. SVM/SVR
3.2.7. Naive Bayes Classifier (NB)
3.2.8. K-Means
4. Deep Learning (DL)
4.1. DL Algorithms
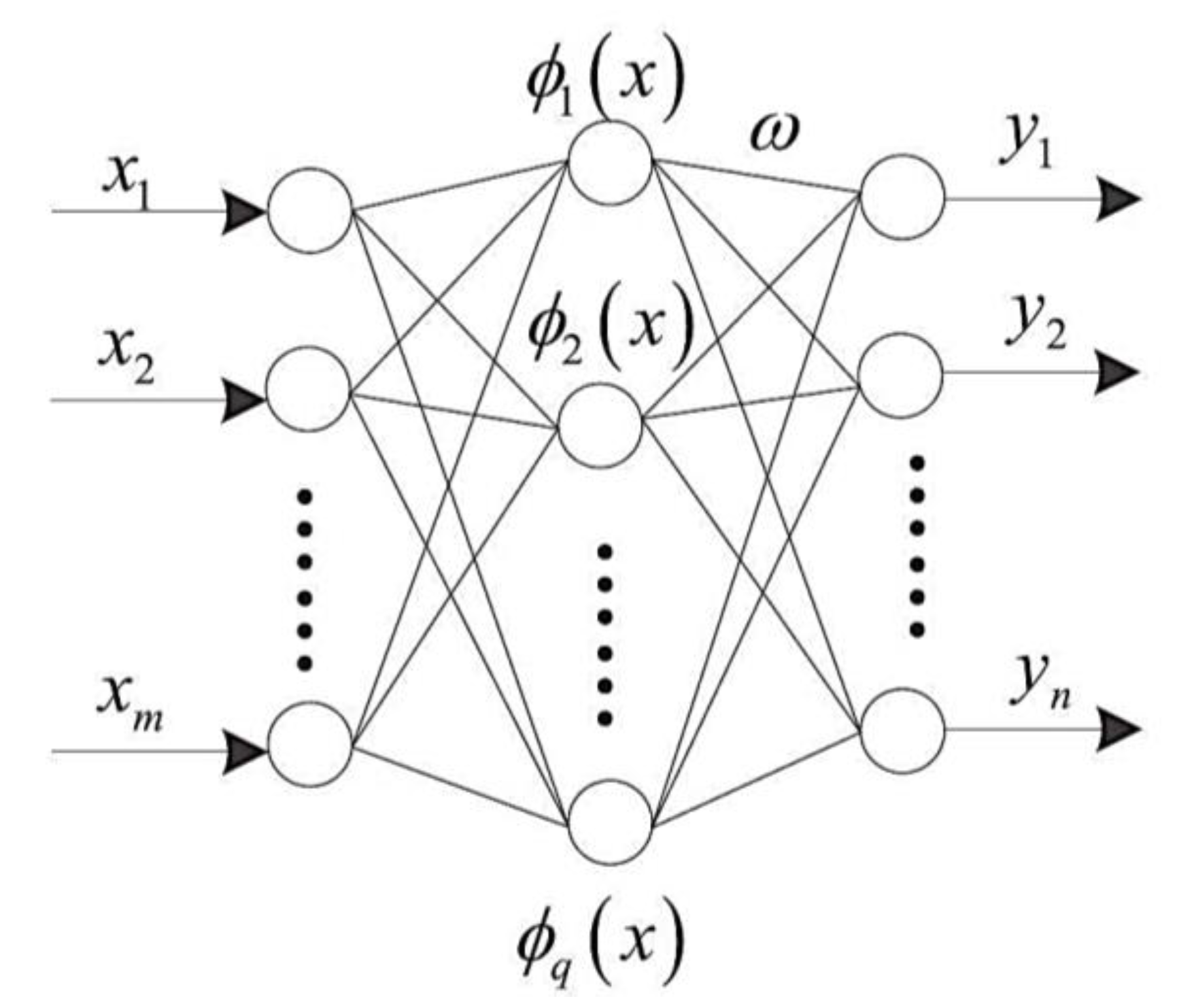
4.1.1. Artificial Neural Network (ANN)
| Name of the Activation Function | Formula | Graphical Representation | Number of Equations |
|---|---|---|---|
| Linear |  | (3) | |
| Sigmoid | 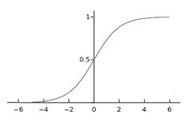 | (4) | |
| Hyperbolic tangent sigmoid (tanh-sig) |  | (5) | |
| Binary step |  | (6) | |
| Rectified Linear Units (ReLU) | 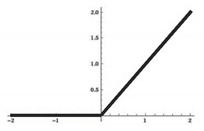 | (7) | |
| Leaky ReLU | 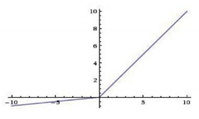 | (8) | |
| Exponential Linear Unit (ELU) | 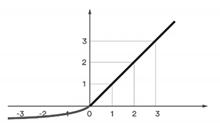 | (9) | |
| Gaussian Radial Basis |  | (10) | |
| Softmax | 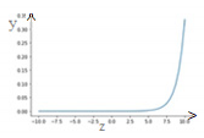 | (11) |
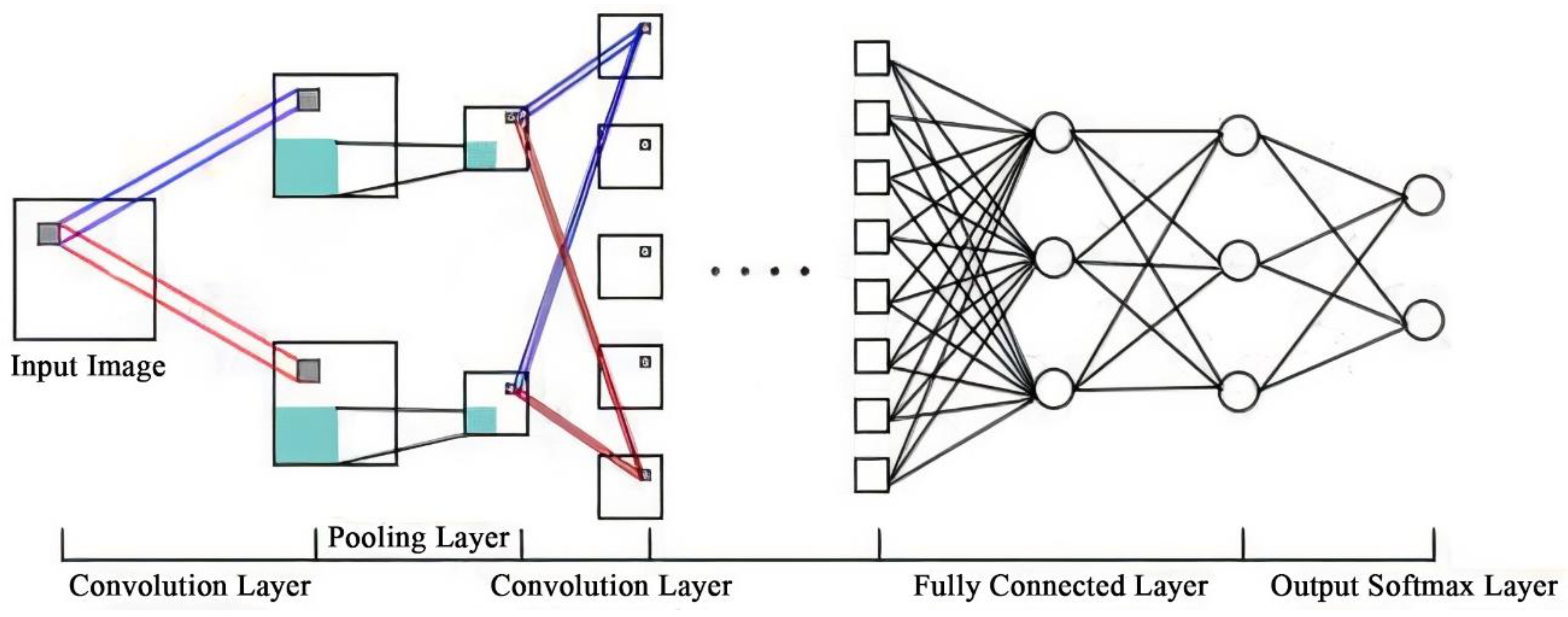
4.1.2. Convolutional Neural Network (CNN)
Input Layer
Convolutional Layer
Pooling Layer
Activation Function
Fully Connected Layer (FCL)
Loss Function
Back Propagation and Feedforward
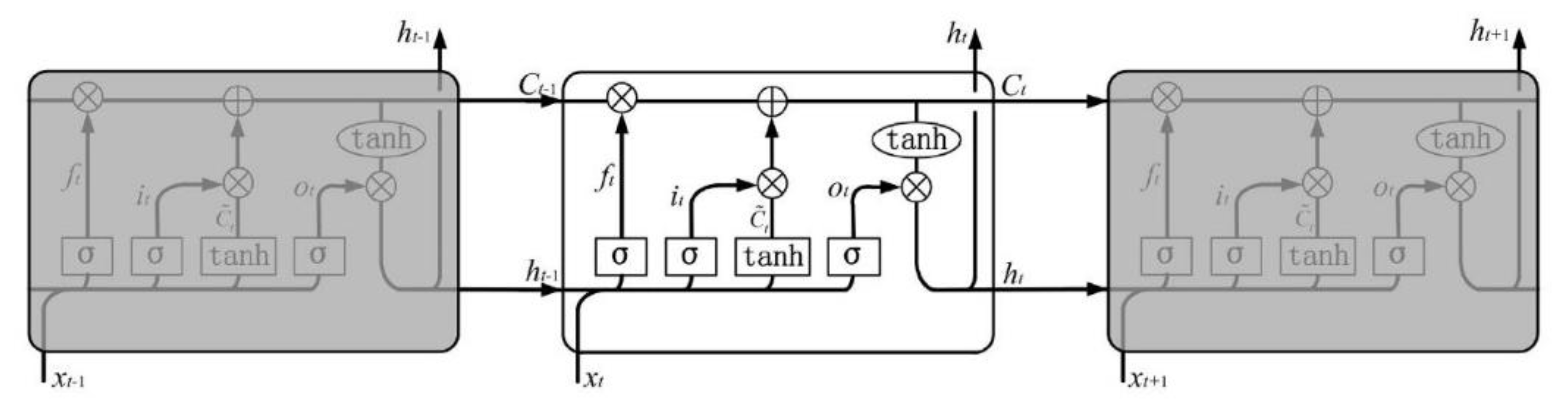
4.1.3. Recurrent Neural Network (RNN)
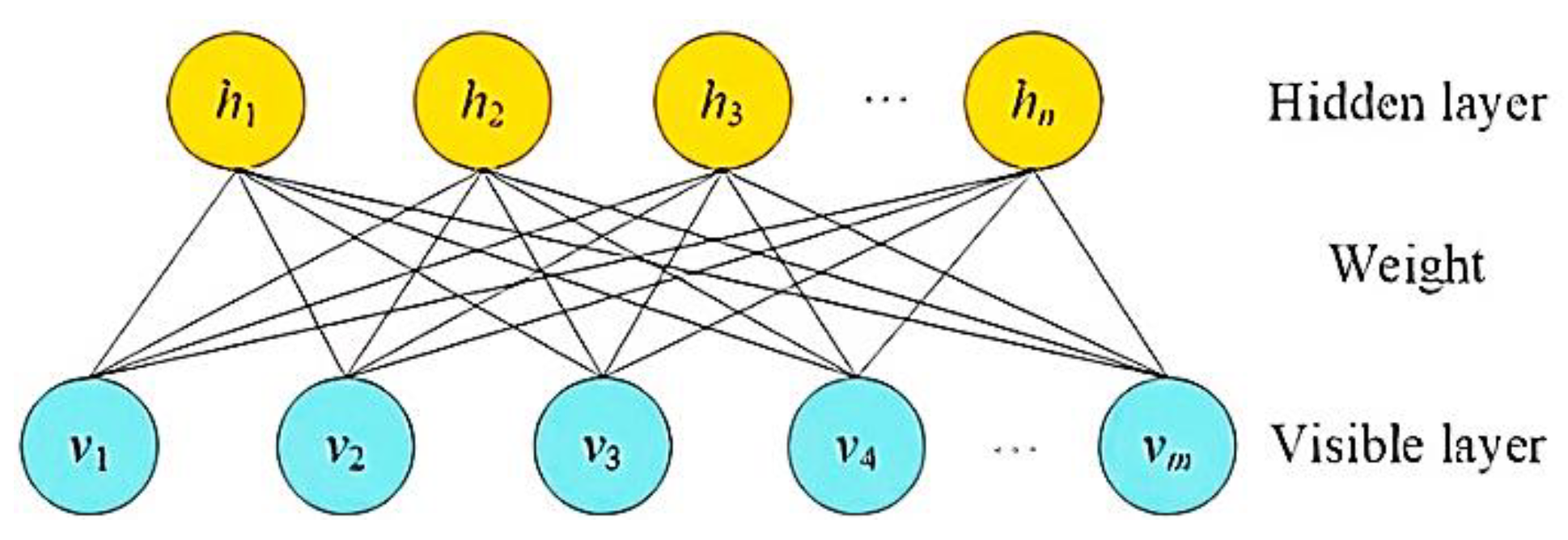
4.1.4. Restricted Boltzmann Machine (RBM)
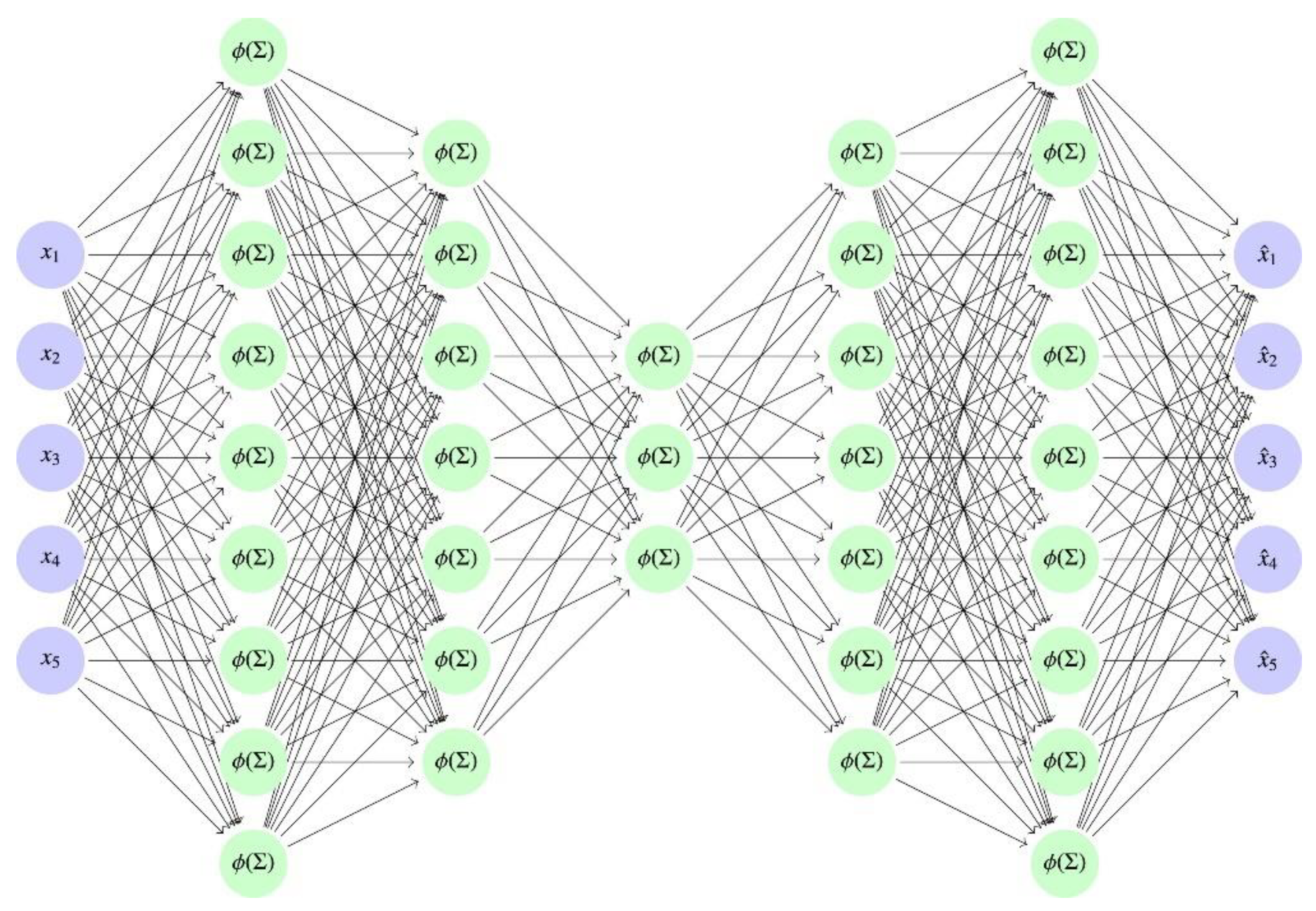
4.1.5. Auto Encoder (AE)
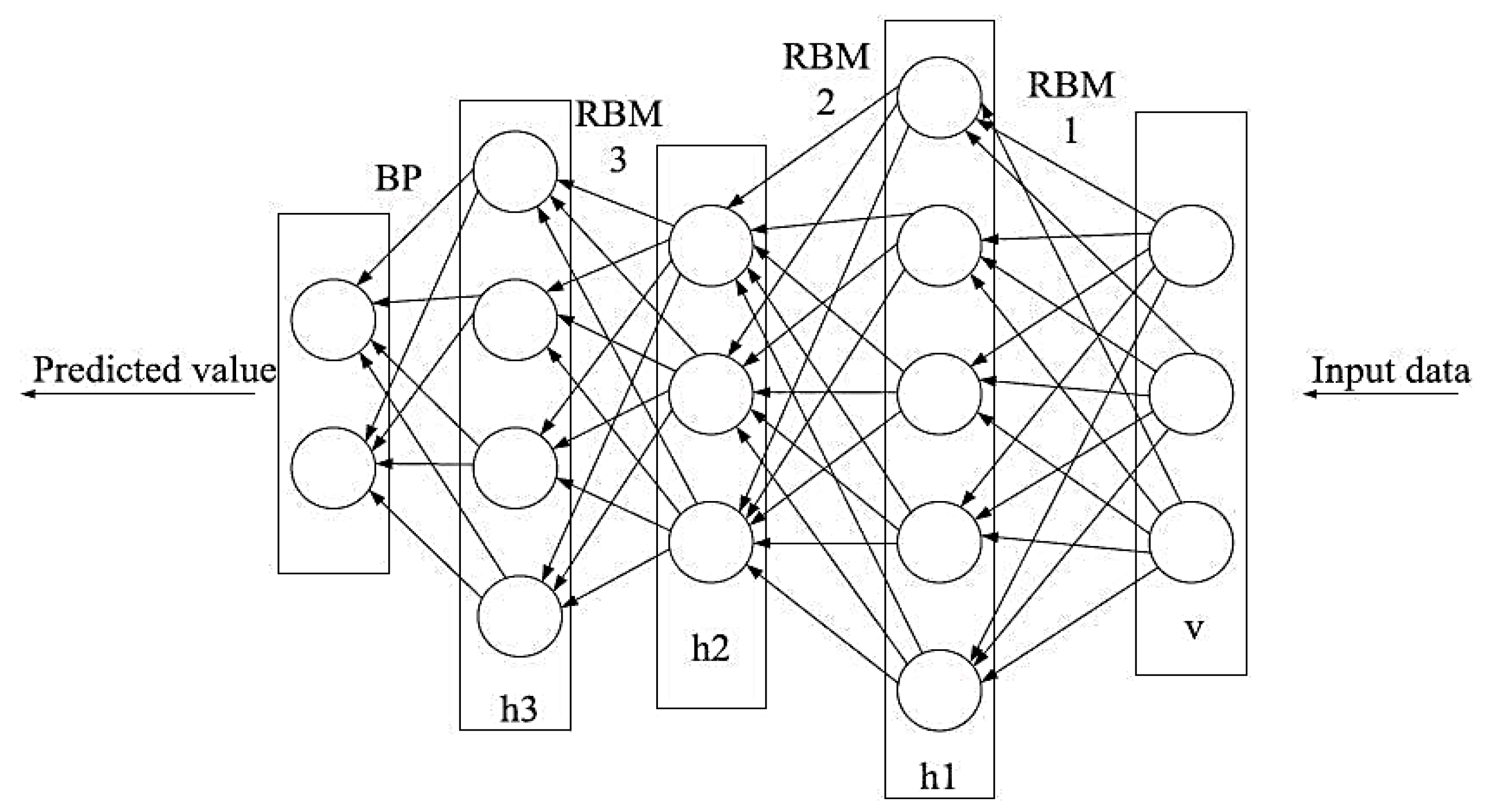
4.1.6. Deep Belief Neural Networks (DBN)
4.1.7. Generative Adversarial Network (GAN)
4.1.8. Adaptive Neuro-Fuzzy Inference System (ANFIS)
4.1.9. Wavelet Neural Network (WNN)
4.1.10. Radial Basis Neural Network (RBNN)
4.1.11. General Regression Neural Network (GRNN)
4.1.12. Extreme Learning Machine (ELM)
4.1.13. Ensemble Learning (EL)
Boosting
Adaptive Boosting (AdaBoost)
Extreme Gradient Boost (XGBoost)
AdaBoost.MRT
Bagging
Stacking
4.1.14. Hybrid Model (HM)
4.1.15. Transfer Learning (TL)
5. Time Series (TS)
5.1. TS Algorithms
5.1.1. Moving Average (MA) & Exponential Smoothing (ES)
5.1.2. Autoregressive Moving Average (ARMA)
5.1.3. Autoregressive Integrated Moving Average (ARIMA)
5.1.4. Case-Based Reasoning (CBR)
5.1.5. Fuzzy Time SERIES (FTS)
5.1.6. Grey Prediction Model (GPM)
5.1.7. Prophet Model
6. Performance Evaluation Metrics
6.1. Mean Squared Error (MSE)
6.2. R-Squared (R2)
6.3. Mean Absolute Error (MAE)
6.4. Root Mean Square Error (RMSE)
6.5. Normalised Root Mean Square Error (nRMSE)
6.6. Mean Absolute Percentage Error (MAPE)
6.7. Mean Bias Error (MBE)
6.8. t-Statistics
6.9. Coefficient of Variation of the Root Mean Square Error (CV-RMSE)
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| DL | Deep Learning |
| SL | Supervised Learning |
| SSL | Semi-Supervised Learning |
| ANN | Artificial Neural Network |
| R2 | Coefficient of Determination |
| DNN | Deep Neural Network |
| CNN | Convolutional Neural Network |
| CL | Convolutional Layer |
| nRMSE% | Normalized Root Mean Square Error |
| GAN | Generative Adversarial Network |
| RNN | Recurrent Neural Network |
| LSTM | Long-Short term Memory |
| RBM | Restricted Boltzmann Machine |
| RE | Reconstruction Error |
| AE | Auto Encoder |
| DBN | Deep Belief Networks |
| GAN | Generative Adversarial Network |
| ARMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| CBR | Case-Based Reasoning |
| HM | Hybrid Model |
| FCL | Fully Connected Layer |
| GRNN | General Regression Neural Network |
| TL | Transfer Learning |
| LASSO | Least Absolute Shrinkage Selector Operator |
| kNN | k Nearest Neighbor |
| SVR | Support Vector Regression |
| KELM | Kernel Extreme Learning Machine |
| NARX | Nonlinear Autoregressive Exogenous |
| NN | Neural Networks |
| DNI | Direct Normal Irradiance |
| GHI | Global Horizontal Irradiance |
| ANFIS-FCM | ANFIS based on Fuzzy C-means Clustering |
| ANFIS-SC | ANFIS based on Subtractive Clustering |
| SP | Smart Persistence |
| BT | Boosted-Tree |
| MMI | Modified Mutual Information |
| FCRBM | Factored Conditional Restricted Boltzmann Machine |
| GWDO | Genetic Wind-Driven Optimization |
| APSONN | Accelerated Particle Swarm Optimization Neural Network |
| GANN | Genetic Algorithm Neural Network |
| ABCNN | Artificial Bee Colony Neural Network |
| MLR | Multiple Linear Regression |
| GRU | Gated Recurrent Unit |
| AEM | Actual Engineering Model |
| GSA | Gravitational Search Algorithm |
| ICBR | Improved Case Based Reasoning |
| FDD | Fault Detection and Diagnosis |
| IDA | Improved Dragonfly Algorithm |
| MSSM | Mahalanobis Semi-Supervised Mapping |
| SM | Surrogate Model |
| HOA | Hybrid Optimization Algorithm |
| LSSVM | Least Square SVM |
| FA | Firefly Algorithm |
| HVAC | Heating Ventilating and Air Conditioning |
| PV | Photovoltaic |
| EM | Energy Management |
| LR | Linear Regression |
| DT | Decision Tree |
| WNN | Wavelet Neural Network |
| BP | Back Propagation |
| AIC | Akaike Information Criterion |
| ReLU | Rectified Linear Unit |
| GB | Gradient Boosting |
| DA | Dragonfly algorithm |
| ELU | Exponential Linear Unit |
| DM | Discriminator Model |
| GM | Generative Model |
| USL | Unsupervised Learning |
| RL | Reinforcement Learning |
| EORV | Expectation of a Random Variable(Expected Value) |
| UE | Uncorrelated Error |
| NB | Naive Bayes |
| WT | Wavelet Transform |
| ELM | Extreme Learning Machine |
| PCA | Principal Component Analysis |
| SLFN | Single Hidden Layer Feed-Forward Neural Networks |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| MRE | Mean Relative Error |
| MBE | Mean Bias Error |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Square Error |
| MA | Moving Average |
| AR | Autoregressive |
| ES | Exponential Smoothing |
| FTS | Fuzzy Time Series |
| MLP | Multilayer Perceptron Network |
| GPM | Gray Prediction Model |
| TS | Time Series |
| SVM | Support Vector Machine |
| XGBoost | eXtreme Gradient Boost |
| RF | Random Forest |
| NWP | Numerical Weather Prediction |
| WRF | Weather Research and Forecasting |
| CIADCast | Cloud Index Advection and Diffusion |
| GBT | Gradient Boosting Tree |
| MLPNN | Multi Layer Perceptron Neural Network |
| ANFIS | Adaptive Neuro-Fuzzy Inference Systems |
| MARS | Multivariate Adaptive Regression Spline |
| CART | classification and regression tree |
| MI-ANN | Mutual Information-Based Artificial Neural Network |
| AFC-ANN | Accurate and Fast Converging based on ANN |
| CSNN | Cuckoo Search Neural Network |
| CS | Cuckoo Search |
| OPEC | Organization of Petroleum Exporting Countries |
| GARCH | Generalized Autoregressive Conditional Heteroscedasticity |
| EMD | Empirical Mode Decomposition |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| DRNN | Deep Recurrent Neural Network |
| SMTL | Surrogate Model trained using Transfer Learning |
| VPSO | Vibration Particle Swarm Optimization |
| DST | Decision Support Tool |
| PNN | Probabilistic Neural Networks |
| LMD | Local Mean Decomposition |
| BAS-SVM | Beetle Antennae Search based Support Vector Machine |
| SMANN | Surrogate Model trained using ANN |
| EM | Energy Management |
| GPR | Gaussian Process Regression |
| RBNN | Radial Basis Neural Network |
| AI | Artificial Intelligence |
| EWT | Empirical Wavelet Transform |
| EL | Ensemble Learning |
| SLR | Simple Linear Regression |
| LOR | Logistic Regression |
| RBF | Radial Basis Function |
| AdaBoost | Adaptive Boosting |
| IoT | Internet of Things |
| CA | Cluster Analysis |
| GP | Gaussian Processes |
| FDA | Fischer Discriminant Analysis |
References
- Mosavi, A.; Salimi, M.; Faizollahzadeh Ardabili, S.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the art of machine learning models in energy systems, a systematic review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
- Shivam, K.; Tzou, J.-C.; Wu, S.-C. A multi-objective predictive energy management strategy for residential grid-connected PV-battery hybrid systems based on machine learning technique. Energy Convers. Manag. 2021, 237, 114103. [Google Scholar] [CrossRef]
- Somu, N.; MR, G.R.; Ramamritham, K. A deep learning framework for building energy consumption forecast. Renew. Sustain. Energy Rev. 2021, 137, 110591. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- Musbah, H.; Aly, H.H.; Little, T.A. Energy management of hybrid energy system sources based on machine learning classification algorithms. Electr. Power Syst. Res. 2021, 199, 107436. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Rangel-Martinez, D.; Nigam, K.; Ricardez-Sandoval, L.A. Machine learning on sustainable energy: A review and outlook on renewable energy systems, catalysis, smart grid and energy storage. Chem. Eng. Res. Des. 2021, 174, 414–441. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, T.; Zhang, X.; Zhang, C. Artificial intelligence-based fault detection and diagnosis methods for building energy systems: Advantages, challenges and the future. Renew. Sustain. Energy Rev. 2019, 109, 85–101. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Tan, Y.; Yuan, J. Fault detection based on Bayesian network and missing data imputation for building energy systems. Appl. Therm. Eng. 2021, 182, 116051. [Google Scholar] [CrossRef]
- Li, H.; Yang, D.; Cao, H.; Ge, W.; Chen, E.; Wen, X.; Li, C. Data-driven hybrid petri-net based energy consumption behaviour modelling for digital twin of energy-efficient manufacturing system. Energy 2022, 239, 122178. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Brandt, A.R. Time-series aggregation for the optimization of energy systems: Goals, challenges, approaches, and opportunities. Renew. Sustain. Energy Rev. 2022, 157, 111984. [Google Scholar] [CrossRef]
- Frequency Chart of the Number of Articles Related to ML and DL in the Field of Energy Systems. Available online: https://www.scopus.com (accessed on 16 October 2021).
- Turetskyy, A.; Wessel, J.; Herrmann, C.; Thiede, S. Battery production design using multi-output machine learning models. Energy Storage Mater. 2021, 38, 93–112. [Google Scholar] [CrossRef]
- Yun, G.Y.; Kong, H.J.; Kim, H.; Kim, J.T. A field survey of visual comfort and lighting energy consumption in open plan offices. Energy Build. 2012, 46, 146–151. [Google Scholar] [CrossRef]
- Xuan, Z.; Xuehui, Z.; Liequan, L.; Zubing, F.; Junwei, Y.; Dongmei, P. Forecasting performance comparison of two hybrid machine learning models for cooling load of a large-scale commercial building. J. Build. Eng. 2019, 21, 64–73. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R.; le Cam, M. Hybrid short-term forecasting of the electric demand of supply fans using machine learning. J. Build. Eng. 2020, 29, 101144. [Google Scholar] [CrossRef]
- Ghodrati, A.; Zahedi, R.; Ahmadi, A. Analysis of cold thermal energy storage using phase change materials in freezers. J. Energy Storage 2022, 51, 104433. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Wang, S. Development of prediction models for next-day building energy consumption and peak power demand using data mining techniques. Appl. Energy 2014, 127, 1–10. [Google Scholar] [CrossRef]
- Bot, K.; Ruano, A.; Ruano, M. Forecasting Electricity Demand in Households using MOGA-designed Artificial Neural Networks. IFAC-Pap. 2020, 53, 8225–8230. [Google Scholar] [CrossRef]
- Bian, H.; Zhong, Y.; Sun, J.; Shi, F. Study on power consumption load forecast based on K-means clustering and FCM–BP model. Energy Rep. 2020, 6, 693–700. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Walker, S.; Khan, W.; Katic, K.; Maassen, W.; Zeiler, W. Accuracy of different machine learning algorithms and added-value of predicting aggregated-level energy performance of commercial buildings. Energy Build. 2020, 209, 109705. [Google Scholar] [CrossRef]
- Grimaldo, A.I.; Novak, J. Combining Machine Learning with Visual Analytics for Explainable Forecasting of Energy Demand in Prosumer Scenarios. Procedia Comput. Sci. 2020, 175, 525–532. [Google Scholar] [CrossRef]
- Haq, E.U.; Lyu, X.; Jia, Y.; Hua, M.; Ahmad, F. Forecasting household electric appliances consumption and peak demand based on hybrid machine learning approach. Energy Rep. 2020, 6, 1099–1105. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Khan, I. Electric load forecasting based on deep learning and optimized by heuristic algorithm in smart grid. Appl. Energy 2020, 269, 114915. [Google Scholar] [CrossRef]
- Khan, A.; Chiroma, H.; Imran, M.; Bangash, J.I.; Asim, M.; Hamza, M.F.; Aljuaid, H. Forecasting electricity consumption based on machine learning to improve performance: A case study for the organization of petroleum exporting countries (OPEC). Comput. Electr. Eng. 2020, 86, 106737. [Google Scholar] [CrossRef]
- Kazemzadeh, M.-R.; Amjadian, A.; Amraee, T. A hybrid data mining driven algorithm for long term electric peak load and energy demand forecasting. Energy 2020, 204, 117948. [Google Scholar] [CrossRef]
- Fathi, S.; Srinivasan, R.; Fenner, A.; Fathi, S. Machine learning applications in urban building energy performance forecasting: A systematic review. Renew. Sustain. Energy Rev. 2020, 133, 110287. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Zhang, L.; Wu, X.; Wang, X.-j. Energy consumption prediction and diagnosis of public buildings based on support vector machine learning: A case study in China. J. Clean. Prod. 2020, 272, 122542. [Google Scholar] [CrossRef]
- Kaytez, F. A hybrid approach based on autoregressive integrated moving average and least-square support vector machine for long-term forecasting of net electricity consumption. Energy 2020, 197, 117200. [Google Scholar] [CrossRef]
- Fan, G.-F.; Wei, X.; Li, Y.-T.; Hong, W.-C. Forecasting electricity consumption using a novel hybrid model. Sustain. Cities Soc. 2020, 61, 102320. [Google Scholar] [CrossRef]
- Jamil, R. Hydroelectricity consumption forecast for Pakistan using ARIMA modeling and supply-demand analysis for the year 2030. Renew. Energy 2020, 154, 1–10. [Google Scholar] [CrossRef]
- Beyca, O.F.; Ervural, B.C.; Tatoglu, E.; Ozuyar, P.G.; Zaim, S. Using machine learning tools for forecasting natural gas consumption in the province of Istanbul. Energy Econ. 2019, 80, 937–949. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S. Load demand forecasting of residential buildings using a deep learning model. Electr. Power Syst. Res. 2020, 179, 106073. [Google Scholar] [CrossRef]
- Moosavian, S.F.; Zahedi, R.; Hajinezhad, A. Economic, environmental and social impact of carbon tax for Iran: A computable general equilibrium analysis. Energy Sci. Eng. 2022, 10, 13–29. [Google Scholar] [CrossRef]
- Narvaez, G.; Giraldo, L.F.; Bressan, M.; Pantoja, A. Machine learning for site-adaptation and solar radiation forecasting. Renew. Energy 2021, 167, 333–342. [Google Scholar] [CrossRef]
- Feng, Y.; Gong, D.; Zhang, Q.; Jiang, S.; Zhao, L.; Cui, N. Evaluation of temperature-based machine learning and empirical models for predicting daily global solar radiation. Energy Convers. Manag. 2019, 198, 111780. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Zeng, W.; Wang, X.; Zou, H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renew. Sustain. Energy Rev. 2019, 100, 186–212. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Time series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Huertas-Tato, J.; Aler, R.; Galván, I.M.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Pozo-Vázquez, D. A short-term solar radiation forecasting system for the Iberian Peninsula. Part 2: Model blending approaches based on machine learning. Sol. Energy 2020, 195, 685–696. [Google Scholar] [CrossRef]
- Govindasamy, T.R.; Chetty, N. Machine learning models to quantify the influence of PM10 aerosol concentration on global solar radiation prediction in South Africa. Clean. Eng. Technol. 2021, 2, 100042. [Google Scholar] [CrossRef]
- Gürel, A.E.; Ağbulut, Ü.; Biçen, Y. Assessment of machine learning, time series, response surface methodology and empirical models in prediction of global solar radiation. J. Clean. Prod. 2020, 277, 122353. [Google Scholar] [CrossRef]
- Alizamir, M.; Kim, S.; Kisi, O.; Zounemat-Kermani, M. A comparative study of several machine learning based non-linear regression methods in estimating solar radiation: Case studies of the USA and Turkey regions. Energy 2020, 197, 117239. [Google Scholar] [CrossRef]
- Srivastava, R.; Tiwari, A.; Giri, V. Solar radiation forecasting using MARS, CART, M5, and random forest model: A case study for India. Heliyon 2019, 5, e02692. [Google Scholar] [CrossRef] [PubMed]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.N.N.; Machado, L.; Pabon, J.J.G. Prediction of hourly solar radiation in Abu Musa Island using machine learning algorithms. J.Clean.Prod. 2018, 176, 63–75. [Google Scholar]
- Li, C.; Lin, S.; Xu, F.; Liu, D.; Liu, J. Short-term wind power prediction based on data mining technology and improved support vector machine method: A case study in Northwest China. J. Clean. Prod. 2018, 205, 909–922. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Lu, H.; Niu, T.; Du, P. Hybrid wind energy forecasting and analysis system based on divide and conquer scheme: A case study in China. J. Clean. Prod. 2019, 222, 942–959. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X. Wind power forecasting of an offshore wind turbine based on high-frequency SCADA data and deep learning neural network. Energy 2020, 201, 117693. [Google Scholar] [CrossRef]
- Zendehboudi, A.; Baseer, M.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J. A robust combination approach for short-term wind speed forecasting and analysis–Combination of the ARIMA (Autoregressive Integrated Moving Average), ELM (Extreme Learning Machine), SVM (Support Vector Machine) and LSSVM (Least Square SVM) forecasts using a GPR (Gaussian Process Regression) model. Energy 2015, 93, 41–56. [Google Scholar]
- Demolli, H.; Dokuz, A.S.; Ecemis, A.; Gokcek, M. Wind power forecasting based on daily wind speed data using machine learning algorithms. Energy Convers. Manag. 2019, 198, 111823. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Jin, F.; Wu, Z. A self-adaptive kernel extreme learning machine for short-term wind speed forecasting. Appl. Soft Comput. 2021, 99, 106917. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind speed prediction using a univariate ARIMA model and a multivariate NARX model. Energies 2016, 9, 109. [Google Scholar] [CrossRef]
- Li, L.-L.; Zhao, X.; Tseng, M.-L.; Tan, R.R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Tian, Z. Short-term wind speed prediction based on LMD and improved FA optimized combined kernel function LSSVM. Eng. Appl. Artif. Intell. 2020, 91, 103573. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Satriani, T.R.A. Day-ahead spatiotemporal wind speed forecasting using robust design-based deep learning neural network. Energy 2020, 209, 118441. [Google Scholar] [CrossRef]
- Zahedi, R.; Ahmadi, A.; Eskandarpanah, R.; Akbari, M. Evaluation of Resources and Potential Measurement of Wind Energy to Determine the Spatial Priorities for the Construction of Wind-Driven Power Plants in Damghan City. Int. J. Sustain. Energy Environ. Res. 2022, 11, 1–22. [Google Scholar] [CrossRef]
- Zhang, R.Y.; Josz, C.; Sojoudi, S. Conic optimization for control, energy systems, and machine learning: Applications and algorithms. Annu. Rev. Control 2019, 47, 323–340. [Google Scholar] [CrossRef]
- Narciso, D.A.; Martins, F. Application of machine learning tools for energy efficiency in industry: A review. Energy Rep. 2020, 6, 1181–1199. [Google Scholar] [CrossRef]
- Azad, A.S.; Rahaman, M.S.A.; Watada, J.; Vasant, P.; Vintaned, J.A.G. Optimization of the hydropower energy generation using Meta-Heuristic approaches: A review. Energy Rep. 2020, 6, 2230–2248. [Google Scholar] [CrossRef]
- Acarer, S.; Uyulan, Ç.; Karadeniz, Z.H. Optimization of radial inflow wind turbines for urban wind energy harvesting. Energy 2020, 202, 117772. [Google Scholar] [CrossRef]
- Salimi, S.; Hammad, A. Optimizing energy consumption and occupants comfort in open-plan offices using local control based on occupancy dynamic data. Build. Environ. 2020, 176, 106818. [Google Scholar] [CrossRef]
- Teng, T.; Zhang, X.; Dong, H.; Xue, Q. A comprehensive review of energy management optimization strategies for fuel cell passenger vehicle. Int. J. Hydrog. Energy 2020, 45, 20293–20303. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Wickramasinghe, P.U.; Nik, V.M.; Scartezzini, J.-L. Machine learning methods to assist energy system optimization. Appl. Energy 2019, 243, 191–205. [Google Scholar] [CrossRef]
- Ikeda, S.; Nagai, T. A novel optimization method combining metaheuristics and machine learning for daily optimal operations in building energy and storage systems. Appl. Energy 2021, 289, 116716. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Artificial neural network based multivariable optimization of a hybrid system integrated with phase change materials, active cooling and hybrid ventilations. Energy Convers. Manag. 2019, 197, 111859. [Google Scholar] [CrossRef]
- Ilbeigi, M.; Ghomeishi, M.; Dehghanbanadaki, A. Prediction and optimization of energy consumption in an office building using artificial neural network and a genetic algorithm. Sustain. Cities Soc. 2020, 61, 102325. [Google Scholar] [CrossRef]
- Naserbegi, A.; Aghaie, M. Multi-objective optimization of hybrid nuclear power plant coupled with multiple effect distillation using gravitational search algorithm based on artificial neural network. Therm. Sci. Eng. Prog. 2020, 19, 100645. [Google Scholar] [CrossRef]
- Abbas, F.; Habib, S.; Feng, D.; Yan, Z. Optimizing generation capacities incorporating renewable energy with storage systems using genetic algorithms. Electronics 2018, 7, 100. [Google Scholar] [CrossRef]
- Li, Y.; Jia, M.; Han, X.; Bai, X.-S. Towards a comprehensive optimization of engine efficiency and emissions by coupling artificial neural network (ANN) with genetic algorithm (GA). Energy 2021, 225, 120331. [Google Scholar] [CrossRef]
- Xu, L.; Huang, C.; Li, C.; Wang, J.; Liu, H.; Wang, X. A novel intelligent reasoning system to estimate energy consumption and optimize cutting parameters toward sustainable machining. J. Clean. Prod. 2020, 261, 121160. [Google Scholar] [CrossRef]
- Wen, H.; Sang, S.; Qiu, C.; Du, X.; Zhu, X.; Shi, Q. A new optimization method of wind turbine airfoil performance based on Bessel equation and GABP artificial neural network. Energy 2019, 187, 116106. [Google Scholar] [CrossRef]
- El Koujok, M.; Ragab, A.; Amazouz, M. A Multi-Agent Approach Based on Machine-Learning for Fault Diagnosis. IFAC-Pap. 2019, 52, 103–108. [Google Scholar] [CrossRef]
- Deleplace, A.; Atamuradov, V.; Allali, A.; Pellé, J.; Plana, R.; Alleaume, G. Ensemble Learning-based Fault Detection in Nuclear Power Plant Screen Cleaners. IFAC-Pap. 2020, 53, 10354–10359. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Federated learning for machinery fault diagnosis with dynamic validation and self-supervision. Knowl.-Based Syst. 2021, 213, 106679. [Google Scholar] [CrossRef]
- Pang, Y.; Jia, L.; Zhang, X.; Liu, Z.; Li, D. Design and implementation of automatic fault diagnosis system for wind turbine. Comput. Electr. Eng. 2020, 87, 106754. [Google Scholar] [CrossRef]
- Zahedi, R.; Ahmadi, A.; Dashti, R. Energy, exergy, exergoeconomic and exergoenvironmental analysis and optimization of quadruple combined solar, biogas, SRC and ORC cycles with methane system. Renew. Sustain. Energy Rev. 2021, 150, 111420. [Google Scholar] [CrossRef]
- Rivas, A.E.L.; Abrão, T. Faults in smart grid systems: Monitoring, detection and classification. Electr. Power Syst. Res. 2020, 189, 106602. [Google Scholar] [CrossRef]
- Yang, C.; Liu, J.; Zeng, Y.; Xie, G. Real-time condition monitoring and fault detection of components based on machine-learning reconstruction model. Renew. Energy 2019, 133, 433–441. [Google Scholar] [CrossRef]
- Choi, W.H.; Kim, J.; Lee, J.Y. Development of Fault Diagnosis Models Based on Predicting Energy Consumption of a Machine Tool Spindle. Procedia Manuf. 2020, 51, 353–358. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y.; Zhang, J. Mahalanobis semi-supervised mapping and beetle antennae search based support vector machine for wind turbine rolling bearings fault diagnosis. Renew. Energy 2020, 155, 1312–1327. [Google Scholar] [CrossRef]
- Han, H.; Cui, X.; Fan, Y.; Qing, H. Least squares support vector machine (LS-SVM)-based chiller fault diagnosis using fault indicative features. Appl. Therm. Eng. 2019, 154, 540–547. [Google Scholar] [CrossRef]
- Helbing, G.; Ritter, M. Deep Learning for fault detection in wind turbines. Renew. Sustain. Energy Rev. 2018, 98, 189–198. [Google Scholar] [CrossRef]
- Wang, H.; Peng, M.-J.; Hines, J.W.; Zheng, G.-y.; Liu, Y.-K.; Upadhyaya, B.R. A hybrid fault diagnosis methodology with support vector machine and improved particle swarm optimization for nuclear power plants. ISA Trans. 2019, 95, 358–371. [Google Scholar] [CrossRef]
- Sarwar, M.; Mehmood, F.; Abid, M.; Khan, A.Q.; Gul, S.T.; Khan, A.S. High impedance fault detection and isolation in power distribution networks using support vector machines. J. King Saud Univ. Eng. Sci. 2019, 32, 524–535. [Google Scholar] [CrossRef]
- Eskandari, A.; Milimonfared, J.; Aghaei, M. Line-line fault detection and classification for photovoltaic systems using ensemble learning model based on IV characteristics. Sol. Energy 2020, 211, 354–365. [Google Scholar] [CrossRef]
- Han, H.; Zhang, Z.; Cui, X.; Meng, Q. Ensemble learning with member optimization for fault diagnosis of a building energy system. Energy Build. 2020, 226, 110351. [Google Scholar] [CrossRef]
- Tightiz, L.; Nasab, M.A.; Yang, H.; Addeh, A. An intelligent system based on optimized ANFIS and association rules for power transformer fault diagnosis. ISA Trans. 2020, 103, 63–74. [Google Scholar] [CrossRef]
- Dash, P.; Prasad, E.N.; Jalli, R.K.; Mishra, S. Multiple power quality disturbances analysis in photovoltaic integrated direct current microgrid using adaptive morphological filter with deep learning algorithm. Appl. Energy 2022, 309, 118454. [Google Scholar] [CrossRef]
- Yılmaz, A.; Küçüker, A.; Bayrak, G. Automated classification of power quality disturbances in a SOFC&PV-based distributed generator using a hybrid machine learning method with high noise immunity. Int. J. Hydrog. Energy 2022. [Google Scholar] [CrossRef]
- Manojlović, V.; Kamberović, Ž.; Korać, M.; Dotlić, M. Machine learning analysis of electric arc furnace process for the evaluation of energy efficiency parameters. Appl. Energy 2022, 307, 118209. [Google Scholar] [CrossRef]
- Sarmas, E.; Spiliotis, E.; Marinakis, V.; Koutselis, T.; Doukas, H. A meta-learning classification model for supporting decisions on energy efficiency investments. Energy Build. 2022, 258, 111836. [Google Scholar] [CrossRef]
- Tschora, L.; Pierre, E.; Plantevit, M.; Robardet, C. Electricity price forecasting on the day-ahead market using machine learning. Appl. Energy 2022, 313, 118752. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, Z.; Wu, J.; Du, X.; Chen, K. Short term electricity price forecasting using a new hybrid model based on two-layer decomposition technique and ensemble learning. Electr. Power Syst. Res. 2022, 205, 107762. [Google Scholar] [CrossRef]
- Homod, R.Z.; Togun, H.; Hussein, A.K.; Al-Mousawi, F.N.; Yaseen, Z.M.; Al-Kouz, W.; Abd, H.J.; Alawi, O.A.; Goodarzi, M.; Hussein, O.A. Dynamics analysis of a novel hybrid deep clustering for unsupervised learning by reinforcement of multi-agent to energy saving in intelligent buildings. Appl. Energy 2022, 313, 118863. [Google Scholar] [CrossRef]
- Anwar, M.B.; El Moursi, M.S.; Xiao, W. Novel power smoothing and generation scheduling strategies for a hybrid wind and marine current turbine system. IEEE Trans. Power Syst. 2016, 32, 1315–1326. [Google Scholar] [CrossRef]
- Leerbeck, K.; Bacher, P.; Junker, R.G.; Goranović, G.; Corradi, O.; Ebrahimy, R.; Tveit, A.; Madsen, H. Short-term forecasting of CO2 emission intensity in power grids by machine learning. Appl. Energy 2020, 277, 115527. [Google Scholar] [CrossRef]
- Gallagher, C.V.; Bruton, K.; Leahy, K.; O’Sullivan, D.T. The suitability of machine learning to minimise uncertainty in the measurement and verification of energy savings. Energy Build. 2018, 158, 647–655. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. Crack detection and localization on wind turbine blade using machine learning algorithms: A data mining approach. Struct. Durab. Health Monit. 2019, 13, 181. [Google Scholar] [CrossRef]
- Bassam, A.; May Tzuc, O.; Escalante Soberanis, M.; Ricalde, L.; Cruz, B. Temperature estimation for photovoltaic array using an adaptive neuro fuzzy inference system. Sustainability 2017, 9, 1399. [Google Scholar] [CrossRef]
- Zahedi, R.; Daneshgar, S. Exergy analysis and optimization of Rankine power and ejector refrigeration combined cycle. Energy 2022, 240, 122819. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Universal domain adaptation in fault diagnostics with hybrid weighted deep adversarial learning. IEEE Trans. Ind. Inform. 2021, 17, 7957–7967. [Google Scholar] [CrossRef]
- Osisanwo, F.; Akinsola, J.; Awodele, O.; Hinmikaiye, J.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: Classification and comparison. Int. J. Comput. Trends Technol. (IJCTT) 2017, 48, 128–138. [Google Scholar]
- Ozbas, E.E.; Aksu, D.; Ongen, A.; Aydin, M.A.; Ozcan, H.K. Hydrogen production via biomass gasification, and modeling by supervised machine learning algorithms. Int. J. Hydrog. Energy 2019, 44, 17260–17268. [Google Scholar] [CrossRef]
- Samuel, A.L. Machine learning. Technol. Rev. 1959, 62, 42–45. [Google Scholar]
- Daneshgar, S.; Zahedi, R.; Farahani, O. Evaluation of the concentration of suspended particles in underground subway stations in Tehran and its comparison with ambient concentrations. Ann. Env. Sci. Toxicol. 2022, 6, 019–025. [Google Scholar]
- Ayodele, T.O. Types of machine learning algorithms. New Adv. Mach. Learn. 2010, 3, 19–48. [Google Scholar]
- Mohajeri, N.; Assouline, D.; Guiboud, B.; Bill, A.; Gudmundsson, A.; Scartezzini, J.-L. A city-scale roof shape classification using machine learning for solar energy applications. Renew. Energy 2018, 121, 81–93. [Google Scholar] [CrossRef]
- Dery, L.M.; Nachman, B.; Rubbo, F.; Schwartzman, A. Weakly supervised classification in high energy physics. J. High Energy Phys. 2017, 2017, 145. [Google Scholar] [CrossRef]
- Catalina, T.; Iordache, V.; Caracaleanu, B. Multiple regression model for fast prediction of the heating energy demand. Energy Build. 2013, 57, 302–312. [Google Scholar] [CrossRef]
- Haider, S.A.; Sajid, M.; Iqbal, S. Forecasting hydrogen production potential in islamabad from solar energy using water electrolysis. Int. J. Hydrog. Energy 2021, 46, 1671–1681. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S. Stochastic uncertainty-based optimisation on an aerogel glazing building in China using supervised learning surrogate model and a heuristic optimisation algorithm. Renew. Energy 2020, 155, 810–826. [Google Scholar] [CrossRef]
- Alkhayat, G.; Mehmood, R. A review and taxonomy of wind and solar energy forecasting methods based on deep learning. Energy AI 2021, 4, 100060. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Perera, A.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar] [CrossRef]
- Li, H.; Misra, S. Reinforcement learning based automated history matching for improved hydrocarbon production forecast. Appl. Energy 2021, 284, 116311. [Google Scholar] [CrossRef]
- Zhou, B.; Duan, H.; Wu, Q.; Wang, H.; Or, S.W.; Chan, K.W.; Meng, Y. Short-term prediction of wind power and its ramp events based on semi-supervised generative adversarial network. Int. J. Electr. Power Energy Syst. 2021, 125, 106411. [Google Scholar] [CrossRef]
- Li, B.; Cheng, F.; Zhang, X.; Cui, C.; Cai, W. A novel semi-supervised data-driven method for chiller fault diagnosis with unlabeled data. Appl. Energy 2021, 285, 116459. [Google Scholar] [CrossRef]
- Fumo, N.; Biswas, M.R. Regression analysis for prediction of residential energy consumption. Renew. Sustain. Energy Rev. 2015, 47, 332–343. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Deo, R.C. Near real-time significant wave height forecasting with hybridized multiple linear regression algorithms. Renew. Sustain. Energy Rev. 2020, 132, 110003. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- Panchabikesan, K.; Haghighat, F.; El Mankibi, M. Data driven occupancy information for energy simulation and energy use assessment in residential buildings. Energy 2021, 218, 119539. [Google Scholar] [CrossRef]
- Gung, R.R.; Huang, C.-C.; Hung, W.-I.; Fang, Y.-J. The use of hybrid analytics to establish effective strategies for household energy conservation. Renew. Sustain. Energy Rev. 2020, 133, 110295. [Google Scholar] [CrossRef]
- Becker, R.; Thrän, D. Completion of wind turbine data sets for wind integration studies applying random forests and k-nearest neighbors. Appl. Energy 2017, 208, 252–262. [Google Scholar] [CrossRef]
- Guo, H.; Hou, D.; Du, S.; Zhao, L.; Wu, J.; Yan, N. A driving pattern recognition-based energy management for plug-in hybrid electric bus to counter the noise of stochastic vehicle mass. Energy 2020, 198, 117289. [Google Scholar] [CrossRef]
- Olatunji, O.O.; Akinlabi, S.; Madushele, N.; Adedeji, P.A. Property-based biomass feedstock grading using k-Nearest Neighbour technique. Energy 2020, 190, 116346. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Hour-ahead wind power forecast based on random forests. Renew. Energy 2017, 109, 529–541. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Coşgun, A.; Günay, M.E.; Yıldırım, R. Exploring the critical factors of algal biomass and lipid production for renewable fuel production by machine learning. Renew. Energy 2021, 163, 1299–1317. [Google Scholar] [CrossRef]
- Daneshgar, S.; Zahedi, R. Investigating the hydropower plants production and profitability using system dynamics approach. J. Energy Storage 2022, 46, 103919. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C. Identifying the influential features on the regional energy use intensity of residential buildings based on Random Forests. Appl. Energy 2016, 183, 193–201. [Google Scholar] [CrossRef]
- Smarra, F.; Jain, A.; De Rubeis, T.; Ambrosini, D.; D’Innocenzo, A.; Mangharam, R. Data-driven model predictive control using random forests for building energy optimization and climate control. Appl. Energy 2018, 226, 1252–1272. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Golabi, M.R. Modeling and predicting the electricity production in hydropower using conjunction of wavelet transform, long short-term memory and random forest models. Renew. Energy 2021, 170, 1367–1381. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Özdemir, S.; Demirtaş, M.; Aydın, S. Harmonic Estimation Based Support Vector Machine for Typical Power Systems. Neural Netw. World 2016, 26, 233–252. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Chen, Y.; Wang, D.; Wang, Y.; Zhu, Y. Comparison of support vector machine and copula-based nonlinear quantile regression for estimating the daily diffuse solar radiation: A case study in China. Renew. Energy 2020, 146, 1101–1112. [Google Scholar] [CrossRef]
- Sheikh, M.F.; Kamal, K.; Rafique, F.; Sabir, S.; Zaheer, H.; Khan, K. Corrosion detection and severity level prediction using acoustic emission and machine learning based approach. Ain Shams Eng. J. 2021, 12, 3891–3903. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Martínez-Durbán, M.; del Sagrado, J.; del Águila, I.; Batlles, F. The application of Bayesian network classifiers to cloud classification in satellite images. Renew. Energy 2016, 97, 155–161. [Google Scholar] [CrossRef]
- Liu, G.; Yang, J.; Hao, Y.; Zhang, Y. Big data-informed energy efficiency assessment of China industry sectors based on K-means clustering. J. Clean. Prod. 2018, 183, 304–314. [Google Scholar] [CrossRef]
- Niu, G.; Ji, Y.; Zhang, Z.; Wang, W.; Chen, J.; Yu, P. Clustering analysis of typical scenarios of island power supply system by using cohesive hierarchical clustering based K-Means clustering method. Energy Rep. 2021, 7, 250–256. [Google Scholar] [CrossRef]
- Zhang, T.; Bai, H.; Sun, S. A self-adaptive deep learning algorithm for intelligent natural gas pipeline control. Energy Rep. 2021, 7, 3488–3496. [Google Scholar] [CrossRef]
- Su, Q.; Khan, H.U.; Khan, I.; Choi, B.J.; Wu, F.; Aly, A.A. An optimized algorithm for optimal power flow based on deep learning. Energy Rep. 2021, 7, 2113–2124. [Google Scholar] [CrossRef]
- Zahedi, R.; Ahmadi, A.; Sadeh, M. Investigation of the load management and environmental impact of the hybrid cogeneration of the wind power plant and fuel cell. Energy Rep. 2021, 7, 2930–2939. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- Premalatha, M.; Naveen, C. Analysis of different combinations of meteorological parameters in predicting the horizontal global solar radiation with ANN approach: A case study. Renew. Sustain. Energy Rev. 2018, 91, 248–258. [Google Scholar]
- Ramezanizadeh, M.; Ahmadi, M.H.; Nazari, M.A.; Sadeghzadeh, M.; Chen, L. A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids. Renew. Sustain. Energy Rev. 2019, 114, 109345. [Google Scholar] [CrossRef]
- Zhong, X.; Enke, D. Predicting the daily return direction of the stock market using hybrid machine learning algorithms. Financ. Innov. 2019, 5, 1–20. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Y.; Pang, J.; Wang, K. Remaining useful life prediction for supercapacitor based on long short-term memory neural network. J. Power Sources 2019, 440, 227149. [Google Scholar] [CrossRef]
- Zhang, W.; Du, Y.; Yoshida, T.; Yang, Y. DeepRec: A deep neural network approach to recommendation with item embedding and weighted loss function. Inf. Sci. 2019, 470, 121–140. [Google Scholar] [CrossRef]
- Jahirul, M.; Rasul, M.; Brown, R.; Senadeera, W.; Hosen, M.; Haque, R.; Saha, S.; Mahlia, T. Investigation of correlation between chemical composition and properties of biodiesel using principal component analysis (PCA) and artificial neural network (ANN). Renew. Energy 2021, 168, 632–646. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Zhang, J.; Shi, J.; Gao, B.; Liu, W. Hybrid deep neural model for hourly solar irradiance forecasting. Renew. Energy 2021, 171, 1041–1060. [Google Scholar] [CrossRef]
- Apicella, A.; Donnarumma, F.; Isgrò, F.; Prevete, R. A survey on modern trainable activation functions. Neural Netw. 2021, 138, 14–32. [Google Scholar] [CrossRef]
- Mittal, A.; Soorya, A.; Nagrath, P.; Hemanth, D.J. Data augmentation based morphological classification of galaxies using deep convolutional neural network. Earth Sci. Inform. 2020, 13, 601–617. [Google Scholar] [CrossRef]
- Akram, M.W.; Li, G.; Jin, Y.; Chen, X.; Zhu, C.; Zhao, X.; Khaliq, A.; Faheem, M.; Ahmad, A. CNN based automatic detection of photovoltaic cell defects in electroluminescence images. Energy 2019, 189, 116319. [Google Scholar] [CrossRef]
- Chou, J.-S.; Truong, D.-N.; Kuo, C.-C. Imaging time-series with features to enable visual recognition of regional energy consumption by bio-inspired optimization of deep learning. Energy 2021, 224, 120100. [Google Scholar] [CrossRef]
- Zhou, D.; Yao, Q.; Wu, H.; Ma, S.; Zhang, H. Fault diagnosis of gas turbine based on partly interpretable convolutional neural networks. Energy 2020, 200, 117467. [Google Scholar] [CrossRef]
- Imani, M. Electrical load-temperature CNN for residential load forecasting. Energy 2021, 227, 120480. [Google Scholar] [CrossRef]
- Qian, C.; Xu, B.; Chang, L.; Sun, B.; Feng, Q.; Yang, D.; Ren, Y.; Wang, Z. Convolutional neural network based capacity estimation using random segments of the charging curves for lithium-ion batteries. Energy 2021, 227, 120333. [Google Scholar] [CrossRef]
- Eom, Y.H.; Yoo, J.W.; Hong, S.B.; Kim, M.S. Refrigerant charge fault detection method of air source heat pump system using convolutional neural network for energy saving. Energy 2019, 187, 115877. [Google Scholar] [CrossRef]
- Poernomo, A.; Kang, D.-K. Content-aware convolutional neural network for object recognition task. Int. J. Adv. Smart Converg. 2016, 5, 1–7. [Google Scholar] [CrossRef][Green Version]
- Geng, Z.; Zhang, Y.; Li, C.; Han, Y.; Cui, Y.; Yu, B. Energy optimization and prediction modeling of petrochemical industries: An improved convolutional neural network based on cross-feature. Energy 2020, 194, 116851. [Google Scholar] [CrossRef]
- Alves, R.H.F.; de Deus Júnior, G.A.; Marra, E.G.; Lemos, R.P. Automatic fault classification in photovoltaic modules using Convolutional Neural Networks. Renew. Energy 2021, 179, 502–516. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Li, X. Deep learning-based prognostic approach for lithium-ion batteries with adaptive time-series prediction and on-line validation. Measurement 2020, 164, 108052. [Google Scholar] [CrossRef]
- Fekri, M.N.; Patel, H.; Grolinger, K.; Sharma, V. Deep learning for load forecasting with smart meter data: Online adaptive recurrent neural network. Appl. Energy 2021, 282, 116177. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Y.; Li, X. Prediction of the NOx emissions from thermal power plant using long-short term memory neural network. Energy 2020, 192, 116597. [Google Scholar] [CrossRef]
- Sun, L.; Liu, T.; Xie, Y.; Zhang, D.; Xia, X. Real-time power prediction approach for turbine using deep learning techniques. Energy 2021, 233, 121130. [Google Scholar] [CrossRef]
- Pang, Z.; Niu, F.; O’Neill, Z. Solar radiation prediction using recurrent neural network and artificial neural network: A case study with comparisons. Renew. Energy 2020, 156, 279–289. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y. Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models. Renew. Energy 2021, 177, 101–112. [Google Scholar] [CrossRef]
- Dedinec, A.; Filiposka, S.; Dedinec, A.; Kocarev, L. Deep belief network based electricity load forecasting: An analysis of Macedonian case. Energy 2016, 115, 1688–1700. [Google Scholar] [CrossRef]
- Hu, S.; Xiang, Y.; Huo, D.; Jawad, S.; Liu, J. An improved deep belief network based hybrid forecasting method for wind power. Energy 2021, 224, 120185. [Google Scholar] [CrossRef]
- Harrou, F.; Dairi, A.; Kadri, F.; Sun, Y. Effective forecasting of key features in hospital emergency department: Hybrid deep learning-driven methods. Mach. Learn. Appl. 2022, 7, 100200. [Google Scholar] [CrossRef]
- Yang, W.; Liu, C.; Jiang, D. An unsupervised spatiotemporal graphical modeling approach for wind turbine condition monitoring. Renew. Energy 2018, 127, 230–241. [Google Scholar] [CrossRef]
- Daneshgar, S.; Zahedi, R. Optimization of power and heat dual generation cycle of gas microturbines through economic, exergy and environmental analysis by bee algorithm. Energy Rep. 2022, 8, 1388–1396. [Google Scholar] [CrossRef]
- Roelofs, C.M.; Lutz, M.-A.; Faulstich, S.; Vogt, S. Autoencoder-based anomaly root cause analysis for wind turbines. Energy AI 2021, 4, 100065. [Google Scholar] [CrossRef]
- Renström, N.; Bangalore, P.; Highcock, E. System-wide anomaly detection in wind turbines using deep autoencoders. Renew. Energy 2020, 157, 647–659. [Google Scholar] [CrossRef]
- Das, L.; Garg, D.; Srinivasan, B. NeuralCompression: A machine learning approach to compress high frequency measurements in smart grid. Appl. Energy 2020, 257, 113966. [Google Scholar] [CrossRef]
- Qi, Y.; Hu, W.; Dong, Y.; Fan, Y.; Dong, L.; Xiao, M. Optimal configuration of concentrating solar power in multienergy power systems with an improved variational autoencoder. Appl. Energy 2020, 274, 115124. [Google Scholar] [CrossRef]
- Hinton, G.E. Deep belief networks. Scholarpedia 2009, 4, 5947. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
- Hao, X.; Guo, T.; Huang, G.; Shi, X.; Zhao, Y.; Yang, Y. Energy consumption prediction in cement calcination process: A method of deep belief network with sliding window. Energy 2020, 207, 118256. [Google Scholar] [CrossRef]
- Sun, X.; Wang, G.; Xu, L.; Yuan, H.; Yousefi, N. Optimal Estimation of the PEM Fuel Cells applying Deep Belief Network Optimized by Improved Archimedes Optimization Algorithm. Energy 2021, 237, 121532. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, Y.; Yousefi, N. Nonlinear modeling of the polymer Membrane Fuel Cells using Deep Belief Networks and Modified Water Strider Algorithm. Energy Rep. 2021, 7, 2460–2469. [Google Scholar] [CrossRef]
- Wei, H.; Hongxuan, Z.; Yu, D.; Yiting, W.; Ling, D.; Ming, X. Short-term optimal operation of hydro-wind-solar hybrid system with improved generative adversarial networks. Appl. Energy 2019, 250, 389–403. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Feng, J.; Feng, X.; Chen, J.; Cao, X.; Zhang, X.; Jiao, L.; Yu, T. Generative adversarial networks based on collaborative learning and attention mechanism for hyperspectral image classification. Remote Sens. 2020, 12, 1149. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Rao, Y. Establishment of a generalizable model on a small-scale dataset to predict the surface pressure distribution of gas turbine blades. Energy 2021, 214, 118878. [Google Scholar] [CrossRef]
- Zahedi, R.; Ghorbani, M.; Daneshgar, S.; Gitifar, S.; Qezelbigloo, S. Potential measurement of Iran’s western regional wind energy using GIS. J. Clean. Prod. 2022, 330, 129883. [Google Scholar] [CrossRef]
- Amirkhani, S.; Nasirivatan, S.; Kasaeian, A.; Hajinezhad, A. ANN and ANFIS models to predict the performance of solar chimney power plants. Renew. Energy 2015, 83, 597–607. [Google Scholar] [CrossRef]
- Noushabadi, A.S.; Dashti, A.; Raji, M.; Zarei, A.; Mohammadi, A.H. Estimation of cetane numbers of biodiesel and diesel oils using regression and PSO-ANFIS models. Renew. Energy 2020, 158, 465–473. [Google Scholar] [CrossRef]
- Anicic, O.; Jovic, S. Adaptive neuro-fuzzy approach for ducted tidal turbine performance estimation. Renew. Sustain. Energy Rev. 2016, 59, 1111–1116. [Google Scholar] [CrossRef]
- Walia, N.; Singh, H.; Sharma, A. ANFIS: Adaptive neuro-fuzzy inference system-a survey. Int. J. Comput. Appl. 2015, 123, 32–38. [Google Scholar] [CrossRef]
- Akkaya, E. ANFIS based prediction model for biomass heating value using proximate analysis components. Fuel 2016, 180, 687–693. [Google Scholar] [CrossRef]
- Aldair, A.A.; Obed, A.A.; Halihal, A.F. Design and implementation of ANFIS-reference model controller based MPPT using FPGA for photovoltaic system. Renew. Sustain. Energy Rev. 2018, 82, 2202–2217. [Google Scholar] [CrossRef]
- Balabin, R.M.; Safieva, R.Z.; Lomakina, E.I. Wavelet neural network (WNN) approach for calibration model building based on gasoline near infrared (NIR) spectra. Chemom. Intell. Lab. Syst. 2008, 93, 58–62. [Google Scholar] [CrossRef]
- Aly, H.H. A novel deep learning intelligent clustered hybrid models for wind speed and power forecasting. Energy 2020, 213, 118773. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Mizzi, S. Combination of cuckoo search and wavelet neural network for midterm building energy forecast. Energy 2020, 202, 117728. [Google Scholar] [CrossRef]
- Aly, H.H. A novel approach for harmonic tidal currents constitutions forecasting using hybrid intelligent models based on clustering methodologies. Renew. Energy 2020, 147, 1554–1564. [Google Scholar] [CrossRef]
- Wu, Z.-Q.; Jia, W.-J.; Zhao, L.-R.; Wu, C.-H. Maximum wind power tracking based on cloud RBF neural network. Renew. Energy 2016, 86, 466–472. [Google Scholar] [CrossRef]
- Han, Y.; Fan, C.; Geng, Z.; Ma, B.; Cong, D.; Chen, K.; Yu, B. Energy efficient building envelope using novel RBF neural network integrated affinity propagation. Energy 2020, 209, 118414. [Google Scholar] [CrossRef]
- Cherif, H.; Benakcha, A.; Laib, I.; Chehaidia, S.E.; Menacer, A.; Soudan, B.; Olabi, A. Early detection and localization of stator inter-turn faults based on discrete wavelet energy ratio and neural networks in induction motor. Energy 2020, 212, 118684. [Google Scholar] [CrossRef]
- Hussain, M.; Dhimish, M.; Titarenko, S.; Mather, P. Artificial neural network based photovoltaic fault detection algorithm integrating two bi-directional input parameters. Renew. Energy 2020, 155, 1272–1292. [Google Scholar] [CrossRef]
- Karamichailidou, D.; Kaloutsa, V.; Alexandridis, A. Wind turbine power curve modeling using radial basis function neural networks and tabu search. Renew. Energy 2021, 163, 2137–2152. [Google Scholar] [CrossRef]
- Zahedi, R.; Ahmadi, A.; Gitifar, S. Reduction of the environmental impacts of the hydropower plant by microalgae cultivation and biodiesel production. J. Environ. Manag. 2022, 304, 114247. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Salazar, G.A.; Zhu, Z.; Gong, W. Solar radiation prediction using different techniques: Model evaluation and comparison. Renew. Sustain. Energy Rev. 2016, 61, 384–397. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Hu, B.; Gong, W. Modeling and comparison of hourly photosynthetically active radiation in different ecosystems. Renew. Sustain. Energy Rev. 2016, 56, 436–453. [Google Scholar] [CrossRef]
- Sakiewicz, P.; Piotrowski, K.; Kalisz, S. Neural network prediction of parameters of biomass ashes, reused within the circular economy frame. Renew. Energy 2020, 162, 743–753. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Feng, Y.; Hao, W.; Li, H.; Cui, N.; Gong, D.; Gao, L. Machine learning models to quantify and map daily global solar radiation and photovoltaic power. Renew. Sustain. Energy Rev. 2020, 118, 109393. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mohammadi, K.; Yee, L.; Petković, D.; Mostafaeipour, A. A comparative evaluation for identifying the suitability of extreme learning machine to predict horizontal global solar radiation. Renew. Sustain. Energy Rev. 2015, 52, 1031–1042. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Gunturi, S.K.; Sarkar, D. Ensemble machine learning models for the detection of energy theft. Electr. Power Syst. Res. 2021, 192, 106904. [Google Scholar] [CrossRef]
- Tama, B.A.; Lim, S. Ensemble learning for intrusion detection systems: A systematic mapping study and cross-benchmark evaluation. Comput. Sci. Rev. 2021, 39, 100357. [Google Scholar] [CrossRef]
- Dogan, A.; Birant, D. Machine learning and data mining in manufacturing. Expert Syst. Appl. 2020, 114060. [Google Scholar] [CrossRef]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Lu, H.; Cheng, F.; Ma, X.; Hu, G. Short-term prediction of building energy consumption employing an improved extreme gradient boosting model: A case study of an intake tower. Energy 2020, 203, 117756. [Google Scholar] [CrossRef]
- Li, Y.; Shi, H.; Han, F.; Duan, Z.; Liu, H. Smart wind speed forecasting approach using various boosting algorithms, big multi-step forecasting strategy. Renew. Energy 2019, 135, 540–553. [Google Scholar] [CrossRef]
- Freund, Y. Boosting a weak learning algorithm by majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.; Srikanth, N. Ensemble methods for wind and solar power forecasting—A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 82–91. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.-q.; Li, Y.-f.; Zhang, L. Comparison of four Adaboost algorithm based artificial neural networks in wind speed predictions. Energy Convers. Manag. 2015, 92, 67–81. [Google Scholar] [CrossRef]
- Wang, L.; Lv, S.-X.; Zeng, Y.-R. Effective sparse adaboost method with ESN and FOA for industrial electricity consumption forecasting in China. Energy 2018, 155, 1013–1031. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Fan, J.; Wu, L.; Ma, X.; Zhou, H.; Zhang, F. Hybrid support vector machines with heuristic algorithms for prediction of daily diffuse solar radiation in air-polluted regions. Renew. Energy 2020, 145, 2034–2045. [Google Scholar] [CrossRef]
- Zhong, W.; Huang, W.; Lin, X.; Li, Z.; Zhou, Y. Research on data-driven identification and prediction of heat response time of urban centralized heating system. Energy 2020, 212, 118742. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, T.; Yue, B.; Ding, Y.; Xiao, R.; Wang, R.; Zhai, X. Prediction of residential district heating load based on machine learning: A case study. Energy 2021, 231, 120950. [Google Scholar] [CrossRef]
- Kummer, N.; Najjaran, H. Adaboost. MRT: Boosting regression for multivariate estimation. Artif. Intell. Res. 2014, 3, 64–76. [Google Scholar] [CrossRef]
- Liu, H.; Duan, Z.; Li, Y.; Lu, H. A novel ensemble model of different mother wavelets for wind speed multi-step forecasting. Appl. Energy 2018, 228, 1783–1800. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Spatial air quality index prediction model based on decomposition, adaptive boosting, and three-stage feature selection: A case study in China. J. Clean. Prod. 2020, 265, 121777. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Meira, E.; Oliveira, F.L.C.; de Menezes, L.M. Point and interval forecasting of electricity supply via pruned ensembles. Energy 2021, 232, 121009. [Google Scholar] [CrossRef]
- de Oliveira, E.M.; Oliveira, F.L.C. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tsai, C.-F.; Pham, A.-D.; Lu, Y.-H. Machine learning in concrete strength simulations: Multi-nation data analytics. Constr. Build. Mater. 2014, 73, 771–780. [Google Scholar] [CrossRef]
- Chen, J.; Yin, J.; Zang, L.; Zhang, T.; Zhao, M. Stacking machine learning model for estimating hourly PM2. 5 in China based on Himawari 8 aerosol optical depth data. Sci. Total Environ. 2019, 697, 134021. [Google Scholar] [CrossRef]
- Ngo, N.-T. Early predicting cooling loads for energy-efficient design in office buildings by machine learning. Energy Build. 2019, 182, 264–273. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, Y.; Xiao, J.; Zhang, W.; Feng, R. Hybrid wind speed forecasting model based on multivariate data secondary decomposition approach and deep learning algorithm with attention mechanism. Renew. Energy 2021, 174, 688–704. [Google Scholar] [CrossRef]
- Zahedi, R.; Zahedi, A.; Ahmadi, A. Strategic Study for Renewable Energy Policy, Optimizations and Sustainability in Iran. Sustainability 2022, 14, 2418. [Google Scholar] [CrossRef]
- Akram, M.W.; Li, G.; Jin, Y.; Chen, X.; Zhu, C.; Ahmad, A. Automatic detection of photovoltaic module defects in infrared images with isolated and develop-model transfer deep learning. Sol. Energy 2020, 198, 175–186. [Google Scholar] [CrossRef]
- Chen, W.; Qiu, Y.; Feng, Y.; Li, Y.; Kusiak, A. Diagnosis of wind turbine faults with transfer learning algorithms. Renew. Energy 2021, 163, 2053–2067. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, R.; Zhou, Y. Transfer learning for short-term wind speed prediction with deep neural networks. Renew. Energy 2016, 85, 83–95. [Google Scholar] [CrossRef]
- Gonzalez-Vidal, A.; Jimenez, F.; Gomez-Skarmeta, A.F. A methodology for energy multivariate time series forecasting in smart buildings based on feature selection. Energy Build. 2019, 196, 71–82. [Google Scholar] [CrossRef]
- Winters, P.R. Forecasting sales by exponentially weighted moving averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Cadenas, E.; Jaramillo, O.A.; Rivera, W. Analysis and forecasting of wind velocity in chetumal, quintana roo, using the single exponential smoothing method. Renew. Energy 2010, 35, 925–930. [Google Scholar] [CrossRef]
- Flores, J.J.; Graff, M.; Rodriguez, H. Evolutive design of ARMA and ANN models for time series forecasting. Renew. Energy 2012, 44, 225–230. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.-L. Hybrid methodology for hourly global radiation forecasting in Mediterranean area. Renew. Energy 2013, 53, 1–11. [Google Scholar] [CrossRef]
- Doorga, J.R.S.; Dhurmea, K.R.; Rughooputh, S.; Boojhawon, R. Forecasting mesoscale distribution of surface solar irradiation using a proposed hybrid approach combining satellite remote sensing and time series models. Renew. Sustain. Energy Rev. 2019, 104, 69–85. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Z.; Hu, W.; Wang, Y.; Dong, L.; Zhang, J. Coordinated optimal operation of hydro–wind–solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Zahedi, R.; Rad, A.B. Numerical and experimental simulation of gas-liquid two-phase flow in 90-degree elbow. Alex. Eng. J. 2021, 61, 2536–2550. [Google Scholar] [CrossRef]
- Hassan, J. ARIMA and regression models for prediction of daily and monthly clearness index. Renew. Energy 2014, 68, 421–427. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Seetharaman, K. Day-ahead wind speed forecasting using f-ARIMA models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Moreno, S.R.; Mariani, V.C.; dos Santos Coelho, L. Hybrid multi-stage decomposition with parametric model applied to wind speed forecasting in Brazilian Northeast. Renew. Energy 2021, 164, 1508–1526. [Google Scholar] [CrossRef]
- Reikard, G.; Hansen, C. Forecasting solar irradiance at short horizons: Frequency and time domain models. Renew. Energy 2019, 135, 1270–1290. [Google Scholar] [CrossRef]
- Hong, T.; Koo, C.; Kim, D.; Lee, M.; Kim, J. An estimation methodology for the dynamic operational rating of a new residential building using the advanced case-based reasoning and stochastic approaches. Appl. Energy 2015, 150, 308–322. [Google Scholar] [CrossRef]
- Ju, K.; Su, B.; Zhou, D.; Zhang, Y. An incentive-oriented early warning system for predicting the co-movements between oil price shocks and macroeconomy. Appl. Energy 2016, 163, 452–463. [Google Scholar] [CrossRef]
- Koo, C.; Li, W.; Cha, S.H.; Zhang, S. A novel estimation approach for the solar radiation potential with its complex spatial pattern via machine-learning techniques. Renew. Energy 2019, 133, 575–592. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Singh, S. A simple method of forecasting based on fuzzy time series. Appl. Math. Comput. 2007, 186, 330–339. [Google Scholar] [CrossRef]
- Severiano, C.A.; e Silva, P.C.d.L.; Cohen, M.W.; Guimarães, F.G. Evolving fuzzy time series for spatio-temporal forecasting in renewable energy systems. Renew. Energy 2021, 171, 764–783. [Google Scholar] [CrossRef]
- Ju-Long, D. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Lin, C.-S.; Liou, F.-M.; Huang, C.-P. Grey forecasting model for CO2 emissions: A Taiwan study. Appl. Energy 2011, 88, 3816–3820. [Google Scholar] [CrossRef]
- Tsai, S.-B.; Xue, Y.; Zhang, J.; Chen, Q.; Liu, Y.; Zhou, J.; Dong, W. Models for forecasting growth trends in renewable energy. Renew. Sustain. Energy Rev. 2017, 77, 1169–1178. [Google Scholar] [CrossRef]
- Huang, L.; Liao, Q.; Qiu, R.; Liang, Y.; Long, Y. Prediction-based analysis on power consumption gap under long-term emergency: A case in China under COVID-19. Appl. Energy 2021, 283, 116339. [Google Scholar] [CrossRef]
- Duan, H.; Pang, X. A multivariate grey prediction model based on energy logistic equation and its application in energy prediction in China. Energy 2021, 229, 120716. [Google Scholar] [CrossRef]
- Žunić, E.; Korjenić, K.; Hodžić, K.; Đonko, D. Application of Facebook’s Prophet Algorithm for Successful Sales Forecasting Based on Real-world Data. Int. J. Comput. Sci. Inf. Technol. 2020, 12, 23–36. [Google Scholar] [CrossRef]
- Yan, J.; Wang, L.; Song, W.; Chen, Y.; Chen, X.; Deng, Z. A time-series classification approach based on change detection for rapid land cover mapping. ISPRS J. Photogramm. Remote Sens. 2019, 158, 249–262. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Li, H.; Ann Piette, M. Predicting city-scale daily electricity consumption using data-driven models. Adv. Appl. Energy 2021, 2, 100025. [Google Scholar] [CrossRef]
- Ağbulut, Ü.; Gürel, A.E.; Biçen, Y. Prediction of daily global solar radiation using different machine learning algorithms: Evaluation and comparison. Renew. Sustain. Energy Rev. 2021, 135, 110114. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.; Machado, L.; Pabon, J. Prediction of wind speed and wind direction using artificial neural network, support vector regression and adaptive neuro-fuzzy inference system. Sustain. Energy Technol. Assess. 2018, 25, 146–160. [Google Scholar] [CrossRef]
- Maino, C.; Misul, D.; Di Mauro, A.; Spessa, E. A deep neural network based model for the prediction of hybrid electric vehicles carbon dioxide emissions. Energy AI 2021, 5, 100073. [Google Scholar] [CrossRef]
- Voyant, C.; Paoli, C.; Muselli, M.; Nivet, M.-L. Multi-horizon solar radiation forecasting for Mediterranean locations using time series models. Renew. Sustain. Energy Rev. 2013, 28, 44–52. [Google Scholar] [CrossRef]
- Royapoor, M.; Roskilly, T. Building model calibration using energy and environmental data. Energy Build. 2015, 94, 109–120. [Google Scholar] [CrossRef]
- Uyanık, T.; Karatuğ, Ç.; Arslanoğlu, Y. Machine learning approach to ship fuel consumption: A case of container vessel. Transp. Res. Part D Transp. Environ. 2020, 84, 102389. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. Solar power forecasting using deep learning techniques. IEEE Access 2022, 10, 31692–31698. [Google Scholar] [CrossRef]
- de Medeiros, R.K.; da Nóbrega Besarria, C.; de Jesus, D.P.; de Albuquerquemello, V.P. Forecasting oil prices: New approaches. Energy 2022, 238, 121968. [Google Scholar] [CrossRef]
- Nsangou, J.C.; Kenfack, J.; Nzotcha, U.; Ekam, P.S.N.; Voufo, J.; Tamo, T.T. Explaining household electricity consumption using quantile regression, decision tree and artificial neural network. Energy 2022, 250, 123856. [Google Scholar] [CrossRef]
- Kato, T. Prediction of photovoltaic power generation output and network operation. In Integration of Distributed Energy Resources in Power Systems; Elsevier: Amsterdam, The Netherlands, 2016; pp. 77–108. [Google Scholar]
- Moslehi, S.; Reddy, T.A.; Katipamula, S. Evaluation of data-driven models for predicting solar photovoltaics power output. energy 2018, 142, 1057–1065. [Google Scholar] [CrossRef]











| Year | Reference | The Algorithms Investigated in This Study | Application |
|---|---|---|---|
| 2017 | Deb et al. [22] | SVM, MA & ES, CBR, NN, ARIMA, Grey, HM, ANN, Fuzzy | Energy consumption and demand forecast |
| 2018 | Amasyali et al. [21] | SVM, ANN, LSSVM, DT, GLR, MLR, FFNN, LASSO, NARIX, PENN, GRNN, ARIMA, AR, BN, CBR, RBF, MARS, ELM | |
| 2019 | Beyca et al. [34] | MLR, SVR, ANN | |
| 2020 | Walker et al. [23] | ANN, SVM, RF, BT | |
| Grimaldo et al. [24] | kNN | ||
| Haq et al. [25] | SVM, ANN, K-mean | ||
| Hafeez et al. [26] | FCRBM | ||
| Khan et al. [27] | CSNNN | ||
| Kazemzadeh et al. [28] | PSO-SVR, ANN, ARIMA, HM | ||
| Fathi et al. [29] | MLR, ANN, SVR, GA, RF, CA, BN, GP, GB, PCA, DL, RL, ARIMA, ENS | ||
| Liu et al. [30] | SVM | ||
| Kaytez et al. [31] | LSSVM, ARIMA, HM, MLR | ||
| Fan et al. [32] | EMD-SVR-PSO-AR-GARCH, EMD-SVR-AR, SVR-GA, AR-GARCH, ARMA | ||
| Wen et al. [35] | DRNN-GRU, DRNN-LSTM, DRNN, MLP, ARIMA, SVM, MLR | ||
| Jamil [33] | ARIMA | ||
| 2017 | Voyant et al. [6] | LR, GLM, ANN, SVR/SVM, DT, kNN, Markov Chain, HM, ARIMA | Predicting the output power of solar systems |
| 2019 | Srivastava et al. [45] | RF, CART, MARS, M5 | |
| Benali et al. [46] | ANN, RF, SP | ||
| 2020 | Huertas-Tato et al. [41] | SVR-HM | |
| Gürel et al. [43] | ANN | ||
| Alizamir et al. [44] | GBT, MLPNN, ANFIS-FCM, ANFIS-SC, MARS, CART | ||
| 2021 | Govindasamy et al. [42] | ANN, SVR, GRNN, RF | |
| Khosravi et al. [47] | SVM, ANN, DL, kNN | ||
| 2015 | Wang et al. [52] | ARIMA, SVM, ELM, EWT, LSSVM, GPR, HM | Predicting the output power of wind systems |
| 2016 | Cadenas et al. [55] | ARIMA, NARX | |
| 2018 | Zendehboudi et al. [51] | SVM-HM, ANN, SVM | |
| 2019 | Demolli et al. [53] | LASSO, kNN, RF, XGBoost, SVR | |
| 2020 | Li et al. [56] | IDA-SVM, DA-SVM, GA-SVM, Grid-SVM, GPR, BPNN | |
| Tian et al. [57] | LSSVM, HM, LMD | ||
| Hong et al. [58] | CNN | ||
| 2021 | Xiao et al. [54] | ANN, KELM | |
| 2018 | Abbas et al. [71] | ANN-GA | Optimization |
| 2019 | Perera et al. [66] | TL, HM | |
| Wen et al. [74] | ANN, GABP-ANN | ||
| Zhou et al. [68] | ANN, PSO | ||
| 2020 | Ilbeigi et al. [69] | ANN, MLP, GA, HM | |
| Naserbegi et al. [70] | GSA-ANN | ||
| Xu et al. [73] | VPSO, ANN, ANFIS, ANFIS-VPSO, ICBR | ||
| 2021 | Li et al. [72] | ANN-GA, CFD-GA | |
| Ikeda et al. [67] | DNN, HM | ||
| 2018 | Zhao et al. [8] | AE, MLP, CNN, DBN | Fault and defect detection |
| 2019 | Wang et al. [83] | LSSVM, SVM, PNN | |
| Han et al. [84] | ANN, SVM, PCA, BN, SVR, Fuzzy | ||
| Helbinget al. [85] | SV-PSO, BPNN, ANFIS | ||
| Sarwar et al. [87] | SVM, kNN, NB | ||
| Wang et al. [86] | SVM, PCA, FDA | ||
| 2020 | Yang et al. [81] | RF, DT, kNN | |
| Choi et al. [82] | BAS-SVM, SVM, PSO-SVM, GA-SVM, ABS-SVM | ||
| Rivas et al. [80] | SVM | ||
| Eskandari et al. [88] | kNN, SVM, RF, EL | ||
| Han et al. [89] | ANFIS-BWOA, AR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forootan, M.M.; Larki, I.; Zahedi, R.; Ahmadi, A. Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability 2022, 14, 4832. https://doi.org/10.3390/su14084832
Forootan MM, Larki I, Zahedi R, Ahmadi A. Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability. 2022; 14(8):4832. https://doi.org/10.3390/su14084832
Chicago/Turabian StyleForootan, Mohammad Mahdi, Iman Larki, Rahim Zahedi, and Abolfazl Ahmadi. 2022. "Machine Learning and Deep Learning in Energy Systems: A Review" Sustainability 14, no. 8: 4832. https://doi.org/10.3390/su14084832
APA StyleForootan, M. M., Larki, I., Zahedi, R., & Ahmadi, A. (2022). Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability, 14(8), 4832. https://doi.org/10.3390/su14084832








