Manta Ray Foraging Optimization for the Virtual Inertia Control of Islanded Microgrids Including Renewable Energy Sources

Abstract

Nowadays, the penetration level of renewable energy sources (RESs) has increased dramatically in electrical networks, especially in microgrids. Due to the replacement of conventional synchronous generators by RESs, the inertia of the microgrid is significantly reduced. This has a negative impact on the dynamics and performance of the microgrid in the face of uncertainties, resulting in a weakening of microgrid stability, especially in an islanded operation. Hence, this paper focuses on enhancing the dynamic security of an islanded microgrid using a frequency control concept based on virtual inertia control. The control in the virtual inertia control loop was based on a proportional-integral (PI) controller optimally designed by the Manta Ray Foraging Optimization (MRFO) algorithm. The performance of the MRFO-based PI controller was investigated considering various operating conditions and compared with that of other evolutionary optimization algorithm-based PI controllers. To achieve realistic simulations conditions, actual wind data and solar power data were used, and random load fluctuations were implemented. The results show that the MRFO-based PI controller has a superior performance in frequency disturbance alleviation and reference frequency tracking compared with the other considered optimization techniques.

1. Introduction

The high deployment of RESs, especially solar and wind systems, in modern power grids is a promising solution for the reduction of greenhouse gas emissions produced from traditional power generators [1]. Despite their numerous economic and environmental benefits, the widespread integration of RESs lowers the overall inertia of power grids, which causes negative impacts on frequency stability [2,3], especially in the case of islanded microgrids.

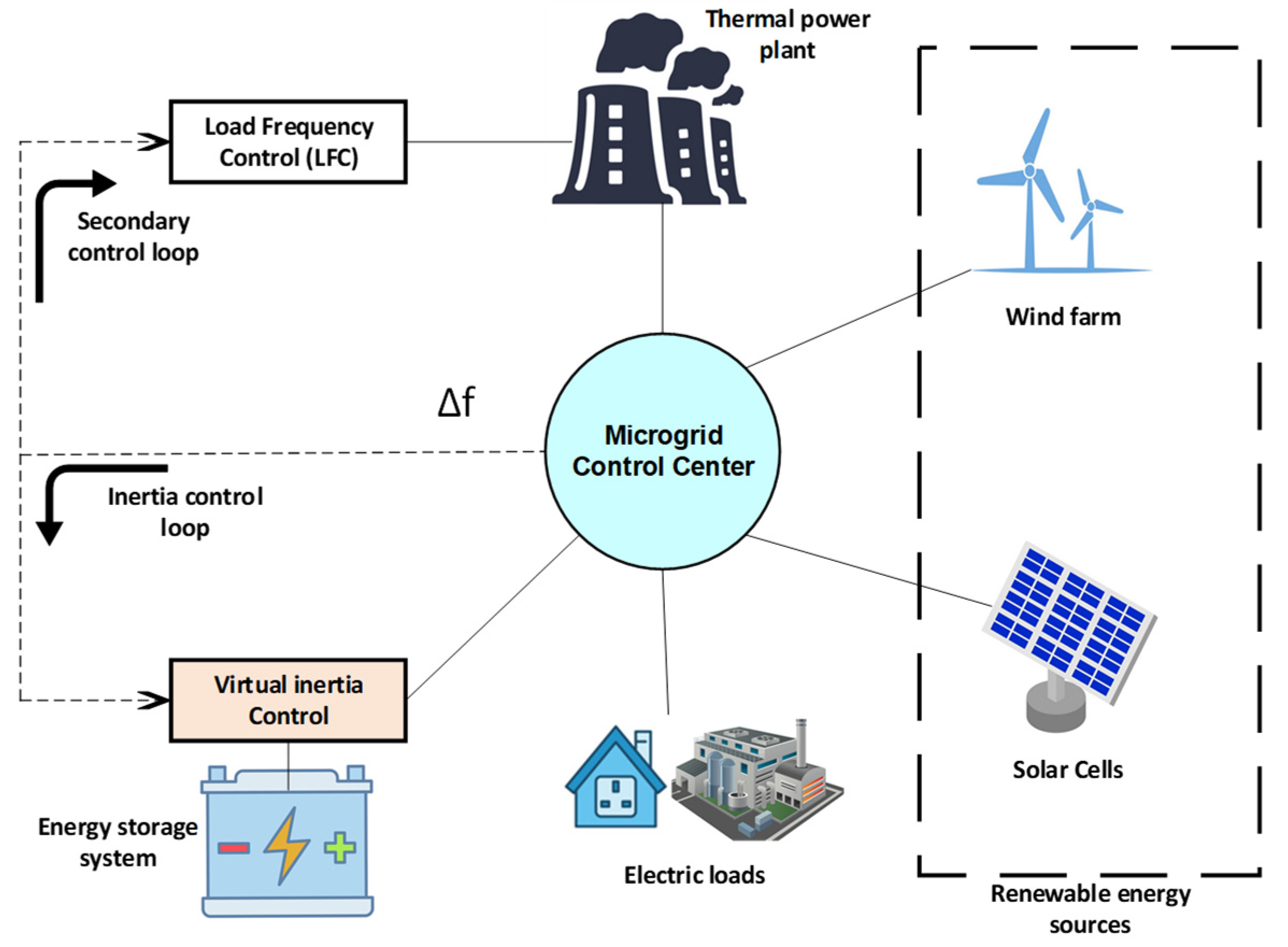
A microgrid can be considered as a micro electric system with a group of RESs, small thermal generating units, energy storage units, and domestic loads, that can be operated in either a grid-connected mode or an islanded mode [4,5,6]. In the grid-connected mode, the microgrid can receive power from both the utility grid and distributed generators (DGs). In this mode, most of the load consumed power is provided by the DGs in the microgrid, and the rest is supplied by the utility grid to meet actual fluctuations in power demand [7]. On the other hand, in the islanded mode of operation, either load or generation shedding may be performed to maintain power balance [8,9]. In this regard, some studies have addressed the challenges of microgrid operations in terms of grid-connected mode [10,11] and islanded mode operation [12,13,14,15]. According to the previous studies, microgrid control is more demanding in islanded mode than in grid-connected mode, since the frequency and voltage are not supported by the utility grid [16].

With the noticeable increased integration of power electronics-based RESs in microgrids, a shortage of system inertia appears, leading to possible frequency instability. Consequently, power electronics-based RESs generate high fluctuations in frequency compared with other conventional power plants [17,18,19]. Hence, islanded microgrids might not be secure for high penetration levels of power electronics-based RESs.

Due to the aforementioned frequency stability issues, a new control concept called virtual synchronous generator (VSG) or virtual synchronous machine (VSM) was introduced to mimic the conventional generating machines’ behavior [1,20]. 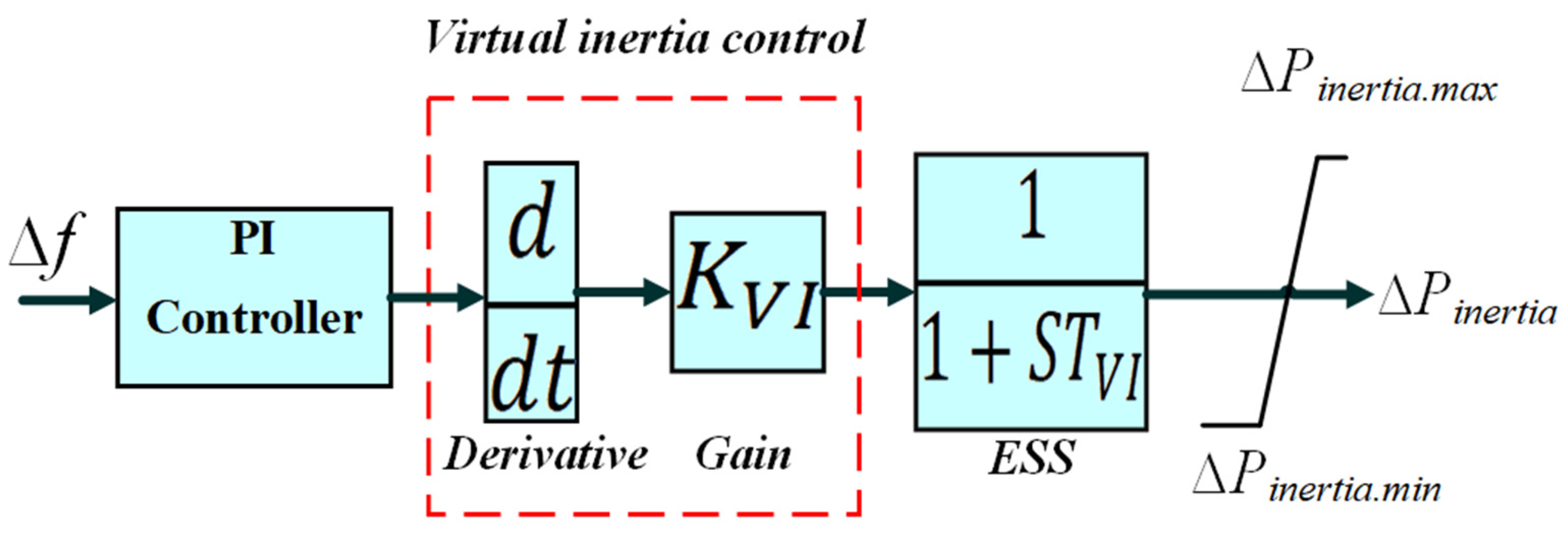The virtual inertia control concept is considered a specific part of VSM operation, which depends on imitating the prime mover characteristics to provide the inertia power for the support of frequency stability [21]. Virtual inertia control is provided by connecting energy storage systems (ESS) with the grid through inverters to provide damping and inertia characteristics of conventional machines to the grid. The control approach depends on measuring the rate of change of frequency (RCF), where the frequency change is calculated to provide the necessary power to the microgrid through ESS and, hence, enhance the frequency stability of the microgrid [22].

In the past few years, numerous control strategies were utilized with virtual inertia control to enhance the microgrid frequency stability [23,24,25,26,27,28]. For example, the enhanced derivative technique was applied to a virtual inertia control model to mimic the damping and inertia properties for frequency stability support of the microgrid [23,24]. In [25], a fuzzy logic control was implemented with a virtual inertia control loop for regulating the microgrid frequency. Robust virtual inertia control based on H-infinite control was proposed in [26] for the enhancement of frequency stability in a microgrid with a high penetration level of RESs. In [27], the coefficient diagram method was implemented in a virtual inertia control model to alleviate the frequency disturbances in islanded microgrids in case of contingencies. In [28], a model predictive control was provided with virtual inertia control for microgrid frequency stabilization in the face of disturbances and system uncertainties. Though the aforementioned controllers have a decent performance when dealing with the system’s dynamics, they struggle with several drawbacks such as (i) their reliance on the designer’s knowledge to obtain the appropriate deign structure, (ii) their requirement of a long time for computation and operation, (iii) their complex design procedures, (iv) their higher cost compared with conventional controllers [29]. Moreover, proportional integral derivative (PID) or PI controllers are the most commonly used to study the frequency regulation problem, since they provide many benefits such as a wide-ranging stability margin, simplicity in structure, and low cost. However, these controllers are sensitive to disturbances and system uncertainties (i.e., system parameters variations). Therefore, the optimal design of these controllers is considered a challenge in the face of disturbances and system uncertainties. Various heuristic optimization techniques such as particle swarm optimization (PSO) [30], genetic algorithms (GA) [31], and chicken swarm optimizer (CSO) [32] were applied to optimally design these controllers and improve frequency stability. Though these techniques are used in solving various optimization problems [30,31,32], they have a slow convergence rate during the iterative process, and it is difficult to achieve global optimal solutions dealing with high dimensional problems. On the other hand, the MRFO algorithm has proven its effectiveness in tackling challenging problems in terms of computational cost and solution precision. According to the previous observations, the continuous advance and great progress of optimization of revolutionary algorithms promotes the application of the MRFO algorithm to design optimal parameters of PI controllers within the virtual inertia control loop.

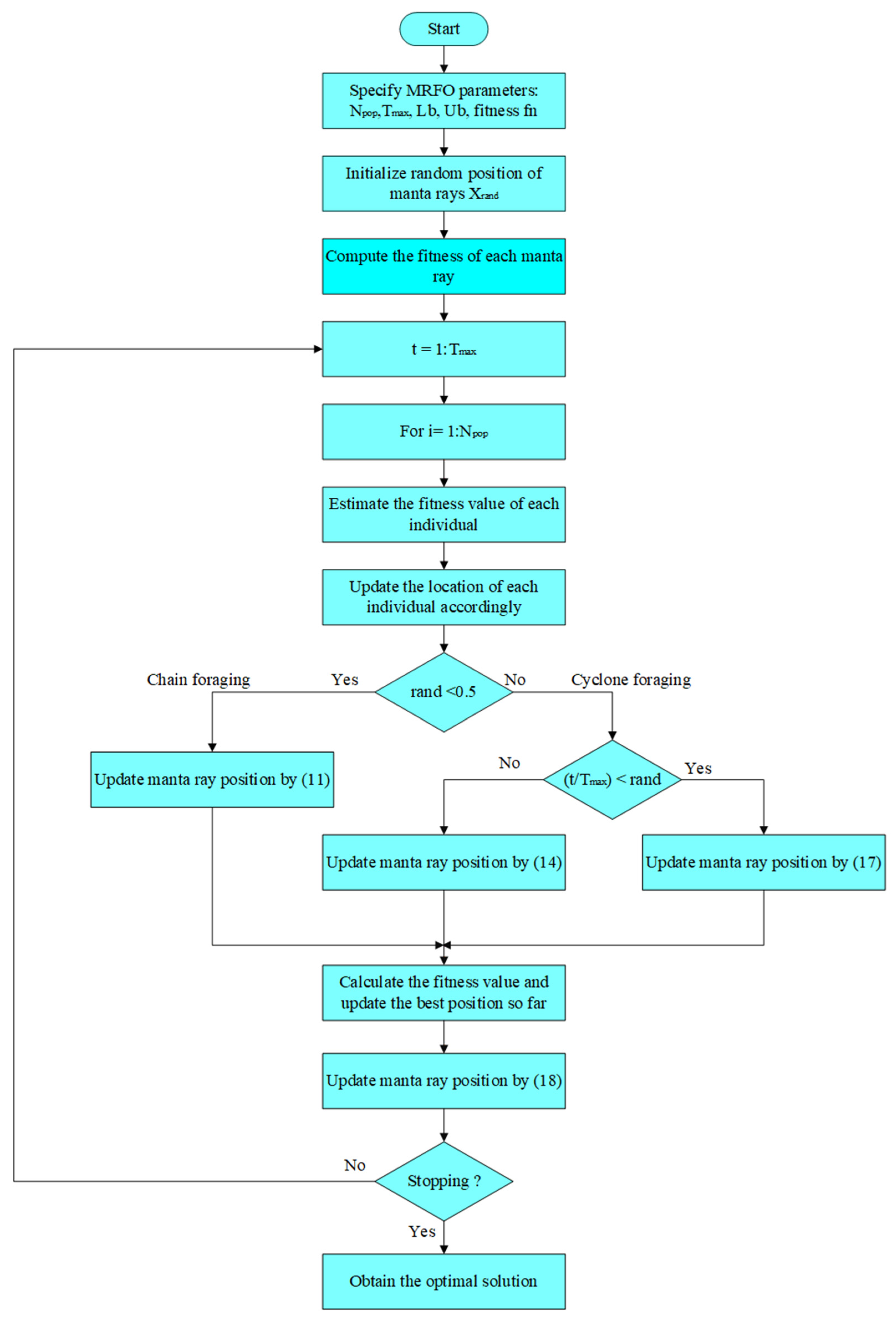
Manta ray foraging optimization (MRFO) is a new metaheuristic algorithm inspired by the foraging behaviors of manta rays. Manta rays have intelligent and different foraging strategies for finding plentiful plankton. These foraging strategies are chain, cyclone, and somersault foraging [33]. MRFO is simple in execution and provides great potential for many applications in numerous designing engineering fields.

The research contributions obtained by using an MRFO-based PI controller in the virtual inertia control loop of islanded microgrid are the following:

i.

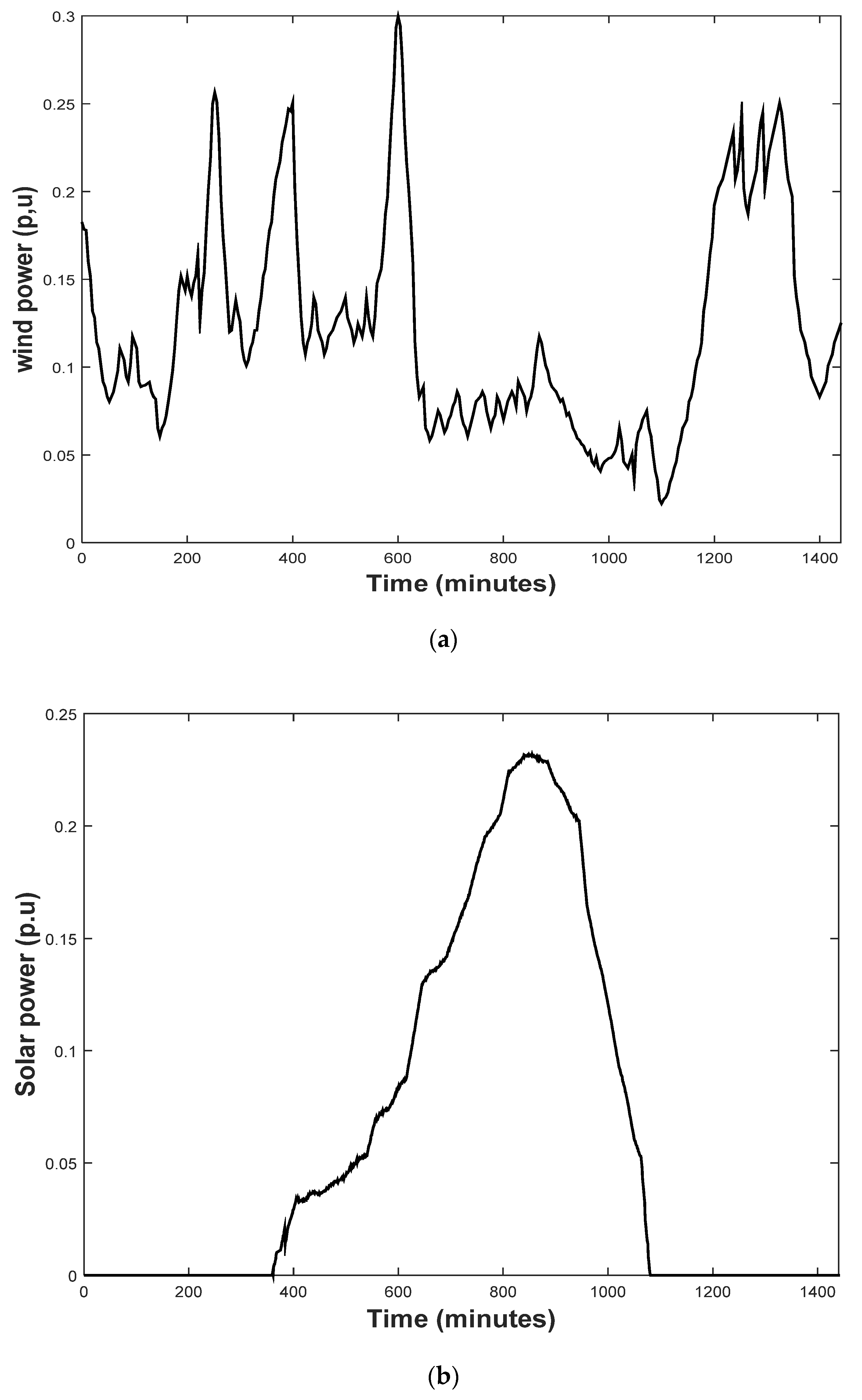
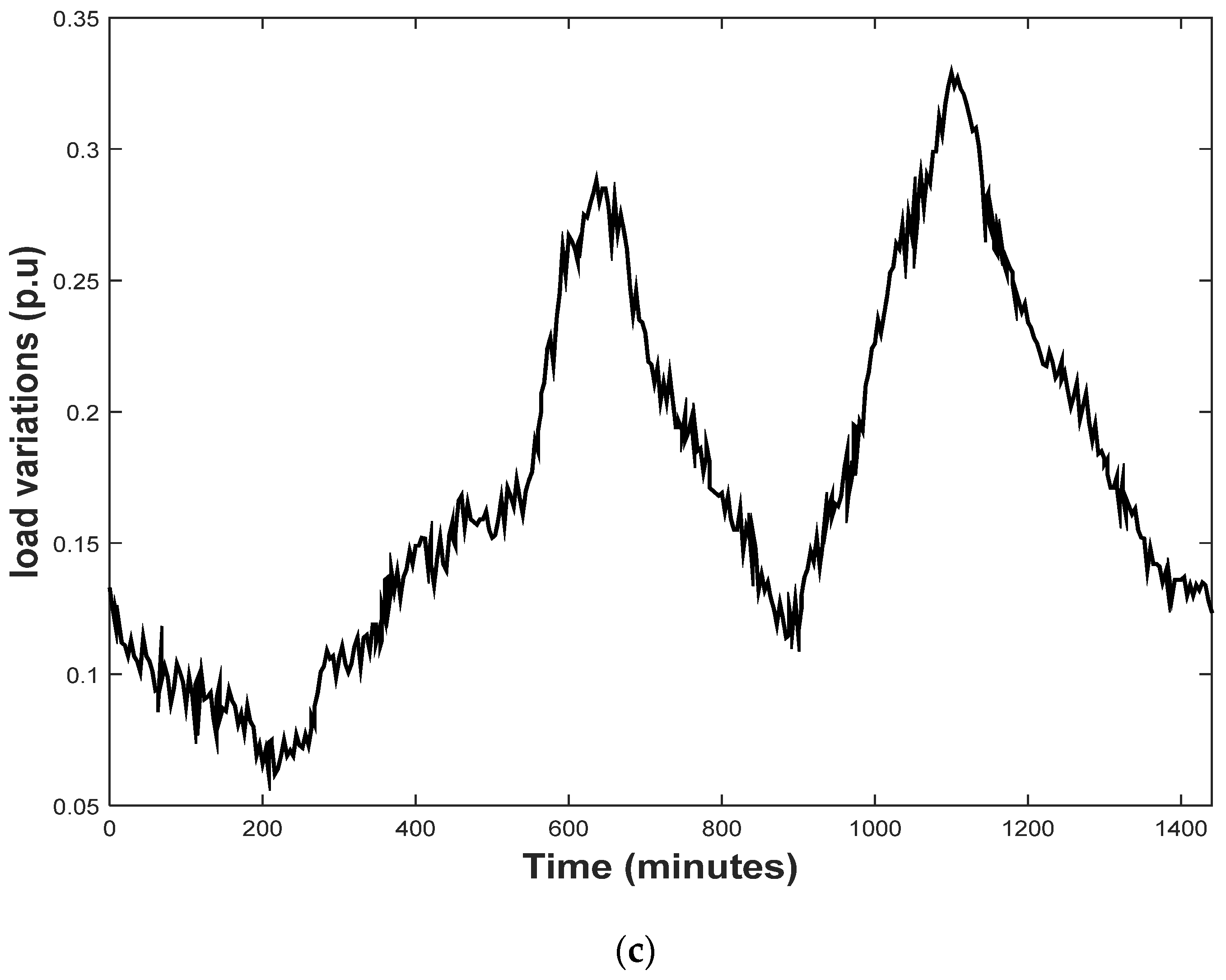
The uncertainties in RESs and load powers were considered to check the performance of the microgrid under different operating conditions.

ii.

Actual wind data from the Al-Zaafrana wind farm in Egypt were extracted and used, solar power data extracted from field tests and random load fluctuations were implemented to achieve the presented results.

iii.

The wind, solar, and load data showed signs of partial and complete shedding, validating the effectiveness of the presented control approach under severe scenarios.

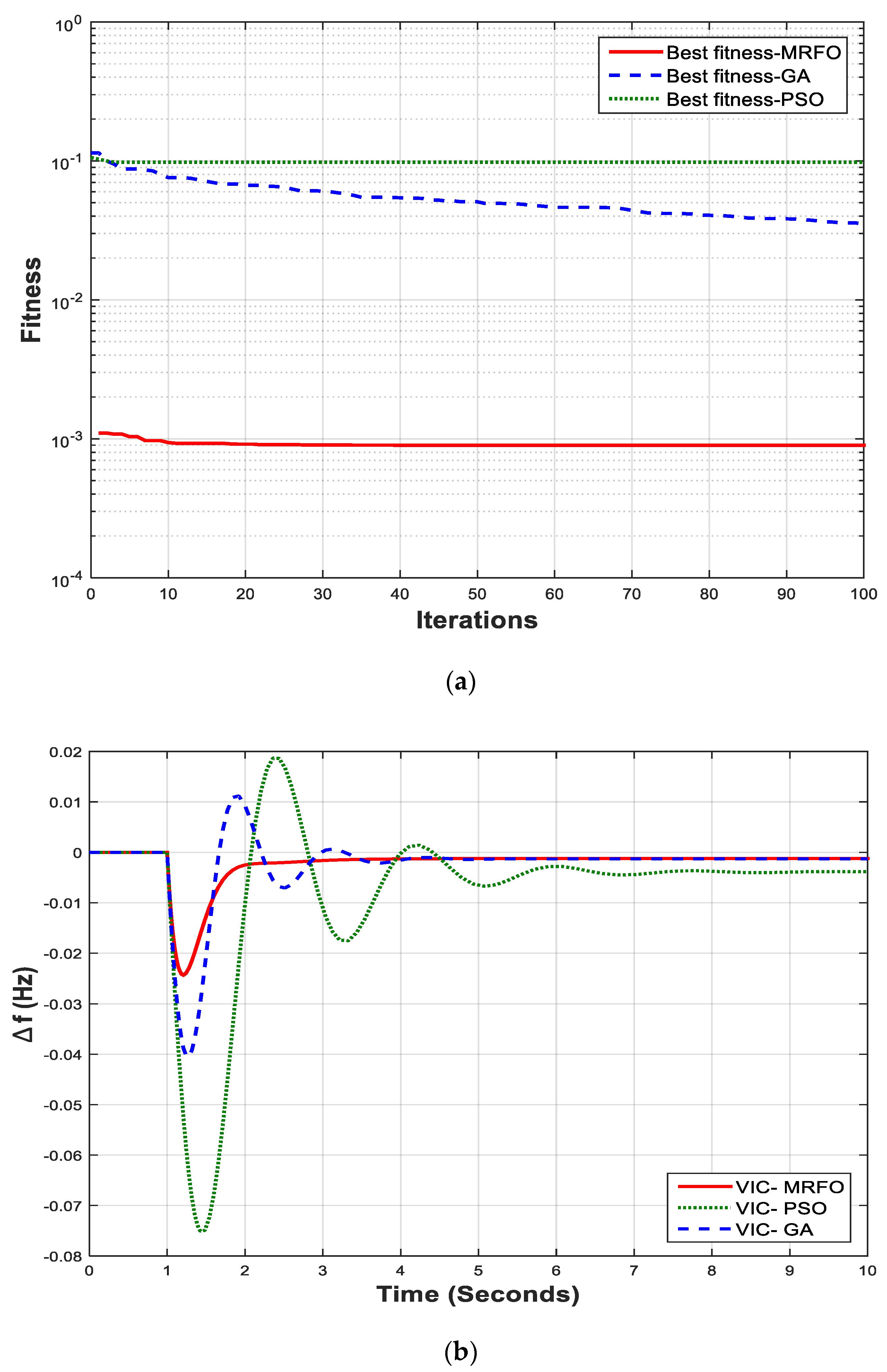
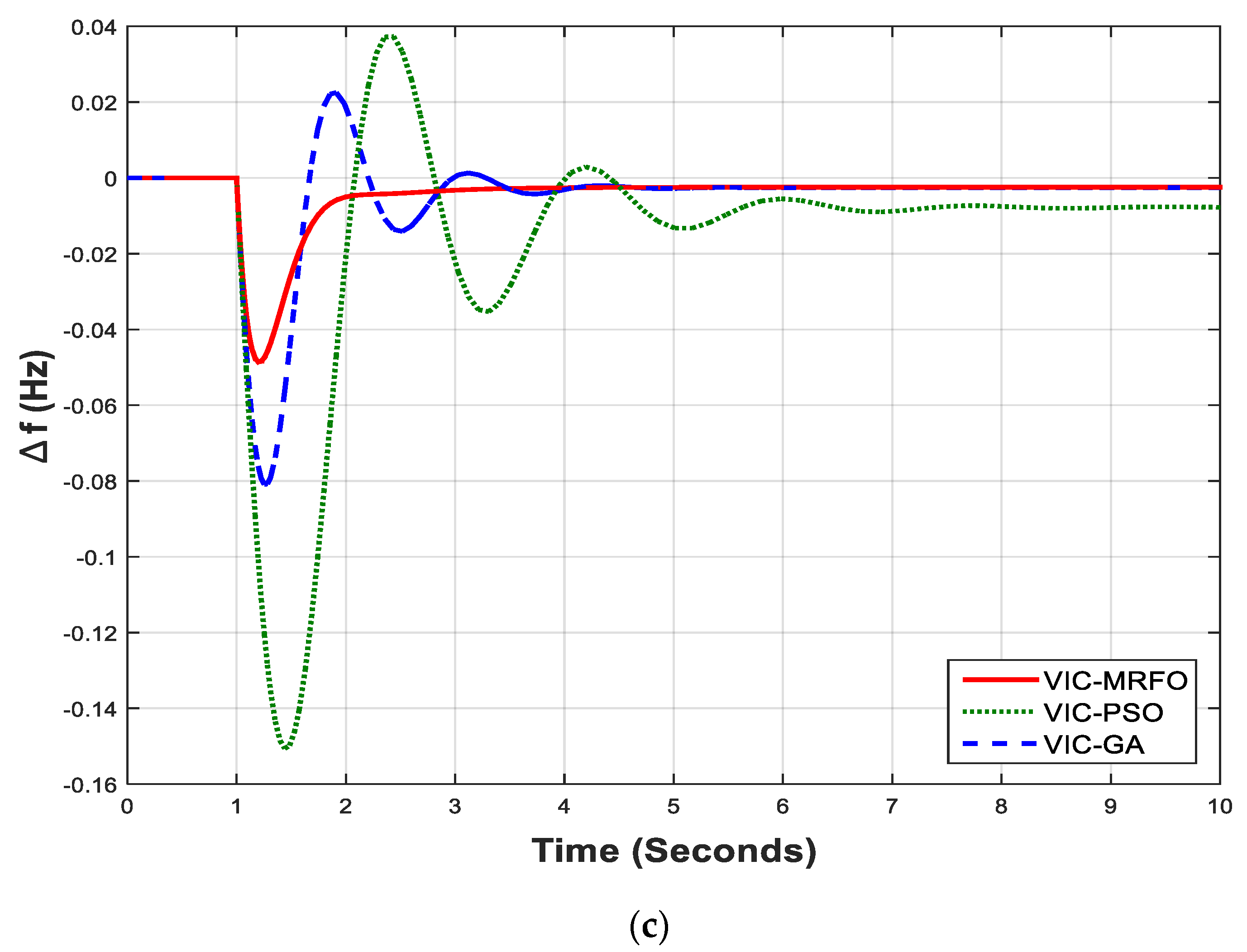
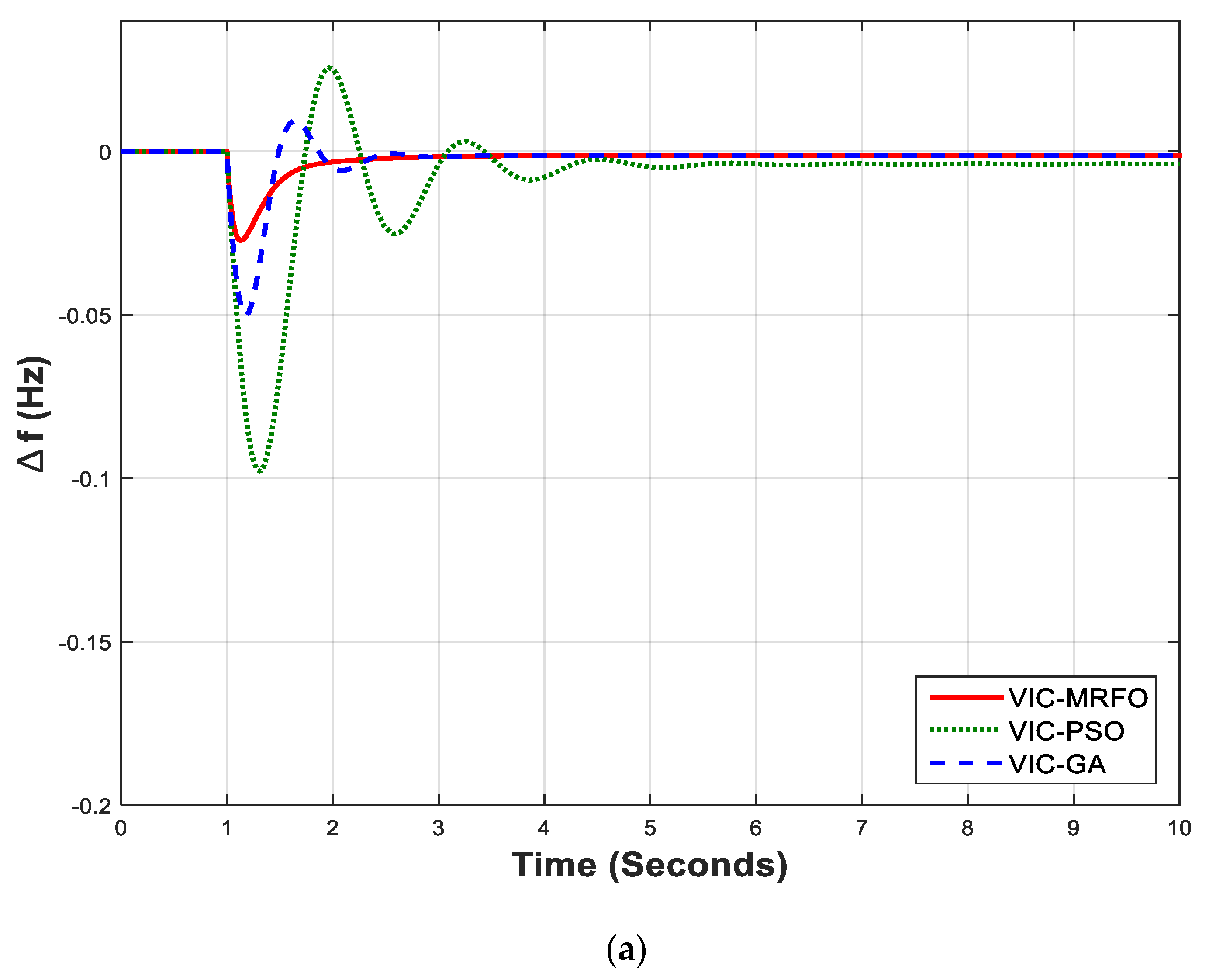
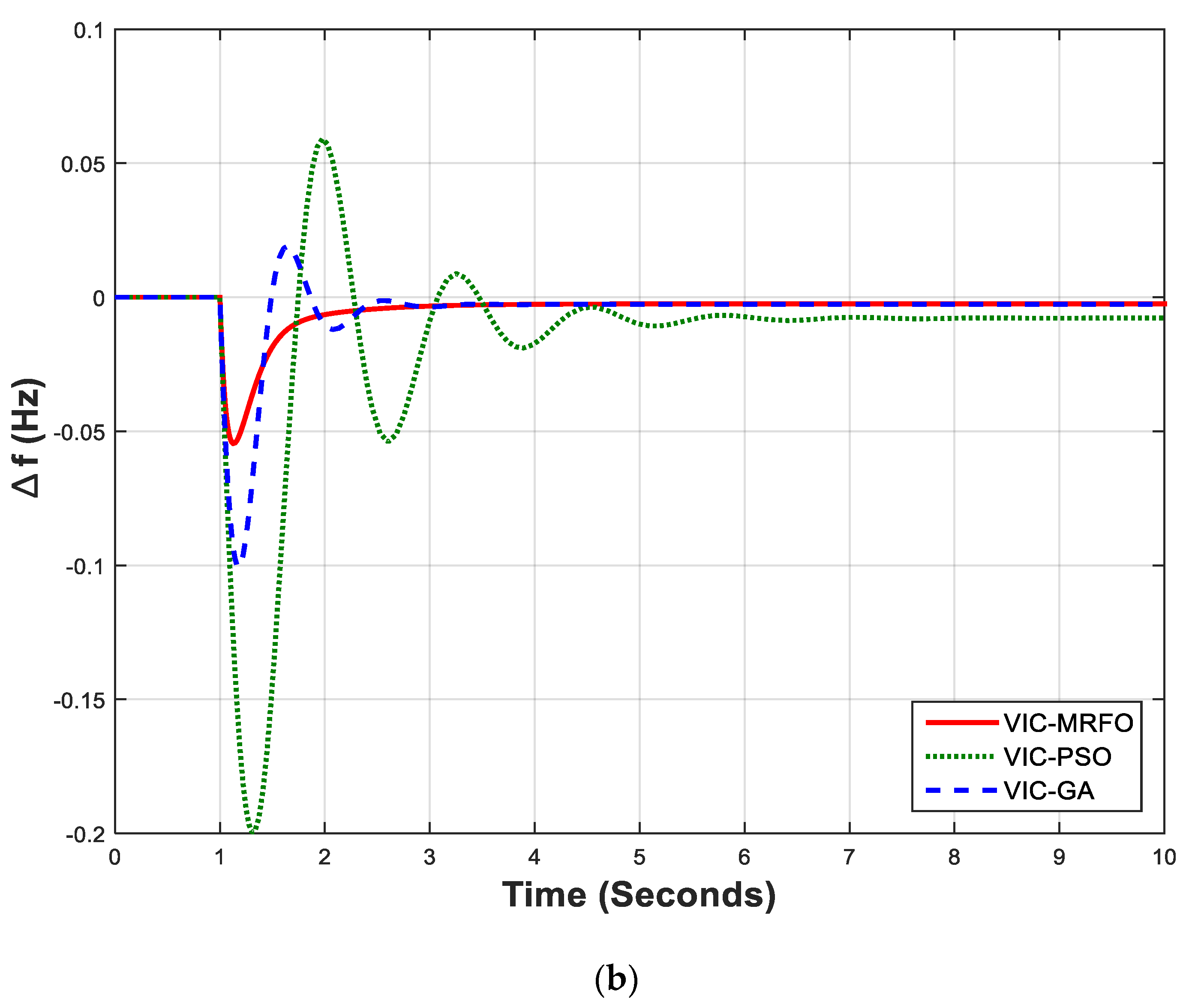
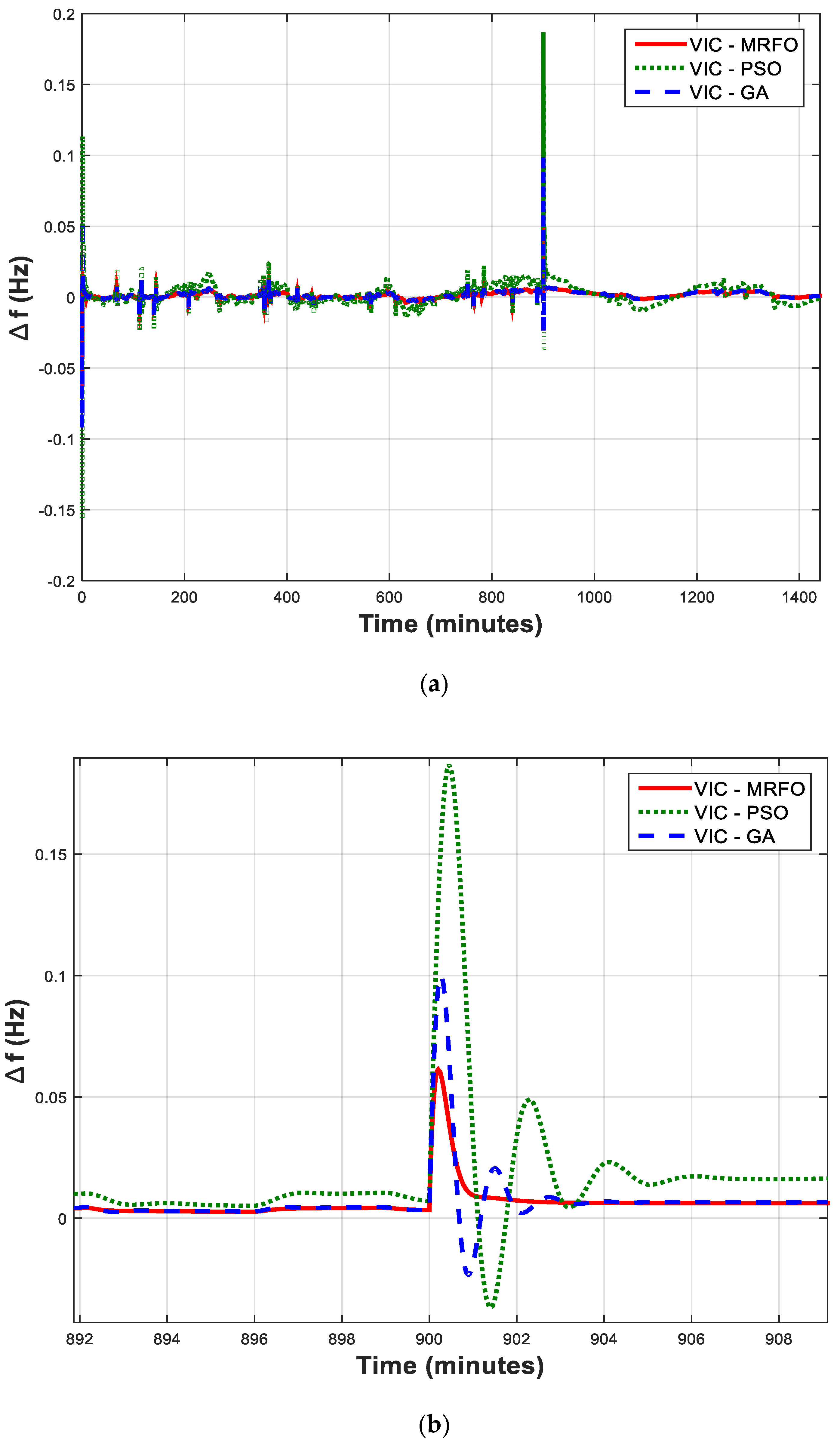
The optimization problem is defined using the criterion of integral square error (ISE), that is the most commonly utilized within the frequency control loops [30]. The effectiveness of MRFO-based PI controller is compared with PSO-based and GA-based PI controllers. The performance of the proposed control approach is checked using the time domain simulations, that are performed using MATLAB software.

The remainder of the paper is organized as follows: Section 2 describes the structure and dynamic modelling of the microgrid including virtual inertia control concept. The control approach and problem formulation are presented in Section 3. Section 4 describes the MRFO while Section 5 presents the simulation results and discussion. Finally, the paper is concluded in Section 6.

2. System Configuration

2.1. Microgrid Structure

An islanded microgrid is considered as an independent microsystem consisting of DGs and interconnected loads. DGs can be of two types; the first type is RES, which produces an uncertain output power like wind and solar photovoltaic (PV) power [34]. The second type of DGs is dispatchable generators that can produce controllable power such as small thermal plants and small hydro-electric turbines [35]. The microgrid system utilized in this study is shown in Figure 1. The system consists of a non-reheat thermal power plant, a wind farm, a PV farm, ESS, and domestic loads.

Figure 2 describes the frequency response dynamic model of the microgrid under study with RESs penetration including the proposed PI controller in the virtual inertia control loop. This figure shows the modelling of different control areas (i.e., primary and secondary control loops) in the microgrid with RESs like solar and wind farms, a conventional power unit like a thermal power station, and domestic loads. This study depended on the first-order dynamic model for RESs. According to references [26,30], the first-order dynamic model for RESs is adequate for frequency stability studies in microgrids. This study takes into accounts the significant inherent constraints and essential requirements needed by the dynamic actions of the conventional generator in order to obtain the exact modelling of the studied microgrid. One of the most essential dynamic limits of the non-reheat thermal generating unit is the power generation change rate because of the restriction of thermal and mechanical actions. In this work, two physical constraints of conventional generators were applied. The first one was the generation rate constraint (GRC) of thermal power plants, that was set as 0.2 p.u.MW/minute [36]. The second physical constraint was the maximum/minimum gate valve limit (i.e., governor dead band (GDB)). The maximum/minimum gate valve limits (V_U, V_L) were set as 0.3 and −0.3 p.u.MW, respectively. The control dynamic equations that describe each component in the studied microgrid are expressed as

$$\Delta P_m=\frac{1}{1+S{T}_t}\Delta P_g$$

(1)

$$\Delta P_g=\frac{1}{1+S{T}_g}\left(\Delta P_{ACE}-\frac{1}{R}\Delta f\right)$$

(2)

$$\Delta P_{ACE}=\frac{K_i}{S}\Delta f$$

(3)

$$\Delta P_{wt}=\frac{1}{1+S{T}_{wt}}\Delta P_{wind}$$

(4)

$$\Delta P_{pv}=\frac{1}{1+S{T}_{pv}}\Delta P_{solar}$$

(5)

where ∆P_m represents the change in thermal power generation, ∆P_g is the change in governor power, ∆P_ACE is the change in control signal from the secondary control, ∆f is the deviation in frequency, ∆P_wind is the wind power variation, ∆P_wt is the wind farm real output power deviation, and ∆P_pv is the solar farm real output power deviation. Therefore, the studied microgrid frequency change taking into accounts the primary and secondary frequency control loops in addition to the virtual inertial control can be obtained as:

$$\Delta f=\frac{1}{2HS+D}\left(\Delta P_m+\Delta P_{wt}+\Delta P_{pv}+\Delta P_{inertia}-\Delta P_L \right)$$

(6)

where $\Delta P_{inertia}$ is the change in the inertia power, and $\Delta P_L$ is the load power variation.

2.2. Virtual Inertia Control Concept for a Microgrid

The modelling of a virtual inertia control block can provide the necessary inertia power to a microgrid to compensate the lack in system inertia because of the high integration of RESs, as shown in Figure 2. In this work, the proposed virtual inertia control consisted of a derivative element, ESS, virtual inertia gain, and a power limiter, as indicated in Figure 3. One of the most significant components in virtual inertia control is the derivative control element, as it calculates the RCF to provide the necessary compensated inertia power to the microgrid through ESS and power inverters during high penetration of RESs and disturbances [22,30]. The RCF can be calculated as follows:

$$RCF=\left[ \frac{d}{dt}\left(\Delta f\right) \right]$$

(7)

In this work, the inertia properties to imitate the stored kinetic power in the rotating elements of traditional generators was provided by the ESS. Therefore, ESS has become an important part in microgrids with RESs, since they provide frequency balance and regulation for further dispatch. To achieve an actual condition of ESS, the system was provided with a low-pass filter obtain a dynamic response. The low-pass filter could eliminate the noise signals produced by the frequency measurement, as the noise signal can significantly affect the derivative control component. Moreover, the power limiter was employed to limit the minimum and maximum ESS capacity and add a real representation of the ESS. Hence, the virtual inertia controller with its dynamic modelling shown in Figure 3 could eventually imitate the inertia characteristics and provide the inertia power to the microgrid for frequency regulation and control in case of RESs penetration and disturbances. The dynamic equation that describes the emulation of the inertia power virtually is presented below [37].

$$\Delta P_{inertia}=\frac{K_{VI}}{1+S{T}_{VI}}\left[\frac{d}{dt}\left(\Delta f\right)\right]$$

(8)

where $K_{VI}$ is the virtual inertia control gain, $T_{VI}$ is the time constant of the low-pass filter to emulate the dynamic response of the ESS, and $\Delta f$ is the deviation in frequency.

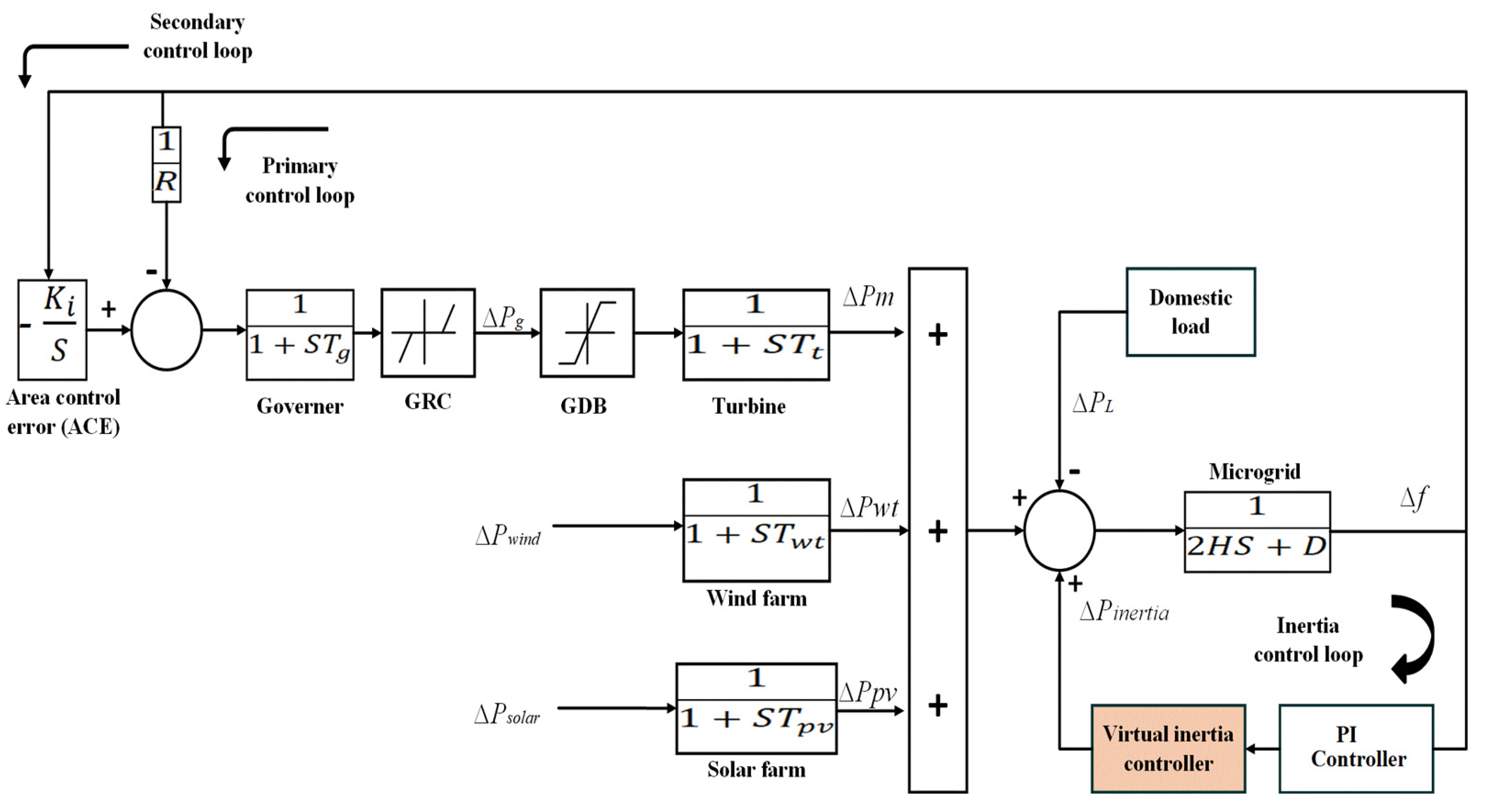
3. Virtual Inertia Control Based on a PI Controller

In traditional networks, the main source of inertia consists of the rotating elements in conventional generating units. Therefore, these generating units play a significant role in restricting the RCF. However, the overall microgrid inertia might be significantly reduced with a high integration of renewables. Therefore, RESs supported by power electronics negatively affect the microgrid frequency resilience. Hence, this will create working restrictions for a virtual inertia control device which cannot deliver sufficient frequency support in the face of contingencies and high RESs integration into the microgrid [29]. Therefore, an additional reliable controller must be provided to deal with uncertainties and contingencies in a low-inertia system and reduce the frequency deviations in case of sudden disturbances or contingencies such as sudden generation loss or load shedding [26,38]. Regarding this issue, a PI controller is proposed to be added in loop to a virtual inertia controller model to emulate the inertia response in the microgrid, thus improving the frequency stability of the studied microgrid. Furthermore, the optimal tuning of the parameters of the PI controller was achieved using an MRFO algorithm under different operating conditions of the microgrid. The parameters of the PI controller are the proportional gain $K_p$ and the integral gain $K_i$. Its transfer function is described as follows:

$$G\left(S\right)=K_p+\frac{K_i}{S}$$

(9)

The MRFO was used to find the optimum design parameters for minimizing the system frequency deviation. In this study, the integral square error (ISE) criterion was used as the objective function to be minimized for optimum tuning of the parameters [30,39]. Therefore, the objective function of the optimization problem, depending on the ISE, can be formulated as follows:

$$ISE={{\displaystyle \int }}_0^{t_{sim}}{\left(\Delta f\right)}^{2}dt$$

(10)

the lower and upper limits of the controller parameters are 0 and 100, respectively; $\Delta f$ is the frequency deviation, and $t_{sim}$ is the simulation time for one run.

4. Manta Ray Foraging Optimization Algorithm

The Manta ray foraging optimizer is a relatively new metaheuristic optimization method based on the foraging attitude that manta rays have to search for their food. These sea creatures possess two fleshly pectoral fins that look like wings on their flat body. They also possess two cephalic lobes that expand in front of their end mouths. Manta rays have intelligent and different foraging strategies to find plentiful plankton. These foraging strategies are chain, cyclone, and somersault foraging. These three foraging strategies were mathematically modelled to provide a modern bio-inspired optimization algorithm named MRFO to solve global optimization problems [40]. The mathematical modelling is further explained in the subsequent sections.

4.1. Chain Foraging

In this strategy, plentiful plankton with high concentration can be considered as the main target (i.e., best solution) by manta rays. Thus, they can detect the position of their food and swim in its direction. Hence, an orderly foraging chain is formed by manta rays by lining up head to tail. Each manta ray moves towards the food and the preceding individual. Consequently, each individual moves depending not only on the food (i.e., best solution) found during one iteration, but also on the solution of the preceding manta rays. This foraging approach can be mathematically expressed as [33]

$$x_i\left(t+1\right)=\{\begin{array}{c}{x}_i\left(t\right)+r\left(x_{best}\left(t\right)-x_i\left(t\right)\right)+a\left(x_{best}\left(t\right)-x_i\left(t\right)\right) i=1\\ x_i\left(t\right)+r\left(x_{i-1}\left(t\right)-x_i\left(t\right)\right)+a\left(x_{best}\left(t\right)-x_i\left(t\right)\right) i=2,3,\dots \dots \dots ,N\end{array}$$

(11)

$$a=2r· \sqrt{\left|log\left(r\right)\right|}$$

(12)

where $x_i\left(t\right)$ is the location of the ith individual at iteration t, a is a weighting factor, r is a random value between 0 and 1 [41], N is the population size (i.e., number of manta rays), and $x_{best}\left(t\right)$ is the best solution at time t. Equation (11) shows that the location of the ith individual, except the first one, depends on the location of the (i−1)th individual $x_{i-1}\left(t\right)$ and the best solution $x_{best}\left(t\right)$ so far.

4.2. Cyclone Foraging

When the desired food is identified by manta ray groups, a foraging chain with a spiral shape is formed by manta rays that search for their plankton. This strategy is similar to the spiral foraging approach of the whale optimization algorithm. Moreover, in the cyclone foraging strategy, each individual swims towards the preceding manta ray. Therefore, each individual not only observes the target plankton, but also swims to it moving along a spiral. The mathematical equations that describe the spiral movements of manta ray swarms in a two-dimensional field can be defined as follows [33,42]:

$$\{\begin{array}{c}{X}_i\left(t+1\right)=X_{best}+r\left(X_{i-1}\left(t\right)-X_i\left(t\right)\right)+e^{bw}·cos\left(2\pi w\right)\left(X_{best}-X_i\left(t\right)\right)\\ Y_i\left(t+1\right)=Y_{best}+r\left(Y_{i-1}\left(t\right)-Y_i\left(t\right)\right)+e^{bw}·sin\left(2\pi w\right)\left(Y_{best}-Y_i\left(t\right)\right)\end{array}$$

(13)

where w is a random value between 0 and 1. The cyclone foraging approach can be mathematically modeled as follows:

$$x_i\left(t+1\right)=\{\begin{array}{c}{x}_{best}+r\left(x_{best}\left(t\right)-x_i\left(t\right)\right)+\beta \left(x_{best}\left(t\right)-x_i\left(t\right)\right) i=1\\ x_{best}+r\left(x_{i-1}\left(t\right)-x_i\left(t\right)\right)+\beta \left(x_{best}\left(t\right)-x_i\left(t\right)\right) i=2,3,\dots \dots \dots ,N\end{array}$$

(14)

where $\beta$ is a weighting factor given by

$$\beta =2e^{r_1\frac{T-t+1}{T}}·sin\left(2\pi r_1\right)$$

(15)

where $r_1$ is a value selected randomly between 0 and 1, t represents the iteration number, and T represents the total number of performed iterations. The cyclone foraging approach incorporates a great exploitation of the area with the feasible solution since each individual searches for the plankton according to its reference location. This behavior indeed improves the exploration procedure by making the manta rays search for different food locations that are far away from the existing best one. The process is achieved by allocating a location randomly within the field area as follows:

$$x_{rand}=Lb+r·\left(Ub-Lb\right)$$

(16)

$$x_i\left(t+1\right)=\{\begin{array}{c}{x}_{rand}+r\left(x_{rand}-x_i\left(t\right)\right)+\beta \left(x_{rand}-x_i\left(t\right)\right) i=1\\ x_{rand}+r\left(x_{i-1}\left(t\right)-x_i\left(t\right)\right)+\beta \left(x_{rand}\left(t\right)-x_i\left(t\right)\right) i=2,3,\dots \dots \dots ,N\end{array}$$

(17)

where $x_{rand}$ is a random position allocated for the search area, and $Lb$ and $Ub$ are the lower and upper limits of the problem variables.

4.3. Somersault Foraging

In this strategy, manta rays observe the food as a pivot. When manta rays locate the plankton, they perform a set of backwards somersaults, circling across the food and somersaulting to a new location. Consequently, the locations of manta rays are always updated around the best identified location moment by moment. This foraging approach is mathematically modeled according to Equation (18)

$$x_i\left(t+1\right)=x_i\left(t\right)+S\left(r_2·x_{best}-r_3·x_i\left(t\right)\right) i=1,2,\dots \dots \dots ,N$$

(18)

where $r_2$ and $r_3$ are random values between 0 and 1, S is the somersault coefficient for determining the somersault range. Equation (18) shows that each manta ray is able to reach any location among the current location and symmetrical locations in relation to the pivot in the searching area. Thus, the distance is reduced between the individual location and the best location found moment by moment through this strategy. Therefore, each individual moves regularly to the optimum location in the searching area. Moreover, the somersault coefficient for determining the somersault range decreases as iterations increase. Figure 4 shows the flowchart that describes the operation of MRFO [41]. The exploration and exploitation behavior are controlled by the MRFO by controlling ($t/T_{max}$). When ($t/T_{max}$) > rand, the exploration behavior is performed; when ($t/T_{max}$) < rand, the exploitation process is performed, and the individual in the optimal position is used as a reference. A random number is also used to select between chain or cyclone foraging. Then, somersault foraging is performed.

5. Time Domain Simulations

5.1. Description of the Case Study

The frequency response dynamic model of the islanded microgrid under study with RESs penetration including the proposed PI controller in the virtual inertia control loop is described in Figure 2. The microgrid model was built with the help of the Simulink feature in MATLAB program. The system consisted of a 12 MW of non-reheat thermal power plant, 15 MW of domestic loads, a 10 MW wind farm with an 8 MW PV farm, and ESS with 6 MW capacity. The base power of the system was 25 MW. Moreover, the disturbances signals to the studied microgrid were solar power variation $\Delta P_{solar}$, variations in wind power $\Delta P_{wind}$, and variations in demand power $\Delta P_L$. The microgrid parameters are presented in

Table 1. Microgrid’s dynamic parameters.

Parameter	Physical Meaning	Value
D (p.u.MW/Hz)	Microgrid damping coefficient	0.015
H (p.u.MW s)	Overall inertia constant	0.083
Tg (S)	Governor time constant	0.1
Tt (S)	Turbine time constant	0.4
Twt (S)	Wind turbine time constant	1.5
Tpv (S)	Solar system time constant	1.8
Ki	Integral control gain	0.05
R (Hz/p.u.MW)	Speed droop charcharis	2.4
TVI (S)	Virtual inertia time constant	10
KVI	Virtual inertia gain	0.5
VU (p.u.MW)	Maximum valve gate limit	0.3
VL(p.u.MW)	Minimum valve gate limit	−0.3
GRC (p.u.MW/minute)	Generation rate constraint	0.2
∆Pinertia.max (p.u.MW)	Maximum ESS capacity	0.24
∆Pinertia.min(p.u.MW)	Minimum ESS capacity	−0.24

. The microgrid parameters were chosen according to [22,30]. The optimization problem was solved through the interface between the m-files of the MRFO code with the microgrid model [43]. The performance of the microgrid was investigated considering various operating conditions through the following scenarios.

5.2. Scenario 1: Microgrid Performance without RESs

This scenario introduces the optimal tuning of the PI controller-based virtual inertia controller without RESs integration into the microgrid with the help of the suggested MRFO under load disturbances. This scenario mainly aimed at checking the performance of the studied microgrid by doing a comparison between the MRFO-based PI controller and PI controllers based on other optimization techniques, such as GA and PSO algorithms. In this scenario, the RESs were not taken into consideration for a fair comparison. The studied microgrid was subjected to step load changes of 5% and 10% at time = 1 s under nominal microgrid system inertia. The optimal characteristics involved 20 manta rays with 100 iterations. A trial-and-error approach was used to define the optimal characteristics, as this approach is commonly used with different computation optimization techniques. For investigating the robustness of the MRFO technique, the optimization process was repeated 10 times, leading to an objective fitness value of 9.2 × 10⁻³ and an approximately zero standard deviation. Figure 5a illustrates the convergence curve of the fitness function of the MRFO compared with the objective function of the GA and PSO. It is clear that the MRFO has a lower fitness value compared to GA and PSO under a constant number of iterations, which proves the effectiveness of the MRFO-based PI controller in frequency reference tracking and damping frequency oscillations. The optimal tuning of the PI controller led to an optimal proportional gain of K_p = 28.5 and an integral gain of K_i = 78.3. Figure 5b,c indicates the frequency deviation ∆f of the microgrid under 5% and 10% step increases in load using the proposed PI controller in virtual inertia control loop. The obtained dynamic responses showed that the microgrid response when using the PI controller with MRFO produced a fast response, a low steady state error, and a better dampening of the frequency fluctuations than when different optimization algorithms such as GA and PSO algorithms were used [30].

Table 2. Transient parameters of the studied microgrid frequency deviation for scenario 1.

Algorithm	SLP	MPUS (Hz)	MPOS (Hz)	Ts(s)	ess (Hz)
MRFO	5%	0.02431	0	1.35	0.0012
GA		0.04041	0.01117	1.5	0.0013
PSO		0.0751	0.01868	1.93	0.0038
MRFO	10%	0.04856	0	1.56	0.0024
GA		0.08091	0.02252	1.97	0.0026
PSO		0.1506	0.03731	3.64	0.0077

shows the transient parameters of the microgrid frequency deviation under load perturbations. It can be observed that the maximum percentage overshoot (MPOS), maximum percentage undershoot (MPUS), steady-state error (e_ss) of the microgrid frequency deviation and settling time (T_s) of 2% criterion using the suggested controller had lower values compared with PSO-based and GA-based PI controllers. Furthermore, the MRFO algorithm was tested for different values of system inputs to accomplish the sensitivity analysis.

Table 3. Transient parameters of the studied microgrid for different input values.

Parameter	Value	MPUS (Hz)	MPOS (Hz)	Ts (s)	ess (Hz)
H (p.u.MW s)	0.083 (nominal)	0.04856	0	1.565	0.0024
	0.08715 (+5%)	0.0482	0	1.556	0.0024
	0.07885 (−5%)	0.0492	0	1.563	0.0024
D (p.u.MW/Hz)	0.015 (nominal)	0.04856	0	1.565	0.0024
	0.01575 (+5%)	0.0484	0	1.563	0.0024
	0.01425 (−5%)	0.0486	0	1.567	0.0024
R (Hz/p.u.MW)	2.4 (nominal)	0.04856	0	1.565	0.0024
	2.52 (+5%)	0.0487	0	1.566	0.0024
	2.28 (−5%)	0.0486	0	1.560	0.0024
Tg (S)	0.1 (nominal)	0.04856	0	1.565	0.0024
	0.105 (+5%)	0.0487	0	1.567	0.0024
	0.095 (−5%)	0.0486	0	1.563	0.0024
Tt (S)	0.4 (nominal)	0.04856	0	1.565	0.0024
	0.42 (+5%)	0.0487	0	1.568	0.0024
	0.38 (−5%)	0.04850	0	1.561	0.0024

shows the transient parameters of the studied microgrid when it was subjected to a 10% step load change for a $\pm$5% change from the nominal value of the different input parameters. It can be seen that the settling time, steady-state error, maximum overshoot, and maximum undershoot were almost the same and within acceptable limits while using the proposed PI controller with the MRFO algorithm.

5.3. Scenario 2: Microgrid Performance under Reduced System Inertia

In this scenario, the studied microgrid was subjected to step load changes of 5% and 10% in case of a 50% reduction in microgrid overall inertia (i.e., uncertainty). The studied microgrid performance was investigated under load disturbances and system uncertainties (i.e., low system inertia). Figure 6a,b indicates the frequency deviation of the microgrid under 5% and 10% step increases in load under a 50% reduction in system inertia. It can be seen that there were high fluctuations in the microgrid frequency and large frequency deviations in the case of low microgrid inertia.

Table 4. Transient parameters of the studied microgrid frequency deviation for scenario 2.

Algorithm	SLP	MPUS (Hz)	MPOS (Hz)	Ts(s)	ess (Hz)
MRFO	5%	0.0273	0	1.28	0.0012
GA		0.0502	0.0094	1.38	0.0015
PSO		0.098	0.026	2.75	0.0039
MRFO	10%	0.0545	0	1.48	0.0026
GA		0.1005	0.019	1.65	0.0028
PSO		0.2	0.059	3.12	0.0079

shows that a more satisfactory result was obtained by an MRFO-based PI controller with a virtual inertia controller dealing with disturbance alleviation and frequency reference tracking quality and minimizing steady-state error during low microgrid inertia conditions. The simulation results indicated that the MRFO-based PI controller was better in tracking the microgrid frequency reference point during a sudden load power increase compared with PSO-based and GA-based PI controllers in the virtual inertia control loop.

5.4. Scenario 3: Microgrid Performance Including RESs

The intermittent power of RESs, generation/demand power, and permanent changes of system control are considered as important qualities of the actual islanded microgrids. Therefore, in this scenario, the microgrid frequency performance was investigated, taking into account the RESs and load power fluctuations. To achieve a realistic study, actual wind data were extracted and used from Al-Zaafrana wind farm in Egypt, in 2014, with rated wind speed = 15 m/s [44]. Figure 7a shows the wind power pattern, where the output wind power had a rated power of 0.4 p.u.MW and fluctuated below the rated power. Moreover, solar power data obtained from a test location in Riyadh city, Saudi Arabia, in 2015 were implemented [44]. These real data refer to a completely sunny day (from 6 am to 6 pm). The output power pattern of the solar farm is shown in Figure 7b; the solar farm had 0.32 p.u.MW that changed gradually in different conditions of shading below the rated power. In addition, an actual random load pattern was implemented as shown in Figure 7c [45].

Table 5. Multiple operating conditions of the studied microgrid.

Disturbance	Starting Time	Stopping Time	Size
Wind farm	initial	-	10 MW
Solar farm	initial	-	8 MW
Domestic load	initial	900	15 MW

shows various working conditions to realize multiple operations of the studied microgrid and investigate the proficiency of the MRFO-based PI controller in the virtual inertia control loop against RESs integration and load permanent disturbances, as well as the microgrid inertia change.

The system frequency response was investigated under nominal microgrid inertia. Figure 8a shows that the microgrid frequency response was affected by RESs penetration and load power fluctuations. For a clear comparison between the MRFO-based PI controller and other optimization algorithm-based PI controllers in the virtual inertia control loop, Figure 8b shows a zoom view of the microgrid frequency response at time = 900 min when the load was disconnected. This can be considered a complete load shedding case in the islanded microgrid to test the system response under severe operating conditions. The evaluation parameters of the studied microgrid frequency deviation with different control techniques were compared and are presented in

Table 6. Evaluation indices of the studied microgrid frequency deviation for scenario 3.

Algorithm	MPUS (Hz)	MPOS (Hz)
MRFO	0.057	0.061
GA	0.092	0.1
PSO	0.16	0.19

. It can be noted that the PSO-based PI controller was able to regulate the frequency within $\pm$0.2 Hz, and the GA based-PI controller was able to regulate the frequency within ±0.1 Hz. On the other hand, the MRFO-PI controller-based controller was able to regulate the frequency within ±0.06 Hz. Therefore, the MRFO-PI controller in the virtual inertia control loop was found to be the best when dealing with RESs variations and random load power disturbances.

6. Concluding Remarks

The increased penetration rate of RESs integrated into the microgrids affects the system frequency stability due to the reduction in the overall grid inertia, leading to serious frequency instability issues. Therefore, this work proposes a frequency control model imitating the inertia power to support the frequency control loops in islanded microgrids. The control approach used with a virtual inertia controller depended on a PI controller optimally designed with the MRFO algorithm. The performance of the MRFO-based PI controller implemented in the loop of the proposed virtual inertia controller was investigated and compared with that of PI controller based on other optimization algorithms, taking into accounts RESs penetration, load power fluctuations, and system uncertainties to check the performance. The simulation results indicates that the MRFO-based PI controller was four times better in tracking the microgrid frequency reference point compared with the PSO-based PI controller, and two times better compared with the GA-based PI controller in the virtual inertia control loop. In the near future, the proposed controller shall be used in many renewable energy systems and smart grids.