An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices
Abstract
:1. Introduction
- Developing an IVIF-similarity measure to compute weights of DMs. The similarity measure method is conducted based on the distance from the ideal decision matrix under IVIF conditions that considers membership and non-membership degrees to control vagueness and uncertain conditions.
- Extending an IVIF-Shannon entropy method to obtain the weights of the criteria. This method calculates the criteria weights with respecting entropy measures under IVIF situations.
- Developing an IVIF-E-VIKOR method for ranking the alternatives. In the IVIF-E-VIKOR method, a new indicator is presented for evaluating the alternatives under IVIF conditions by considering membership and non-membership degrees closer to the outcomes of real-world problems.
- Extending an IVIF-MARCOS approach to rank the alternatives. This method obtains the alternative ranking based on the utility function that is computed based on the utility degree by respecting membership and non-membership values to handle uncertain situations.
- Proposing a new hybrid ranking model to concurrently appraise alternatives based on two IVIF-E-VIKOR and IVIF-MARCOS approaches.
2. Preliminaries
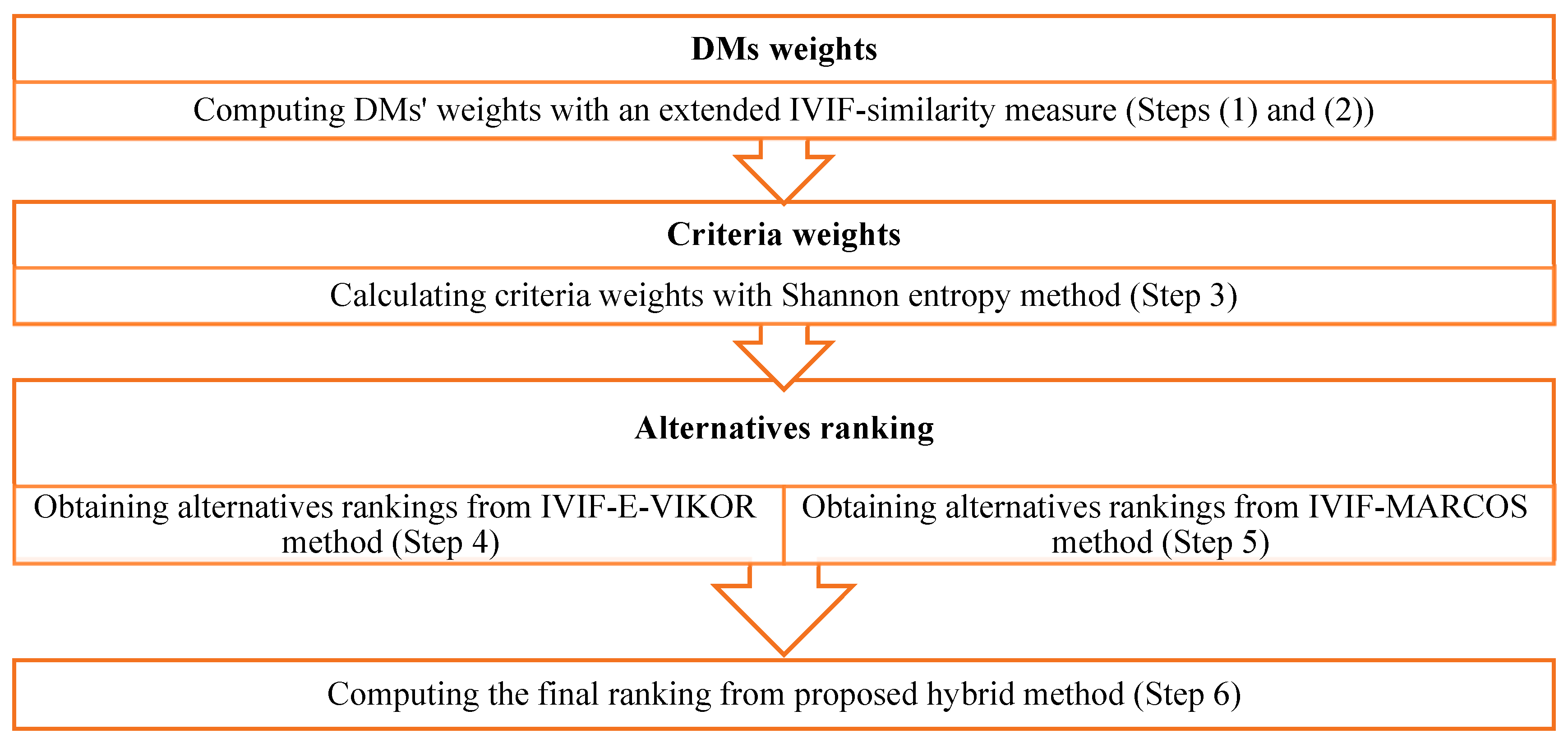
3. Proposed Soft Computing Model
4. Illustrative Example
4.1. Computational Results
4.2. Comparative Analysis
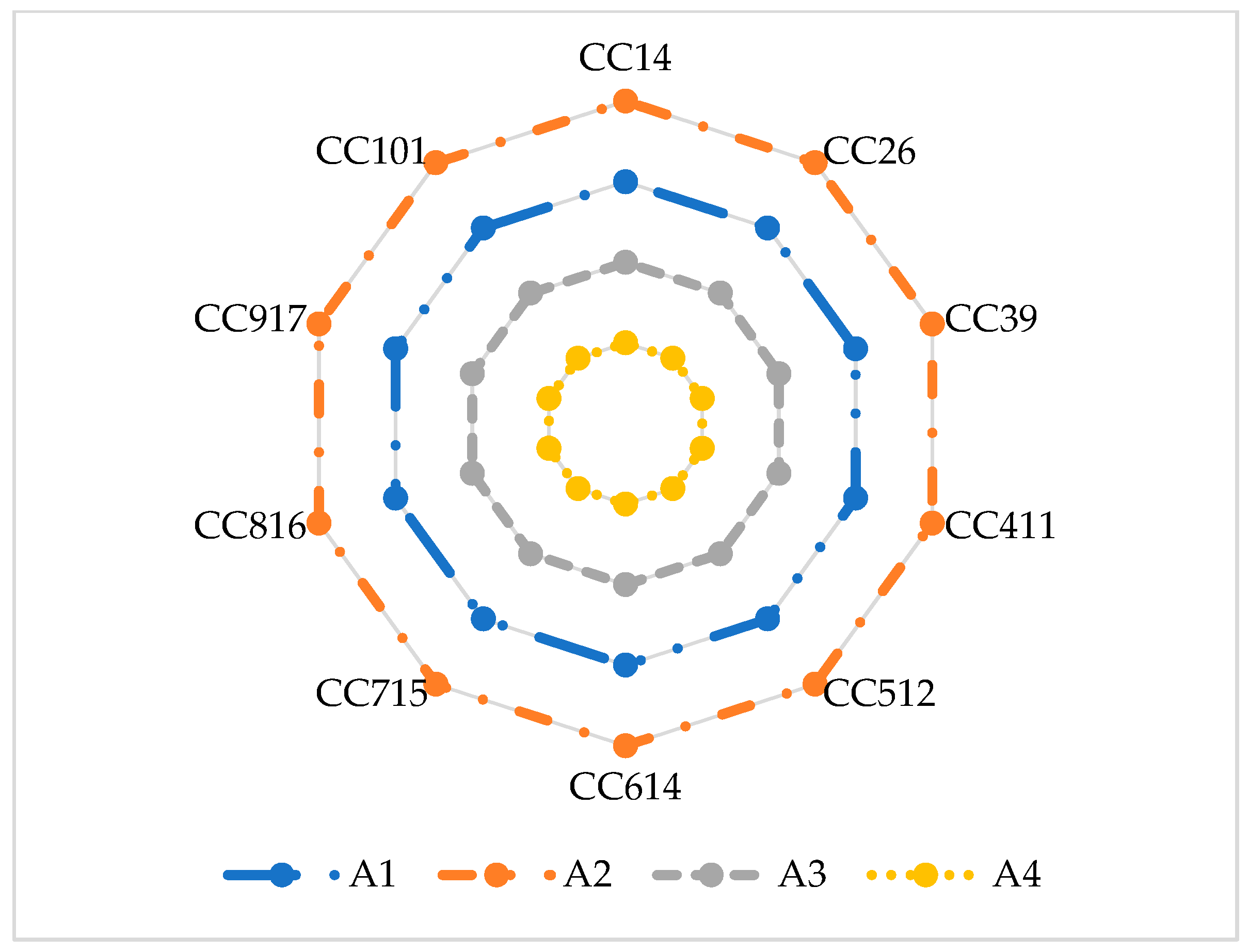
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, A.; Ozdamar, L.; Zhang, C.N. Supply chain redesign in the healthcare industry of Singapore. Supply Chain Manag. Int. J. 2008, 13, 95–103. [Google Scholar] [CrossRef]
- Foroozesh, N.; Tavakkoli-Moghaddam, R.; Mousavi, S.M. An interval-valued fuzzy statistical group decision making approach with new evaluating indices for sustainable supplier selection problem. J. Intell. Fuzzy Syst. 2019, 36, 1855–1866. [Google Scholar] [CrossRef]
- Krysiak, F.C. Risk management as a tool for sustainability. J. Bus. Ethics 2009, 85, 483–492. [Google Scholar] [CrossRef] [Green Version]
- Baltacioglu, T.; Ada, E.; Kaplan, M.D.; Yurt And, O.; Cem Kaplan, Y. A new framework for service supply chains. Serv. Ind. J. 2007, 27, 105–124. [Google Scholar] [CrossRef]
- Mustaffa, N.H.; Potter, A. Healthcare supply chain management in Malaysia: A case study. Supply Chain Manag. Int. J. 2009, 14. [Google Scholar]
- Beliën, J.; De Boeck, L.; Colpaert, J.; Devesse, S.; Van den Bossche, F. Optimizing the facility location design of organ transplant centers. Decis. Support Syst. 2013, 54, 1568–1579. [Google Scholar] [CrossRef]
- Zahiri, B.; Tavakkoli-Moghaddam, R.; Mohammadi, M.; Jula, P. Multi-objective design of an organ transplant network under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2014, 72, 101–124. [Google Scholar] [CrossRef]
- Ghadimi, P.; Heavey, C. Sustainable supplier selection in medical device industry: Toward sustainable manufacturing. Procedia Cirp 2014, 15, 165–170. [Google Scholar] [CrossRef] [Green Version]
- Hashemkhani Zolfani, S.H.; Pourhossein, M.; Yazdani, M.; Zavadskas, E.K. Evaluating construction projects of hotels based on environmental sustainability with MCDM framework. Alex. Eng. J. 2018, 57, 357–365. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Vilutiene, T.; Adeli, H. Sustainable decision-making in civil engineering, construction and building technology. Sustainability 2018, 10, 14. [Google Scholar] [CrossRef] [Green Version]
- Zavadskas, E.K.; Šaparauskas, J.; Antucheviciene, J. Sustainability in construction engineering. Sustainability 2018, 10, 2236. [Google Scholar] [CrossRef] [Green Version]
- Hajighasemi, Z.; Mousavi, S.M. A new approach in failure modes and effects analysis based on compromise solution by considering objective and subjective weights with interval-valued intuitionistic fuzzy sets. Iran. J. Fuzzy Syst. 2018, 15, 139–161. [Google Scholar]
- Mousavi, S.M.; Mirdamadi, S.; Siadat, A.; Dantan, J.; Tavakkoli-Moghaddam, R. An intuitionistic fuzzy grey model for selection problems with an application to the inspection planning in manufacturing firms. Eng. Appl. Artif. Intell. 2015, 39, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.; Vahdani, B.; Behzadi, S.S. Designing a model of intuitionistic fuzzy VIKOR in multi-attribute group decision-making problems. Iran. J. Fuzzy Syst. 2016, 13, 45–65. [Google Scholar]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. Interval valued intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets; Physica: Heidelberg, Germany, 1999; pp. 139–177. [Google Scholar]
- Davoudabadi, R.; Mousavi, S.M.; Šaparauskas, J.; Gitinavard, H. Solving construction project selection problem by a new uncertain weighting and ranking based on compromise solution with linear assignment approach. J. Civ. Eng. Manag. 2019, 25, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Hayat, K.; Ali, M.I.; Cao, B.Y.; Karaaslan, F.; Yang, X.P. Another view of aggregation operators on group-based generalized intuitionistic fuzzy soft sets: Multi-attribute decision making methods. Symmetry 2018, 10, 753. [Google Scholar] [CrossRef] [Green Version]
- Hayat, K.; Ali, M.I.; Alcantud, J.C.R.; Cao, B.Y.; Tariq, K.U. Best concept selection in design process: An application of generalized intuitionistic fuzzy soft sets. J. Intell. Fuzzy Syst. 2018, 35, 5707–5720. [Google Scholar] [CrossRef]
- Bolturk, E.; Kahraman, C. Interval-valued intuitionistic fuzzy CODAS method and its application to wave energy facility location selection problem. Intell. Fuzzy Syst. 2018, 35, 4865–4877. [Google Scholar] [CrossRef]
- Liu, H.C.; Quan, M.Y.; Li, Z.; Wang, Z.L. A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment. Inf. Sci. 2019, 486, 254–270. [Google Scholar] [CrossRef]
- Abdullah, L.; Zulkifli, N.; Liao, H.; Herrera-Viedma, E.; Al-Barakati, A. An interval-valued intuitionistic fuzzy DEMATEL method combined with Choquet integral for sustainable solid waste management. Eng. Appl. Artif. Intell. 2019, 82, 207–215. [Google Scholar] [CrossRef]
- Roy, J.; Das, S.; Kar, S.; Pamučar, D. An extension of the CODAS approach using interval-valued intuitionistic fuzzy set for sustainable material selection in construction projects with incomplete weight information. Symmetry 2019, 11, 393. [Google Scholar] [CrossRef] [Green Version]
- Davoudabadi, R.; Mousavi, S.M.; Mohagheghi, V. A new last aggregation method of multi-attributes group decision making based on concepts of TODIM, WASPAS and TOPSIS under interval-valued intuitionistic fuzzy uncertainty. Knowl. Inf. Syst. 2020, 62, 1371–1391. [Google Scholar] [CrossRef]
- Davoudabadi, R.; Mousavi, S.M.; Mohagheghi, V.; Vahdani, B. Resilient supplier selection through introducing a new interval-valued intuitionistic fuzzy evaluation and decision-making framework. Arab. J. Sci. Eng. 2019, 44, 7351–7360. [Google Scholar] [CrossRef]
- Mao, R.J.; You, J.X.; Duan, C.Y.; Shao, L.N. A heterogeneous MCDM framework for sustainable supplier evaluation and selection based on the IVIF-TODIM method. Sustainability 2019, 11, 5057. [Google Scholar] [CrossRef] [Green Version]
- Seker, S.; Aydin, N. Sustainable public transportation system evaluation: A novel two-stage hybrid method based on IVIF-AHP and CODAS. Int. J. Fuzzy Syst. 2020, 22, 257–272. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wu, Y.; Dong, Y. Ranking range-based approach to MADM under incomplete context and its application in venture investment evaluation. Technol. Econ. Dev. Econ. 2019, 25, 877–899. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Dong, Y.; Chiclana, F.; Herrera-Viedma, E. Social trust-driven consensus reaching model with a minimum adjustment feedback mechanism considering assessments-modifications willingness. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Qi, W.; Huang, Z.; Dinçer, H.; Korsakienė, R.; Yüksel, S. Corporate governance-based strategic approach to sustainability in energy industry of emerging economies with a novel interval-valued intuitionistic fuzzy hybrid decision making model. Sustainability 2020, 12, 3307. [Google Scholar] [CrossRef] [Green Version]
- Davoudabadi, R.; Mousavi, S.M.; Mohagheghi, V. A new decision model based on DEA and simulation to evaluate renewable energy projects under interval-valued intuitionistic fuzzy uncertainty. Renew. Energy 2020, 164, 1588–1601. [Google Scholar] [CrossRef]
- Bolturk, E.; Gülbay, M.; Kahraman, C. Sustainable energy selection based on interval-valued intuitionistic fuzzy and neutrosophic aggregation operators. J. Intell. Fuzzy Syst. 2020, 39, 6553–6563. [Google Scholar] [CrossRef]
- Alrasheedi, M.; Mardani, A.; Mishra, A.R.; Streimikiene, D.; Liao, H.; Al-nefaie, A.H. Evaluating the green growth indicators to achieve sustainable development: A novel extended interval-valued intuitionistic fuzzy-combined compromise solution approach. Sustain. Dev. 2021, 29, 120–142. [Google Scholar] [CrossRef]
- Alimohammadlou, M.; Khoshsepehr, Z. Investigating organizational sustainable development through an integrated method of interval-valued intuitionistic fuzzy AHP and WASPAS. Environ. Dev. Sustain. 2021, 24, 2193–2224. [Google Scholar] [CrossRef]
- Chen, L.; Duan, D.; Mishra, A.R.; Alrasheedi, M. Sustainable third-party reverse logistics provider selection to promote circular economy using new uncertain interval-valued intuitionistic fuzzy-projection model. J. Enterp. Inf. Manag. 2021. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chandel, A.; Saeidi, P. Low-carbon tourism strategy evaluation and selection using interval-valued intuitionistic fuzzy additive ratio assessment approach based on similarity measures. Environ. Dev. Sustain. 2021, 1–47. [Google Scholar] [CrossRef]
- Ayyildiz, E. Interval valued intuitionistic fuzzy analytic hierarchy process-based green supply chain resilience evaluation methodology in post COVID-19 era. Environ. Sci. Pollut. Res. 2021, 1–19. [Google Scholar] [CrossRef]
- Tumsekcali, E.; Ayyildiz, E.; Taskin, A. Interval valued intuitionistic fuzzy AHP-WASPAS based public transportation service quality evaluation by a new extension of SERVQUAL Model: P-SERVQUAL 4.0. Expert Syst. Appl. 2021, 186, 115757. [Google Scholar] [CrossRef]
- Perçin, S. Circular supplier selection using interval-valued intuitionistic fuzzy sets. Environ. Dev. Sustain. 2021, 24, 5551–5581. [Google Scholar] [CrossRef]
- Tavana, M.; Shaabani, A.; Di Caprio, D.; Bonyani, A. An integrated group fuzzy best-worst method and combined compromise solution with Bonferroni functions for supplier selection in reverse supply chains. Clean. Logist. Supply Chain 2021, 2, 100009. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, S.C.; Li, X. An order-splitting model for supplier selection and order allocation in a multi-echelon supply chain. Comput. Oper. Res. 2022, 137, 105515. [Google Scholar] [CrossRef]
- Jiang, W.H.; Xu, L.; Chen, Z.S.; Govindan, K.; Chin, K.S. Financing equilibrium in a capital constrained supply Chain: The impact of credit rating. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102559. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhang, X.; Govindan, K.; Wang, X.J.; Chin, K.S. Third-party reverse logistics provider selection: A computational semantic analysis-based multi-perspective multi-attribute decision-making approach. Expert Syst. Appl. 2021, 166, 114051. [Google Scholar] [CrossRef]
- Xue, Y.X.; You, J.X.; Lai, X.D.; Liu, H.C. An interval-valued intuitionistic fuzzy MABAC approach for material selection with incomplete weight information. Appl. Soft Comput. 2016, 38, 703–713. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment. Comput. Appl. Math. 2018, 37, 1319–1329. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, J. On geometric aggregation over interval-valued intuitionistic fuzzy information. In Proceedings of the IEEE Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; Volume 2, pp. 466–471. [Google Scholar]
- Bai, Z.Y. An interval-valued intuitionistic fuzzy TOPSIS method based on an improved score function. Sci. World J. 2013, 2013, 879089. [Google Scholar] [CrossRef] [Green Version]
- Ze-Shui, X. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2007, 22, 215–219. [Google Scholar]
- Mousavi, S.M.; Antuchevičienė, J.; Zavadskas, E.K.; Vahdani, B.; Hashemi, H. A new decision model for cross-docking center location in logistics networks under interval-valued intuitionistic fuzzy uncertainty. Transport 2019, 34, 30–40. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.S.; Chen, J. An overview of distance and similarity measures of intuitionistic fuzzy sets. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2008, 16, 529–555. [Google Scholar] [CrossRef]
- Rajaram, R.; Castellani, B.; Wilson, A.N. Advancing Shannon entropy for measuring diversity in systems. Complexity 2017, 2017, 8715605. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.; Samuel, C. Selection of best renewable energy source by using VIKOR method. Technol. Econ. Smart Grids Sustain. Energy 2017, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A new fuzzy MARCOS method for road traffic risk analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xu, Z. Soft computing based on maximizing consensus and fuzzy TOPSIS approach to interval-valued intuitionistic fuzzy group decision making. Appl. Soft Comput. 2015, 26, 42–56. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Luthra, S.; Govindan, K.; Kannan, D.; Mangla, S.K.; Garg, C.P. An integrated framework for sustainable supplier selection and evaluation in supply chains. J. Clean. Prod. 2017, 140, 1686–1698. [Google Scholar] [CrossRef]
- Puška, L.A.; Kozarević, S.; Stević, Ž.; Stovrag, J. A New Way Of Applying Interval Fuzzy Logic in Group Decision Making For Supplier Selection. Econ. Comput. Econ. Cybern. Stud. Res. 2018, 52. [Google Scholar] [CrossRef]
- Chatterjee, K.; Pamucar, D.; Zavadskas, E.K. Evaluating the performance of suppliers based on using the R’AMATEL-MAIRCA method for green supply chain implementation in electronics industry. J. Clean. Prod. 2018, 184, 101–129. [Google Scholar] [CrossRef]
- Stojić, G.; Stević, Ž.; Antuchevičienė, J.; Pamučar, D.; Vasiljević, M. A novel rough WASPAS approach for supplier selection in a company manufacturing PVC carpentry products. Information 2018, 9, 121. [Google Scholar] [CrossRef] [Green Version]
- Vasiljević, M.; Fazlollahtabar, H.; Stević, Ž.; Vesković, S. A rough multicriteria approach for evaluation of the supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar] [CrossRef]
- Oztaysi, B.; Onar, S.C.; Goztepe, K.; Kahraman, C. Evaluation of research proposals for grant funding using interval-valued intuitionistic fuzzy sets. Soft Comput. 2017, 21, 1203–1218. [Google Scholar] [CrossRef]
- Park, J.H.; Cho, H.J.; Kwun, Y.C. Extension of the VIKOR method for group decision making with interval-valued intuitionistic fuzzy information. Fuzzy Optim. Decis. Mak. 2011, 10, 233–253. [Google Scholar] [CrossRef]
- Park, J.H.; Park, I.Y.; Kwun, Y.C.; Tan, X. Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment. Appl. Math. Model. 2011, 35, 2544–2556. [Google Scholar] [CrossRef]
- Foroozesh, N.; Jolai, F.; Mousavi, S.M.; Karimi, B. A new fuzzy-stochastic compromise ratio approach for green supplier selection problem with interval-valued possibilistic statistical information. Neural Comput. Appl. 2021, 33, 7893–7911. [Google Scholar] [CrossRef]
- Mirnezami, S.A.; Mousavi, S.M.; Mohagheghi, V. An innovative interval type-2 fuzzy approach for multi-scenario multi-project cash flow evaluation considering TODIM and critical chain with an application to energy sector. Neural Comput. Appl. 2021, 33, 2263–2284. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Foroozesh, N.; Zavadskas, E.K.; Antucheviciene, J. A new soft computing approach for green supplier selection problem with interval type-2 trapezoidal fuzzy statistical group decision and avoidance of information loss. Soft Comput. 2020, 24, 12313–12327. [Google Scholar] [CrossRef]
- Dorfeshan, Y.; Tavakkoli-Moghaddam, R.; Mousavi, S.M.; Vahedi-Nouri, B. A new weighted distance-based approximation methodology for flow shop scheduling group decisions under the interval-valued fuzzy processing time. Appl. Soft Comput. 2020, 91, 106248. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M.; Mojtahedi, M.; Newton, S. Evaluating large, high-technology project portfolios using a novel interval-valued Pythagorean fuzzy set framework: An automated crane project case study. Expert Syst. Appl. 2020, 162, 113007. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M. D-WASPAS: Addressing social cognition in uncertain decision-making with an application to a sustainable project portfolio problem. Cogn. Comput. 2020, 12, 619–641. [Google Scholar] [CrossRef]
| References | Method Features | |||||
|---|---|---|---|---|---|---|
| Applying Linguistic Terms | IVIF | DM Weights | Criteria Weights | Hybrid/New Ranking Method | Group Decision Making | |
| [20] | * | |||||
| [21] | * | * | * | |||
| [23] | * | * | * | |||
| [25] | * | * | * | * | * | * |
| [30] | * | * | * | * | ||
| [32] | * | * | * | |||
| [33] | * | * | * | |||
| [36] | * | * | * | |||
| [38] | * | * | * | |||
| [43] | * | * | * | * | * | |
| This paper | * | * | * | * | * | * |
| Segments | Criteria | Definition |
|---|---|---|
| Economic | C1 | Price |
| C2 | Quality | |
| C3 | Delivery on time | |
| C4 | Contributions | |
| C5 | Management | |
| C6 | Reliability | |
| Social | C7 | Credibility |
| C8 | Safety | |
| C9 | Information revelation | |
| C10 | Employee benefits and rights | |
| C11 | Security acts | |
| C12 | Education | |
| C13 | Policies | |
| Environmental | C14 | Environmental suitability |
| C15 | Management systems of environment | |
| C16 | Pollution control | |
| C17 | Consider the requirements of ISO |
| Linguistic Terms | IVIF Values |
|---|---|
| Absolutely low (AL) | ([0.1,0.25],[0.65,0.75]) |
| Very low (VL) | ([0.15,0.30],[0.60,0.70]) |
| Low (L) | ([0.20,0.35],[0.55,0.65]) |
| Medium low (ML) | ([0.25,0.40],[0.50,0.60]) |
| Equal (E) | ([0.45,0.55],[0.30,0.45]) |
| Medium high (MH) | ([0.50,0.60],[0.25,0.40]) |
| High (H) | ([0.55,0.65],[0.20,0.35]) |
| Very high (VH) | ([0.60,0.70],[0.15,0.30]) |
| Absolutely high (AH) | ([0.65,0.75],[0.10,0.25]) |
| Criteria | DMs | Alternatives | |||
|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | ||
| C1 | DM1 | E | MH | VH | AH |
| DM2 | AH | E | AH | MH | |
| DM3 | MH | ML | VH | E | |
| C2 | DM1 | MH | MH | ML | MH |
| DM2 | VH | VH | AH | H | |
| DM3 | MH | MH | ML | ML | |
| C3 | DM1 | ML | E | MH | E |
| DM2 | MH | VH | MH | H | |
| DM3 | MH | AH | MH | MH | |
| C4 | DM1 | E | MH | MH | MH |
| DM2 | AH | MH | AH | MH | |
| DM3 | VH | MH | MH | H | |
| C5 | DM1 | MH | VH | MH | VH |
| DM2 | VH | AH | VH | AH | |
| DM3 | AH | VH | MH | MH | |
| C6 | DM1 | MH | ML | MH | ML |
| DM2 | E | AH | ML | E | |
| DM3 | ML | ML | H | ML | |
| C7 | DM1 | MH | MH | MH | VH |
| DM2 | VH | MH | E | AH | |
| DM3 | MH | MH | MH | VH | |
| C8 | DM1 | E | MH | VH | MH |
| DM2 | VH | AH | VH | AH | |
| DM3 | AH | MH | VH | MH | |
| C9 | DM1 | MH | MH | VH | MH |
| DM2 | MH | VH | AH | MH | |
| DM3 | MH | MH | VH | MH | |
| C10 | DM1 | VH | MH | ML | MH |
| DM2 | AH | ML | AH | AH | |
| DM3 | VH | H | ML | MH | |
| C11 | DM1 | ML | L | E | MH |
| DM2 | AH | MH | AH | VH | |
| DM3 | ML | MH | MH | MH | |
| C12 | DM1 | MH | MH | MH | MH |
| DM2 | MH | H | VH | ML | |
| DM3 | MH | VH | MH | H | |
| C13 | DM1 | MH | AH | ML | MH |
| DM2 | AH | E | MH | E | |
| DM3 | MH | VH | MH | MH | |
| C14 | DM1 | MH | AH | E | VH |
| DM2 | VH | VH | AH | VH | |
| DM3 | MH | H | VH | VH | |
| C15 | DM1 | MH | E | MH | VH |
| DM2 | ML | MH | VH | AH | |
| DM3 | H | AH | AH | VH | |
| C16 | DM1 | MH | H | MH | ML |
| DM2 | E | E | E | AH | |
| DM3 | MH | MH | E | H | |
| C17 | DM1 | VH | MH | MH | MH |
| DM2 | VH | H | VH | MH | |
| DM3 | VH | MH | MH | MH | |
| DMs | We | |
|---|---|---|
| DM1 | 0.630 | 0.337 |
| DM2 | 0.617 | 0.330 |
| DM3 | 0.623 | 0.333 |
| DMs | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DM1 | 0.429 | 0.464 | 0.471 | 0.467 | 0.436 | 0.464 | 0.450 | 0.453 | 0.450 | 0.450 | 0.462 | 0.464 | 0.444 | 0.429 | 0.453 | 0.458 | 0.450 |
| DM2 | 0.418 | 0.405 | 0.444 | 0.414 | 0.386 | 0.446 | 0.429 | 0.386 | 0.425 | 0.389 | 0.400 | 0.444 | 0.446 | 0.397 | 0.425 | 0.450 | 0.430 |
| DM3 | 0.453 | 0.464 | 0.439 | 0.444 | 0.425 | 0.458 | 0.450 | 0.425 | 0.450 | 0.444 | 0.464 | 0.444 | 0.450 | 0.430 | 0.394 | 0.462 | 0.450 |
| DMs | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DM1 | 0.046 | 0.050 | 0.051 | 0.050 | 0.047 | 0.050 | 0.048 | 0.049 | 0.048 | 0.048 | 0.050 | 0.050 | 0.048 | 0.046 | 0.049 | 0.049 | 0.048 |
| DM2 | 0.042 | 0.041 | 0.045 | 0.042 | 0.039 | 0.045 | 0.043 | 0.039 | 0.043 | 0.039 | 0.041 | 0.045 | 0.045 | 0.040 | 0.043 | 0.046 | 0.044 |
| DM3 | 0.048 | 0.049 | 0.046 | 0.047 | 0.045 | 0.048 | 0.048 | 0.045 | 0.048 | 0.047 | 0.049 | 0.047 | 0.048 | 0.045 | 0.042 | 0.049 | 0.048 |
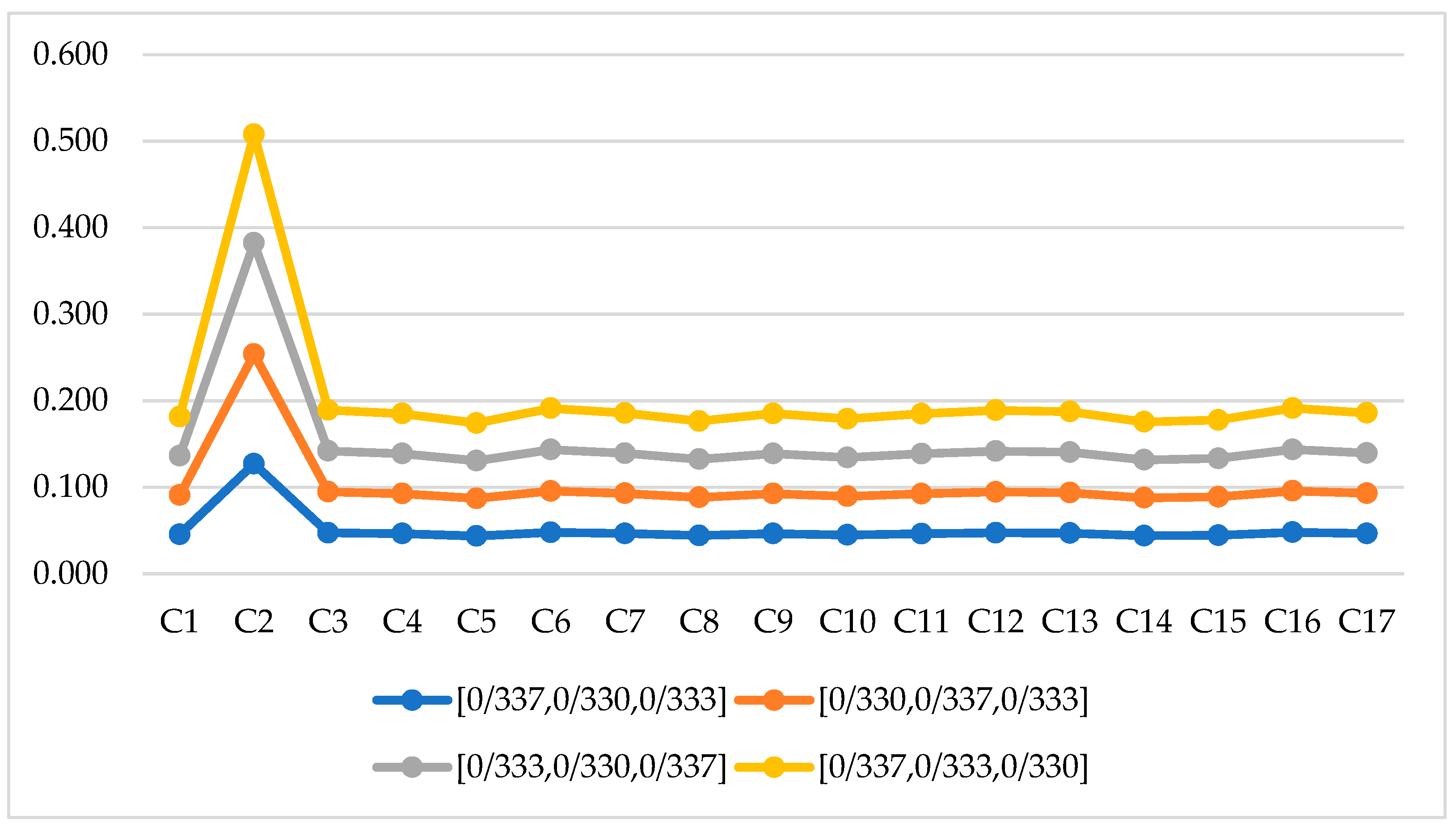
| Criteria | Weights |
|---|---|
| 0.045 | |
| 0.127 | |
| 0.047 | |
| 0.046 | |
| 0.044 | |
| 0.048 | |
| 0.046 | |
| 0.044 | |
| 0.046 | |
| 0.045 | |
| 0.046 | |
| 0.047 | |
| 0.047 | |
| 0.044 | |
| 0.044 | |
| 0.048 | |
| 0.046 |
| Alternatives | Final Score Values | |||
|---|---|---|---|---|
| ([0.379,0.391], [0.462,0.455]) | ([0.047,0.047], [0.127,0.127]) | ([0.032,0.030], [1.000,0.991]) | 0.030 | |
| ([0.369,0.381], [0.458,0.458]) | ([0.046,0.046], [0.127,0.127]) | ([0.010,0.010], [0.987,1.000]) | 0.010 | |
| ([0.443,0.460], [0.406,0.399]) | ([0.127,0.127], [0.048,0.048]) | ([0.198,0.192], [0.828,0.824]) | 0.191 | |
| ([0.465,0.492], [0.375,0.370]) | ([0.096,0.112], [0.046,0.046]) | ([0.266,0.279], [0.749,0.752]) | 0.266 |
| ([0.369,0.381], [0.375,0.370]) | ([0.465,0.492], [0.462,0.458]) | ([0.046,0.046], [0.046,0.046]) | ([0.127,0.127], [0.127,0.127]) |
| Alternatives | |||||
|---|---|---|---|---|---|
| ([0.588,0.592], [0.226,0.363]) | ([2.222,2.237], [0.855,1.374]) | ([0.791,0.791], [0.791,0.791]) | ([0.209,0.209], [0.209,0.209]) | ([0.557,0.561], [0.214,0.344]) | |
| ([0.490,0.590], [0.229,0.366]) | ([1.852,2.228], [0.865,1.384]) | ([0.791,0.791], [0.791,0.791]) | ([0.209,0.209], [0.209,0.209]) | ([0.464,0.559], [0.217,0.347]) | |
| ([0.483,0.586], [0.242,0.375]) | ([1.824,2.215], [0.915,1.419]) | ([0.791,0.791], [0.791,0.791]) | ([0.209,0.209], [0.209,0.209]) | ([0.457,0.555], [0.229,0.356]) | |
| ([0.484,0.584], [0.235,0.371]) | ([1.824,2.209], [0.889,1.402]) | ([0.791,0.791], [0.791,0.791]) | ([0.209,0.209], [0.209,0.209]) | ([0.458,0.554], [0.223,0.351]) |
| Alternatives | Final Score Values | Final Ranking Results |
|---|---|---|
| 0.340 | 3 | |
| 0.311 | 4 | |
| 0.397 | 2 | |
| 0.436 | 1 |
| Alternatives | IVIF-VIKOR [62] | IVIF-VIKOR Ranking | IVIF-TOPSIS [63] | IVIF-TOPSIS Ranking | IVIF-Hybrid Proposed Model | Proposed Model Ranking |
|---|---|---|---|---|---|---|
| 0.052 | 3 | 0.522 | 3 | 0.340 | 3 | |
| 0.006 | 4 | 0.496 | 4 | 0.311 | 4 | |
| 0.359 | 2 | 0.524 | 2 | 0.397 | 2 | |
| 0.461 | 1 | 0.653 | 1 | 0.436 | 1 |
| Ranking Results | ||
|---|---|---|
| 0.100 | 0.900 | |
| 0.200 | 0.800 | |
| 0.300 | 0.700 | |
| 0.400 | 0.600 | |
| 0.500 | 0.500 | |
| 0.600 | 0.400 | |
| 0.700 | 0.300 | |
| 0.800 | 0.200 | |
| 0.900 | 0.100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salimian, S.; Mousavi, S.M.; Antucheviciene, J. An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices. Sustainability 2022, 14, 3795. https://doi.org/10.3390/su14073795
Salimian S, Mousavi SM, Antucheviciene J. An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices. Sustainability. 2022; 14(7):3795. https://doi.org/10.3390/su14073795
Chicago/Turabian StyleSalimian, Sina, Seyed Meysam Mousavi, and Jurgita Antucheviciene. 2022. "An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices" Sustainability 14, no. 7: 3795. https://doi.org/10.3390/su14073795
APA StyleSalimian, S., Mousavi, S. M., & Antucheviciene, J. (2022). An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices. Sustainability, 14(7), 3795. https://doi.org/10.3390/su14073795









