Ranking Decision Making for Eco-Efficiency Using Operational, Energy, and Environmental Efficiency

Abstract

The objective of this paper is to propose a method for evaluating the eco-efficiency of business organizations. In order to adequately capture the inherent properties of eco-efficiency, we present a decision support model that can evaluate an organization based on ranking the derived efficiencies at the operational, energy, and environmental dimensions and taking these factors into account comprehensively. The proposed model was designed in the form of a combination of data envelopment analysis (DEA) and TOPSIS, and we tried to make use of the advantages of each method and offset the disadvantages. Specifically, the operational, energy, and environmental efficiencies were derived through DEA. Then, each efficiency was set as the criteria, and the eco-efficiency ranking was determined through TOPSIS. This study shows that it has the advantage of not requiring preference information from the decision maker and, at the same time, can improve the discriminatory power between efficient and inefficient decision-making units. To apply the proposed model, the analysis results are presented through an illustrative example, and the theoretical significance is described. It is also explained that the proposed model can provide a more realistic and convincing evaluation.

1. Introduction

Over the past 30 years, the discussion of efficiency measures related to the environment has continued. In the 1990s, Schalteger and Sturm [1] introduced and defined eco-efficiency as “business connections to sustainable development.” Since then, scholars have paid attention to measuring and evaluating eco-efficiency. Specifically, measurement and evaluation models have been developed by operations research scholars [2,3,4,5,6,7], and the developed models have been applied to various fields [8,9,10,11,12,13,14,15]. The concept of eco-efficiency is analyzed at the national level, used in the evaluation of industries or regions within a country and used to measure and evaluate efficiency at the organizational level. Regardless of the level of evaluation, obviously, the main concern of measuring eco-efficiency is to improve economic performance by simultaneously reducing environmental impact and energy use. In addition, the definition of eco-efficiency differs somewhat among the scholars who present this concept, but fundamentally, they shed light on the common core of “producing appropriate pollutants and energy efficiently”. There has been growing interest in eco-efficiency in many business sectors, and it is believed that eco-efficiency evaluation can supplement the traditional evaluation system that is obsessed with technological and economic evaluation and support the decision-making process [16].

Data Envelopment Analysis (DEA) has been widely used since it was first proposed by Charnes et al. [17] as an effective tool to evaluate the productivity and efficiency of organizations. DEA has the advantage of considering many inputs and outputs. In addition, DEA does not require a parameter specification of a particular function, nor does it require a predetermination of the weights of each input and output. For these reasons, since the original model was carried out, many researchers have contributed to the refinement and extension of DEA for their various fields of interest.

Traditional DEA models allow the users to evaluate the economic performance of individual decision-making units (DMUs) depending on a profitability perspective. However, addressing the environmental performance and energy utilization has become one of the important issues for analyzing the performance of organizations. Therefore, extended DEA methods that take into account those issues are required. For the past 20 years, DEA has been widely used as a methodology for measuring efficiency while considering environmental factors (e.g., [2,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]) and energy factors (e.g., [20,29,32,35,36,37,38,39]). Although somewhat different, scholars have presented measures for environmental and energy efficiency while taking into account the above two factors. In DEA studies, environmental efficiency has been measured by incorporating environmentally detrimental factors, which can be considered undesirable outputs. Theoretically, DEA methods taking into account undesirable outputs were developed by Färe and Grosskopf [40], Korhonen and Luptacik [2], Seiford and Zhu [41], and Liu et al. [42]. Since Färe et al. [43] studied energy efficiency, numerous studies have proposed the method for evaluating energy efficiency by employing DEA. As such, efforts have been made to evaluate the organization’s performance through environmental efficiency and energy efficiency, but they have not reached the point of deriving eco-efficiency by integrating these measures. Recalling the meaning of eco-efficiency defined above, it would be the most reasonable approach to consider both environmental efficiency and energy efficiency as well as operational efficiency, which is fundamental for business organizations.

Nevertheless, the reason why there are not many studies trying to integrate these three efficiencies is that the preference information indicating the relative importance of each is not known. In other words, when these three efficiencies are integrated through DEA, decision makers are required to judge their relative importance in relation to operation, the environment, and energy. As in Lee and Park [44], demanding relative importance from decision makers can be an advantage in that it can increase the degree of freedom, but on the contrary, it can be pointed out as a disadvantage in that it can burden decision makers. In addition, it may be difficult to use weights because the distribution of efficiency scores is not homogeneous due to the characteristics of the variables used in each efficiency calculation.

How can an eco-efficiency evaluation be performed that reasonably synthesizes operational, energy, and environmental efficiency? In this context, can the evaluation of eco-efficiency be sound mathematically and make a sufficiently discriminatory evaluation? While answering the above questions, we would like to suggest a method that practitioners can easily understand and apply. Overall, this study proposes a model for evaluating organizational efficiency in terms of operation, environment, and energy and proposes a method of assessing eco-efficiency without information on the preference of decision makers. The relationship between each efficiency derived through DEA and overall efficiency will be identified, and a ranking method for eco-efficiency by combining with TOPSIS, a representative Multi-Criteria Decision Making (MCDM) technique, will be presented. The reasons for using TOPSIS in this study can be summarized in three ways. First, TOPSIS is intuitive and simple [45]. Second, it does not require the decision makers’ preference information [46]. Third, the performance measures of all alternatives to the attributes can be easily visualized. Finally, it allows for a compromise between criteria, where a poor outcome of one criterion may be overruled by a good outcome for another criterion [47]. These characteristics show that TOPSIS can be one of the most suitable methods for deriving a ranking without decision makers’ preference information in consideration of the fragmentation of multiple efficiency scores derived through DEA. It should be noted that this does not mean that TOPSIS is the only technique that should be used in combination with DEA, and other ranking-based MCDM techniques that share the above advantages can also be utilized.

The rest of the paper is organized as follows. Section 2 describes the models for deriving the overall efficiency and partial efficiency and examines the relationship between the efficiency measures. In addition, a description of the application of the methodology is presented along with a theoretical review. Section 3 explains how to derive eco-efficiency rankings by synthesizing the operational, energy and environmental efficiencies through the example of an agricultural production system. Section 4 discusses the theoretical and practical implications of the study. Section 5 concludes the study by discussing the limitations of the study and seeking paths for future research.

2. Methods

2.1. Overall Efficiency

In DEA terminology, the organization under evaluation is called a decision-making unit (DMU). The efficiency of a DMU is expressed as a ratio of the weighted sum of its outputs to the weighted sum of its inputs. Thus, it is necessary to classify all variables according to their functional uses in order to define the overall efficiency. In this study, we decompose the input variables into three types: operational inputs, energy inputs, and environmental inputs. The output variables are also divided into two types: (general) outputs and environmental outputs. Given these types of variables, we can define the operational, energy, and environmental efficiencies as follows:

$${\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}/}{\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}$$

(1)

$${\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}/{\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}}$$

(2)

$${\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}/{\displaystyle \sum _{h=1}^q{\mu }_h{y}_{ho}^{-}}}$$

(3)

Generally, the outputs have the characteristic of being better when having larger values. For this reason, these outputs are also called desirable outputs. In this study, we set the (general) outputs $y_r^{+}$ as desirable outputs. We define the input variables $x_i$ as operational inputs, typically used in the production process for ensuring greater efficiency as they are reduced (e.g., labor, machinery, and resources). Now, the operational efficiency of DMU o is expressed as in Equation (1), where $v_i$ and $u_r$ are unknown non-negative weights for the operational inputs and outputs, respectively. The energy efficiency is measured by separating the energy-related components from the general production resources. Thus, energy inputs $z_k$ are considered input variables, and accordingly, the energy efficiency of DMU o can be calculated by Equation (2), where $w_k$ is the unknown non-negative weights for the energy inputs. Equation (3) expresses the environmental efficiency. Simply, environmental efficiency explains how to efficiently produce the outputs relative to the environmental inputs, and environmental efficiency is calculated as the ratio of the outputs to the environmental inputs. However, in this study, we define $y_h^{-}$ as a set of variables consisting of environmental inputs and environmental outputs, because the environmental outputs are also treated as behaving inputs in a fractional form for efficiency calculation. This idea was also proposed and utilized by Korhonen and Luptacik [2], Zhang et al. [29], Lee and Park [44], and Cecchini et al. [48].

The conventional DEA method is followed the assumption that all input variables affected all the output variables. This model implicitly assumes that all DMUs operate a constant returns to scale (CRS) transformation of the inputs into outputs. We adopt the CRS assumption in this study. When there are total of m + p + q inputs and s outputs for each DMU j (j = 1,2,…,n), the overall efficiency of a particular DMU o can be formulated as in the following fractional programming model:

$$\begin{array}{l}\max \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}}}{{\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}+{\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}+{\displaystyle \sum _{h=1}^q{\mu }_h{y}_{ho}^{-}}}\\ \mathrm{s}.\mathrm{t}.\\ \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}^{+}}}{{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}+{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}+{\displaystyle \sum _{h=1}^q{\mu }_h{y}_{hj}^{-}}}}}\le 1\\ v_i\ge 0\\ w_k\ge 0\\ {\mu }_h\ge 0\\ u_r\ge 0\end{array}$$

(4)

Additionally, Equation (4) can be transformed into a linear model by using the Charnes–Cooper transformation [49]:

$$\begin{array}{l}\max \theta ={\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}^{+}}-{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}-{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}-{\displaystyle \sum _{h=1}^q{\mu }_h{y}_{rj}^{-}}}}\le 0\\ {\displaystyle \sum _{i=1}^m{v}_i{x}_{io}+{\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}+{\displaystyle \sum _{h=1}^q{\mu }_h{y}_{ro}^{-}}}}=1\\ v_i\ge 0\\ w_k\ge 0\\ {\mu }_h\ge 0\\ u_r\ge 0\end{array}$$

(5)

2.2. Partial Efficiency

In Equation (5), the optimal objective function value becomes the efficiency score of DMU o. If the efficiency score equals one, DMU o is regarded as efficient and is also on the efficient frontier; otherwise, it is inefficient. Equations (4) and (5) allow the DMU o to assign the most favorable weights in calculating the ratio of the aggregated output to the aggregated input. However, the weighting scheme of the traditional DEA model is not applicable for some cases, since one or very few variables may be heavily weighted, and the effect of the other variables may be completely ignored. In addition, not all inputs in the production process necessarily affect all of the output factors. Namely, some inputs may not influence certain outputs in many settings measured for efficiency. Therefore, it is necessary to convert the aggregated form of the input-output setting into a form that can measure the partial efficiency. In addition, we can point out the difficulties that arise when evaluating performance across multiple dimensions through a measure of efficiency in DEA. In this case, for a detailed analysis of the efficiency of the DMUs, it was necessary to determine the efficiency of each individual dimension. The partial efficiency measures provide deeper insight into how an organization operates and can have significant business implications [50]. This is also consistent with the DEA’s general purpose of finding areas where certain inefficiencies are occurring and supporting performance improvement actions.

We propose a model that disaggregates efficiency by considering the nature of the variables. From Equations (1–3), the partial efficiency models for measuring the operational, energy, and environmental efficiencies can be formulated as follows:

$$\begin{array}{l}\max {\theta }^1={\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}^{+}}-{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}\le 0\\ {\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}=1\\ v_i\ge 0\\ u_r\ge 0\end{array}$$

(6)

If the optimal value of the objective function in Equation (6) equals one, then the specific DMU o is on the operationally efficient frontier:

$$\begin{array}{l}\max {\theta }^2={\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}^{+}}-{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}\le 0\\ {\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}=1\\ w_k\ge 0\\ u_r\ge 0\end{array}$$

(7)

If the optimal value of the objective function in Equation (7) equals one, then the specific DMU o is on the energy efficient frontier:

$$\begin{array}{l}\max {\theta }^3={\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}^{+}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}^{+}}-{\displaystyle \sum _{h=1}^q{\mu }_h{y}_{hj}^{-}}\le 0\\ {\displaystyle \sum _{h=1}^q{\mu }_h{y}_{ho}^{-}}=1\\ {\mu }_h\ge 0\\ u_r\ge 0\end{array}$$

(8)

If the optimal value of the objective function in Equation (8) equals one, then the specific DMU o is on the environmentally efficient frontier.

Definition 1.

A DMU o is said to be operationally efficient if its partial efficiency score${\theta }^1=1$.

Definition 2.

A DMU o is said to be energy efficient if its partial efficiency score${\theta }^2=1$.

Definition 3.

A DMU o is said to be environmentally efficient if its partial efficiency score${\theta }^3=1$.

Theorem 1.

If a DMU is partially efficient, it is efficient overall.

Obviously, the overall efficiency score is larger than or equal to the maximum value of the three partial efficiency scores. As shown in Equation (5), the overall efficiency evaluation model includes all the variables used in each of the partial efficiency evaluations, and thus it has more choices for having the most favorable weight.

Theorem 2.

For any DMU j,${\theta }_j^{*}\ge \max \{{\theta }_j^1,{\theta }_j^2,{\theta }_j^3\}$.

Proof. 

(1) When assuming that $\max \{{\theta }_j^1,{\theta }_j^2,{\theta }_j^3\}={\theta }_j^1<1$, the first constraint in Equation (6) is a more restricted version than that in Equation (5). Thus, Equation (5) permits multipliers which identify other input variables. The more variables considered, the greater the chance some inefficient DMUs will dominate the added dimension. (2) When assuming that $\max \{{\theta }_j^1,{\theta }_j^2,{\theta }_j^3\}={\theta }_j^1=1$, by Theorem 1, ${\theta }_j^{*}=1$. By combining (1) and (2), the theorem is proven. □

Furthermore, DMUs that were not efficient through partial efficiency evaluation could be classified as efficient units in overall terms. From the above discussion, we can conclude that the overall efficiency model overestimates the efficiency of DMUs, although it contains variables related to operation, energy, and environment.

2.3. No Preference Information

The original DEA model minimizes decision maker intervention in that it measures the relative efficiency without including judgment on the decision maker’s preferences. Various DEA techniques that can utilize a decision maker’s preference information have been proposed. Examples include Golany’s method of setting targets [51], Athanassopoulis’s method of using weight restrictions [52], and Charnes et al.’s method of using the cone ratio [53]. However, all of the above-mentioned methods require the decision maker’s preference information, and in most cases, it is subjective and can be difficult to obtain. In addition, these methods focus on capturing preference information for the variables used in DEA. In such a situation, if the number of variables increases, it becomes difficult to reflect the preference information, which increases the burden on decision makers. Furthermore, if preference information for each variable is considered in the form of weights, there is a possibility that the merits of DEA, which is based on optimistic self-evaluation, may be diluted. Therefore, it can be said that a method that can reflect the common characteristics of variables while maintaining the advantage of DEA that does not utilize the decision maker’s preference information is required.

In this study, using the concept of partial efficiency presented in the above subsection, we derive efficiency measures that convey the common characteristics of the inputs and outputs and propose a method to evaluate the overall performance based on this. If the operational, energy, and environmental efficiencies, which are the main interest of this study, are defined as partial efficiency, and each efficiency score is derived, the distribution of each efficiency score will not be homogeneous. In a situation where there are multiple partial efficiency scores, how to make a comprehensive judgment without the decision maker’s preference information becomes a critical problem. MCDM techniques can help solve this problem. In this study, we propose a method for evaluating performance based on ranking by synthesizing multiple partial efficiencies using TOPSIS, one of the most popular MCDM techniques.

2.4. TOPSIS

TOPSIS (a technique for order preference by similarity to an ideal solution) is one of the major classical MCDM methods that was originally developed by Hwang and Yoon in 1981 [54]. The mechanism of this approach is based on the relative distance measure by calculating the distance from each alternative to the ideal solution (PIS) and negative ideal solution (NIS), where n is the number of criteria in the decision problem. With TOPSIS, the best alternative is determined with the greatest relative closeness to the ideal. In this study, the partial efficiency scores are recognized as criteria, and the DMUs are regarded as the alternatives to determine the ranking order of all DMUs. The procedure of TOPSIS is presented below in five steps. In Step 1, the alternative data are normalized via Equation (9), where ${\theta }_{ij}$ is the appraisal matrix R of alternative (DMU) i under the appraisal criterion (partial efficiency) j and $r_{ij}$ is the normalized appraisal matrix R:

$$r_{ij}={\theta }_{ij}/\sqrt{{\displaystyle \sum _{j=1}^n{\theta }_{ij}^2}},i=1,2,\dots ,m$$

(9)

In Step 2, these normalized values $r_{ij}$ are weighted via Equation (10), where $v_{ij}$ is the weighted normalized values of DMU i under partial efficiency j:

$$v_{ij}=w_i{r}_{ij},i=1,2,\dots ,m;j=1,2,\dots ,n$$

(10)

In Step 3, the PIS and NIS are determined via Equations (11) and (12), respectively:

$$A^{+}=\{v_1^{+},\dots ,v_n^{+}\}=\{({\max }_i{v}_{ij})|i=1,2,\dots ,m\}$$

(11)

$$A^{-}=\{v_1^{-},\dots ,v_n^{-}\}=\{({\min }_i{v}_{ij})|i=1,2,\dots ,m\}$$

(12)

The original TOPSIS method can also obtain the PIS and NIS for the lager-the-better criteria as well as the smaller-the-better criteria. However, since the criteria used in this study are efficiency scores, the lager-the-better criteria applies, and Step 3 is more simplified. Step 4 calculates the separation of each alternative from the PIS and NIS for each partial efficiency using the n-dimensional Euclidean distance:

$$S_i^{+}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_{ij}-v_j^{+})}^2}},i=1,2,\dots ,m$$

(13)

$$S_i^{-}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_{ij}-v_j^{-})}^2}},i=1,2,\dots ,m$$

(14)

Lastly, Step 5 calculates the relative closeness to the ideal solution ($C_i^{*}$):

$$C_i^{*}=\frac{S_i^{-}}{S_i^{+}+S_i^{-}},i=1,2,\dots ,m$$

(15)

This indicates that the smaller the difference between the partial efficiency and ideal values, the better the performance the DMU will have.

3. Illustrative Example

In this section, we describe how we used our approach to evaluate the operational, energy, and environmental efficiencies. The LCI data of the agricultural production systems for 94 soybean farms were first presented by Mohammadi et al. [55]. The data presented herein were collected for a combinational use of LCI and DEA in the work of Mohammadi et al. [55]. In addition, Lee and Park [44] modified this dataset to be suitable for DEA. The reader is referred to Mohammadi et al. [55] for the original data source.

It is very important to select the input and output variables prior to performing DEA (

Table 1. Input and output variables.

Category	Variables
Operational Inputs	Labor, Machinery
Energy Inputs	Diesel, Electricity
Environmental Inputs	Herbicides, Insecticides, Urea, FYM, P2O5
Environmental Output	Straw
General Output	Soybeans

). Correlation analysis was performed to validate the isotonic relationship between the input and output variables, and three inputs were eliminated that were negative to the output variable (correlation coefficients: −0.04 (water), −0.15 (seed), and −0.03 (CH4)). All remaining inputs were positively correlated with the output variable; that is, an increase in any input would not result in a decrease in the output [56,57,58]. In addition, K2O, an environmental input, was consumed by only 12 out of 94 farms, so it was also removed. Therefore, in this illustration, 94 soybean farms were defined as DMUs, and each DMU had two operational inputs, two energy inputs, five environmental inputs, one environmental output, and one (general) output. The data are shown in

Table A1. Data.

DMU	Labor (h)	Machinery (h)	Diesel (L)	Electricity (kWh)	Herbicides (kg)	Insecticides (kg)	Urea (kg)	P2O5 (kg)	FYM (kg)	Soybean (kg)	Straw (kg)
1	169	16	70	0	4	1.5	110	46	0	3500	4312
2	142	15	65	0	3	0.5	55	23	2500	3000	3889
3	197	22	88	1953	2	1	96	69	2500	3000	3889
4	254	35	122	1286	3	2	110	46	7500	3600	4397
5	138	32	111	1432	2	2.5	78	23	2222	3000	3889
6	152	28	98	0	3	2	110	46	2000	3150	4016
7	148	28	109	703	3	3	110	46	563	4150	4862
8	213	27	109	1406	1	2	137	115	1250	3500	4312
9	159	18	76	0	0	2	76	46	0	2300	3296
10	137	28	96	0	3	3.5	76	46	0	2300	3296
11	272	26	105	0	3	2	103	115	750	3500	4312
12	185	31	126	1406	3	4.5	82	92	1500	3400	4227
13	228	35	119	781	3	5	82	92	7500	3000	3889
14	264	22	91	0	3	2	100	72	0	2315	3309
15	200	45	150	1758	0	1.5	92	0	16,667	3750	4524
16	289	32	115	2179	3	1.5	114	115	7500	3250	4100
17	282	35	130	1758	3	2.5	105	92	4500	3500	4312
18	209	24	83	1524	3	1	92	0	6000	2600	3550
19	268	33	119	2901	3	8	92	0	12,500	3000	3889
20	210	55	168	1538	0	1	64	46	10,000	35,007	4312
21	139	27	108	732	3	4.5	114	115	9375	3500	4312
22	179	23	109	1154	5	0.5	69	0	4000	4000	4735
23	200	40	131	820	3	3.5	114	115	1111	3115	3986
24	245	29	106	1172	3	1.5	87	46	3750	3500	4312
25	222	31	93	1289	3	8	0	0	11,000	4200	4904
26	263	54	175	2175	3	3.5	92	0	12,500	3100	3974
27	285	64	203	2175	3	2.5	92	0	25,000	3000	3889
28	124	17	69	0	3	0.5	78	23	0	3200	4058
29	215	15	88	3282	0	1	87	46	0	3500	4312
30	134	14	76	1406	0	1.5	69	0	0	2000	3043
31	137	17	64	1318	3	3	78	23	833	3300	4143
32	201	17	68	879	3	0.5	110	46	0	3600	4397
33	159	38	128	2051	3	2.5	110	46	7500	3500	4312
34	269	50	160	732	3	5.5	64	46	0	4200	4904
35	223	10	65	2813	3	4.5	64	46	1500	3000	3889
36	145	24	101	2075	0	3	64	46	0	2500	3466
37	176	29	108	1172	3	2	64	46	2083	3500	4312
38	183	29	100	1450	3	10.6	48	35	208	2800	3720
39	167	23	93	3076	3	2.5	50	69	0	3000	3889
40	238	26	95	879	3	2.5	64	46	0	3330	4168
41	290	34	117	3516	3	6	197	92	0	3500	4312
42	206	24	93	2051	3	5	128	92	3000	4000	4735
43	350	21	120	1538	4	5	159	92	3000	3400	4227
44	133	31	100	1154	3	6.5	96	69	0	3500	4312
45	169	25	92	1025	3	3.5	0	0	6250	4000	4735
46	157	34	108	820	3	3	110	46	3750	2800	3720
47	239	35	120	1641	3	3.6	156	46	15,000	4000	4735
48	170	21	89	855	3	1.5	115	0	0	3500	4312
49	220	50	146	1582	3	4	135	81	10,000	3500	4312
50	277	29	117	2813	1.25	4.5	110	46	0	3800	4566
51	186	48	165	1791	1.5	3	92	0	21,429	3700	4481
52	189	20	81	781	0	1.5	64	46	0	2666	3606
53	104	35	124	2110	3	3	83	23	12,000	2600	3550
54	170	19	75	1465	3	2	92	0	0	2700	3635
55	112	20	101	2110	2	3	92	0	0	3400	4227
56	144	25	106	1074	3.5	0.3	110	46	1500	3570	4371
57	179	15	86	1978	0	1.5	92	0	0	3000	3889
58	215	30	109	769	3	3	123	138	22,500	3500	4312
59	146	34	134	1846	3	2.5	87	46	15,000	3800	4566
60	162	40	147	2369	3	2.5	87	46	15,000	3500	4312
61	245	34	119	1410	3	3	92	0	10,000	3000	3889
62	196	9	61	513	3	2.5	32	23	417	2500	3466
63	187	19	79	1934	2	2.5	137	115	0	2800	3720
64	163	21	88	1465	3	3	115	0	2500	3570	4371
65	243	21	86	824	3	3	123	138	5000	3700	4481
66	196	22	103	2175	3	2.5	137	115	0	2800	3720
67	178	26	100	0	3.5	0.3	110	46	1500	3000	3889
68	214	33	132	1367	3.5	3	110	46	7500	3500	4312
69	169	27	92	1282	3.5	0.5	92	0	7500	3600	4397
70	208	28	104	1432	3	3	123	138	20,000	2800	3720
71	165	37	124	1758	3	2	77	0	15,000	3500	4312
72	261	32	124	2179	3	1.5	114	115	7500	2900	3804
73	283	38	138	1758	3	1.5	69	0	5000	3550	4354
74	167	37	136	1904	3	1	92	0	7500	2600	3550
75	211	31	122	1477	0	1	46	0	10,000	3400	4227
76	155	36	129	1030	3	2.5	69	0	10,000	3800	4566
77	154	30	96	1007	3	2	110	46	7500	3300	4143
78	176	28	119	2344	3	2.5	92	0	0	2600	3550
79	195	18	89	1846	3	6	119	69	10,000	3300	4143
80	144	21	93	1641	2	3	137	115	0	3900	4651
81	108	29	98	820	3.5	1.5	64	46	7500	3700	4481
82	279	27	116	916	4	4.5	160	115	15,000	3300	4143
83	309	12	55	820	1	1	128	92	0	3600	4397
84	95	12	66	0	3.5	2.5	87	46	10,000	3400	4227
85	141	25	105	0	2	1.5	174	92	0	3200	4058
86	152	27	103	0	0	2.5	91	115	12,500	3150	4016
87	127	19	82	0	3	4.5	114	115	9375	3050	3931
88	121	21	84	1172	3	2	46	0	10,000	3100	3974
89	213	6	47	1074	2	1.5	105	92	0	2000	3043
90	171	17	69	2344	3	1	92	0	0	2500	3466
91	192	18	87	328	3	1	64	46	18,667	3000	3889
92	217	6	48	1074	3	1.5	105	92	0	2000	3043
93	199	19	72	2110	3	2	64	46	0	3000	3889
94	211	16	58	1007	3	1.5	110	46	0	3200	4058

of Appendix A.

To verify the relationship between the number of variables and the number of DMUs used in this case, it is noted that the rule of thumb by Golany and Roll [57] and Cooper et al. [59] was satisfied, because the number of DMUs was over three times higher than the total number of input and output variables.

3.1. Overall Efficiency and Partial Efficiency Scores

The operational, energy, and environmental efficiency scores were derived through Equations (6)–(8), respectively, and the overall efficiency via Equation (5) was derived to compare the results. Through this result, it was possible to identify the flaws of utilizing the overall efficiency. First, the discriminant power was very low. Among the 94 DMUs, 57 were efficient. The parsimonious variable setting was particularly important. As more variables are included in a DEA model, the ability to distinguish between efficient and inefficient DMUs decreases, as more DMUs appear to be efficient due to increased dimensionality. In the overall efficiency evaluation model set up for comparison with the partial efficiencies we would utilize, all inputs were included, making the efficiency difficult to judge. Second, the overall efficiency model did not address the characteristics of the variables (whether an operational variable, an energy variable, or an environmental variable). Through this model, it was possible to figure out which variables were contributing to the efficiency score through multipliers, but since a large number of variables was included in the model, it was difficult to determine what role the common characteristics of the input variables played in deriving the efficiency.

The concept of partial efficiency, defined as the partitioning of input variables, leads to specific implications for the efficiency evaluation of DMUs. The partial efficiency model increased the discriminant power by reducing the number of efficient DMUs. This was a natural result because we reduced the number of variables in each model by decomposing the input variables into three groups. Through Equations (6–8), 12, 2, and 34 DMUs were derived as efficient DMUs in terms of operation, energy, and the environment, respectively. The distribution of efficiency scores gives an idea of how partial efficiencies can be used for a comprehensive assessment.

Table 2. Descriptive statistics of efficiency scores.

	Operational Efficiency	Energy Efficiency	Environmental Efficiency	Overall Efficiency
Mean	0.787	0.543	0.872	0.934
Median	0.795	0.529	0.891	1.000
S. D.	0.144	0.155	0.129	0.099
Range	0.491	0.760	0.465	0.344
Minimum	0.509	0.240	0.535	0.656
Maximum	1.000	1.000	1.000	1.000

shows that, overall, the environmental efficiency was higher than the operational and energy efficiencies. This phenomenon was due to the number of variables for calculating the efficiency scores; that is, a large number of environmental inputs made the environmental efficiency score higher. Thus, the overall efficiency highly depended on the environmental efficiency. The correlation coefficients presented in

Table 3. Spearman’s correlation coefficients.

	Energy Efficiency	Environmental Efficiency	Overall Efficiency
Operational Efficiency	0.666 (0.00) *	0.216 (0.03)	0.565 (0.00)
Energy Efficiency		0.350 (0.00)	0.628 (0.00)
Environmental Efficiency			0.722 (0.00)

* Values in parentheses indicate p-values.

are helpful in understanding this phenomenon. The values in parentheses shown in Table 3 indicate p-values.

It can be found that there was a significant difference in the dispersion as well as the locations of the efficiency scores. In particular, in the case of energy efficiency, it can be observed from Table 2 and Figure 1 that the degree of dispersion was significantly larger than those of the other efficiencies. Here, since the order of the DMUs was nominal, there was no need to give meaning to the pattern along the horizontal axis. If eco-efficiency is derived by simply integrating the three partial efficiencies with different distributions in this way, it is inevitably biased to a specific efficiency value. In this analysis, a high degree of bias for the environmental efficiency may have occurred.

3.2. Ranking Evaluation

Because it was impossible to show the calculation results of all 94 DMUs due to space limitations, only the efficiency scores, the indicators used in the final calculation of TOPSIS, and the derived rankings were reported. These results are presented in

Table 4. Efficiency scores and eco-efficiency ranks.

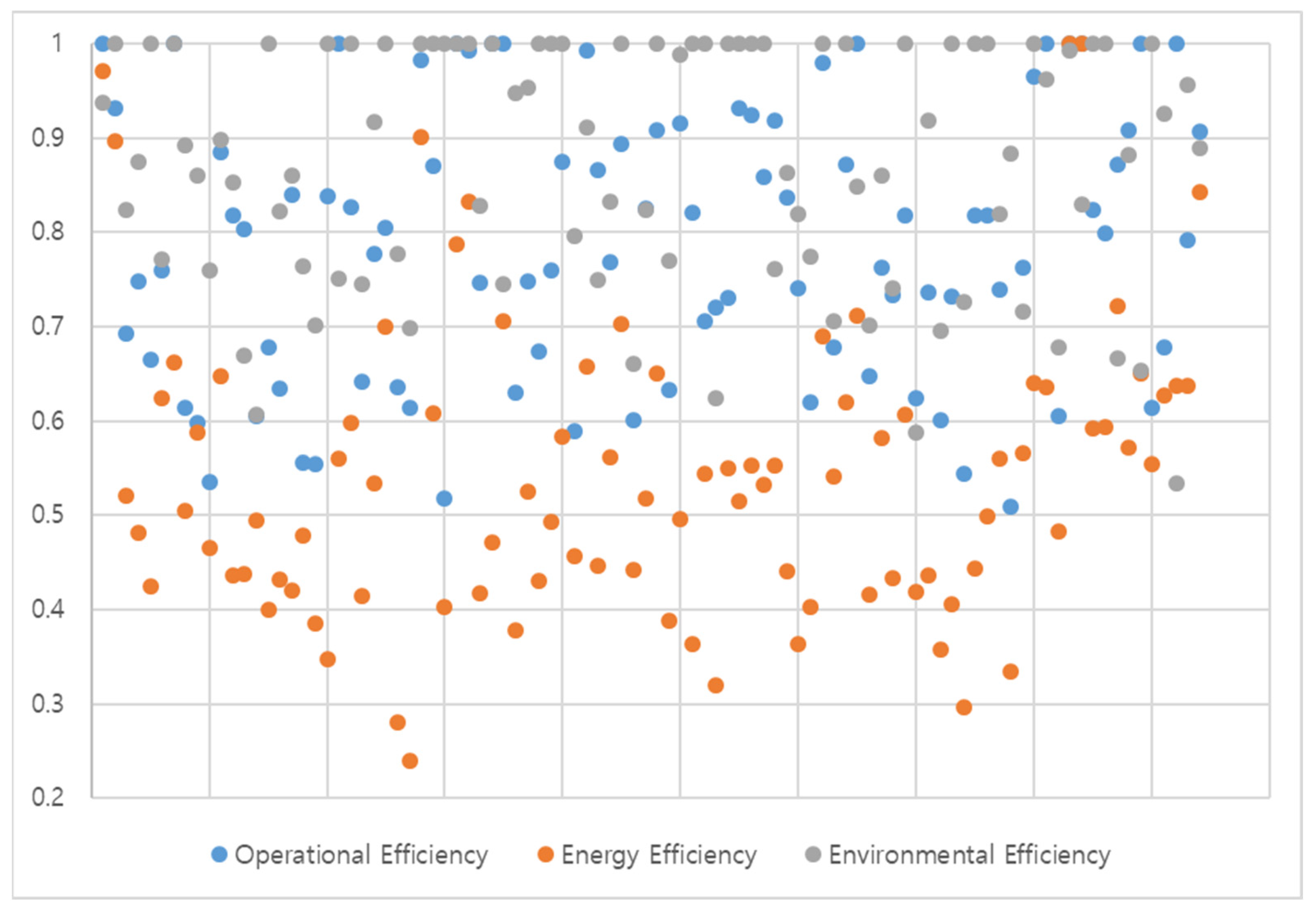
DMU	Operational Efficiency	Energy Efficiency	Environmental Efficiency	Overall Efficiency	S+	S−	C	Eco-Efficiency Rank
1	1.000	0.971	0.937	1.000	0.018	0.200	0.918	2
2	0.931	0.896	1.000	1.000	0.040	0.178	0.817	5
3	0.693	0.521	0.823	0.836	0.154	0.067	0.302	69
4	0.748	0.481	0.874	0.888	0.154	0.075	0.328	64
5	0.665	0.425	1.000	1.000	0.166	0.090	0.351	56
6	0.759	0.624	0.772	1.000	0.133	0.082	0.380	50
7	1.000	0.662	1.000	1.000	0.103	0.145	0.585	11
8	0.613	0.505	0.892	0.970	0.160	0.071	0.309	68
9	0.598	0.587	0.861	1.000	0.149	0.076	0.338	61
10	0.535	0.465	0.760	1.000	0.177	0.045	0.202	80
11	0.885	0.647	0.897	1.000	0.112	0.112	0.500	21
12	0.818	0.436	0.852	0.895	0.157	0.078	0.330	62
13	0.804	0.437	0.669	0.903	0.168	0.059	0.259	73
14	0.606	0.494	0.607	0.783	0.177	0.038	0.177	86
15	0.678	0.400	1.000	1.000	0.169	0.089	0.347	57
16	0.635	0.432	0.823	0.823	0.172	0.055	0.242	75
17	0.840	0.420	0.860	0.872	0.158	0.081	0.339	60
18	0.555	0.479	0.764	0.923	0.174	0.047	0.214	79
19	0.555	0.385	0.701	0.704	0.189	0.030	0.136	90
20	0.838	0.347	1.000	1.000	0.165	0.102	0.381	49
21	1.000	0.560	0.751	1.000	0.135	0.111	0.451	37
22	0.827	0.598	1.000	1.000	0.124	0.114	0.478	28
23	0.642	0.414	0.745	0.745	0.177	0.043	0.194	83
24	0.777	0.534	0.917	0.983	0.142	0.089	0.386	47
25	0.805	0.700	1.000	1.000	0.104	0.126	0.548	17
26	0.635	0.281	0.777	0.797	0.191	0.042	0.179	85
27	0.614	0.240	0.699	0.780	0.199	0.028	0.124	94
28	0.982	0.900	1.000	1.000	0.035	0.185	0.841	4
29	0.870	0.608	1.000	1.000	0.119	0.120	0.500	20
30	0.517	0.402	1.000	1.000	0.180	0.086	0.323	66
31	1.000	0.788	1.000	1.000	0.069	0.163	0.702	8
32	0.992	0.832	1.000	1.000	0.056	0.171	0.753	6
33	0.747	0.418	0.828	0.841	0.165	0.064	0.279	71
34	1.000	0.470	1.000	1.000	0.142	0.130	0.478	27
35	1.000	0.705	0.745	1.000	0.106	0.129	0.549	16
36	0.629	0.378	0.948	1.000	0.175	0.075	0.301	70
37	0.747	0.526	0.953	0.964	0.144	0.091	0.388	46
38	0.674	0.430	1.000	1.000	0.165	0.090	0.354	55
39	0.760	0.493	1.000	1.000	0.149	0.099	0.400	44
40	0.875	0.583	1.000	1.000	0.124	0.118	0.487	24
41	0.589	0.457	0.796	0.834	0.173	0.051	0.226	78
42	0.993	0.657	0.911	1.000	0.106	0.132	0.556	15
43	0.866	0.446	0.750	0.881	0.158	0.076	0.323	65
44	0.768	0.562	0.832	1.000	0.140	0.079	0.361	53
45	0.894	0.702	1.000	1.000	0.096	0.135	0.583	12
46	0.600	0.442	0.661	0.666	0.181	0.033	0.156	89
47	0.825	0.518	0.824	0.901	0.145	0.081	0.359	54
48	0.907	0.650	1.000	1.000	0.108	0.129	0.545	18
49	0.634	0.389	0.770	0.770	0.180	0.044	0.196	82
50	0.915	0.496	0.988	1.000	0.139	0.115	0.452	35
51	0.821	0.364	1.000	1.000	0.164	0.100	0.379	51
52	0.706	0.544	1.000	1.000	0.144	0.099	0.408	41
53	0.721	0.320	0.623	0.830	0.189	0.037	0.162	88
54	0.731	0.550	1.000	1.000	0.141	0.101	0.418	39
55	0.932	0.514	1.000	1.000	0.135	0.121	0.471	31
56	0.924	0.552	1.000	1.000	0.128	0.122	0.487	23
57	0.858	0.533	1.000	1.000	0.135	0.112	0.452	34
58	0.918	0.553	0.761	0.920	0.138	0.094	0.406	42
59	0.837	0.440	0.862	0.932	0.155	0.082	0.346	58
60	0.741	0.364	0.819	0.837	0.173	0.060	0.258	74
61	0.619	0.403	0.775	0.780	0.179	0.044	0.199	81
62	0.980	0.690	1.000	1.000	0.096	0.145	0.602	9
63	0.678	0.541	0.705	0.781	0.158	0.056	0.261	72
64	0.871	0.620	1.000	1.000	0.117	0.121	0.509	19
65	1.000	0.711	0.848	1.000	0.096	0.136	0.586	10
66	0.647	0.415	0.701	0.750	0.179	0.038	0.175	87
67	0.762	0.582	0.859	1.000	0.136	0.085	0.384	48
68	0.733	0.433	0.740	0.766	0.168	0.053	0.239	76
69	0.818	0.606	1.000	1.000	0.123	0.114	0.480	26
70	0.625	0.418	0.587	0.656	0.187	0.028	0.131	92
71	0.736	0.436	0.919	0.958	0.160	0.079	0.329	63
72	0.601	0.357	0.695	0.695	0.189	0.029	0.135	91
73	0.731	0.406	1.000	1.000	0.164	0.093	0.362	52
74	0.544	0.296	0.726	0.798	0.198	0.029	0.128	93
75	0.818	0.444	1.000	1.000	0.153	0.102	0.400	43
76	0.818	0.499	1.000	1.000	0.144	0.105	0.422	38
77	0.739	0.561	0.820	0.855	0.144	0.075	0.343	59
78	0.509	0.334	0.883	0.883	0.190	0.059	0.236	77
79	0.762	0.566	0.716	0.853	0.147	0.069	0.319	67
80	0.965	0.641	1.000	1.000	0.108	0.137	0.558	13
81	1.000	0.636	0.962	1.000	0.109	0.137	0.556	14
82	0.606	0.483	0.678	0.715	0.174	0.040	0.188	84
83	1.000	1.000	0.992	1.000	0.002	0.213	0.991	1
84	1.000	1.000	0.829	1.000	0.037	0.202	0.847	3
85	0.824	0.592	1.000	1.000	0.126	0.113	0.473	30
86	0.799	0.594	1.000	1.000	0.127	0.111	0.465	32
87	0.871	0.722	0.666	1.000	0.113	0.108	0.488	22
88	0.909	0.572	0.882	1.000	0.128	0.105	0.452	36
89	1.000	0.650	0.653	1.000	0.125	0.118	0.485	25
90	0.613	0.554	1.000	1.000	0.150	0.096	0.391	45
91	0.678	0.627	0.926	1.000	0.132	0.094	0.416	40
92	1.000	0.637	0.535	1.000	0.137	0.115	0.455	33
93	0.791	0.637	0.957	1.000	0.119	0.108	0.475	29
94	0.906	0.843	0.889	1.000	0.063	0.152	0.707	7

. In addition, to help the reader understand, the calculation process and its results are explained with the example of DMU 11. The partial efficiency of DMU 11 showed the scores of 0.885 (operational efficiency), 0.647 (energy efficiency), and 0.897 (environmental efficiency) through Equations (6)–(8), respectively. It is noteworthy that the overall efficiency score of this DMU was one, and Equation (5) classified this DMU as an efficient unit. The efficiency results of DMU 11 show that the DMU, which was inefficient through partial efficiency evaluation, could be classified as an efficient unit in the overall aspect (Theorem 2). It can be confirmed that this phenomenon also appeared in other DMUs such as DMU 6, 9, 10, 36, 42, 44, 50, 67, 87, 88, 91, 93, and 94. In sum, a total of 13 DMUs demonstrated this phenomenon.

The first step of TOPSIS is normalization. The partial efficiency scores ${\theta }_j$ were normalized by Equation (9). Thus, the normalized vector for DMU 11 was calculated as $r_j$ = (0.129, 0.172, 0.103). Next, a process was required to apply weights for the operational, energy, and environmental factors. However, in this study, an equal weight was applied to each partial efficiency to reflect the situation in which the preference information of the decision maker was not considered; that is, all $w_j$ became one, and hence $v_j$ was considered equal to the normalized vector $r_j$. This process was executed for all DMUs to derive all $v_{ij}$, and the PIS and NIS for each partial efficiency were found to be $A^{+}$ = (0.129, 0.183, 0.117) and $A^{-}$ = (0.033, 0.011, 0.033), respectively; that is, the PIS and NIS of the operational efficiency were 0.129 and 0.033. The separation measures were derived by substituting the ideal solutions of each partial efficiency and the weighted normalized vector into Equations (13) and (14). The calculated separation indices were $S^{+}$ = 0.018 and $S^{-}$ = 0.200. Finally, the relative closeness to the ideal solution was calculated to be $C^{*}=0.200/(0.018+0.200)=0.918$. All the relative closeness indices were derived for all DMUs, and the ranks were derived in descending order. The ranking of DMU 11 used in the example was analyzed as the 21st-ranked DMU.

The analysis of the ranking of eco-efficiency obtained by the proposed method showed different results from the analysis using aggregated measures. First, the analysis results indicate that all DMUs from the 1st to 41st in the derived eco-efficiency ranking were organizations with an overall efficiency that satisfied one. In other words, the DMUs analyzed as being efficient overall through DEA using an aggregated measure were ranked high in the eco-efficiency evaluation. However, our analysis shows that these 41 DMUs were specifically identified by presenting their ranks. Second, this analysis showed a ranking reversal. The overall efficiency of DMU 58, ranked 42nd in eco-efficiency, was 0.920, which was analyzed to be an inefficient DMU. However, 16 DMUs which ranked lower in eco-efficiency than DMU 58 were overall efficient DMUs. For example, DMU 10 was evaluated as an overall efficient DMU, but the eco-efficiency ranking was 80th, a fairly low ranking.

This was because the environmental efficiency score of DMU 10 was higher than the other partial efficiency scores, and it seems that it was because the environmental efficiency had the lowest discriminant power in the partial efficiency analysis. More comprehensively, it can be said that the overall efficiency was highly dependent on the environmental efficiency, and on the contrary, it was the result of a lack of correlation with the operational and energy efficiencies. In this paper, we discussed in Section 3.1 that the reason for these results was related to the number of variables involved in DEA. In order to support the empirical results of this discussion, Spearman and Kendall’s rank correlation analysis was performed. The rank correlation coefficient was derived according to how each partial efficiency showed a correlation to the overall efficiency and eco-efficiency, and the results are summarized in

Table 5. Spearman and Kendall’s Tau correlation coefficients.

	Overall Efficiency Rank		Eco-Efficiency Rank
	Spearman	Kendall	Spearman	Kendall
Operational Efficiency Rank	0.590	0.472	0.858	0.658
Energy Efficiency Rank	0.618	0.485	0.683	0.686
Environmental Efficiency Rank	0.712	0.616	0.618	0.473

.

4. Discussion

4.1. Theoretical Contribution

In the case of evaluating the eco-efficiency using aggregated measures through DEA, it was shown that, theoretically, even if only one of the partial efficiencies was analyzed to be efficient, it was determined to be an overall efficient DMU (Theorem 1). In addition, it was shown that the overall efficiency could be expressed as one even if it was not classified as an efficient DMU in any partial efficiency (Theorem 2). It was also empirically demonstrated that a significant number of DMUs exhibited this phenomenon through a case study. This study explained that when evaluating the eco-efficiency inherent in the concept of multiple partial efficiencies such as operational, energy, and environmental, a method that can supplement DEA is required, and TOPSIS is presented as one of the complementary methods.

Another contribution relates to the use of preference information. Prior studies have evaluated eco-efficiency by applying weights according to subjective judgment by asking the decision makers for their preference information or using equal weights [16,29,57,58]. However, since the use of these weighting schemes involves the subjectivity of the decision maker, it may be difficult for stakeholders to trust the results. Therefore, based on the independent evaluation of each partial efficiency, we proposed a decision support tool that could evaluate the partial efficiencies in a balanced manner without incorporating the preference information. The key to balancing here is that it reflects the distribution of the derived partial efficiency scores, which can add credibility to the evaluation of the eco-efficiency.

4.2. Practical Implication

This study presented a method for explicitly classifying the state of each DMU, even when evaluating the eco-efficiency of a large number of DMUs. When practitioners evaluate a number of input and output variables through DEA, discriminant power often decreases, making practical application difficult and often meaningless. In addition, the results are only explained by relying on specific variables, failing to derive practical implications for how the eco-efficiency score is good or poor in terms of operation, energy, or the environment. This study pointed out the problems of previous studies using integrated measures that offset the characteristics of each variable, even though it is possible to develop partial efficiency indicators suitable for each aspect when variables can be classified in terms of operation, energy, and the environment. In other words, it helps practitioners understand by structuring the factors involved in measuring eco-efficiency into operational, energy, and environmental dimensions and presenting a way to illuminate the nature of each dimension. In addition, through the combined use of DEA and TOPSIS, the evaluation results for eco-efficiency can be presented in a discriminative ranking, which means that it is easy for practitioners to actually use them.

In addition, it conveys to practitioners and stakeholders that environmental efficiency and eco-efficiency cannot be regarded as the same concept. Practitioners must remember that in order to consider the operational perspective of the organization and to properly follow the definition of eco-efficiency, measurements and evaluation must be carried out in a form that encompasses operation, energy, and the environment, as in this study.

5. Conclusions

In this paper, a performance evaluation model based on the concept of eco-efficiency was proposed, which was constructed by combining DEA and TOPSIS. The analysis was performed through calculations of the operational, energy, and environmental efficiencies, and the eco-efficiency ranking was finally derived. The model proposed in this paper can provide a more realistic and persuasive evaluation, and its value can be summarized in three aspects as follows:

• Considering the characteristics of DEA, it was shown that the derivation of the overall efficiency could not actually capture the eco-efficiency. Theoretically, this part was pointed out, and this phenomenon was confirmed and explained through an illustrative example.
• An analysis technique that can make a ranking evaluation considering the distribution of partial efficiencies, even in a situation where preference information is not requested from the decision makers, is presented.
• Another research value is that a decision-making support tool that could balance the operational, energy, and environmental aspects at the same time was presented.

The analysis presented in this study provides clues to future research along with several limitations. Although the rank-based DEA methods have the advantage of specifying the ranking of efficient DMUs, this study did not directly derive the eco-efficiency measure for the rankings. This phenomenon occurs when evaluating alternatives by ranking and may make numerical comparison difficult when comparing the performance with other alternatives. Specifically, for example, it is difficult to determine at a glance how much the eco-efficiency of a specific DMU is better than those of other DMUs. Therefore, it may be difficult to utilize this in research where the measurement of the eco-efficiency is important in itself. When it is necessary to directly derive the eco-efficiency, the preference information of the decision makers is inevitably required. If the decision maker can sufficiently present preference information, it may be possible to derive the eco-efficiency by aggregated partial efficiency using weights. It is expected that future studies will find ways to capture the eco-efficiency by designing aggregated measures without increasing the burden on decision makers.

Another remark relates to the use of MCDM techniques, which consider multiple efficiency measures as the criteria. However, this study is meaningful in that it showed that the shortcomings of the comprehensive evaluation through DEA can be supplemented through other mathematical analysis techniques. Although this study utilized TOPSIS, it should be noted that this is not necessarily the only tool that can overcome the shortcomings of DEA. In this study, it was explained that TOPSIS, as one of the intuitive and simple MCDM techniques, does not require decision maker preference information and allows a compromise that does not depend on a single criterion. However, other MCDM techniques (especially VIKOR) that have the above advantages can also be used in combination with DEA. Comparing the results using MCDM techniques other than TOPSIS to evaluate the eco-efficiency ranking will also be a task to be addressed in future research. Furthermore, even if the methods do not have the above advantages, it is possible to develop methodologies through appropriate modifications according to the decision-making situation. For example, it is expected that techniques such as the analytic hierarchy process and best-worst method can be used if sufficient resources are available for pairwise comparison.