Prediction of Penetration Resistance of a Spherical Penetrometer in Clay Using Multivariate Adaptive Regression Splines Model
Abstract
:1. Introduction
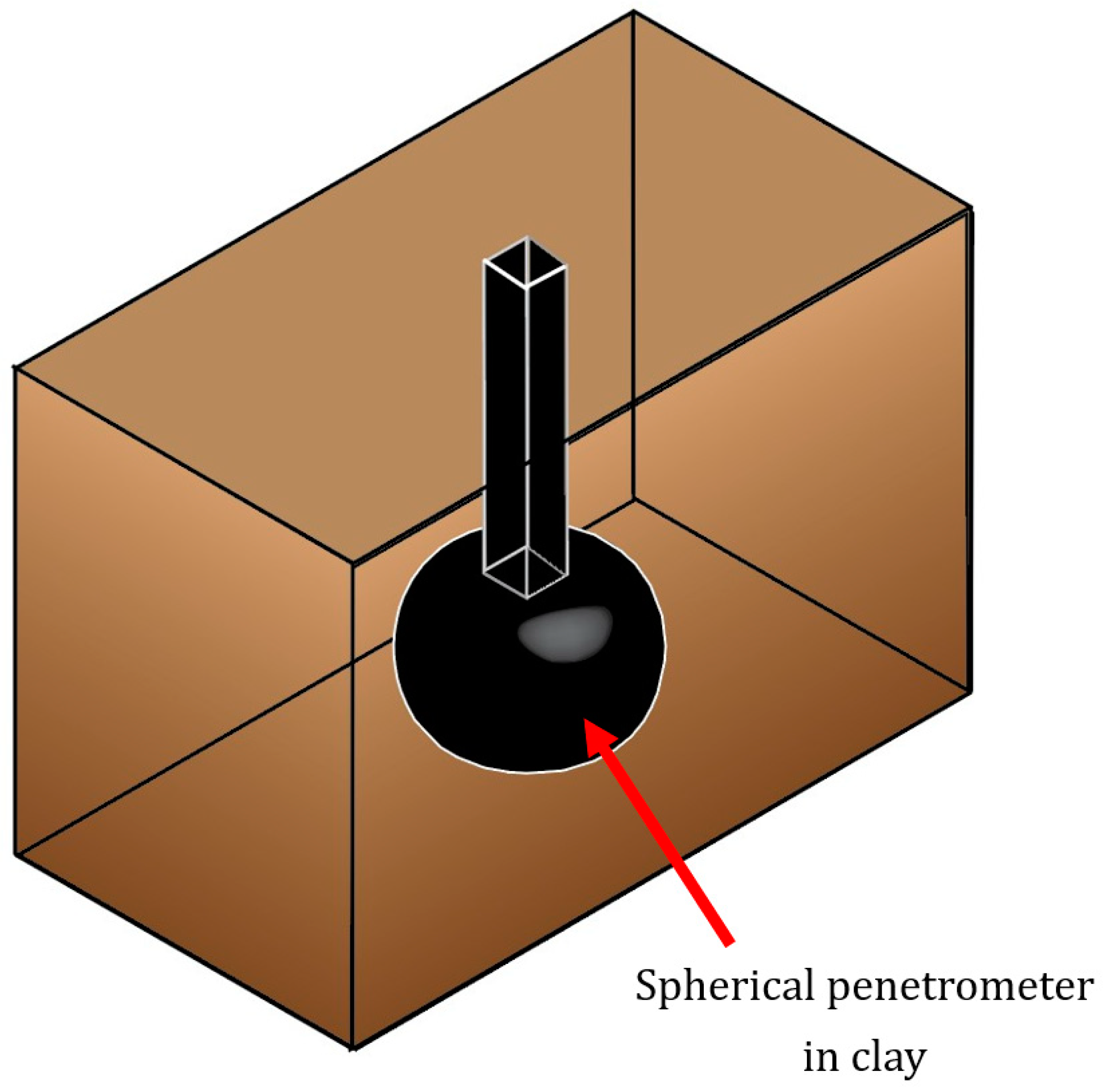
2. Problem Definition
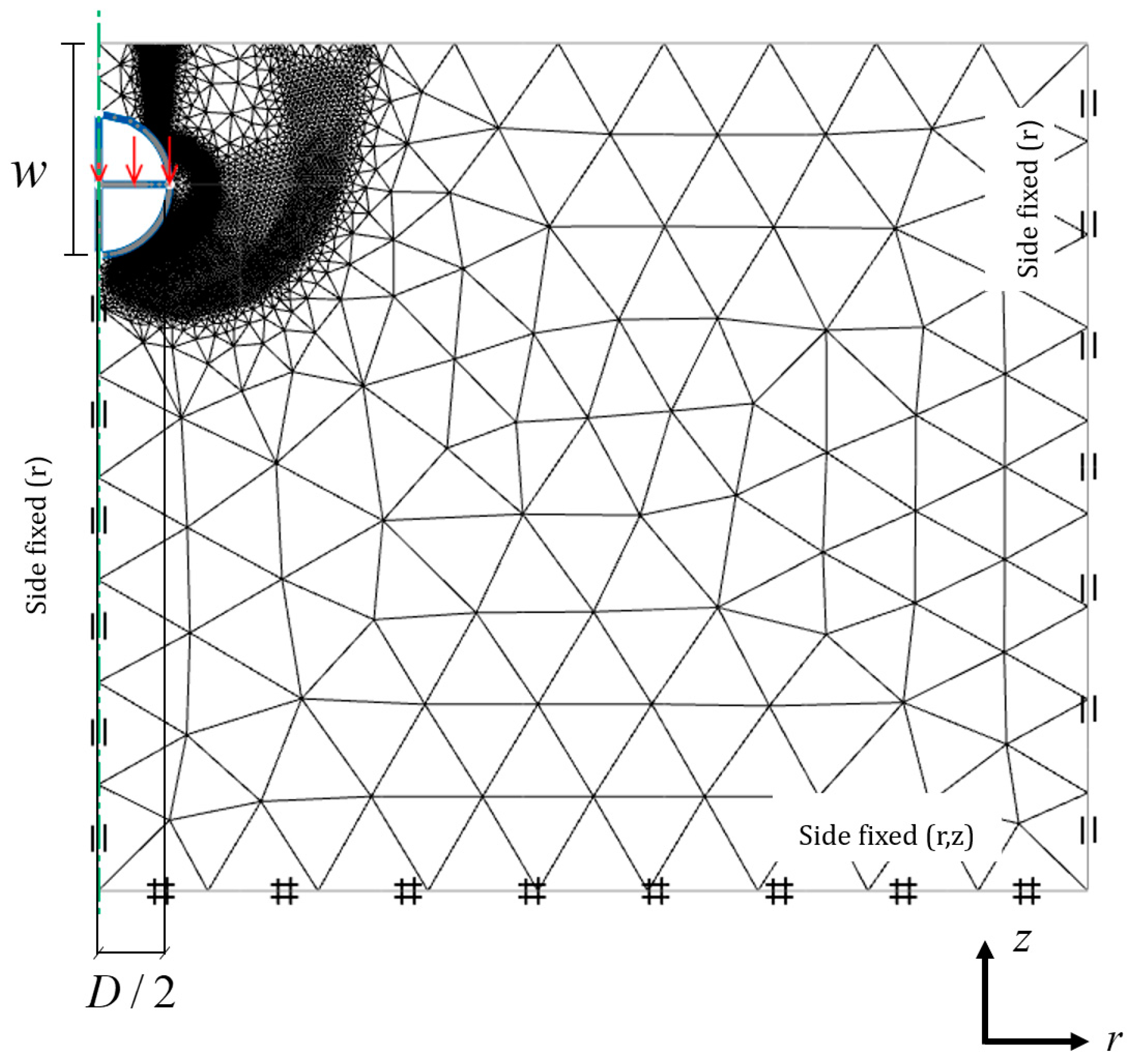
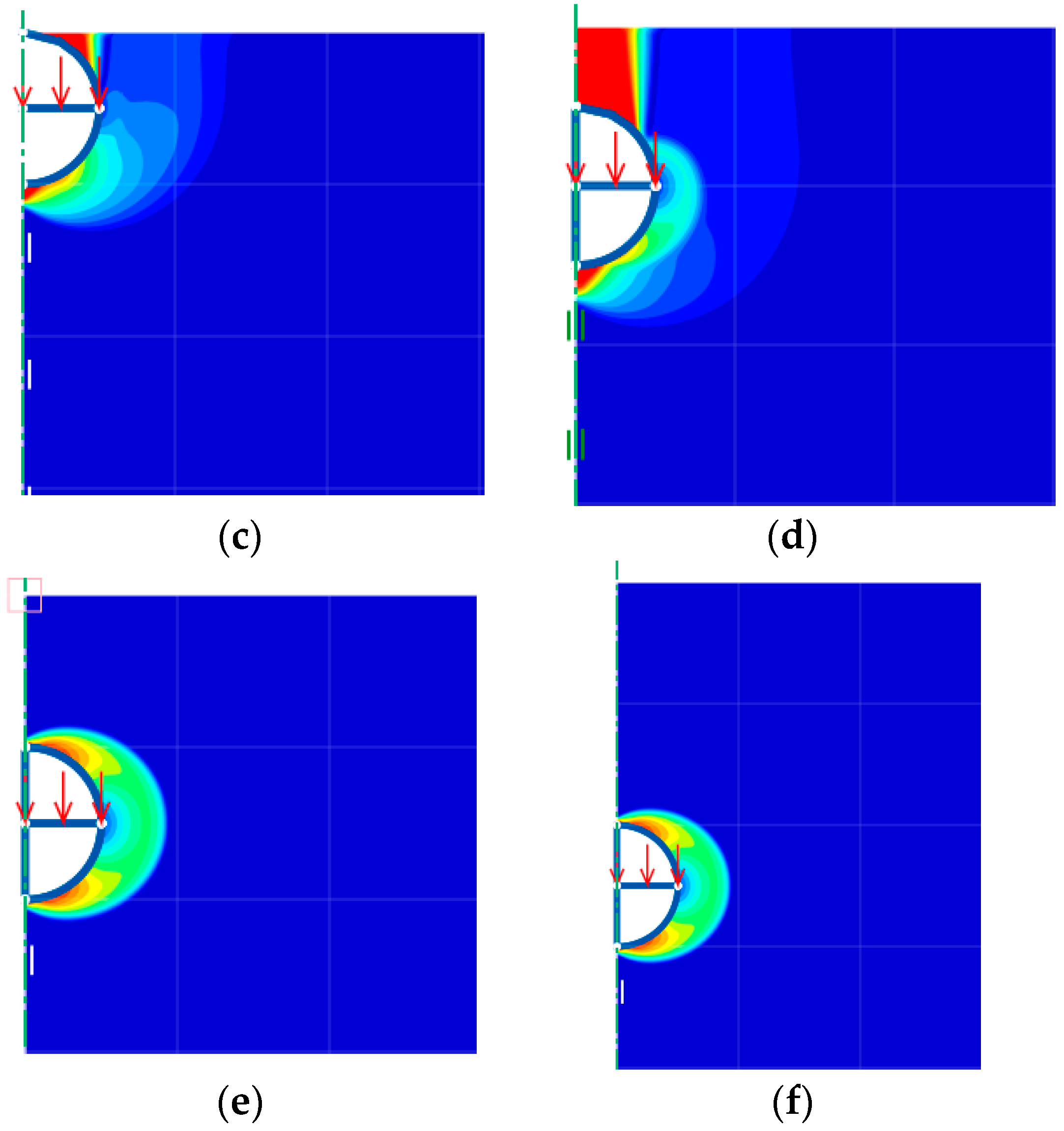
3. FELA
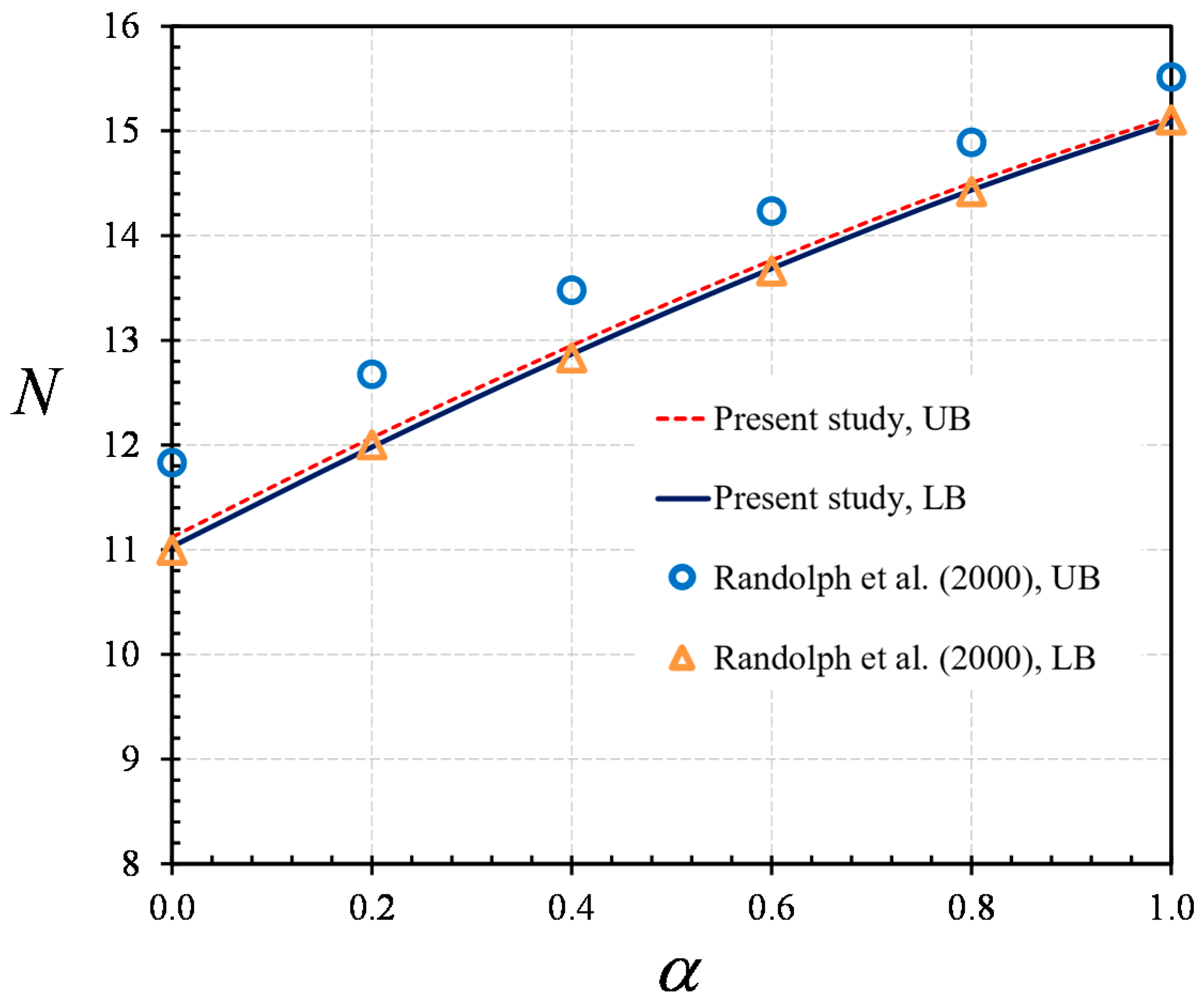
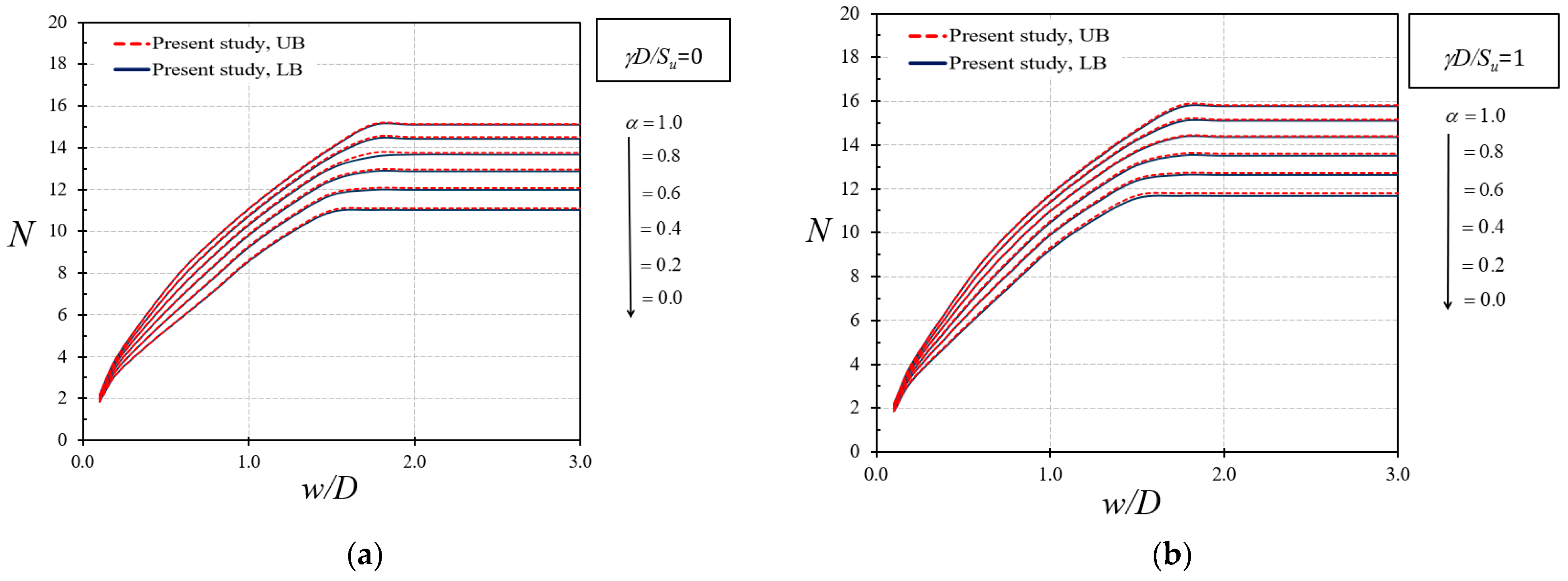
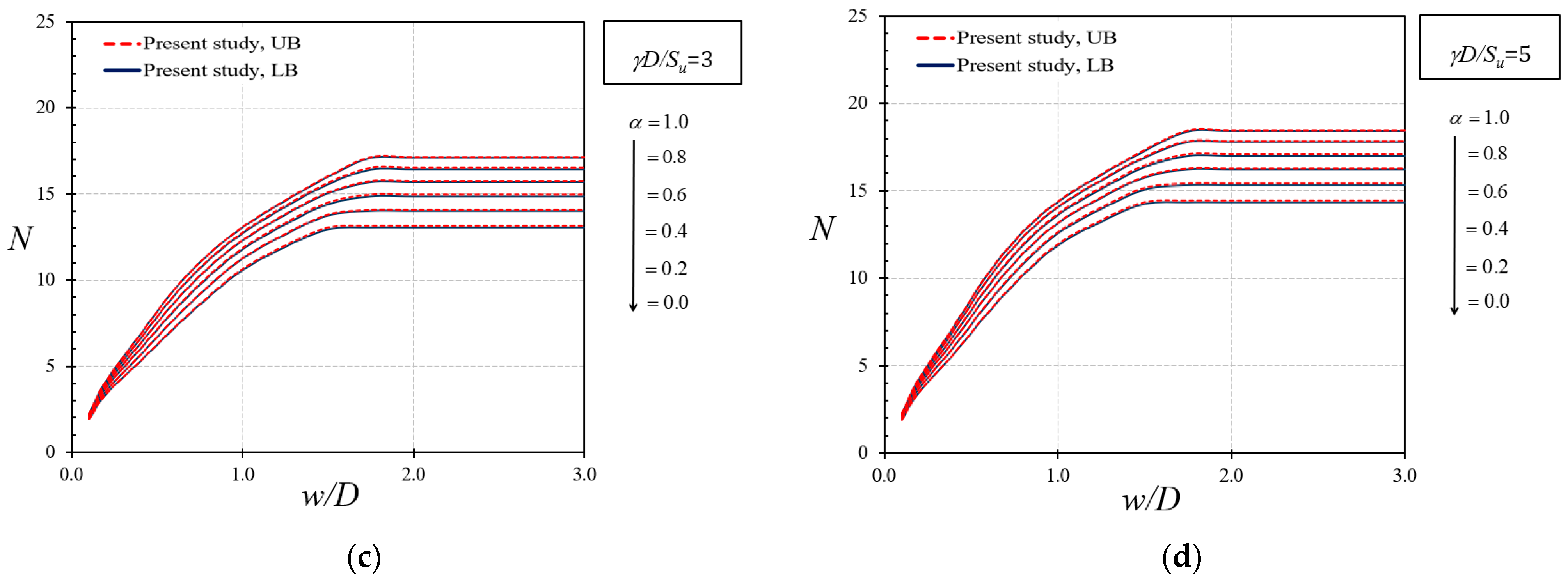
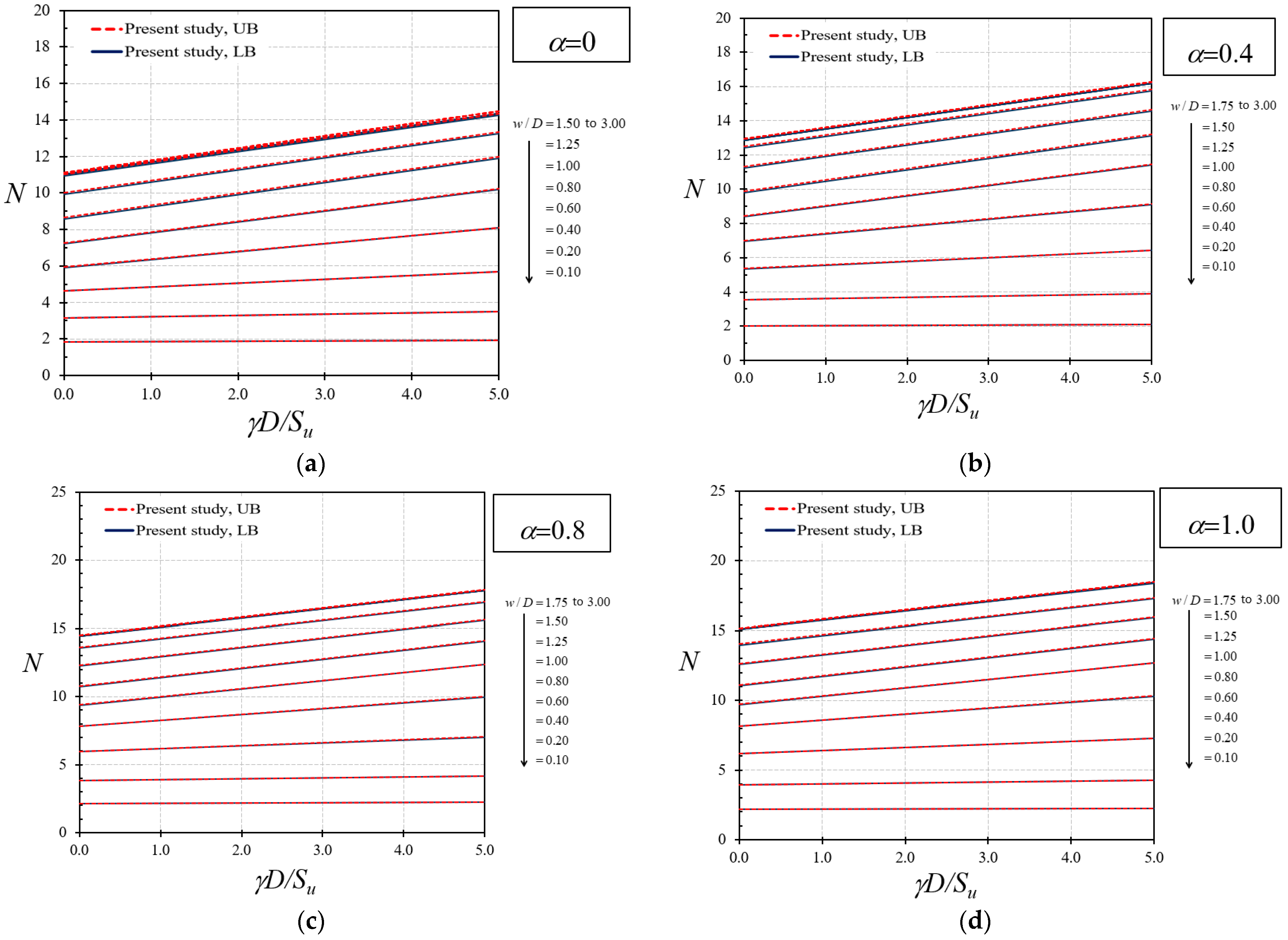
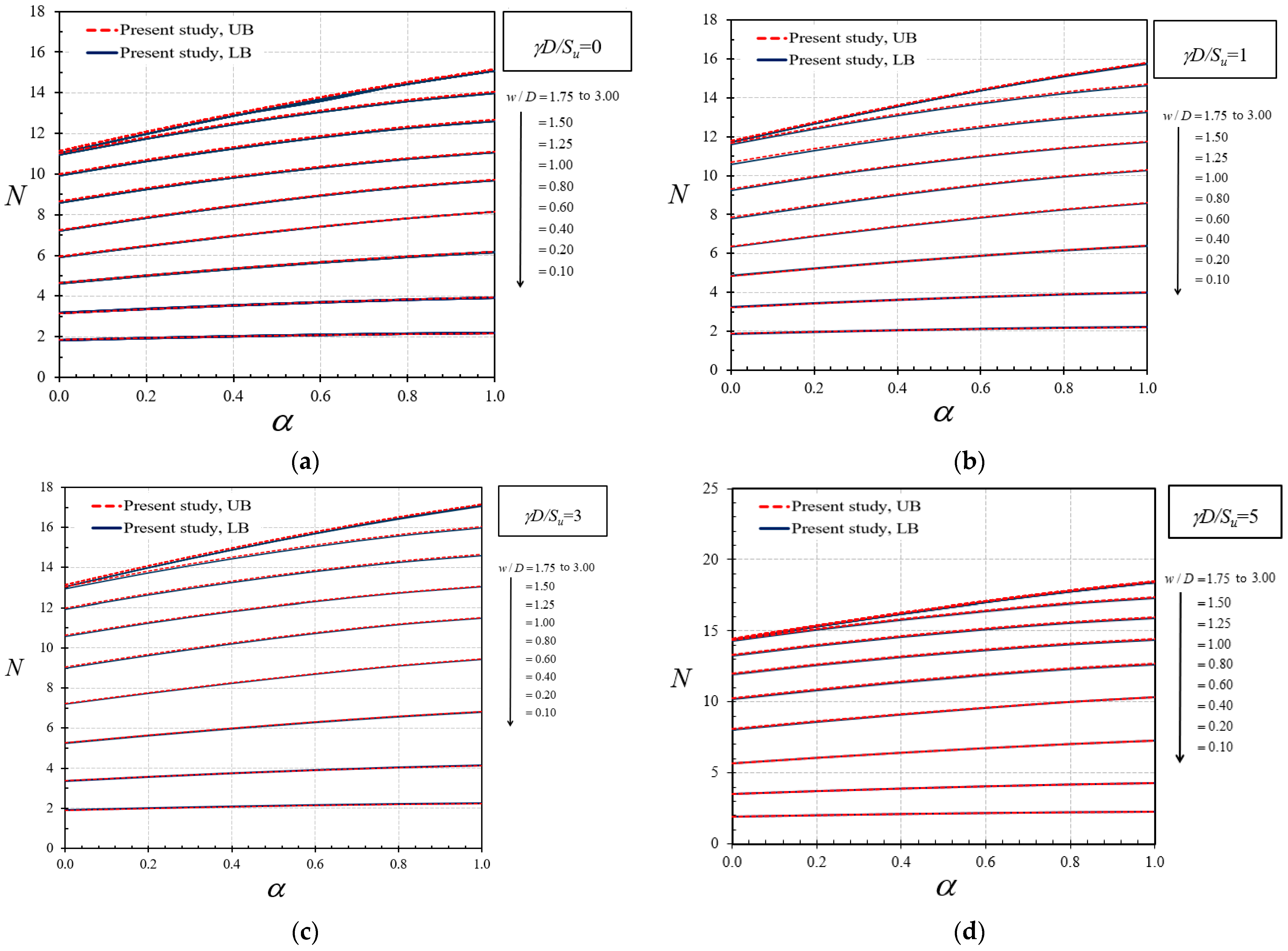
4. Numerical Results and Discussion
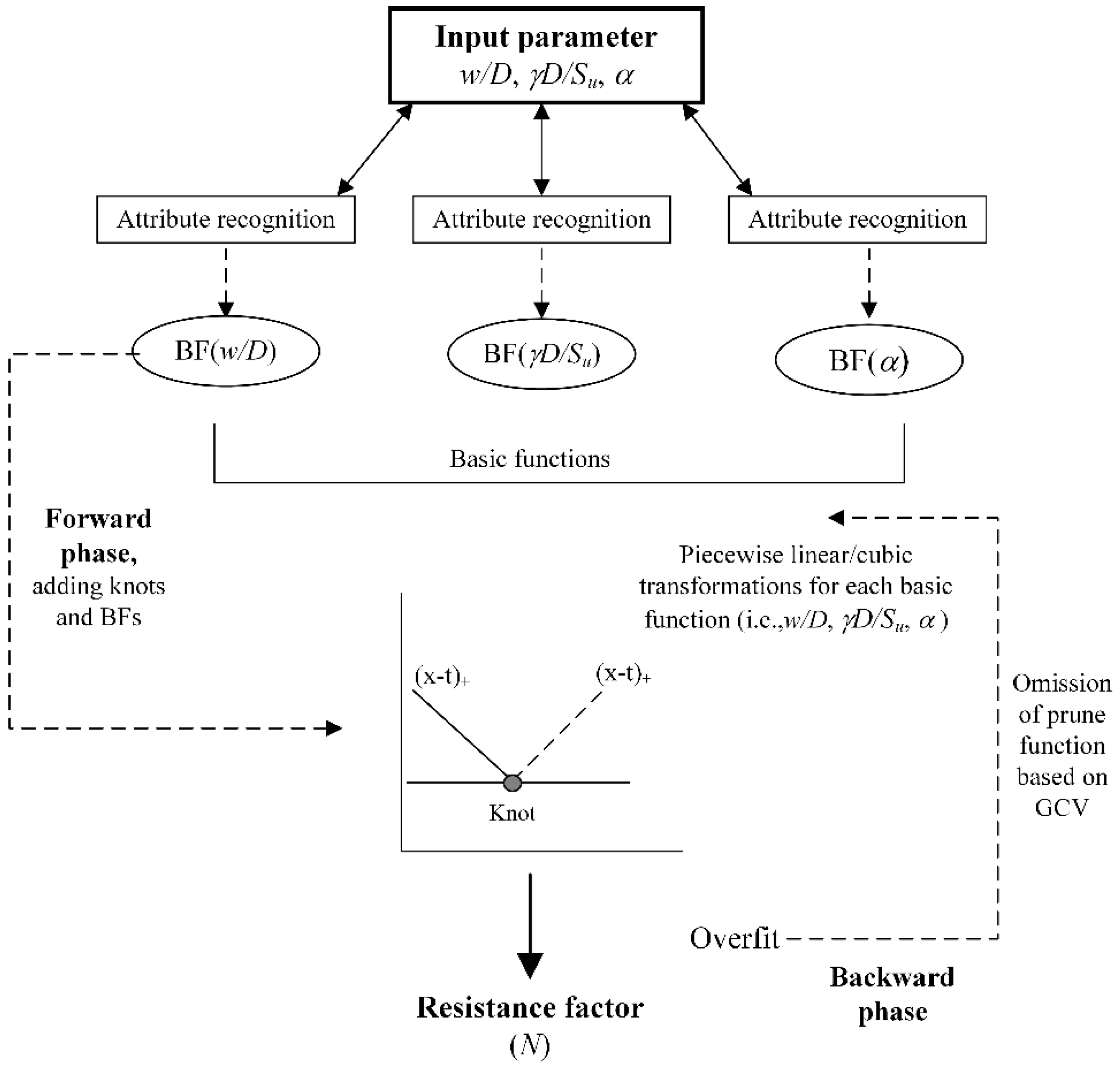
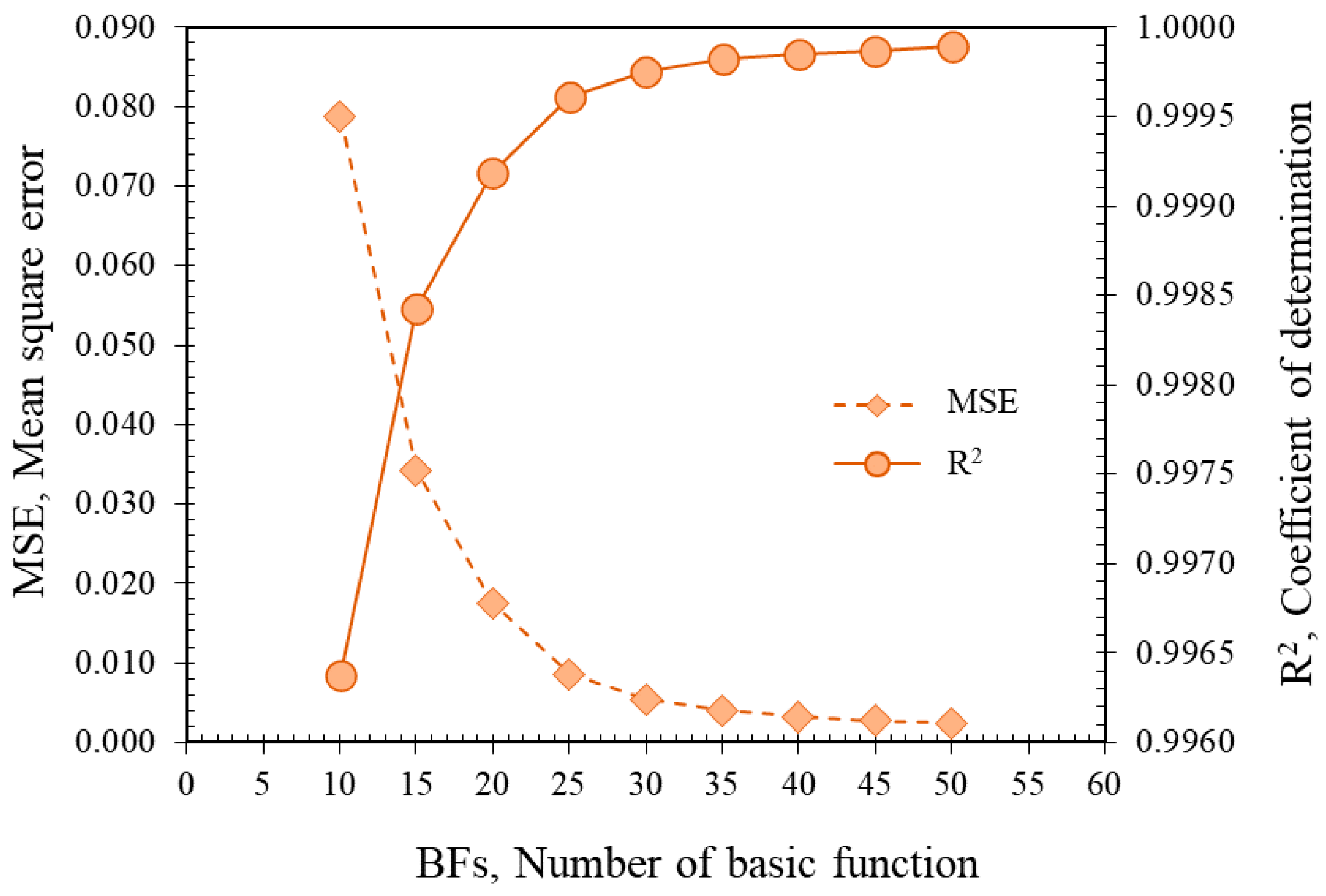
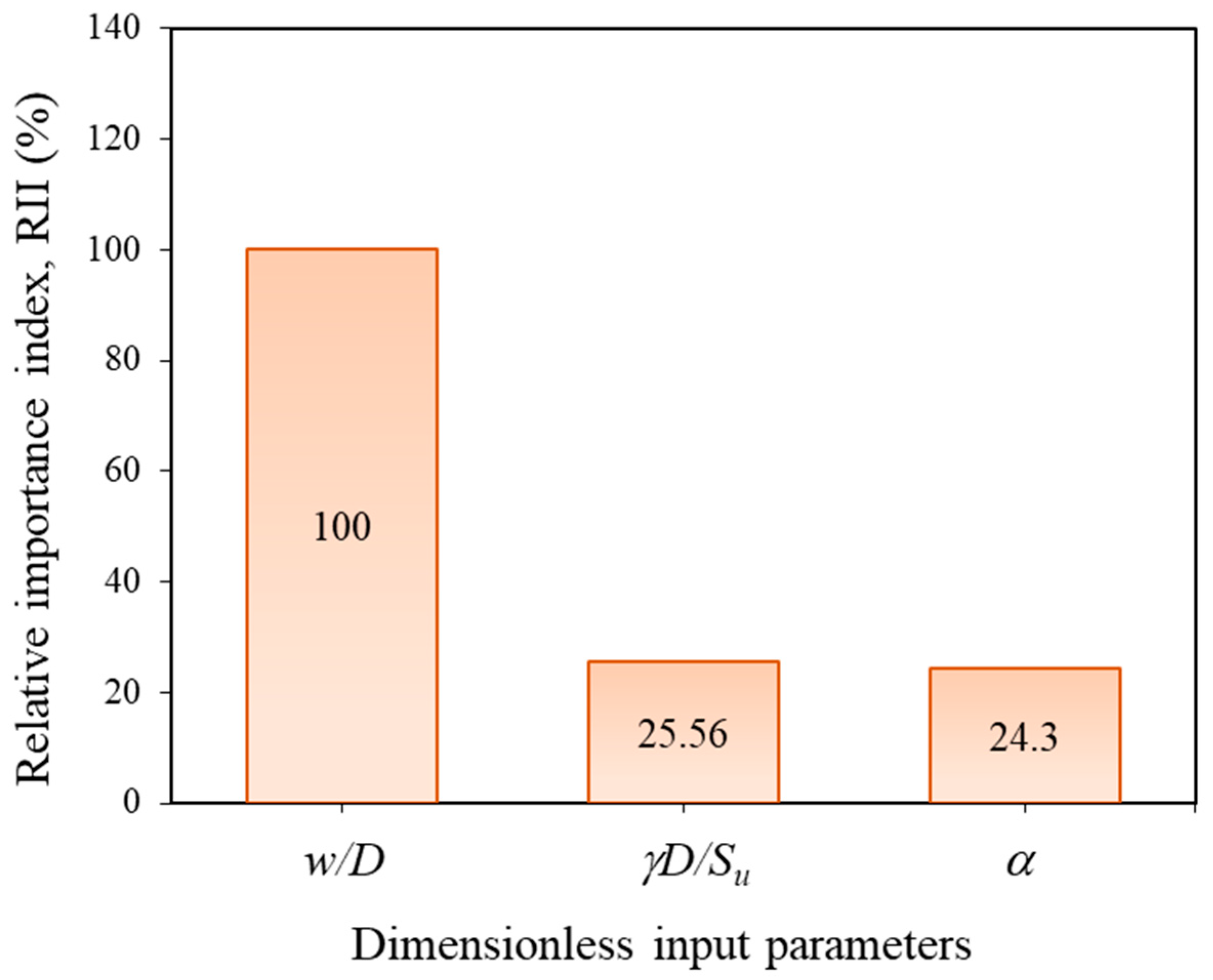
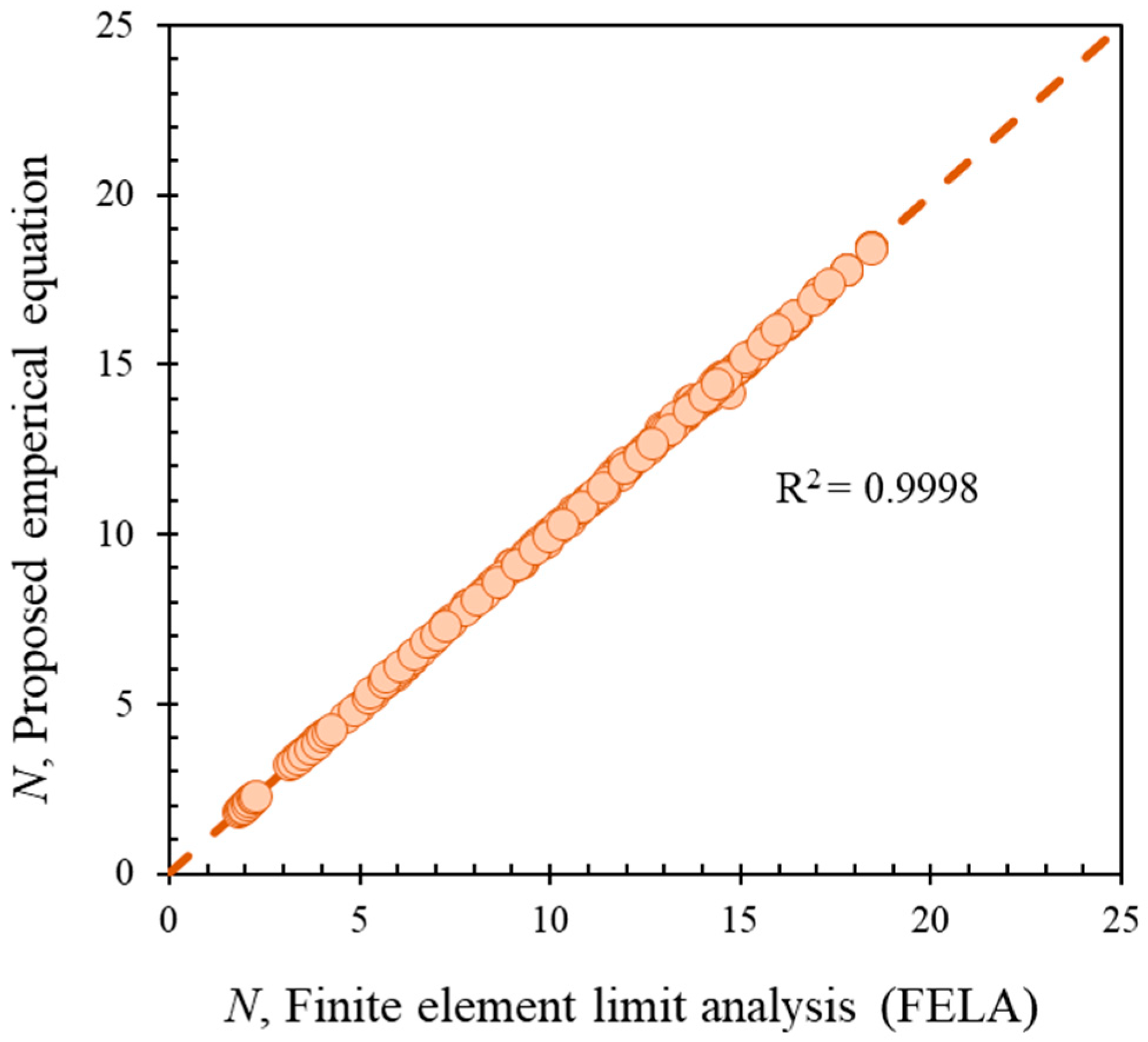
5. MARS Model
× BF6 + 3.85193 × BF7 − 8.16031 × BF8 − 1.52479 × BF11 − 0.511563 × BF15 + 1.08646 × BF18 − 2.25835 ×
BF19 + 2.71541 × BF21 − 2.92672 × BF22 − 6.38501 × BF23 − 2.68077 × BF25 − 1.31827 × BF27 + 0.533877 ×
BF29 − 0.429556 × BF30 − 0.309733 × BF31 − 0.225152 × BF32 − 0.2951 × BF33 + 1.11913 × BF35
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Randolph, M.F.; Hefer, P.A.; Geise, J.; Watson, P.G. Improved seabed strength profiling using T-bar penetrometer. In Proceedings of the Offshore Site Investigation and Foundation Behaviour: New Frontiers—Proceedings of an International Conference, London, UK, 22–24 September 1998; OnePetro: Richardson, TX, USA, 1998; pp. 221–235. [Google Scholar]
- Hefer, P.A.; Neubecker, S.R. A recent development in offshore site investigation tools: The T-bar. In Proceedings of the Australian Oil and Gas Conference, Perth, Australia, 18–22 April 1999. [Google Scholar]
- Randolph, M.F.; Houlsby, G.T. The Limiting Pressure on a Circular Pile Loaded Laterally in Cohesive Soil. Geotechnique 1984, 34, 613–623. [Google Scholar] [CrossRef]
- Martin, C.M.; Randolph, M.F. Upper bound analysis of lateral pile capacity in cohesive soil. Geotechnique 2006, 56, 141–145. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Ultimate lateral capacity of two dimensional plane strain rectangular pile in clay. Geomech. Eng. 2016, 11, 235–251. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Undrained lateral capacity of I-shaped concrete piles. Songklanakarin J. Sci. Technol. 2017, 39, 751–758. [Google Scholar]
- Ukritchon, B.; Keawsawasvong, S. Undrained lateral capacity of rectangular piles under a general loading direction and full flow mechanism. KSCE J. Civil. Eng. 2018, 22, 2256–2265. [Google Scholar] [CrossRef]
- Vallejo, L.E. Evaluation of test methods designed to obtain the undrained shear strength of muds. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1982; OnePetro: Richardson, TX, USA, 1982. [Google Scholar]
- Watson, P.G.; Newson, T.A.; Randolph, M.F. Strength Profiling in Soft Offshore Soils; CRC Press/Balkema: Boca Raton, FL, USA, 1998; pp. 1389–1394. [Google Scholar]
- Newson, T.A.; Watson, P.G.; Bransby, M.F. Undrained shear strength profiling using a spherical penetrometer. Submitt. Publ. 1999. [Google Scholar]
- Randolph, M.F.; Martin, C.M.; Hu, Y. Limiting resistance of a spherical penetrometer in cohesive material. Geotechnique 2000, 50, 573–582. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Undrained basal stability of braced circular excavations in non-homogeneous clays with linear increase of strength with depth. Comput. Geotech. 2019, 115, 103180. [Google Scholar] [CrossRef]
- Keawsawasvong, S. Bearing capacity of conical footings on clays considering combined effects of anisotropy and non-homogeneity. Ships Offshore Struct. 2021, 1–12. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Finite element analysis of undrained stability of cantilever flood walls. Int. J. Geotech. Eng. 2017, 11, 355–367. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Undrained stability of plane strain active trapdoors in anisotropic and non-homogeneous clays. Tunn. Undergr. Space Technol. 2021, 107, 103628. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Shiau, J.; Ngamkhanong, C.; Lai, V.Q.; Thongchom, C. Undrained stability of ring foundations: Axisymmetry, anisotropy, and non-homogeneity. Int. J. Geomech. 2022, 22, 04021253. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Design equation for stability of shallow unlined circular tunnels in Hoek-Brown rock masses. Bull. Eng. Geol. Environ. 2020, 79, 4167–4190. [Google Scholar] [CrossRef]
- Yodsomjai, W.; Keawsawasvong, S.; Senjuntichai, T. Undrained stability of unsupported conical slopes in anisotropic clays based on Anisotropic Undrained Shear failure criterion. Transp. Infrastruct. Geotechnol. 2021, 8, 557–568. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Error in Ito and Matsui’s limit equilibrium solution of lateral force on a row of stabilizing piles. J. Geotech. Geoenviron. Eng. 2017, 143, 02817004. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Undrained lower bound solutions for end bearing capacity of shallow circular piles in non-homogeneous and anisotropic clays. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 596–632. [Google Scholar] [CrossRef]
- Ukritchon, B.; Yoang, S.; Keawsawasvong, S. Three-dimensional stability analysis of the collapse pressure on flexible pavements over rectangular trapdoors. Transp. Geotech. 2019, 21, 100277. [Google Scholar] [CrossRef]
- Ukritchon, B.; Yoang, S.; Keawsawasvong, S. Undrained stability of unsupported rectangular excavations in non-homogeneous clays. Comput. Geotech. 2020, 117, 103281. [Google Scholar] [CrossRef]
- Sloan, S.W. Geotechnical stability analysis. Géotechnique 2013, 63, 531–572. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W. MARS Applications in Geotechnical Engineering Systems; Springer Nature Customer Service Center LLC: New York, NY, USA, 2020. [Google Scholar]
- Keawsawasvong, S.; Lai, V.Q. End bearing capacity factor for annular foundations embedded in clay considering the effect of the adhesion factor. Int. J. Geosynth. Ground Eng. 2021, 7, 15. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Unsafe error in conventional shape factor for shallow circular foundations in normally consolidated clays. J. Geotech. Geoenviron. Eng. 2017, 143, 02817001. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Design equations of uplift capacity of circular piles in sands. Appl. Ocean Res. 2019, 90, 101844. [Google Scholar] [CrossRef]
- Ukritchon, B.; Wongtoythong, P.; Keawsawasvong, S. New design equation for undrained pullout capacity of suction caissons considering combined effects of caisson aspect ratio, adhesion factor at interface, and linearly increasing strength. Appl. Ocean Res. 2018, 75, 1–14. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.; Krabbenhoft, J. Optum Computational Engineering (OptumG2). 2015. Available online: www.optumce.com (accessed on 20 January 2021).
- Ciria, H.; Peraire, J.; Bonet, J. Mesh adaptive computation of upper and lower bounds in limit analysis. Int. J. Numer. Methods Eng. 2008, 75, 899–944. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. Effective hybrid soft computing approach for optimum design of shallow foundations. Sustainability 2022, 14, 1847. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Keawsawasvong, S.; Mirzaei, H.; Jebeli, M. An effective artificial intelligence approach for slope stability evaluation. IEEE Access 2022, 10, 5660–5671. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Gocheva-Ilieva, S.; Ivanov, A.; Stoimenova-minova, M. Prediction of Daily Mean PM10 Concentrations Using Random Forest, CART Ensemble and Bagging Stacked by MARS. Sustainability 2022, 14, 798. [Google Scholar] [CrossRef]
- Kim, S.; Alizamir, M.; Kim, N.W.; Kisi, O. Bayesian Model Averaging: A Unique Model Enhancing Forecasting Accuracy for Daily Streamflow Based on Different Antecedent Time Series. Sustainability 2022, 12, 9720. [Google Scholar] [CrossRef]
- Halecki, W.; Kowalik, T.; Bogdał, A. Multiannual Assessment of the Risk of Surface Water Erosion and Metal Accumulation Indices in the Flysch Stream Using the MARS Model in the Polish Outer Western Carpathians. Sustainability 2019, 11, 7189. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Fan, J. Comparison of neuron-based, kernel-based, tree-based and curve-based machine learning models for predicting daily reference evapotranspiration. PLoS ONE 2019, 14, e0217520. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raja, M.N.A.; Shukla, S.K. Multivariate adaptive regression splines model for reinforced soil foundations. Geosynth. Int. 2021, 28, 368–390. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Goh, A.T.C. MARS inverse analysis of 954 soil and wall properties for braced excavations in clays. Geomech. Eng. 2018, 16, 577–588. [Google Scholar]
- Zheng, G.; Yang, P.; Zhou, H.; Zeng, C.; Yang, X.; He, X.; Yu, X. Evaluation of the earthquake induced uplift displacement of tunnels using multivariate adaptive regression splines. Comput. Geotech. 2019, 113, 103099. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, H.; Yu, X.; Guo, Z.; Zheng, G.; Yang, X.; Tian, Y. Evaluation of the bending failure of columns under an embankment loading. Int. J. Geomech. 2021, 21, 04021112. [Google Scholar] [CrossRef]
- Lai, F.; Zhang, N.; Liu, S.; Sun, Y.; Li, Y. Ground movements induced by installation of twin large diameter deeply-buried caissons: 3D numerical modeling. Acta Geotech. 2021, 16, 2933–2961. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Wang, W.; Zhang, F.; Goh, A.T.C. A multivariate adaptive regression splines model for determining horizontal wall deflection envelope for braced excavations in clays. Tunn. Undergr. Space Technol. 2019, 84, 461–471. [Google Scholar] [CrossRef]
- Caraka, R.E.; Chen, R.C.; Bakar, S.A.; Tahmid, M.; Toharudin, T.; Pardamean, B. Employing Best Input SVR Robust Lost Function with Nature-Inspired Metaheuristics in Wind Speed Energy Forecasting. IAENG Int. J. Comput. Sci. 2020, 47, 572–584. [Google Scholar]
- Stoklosa, J.; Warton, D.I. A Generalized Estimating Equation Approach to Multivariate Adaptive Regression Splines. J. Comput. Graph. Stat. 2018, 27, 245–253. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef] [Green Version]
- De Boor, C. Spline basics. In Handbook of Computer Aided Geometric Design; Chapter 6; Academic Press: Cambridge, MA, USA, 2002; ISBN 978-0-444-51104-1. [Google Scholar]
- Ruppert, D.; Wand, M.P.; Carroll, R.J. Semiparametric regression during 2003–2007. Electron. J. Stat. 2009, 3, 1193–1256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barry, D.; Hardle, W. Applied Nonparametric Regression. J. R. Stat. Soc. Ser. A 1993, 156, 128. [Google Scholar] [CrossRef]




| BF | Equation | BF | Equation |
|---|---|---|---|
| BF1 | max (0, (w/D − 1.25)) | BF20 | max (0, (1.5 − w/D)) |
| BF2 | max (0, (1.25 − w/D)) | BF21 | max (0, (α − 0.6)) × BF20 |
| BF3 | max (0, (γD/Su − 0)) | BF22 | max (0, (0.6 − α)) × BF20 |
| BF4 | max (0, (α + 5.96046 × 10−8)) | BF23 | max (0, (w/D − 0.2)) |
| BF5 | max (0, (w/D − 0.6)) × BF3 | BF25 | max (0, (w/D − 0.6)) × BF4 |
| BF6 | max (0, (0.6 − w/D)) × BF3 | BF27 | max (0, (α − 0.6)) × BF23 |
| BF7 | max (0, (w/D − 1.75)) × BF4 | BF29 | max (0, (γD/Su − 1)) × BF23 |
| BF8 | max (0, (1.75 − w/D)) × BF4 | BF30 | max (0, (1 − γD/Su)) × BF23 |
| BF11 | max (0, (w/D − 0.8)) | BF31 | max (0, (α − 0.6)) × BF30 |
| BF15 | max (0, (w/D − 1)) × BF3 | BF32 | max (0, (0.6 − α)) × BF30 |
| BF18 | max (0, (0.6 − α)) × BF11 | BF33 | max (0, (w/D − 0.8)) × BF3 |
| BF19 | max (0, (w/D − 1.5)) | BF35 | max (0, (α + 5.96046 × 10−8)) |
| N = 18.1381 + 10.1002 × BF1 − 12.0408 × BF2 + 0.209064 × BF3 + 8.54367 × BF4 + 0.259794 × BF5 − 0.380723 × BF6 + 3.85193 × BF7 − 8.16031 × BF8 − 1.52479 × BF11 − 0.511563 × BF15 + 1.08646 × BF18 − 2.25835 × BF19 + 2.71541 × BF21 − 2.92672 × BF22 − 6.38501 × BF23 − 2.68077 × BF25 − 1.31827 × BF27 + 0.533877 × BF29 − 0.429556 × BF30 − 0.309733 × BF31 − 0.225152 × BF32 − 0.2951 × BF33 + 1.11913 × BF35 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirimontree, S.; Jearsiripongkul, T.; Lai, V.Q.; Eskandarinejad, A.; Lawongkerd, J.; Seehavong, S.; Thongchom, C.; Nuaklong, P.; Keawsawasvong, S. Prediction of Penetration Resistance of a Spherical Penetrometer in Clay Using Multivariate Adaptive Regression Splines Model. Sustainability 2022, 14, 3222. https://doi.org/10.3390/su14063222
Sirimontree S, Jearsiripongkul T, Lai VQ, Eskandarinejad A, Lawongkerd J, Seehavong S, Thongchom C, Nuaklong P, Keawsawasvong S. Prediction of Penetration Resistance of a Spherical Penetrometer in Clay Using Multivariate Adaptive Regression Splines Model. Sustainability. 2022; 14(6):3222. https://doi.org/10.3390/su14063222
Chicago/Turabian StyleSirimontree, Sayan, Thira Jearsiripongkul, Van Qui Lai, Alireza Eskandarinejad, Jintara Lawongkerd, Sorawit Seehavong, Chanachai Thongchom, Peem Nuaklong, and Suraparb Keawsawasvong. 2022. "Prediction of Penetration Resistance of a Spherical Penetrometer in Clay Using Multivariate Adaptive Regression Splines Model" Sustainability 14, no. 6: 3222. https://doi.org/10.3390/su14063222
APA StyleSirimontree, S., Jearsiripongkul, T., Lai, V. Q., Eskandarinejad, A., Lawongkerd, J., Seehavong, S., Thongchom, C., Nuaklong, P., & Keawsawasvong, S. (2022). Prediction of Penetration Resistance of a Spherical Penetrometer in Clay Using Multivariate Adaptive Regression Splines Model. Sustainability, 14(6), 3222. https://doi.org/10.3390/su14063222










