Precipitation Forecasting in Northern Bangladesh Using a Hybrid Machine Learning Model
Abstract
:1. Introduction
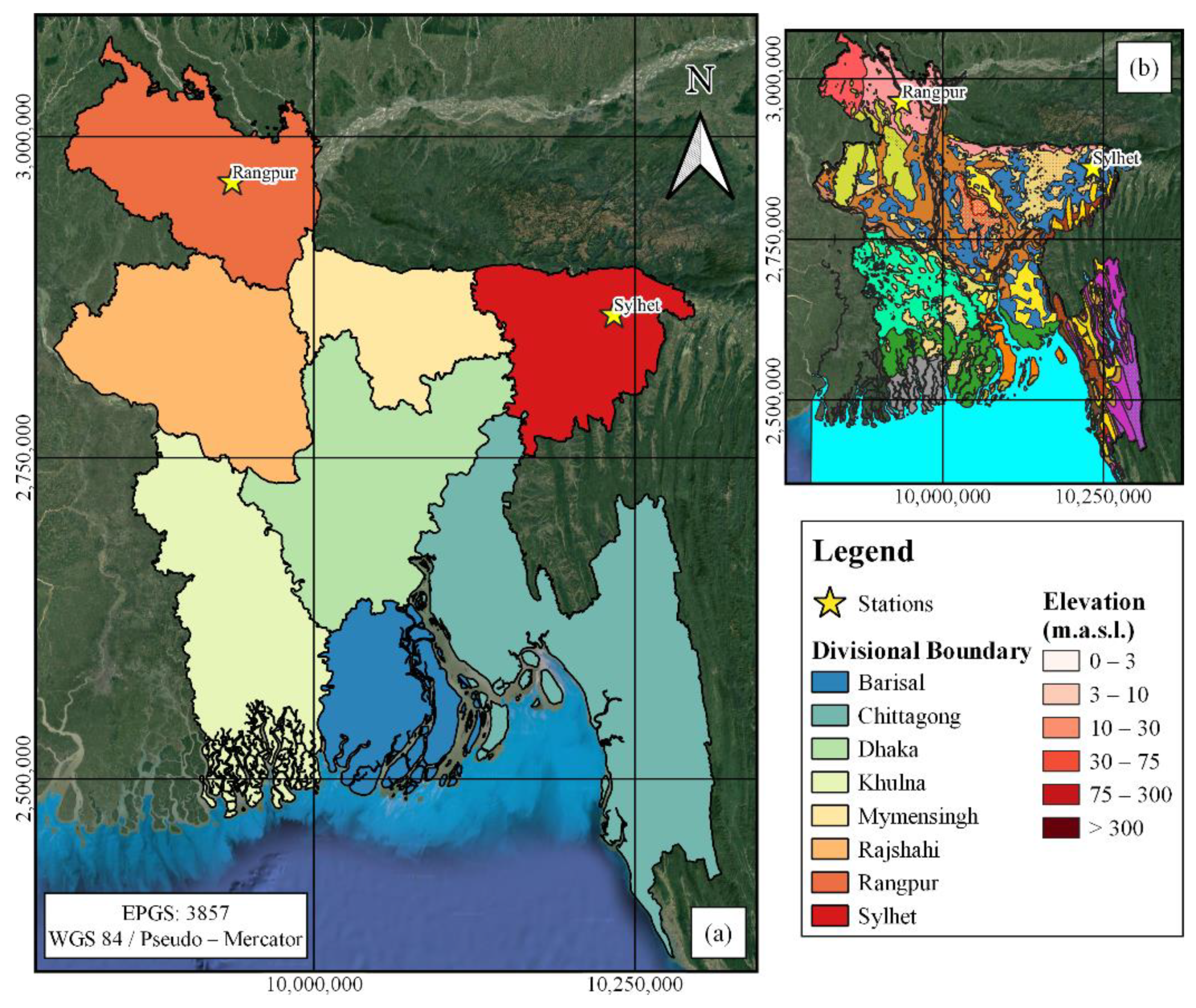
2. Study Area and Datasets
3. Methods
3.1. M5P
3.2. Support Vector Regression (SVR)
3.3. Hybrid Model M5P-SVR
3.4. Particle Swarm Optimization (PSO)
4. Results
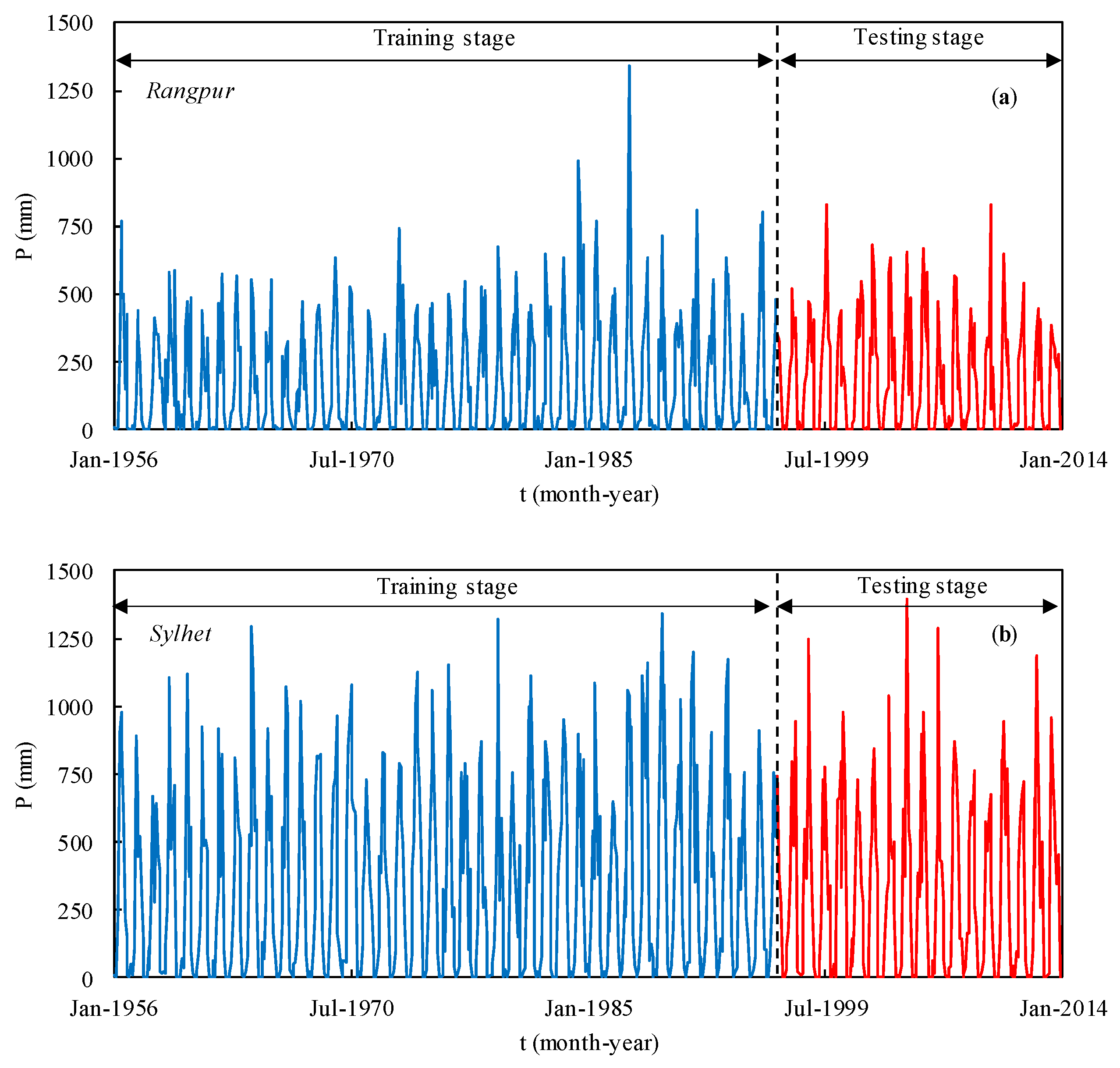
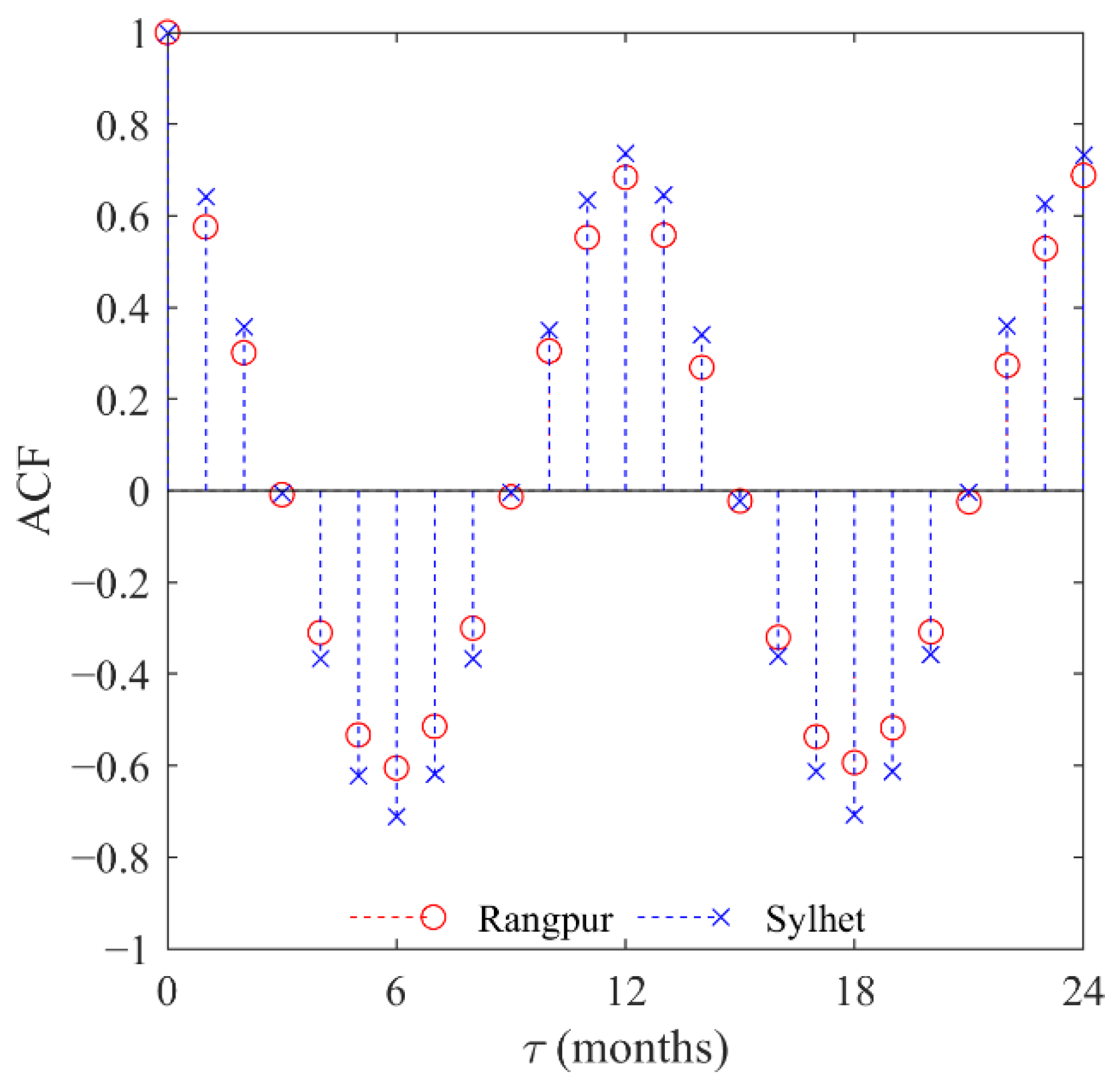
4.1. Time Series Analysis
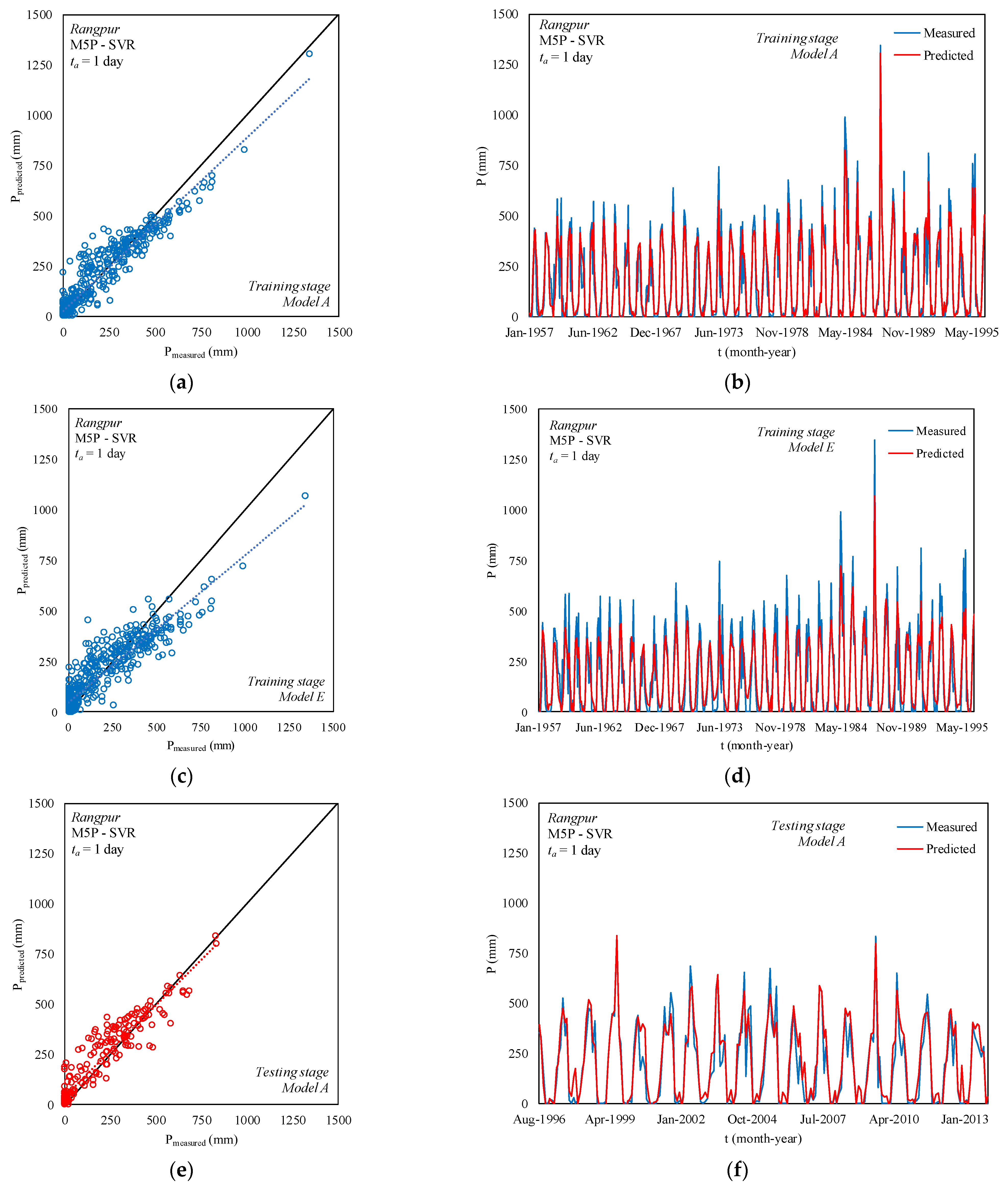
4.2. Rangpur Station
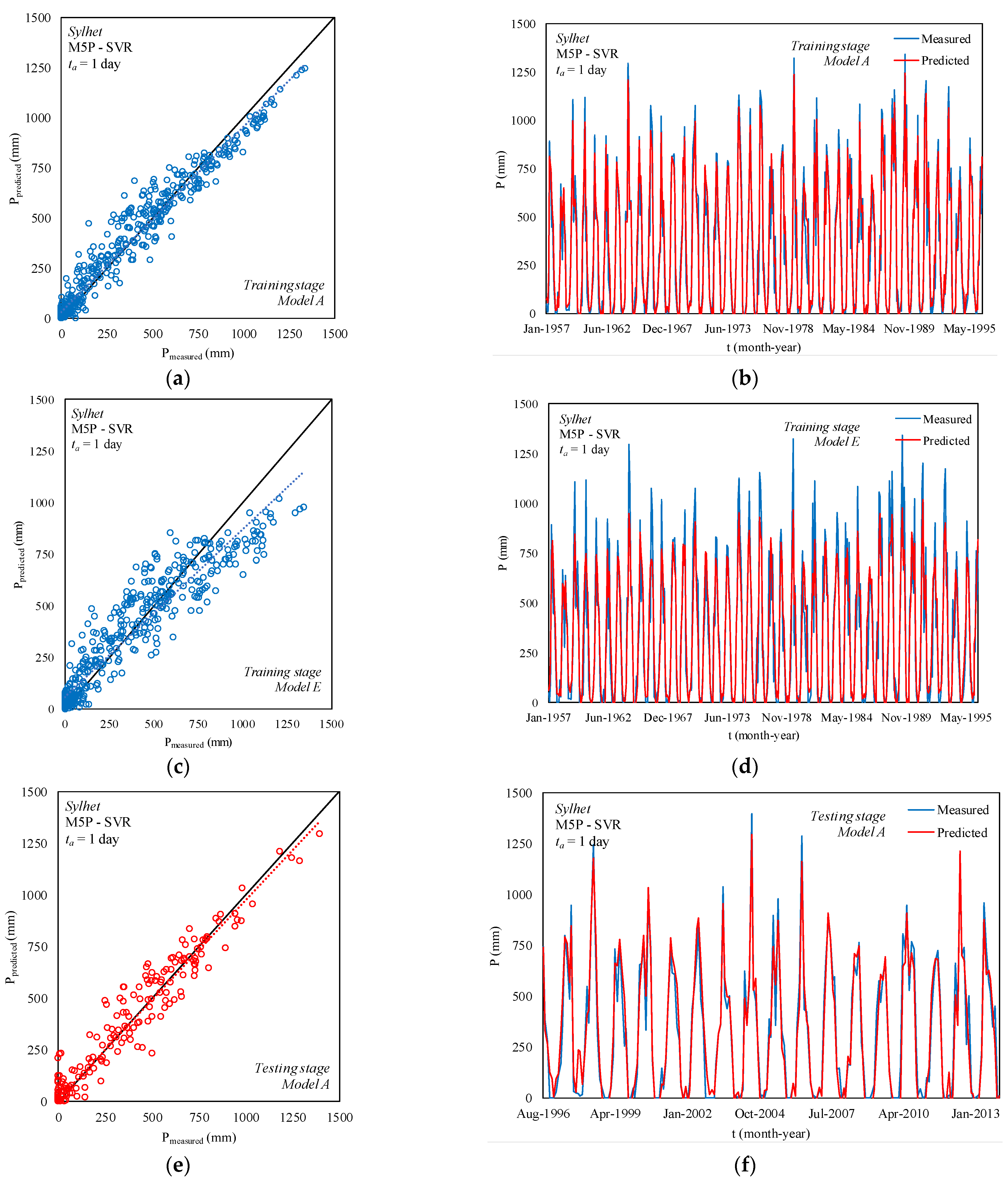
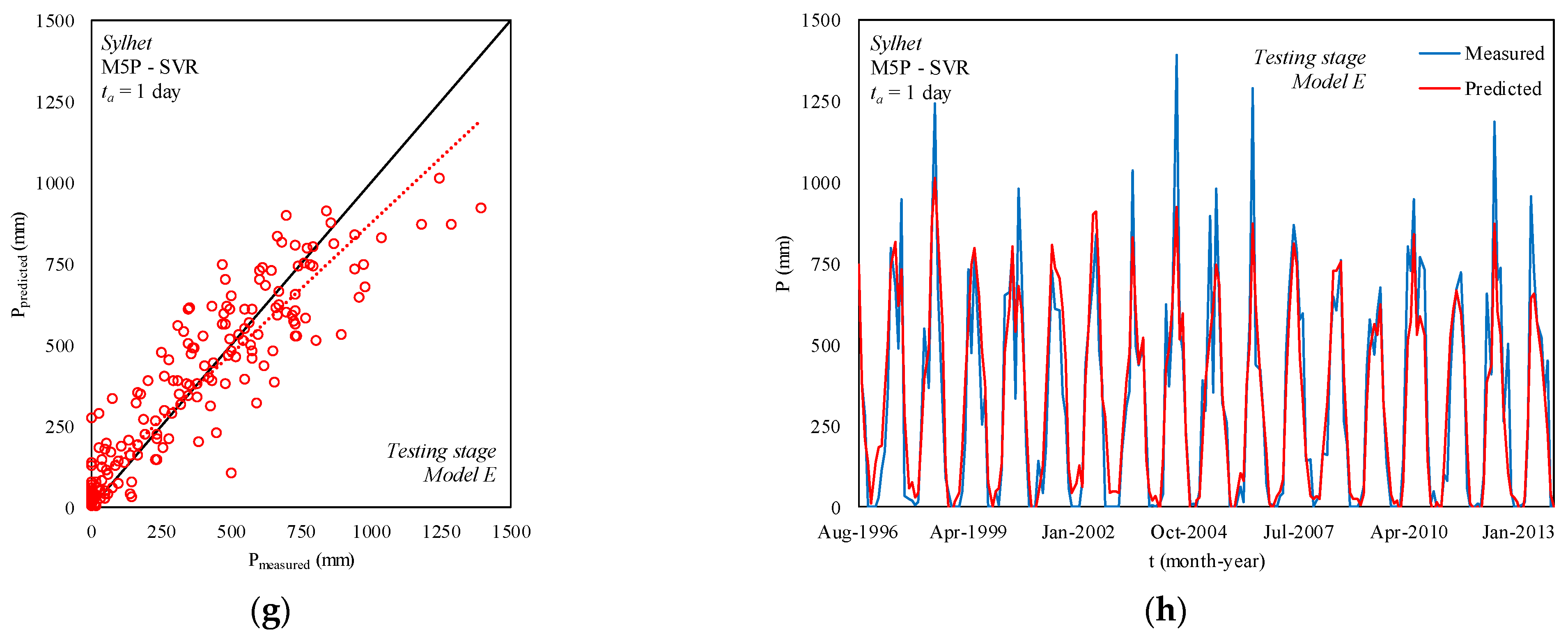
4.3. Sylhet Station
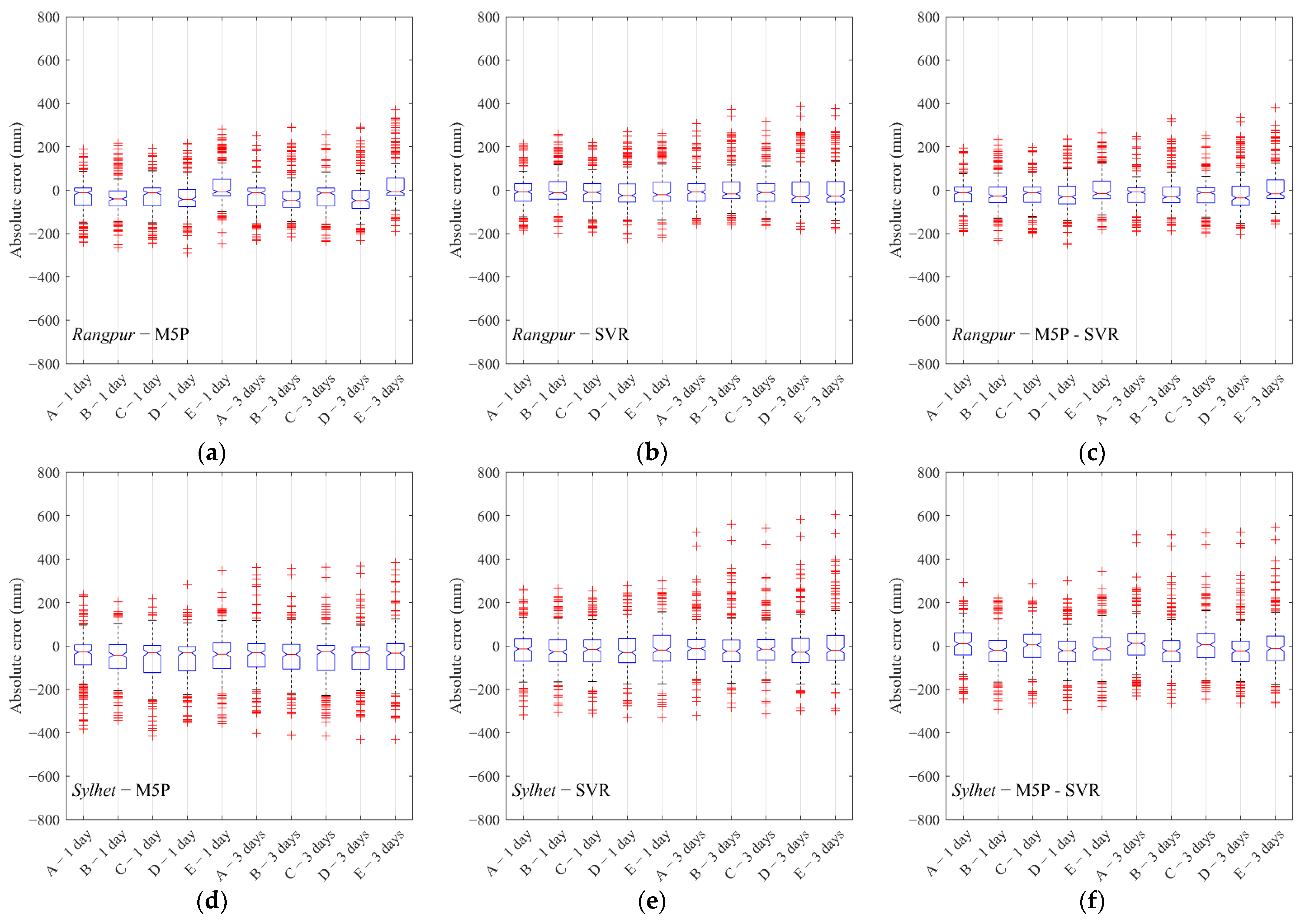
4.4. Performance Comparisons of the Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Murali, J.; Afifi, T. Rainfall variability, food security and human mobility in the Janjgir-Champa district of Chhattisgarh state, India. Clim. Dev. 2014, 6, 28–37. [Google Scholar] [CrossRef]
- Lockart, N.; Willgoose, G.; Kuczera, G.; Kiem, A.S.; Chowdhury, A.K.; Parana Manage, N.; Twomey, C. Case study on the use of dynamically downscaled climate model data for assessing water security in the Lower Hunter region of the eastern seaboard of Australia. J. South. Hemisph. Earth Syst. Sci. 2016, 66, 177–202. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T.; Kaspar, F. Estimating the impact of global change on flood and drought risks in Europe: A continental, integrated analysis. Clim. Chang. 2006, 75, 273–299. [Google Scholar] [CrossRef]
- Kang, J.; Wang, H.; Yuan, F.; Wang, Z.; Huang, J.; Qiu, T. Prediction of Precipitation Based on Recurrent Neural Networks in Jingdezhen, Jiangxi Province, China. Atmosphere 2020, 11, 246. [Google Scholar] [CrossRef] [Green Version]
- Chiang, Y.M.; Chang, L.C.; Jou, B.J.D.; Lin, P.F. Dynamic ANN for precipitation estimation and forecasting from radar observations. J. Hydrol. 2007, 334, 250–261. [Google Scholar] [CrossRef]
- Grecu, M.; Krajewski, W.F. A large-sample investigation of statistical procedures for radar-based short-term quantitative precipitation forecasting. J. Hydrol. 2000, 239, 69–84. [Google Scholar] [CrossRef]
- Peleg, N.; Ben-Asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lessons learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef] [Green Version]
- Morin, E.; Krajewski, W.F.; Goodrich, D.C.; Gao, X.; Sorooshian, S. Estimating rainfall intensities from weather radar data: The scale-dependency problem. J. Hydrometeorol. 2003, 4, 782–797. [Google Scholar] [CrossRef] [Green Version]
- Barszcz, M.P. Quantitative rainfall analysis; flow simulation for an urban catchment using input from a weather radar. Geomat. Nat. 2019, 10, 2129–2144. [Google Scholar] [CrossRef]
- Dash, S.S.; Sahoo, B.; Raghuwanshi, N.S. Comparative Assessment of Model Uncertainties in Streamflow Estimation from a Paddy-Dominated Integrated Catchment Reservoir Command; AGU Fall Meeting: Washington, DC, USA, 2018; p. H43C-2386. [Google Scholar]
- Chen, C.; Zhang, Q.; Kashani, M.H.; Jun, C.; Bateni, S.M.; Band, S.S.; Dash, S.S.; Chau, K.W. Forecast of rainfall distribution based on fixed sliding window long short-term memory. Eng. Appl. Comput. Fluid Mech. 2022, 16, 248–261. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; de Marinis, G. Prediction of spring flows using nonlinear autoregressive exogenous (NARX) neural network models. Environ. Monitor. Assess. 2021, 193, 350. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting evapotranspiration in different climates using ensembles of recurrent neural networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Fathi, M.; Kashani, M.H.; Jameii, S.M.; Mahdipour, E. Big Data Analytics in Weather Forecasting: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 1247–1275. [Google Scholar] [CrossRef]
- Ramesh Babu, N.; Bandreddy Anand Babu, C.; Dhanikar, P.R.; Medda, G. Comparison of ANFIS and ARIMA Model for Weather Forecasting. Indian J. Sci. Technol. 2015, 8 (Suppl. S2), 70–73. [Google Scholar] [CrossRef]
- Xiang, Y.; Gou, L.; He, L.; Xia, S.; Wang, W. A SVR–ANN combined model based on ensemble EMD for rainfall prediction. Appl. Soft Comput. 2018, 73, 874–883. [Google Scholar] [CrossRef]
- Tran Anh, D.; Duc Dang, T.; Pham Van, S. Improved Rainfall Prediction Using Combined Pre-Processing Methods and Feed-Forward Neural Networks. J 2019, 2, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Danandeh Mehr, A.; Nourani, V.; Karimi Khosrowshahi, V.; Ghorbani, M.A. A hybrid support vector regression–firefly model for monthly rainfall forecasting. Int. J. Environ. Sci. Technol. 2019, 16, 335–346. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Jabarnejad, M.; Nourani, V. Pareto-optimal MPSA-MGGP: A new gene-annealing model for monthly rainfall forecasting. J. Hydrol. 2019, 571, 406–415. [Google Scholar] [CrossRef]
- Pham, B.T.; Le, L.M.; Le, T.T.; Bui, K.T.T.; Le, V.M.; Ly, H.B.; Prakash, I. Development of Advanced Artificial Intelligence Models for Daily Rainfall Prediction. Atmos. Res. 2020, 237, 104845. [Google Scholar] [CrossRef]
- Diez-Sierra, J.; Jesus, M.d. Long-term rainfall prediction using atmospheric synoptic patterns in semi-arid climates with statistical and machine learning methods. J. Hydrol. 2020, 586, 124789. [Google Scholar] [CrossRef]
- Ghamariadyan, M.; Imteaz, M.A. A Wavelet Artificial Neural Network method for medium-term rainfall prediction in Queensland (Australia) and the comparisons with conventional methods. Int. J. Climatol. 2021, 41, E1396–E1416. [Google Scholar] [CrossRef]
- Danandeh Mehr, A. Seasonal rainfall hindcasting using ensemble multi-stage genetic programming. Theor. Appl. Climatol. 2021, 143, 461–472. [Google Scholar] [CrossRef]
- Jahan, C.S.; Mazumder, Q.H.; Islam, A.T.M.M.; Adham, M.I. Impact of irrigation in Barind area, NW Bangladesh—an evaluation based on the meteorological parameters and fluctuation trend in groundwater table. J. Geol. Soc. India 2010, 76, 134–142. [Google Scholar] [CrossRef]
- Rahman, M.S.; Islam, A.R.M.T. Are precipitation concentration and intensity changing in Bangladesh overtimes? Analysis of the possible causes of changes in precipitation systems. Sci. Total Environ. 2019, 690, 370–387. [Google Scholar] [CrossRef] [PubMed]
- Di Nunno, F.; de Marinis, G.; Gargano, R.; Granata, F. Tide prediction in the Venice Lagoon using Nonlinear Autoregressive Exogenous (NARX) neural network. Water 2021, 13, 1173. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Aravena, R.; Bobee, B. Artificial neural network modeling of water table depth fluctuations. Water Resour. Res. 2001, 37, 885–896. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A.E. Evaluation of seasonally classified inputs for the prediction of daily groundwater levels: NARX networks vs support vector machines. Environ. Model. Assess. 2019, 24, 223–234. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S.; Ahmadi, F.; Lien, N.T.T.; Linh, N.T.T.; Pham, Q.B. Developing hybrid time series and artificial intelligence models for estimating air temperatures. Stoch. Environ. Res. Risk Assess. 2021, 35, 1189–1204. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Groundwater level prediction in Apulia region (Southern Italy) using NARX neural network. Environ. Res. 2020, 190, 110062. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; de Marinis, G. Forecasting of Extreme Storm Tide Events Using NARX Neural Network-Based Models. Atmosphere 2021, 12, 512. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Australia, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Granata, F.; Di Nunno, F. Artificial Intelligence models for prediction of the tide level in Venice. Stoch. Environ. Res. Risk Assess. 2021, 35, 2537–2548. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; J. Wiley: New York, NY, USA, 1998. [Google Scholar]
- Collobert, R.; Bengio, S. SVMTorch: Support vector machines for large-scale regression problems. J. Mach. Learn. Res. 2001, 1, 143–160. [Google Scholar]
- Granata, F.; Di Nunno, F. Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models. Fluids 2022, 7, 20. [Google Scholar] [CrossRef]
- Kittler, J.; Hatef, M.; Duin, R.P.W.; Matas, J. On Combining Classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef] [Green Version]
- Gandhi, I.; Pandey, M. Hybrid Ensemble of classifiers using voting. In Proceedings of the 2015 International Conference on Green Computing and Internet of Things (ICGCIoT), Greater Noida, India, 8–10 October 2015; pp. 399–404. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Kisi, O.; Yaseen, Z.; Shahid, S.; Zounemat-Kermani, M. Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl.-Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Kilinc, H.C. Daily Streamflow Forecasting Based on the Hybrid Particle Swarm Optimization and Long Short-Term Memory Model in the Orontes Basin. Water 2022, 14, 490. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Zhang, G.; Zhang, Z.; Wang, S. Research on Particle Swarm Optimization in LSTM Neural Networks for Rainfall-Runoff Simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neutral Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Zhang, F.; Dai, H.; Tang, D. A Conjunction Method of Wavelet Transform-Particle Swarm Optimization-Support Vector Machine for Streamflow Forecasting. J. Appl. Math. 2014, 2014, 910196. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Amini, A.; Shahabi, H.; Al-Ansari, N.; Hamidi, S.; Singh, S.K.; Thai Pham, B.; Ahmad, B.B.; Ghazvinei, P.T. A Hybrid Intelligence Approach to Enhance the Prediction Accuracy of Local Scour Depth at Complex Bridge Piers. Sustainability 2020, 12, 1063. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.K.; Niu, W.J.; Tang, Z.Y.; Jiang, Z.Q.; Xu, Y.; Liu, Y.; Zhang, H.R. Monthly runoff time series prediction by variational mode decomposition and support vector machine. based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Gandomi, A.H. MSGP-LASSO: An improved multi-stage genetic programming model for streamflow prediction. Inf. Sci. 2021, 561, 181–195. [Google Scholar] [CrossRef]
- Dabral, P.P.; Murry, M.Z. Modelling and Forecasting of Rainfall Time Series Using SARIMA. Environ. Process. 2017, 4, 399–419. [Google Scholar] [CrossRef]
- Alsumaiei, A.A. A Nonlinear Autoregressive Modeling Approach for Forecasting Groundwater Level Fluctuation in Urban Aquifers. Water 2020, 12, 820. [Google Scholar] [CrossRef] [Green Version]
- Di Nunno, F.; Race, M.; Granata, F. A nonlinear autoregressive exogenous (NARX) model to predict nitrate concentration in rivers. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef]
- Iannello, J.P. Time Delay Estimation Via Cross-Correlation in the Presence of Large Estimation Errors. IEEE Trans. Signal Process. 1982, 30, 998–1003. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, A.F.M.K.; Kar, K.K.; Shahid, S.; Chowdhury, R.; Rashid, M.D.M. Evaluation of Spatio-temporal Rainfall Variability and Performance of a Stochastic Rainfall Model in Bangladesh. Int. J. Climatol. 2019, 39, 4256–4273. [Google Scholar] [CrossRef]
- Rahman, M.; Islam, A.H.M.S.; Nadvi, S.Y.M.; Rahman, R.M. Comparative Study of ANFIS and ARIMA Model for Weather Forecasting in Dhaka. In Proceedings of the 2013 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Mahmud, I.; Bari, S.H.; Rahman, M.T.U. Monthly rainfall forecast of Bangladesh using autoregressive integrated moving average method. Environ. Eng. Res. 2017, 22, 162–168. [Google Scholar] [CrossRef] [Green Version]
- Navid, M.A.I.; Niloy, N.H. Multiple Linear Regressions for Predicting Rainfall for Bangladesh. Communications 2018, 6, 1–4. [Google Scholar] [CrossRef] [Green Version]



| Model | Exogenous Inputs |
|---|---|
| A | Tmax, Tmin, H, Vwind, C, S |
| B | H, Vwind, C, S |
| C | Tmax, Tmin, H, Vwind |
| D | H, Vwind |
| E | H |
| Variable | Rangpur | Sylhet | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | σ | CV | Max | Min | Mean | σ | CV | Max | Min | |
| Tmax (°C) | 32.9 | 3.6 | 0.11 | 43.3 | 21.6 | 33.2 | 2.8 | 0.08 | 39.6 | 25.8 |
| Tmin (°C) | 19.9 | 5.5 | 0.28 | 27.7 | 7.3 | 20.3 | 4.5 | 0.22 | 26.3 | 10.6 |
| P (mm) | 179.1 | 203.9 | 1.14 | 1344.0 | 0.0 | 333.7 | 336.3 | 1.01 | 1394.0 | 0.0 |
| H (%) | 80.6 | 7.1 | 0.09 | 92.0 | 40.0 | 78.7 | 8.1 | 0.10 | 93.0 | 47.0 |
| Vwind (m/s) | 1.2 | 0.6 | 0.50 | 3.3 | 0.2 | 1.5 | 0.7 | 0.47 | 5.4 | 0.3 |
| C (okta) | 3.3 | 2.0 | 0.61 | 7.2 | 0.1 | 4.3 | 2.2 | 0.51 | 7.7 | 0.3 |
| S (hours) | 6.4 | 1.5 | 0.23 | 10.8 | 1.7 | 6.3 | 2.0 | 0.32 | 10.6 | 0.0 |
| Stage | ta | Algorithm | Metrics | Model | ||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | ||||
| Training | 1 month | M5P | R2 | 0.88 | 0.85 | 0.87 | 0.80 | 0.79 |
| MAE (mm) | 47 | 53 | 48 | 64 | 67 | |||
| RMSE (mm) | 71 | 77 | 73 | 86 | 90 | |||
| RAE (%) | 28.05 | 30.88 | 28.04 | 37.55 | 39.59 | |||
| SVR | R2 | 0.85 | 0.79 | 0.85 | 0.78 | 0.77 | ||
| MAE (mm) | 51 | 61 | 52 | 62 | 65 | |||
| RMSE (mm) | 75 | 88 | 78 | 89 | 92 | |||
| RAE (%) | 30.13 | 35.55 | 30.09 | 37.05 | 38.12 | |||
| M5P-SVR | R2 | 0.89 | 0.87 | 0.87 | 0.80 | 0.79 | ||
| MAE (mm) | 47 | 49 | 47 | 62 | 64 | |||
| RMSE (mm) | 68 | 71 | 71 | 85 | 88 | |||
| RAE (%) | 27.42 | 28.31 | 27.52 | 36.44 | 37.98 | |||
| 3 months | M5P | R2 | 0.88 | 0.84 | 0.87 | 0.79 | 0.78 | |
| MAE (mm) | 48 | 54 | 49 | 65 | 69 | |||
| RMSE (mm) | 71 | 78 | 73 | 86 | 89 | |||
| RAE (%) | 28.22 | 31.48 | 28.24 | 38.25 | 40.69 | |||
| SVR | R2 | 0.85 | 0.77 | 0.84 | 0.76 | 0.74 | ||
| MAE (mm) | 52 | 62 | 52 | 65 | 67 | |||
| RMSE (mm) | 76 | 91 | 78 | 94 | 95 | |||
| RAE (%) | 30.33 | 36.46 | 30.35 | 38.42 | 39.52 | |||
| M5P-SVR | R2 | 0.89 | 0.87 | 0.87 | 0.79 | 0.78 | ||
| MAE (mm) | 47 | 49 | 47 | 63 | 66 | |||
| RMSE (mm) | 69 | 71 | 71 | 87 | 90 | |||
| RAE (%) | 27.50 | 28.73 | 27.50 | 37.20 | 39.25 | |||
| Testing | 1 month | M5P | R2 | 0.86 | 0.82 | 0.86 | 0.80 | 0.72 |
| MAE (mm) | 69 | 75 | 69 | 83 | 84 | |||
| RMSE (mm) | 96 | 91 | 96 | 95 | 103 | |||
| RAE (%) | 41.99 | 44.84 | 42.02 | 48.64 | 49.41 | |||
| SVR | R2 | 0.84 | 0.79 | 0.83 | 0.78 | 0.78 | ||
| MAE (mm) | 66 | 74 | 67 | 79 | 79 | |||
| RMSE (mm) | 91 | 94 | 92 | 97 | 98 | |||
| RAE (%) | 40.51 | 43.73 | 41.05 | 46.46 | 46.89 | |||
| M5P-SVR | R2 | 0.87 | 0.82 | 0.86 | 0.80 | 0.79 | ||
| MAE (mm) | 62 | 73 | 65 | 76 | 79 | |||
| RMSE (mm) | 88 | 91 | 89 | 92 | 94 | |||
| RAE (%) | 38.09 | 43.15 | 39.65 | 45.04 | 46.56 | |||
| 3 months | M5P | R2 | 0.86 | 0.82 | 0.86 | 0.79 | 0.72 | |
| MAE (mm) | 69 | 75 | 69 | 86 | 87 | |||
| RMSE (mm) | 97 | 93 | 97 | 98 | 104 | |||
| RAE (%) | 42.35 | 50.81 | 42.39 | 44.35 | 51.70 | |||
| SVR | R2 | 0.83 | 0.79 | 0.83 | 0.77 | 0.77 | ||
| MAE (mm) | 67 | 75 | 68 | 82 | 83 | |||
| RMSE (mm) | 92 | 95 | 92 | 99 | 100 | |||
| RAE (%) | 40.81 | 44.83 | 41.40 | 48.38 | 49.05 | |||
| M5P-SVR | R2 | 0.87 | 0.82 | 0.86 | 0.80 | 0.78 | ||
| MAE (mm) | 63 | 75 | 65 | 78 | 83 | |||
| RMSE (mm) | 89 | 93 | 90 | 93 | 96 | |||
| RAE (%) | 38.45 | 44.25 | 39.71 | 46.16 | 48.94 | |||
| Stage | ta | Algorithm | Metrics | Model | ||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | ||||
| Training | 1 month | M5P | R2 | 0.92 | 0.90 | 0.91 | 0.89 | 0.88 |
| MAE (mm) | 62 | 68 | 66 | 73 | 84 | |||
| RMSE (mm) | 85 | 95 | 92 | 102 | 114 | |||
| RAE (%) | 21.14 | 24.21 | 22.98 | 25.32 | 28.87 | |||
| SVR | R2 | 0.90 | 0.86 | 0.88 | 0.84 | 0.84 | ||
| MAE (mm) | 62 | 75 | 68 | 81 | 88 | |||
| RMSE (mm) | 89 | 106 | 98 | 116 | 124 | |||
| RAE (%) | 21.45 | 25.95 | 23.54 | 28.42 | 30.30 | |||
| M5P-SVR | R2 | 0.94 | 0.93 | 0.93 | 0.91 | 0.88 | ||
| MAE (mm) | 55 | 59 | 58 | 64 | 82 | |||
| RMSE (mm) | 76 | 84 | 83 | 91 | 112 | |||
| RAE (%) | 18.64 | 20.67 | 20.28 | 22.38 | 28.28 | |||
| 3 months | M5P | R2 | 0.92 | 0.90 | 0.91 | 0.89 | 0.88 | |
| MAE (mm) | 63 | 70 | 67 | 75 | 86 | |||
| RMSE (mm) | 85 | 97 | 93 | 104 | 118 | |||
| RAE (%) | 21.50 | 24.38 | 23.30 | 26.48 | 34.30 | |||
| SVR | R2 | 0.89 | 0.85 | 0.88 | 0.84 | 0.84 | ||
| MAE (mm) | 64 | 75 | 69 | 82 | 90 | |||
| RMSE (mm) | 90 | 108 | 99 | 117 | 126 | |||
| RAE (%) | 21.89 | 26.24 | 24.08 | 28.77 | 30.64 | |||
| M5P-SVR | R2 | 0.94 | 0.92 | 0.92 | 0.90 | 0.88 | ||
| MAE (mm) | 56 | 62 | 60 | 69 | 85 | |||
| RMSE (mm) | 78 | 85 | 85 | 95 | 114 | |||
| RAE (%) | 19.12 | 21.37 | 20.83 | 24.35 | 28.99 | |||
| Testing | 1 month | M5P | R2 | 0.91 | 0.87 | 0.87 | 0.87 | 0.85 |
| MAE (mm) | 77 | 83 | 83 | 89 | 102 | |||
| RMSE (mm) | 99 | 113 | 111 | 121 | 133 | |||
| RAE (%) | 28.60 | 31.13 | 31.16 | 33.27 | 35.96 | |||
| SVR | R2 | 0.91 | 0.84 | 0.86 | 0.82 | 0.82 | ||
| MAE (mm) | 69 | 78 | 73 | 83 | 92 | |||
| RMSE (mm) | 92 | 106 | 99 | 118 | 125 | |||
| RAE (%) | 25.38 | 27.58 | 27.39 | 31.74 | 34.08 | |||
| M5P-SVR | R2 | 0.92 | 0.89 | 0.89 | 0.88 | 0.85 | ||
| MAE (mm) | 68 | 73 | 73 | 77 | 86 | |||
| RMSE (mm) | 91 | 99 | 99 | 107 | 119 | |||
| RAE (%) | 25.26 | 27.45 | 27.12 | 29.34 | 31.84 | |||
| 3 months | M5P | R2 | 0.90 | 0.87 | 0.87 | 0.85 | 0.83 | |
| MAE (mm) | 80 | 86 | 87 | 92 | 106 | |||
| RMSE (mm) | 103 | 117 | 117 | 130 | 147 | |||
| RAE (%) | 29.31 | 32.26 | 32.63 | 34.79 | 37.70 | |||
| SVR | R2 | 0.90 | 0.84 | 0.87 | 0.83 | 0.82 | ||
| MAE (mm) | 70 | 80 | 75 | 86 | 93 | |||
| RMSE (mm) | 93 | 108 | 102 | 116 | 126 | |||
| RAE (%) | 25.86 | 28.03 | 27.95 | 32.03 | 34.37 | |||
| M5P-SVR | R2 | 0.91 | 0.87 | 0.88 | 0.86 | 0.83 | ||
| MAE (mm) | 69 | 75 | 74 | 79 | 89 | |||
| RMSE (mm) | 93 | 102 | 100 | 109 | 122 | |||
| RAE (%) | 25.57 | 27.94 | 27.73 | 30.07 | 32.87 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nunno, F.; Granata, F.; Pham, Q.B.; de Marinis, G. Precipitation Forecasting in Northern Bangladesh Using a Hybrid Machine Learning Model. Sustainability 2022, 14, 2663. https://doi.org/10.3390/su14052663
Di Nunno F, Granata F, Pham QB, de Marinis G. Precipitation Forecasting in Northern Bangladesh Using a Hybrid Machine Learning Model. Sustainability. 2022; 14(5):2663. https://doi.org/10.3390/su14052663
Chicago/Turabian StyleDi Nunno, Fabio, Francesco Granata, Quoc Bao Pham, and Giovanni de Marinis. 2022. "Precipitation Forecasting in Northern Bangladesh Using a Hybrid Machine Learning Model" Sustainability 14, no. 5: 2663. https://doi.org/10.3390/su14052663
APA StyleDi Nunno, F., Granata, F., Pham, Q. B., & de Marinis, G. (2022). Precipitation Forecasting in Northern Bangladesh Using a Hybrid Machine Learning Model. Sustainability, 14(5), 2663. https://doi.org/10.3390/su14052663









