Reliability Analysis of an Embankment Built and Reinforced in Soft Ground Using LE and FE
Abstract
:1. Introduction
2. Reliability Proposed Analysis Based on the Coupling Method
2.1. Reliability Method-FORM
- I
- Transforming the correlated variables to equivalent normal ones (still correlated) by the principle of normal approximation;
- II
- Calculating the equivalent coefficients of correction in the space;
- III
- Eliminating the correlation by orthogonal decomposition or Cholesky factorization.
2.2. Correlation among Variable Pairs
2.3. Procedure for Coupling—Modeling and Reliability Software
2.4. Procedure for Carrying Out a Reliability Analysis via the Coupling Method
- I
- Modeling the structure into commercial software by inserting the mean values of the parameters and discretizing each layer and reinforcement type (if they exist);
- II
- Defining which variables (input parameters of the model) are random variables. Usually the most common random variables used in probabilistic analyses of geotechnical problems are the bulk unit weight (), cohesion (c), undrained shear strength (), and friction angle ();
- III
- Inserting information into the reliability program about the defined random variables, such as the mean (), the distribution type (∼), and the standard deviation () or the coefficient of variation ();
- IV
- Sometimes, when necessary, a few alterations can be made to the algorithm.
- V
- Performing the coupling algorithm, which obtains the desired results and stores them in a text file. The file contains the results about the search for the design point, the number of iterations, the number of evaluations of the performance equation, convergence history, reliability index, probability of failure, the sensitivity of the random variables at the design point, and the evaluation time.
3. Application in a Case Study
3.1. Model Information
- I
- For the embankment fill material, foundation sand, and interface element: Drained Elastic-Plastic for the SIGMA/W, and Mohr–Coulomb for the SLOPE/W and SLIDE;
- II
- For the soft clay material: Soft Clay (Modified Cam-Clay with pore water pressure change) for the SIGMA/W, and Undrained () for the SLOPE/W and SLIDE;
- III
- For the reinforcement material (geogrid): Structural Beam by considering the Moment of Inertia = 0 m (allowing only tension stress) for the SIGMA/W, and Reinforcement Load by choosing the model developed for geosynthetics for SLOPE/W and SLIDE.
3.2. Statistical Information
3.3. Limit State (LS) Function
3.3.1. Slope Stability
3.3.2. Postconstruction Settlement
4. Results
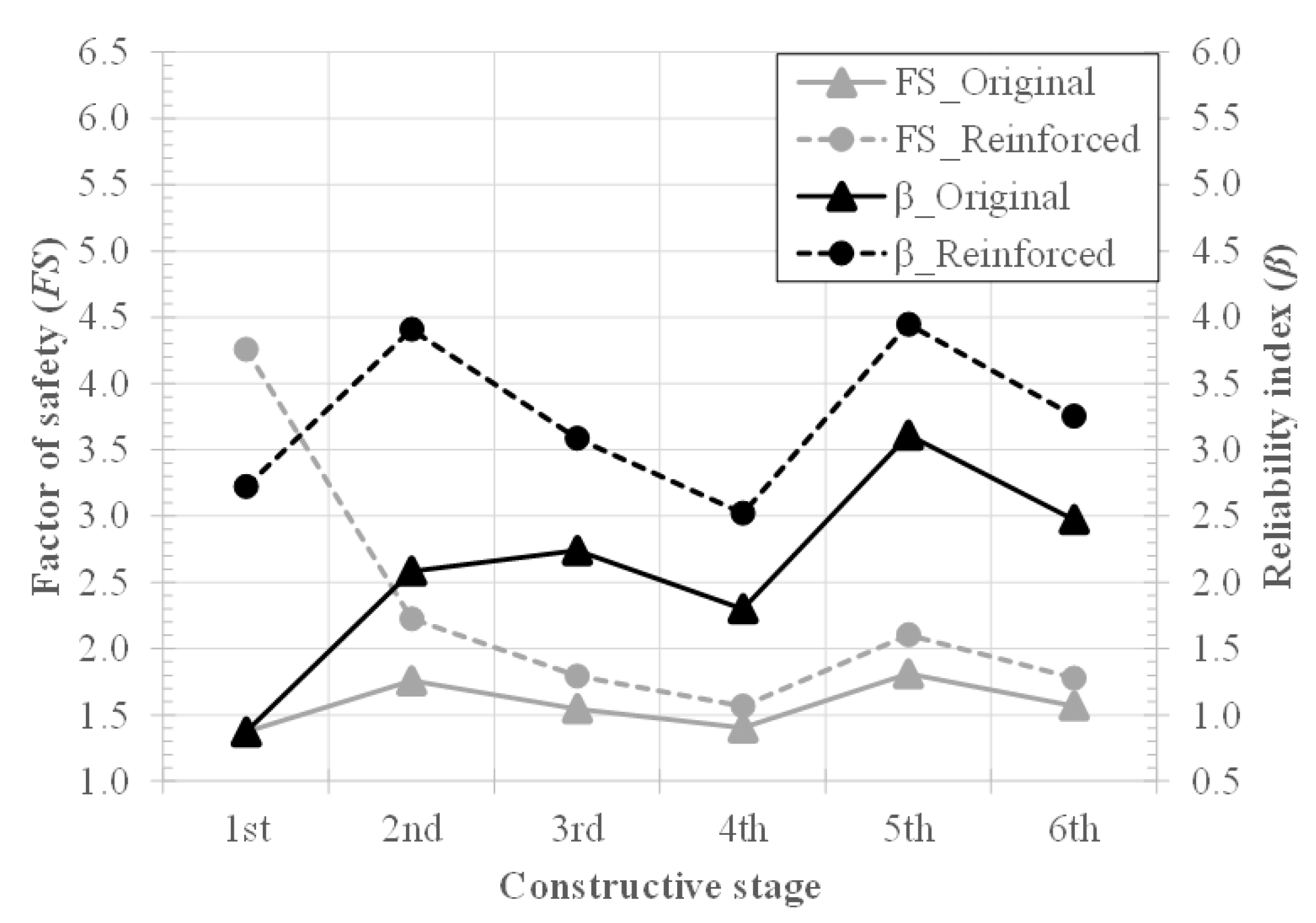
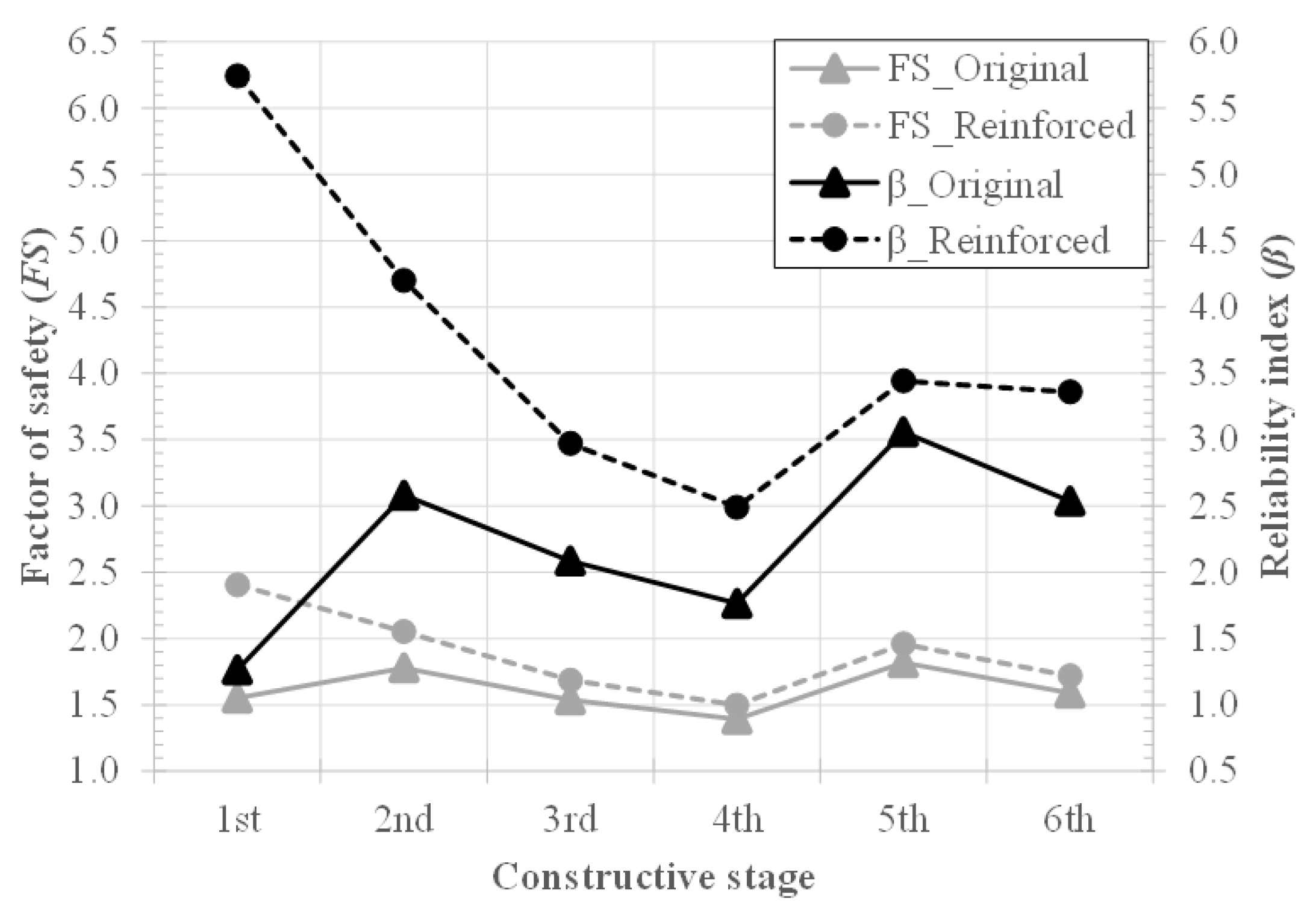
4.1. Deterministic and Probabilistic Stability Analysis
4.2. Comparison of the Probabilistic Performance of Both Couplings
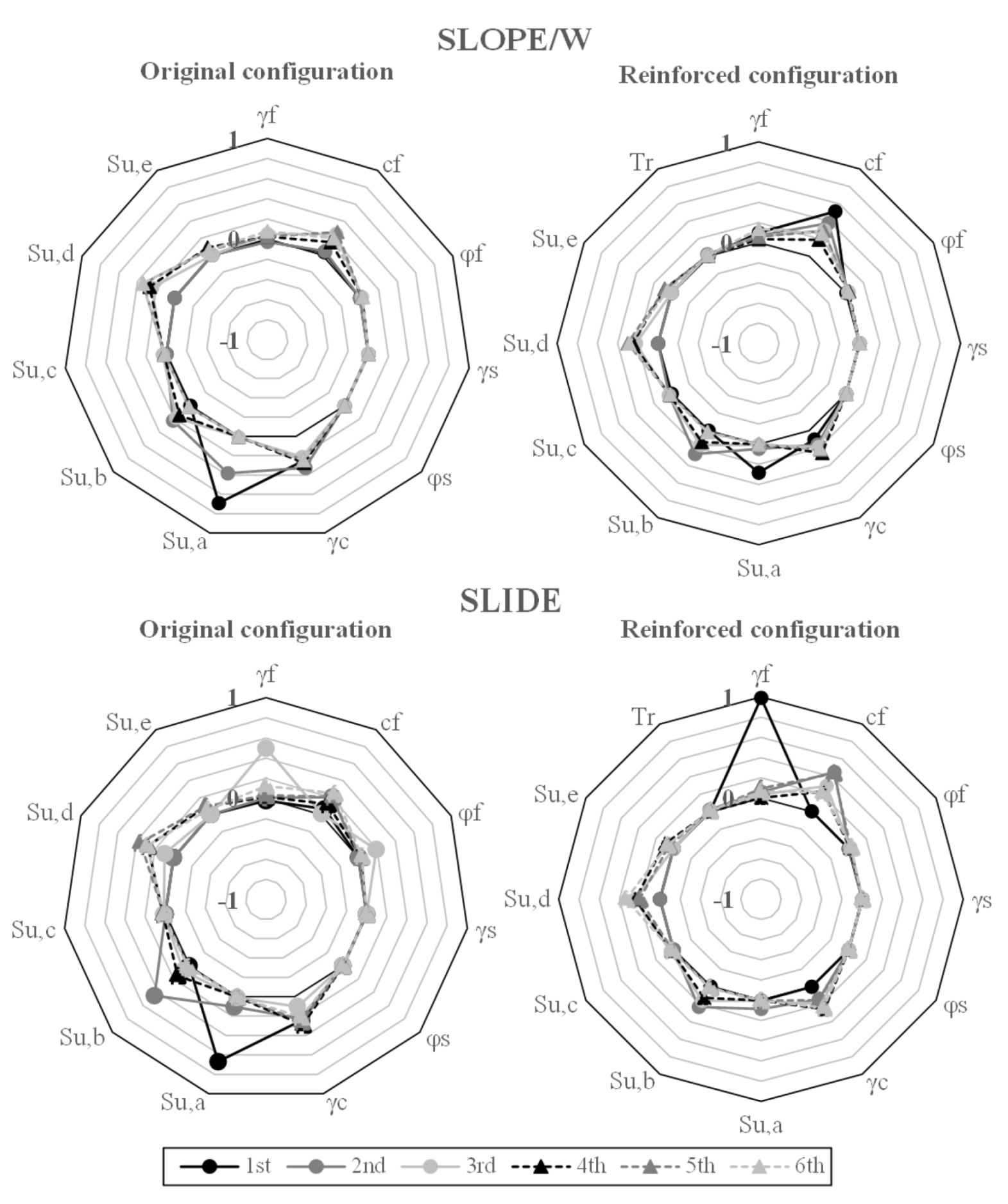
- About how programs assumed the behavior of the reinforcement in the simulation: Precisely, in this study, SLOPE/W took the mobilized reinforcement strength to reduce the activating forces/moments. By contrast, SLIDE assumed the reinforcement strength to increase the resisting forces/moments. Since reinforcement is overdesigned for the first stage (i.e., reinforcement is supposed to work for the last stage, operation), the program assumption presents significant effects for this stage. Indeed, reinforcement at the first stage would most likely resist most of the actions due to the beginning of the surface loading. Consequently, the and are likely to assume high initial values because the reinforcement is supposed to help the foundation soil up to after the sixth stage when the excess of pore water pressure dissipates;
- Each software assumed the searching surface method: Simulations with SLOPE were carried out by adopting the entry and exit search method. At the same time, SLIDE evaluated the stability by running the auto search surface algorithm. Then, discrepancies are expected regarding each simulation’s defined critical slip surface. The critical slip surface may also vary according to configurations assumed for the searching method (e.g., iteration number, node numbers);
- Finally, it is essential to note that critical surfaces do not have to be coincident when comparing the deterministic critical slip surface and the probabilistic one [13,14,15]. The likely change of critical slip surface location at each simulation may also affect the results, mainly for the first stages, associated with significant geometry changes because of the equilibrium berms.
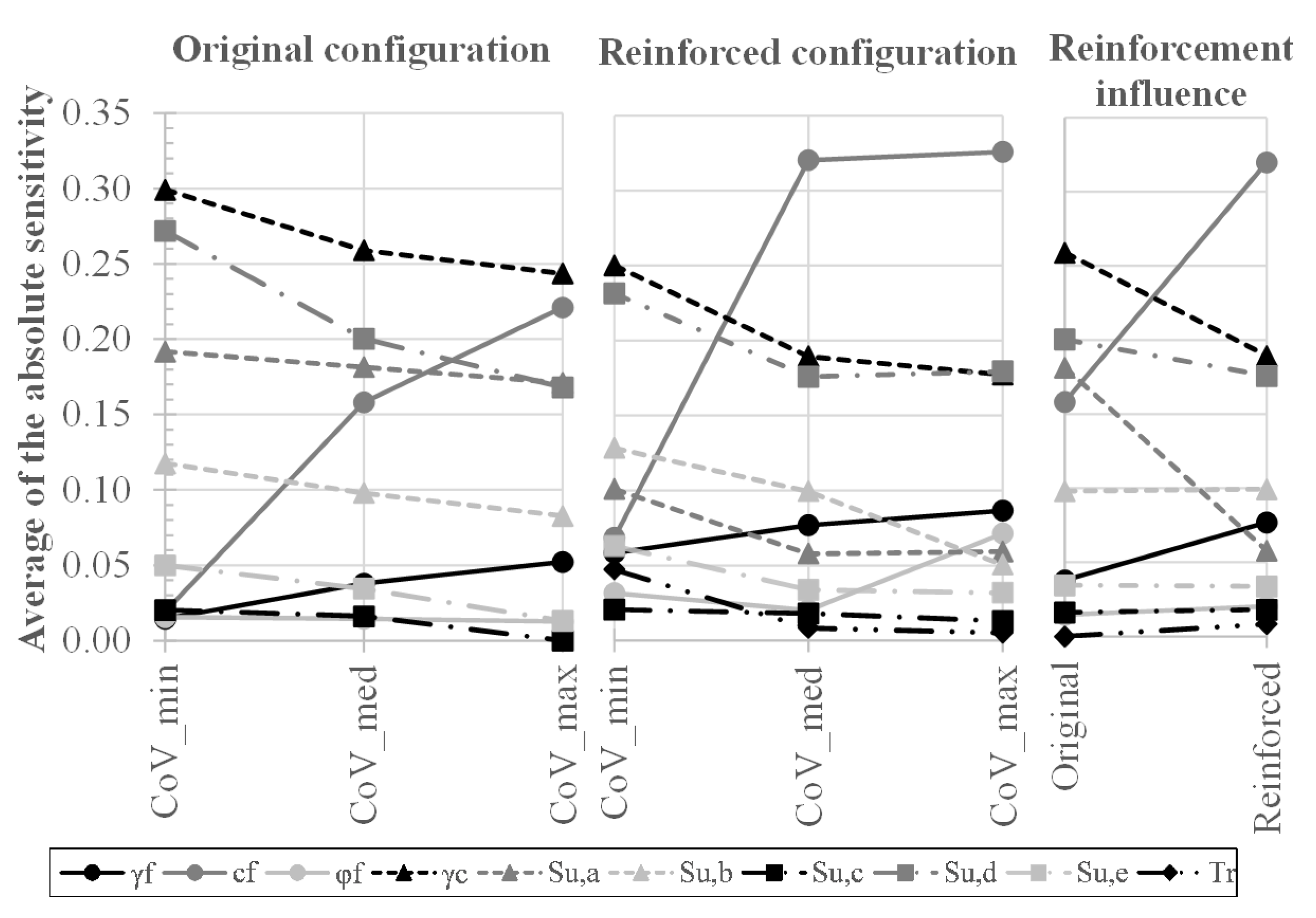
4.3. Influence of the Uncertainty Level of the Stability
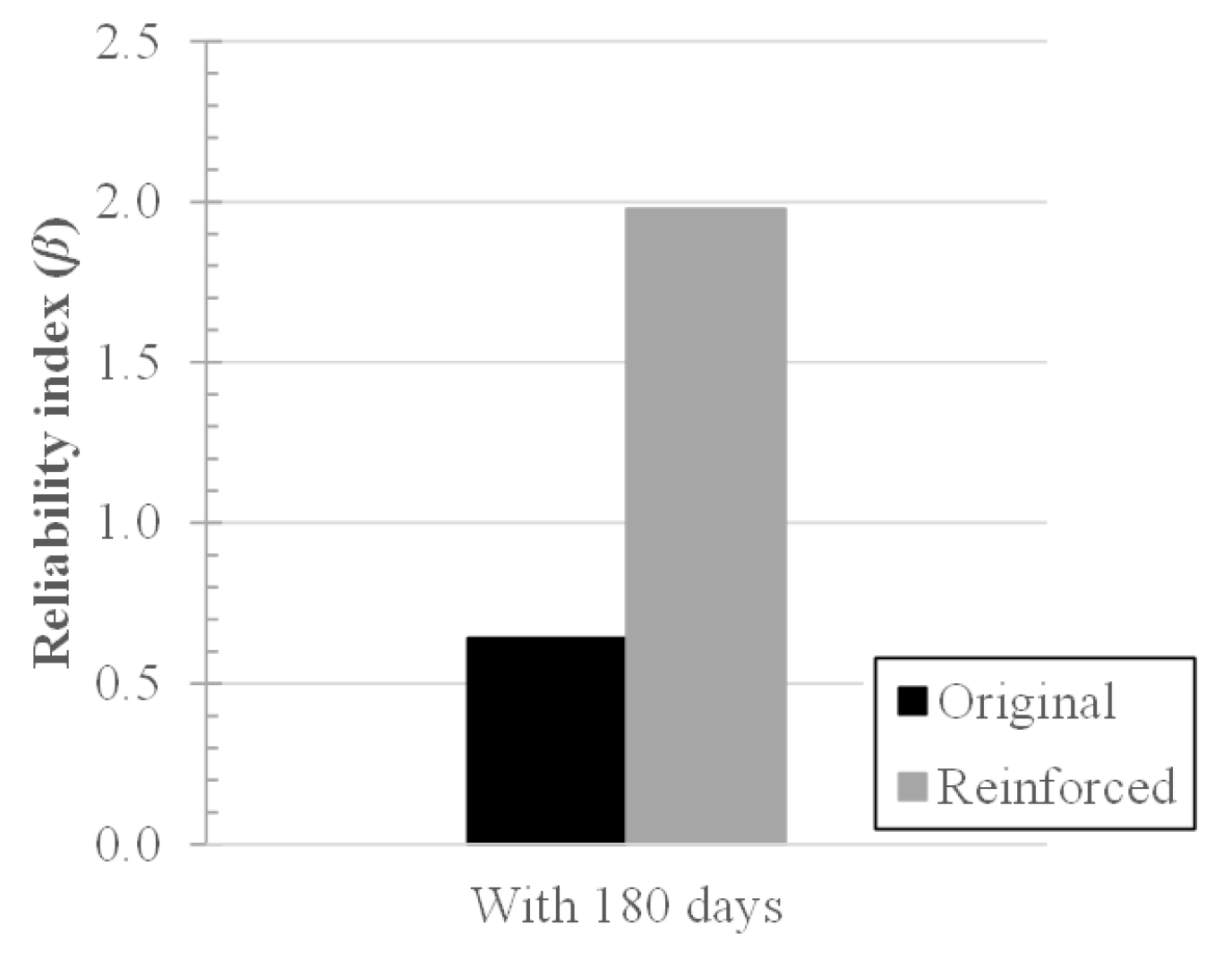
4.4. Probabilistic Performance of the Postconstruction Settlement
4.5. Sensitivity of the Parameters
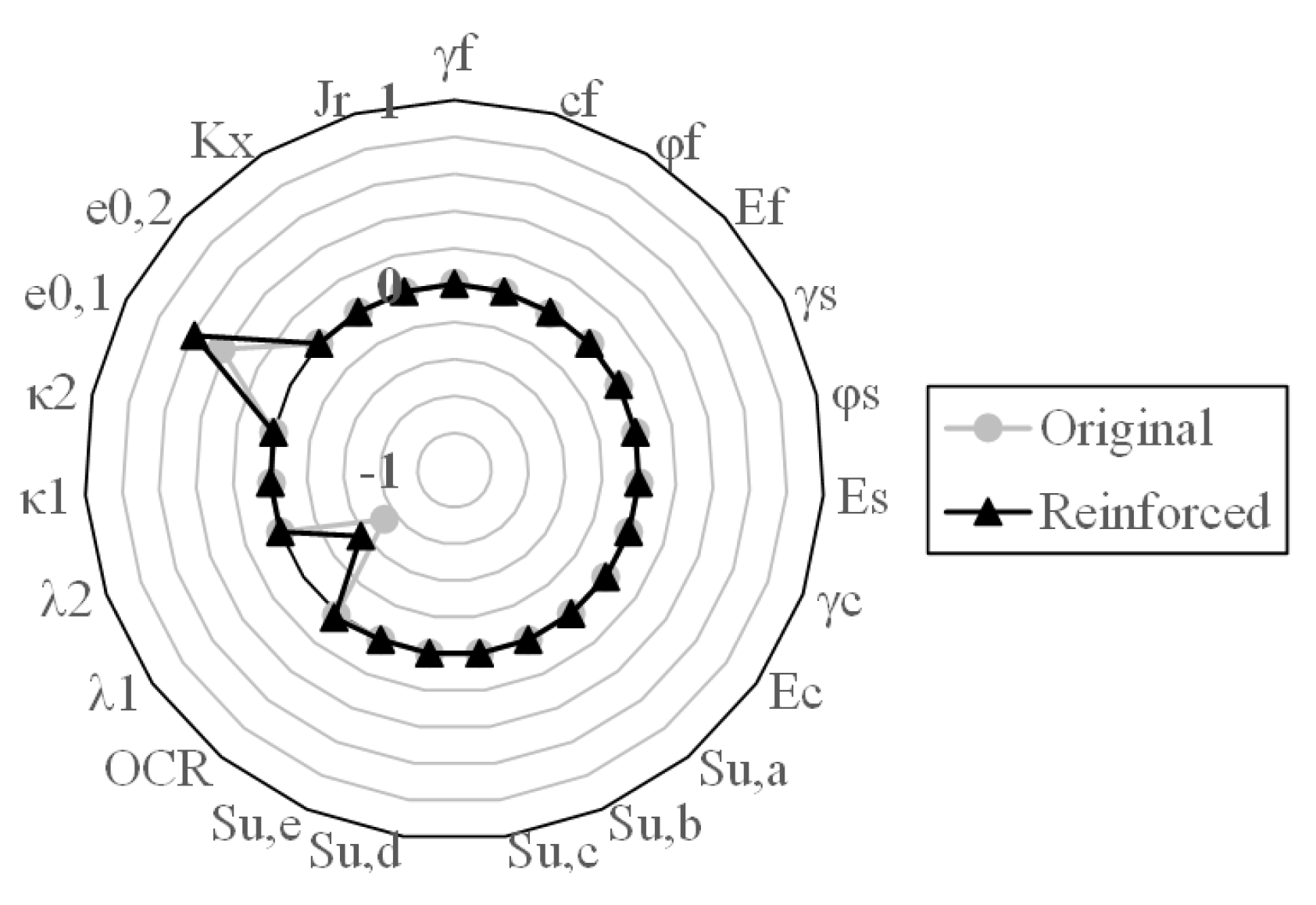
4.6. Validation of the Coupling Method
5. Conclusions
- The coupling method can be used with different commercial programs, widely used in the practical field. In this paper, for example, the reliability analyses were obtained from the application to two well-known commercial programs, GeoStudio (SLOPE/W and SIGMA/W) and RocScience (SLIDE);
- The coupling method can carry an analysis by using LEM and FEM. Indeed, it may be also applied to other methods, such as discrete elements and material point methods;
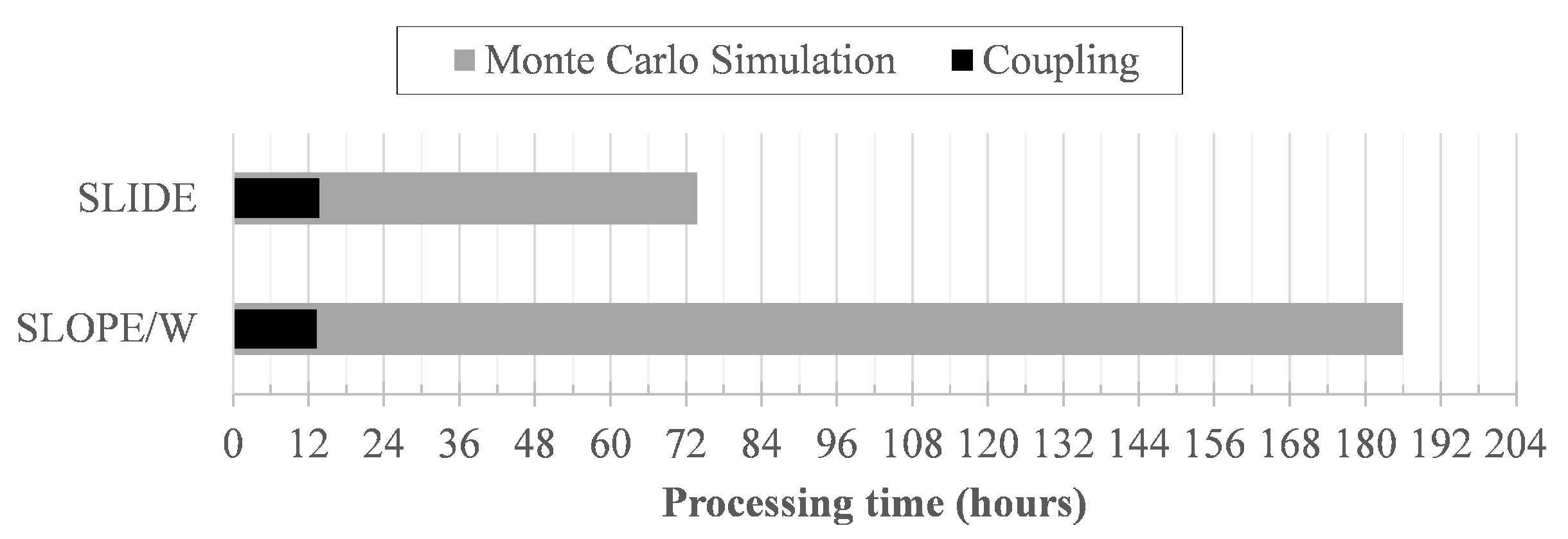
- Comparing the results obtained via the coupling method and the crude MC simulation, the coupling approach presents great precision to approximate the value of using the FORM, as shown by Figure 11. Besides the precision, it is also able to perform a probabilistic analysis with a much lower computational cost; about 7.3% (13.8 times faster) and 18.2% (5.5 times faster) of the total required time by GeoStudio and RocScience, respectively, to process the analysis;
- Besides analyzing the probabilistic stability of the embankment, the coupling method can also carry out probabilistic analysis over several other aspects as these may be described by an LS function. For example, besides the stability condition, a probabilistic analysis was also carried out concerning the postconstruction settlement for the case study;
- By understanding the coupling method, the value of obtained from this cannot be associated with a specific slip surface. As pointed out by the literature, the probabilistic critical slip surface does not coincide with the deterministic one because each evaluation of the model with a different may present different results for the critical slip surface position. Then, it is right to say that the value of obtained by the coupling method refers to the stability or to another aspect associated with the LS function of the entire system, not to a specific slip surface, even though it is the probabilistic one;
- Most probabilistic studies and practice analysis of embankments, even having been constructed by stages and built on soft ground, usually carried out analyses just for the last stage. However, the value of may vary significantly with stages and time, such as those presented by this paper;
- Considering only the deterministic obtained for the models, it can be concluded that the original structure presented a satisfactory safety level (according to the design requirements adopted by the reference). However, the reliability analyses showed another reality where the structure was considered unsatisfactory, according to [48]. As a result, to acquire a good estimation of the safety level and to obtain reliable results during the design conception, both indexes ( and ) need to be tested;
- The probabilistic safety level is strongly influenced by the uncertainty level assumed for the system. This influence may take the structure of a high level of performance to an unsatisfactory level even worse than it. Therefore, it is strongly recommended that be taken according to the tests performed in situ and only if these tests present a satisfactory number of samples, particularly for the most sensitive parameters. The less known about the structure and the parameters involved, the higher the level of uncertainty ( values) is to be adopted;
- The coupling method analyzes the whole process and the convergence history. These data are helpful to identify potential problems or to add other analyses throughout the process, which makes the method more reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cornell, C.A. First order uncertainty analysis of soils deformations and stability. In Proceedings of the 1st International Conference on Application of Statistics and Probability in Soil and Structural Engineering, Hong Kong, China, 13–16 September 1971; pp. 129–144. [Google Scholar]
- Tang, W.; Yucemen, M.; Ang, A. Probability-based short term design of slopes. Can. Geotech. J. 1976, 13, 201–215. [Google Scholar] [CrossRef]
- McGuffey, V.; Grivas, D.; Iori, J.; Kyfor, Z. Conventional and Probabilistic Embankment Design. J. Geotech. Eng. Div. 1982, 108, 1246–1254. [Google Scholar] [CrossRef]
- Oka, Y.; Wu, T.H. System Reliability of Slope Stability. J. Geotech. Eng. 1990, 116, 1185–1189. [Google Scholar] [CrossRef]
- Chowdhury, R.N.; Xu, D.W. Rational Polynomial Technique in Slope Reliability Analysis. J. Geotech. Eng. 1993, 119, 1910–1928. [Google Scholar] [CrossRef]
- Alonso, E.E. Risk analysis of slopes and its application to slopes in Canadian sensitive clays. Géotechnique 1976, 26, 453–472. [Google Scholar] [CrossRef]
- Harr, M.E. Mechanics of Participate Media: A Probabilistic Approach; McGraw-Hill International: New York, NY, USA, 1977; p. 543. [Google Scholar]
- Vanmarcke, E.H. Reliability of earth slopes. J. Geotech. Eng. Div. 1977, 103, 1247–1265. [Google Scholar] [CrossRef]
- Chowdhury, R.N.; A-Grivas, D. Probabilistic Model of Progressive Failure of Slopes. J. Geotech. Eng. Div. 1982, 108, 803–819. [Google Scholar] [CrossRef]
- Bergado, D.; Miura, N.; Chang, J.; Danzuka, M. Reliability assessment of test embankments on soft Bangkok clay by variance reduction and nearest-neighbor methods. Comput. Geotech. 1987, 4, 171–194. [Google Scholar] [CrossRef]
- Christian, J.T.; Ladd, C.C.; Baecher, G.B. Reliability Applied to Slope Stability Analysis. J. Geotech. Eng. 1994, 120, 2180–2207. [Google Scholar] [CrossRef]
- Bergado, D.T.; Patron, B.C.; Youyongwatana, W.; Chai, J.C.; Yudhbir. Reliability-based analysis of embankment on soft Bangkok clay. Struct. Saf. 1994, 13, 247–266. [Google Scholar] [CrossRef]
- Chowdhury, R.N.; Tang, W.H. Comparison of risk models for slopes. In Proceedings of the 5th International Conference on Application of Statistics and Probability in Soil and Structural Engineering; University of British Columbia: Vancouver, BC, Canada, 1987; pp. 863–869. [Google Scholar]
- Li, K.S.; Lumb, P. Probabilistic design of slopes. Can. Geotech. J. 1987, 24, 520–535. [Google Scholar] [CrossRef]
- Hassan, A.M.; Wolff, T.F. Search Algorithm for Minimum Reliability Index of Earth Slopes. J. Geotech. Geoenviron. Eng. 1999, 125, 301–308. [Google Scholar] [CrossRef]
- Low, B.; Tang, W.H. Probabilistic slope analysis using Janbu’s generalized procedure of slices. Comput. Geotech. 1997, 21, 121–142. [Google Scholar] [CrossRef]
- Low, B.; Tang, W.H. Reliability analysis of reinforced embankments on soft ground. Can. Geotech. J. 1997, 34, 672–685. [Google Scholar] [CrossRef]
- Low, B.K.; Gilbert, R.B.; Wright, S.G. Slope Reliability Analysis Using Generalized Method of Slices. J. Geotech. Geoenviron. Eng. 1998, 124, 350–362. [Google Scholar] [CrossRef]
- El-Ramly, H.; Morgenstern, N.; Cruden, D. Probabilistic slope stability analysis for practice. Can. Geotech. J. 2002, 39, 665–683. [Google Scholar] [CrossRef]
- Bhattacharya, G.; Jana, D.; Ojha, S.; Chakraborty, S. Direct search for minimum reliability index of earth slopes. Comput. Geotech. 2003, 30, 455–462. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Z.; Au, S.K. Efficient Monte Carlo Simulation of parameter sensitivity in probabilistic slope stability analysis. Comput. Geotech. 2010, 37, 1015–1022. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Zhang, L.; Tang, W. Back analysis of slope failure with Markov chain Monte Carlo simulation. Comput. Geotech. 2010, 37, 905–912. [Google Scholar] [CrossRef]
- Kang, F.; Han, S.; Salgado, R.; Li, J. System probabilistic stability analysis of soil slopes using Gaussian process regression with Latin hypercube sampling. Comput. Geotech. 2015, 63, 13–25. [Google Scholar] [CrossRef]
- Marandi, S.; Anvar, M.; Bahrami, M. Uncertainty analysis of safety factor of embankment built on stone column improved soft soil using fuzzy logic α-cut technique. Comput. Geotech. 2016, 75, 135–144. [Google Scholar] [CrossRef]
- Ferreira, F.B.; Topa Gomes, A.; Vieira, C.S.; Lopes, M.L. Reliability analysis of geosynthetic-reinforced steep slopes. Geosynth. Int. 2016, 23, 301–315. [Google Scholar] [CrossRef]
- Xia, Y.; Mahmoodian, M.; Li, C.Q.; Zhou, A. Stochastic Method for Predicting Risk of Slope Failure Subjected to Unsaturated Infiltration Flow. Int. J. Geomech. 2017, 17, 04017037. [Google Scholar] [CrossRef]
- Wang, F.; Li, H.; Zhang, Q.L. Response-Surface-Based Embankment Reliability under Incomplete Probability Information. Int. J. Geomech. 2017, 17, 06017021. [Google Scholar] [CrossRef]
- Javankhoshdel, S.; Bathurst, R.J. Deterministic and probabilistic failure analysis of simple geosynthetic reinforced soil slopes. Geosynth. Int. 2017, 24, 14–29. [Google Scholar] [CrossRef]
- Mouyeaux, A.; Carvajal, C.; Bressolette, P.; Peyras, L.; Breul, P.; Bacconnet, C. Probabilistic stability analysis of an earth dam by Stochastic Finite Element Method based on field data. Comput. Geotech. 2018, 101, 34–47. [Google Scholar] [CrossRef]
- Santos, M.G.C.; Silva, J.L.; Beck, A.T. Reliability-based design optimization of geosynthetic-reinforced soil walls. Geosynth. Int. 2018, 25, 442–455. [Google Scholar] [CrossRef]
- Ji, J.; Liao, H.; Low, B. Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations. Comput. Geotech. 2012, 40, 135–146. [Google Scholar] [CrossRef]
- Low, B. FORM, SORM, and spatial modeling in geotechnical engineering. Struct. Saf. 2014, 49, 56–64. [Google Scholar] [CrossRef]
- Jia, J.; Wang, S.; Zheng, C.; Chen, Z.; Wang, Y. FOSM-based shear reliability analysis of CSGR dams using strength theory. Comput. Geotech. 2018, 97, 52–61. [Google Scholar] [CrossRef]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction, 3th ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; p. 506. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and Invariant Second-Moment Code Format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Rackwitz, R.; Flessler, B. Structural reliability under combined random load sequences. Comput. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Ellingwood, B.R. Reliability-based condition assessment and LRFD for existing structures. Struct. Saf. 1996, 18, 67–80. [Google Scholar] [CrossRef]
- Nataf, A. Détermination des distributions de probabilités dont les marges sont données. Comptes Rendus L’AcadéMie Des Sci. 1962, 225, 42–43. [Google Scholar]
- Lebrun, R.; Dutfoy, A. A generalization of the Nataf transformation to distributions with elliptical copula. Probabilistic Eng. Mech. 2009, 24, 172–178. [Google Scholar] [CrossRef]
- Lebrun, R.; Dutfoy, A. An innovating analysis of the Nataf transformation from the copula viewpoint. Probabilistic Eng. Mech. 2009, 24, 312–320. [Google Scholar] [CrossRef]
- Lebrun, R.; Dutfoy, A. Do Rosenblatt and Nataf isoprobabilistic transformations really differ? Probabilistic Eng. Mech. 2009, 24, 577–584. [Google Scholar] [CrossRef]
- Baecher, G.; Christian, J. Reliability and Statistics in Geotechnical Engineering; John Wiley & Sons Ltd.: London, UK, 2003; p. 618. [Google Scholar]
- Beck, A.; Verzenhassi, C. Risk optimization of a steel frame communications tower subject to tornado winds. Lat. Am. J. Solids Struct. 2008, 5, 187–203. [Google Scholar]
- Nascimento, C.M.C. Avaliação de Alternativas de Processos Construtivos de Ferrovias Sobre Solos Moles. Specialization Thesis, Military Institute of Engineering, Rio de Janeiro, RJ, Brazil, 2008. (In Portuguese). [Google Scholar]
- Mesri, G. New design procedure for stability of soft clays. J. Geotech. Geoenvironmental Eng. 1975, 101, 409–412. [Google Scholar] [CrossRef]
- Belo, J.L.P.; Silva, J.L. Reliability Analysis of a Controlled Stage-Constructed and Reinforced Embankment on Soft Ground Using 2D and 3D Models. Front. Built Environ. 2020, 5, 150. [Google Scholar] [CrossRef] [Green Version]
- Azzouz, A.S.; Krizek, R.J.; Corotis, R.B. Regression Analysis of Soil Compressibility. Soils Found. 1976, 16, 19–29. [Google Scholar] [CrossRef] [Green Version]
- USACE. Engineering and Design: Introduction to Probability and Reliability Methods for Use in Geotechnical Engineering; Technical Letter CECW-EG – ETL 1110-2-547; U.S. Army Corps of Engineers: Washington, DC, USA, 1997. [Google Scholar]

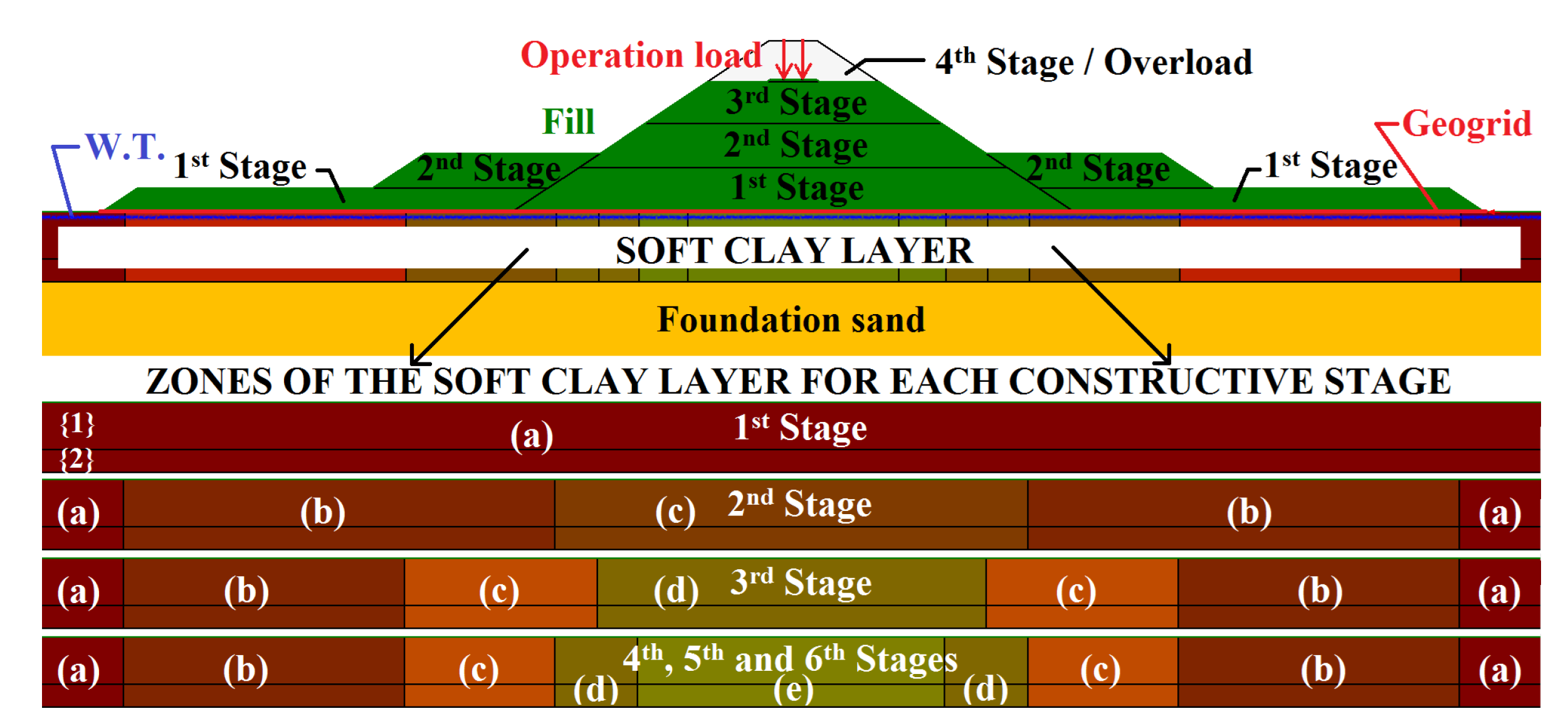



| Stage | Operation | Zone Configuration |
|---|---|---|
| 1 | First fill layer, height of 3.80 m | |
| 2 | Second fill layer, height of 3.70 m | , , |
| 3 | Third fill layer, height of 3.60 m | , , , |
| 4 | Overload fill layer, height of 3.54 m | , , , , |
| 5 | Remove the overload fill layer | , , , , |
| 6 | Execution and operation of the railway | , , , , |
| Parameters | Fill | Sand | Interface | Soft Clay | Reinf | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (kN/m) | 18 | 17 | 18 | 15 | - | |||||||||||||||||
| ’ () | 25.0 | 35.0 | 12.5 | 29.0 | - | |||||||||||||||||
| c’ (kPa) | 25.0 | 0.0 | 12.5 | - | - | |||||||||||||||||
| (kPa) | - | 8 | 16 | 18 | 31 | 45 | 18 | 26 | 28 | 58 | - | |||||||||||
| - | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | - | |||
| - | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | 0.456 | 0.195 | - | |||
| - | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | 0.060 | 0.025 | - | |||
| E (MPa) | 15 | 35 | 15 | 2 | - | |||||||||||||||||
| v | 0.3 | 0.3 | 0.3 | 0.45 | - | |||||||||||||||||
| - | 1.2 | - | ||||||||||||||||||||
| (m/d) | - | 0.001 | - | |||||||||||||||||||
| (MPa) | - | - | 1.5 | |||||||||||||||||||
| (kN/m) | - | - | 200 | |||||||||||||||||||
| Parameter | Distribution | (%) | ||
|---|---|---|---|---|
| min | med | max | ||
| Bulk unit weight () | Normal | 2.5 | 7.5 | 12.5 |
| Cohesion (c) | Normal | 10.0 | 40.0 | 70.0 |
| Friction angle () | Log-Normal | 5.0 | 10.0 | 15.5 |
| E-Modulus (E) | Normal | 2.0 | 22.0 | 42.0 |
| Overconsolidation ratio () | Normal | 10.0 | 22.5 | 35.0 |
| Parameter of the MCC model | Normal | 25.0 | 27.5 | 30.0 |
| Parameter of the MCC model | Normal | 25.0 | 27.5 | 30.0 |
| Initial void ratio () | Normal | 13.0 | 27.5 | 42.0 |
| Hydraulic conductivity (K) | Log-Normal | 200.0 | 250.0 | 300.0 |
| Undrained shear strength () | Log-Normal | 20.0 | 35.0 | 50.0 |
| Reinforcement stiffness () | Normal | 5.0 | 10.0 | 15.0 |
| Reinforcement tensile strength () | Normal | 5.0 | 10.0 | 15.0 |
| Pair | c | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.5 | 1 | −0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.5 | -0.3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 1 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0.5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0.5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 1 | 0.512 | 0.354 | 0.290 | 0.208 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.512 | 1 | 0.692 | 0.567 | 0.407 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.354 | 0.692 | 1 | 0.820 | 0.587 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.290 | 0.567 | 0.820 | 1 | 0.717 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.5 | 0.208 | 0.407 | 0.587 | 0.717 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.368 | 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.368 | 1 | 0 | 0.7 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.368 | 0.5 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.368 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.5 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belo, J.L.d.P.; Lins da Silva, J.; de Queiroz, P.I.B. Reliability Analysis of an Embankment Built and Reinforced in Soft Ground Using LE and FE. Sustainability 2022, 14, 2224. https://doi.org/10.3390/su14042224
Belo JLdP, Lins da Silva J, de Queiroz PIB. Reliability Analysis of an Embankment Built and Reinforced in Soft Ground Using LE and FE. Sustainability. 2022; 14(4):2224. https://doi.org/10.3390/su14042224
Chicago/Turabian StyleBelo, Jean Lucas dos Passos, Jefferson Lins da Silva, and Paulo Ivo Braga de Queiroz. 2022. "Reliability Analysis of an Embankment Built and Reinforced in Soft Ground Using LE and FE" Sustainability 14, no. 4: 2224. https://doi.org/10.3390/su14042224
APA StyleBelo, J. L. d. P., Lins da Silva, J., & de Queiroz, P. I. B. (2022). Reliability Analysis of an Embankment Built and Reinforced in Soft Ground Using LE and FE. Sustainability, 14(4), 2224. https://doi.org/10.3390/su14042224







