A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty
Abstract
:1. Introduction
2. Literature Review
2.1. Multi-Attribute Reverse Auctions (MARA) and Its Extentions
2.2. Supplier Selection and Green Supplier Selection
2.3. Hesitant Fuzzy Sets (HFS) and Its Applications
3. Preliminaries
- (1)
- If , then ; If , then ;
- (2)
- If , then , ; , ; , .
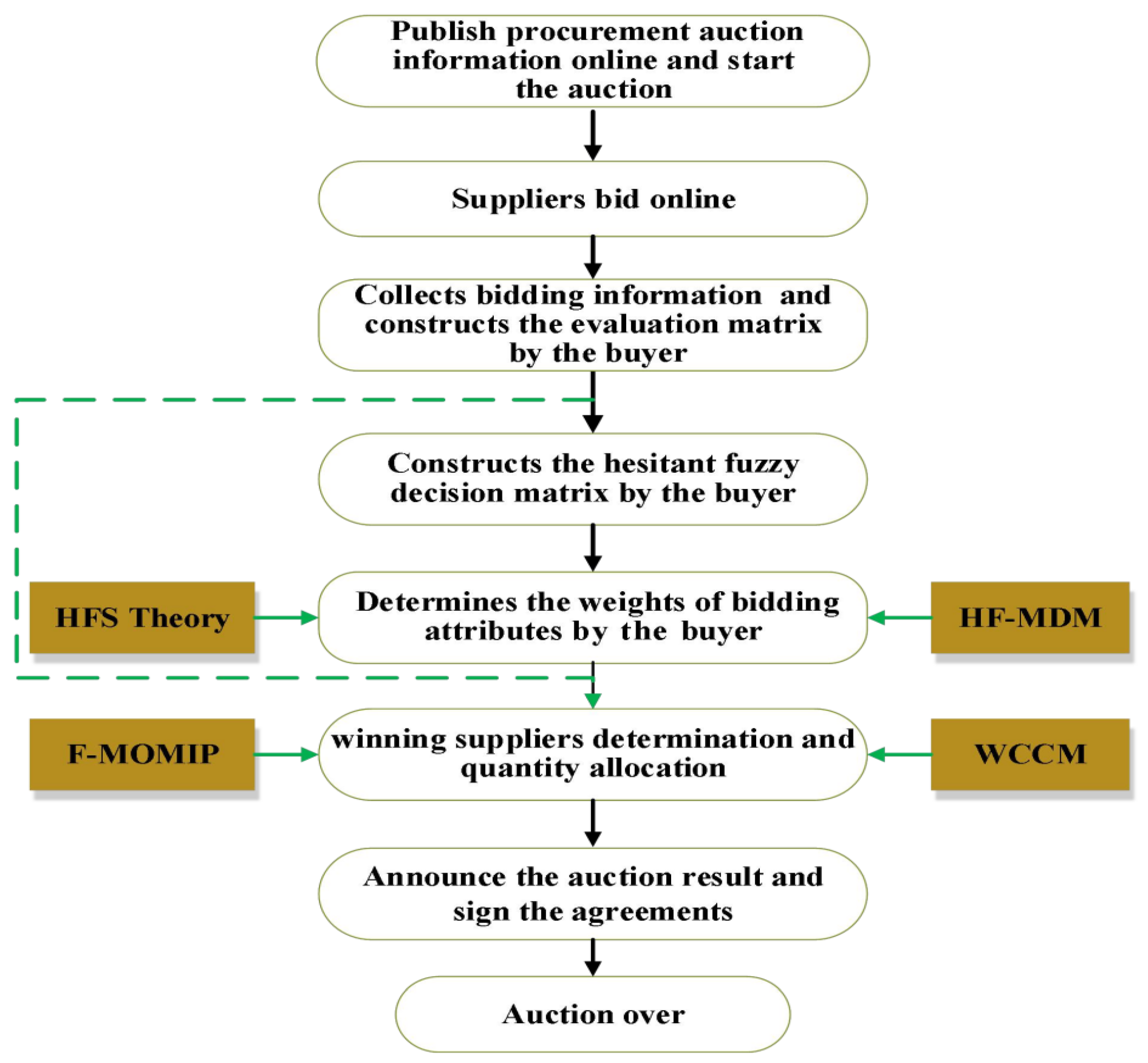
4. Description of the Online Multi-Sourcing Multi-Attribute Reverse Auction (OMSMARA)
- ①
- It is assumed that the purchaser is taking a sealed OMARA, all the suppliers participating in the online auction bid truthfully and independently, and supposing that there is no collusion among them.
- ②
- The buyer does not precisely know the importance of the relevant attributes of the product, and incomplete attribute weight information exists.
- ③
- Due to the uncertain market environment and potential risks, it is assumed that each attribute values in the suppliers’ submitted bids are described by TrFNs.
- ④
- Due to the limitation of cognition and specialty, the purchaser gives a preliminary evaluation value on the membership (satisfaction) degree that the attribute value of each bidding alternatives meets the requirement using HFS.
- ⑤
- It is assumed that the reverse auction in this paper only considers the form of single-round auction. Multiple rounds and interactive situations are not considered temporarily.
- ⑥
- It is assumed that the online procurement auction process generates a certain amount of setup cost for the buyer when signing the auction agreements with the winning bidders. We do not consider the auction participation fee of suppliers temporarily.
5. The Proposed Decision Framework of OMSMARA for Green Supplier Selection under Mixed Uncertainty
5.1. Initial Bidding Evaluation Matrix Construction
5.2. Determination of the Attribute Weights
5.3. Determination of the Winning Suppliers and Their Quantity Allocations
6. Numerical Example
7. Sensitivity Analysis
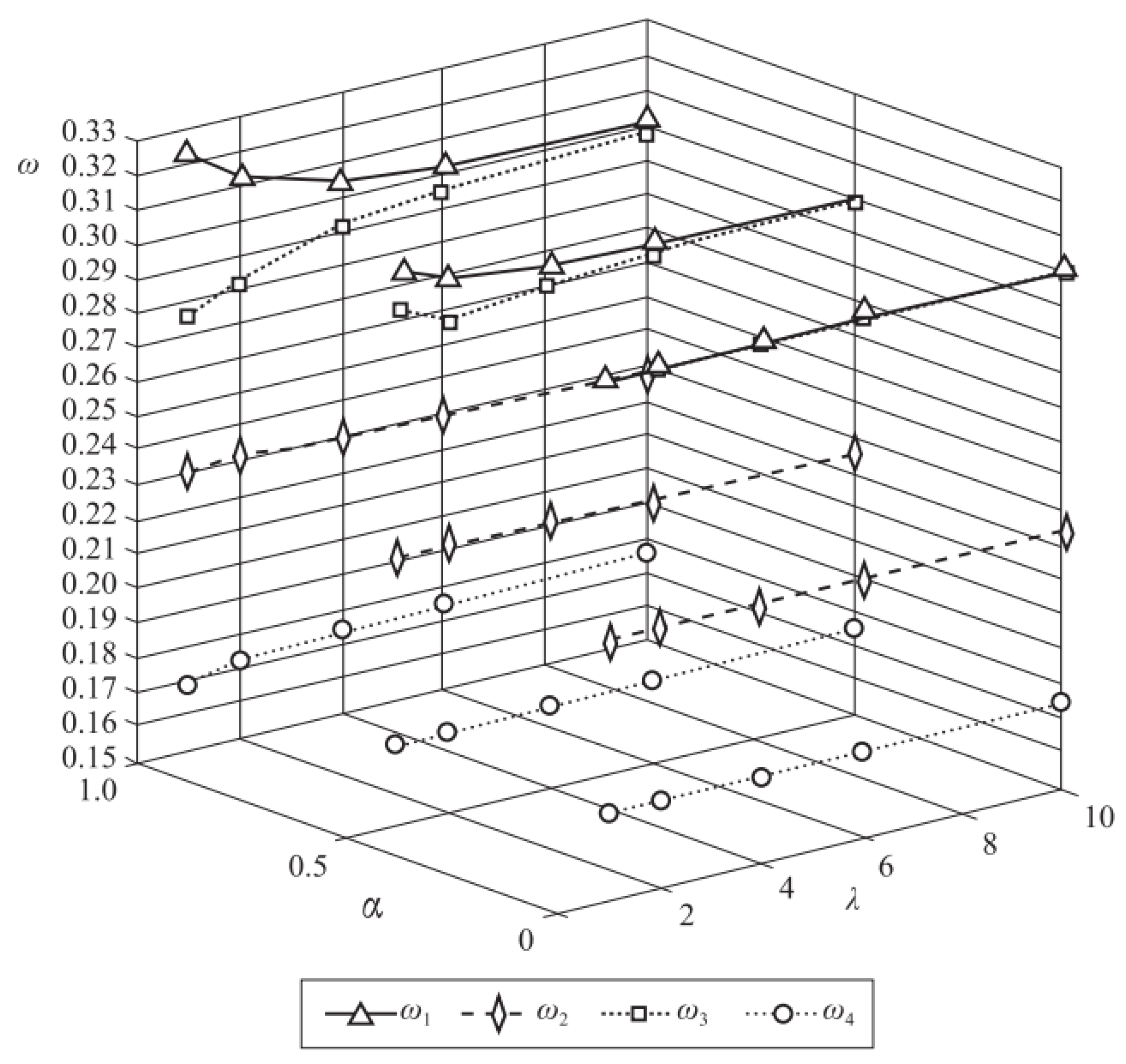
7.1. The Effect of on Attribute Weights
- (1)
- When , the weight vector, , does not change with . When or 1, and are decreasing, while and are increasing.
- (2)
- When = 1, 2, 4, or 6, and are increasing, while and are decreasing. However, = 10, and are increasing, while and are decreasing.
7.2. The Effect of the Changes in the Attribute Weight Vector, , on the Optimal Solutions of Model-6
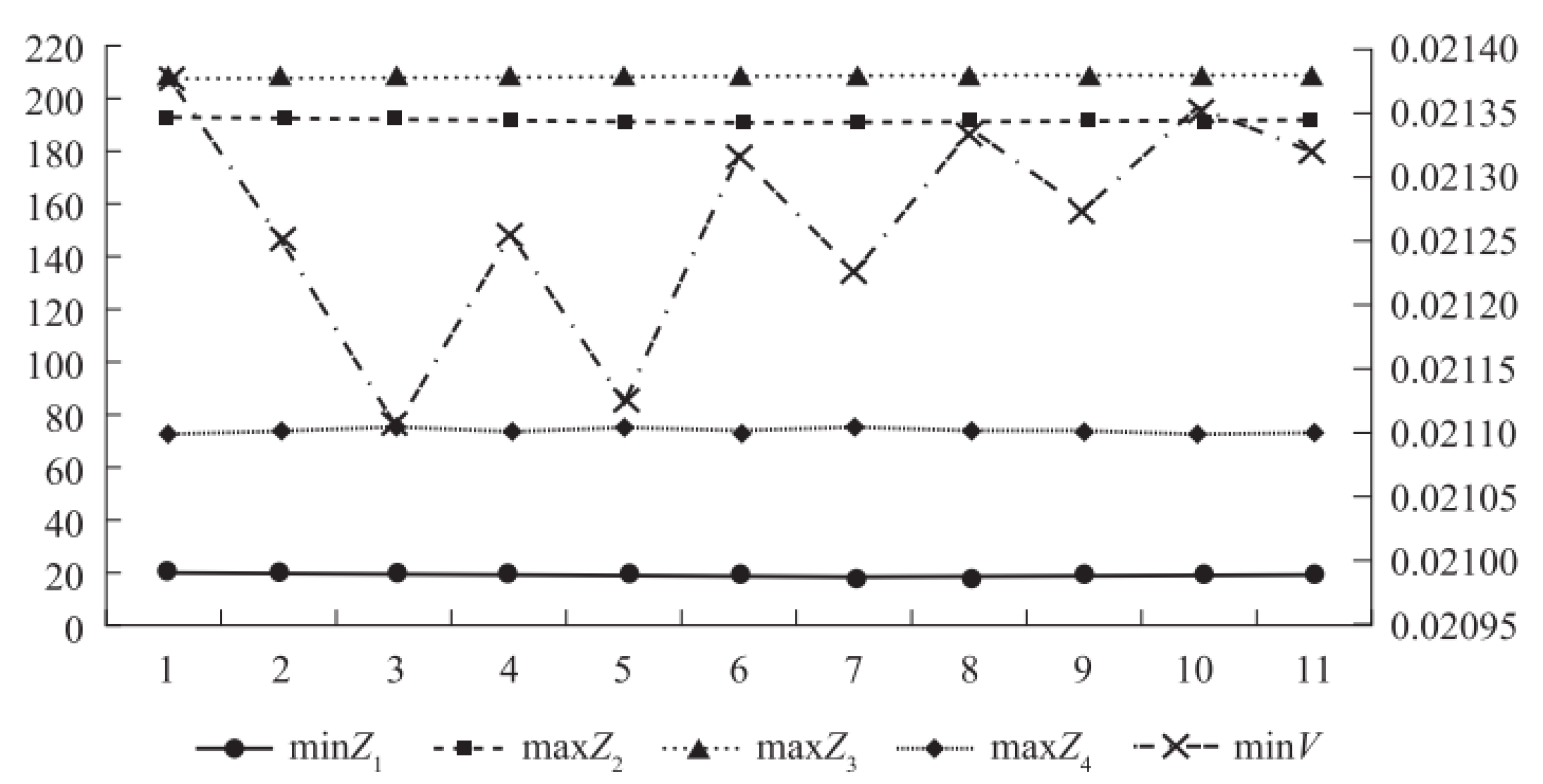
7.3. The Effect of the Changes in the Sub-Objective Weight Vector, (), on the Optimal Solutions of Model-6
8. Comparative Analysis
8.1. The Comparison with the Results Obtained by the Simple Additive Weighting (SAW) Method
8.2. The Comparison with the Results Obtained by -Constraint Method
8.3. The Comprehensive Comparison with the Other Related Literature
- (1)
- Compared with previous theoretical and applied research literatures on reverse auction and multi-attribute reverse auction, most of the previous literatures were developed from the perspective of game theory, such as [11,12,16,17,20,22,23,24,26,27,33], and less from the perspective of decision and optimization. In addition, the existing multi-attribute reverse auction literature from the perspective of decision and optimization, such as [13,14,19,25,28,30], did not consider the complex uncertain situation in the auction process, carried out analysis through simple multi-attribute decision method, or did not consider the real situation of multi-source procurement auction, and almost no online multi-sourcing multi-attribute reverse auction (OMSMARA) has been applied to the selection and order allocation of green suppliers. The most similar to this study in the literature [29], which studied the winner determination of risk-averse buyers in the multi-attribute reverse auction of clean energy equipment procurement with incomplete information and applied MARA to the winner determination of green suppliers of clean energy equipment. However, this paper fails to comprehensively consider the information uncertainty, the psychological influence of hesitation, and the application of fuzzy multi-objective optimization theory, and the proposed method cannot solve the problem of determining and quantitatively allocating multiple winning suppliers at the same time. To sum up, it can be seen that, compared with the previous application research on multi-attribute reverse auction, the research in this paper enriches theoretically and expands the application, which is helpful for promoting the promotion and development of auction theory and its application.
- (2)
- Compared with the previous literature on (green) supplier selection, the previous literature is more about the method of multi-attribute decision making or fuzzy multi-attribute decision making to select the right supplier. For example, [21,30,31,33,46,47] and some literatures model and solve the selection and order allocation problems of suppliers through common mathematical optimization methods, such as [32,34,35,36]. However, some of the above literature studies do not take into account the requirements of green attributes in green procurement, some rarely consider the application efficiency and practicability in real procurement, and almost no literature considers the application of OMSMARA technology to the selection and order allocation problem of green suppliers. The literature that are most similar to this study are [27] and [48]. The former introduces the multi- attribute auction mechanism into the universal supplier selection problem. However, it fails to take into account the possible uncertainties of bidding information in the process of procurement auction, the minds of decision-makers, and other aspects, as well as the requirements of green procurement multi-green attributes, which restricts the practicability and promotion of the research results. While the latter only applies MCDM and multi-objective optimization approach to solving the supplier selection and order allocation with green criteria, it neither considers the existence of uncertainty nor provides a more comprehensive and simple decision-making method to solve the problem of green supplier selection. However, the research in this paper makes up for the shortcomings of the above research. It not only considers the requirements of multi-green attributes in green procurement comprehensively, but also considers the various uncertainties faced by the auction parties. In addition, the decision method framework based on OMSMARA proposed by us can not only improve the value of procurement and reduce the cost of procurement. Moreover, it can effectively improve the efficiency of purchasing decision and the practicability of the decision-making method framework. The research contents of this paper not only enrich the theoretical system of decision-making method of green supplier selection, but also provide more practical decision-making method reference for more purchasing departments.
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| (0.3000, 0.2250, 0.3000, 0.1750) | (0.3103, 0.2276, 0.2897, 0.1724) | (0.3231, 0.2308, 0.2769, 0.1692) | |
| (0.3000, 0.2250, 0.3000, 0.1750) | (0.3052, 0.2281, 0.2927, 0.1740) | (0.3129, 0.2321, 0.2825, 0.1725) | |
| (0.3000, 0.2250, 0.3000, 0.1750) | (0.3015, 0.2271, 0.2964, 0.1749) | (0.3043, 0.2301, 0.2910, 0.1746) | |
| (0.3000, 0.2250, 0.3000, 0.1750) | (0.3004, 0.2265, 0.2979, 0.1752) | (0.3012, 0.2287, 0.2947, 0.1754) | |
| (0.3000, 0.2250, 0.3000, 0.1750) | (0.2998, 0.2260, 0.2989, 0.1753) | (0.2997, 0.2273, 0.2972, 0.1758) |
| Z1 (min) | Z2 (max) | Z3 (max) | Z4 (max) | V (min) | ||
|---|---|---|---|---|---|---|
| (0.3000,0.2250, 0.3000,0.1750)—1 | 19.1408 | 193.4599 | 210.0669 | 73.7783 | 0.021379 | (300,150,0,250,300) |
| (0.3103,0.2276, 0.2897, 0.1724)—2 | 19.2294 | 193.0836 | 209.864 | 74.7148 | 0.021254 | (300,150,0,250,300) |
| (0.3231,0.2308, 0.2769, 0.1692)—3 | 19.3390 | 192.6191 | 209.6138 | 75.8717 | 0.021099 | (300,150,0,250,300) |
| (0.3052,0.2281, 0.2927, 0.1740)—4 | 19.1877 | 193.1053 | 209.8394 | 74.6121 | 0.02125 | (300,150,0,250,300) |
| (0.3129,0.2321, 0.2825, 0.1725)—5 | 19.2551 | 192.6351 | 209.5436 | 75.7261 | 0.021122 | (300,150,0,250,300) |
| (0.3015,0.2271, 0.2964, 0.1749)—6 | 19.1541 | 193.2247 | 209.8943 | 74.2607 | 0.021316 | (300,150,0,250,300) |
| (0.3043,0.2301, 0.2910, 0.1746)—7 | 19.1830 | 192.9330 | 209.7014 | 74.9805 | 0.021224 | (300,150,0,250,300) |
| (0.3004,0.2265, 0.2979, 0.1752)—8 | 19.1408 | 193.4599 | 210.0669 | 73.7783 | 0.021379 | (300,150,0,250,300) |
| (0.3012,0.2287, 0.2947, 0.1754)—9 | 19.1533 | 193.1038 | 209.8053 | 74.5716 | 0.021276 | (300,150,0,250,300) |
| (0.2998,0.2260, 0.2989,0.1753)—10 | 19.1391 | 193.3708 | 209.9971 | 73.9711 | 0.021354 | (300,150,0,250,300) |
| (0.2997,0.2273, 0.2972,0.1758)—11 | 19.1356 | 193.2537 | 209.9056 | 74.2253 | 0.021317 | (300,150,0,250,300) |
References
- Deng, Q.; Qin, Y.; Ahmad, N. Relationship between Environmental Pollution, Environmental Regulation and Resident Health in the Urban Agglomeration in the Middle Reaches of Yangtze River, China: Spatial Effect and Regulating Effect. Sustainability 2022, 14, 7801. [Google Scholar] [CrossRef]
- Qu, S.; Xu, Y.; Ji, Y.; Feng, C.; Wei, J.; Jiang, S. Data-Driven Robust Data Envelopment Analysis for Evaluating the Carbon Emissions Efficiency of Provinces in China. Sustainability 2022, 14, 13318. [Google Scholar] [CrossRef]
- Ehsan, E.; Zainab, K.; Muhammad, Z.T.; Zhang, H.; Xing, L. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation 2022, 117, 102255. [Google Scholar] [CrossRef]
- Ehsan, E.; Zainab, K. Estimating smart energy inputs packages using hybrid optimisation technique to mitigate environmental emissions of commercial fish farms. Appl. Energ. 2022, 326, 119602. [Google Scholar] [CrossRef]
- Abbas, A.; Zhao, C.; Waseem, M.; Ahmad, R. Analysis of Energy Input–Output of Farms and Assessment of Greenhouse Gas Emissions: A Case Study of Cotton Growers. Front. Environ. Sci. 2021, 9, 826838. [Google Scholar] [CrossRef]
- Abbas, A.; Waseem, M.; Yang, M. An ensemble approach for assessment of energy efficiency of agriculture system in Pakistan. Energ. Effic. 2020, 13, 683–696. [Google Scholar] [CrossRef]
- Maditati, D.R.; Munim, Z.H.; Schramm, H.-J.; Kummer, S. A review of green supply chain management: From bibliometric analysis to a conceptual framework and future research directions. Resour. Conserv. Recycl. 2018, 139, 150–162. [Google Scholar] [CrossRef]
- Asha, L.N.; Dey, A.; Yodo, N.; Aragon, L.G. Optimization approaches for multiple conflicting objectives in sustainable green supply chain management. Sustainability 2022, 14, 12790. [Google Scholar] [CrossRef]
- Li, C.; Liu, Q.; Li, Q.; Wang, H. Does Innovative Industrial Agglomeration Promote Environmentally-Friendly Development? Evidence from Chinese Prefecture-Level Cities. Sustainability 2022, 14, 13571. [Google Scholar] [CrossRef]
- Zhu, M.; Yang, H.; Yuan, H.D. Talent internationalization and OFDI of China. Stud. in Sci. of Sci. 2019, 37, 245–253. (In Chinese) [Google Scholar] [CrossRef]
- Teich, J.E.; Wallenius, H.; Wallenius, J.; Zaitsev, A. A multi-attribute e-auction mechanism for procurement: Theoretical foundations. Eur. J. Oper. Res. 2006, 175, 90–100. [Google Scholar] [CrossRef]
- Pinker, E.J.; Seidmann, A.; Vakrat, Y. Managing online auctions: Current business and research issues. Manag. Sci. 2003, 49, 1457–1484. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.-B. Reverse auction with buyer–supplier negotiation using bi-level distributed programming. Eur. J. Oper. Res. 2011, 211, 601–611. [Google Scholar] [CrossRef]
- Huang, M.; Qian, X.; Fang, S.-C.; Wang, X. Winner determination for risk aversion buyers in multi-attribute reverse auction. Omega 2016, 59, 184–200. [Google Scholar] [CrossRef]
- Long, P.; Teich, J.; Wallenius, H.; Wallenius, J. Multi-attribute online reverse auctions: Recent research trends. Eur. J. Oper. Res. 2015, 242, 1–9. [Google Scholar] [CrossRef]
- Xu, S.X.; Huang, G.Q. Efficient Multi-Attribute Multi-Unit Auctions for B2B E-Commerce Logistics. Prod. Oper. Manag. 2016, 26, 292–304. [Google Scholar] [CrossRef]
- Bichler, M.; Kalagnanam, J. Configurable offers and winner determination in multi-attribute auctions. Eur. J. Oper. Res. 2005, 160, 380–394. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, J.; Cheng, T.E.; Hua, G.; Chen, C. An optimal efficient multi-attribute auction for transportation procurement with carriers having multi-unit supplies. Omega 2018, 83, 249–260. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.; Hu, Q. Optimal procurement strategies by reverse auctions with stochastic demand. Econ. Model. 2013, 35, 430–435. [Google Scholar] [CrossRef]
- Xu, J.; Feng, Y.; He, W. Procurement auctions with ex post cooperation between capacity constrained bidders. Eur. J. Oper. Res. 2017, 260, 1164–1174. [Google Scholar] [CrossRef]
- Simić, D.; Kovačević, I.; Svirčević, V.; Simić, S. 50 years of fuzzy set theory and models for supplier assessment and selection: A literature review. J. Appl. Log. 2017, 24, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Che, Y.-K. Design Competition Through Multidimensional Auctions. RAND J. Econ. 1993, 24, 668. [Google Scholar] [CrossRef]
- David, E.; Azoulay-Schwartz, R.; Kraus, S. Bidding in sealed-bid and English multi-attribute auctions. Decis. Support Syst. 2005, 42, 527–556. [Google Scholar] [CrossRef]
- Bellosta, M.-J.; Kornman, S.; Vanderpooten, D. Preference-based English reverse auctions. Artif. Intell. 2011, 175, 1449–1467. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.-B. Solving a sealed-bid reverse auction problem by multiple-criterion decision-making methods. Comput. Math. Appl. 2008, 56, 3261–3274. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Wang, Y.; Li, Y.; Tong, X. An Incentive Mechanism in Mobile Crowdsourcing Based on Multi-Attribute Reverse Auctions. Sensors 2018, 18, 3453. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, V.; Panchal, G.B.; Kumar, S. Universal supplier selection via multi-dimensional auction mechanisms for two-way competition in oligopoly market of supply chain. Omega 2014, 47, 127–137. [Google Scholar] [CrossRef]
- Singh, R.K.; Benyoucef, L. Fuzzy Logic and Interval Arithmetic-Based TOPSIS Method for Multicriteria Reverse Auctions. Serv. Sci. 2012, 4, 101–117. [Google Scholar] [CrossRef]
- Qian, X.; Fang, S.C.; Huang, M.; Wang, X. Winner determination of loss-averse buyers with incomplete information in multi- attribute reverse auctions for clean energy device procurement. Energy 2019, 177, 276–292. [Google Scholar] [CrossRef]
- Wang, S.; Qu, S.; Goh, M.; Wahab, M.I.M.; Zhou, H. Integrated Multi-stage Decision-Making for Winner Determination Problem in Online Multi-attribute Reverse Auctions Under Uncertainty. Int. J. Fuzzy Syst. 2019, 21, 2354–2372. [Google Scholar] [CrossRef]
- Harridan, S.; Cheaitou, A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput. Oper. Res. 2017, 81, 282–304. [Google Scholar] [CrossRef]
- Demirtas, E.A.; Ustun, O. An integrated multi-objective decision making process for supplier selection and order allocation. Omega 2005, 36, 76–90. [Google Scholar] [CrossRef]
- Rao, C.; Xiao, X.; Goh, M.; Zheng, J.; Wen, J. Compound mechanism design of supplier selection based on multi-attribute auction and risk management of supply chain. Comput. Ind. Eng. 2017, 105, 63–75. [Google Scholar] [CrossRef]
- Bohner, C.; Minner, S. Supplier selection under failure risk, quantity and business volume discounts. Comput. Indust. Eng. 2017, 104, 145–155. [Google Scholar] [CrossRef]
- Cheraghalipour, A.; Farsad, S. A bi-objective sustainable supplier selection and order allocation considering quantity discounts under disruption risks: A case study in plastic industry. Comput. Ind. Eng. 2018, 118, 237–250. [Google Scholar] [CrossRef]
- Assellaou, H.; Ouhbi, B.; Frikh, B. Multi-Objective Programming for Supplier Selection and Order Allocation under Disruption Risk and Demand, Quality, and Delay Time Uncertainties. Int. J. Bus. Anal. 2018, 5, 30–56. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Inter. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Tong, X.; Yu, L. MADM based on distance and correlation coefficient measures with decision-maker preferences under a hesitant fuzzy environment. Soft Comput. 2015, 20, 4449–4461. [Google Scholar] [CrossRef]
- Xu, Z.; Xia, M. On distance and correlation measures of hesitant fuzzy information. Int. J. Intell. Syst. 2011, 26, 410–425. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, X. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl.-Based Syst. 2013, 52, 53–64. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. The TODIM analysis approach based on novel measured functions under hesitant fuzzy environment. Knowl.-Based Syst. 2014, 61, 48–58. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.-Q.; Hu, J.-H. Consensus building for hesitant fuzzy preference relations with multiplicative consistency. Comput. Ind. Eng. 2019, 128, 387–400. [Google Scholar] [CrossRef]
- Meng, F.; Chen, X. Correlation Coefficients of Hesitant Fuzzy Sets and Their Application Based on Fuzzy Measures. Cogn. Comput. 2015, 7, 445–463. [Google Scholar] [CrossRef]
- Dong, J.-Y.; Wan, S.-P. A new trapezoidal fuzzy linear programming method considering the acceptance degree of fuzzy constraints violated. Knowl.-Based Syst. 2018, 148, 100–114. [Google Scholar] [CrossRef]
- Wan, S.-P.; Dong, J.-Y. Possibility linear programming with trapezoidal fuzzy numbers. Appl. Math. Model. 2014, 38, 1660–1672. [Google Scholar] [CrossRef]
- Chai, J.; Liu, J.N.; Ngai, E.W. Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Syst. Appl. 2013, 40, 3872–3885. [Google Scholar] [CrossRef]
- Qu, S.; Shu, L.; Yao, J. Optimal pricing and service level in supply chain considering misreport behavior and fairness concern. Comput. Ind. Eng. 2022, 174, 108759. [Google Scholar] [CrossRef]
- Babbar, C.; Amin, S.H. A multi-objective mathematical model integrating environmental concerns for supplier selection and order allocation based on fuzzy QFD in beverages industry. Expert Syst. Appl. 2018, 92, 27–38. [Google Scholar] [CrossRef]
- Qu, S.; Li, Y.; Ji, Y. The mixed integer robust maximum expert consensus models for large-scale GDM under uncertainty circumstances. Appl. Soft Comput. 2021, 107, 107369. [Google Scholar] [CrossRef]
- Qu, S.; Wei, J.; Wang, Q.; Li, Y.; Jin, X.; Chaib, L. Robust minimum cost consensus models with various individual preference scenarios under unit adjustment cost uncertainty. Inform. Fusion 2023, 89, 510–526. [Google Scholar] [CrossRef]
- Qu, S.; Xu, L.; Mangla, S.K.; Chan, F.T.S.; Zhu, J.; Arisian, S. Matchmaking in reward-based crowdfunding platforms: A hybrid machine learning approach. Int. J. Prod. Res. 2022, 60, 7551–7571. [Google Scholar] [CrossRef]
- Ji, Y.; Li, H.; Zhang, H. Risk-Averse Two-Stage Stochastic Minimum Cost Consensus Models with Asymmetric Adjustment Cost. Group Decis. Negot. 2021, 31, 261–291. [Google Scholar] [CrossRef] [PubMed]
| Indices/Sets | Descriptions |
| m | The number of bidding suppliers (or their bidding alternatives). |
| n | The number of evaluation attributes. |
| I | The index set of all suppliers (or bidding alternatives), . |
| J | The index set of all evaluation attributes, |
| J B | The index of benefit-type evaluation attribute. |
| J C | The index of cost-type evaluation attribute. |
| The i-th supplier, | |
| The i-th supplier’s bidding alternatives, | |
| The j-th evaluation attribute, . | |
| The initial bidding evaluation matrix, . | |
| The attribute values in bid alternative i w.r.t attribute j, and . | |
| The normalized fuzzy bid evaluation matrix, . | |
| The normalized attribute values in the bid alternative i with respect to attribute j, and . | |
| The initial hesitant fuzzy decision matrix of buyer, . | |
| The normalized hesitant fuzzy decision matrix, . | |
| Hesitant fuzzy element (HFE) that the evaluation value of Ai with respect to Gj. | |
| The l-th biggest membership degree in , , and indicates the number of membership degrees in . | |
| Z | The total procurement value of the buyer in the OMSMARA. |
| Y | The total procurement cost of the buyer in the OMSMARA. |
| The sub-objective of Z in Model-2. | |
| The normalized sub-objective of Zi in Model-3. | |
| The sub-objective of Y in Model-2. | |
| The normalized sub-objective of Yi in Model-3. | |
| V | The comprehensive objective of Model-3. |
| Parameters | Descriptions |
| The risk preference coefficient of the buyer, . | |
| The distance preference coefficient of the buyer. | |
| Distance measure coefficient, for any positive constant. | |
| The relative weights of the sub-objective in the Model-3. | |
| The relative weights of the sub-objective in the Model-3. | |
| Q | The total demand of the buyer. |
| The budget of the buyer. | |
| N | The max number of winning bidders. |
| The capacity(in quantities of production) of the supplier i. | |
| The unit product price from the supplier i, and . | |
| The possible delay time in delivery of the supplier i, and . | |
| The warranty period of the supplier i, and . | |
| The after-sales service level of the supplier i, and . | |
| A positive constant denotes the fixed setup and contract cost of the buyer for purchasing production from the winning suppliers. | |
| The weight of the j-th evaluation attribute, . | |
| Decision variables | Descriptions |
| The order quantity allocated to supplier i. | |
| 1, if supplier i is selected to allocate the procurement quantity; 0, otherwise; |
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| I | {1,2,3,4,5} | 0 | 300 | ||
| J | {1,2,3,4} | 0.5 | 250 | ||
| JB | {3,4} | 1 | 300 | ||
| JC | {1,2} | 0.125 | 250 | ||
| Q | 1000 | 0.125 | 300 | ||
| N | 4 | 20 | 1 | 8000 |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 () | [5,6,7,8] | [1,2,3,4] | [8,9,10,11] | [90,91,92,93] |
| A2 () | [6,7,8,9] | [2,3,4,5] | [10,11,12,13] | [89,90,91,92] |
| A3 () | [6,7,8,9] | [2,3,4,5] | [8,9,10,11] | [90,91,93,94] |
| A4 () | [4,5,6,7] | [1,2,4,5] | [10,12,13,14] | [92,93,94,95] |
| A5 () | [4,5,6,7] | [1,3,4,5] | [10,11,12,13] | [90,91,93,94] |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 () | [0.1674,0.1913, 0.2232,0.2679] | [0.1127,0.1503, 0.2255,0.4510] | [0.1630,0.1834, 0.2037,0.2241] | [0.2189,0.2214, 0.2238,0.2262] |
| A2 () | [0.1488,0.1674, 0.1913,0.2232] | [0.0902,0.1127, 0.1503,0.2255] | [0.2037,0.2241, 0.2445,0.2649] | [0.2165,0.2189, 0.2214,0.2238] |
| A3 () | [0.1488,0.1674, 0.1913,0.2232] | [0.0902,0.1127, 0.1503,0.2255] | [0.1630,0.1834, 0.2037,0.2241] | [0.2189,0.2214, 0.2262,0.2287] |
| A4 () | [0.1913,0.2232, 0.2679,0.3348] | [0.0902,0.1127, 0.2255,0.4510] | [0.2037,0.2445, 0.2649,0.2852] | [0.2238,0.2262, 0.2287,0.2311] |
| A5 () | [0.1913,0.2232, 0.2679,0.3348] | [0.0902,0.1127, 0.1503,0.4510] | [0.2037,0.2241, 0.2445,0.2649] | [0.2189,0.2214, 0.2262,0.2287] |
| G1 | G2 | G3 | G4 | |
|---|---|---|---|---|
| A1 () | {0.4, 0.5} | {0.6, 0.7} | {0.3, 0.4} | {0.3, 0.4, 0.5} |
| A2 () | {0.3, 0.4} | {0.3, 0.4, 0.5} | {0.4, 0.6, 0.7} | {0.4, 0.5, 0.6} |
| A3 () | {0.3, 0.4} | {0.3, 0.4, 0.5} | {0.3, 0.4} | {0.5, 0.6} |
| A4 () | {0.6, 0.8} | {0.3, 0.5} | {0.6, 0.7, 0.8} | {0.6, 0.7} |
| A5 () | {0.6, 0.8} | {0.2, 0.3, 0.4} | {0.4, 0.6, 0.7} | {0.5, 0.6} |
| H | G1 | G2 | G3 | G4 |
|---|---|---|---|---|
| A1 () | {0.4, 0.5} | {0.6, 0.6, 0.7} | {0.3, 0.3, 0.4} | {0.3, 0.4, 0.5} |
| A2 () | {0.3, 0.4} | {0.3, 0.4, 0.5} | {0.4, 0.6, 0.7} | {0.4, 0.5, 0.6} |
| A3 () | {0.3, 0.4} | {0.3, 0.4, 0.5} | {0.3, 0.3, 0.4} | {0.5, 0.5, 0.6} |
| A4 () | {0.6, 0.8} | {0.3, 0.3, 0.5} | {0.6, 0.7, 0.8} | {0.6, 0.6, 0.7} |
| A5 () | {0.6, 0.8} | {0.2, 0.3, 0.4} | {0.4, 0.6, 0.7} | {0.5, 0.5, 0.6} |
| Bids (Suppliers) | Z1 | Z2 | Z3 | Z4 | Y1 | Y2 | Y3 | Y4 | V |
|---|---|---|---|---|---|---|---|---|---|
| xi/qi | xi/qi | xi/qi | xi/qi | xi/qi | xi/qi | xi/qi | xi/qi | xi/qi | |
| A1 () | 1/150 | 1/300 | 1/300 | 1/300 | 1/300 | 1/300 | 1/300 | 1/300 | 1/300 |
| A2 () | 1/250 | 1/150 | 1/150 | 0/0 | 1/250 | 1/150 | 1/150 | 1/100 | 1/150 |
| A3 () | 1/300 | 0/0 | 0/0 | 1/150 | 1/300 | 0/0 | 0/0 | 1/300 | 0/0 |
| A4 () | 0/0 | 1/250 | 1/250 | 1/250 | 0/0 | 1/250 | 1/250 | 0/0 | 1/250 |
| A5 () | 1/300 | 1/300 | 1/300 | 1/300 | 1/150 | 1/300 | 1/300 | 1/300 | 1/300 |
| Optimal value 2 | 19.2294 | 193.0836 | 209.864 | 74.7148 | 1080 | 6180 | 6680 | 1080 | 0.02125 |
| V (min) | |||
|---|---|---|---|
| (1/8,1/8,1/8,1/8,1/8,1/8,1/8,1/8) | (1,1,0,1,1) | (300,150,0,250,300) | 0.021254 |
| (1/4,1/4,1/4,1/4,0,0,0,0) | (1,1,0,1,1) | (300,150,0,250,300) | 0.042507 |
| (0,0,0,0,1/4,1/4,1/4,1/4) | (1,0,1,1,1) | (300,0,150,250,300) | 9.107 × 10−18 |
| (0,1/2,1/2,0,0,0,0,0) | (1,1,0,1,1) | (300,150,0,250,300) | 6.87 × 10−8 |
| (0,0,0,0,0,1/2,1/2,0) | (1,1,0,1,1) | (300,150,0,250,300) | 1.11 × 10−16 |
| (1/6,2/6,2/6,1/6,0,0,0,0) | (1,1,0,1,1) | (300,150,0,250,300) | 0.0283 |
| (0,0,0,0,1/6,2/6,2/6,1/6) | (1,0,1,1,1) | (300,0,150,250,300) | 9.02 × 10−17 |
| (1/16,3/16,3/16,1/16,1/16,3/16,3/16,1/16) | (1,1,0,1,1) | (300,150,0,250,300) | 0.0106 |
| (1/8,1/8,1/8,1/8, 1/8,1/8,1/8,1/8) | (22.498,193.084, 209.864,74.712) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | −191.895 |
| (1/4,1/4,1/4,1/4, 0, 0, 0, 0) | (22.498,193.084, 209.864,74.712) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | −113.790 |
| (0, 0, 0, 0, 1/4,1/4,1/4,1/4) | (20.257,181.904, 196.533,51.553) | (1080,6980, 7480,1080) | (300,250,300, 150,0) | −270 |
| (0, 0, 0, 0, 0,1/2,1/2,0) | (22.501,191.380, 208.188,74.715) | (1080,6180, 6680,1080) | (300,0,150, 250,300) | 0 |
| (0,1/2,1/2,0, 0, 0, 0, 0) | (22.498,193.084, 209.864,74.712) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | −201.474 |
| (1/6,2/6,2/6,1/6, 0, 0, 0, 0) | (22.498,193.084, 209.864,74.712) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | −143.018 |
| (0, 0, 0, 0, 1/6,2/6,2/6,1/6) | (20.257,181.904, 196.533,51.553) | (1080,6980, 7480,1080) | (300,250,300, 150,0) | −180 |
| (1/16,3/16,3/16,1/16, 1/16,3/16,3/16,1/16) | (22.498,193.084, 209.864,74.712) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | −146.316 |
| (19.2294,193.0836,74.7148 ,1080,6980,7480,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8640 |
| (19.2294,193.0836,74, 1080,6980,7480,1080) | (22.4032,192.9976,74.0000) | (1080,6197, 6681,1080) | (281,169,0, 250,300) | 209.6753 |
| (19.2294,193.0836,74.7148,1080,6180,6680,1080) | (22.4983,193.0836,74.7148) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8639 |
| (19.2294,193,74.7148, 1080,6180,6680,1080) | (22.5009,191.3797,74.7148) | (1080,6180, 6680,1080) | (300,0,150, 250,300) | 208.1875 |
| (19.2294,193.0836,75, 1080,6180,6680,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8639 |
| (22,193,74.7148,1080, 6180,6680,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8640 |
| (22,200,74.7148,1080, 6180,6680,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8640 |
| (22,200,74.7148,1080, 6980,7480,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8640 |
| (19.2294,193.0836,75, 1080,6980,7480,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,150,0, 250,300) | 209.8639 |
| (19.2294,193.0836,74.7148,980,6180,6680,1080) | (22.5009,191.3797,74.7148) | (1080,6180, 6680,1080) | (300,0,150, 250,300) | 208.1875 |
| (19.2294,193.0836,74.7148,980,6980,7480,1080) | (22.4983,193.0836,74.7122) | (1080,6180, 6680,1080) | (300,0,150, 250,300) | 209.8639 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ji, Y.; Wahab, M.I.M.; Xu, D.; Zhou, C. A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty. Sustainability 2022, 14, 16879. https://doi.org/10.3390/su142416879
Wang S, Ji Y, Wahab MIM, Xu D, Zhou C. A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty. Sustainability. 2022; 14(24):16879. https://doi.org/10.3390/su142416879
Chicago/Turabian StyleWang, Shilei, Ying Ji, M. I. M. Wahab, Dan Xu, and Changbao Zhou. 2022. "A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty" Sustainability 14, no. 24: 16879. https://doi.org/10.3390/su142416879
APA StyleWang, S., Ji, Y., Wahab, M. I. M., Xu, D., & Zhou, C. (2022). A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty. Sustainability, 14(24), 16879. https://doi.org/10.3390/su142416879







