Optimal Power Flow in Wind–Photovoltaic Energy Regulation Systems Using a Modified Turbulent Water Flow-Based Optimization
Abstract
1. Introduction
- Improving the convergence speed, exploration, and exploitation capabilities of the conventional TFWO algorithm;
- Introducing an enhanced operator to update the population to increase the power of local search of the original TFWO algorithm;
- Application of the proposed modified algorithm to solve the nonconvex and nonlinear OPF problems;
- Voltage magnitude at WT and PV buses is considered a decision variable, while WT and PV power generation forecasts are dependent variables in the OPF problem.
2. Problem Formulation
2.1. Constraints
2.2. Objective Functions
2.3. Modeling of WT and PV Generation
2.3.1. Modeling of WT Generation
2.3.2. Modeling of PV Generation
3. The Proposed Optimization Algorithm
3.1. TFWO
3.1.1. Formation of Whirlpools
3.1.2. The Effects of Whirlpools on Objects and Particles of Its Set and Other Whirlpools
- Pseudocode 1:
- for
- Pseudocode 2:
- if
3.1.3. Centrifugal Force
- Pseudocode 3:
- end
3.1.4. Interactions between the Whirlpools
- Pseudocode 4:
- for
- end
- Pseudocode 5:
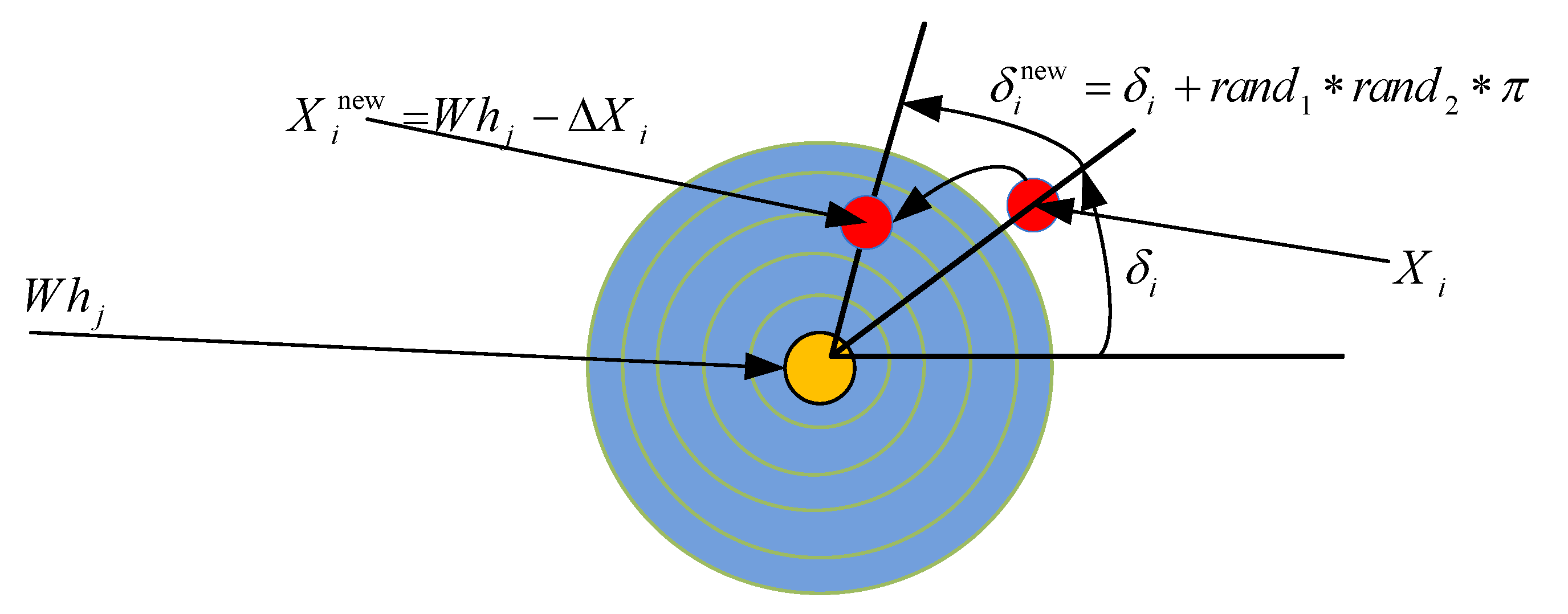
3.2. The Proposed MTFWO
- Pseudocode 6:
4. MTFWO for Different OPF Problems
4.1. OPF Solutions IEEE 30-Bus Network
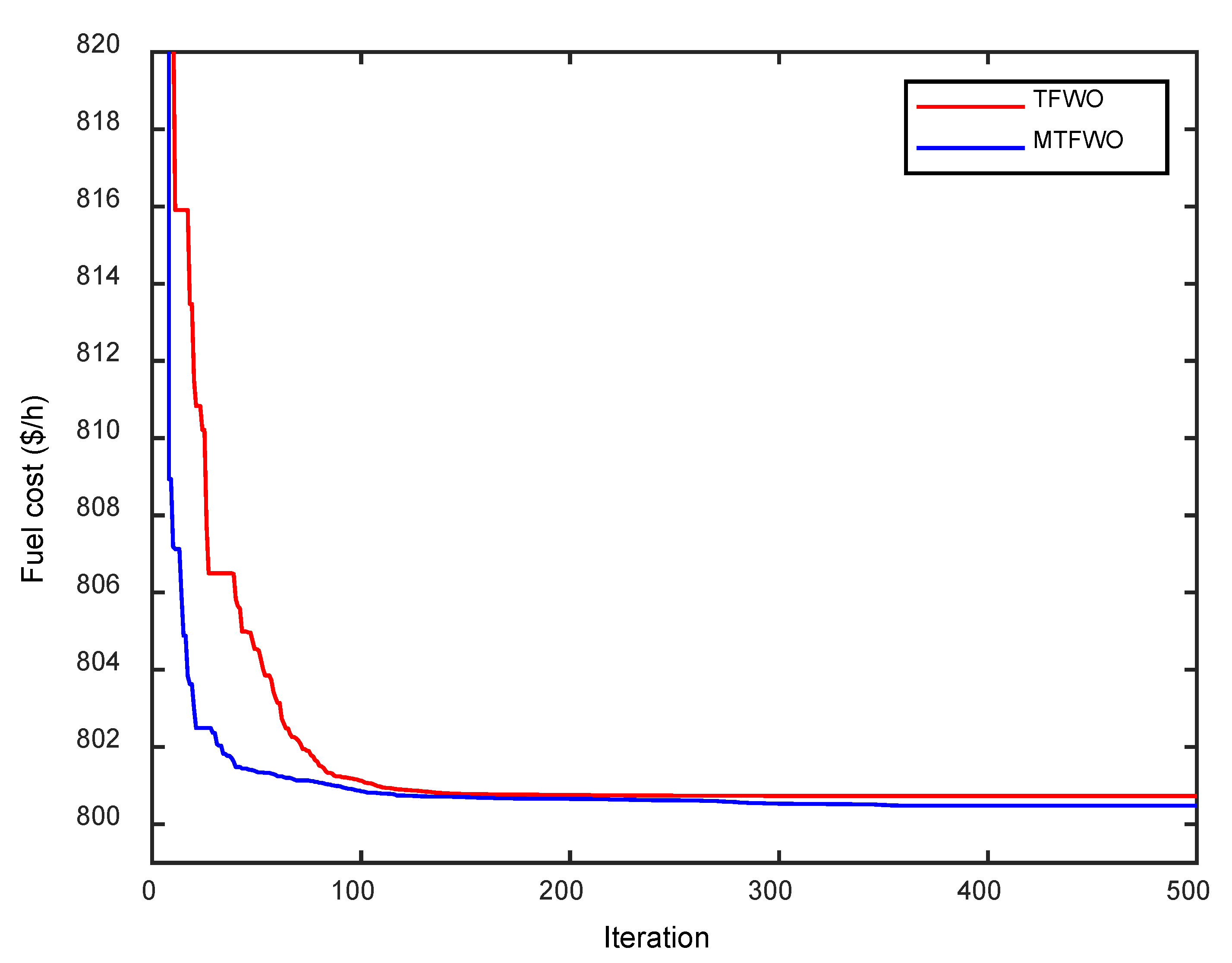
4.1.1. Case 1: Minimization of Fuel Cost
4.1.2. Case 2: Minimization of Piecewise Quadratic Fuel Cost
4.1.3. Case 3: Minimization of Fuel Cost Considering Valve Point Effects (VPEs)
4.1.4. Case 4: Minimization of Fuel Cost and Real Power Loss
4.1.5. Case 5: Minimization of Fuel Cost and V.D.
4.1.6. Case 6: Minimization of Fuel Cost, Emissions, V.D., and Losses
4.2. Solving the OPF Problem Considering WT and PV Generation
4.2.1. Case 7: Minimization of the Generation Cost Incorporating WT and PV Generation
4.2.2. Case 8: Minimization of the Generation Cost Incorporating WT and PV Generation with the Carbon Tax
4.3. Discussions
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sarhan, S.; El-Sehiemy, R.; Abaza, A.; Gafar, M. Turbulent Flow of Water-Based Optimization for Solving Multiobjective Technical and Economic Aspects of Optimal Power Flow Problems. Mathematics 2022, 10, 2106. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Akbel, M.; Duman, S. Optimization of Optimal Power Flow Problem Using Multi-Objective Manta Ray Foraging Optimizer. Appl. Soft Comput. 2022, 116, 108334. [Google Scholar] [CrossRef]
- Ngoko, B.O.; Sugihara, H.; Funaki, T. Optimal Power Flow Considering Line-Conductor Temperature Limits under High Penetration of Intermittent Renewable Energy Sources. Int. J. Electr. Power Energy Syst. 2018, 101, 255–267. [Google Scholar] [CrossRef]
- Baccoli, R.; Frattolillo, A.; Mastino, C.; Curreli, S.; Ghiani, E. A Comprehensive Optimization Model for Flat Solar Collector Coupled with a Flat Booster Bottom Reflector Based on an Exact Finite Length Simulation Model. Energy Convers. Manag. 2018, 164, 482–507. [Google Scholar] [CrossRef]
- Baccoli, R.; Kumar, A.; Frattolillo, A.; Mastino, C.; Ghiani, E.; Gatto, G. Enhancing Energy Production in a PV Collector–Reflector System Supervised by an Optimization Model: Experimental Analysis and Validation. Energy Convers. Manag. 2021, 229, 113774. [Google Scholar] [CrossRef]
- Morshed, M.J.; Hmida, J.B.; Fekih, A. A Probabilistic Multiobjective Approach for Power Flow Optimization in Hybrid Wind-PV-PEV Systems. Appl. Energy 2018, 211, 1136–1149. [Google Scholar] [CrossRef]
- Mura, P.G.; Baccoli, R.; Innamorati, R.; Mariotti, S. An Energy Autonomous House Equipped with a Solar PV Hydrogen Conversion System. Energy Procedia 2015, 78, 1998–2003. [Google Scholar] [CrossRef][Green Version]
- Momoh, J.A.; El-Hawary, M.E.; Adapa, R. A Review of Selected Optimal Power Flow Literature to 1993. II. Newton, Linear Programming and Interior Point Methods. IEEE Trans. Power Syst. 1999, 14, 105–111. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A Review of Selected Optimal Power Flow Literature to 1993. I. Nonlinear and Quadratic Programming Approaches. IEEE Trans. Power Syst. 1999, 14, 96–104. [Google Scholar] [CrossRef]
- Pourakbari-Kasmaei, M.; Mantovani, J.R.S. Logically Constrained Optimal Power Flow: Solver-Based Mixed-Integer Nonlinear Programming Model. Int. J. Electr. Power Energy Syst. 2018, 97, 240–249. [Google Scholar] [CrossRef]
- Ben Hmida, J.; Javad Morshed, M.; Lee, J.; Chambers, T. Hybrid Imperialist Competitive and Grey Wolf Algorithm to Solve Multiobjective Optimal Power Flow with Wind and Solar Units. Energies 2018, 11, 2891. [Google Scholar] [CrossRef]
- Boussa\"\id, I.; Lepagnot, J.; Siarry, P. A Survey on Optimization Metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Abdo, M.; Kamel, S.; Ebeed, M.; Yu, J.; Jurado, F. Solving Non-Smooth Optimal Power Flow Problems Using a Developed Grey Wolf Optimizer. Energies 2018, 11, 1692. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. Modified Honey Bee Mating Optimisation to Solve Dynamic Optimal Power Flow Considering Generator Constraints. IET Gener. Transm. Distrib. 2011, 5, 989. [Google Scholar] [CrossRef]
- Salkuti, S.R. Optimal Power Flow Using Multi-Objective Glowworm Swarm Optimization Algorithm in a Wind Energy Integrated Power System. Int. J. Green Energy 2019, 16, 1547–1561. [Google Scholar] [CrossRef]
- Kumari, B.A.; Vaisakh, K. Integration of Solar and Flexible Resources into Expected Security Cost with Dynamic Optimal Power Flow Problem Using a Novel DE Algorithm. Renew. Energy Focus 2022, 42, 48–69. [Google Scholar] [CrossRef]
- Ali, Z.M.; Aleem, S.H.E.A.; Omar, A.I.; Mahmoud, B.S. Economical-Environmental-Technical Operation of Power Networks with High Penetration of Renewable Energy Systems Using Multi-Objective Coronavirus Herd Immunity Algorithm. Mathematics 2022, 10, 1201. [Google Scholar] [CrossRef]
- Avvari, R.K.; DM, V.K. A Novel Hybrid Multi-Objective Evolutionary Algorithm for Optimal Power Flow in Wind, PV, and PEV Systems. J. Oper. Autom. Power Eng. 2022, 11, 130–143. [Google Scholar]
- Ahmad, M.; Javaid, N.; Niaz, I.A.; Almogren, A.; Radwan, A. A Bio-Inspired Heuristic Algorithm for Solving Optimal Power Flow Problem in Hybrid Power System. IEEE Access 2021, 9, 159809–159826. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and Multiobjective Optimal Power Flow Using Grey Wolf Optimizer and Differential Evolution Algorithms. Electr. Power Components Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Srithapon, C.; Fuangfoo, P.; Ghosh, P.K.; Siritaratiwat, A.; Chatthaworn, R. Surrogate-Assisted Multi-Objective Probabilistic Optimal Power Flow for Distribution Network with Photovoltaic Generation and Electric Vehicles. IEEE Access 2021, 9, 34395–34414. [Google Scholar] [CrossRef]
- Duman, S.; Li, J.; Wu, L. AC Optimal Power Flow with Thermal–Wind–Solar–Tidal Systems Using the Symbiotic Organisms Search Algorithm. IET Renew. Power Gener. 2021, 15, 278–296. [Google Scholar] [CrossRef]
- Elattar, E.E. Optimal Power Flow of a Power System Incorporating Stochastic Wind Power Based on Modified Moth Swarm Algorithm. IEEE Access 2019, 7, 89581–89593. [Google Scholar] [CrossRef]
- Ghasemi, M.; Davoudkhani, I.F.; Akbari, E.; Rahimnejad, A.; Ghavidel, S.; Li, L. A Novel and Effective Optimization Algorithm for Global Optimization and Its Engineering Applications: Turbulent Flow of Water-Based Optimization (TFWO). Eng. Appl. Artif. Intell. 2020, 92, 103666. [Google Scholar] [CrossRef]
- Ullah, Z.; Wang, S.; Radosavljević, J.; Lai, J. A Solution to the Optimal Power Flow Problem Considering WT and PV Generation. IEEE Access 2019, 7, 46763–46772. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Mohamed, Y.S.; El-Gaafary, A.A.M.; Hemeida, A.M. Optimal Power Flow Using Moth Swarm Algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Jabbari, M.; Malekpour, A.R. A Modified Shuffle Frog Leaping Algorithm for Multiobjective Optimal Power Flow. Energy 2011, 36, 6420–6432. [Google Scholar] [CrossRef]
- Narimani, M.R.; Azizipanah-Abarghooee, R.; Zoghdar-Moghadam-Shahrekohne, B.; Gholami, K. A Novel Approach to Multi-Objective Optimal Power Flow by a New Hybrid Optimization Algorithm Considering Generator Constraints and Multi-Fuel Type. Energy 2013, 49, 119–136. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N. Optimal Power Flow Using the Jaya Algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef]
- Alghamdi, A.S. A Hybrid Firefly--JAYA Algorithm for the Optimal Power Flow Problem Considering Wind and Solar Power Generations. Appl. Sci. 2022, 12, 7193. [Google Scholar] [CrossRef]
- Guvenc, U.; Bakir, H.; Duman, S.; Ozkaya, B. Optimal Power Flow Using Manta Ray Foraging Optimization. In Proceedings of the International Conference on Artificial Intelligence and Applied Mathematics in Engineering, Antalya, Turkey, 18–20 April 2020; pp. 136–149. [Google Scholar]
- Khamees, A.K.; Abdelaziz, A.Y.; Eskaros, M.R.; El-Shahat, A.; Attia, M.A. Optimal Power Flow Solution of Wind-Integrated Power System Using Novel Metaheuristic Method. Energies 2021, 14, 6117. [Google Scholar] [CrossRef]
- Ramesh Kumar, A.; Premalatha, L. Optimal Power Flow for a Deregulated Power System Using Adaptive Real Coded Biogeography-Based Optimization. Int. J. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Rahmani, S.; Roosta, A.; Falah, H. A Novel Hybrid Algorithm of Imperialist Competitive Algorithm and Teaching Learning Algorithm for Optimal Power Flow Problem with Non-Smooth Cost Functions. Eng. Appl. Artif. Intell. 2014, 29, 54–69. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal Power Flow Using Tabu Search Algorithm. Electr. Power Components Syst. 2002, 30, 469–483. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential Search Algorithm for Solving Multiobjective Optimal Power Flow Problem. Int. J. Electr. Power Energy Syst. 2016, 79, 1–10. [Google Scholar] [CrossRef]
- Radosavljević, J.; Klimenta, D.; Jevtić, M.; Arsić, N. Optimal Power Flow Using a Hybrid Optimization Algorithm of Particle Swarm Optimization and Gravitational Search Algorithm. Electr. Power Components Syst. 2015, 43, 1958–1970. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gitizadeh, M. Multi-Objective Optimal Electric Power Planning in the Power System Using Gaussian Bare-Bones Imperialist Competitive Algorithm. Inf. Sci. 2015, 294, 286–304. [Google Scholar] [CrossRef]
- Hazra, J.; Sinha, A.K. A Multiobjective Optimal Power Flow Using Particle Swarm Optimization. Eur. Trans. Electr. Power 2011, 21, 1028–1045. [Google Scholar] [CrossRef]
- Sayah, S.; Zehar, K. Modified Differential Evolution Algorithm for Optimal Power Flow with Non-Smooth Cost Functions. Energy Convers. Manag. 2008, 49, 3036–3042. [Google Scholar] [CrossRef]
- Sood, Y. Evolutionary Programming Based Optimal Power Flow and Its Validation for Deregulated Power System Analysis. Int. J. Electr. Power Energy Syst. 2007, 29, 65–75. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. A Solution Network Based on Stud Krill Herd Algorithm for Optimal Power Flow Problems. Soft Comput. 2018, 22, 159–176. [Google Scholar] [CrossRef]
- Ongsakul, W.; Tantimaporn, T. Optimal Power Flow by Improved Evolutionary Programming. Electr. Power Components Syst. 2006, 34, 79–95. [Google Scholar] [CrossRef]
- Jebaraj, L.; Sakthivel, S. A New Swarm Intelligence Optimization Approach to Solve Power Flow Optimization Problem Incorporating Conflicting and Fuel Cost Based Objective Functions. e-Prime-Adv. Electr. Eng. Electron. Energy 2022, 2, 100031. [Google Scholar]
- Ghasemi, M.; Ghavidel, S.; Gitizadeh, M.; Akbari, E. An Improved Teaching–Learning-Based Optimization Algorithm Using Lévy Mutation Strategy for Non-Smooth Optimal Power Flow. Int. J. Electr. Power Energy Syst. 2015, 65, 375–384. [Google Scholar] [CrossRef]
- Roy, R.; Jadhav, H.T. Optimal Power Flow Solution of Power System Incorporating Stochastic Wind Power Using Gbest Guided Artificial Bee Colony Algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 562–578. [Google Scholar] [CrossRef]
- Nguyen, T.T. A High Performance Social Spider Optimization Algorithm for Optimal Power Flow Solution with Single Objective Optimization. Energy 2019, 171, 218–240. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal Power Flow Using an Improved Colliding Bodies Optimization Algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal Power Flow Solutions Using Differential Evolution Algorithm Integrated with Effective Constraint Handling Techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Bentouati, B.; Khelifi, A.; Shaheen, A.M.; El-Sehiemy, R.A. An Enhanced Moth-Swarm Algorithm for Efficient Energy Management Based Multi Dimensions OPF Problem. J. Ambient Intell. Humaniz. Comput. 2020, 12, 9499–9519. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul Wahab, N.I. A Novel Quasi-Oppositional Modified Jaya Algorithm for Multi-Objective Optimal Power Flow Solution. Appl. Soft Comput. 2018, 65, 360–373. [Google Scholar] [CrossRef]
- Herbadji, O.; Slimani, L.; Bouktir, T. Optimal Power Flow with Four Conflicting Objective Functions Using Multiobjective Ant Lion Algorithm: A Case Study of the Algerian Electrical Network. Iran. J. Electr. Electron. Eng. 2019, 15, 94–113. [Google Scholar] [CrossRef]
- Ghoneim, S.S.M.; Kotb, M.F.; Hasanien, H.M.; Alharthi, M.M.; El-Fergany, A.A. Cost Minimizations and Performance Enhancements of Power Systems Using Spherical Prune Differential Evolution Algorithm Including Modal Analysis. Sustainability 2021, 13, 8113. [Google Scholar] [CrossRef]
- Shilaja, C.; Ravi, K. Optimal Power Flow Using Hybrid DA-APSO Algorithm in Renewable Energy Resources. Energy Procedia 2017, 117, 1085–1092. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gharibzadeh, M.; Azizi Vahed, A. Multi-Objective Optimal Power Flow Considering the Cost, Emission, Voltage Deviation and Power Losses Using Multiobjective Modified Imperialist Competitive Algorithm. Energy 2014, 78, 276–289. [Google Scholar] [CrossRef]
- El Sehiemy, R.A.; Selim, F.; Bentouati, B.; Abido, M.A. A Novel Multi-Objective Hybrid Particle Swarm and Salp Optimization Algorithm for Technical-Economical-Environmental Operation in Power Systems. Energy 2020, 193, 116817. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, N.; Srivastava, L.; Malik, H.; Pliego Marugán, A.; García Márquez, F.P. A Hybrid Jaya—Powell’s Pattern Search Algorithm for Multi-Objective Optimal Power Flow Incorporating Distributed Generation. Energies 2021, 14, 2831. [Google Scholar] [CrossRef]
- Ouafa, H.; Linda, S.; Tarek, B. Multi-Objective Optimal Power Flow Considering the Fuel Cost, Emission, Voltage Deviation and Power Losses Using Multiobjective Dragonfly Algorithm. In Proceedings of the International Conference on Recent Advances in Electrical Systems, Hammamet, Tunusia, 22–24 December 2017. [Google Scholar]
- Zhang, J.; Wang, S.; Tang, Q.; Zhou, Y.; Zeng, T. An Improved NSGA-III Integrating Adaptive Elimination Strategy to Solution of Many-Objective Optimal Power Flow Problems. Energy 2019, 172, 945–957. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, G.A.J. Optimal Power Flow Solutions Incorporating Stochastic Wind and Solar Power. Energy Convers. Manag. 2017, 148, 1194–1207. [Google Scholar] [CrossRef]










| Decision Variables | Limitations | Instances | ||||||
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | 1 | 2 | 3 | 4 | 5 | 6 | |
| P G1 (MW) | 49 | 251 | 177.1697 | 140.0001 | 198.7431 | 102.5856 | 176.3452 | 122.15643 |
| P G2 (MW) | 18 | 81 | 48.6955 | 55.0000 | 44.8830 | 55.5630 | 48.8217 | 52.54522 |
| P G5 (MW) | 16 | 51 | 21.3899 | 24.0879 | 18.4621 | 38.1104 | 21.6363 | 31.52471 |
| P G8 (MW) | 11 | 35 | 21.2389 | 34.9985 | 10.0000 | 35.0000 | 22.3212 | 35.00001 |
| P G11 (MW) | 1 | 31 | 11.9284 | 18.3681 | 10.0001 | 30.0000 | 12.1560 | 26.77462 |
| P G13 (MW) | 13 | 41 | 12.0000 | 17.6858 | 12.0002 | 26.6696 | 12.0000 | 20.98255 |
| VG1 | 0.965 | 1.11 | 1.0849 | 1.0744 | 1.0816 | 1.0698 | 1.0420 | 1.073036 |
| VG2 | 0.965 | 1.11 | 1.0607 | 1.0572 | 1.0580 | 1.0576 | 1.0227 | 1.057463 |
| VG5 | 0.965 | 1.11 | 1.0350 | 1.0313 | 1.0304 | 1.0359 | 1.0155 | 1.03283 |
| VG8 | 0.965 | 1.11 | 1.0383 | 1.0392 | 1.0373 | 1.0438 | 1.0076 | 1.04132 |
| VG11 | 0.965 | 1.11 | 1.0990 | 1.0876 | 1.0994 | 1.0830 | 1.0481 | 1.04022 |
| VG13 | 0.965 | 1.11 | 1.0513 | 1.0674 | 1.0636 | 1.0574 | 0.9874 | 1.02364 |
| T6–9 | 0.90 | 1.11 | 1.0721 | 1.0251 | 1.0415 | 1.0853 | 1.0696 | 1.10006 |
| T6–10 | 0.90 | 1.11 | 0.9185 | 0.9578 | 0.9701 | 0.9000 | 0.9000 | 0.95258 |
| T4–12 | 0.90 | 1.11 | 0.9762 | 1.0015 | 0.9951 | 0.9903 | 0.9415 | 1.03145 |
| T28–27 | 0.90 | 1.11 | 0.9738 | 0.9725 | 0.9780 | 0.9751 | 0.9710 | 1.00504 |
| QC10 (MVAR) | 0.00 | 5.01 | 2.6670 | 4.8401 | 4.7382 | 4.5918 | 5.0000 | 3.38923 |
| QC12 (MVAR) | 0.00 | 5.01 | 1.2027 | 0.0025 | 1.9409 | 0.1673 | 1.5141 | 0.06502 |
| QC15 (MVAR) | 0.00 | 5.01 | 4.2890 | 3.0310 | 3.7691 | 4.4881 | 5.0000 | 3.92194 |
| QC17 (MVAR) | 0.00 | 5.01 | 4.9995 | 4.9531 | 4.6145 | 5.0000 | 0 | 5.00006 |
| QC20 (MVAR) | 0.00 | 5.01 | 4.2549 | 4.8434 | 4.3642 | 4.2338 | 5.0000 | 4.98046 |
| QC21 (MVAR) | 0.00 | 5.01 | 4.9976 | 5.0000 | 5.0000 | 5.0000 | 5.0000 | 4.99994 |
| QC23 (MVAR) | 0.00 | 5.01 | 3.3310 | 2.1912 | 2.9300 | 3.2521 | 5.0000 | 4.19076 |
| QC24 (MVAR) | 0.00 | 5.01 | 4.9998 | 4.9990 | 5.0000 | 5.0000 | 5.0000 | 4.99966 |
| QC29 (MVAR) | 0.00 | 5.01 | 2.6262 | 2.5173 | 2.6844 | 2.5592 | 2.6486 | 2.61303 |
| Cost ($/h) | - | - | 800.4781 | 646.4789 | 832.1666 | 859.0401 | 803.8125 | 830.34663 |
| Emission (t/h) | - | - | 0.3663 | 0.2835 | 0.4378 | 0.2289 | 0.3639 | 0.25293 |
| Power losses (MW) | - | - | 9.0222 | 6.7403 | 10.6885 | 4.5286 | 9.8804 | 5.58342 |
| V.D. | - | - | 0.9064 | 0.9193 | 0.8603 | 0.9274 | 0.0941 | 0.2983 |
| Optimizer | Fuel Cost (USD/h) | Emmission (t/h) | Power Losses (MW) | V.D. |
| FPA [26] | 802.7983 | 0.35959 | 9.5406 | 0.36788 |
| MHBMO [20] | 801.985 | - | 9.49 | - |
| SFLA-SA [27] | 801.79 | - | - | - |
| MPSO-SFLA [28] | 801.75 | - | 9.54 | - |
| PPSOGSA [25] | 800.528 | - | 9.02665 | 0.91136 |
| MSA [26] | 800.5099 | 0.36645 | 9.0345 | 0.90357 |
| JAYA [29] | 800.4794 | - | 9.06481 | 0.1273 |
| FA [30] | 800.7502 | 0.36532 | 9.0219 | 0.9205 |
| MRFO [31] | 800.7680 | - | 9.1150 | - |
| AO [32] | 801.83 | - | - | - |
| ARCBBO [33] | 800.5159 | 0.3663 | 9.0255 | 0.8867 |
| MICA-TLA [34] | 801.0488 | - | 9.1895 | - |
| TS [35] | 802.29 | - | - | - |
| ABC [36] | 800.660 | 0.365141 | 9.0328 | 0.9209 |
| HFAJAYA [30] | 800.4800 | 0.3659 | 9.0134 | 0.9047 |
| PSOGSA [37] | 800.49859 | - | 9.0339 | 0.12674 |
| MGBICA [38] | 801.1409 | 0.3296 | - | - |
| AGSO [39] | 801.75 | 0.3703 | - | - |
| DE [40] | 802.39 | - | 9.466 | - |
| MFO [26] | 800.6863 | 0.36849 | 9.1492 | 0.75768 |
| EP [41] | 803.57 | - | - | - |
| GWO [14] | 801.41 | - | 9.30 | - |
| SKH [42] | 800.5141 | 0.3662 | 9.0282 | - |
| IEP [43] | 802.46 | - | - | - |
| TFWO | 800.7308 | 0.3668 | 9.3207 | 0.9044 |
| MTFWO | 800.4781 | 0.3663 | 9.0222 | 0.9064 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. |
|---|---|---|---|---|
| SSA [44] | 646.7796 | 0.2836 | 6.5599 | 0.5320 |
| LTLBO [45] | 647.4315 | 0.2835 | 6.9347 | 0.8896 |
| MFO [26] | 649.2727 | 0.28336 | 7.2293 | 0.47024 |
| MICA-TLA [34] | 647.1002 | - | 6.8945 | - |
| GABC [46] | 647.03 | - | 6.8160 | 0.8010 |
| MDE [40] | 647.846 | - | 7.095 | - |
| SSO [47] | 663.3518 | - | - | - |
| FPA [26] | 651.3768 | 0.28083 | 7.2355 | 0.31259 |
| MPSO-SFLA [28] | 647.55 | - | - | - |
| IEP [43] | 649.312 | - | - | - |
| MSA [26] | 646.8364 | 0.28352 | 6.8001 | 0.84479 |
| TFWO | 646.9716 | 0.2838 | 6.7859 | 0.9099 |
| MTFWO | 646.4789 | 0.2835 | 6.7403 | 0.9193 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. |
|---|---|---|---|---|
| PSO [48] | 832.6871 | - | - | - |
| Self-adaptive penalty based on DE (SP-DE) [49] | 832.4813 | 0.43651 | 10.6762 | 0.75042 |
| FA [30] | 832.5596 | 0.4372 | 10.6823 | 0.8539 |
| HFAJAYA [30] | 832.1798 | 0.4378 | 10.6897 | 0.8578 |
| TFWO | 832.6704 | 0.4380 | 10.8997 | 0.8365 |
| MTFWO | 832.1666 | 0.4378 | 10.6885 | 0.8603 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. | J4 |
|---|---|---|---|---|---|
| Enhanced MSA (EMSA) [50] | 859.9514 | 0.2278 | 4.6071 | 0.7758 | 1044.2354 |
| Quasi-oppositional modified Jaya (QOMJaya) [51] | 826.9651 | - | 5.7596 | - | 1402.9251 |
| Modified Jaya (MJaya) [51] | 827.9124 | - | 5.7960 | - | 1059.7524 |
| Multiobjective ant lion algorithm (MOALO) [52] | 826.4556 | 0.2642 | 5.7727 | 1.2560 | 1057.3636 |
| Spherical prune DE (SpDEA) [53] | 837.8510 | - | 5.6093 | 0.8106 | 1062.223 |
| MSA [26] | 859.1915 | 0.2289 | 4.5404 | 0.92852 | 1040.8075 |
| TFWO | 859.3726 | 0.2290 | 4.5498 | 0.9188 | 1041.3646 |
| MTFWO | 859.0401 | 0.2289 | 4.5286 | 0.9274 | 1040.1841 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. | J5 |
|---|---|---|---|---|---|
| Dragonfly algorithm (DA) with aging PSO (DA-APSO) [54] | 802.63 | - | - | 0.1164 | 814.2700 |
| SpDEA [53] | 803.0290 | - | 9.0949 | 0.2799 | 831.0190 |
| Multiobjective modified bare-bones PSO (BB-MOPSO) [55] | 804.9639 | - | - | 0.1021 | 815.1739 |
| MPSO [26] | 803.9787 | 0.3636 | 9.9242 | 0.1202 | 815.9987 |
| EMSA [50] | 803.4286 | 0.3643 | 9.7894 | 0.1073 | 814.1586 |
| Hybrid PSO and salp swarm Optimization (PSO-SSO) [56] | 803.9899 | 0.367 | 9.961 | 0.0940 | 813.3899 |
| Multiobjective modified ICA (MOMICA) [55] | 804.9611 | 0.3552 | 9.8212 | 0.0952 | 814.4811 |
| MFO [26] | 803.7911 | 0.36355 | 9.8685 | 0.10563 | 814.3541 |
| TFWO [1] | 803.416 | 0.365 | 9.795 | 0.101 | 813.5160 |
| Salp swarm Optimization (SSO) [56] | 803.73 | 0.365 | 9.841 | 0.1044 | 814.1700 |
| PSO [56] | 804.477 | 0.368 | 10.129 | 0.126 | 817.0770 |
| Modified sorting nongenetic algorithm (MNSGA-II) [55] | 805.0076 | - | - | 0.0989 | 814.8976 |
| TFWO | 803.9968 | 0.3641 | 10.1240 | 0.0995 | 813.9468 |
| MTFWO | 803.8125 | 0.3639 | 9.8804 | 0.0941 | 813.2225 |
| Algorithm | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. | J6 |
|---|---|---|---|---|---|
| Hybrid Jaya–Powell’s pattern search 2 (J-PPS2) [57] | 830.8672 | 0.2357 | 5.6175 | 0.2948 | 965.1201 |
| MOALO [52] | 826.2676 | 0.2730 | 7.2073 | 0.7160 | 1005.0512 |
| BB-MOPSO [55] | 833.0345 | 0.2479 | 5.6504 | 0.3945 | 970.3379 |
| PSO [56] | 828.2904 | 0.261 | 5.644 | 0.55 | 968.9674 |
| Hybrid Jaya–Powell’s pattern search 3 (J-PPS3) [57] | 830.3088 | 0.2363 | 5.6377 | 0.2949 | 965.0228 |
| MSA [26] | 830.639 | 0.25258 | 5.6219 | 0.29385 | 965.2907 |
| MNSGA-II [55] | 834.5616 | 0.2527 | 5.6606 | 0.4308 | 972.9429 |
| Hybrid Jaya–Powell’s pattern search 1 (J-PPS1) [57] | 830.9938 | 0.2355 | 5.6120 | 0.2990 | 965.2159 |
| Multiobjective DA (MODA) [58] | 828.49 | 0.265 | 5.912 | 0.585 | 975.8740 |
| MFO [26] | 830.9135 | 0.25231 | 5.5971 | 0.33164 | 965.8080 |
| Improved NSGA-II (I-NSGA-III) [59] | 881.9395 | 0.2209 | 4.7449 | 0.1754 | 994.2078 |
| SSO [56] | 829.978 | 0.25 | 5.426 | 0.516 | 964.9360 |
| TFWO | 830.5073 | 0.2535 | 5.6410 | 0.2987 | 965.6985 |
| MTFWO | 830.3466 | 0.2529 | 5.5834 | 0.2983 | 964.2508 |
| WT Plants | PV Plant | ||||||
|---|---|---|---|---|---|---|---|
| Wind Farm | No. of Turbines | Rated Power, Pwr (MW) | Weibull PDF Parameters | Weibull Mean, Mwbl | Rated Power, Psr (MW) | Lognormal PDF Parameters | Lognormal Mean, Mlgn |
| 1 (bus 5) | 25 | 75 | c = 9, k = 2 | v = 7.976 m/s | 50 (bus 13) | µ = 6, σ = 0.6 | G = 483 W/m2 |
| 2 (bus 11) | 20 | 60 | c = 10, k = 2 | v = 8.862 m/s | |||
| Variables | TFWO | MTFWO |
|---|---|---|
| PG1 (MW) | 134.90791 | 134.90791 |
| PG2 (MW) | 29.1694 | 27.5152 |
| Pws1 (MW) | 44.1115 | 43.1911 |
| PG3 (MW) | 10 | 10 |
| Pws2 (MW) | 37.2235 | 36.4806 |
| Pss (MW) | 33.755 | 37.096 |
| VG1 | 1.0718 | 1.0714 |
| VG2 | 1.0569 | 1.0564 |
| VG5 | 1.035 | 1.0344 |
| VG8 | 1.0612 | 1.0975 |
| VG11 | 1.0997 | 1.1 |
| VG13 | 1.0487 | 1.0497 |
| QG1 (MVAR) | −2.29534 | −2.4284 |
| QG2 (MVAR) | 11.8338 | 11.6775 |
| Qws1 (MVAR) | 22.42 | 22.4327 |
| QG3(MVAR) | 40 | 40 |
| Qws2 (MVAR) | 30 | 30 |
| Qss (MVAR) | 15.0431 | 15.3694 |
| Fuelvlvcost (USD/h) | 442.7995 | 437.3083 |
| Wind gen cost (USD/h) | 248.4581 | 242.7311 |
| Solar gen cost (USD/h) | 91.2925 | 101.8322 |
| Total cost (USD/h) | 782.5501 | 781.8715 |
| Emission (t/h) | 1.76192 | 0.45530 |
| Power losses (MW) | 5.7673 | 5.7908 |
| V.D. | 0.45386 | 0.45530 |
| Variables | TFWO | MTFWO |
|---|---|---|
| PG1 (MW) | 124.05273 | 123.42123 |
| PG2 (MW) | 34.5467 | 32.7675 |
| Pws1 (MW) | 46.79 | 45.8762 |
| PG3 (MW) | 10 | 10 |
| Pws2 (MW) | 39.3703 | 38.6302 |
| Pss (MW) | 33.9203 | 37.9805 |
| VG1 | 1.071 | 1.0705 |
| VG2 | 1.0576 | 1.057 |
| VG5 | 1.0365 | 1.0359 |
| VG8 | 1.0405 | 1.0404 |
| VG11 | 1.0981 | 1.0982 |
| VG13 | 1.0548 | 1.0562 |
| QG1 (MVAR) | −2.54117 | −2.69805 |
| QG2 (MVAR) | 12.4645 | 12.2864 |
| Qws1 (MVAR) | 22.9406 | 22.9691 |
| QG3(MVAR) | 35.4423 | 35.2379 |
| Qws2 (MVAR) | 30 | 30 |
| Qss (MVAR) | 17.3678 | 17.8613 |
| Fuelvlvcost (USD/h) | 435.9284 | 428.3159 |
| Wind gen cost (USD/h) | 265.5061 | 259.5920 |
| Solar gen cost (USD/h) | 91.5097 | 104.5964 |
| Total cost (USD/h) | 792.9442 | 792.5043 |
| Emission (t/h) | 0.91868 | 0.88611 |
| J8 | 811.3178 | 810.2265 |
| Power losses (MW) | 5.2800 | 5.2756 |
| V.D. | 0.46700 | 0.46966 |
| Carbon tax (USD/h) | 18.3736 | 17.7222 |
| Method | Min | Mean | Max | Std. | Time (s) |
|---|---|---|---|---|---|
| Case 1 | |||||
| TFWO | 800.7308 | 800.9731 | 801.4006 | 0.49 | 28 |
| MTFWO | 800.4781 | 800.5693 | 800.7024 | 0.12 | 28 |
| Case 2 | |||||
| TFWO | 646.9716 | 647.2543 | 647.6081 | 0.31 | 28 |
| MTFWO | 646.4789 | 646.5545 | 646.6870 | 0.14 | 28 |
| Case 3 | |||||
| TFWO | 832.6704 | 832.9429 | 833.3842 | 0.54 | 28 |
| MTFWO | 832.1666 | 832.2869 | 832.4130 | 0.16 | 28 |
| Case 4 | |||||
| TFWO | 1041.3646 | 1041.7019 | 1042.1275 | 0.45 | 27 |
| MTFWO | 1040.1841 | 1040.2748 | 1040.5255 | 0.27 | 28 |
| Case 5 | |||||
| TFWO | 813.9468 | 814.2870 | 814.5443 | 0.33 | 28 |
| MTFWO | 813.2225 | 813.3611 | 813.4389 | 0.11 | 28 |
| Case 6 | |||||
| TFWO | 965.6985 | 965.9988 | 966.4672 | 0.50 | 28 |
| MTFWO | 964.2508 | 964.4095 | 964.5010 | 0.17 | 27 |
| Case 7 | |||||
| TFWO | 782.5501 | 782.8716 | 783.3426 | 0.52 | 31 |
| MTFWO | 781.8715 | 781.9663 | 782.2456 | 0.25 | 31 |
| Case 8 | |||||
| TFWO | 811.3178 | 811.6268 | 811.9747 | 0.39 | 31 |
| MTFWO | 810.2265 | 810.3940 | 810.4835 | 0.12 | 31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, A.S. Optimal Power Flow in Wind–Photovoltaic Energy Regulation Systems Using a Modified Turbulent Water Flow-Based Optimization. Sustainability 2022, 14, 16444. https://doi.org/10.3390/su142416444
Alghamdi AS. Optimal Power Flow in Wind–Photovoltaic Energy Regulation Systems Using a Modified Turbulent Water Flow-Based Optimization. Sustainability. 2022; 14(24):16444. https://doi.org/10.3390/su142416444
Chicago/Turabian StyleAlghamdi, Ali S. 2022. "Optimal Power Flow in Wind–Photovoltaic Energy Regulation Systems Using a Modified Turbulent Water Flow-Based Optimization" Sustainability 14, no. 24: 16444. https://doi.org/10.3390/su142416444
APA StyleAlghamdi, A. S. (2022). Optimal Power Flow in Wind–Photovoltaic Energy Regulation Systems Using a Modified Turbulent Water Flow-Based Optimization. Sustainability, 14(24), 16444. https://doi.org/10.3390/su142416444






