Application of Sustainable Concrete in the Seismic Evaluation of an Innovative Type of Buckling Restrained Brace

Abstract

The Buckling Restrained Braced Frame (BRBF), consisting of a ductile steel core in concrete or a steel tube encased in concrete, is constructed to avoid brittle failure modes. The application of ductile materials with improved damping properties, such as tire-derived lightweight aggregate concrete, has not been investigated in BRBF systems, but it enhances the overall performance of the system and contributes to sustainability. Hence, this study aims to investigate the influence of such an application on the response modification, overstrength, and ductility factors, as well as the general earthquake performance, of 4-, 8-, and 14-story special reinforced concrete moment resisting frames equipped with BRBF. The current study compares 48 different BRBF models with TDA infill and conventional concrete infill by considering various bracing configurations, such as Chevron (Inverted V and V), Split X, and Single-Leg BRBF, and different span lengths of 6 m and 8 m. The evaluations include nonlinear response history analyses intended to provide insights into the performance of BRBF when exploiting the available experimental stress–strain characteristics of tire-derived lightweight aggregate concrete as an alternative material. Furthermore, the effectiveness of using tire-derived lightweight aggregate concrete as an alternative damping material in BRBF is examined by comparing BRBF with the new damping properties of concrete. Buildings equipped with BRB encased in TDA showed reduced base shear demand (by an average of 7%) when compared to concrete infill, and the prescribed value for the response modification factor for buildings of 50 m or less provides an acceptable estimation of the lower bond factors in approximately 95% of the cases. Furthermore, when a system requires more damping, the application of BRB encased in TDA is recommended.

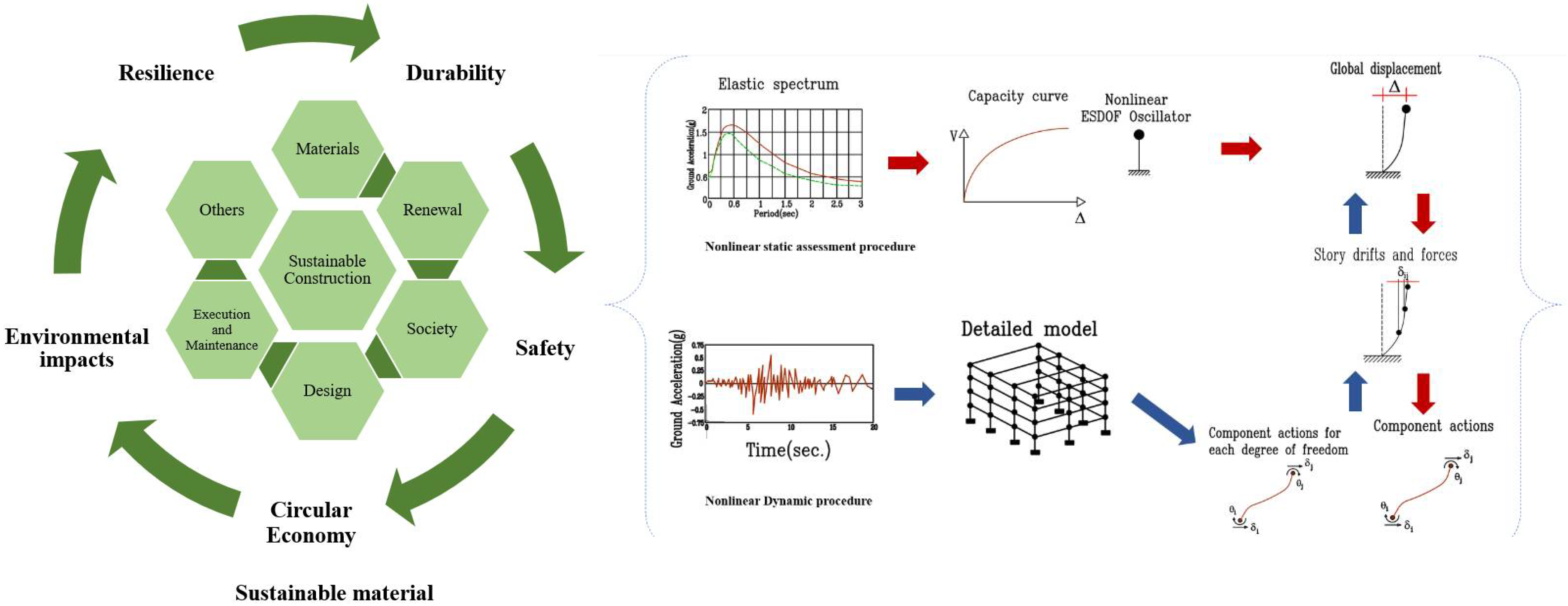
1. Introduction

Predicting structural behavior when subjected to seismic excitation is a challenging task for civil engineering. The damage level can be determined when a structure dissipates a large amount of kinetic energy caused by an earthquake. Since it is not economically feasible to dissipate this energy within the elastic range of materials, building codes allow the structure to yield in controlled/defined areas and a ductile manner in designated elements; in conventional braced frames, these elements are the so-called structural fuses [1]. Three major control system classes can replace conventional bracing systems: passive, active, and semi-active [2]. Among them, passive energy dissipation devices are characterized by an ability to enhance energy dissipation in the structural system, either by transferring the kinetic energy to heat, such as by frictional sliding, by the yielding of metals and viscoelastic solids or fluids, or via vibrating modes, such as using supplemental oscillators [3]. Conventional braces buckle when under compression, which leads to progressive degrading behavior and a loss of stiffness. To resolve this issue, Professor Wada developed an unbounded brace that provides an unbounded layer between the steel core and surrounding concrete to take all axial loads. Unbonded braces can provide both stiffness and a stable energy absorption capability; the brace forces are reduced and do not need to be designed for buckling [1]. This results in lower costs for new construction or retrofitting existing buildings, with lower forces in the superstructure and foundation; this model can be categorized as a passive control system, as presented in Figure 1.

The United Nations world commission on environment and development described sustainable development as “development that meets the needs of the present without compromising the ability of future generations to meet their own needs”. Sustainability is a long-term goal, and to achieve sustainable development, numerous steps should be followed, including enhancing the understanding of the environment, society, economy, and culture and the connection between them [5]. Concrete sustainability has been developed by using alternative fuels and raw materials in cement production, as well as utilizing reclaimed water and reused materials. The selection of materials in the concrete mixture, such as cementitious materials, aggregates, admixtures, and water, directly affects sustainable concrete. Non-conventional aggregates, such as lightweight aggregate, recycled/reused aggregates, recycled concrete, screening, crushed glass aggregate, waste plastic aggregate, recycled scrap tire aggregate, and recycled asphalt pavement aggregate, are becoming more popular. They reduce waste materials, CO₂ emissions, and embodied energy; therefore, their use contributes to sustainability [6]. Rubberized concrete is the general name for tire-derived aggregate concrete. The idea is to enhance ductility by combining flexible and rigid materials [7]. Tire-derived aggregate (TDA) is derived from waste tires fitted to a standard range of practical sizes. TDA is defined as shredded scrap tires with a basic geometrical shape and can be split into two practical types; Type A, ranging from 75 to 100 mm, and Type B, ranging from 150 to 300 mm [8]. Aside from the environmental benefits of TDA, it can be used as a lightweight engineering application, and its engineering properties make TDA suitable for many civil engineering applications. It is also a very durable material and has significant cost advantages. The mechanical properties of tire-derived lightweight aggregate concrete (TDLWAC) were investigated using 38 cylindrical and 36 beam specimens [9]. The compressive, splitting tensile, flexural strength, flexural toughness, and impact flexure properties of rubberized lightweight aggregate were examined. The target strength was 21 MPa. The cylinder and beam specimens contained shale lightweight coarse aggregate, natural sand fine aggregate, cement, and water; the TDA was added to the cylinder and beam specimens in replacement ratios of 0% to 100%. A compression test was carried out using a 500 kN testing machine that applied 0.24 MPa per second to capture the strain gauge. ASTM C469 [10] was used to determine the static modulus of elasticity, and the stress–strain relationship was determined from the load–deflection data obtained during each test. The splitting tensile strength was determined via the load–deflection relationship and in accordance with ASTM C496 [10]. It was concluded that the static mechanical properties decreased when the rubber content increased, and these materials were found to be useful where energy absorption was considered an important aspect. Bracings have been used as the most common lateral load-resisting system. However, they do not perform well in the nonlinear deformation range, given their low ductility, nonsymmetrical hysteresis curve in tension and compression, and stiffness degradation due to buckling in cyclic loading. Therefore, a new generation of bracing systems known as “Buckling Restrained Braced Frames (BRBF)” has been investigated. These bracing systems have symmetric hysteresis curves, high ductility, and large drift capacity [11].

In ASCE 7-22 [12] and NBCC 2015 [13], the minimum earthquake lateral force is divided by the Seismic Force Resisting System (SFRS) reduction factor, known as the response modification factor. This factor does not consider span length, bracing configuration, the building’s height, or the period of the structure. Several studies have been conducted to assess the seismic design factors and performance of conventional BRBFs [11,14,15]. Most of the research carried out in the past focused on the behavior of Buckling Restrained Braced Frames in steel structures, and various approaches have also been proposed to perform their seismic evaluation [16,17,18,19,20,21,22,23]. Further studies are required to characterize the capacities of the overall brace frame system to examine the actual behavior of buckling restrained braces encased with TDA/concrete fillings as new design approaches. This study introduces another application for the use of recycled scrap tire aggregates to reduce waste and contribute to sustainability. Furthermore, the capacities of the overall brace frame system, such as the seismic design factors, are characterized, and the actual behavior of buckling restrained braces encased with TDA/concrete fillings as a new design approach is investigated. For this purpose, the mechanical properties of tire-derived lightweight aggregate concrete (TDLWAC) [24] were used to model the innovative BRB with encased steel composite containing TDA filling. The seismic force reduction factors, including overstrength, ductility, and response modification factors, of four-, eight-, and fourteen-story special reinforced concrete moment frames equipped with BRBF, as well as a comparison between the BRB-encased steel with TDA infill as a new damping feature and the BRB-encased steel with concrete infill, are then discussed. In addition, the effects of building height and span length on four different bracing configurations, including Single-Leg Braces (SLB), Chevron Inverted V Braces (CIVB), Chevron V Braces (CVB), and Split X braces (SXB), were investigated. Moreover, nonlinear response history analyses using twenty-one scaled ground motions based on ASCE 7 [12] and the fundamental period of each structure are performed to demonstrate the efficiency of these bracing systems.

Figure 2 demonstrates the sustainable construction concept as it has been integrated into the analysis procedures. The Nonlinear Static Procedure can consist of different load cases with different distributions in which structural and member stiffness are updated at every step. In this method global displacement, component actions and story drift can be determined. The nonlinear dynamic procedure is based on the mathematical integration of the equations of motions, in this model global displacement, story drifts, and element distortion can be derived from component deformation. When the sustainable material has been selected, its mechanical properties should be extracted using experimental tests. Section 2 concerns the design of a buckling restrained brace frame; Section 3, Section 4 and Section 5 address the calculating of the seismic reduction factors of the integrated sustainable material and conventional concrete in a BRBF, and Section 5 and Section 6 regarding the structural modeling and the calculation of the fundamental period. The application and performance of ductile sustainable material were then verified using nonlinear static procedures (Section 8) and nonlinear response history analysis (Section 9, Section 10, Section 11 and Section 12), followed by results and conclusions in Section 13 and Section 14.

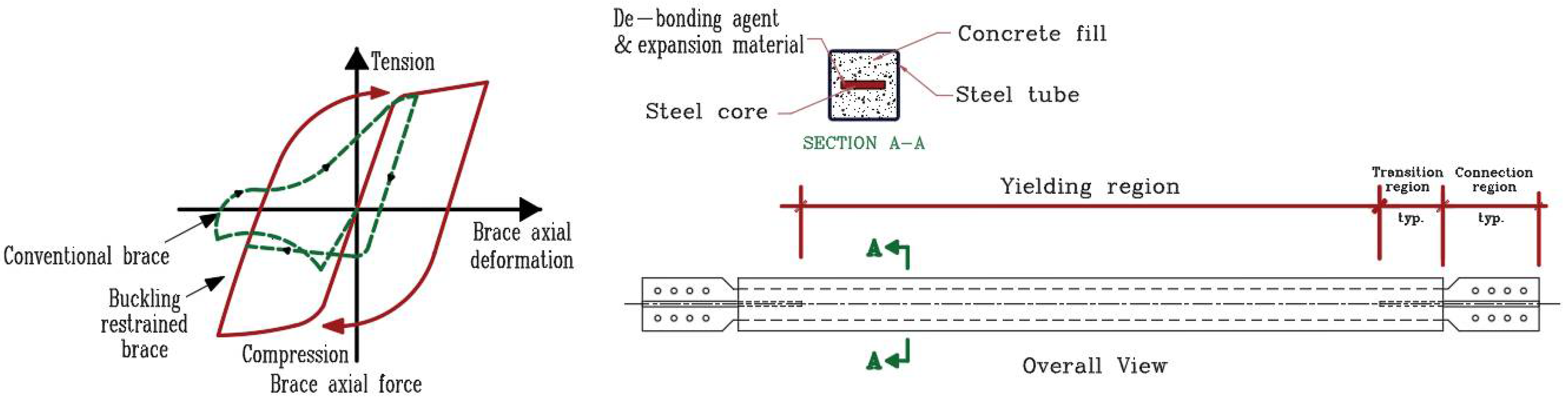
2. Design of Buckling Restrained Braced Frame

A buckling restrained brace (BRB), consisting of a ductile steel core in a concrete or mortar steel tube, can replace conventional braces. The steel core provides the yielding mechanism, while the tube prevents the buckling of the core. The buckling restrained bracing element and hysteretic behavior of conventional and buckling restrained bracing members are presented in Figure 3 [28].

The steel core is the primary source of energy dissipation and is expected to undergo inelastic deformation during a moderate to severe earthquake. The ductility of the BRBF can be achieved by limiting the buckling of the steel core [30].

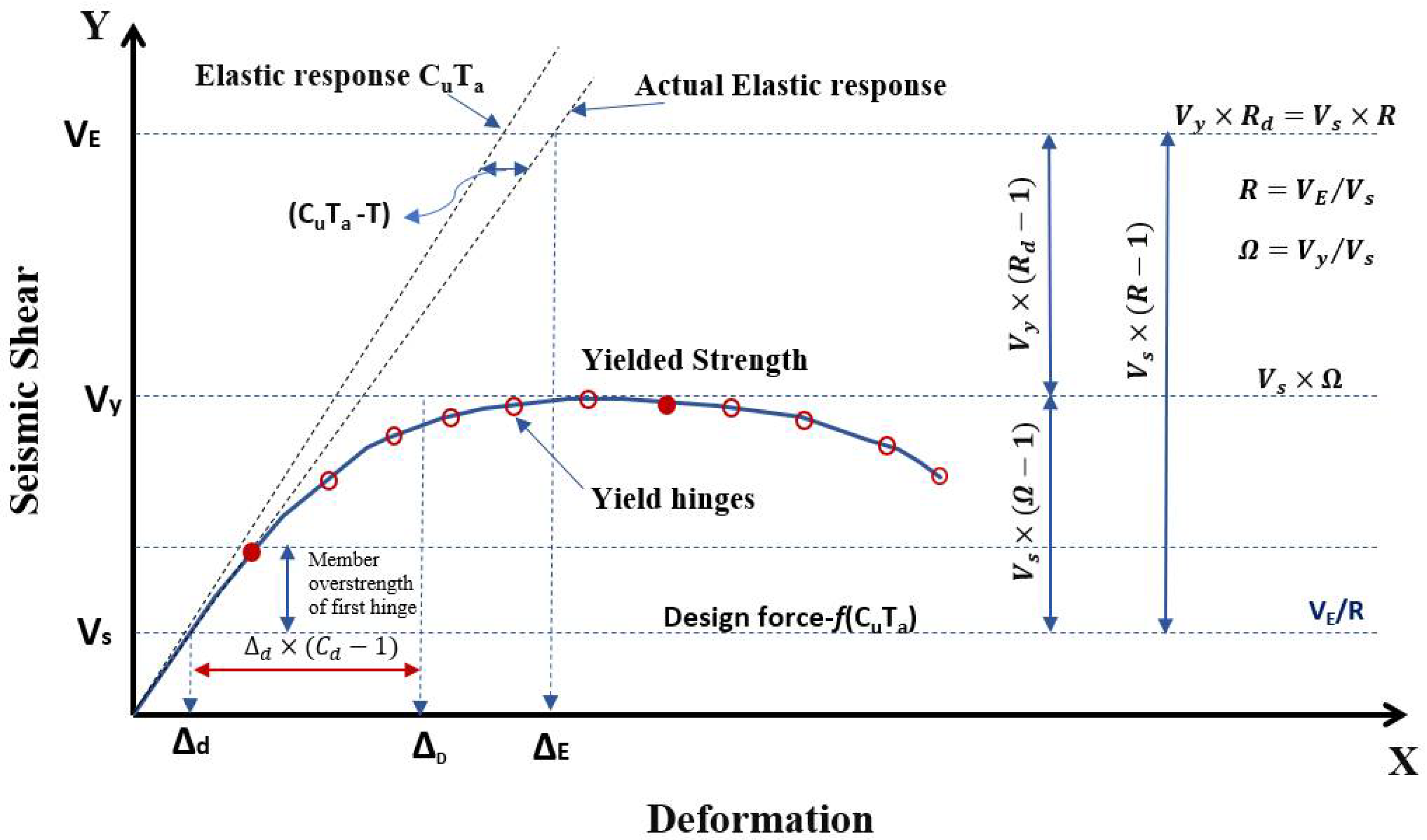
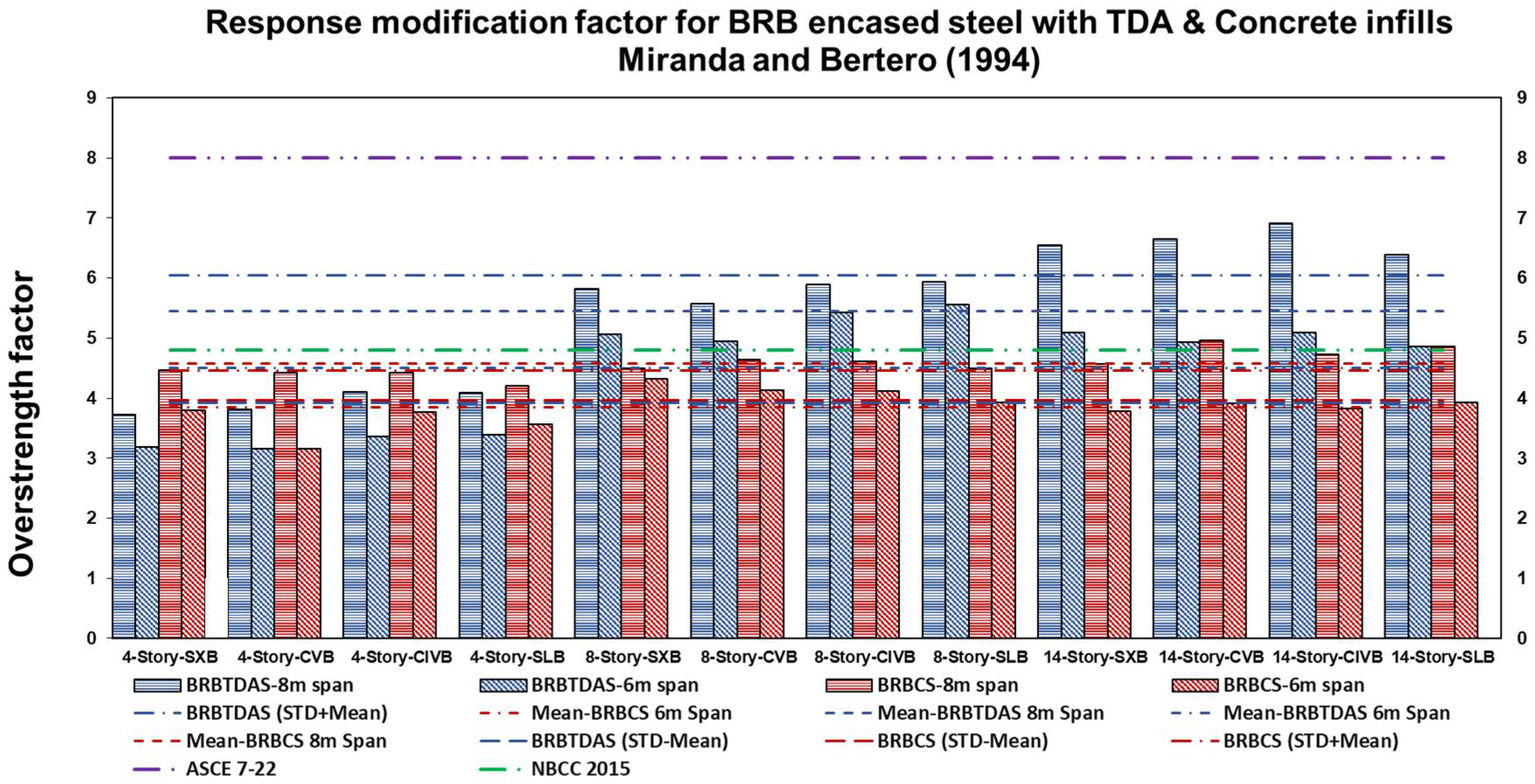
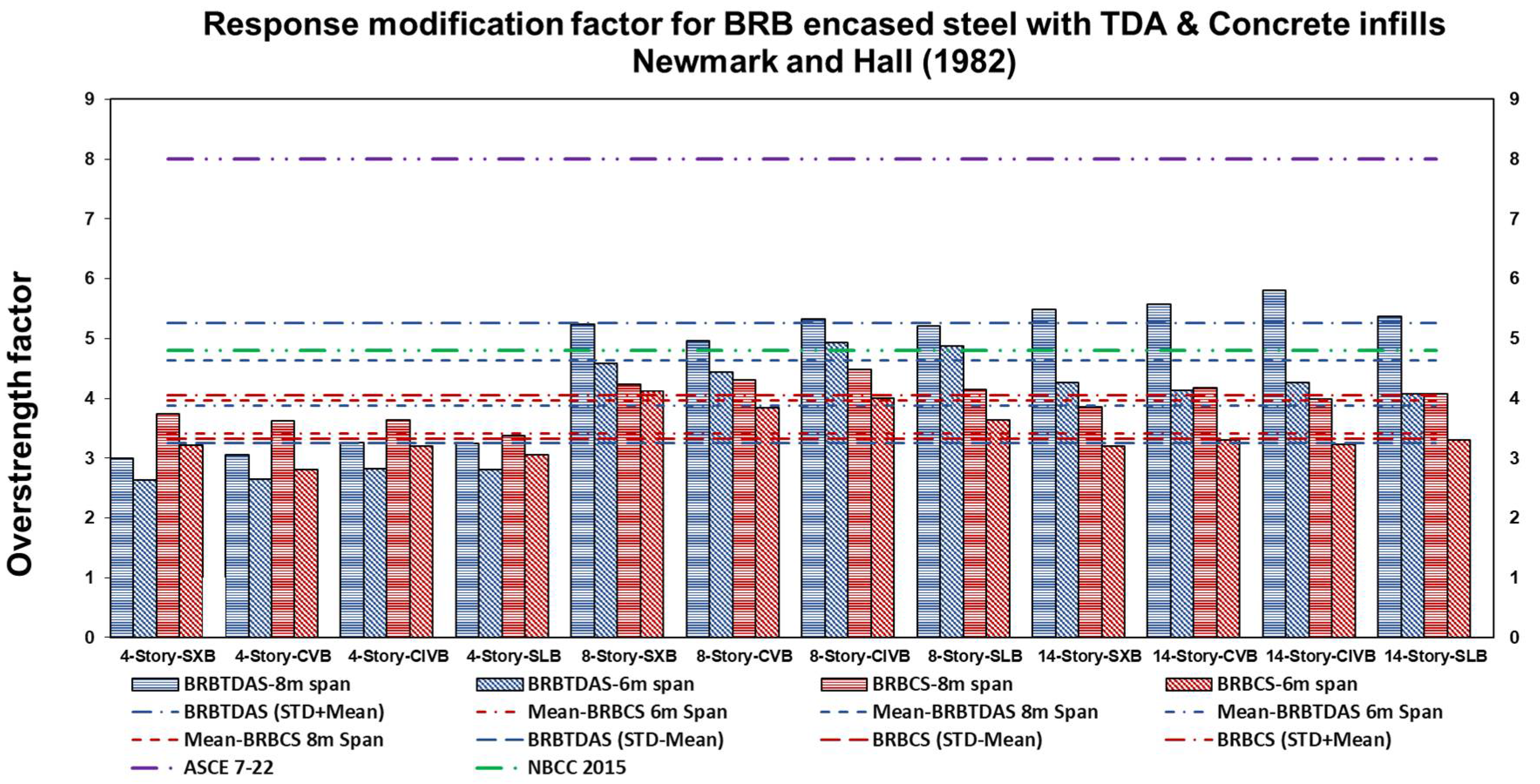
3. Response Modification Factor

The seismic force values are calculated by forces divided by a response modification factor, symbolized as R. Response modification coefficients, including the response modification factor R and the deflection amplification factor C_d, were introduced by ATC 3-06 (1982) [31] based on a detailed seismic framing system. Depending on the performance level of the structure, the component of the response modification factor can be defined in several ways, but the focus of this paper is life safety performance. The general performances of the system types during past earthquakes, their toughness, and the damping of the system were considered for the selection of R values [32].

Two bilinear approximation methods can estimate yield force and yield displacement. The first approximation is the load- or strength-versus-displacement method for reinforced concrete elements [33]. Hereby, the elastic stiffness is based on the secant stiffness of the frame and can be calculated from the force–displacement curve. The second method is the equal energy approach. Utilizing a bilinear approximation of the actual response curve (base shear vs. displacement), it is assumed that the area enclosed by these curves above the actual curve (i.e., area 1) is equal to the enclosed area below the actual response curve (i.e., area 2) (Figure 4), where V_y is the yield force, Δ_y is the yield displacement and Δ_m and Δ_u are the displacements corresponding to a limit state prior to failure. The post-yield stiffness K₁ can be calculated from Equation (1).

$$K_1=\frac{V_{max}-V_y}{{\Delta }_m-{\Delta }_y}$$

(1)

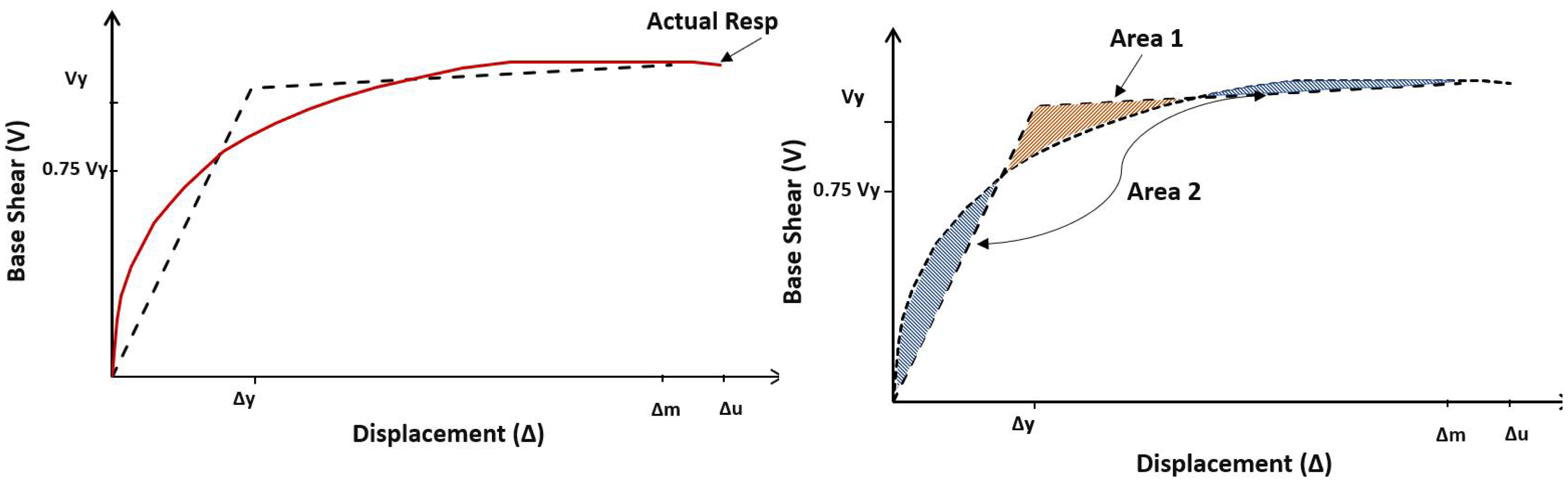
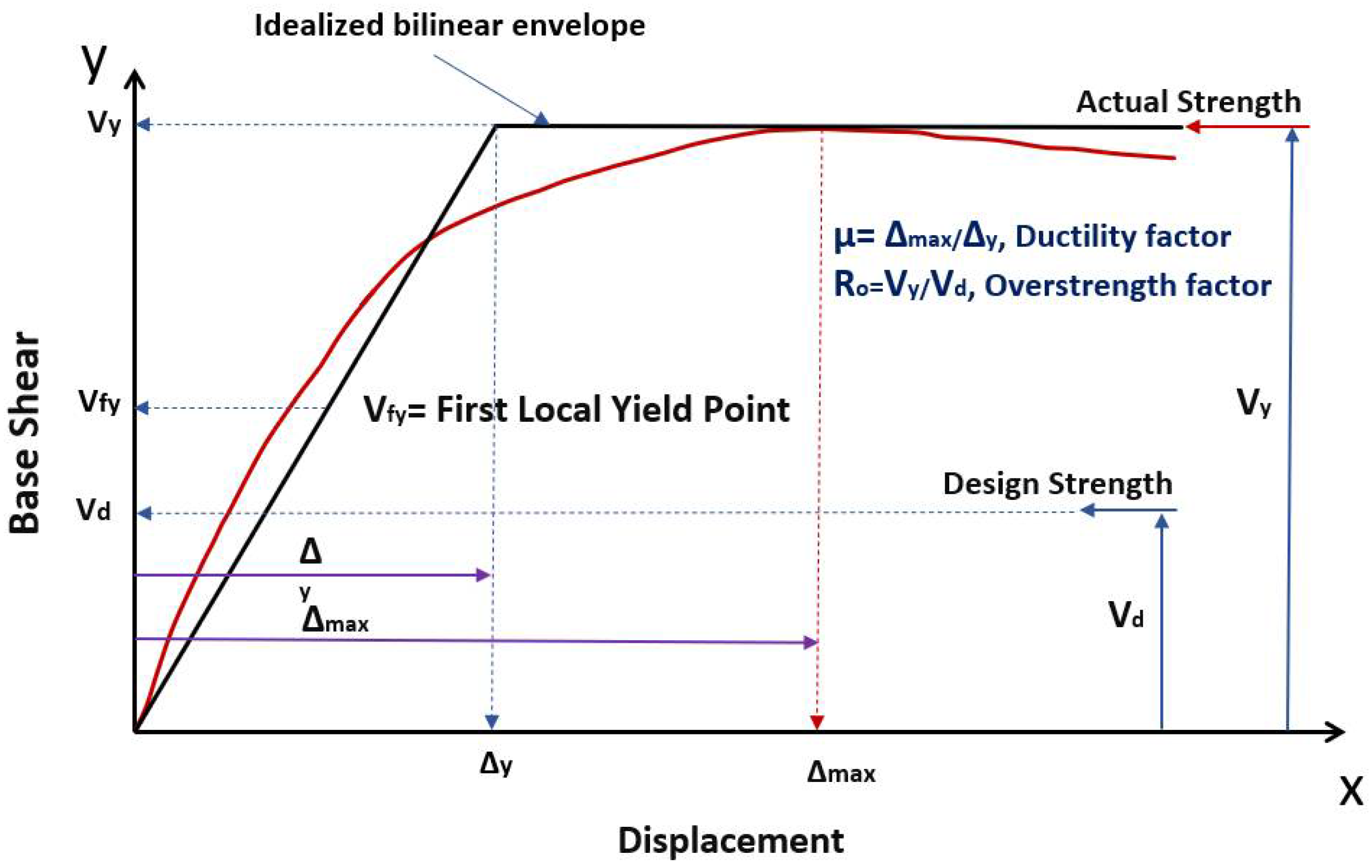
4. Overstrength Factors

Structural analysis under an earthquake in the elastic region can give the reverse strength in the structures, which is more significant than the structural response. The seismic codes take advantage of the fact that structures can dissipate a large amount of earthquake energy via their overstrength and ductility [11,14]. The ratio of the actual lateral strength (V_y) to the lateral design strength (V_d) is defined as the overstrength factor R₀, as shown in Figure 5.

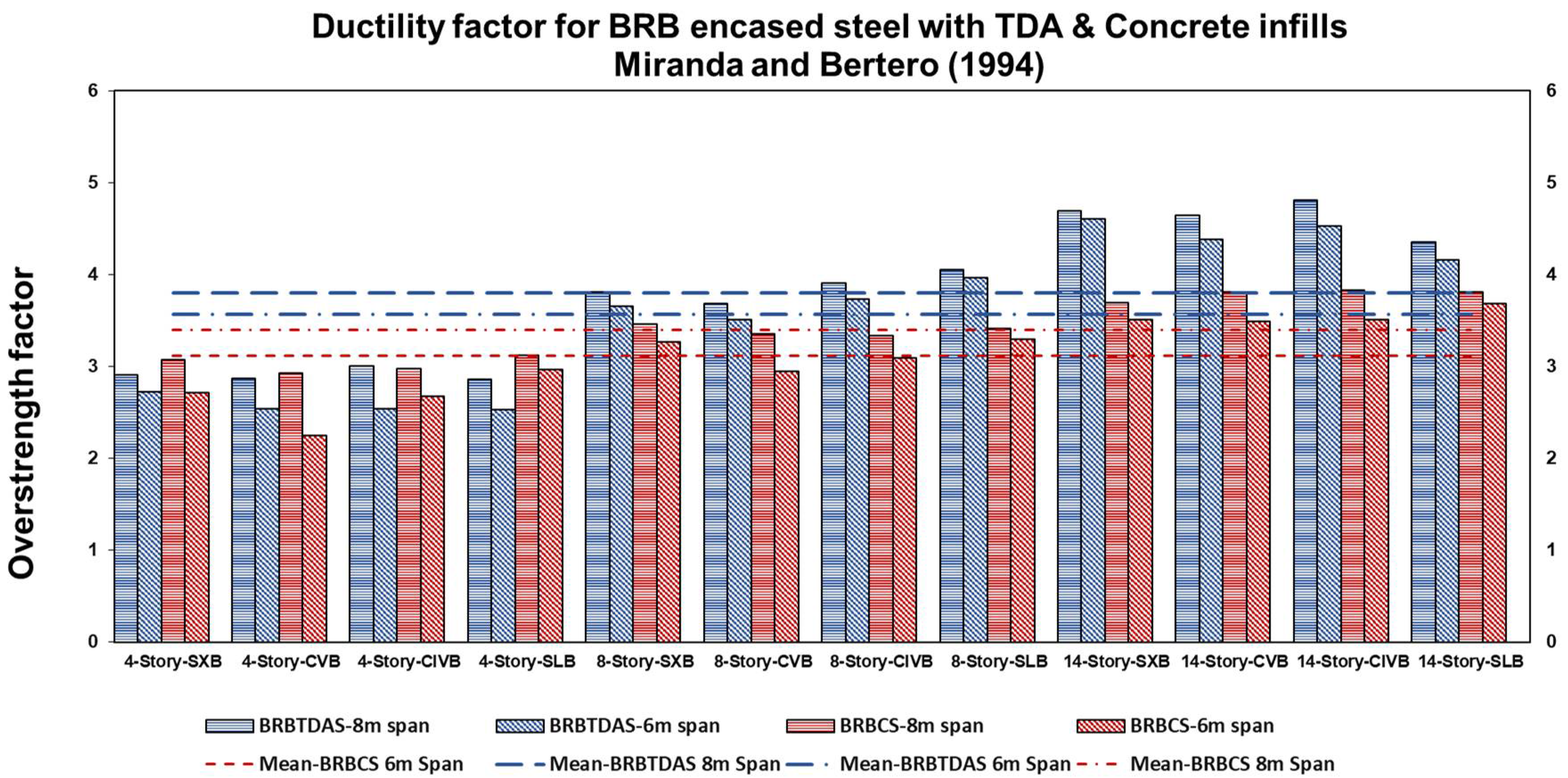
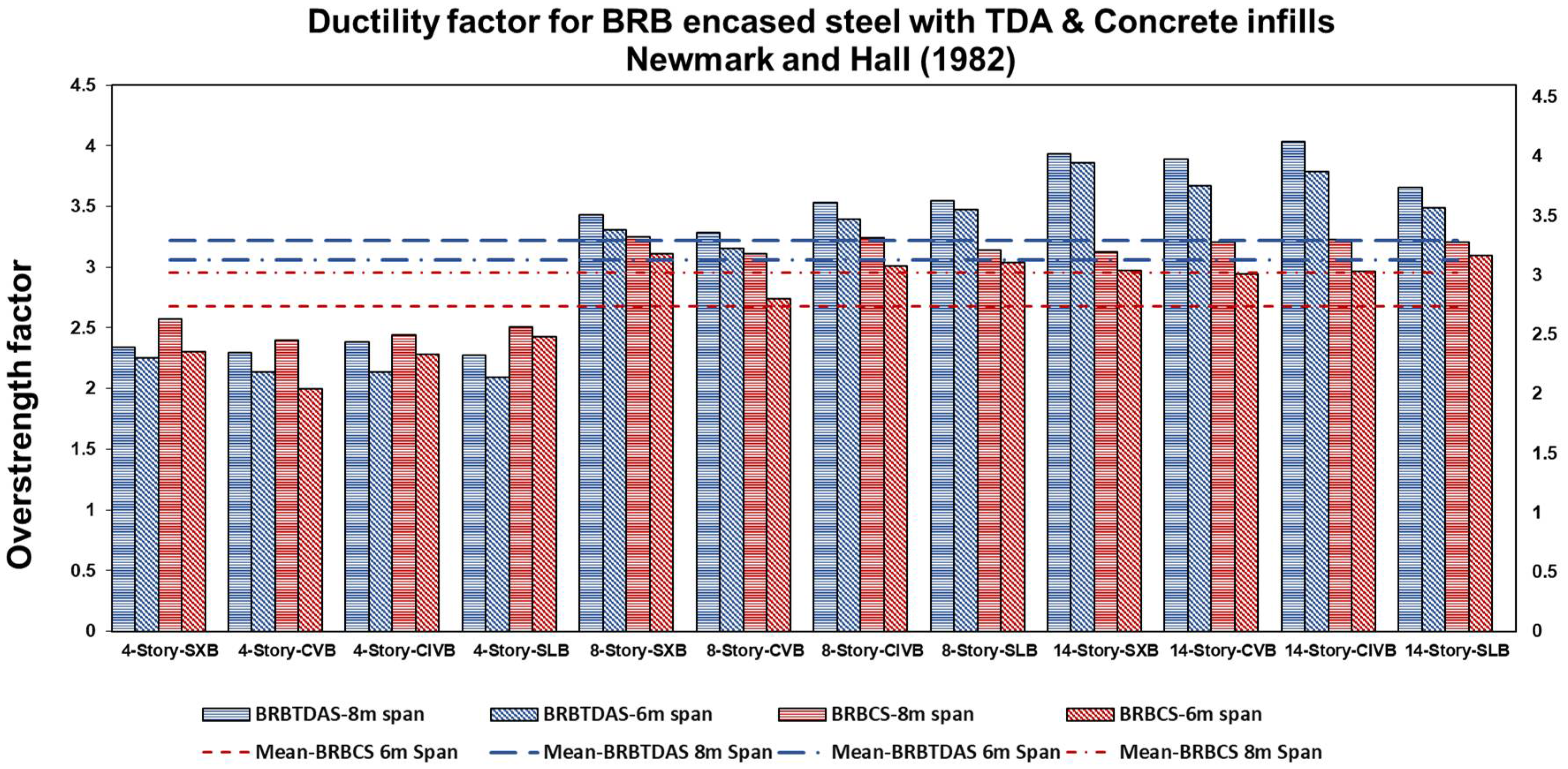
5. Ductility Factors

Several relationships estimate the ductility factor [34,35,36]. R_d is known as the ductility factor, which is the capacity of the structure to dissipate energy in an inelastic range by considering ductility µ, which can be calculated by dividing the maximum displacement over the displacement at the yield point, the soil type and the fundamental period of the structure. The methods proposed by Miranda and Bertero (1994) [35] and Nemark and Hall (1982) [36] were employed and compared in this study. According to Miranda and Bertero (1994) [35], the ductility reduction factor R_µ for stiff soil can be determined with Equations (2) and (3), where µ is ductility, T is the natural period of the structures, and ϕ is a function of ductility, the fundamental period and the soil conditions.

$$R_{\mu }=\frac{\mu -1}{\phi }+1\ge 1$$

(2)

$$\varphi =1+\frac{1}{10T-\mu T}-\frac{1}{2T}{e}^{-1.5{\left|\ln \left(T\right)-0.6\right|}^2}$$

(3)

Newmark and Hall (1982) [36] estimated the ductility reduction factor R_µ based on the structure period presented in

Table 1. Ductility reduction factor [36].

Period of Structure Ta (Sec)	Ductility Reduction Factor Rµ
Ta < 0.1	$R_{\mu }=1.0$
0.12 < Ta < 0.5	$R_{\mu }=\sqrt{2\mu -1}$
Ta > 1	$R_{\mu }=\mu$

.

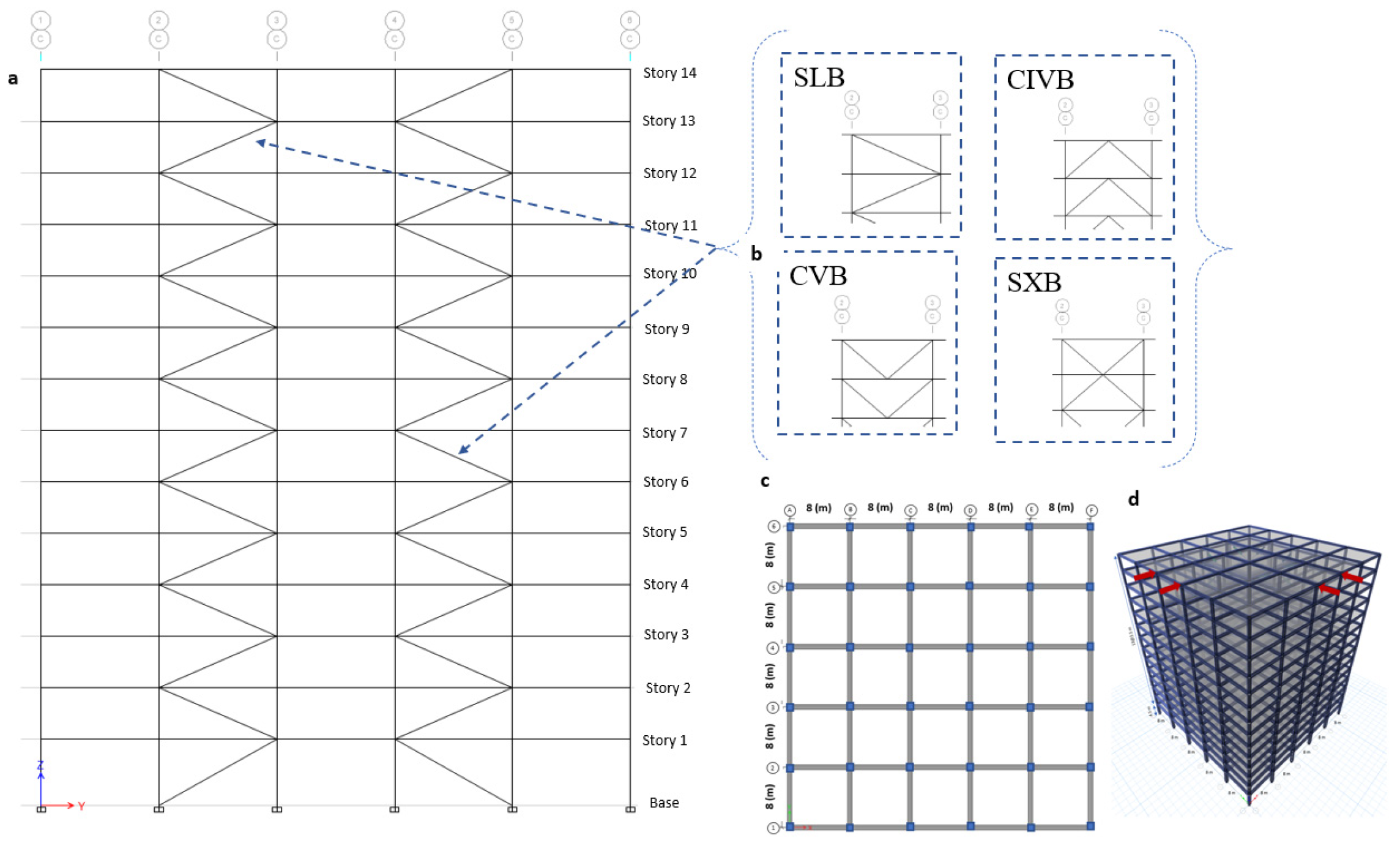
6. Design of Structural Models

The lateral force versus deformation for a seismic force-resisting system is presented in Figure 6. The first plastic hinge occurred above the strength required by analysis due to specific design rules, limits, and material strengths. The system overstrength capacity is the margin at which the maximum strength along the curve is higher than the first highlighted yield. When the lateral load increases, plastic hinges are formed, followed by an increase in resistance until the maximum strength is reached.

In this research, the mechanical properties of tire-derived lightweight aggregate concrete (TDAC) and conventional concrete have been obtained from experimental tests [24] and used to model the BRB with TDA and conventional concrete. Forty-eight different models were created and their influence on the response modification, overstrength, and ductility factors, as well as the general earthquake performance, were assessed and compared against one another. The buildings under consideration are 4-, 8-, and 14-story special reinforced concrete moment frames equipped with buckling restrained braces with an interstory height of 4.5 m at the ground floor and 3.5 m at all levels, consisting of five bays in both east–west and north–south configurations. The buildings are assumed to be located in Los Angeles, California, on stiff soil (Type D). The height restriction for BRBFs risk category D is limited to 50 m, the maximum height restriction in this study. ASCE 7-22 [12] and ACI-19 [37] were used to design the 4-, 8-, and 14-story special reinforced concrete moment frames for BRB-encased steel with TDA and concrete infills to evaluate the overstrength, ductility, and response modification factors. Figure 7 displays the elevation, plan, and 3-D view of a 14-story building with various bracing configurations, such as Chevron (Inverted V and V), Split X, and Single-Leg BRBF, with span lengths of 6 m and 8 m; similar plans are considered for four- and eight-story buildings. The compressive strength f’c is 30 MPa, the modulus of elasticity E_c is 24,500 MPa, the unit weight of reinforced concrete is 24 kN/m³, the design live and dead loads for all models are assumed to be 1.5 kN/m² and 2.4 kN/m², and the snow load acting on the roof is 1.64 kN/m².

7. Modal Analysis

The natural modes calculated from eigenvalue analysis provide the free-vibration mode shapes and frequencies of the system, whereas Ritz value analysis finds modes based on a specific loading. Since the Ritz value offers a better basis than eigenvalue, especially for analyses based on superposition such as response–spectrum or time–history, a Ritz value analysis was performed to determine the natural periods of the friction damper frame system. The fundamental period of the structure is calculated based on the results obtained from the ASCE 7-22 [12] with empirical Equation (4).

$$T_a=C_t{h}_n^x$$

(4)

where T_a is the fundamental lateral period, C_t and x are coefficients, and h_n is the height of the structure. The results of the empirical equation T_a = 0.0731 × (h_n)^0.75 for h_n = 50 m, 29 m, and 15 m, and the analytical results for BRB-encased steel with TDA and concrete infills are presented in

Table 2. The fundamental period of BRB-encased steel with concrete infill.

Span Length	6				8				Ta
Bracing	SLB	CIVB	CVB	SXB	SLB	CIVB	CVB	SXB	(S)
Story
4	0.48	0.46	0.48	0.46	0.49	0.46	0.49	0.47	0.55
8	0.91	0.79	0.89	0.84	0.92	0.80	0.90	0.87	0.92
14	1.36	1.30	1.32	1.29	1.37	1.31	1.33	1.30	1.37

Note: Single-Leg Braces (SLB), Chevron Inverted V Braces (CIVB), Chevron V Braces (CVB), and Split X braces (SXB).

and

Table 3. The fundamental period of BRB-encased steel with TDA infill.

Span Length	6				8				Ta
Bracing	SLB	CIVB	CVB	SXB	SLB	CIVB	CVB	SXB	(S)
Story
4	0.59	0.54	0.54	0.52	0.59	0.55	0.56	0.56	0.55
8	1.08	0.98	1.02	0.99	1.08	0.98	1.02	0.99	0.92
14	1.54	1.46	1.46	1.43	1.55	1.47	1.47	1.44	1.37

Note: Single Leg Braces (SLB), Chevron Inverted V Braces (CIVB), Chevron V Braces (CVB), and Split X braces (SXB).

. It can be observed that for BRB-encased steel with concrete infills, the empirical equation overestimates the fundamental period for four stories and is almost in the same range as the analytical results for eight- and fourteen-story buildings. However, for BRB-encased steel with TDA infills, the empirical equation underestimates the fundamental period for all different levels of buildings. The effect of bracing configuration and span length can be neglected due to minor differences.

8. Nonlinear Static Analysis

The static pushover analysis assumes that the response of the multi-degree-of-freedom structure can be equivalent to a single-degree-of-freedom system. This signifies that a single constant mode controls the response through the time–history regardless of the level of deformation. Although these assumptions are incorrect, several investigations have found that holding them can help yield a good prediction of the maximum seismic response of MDOF [38,39,40,41]. The equation for multi-degree of freedom can be written as Equation (5), based on this assumption [34]. Here, M is the mass matrices, C is the damping matrices, Q is the story force vector, $\ddot{x_g}$ is the ground acceleration, and X is the relative displacement vector equal to shape vector, φ, by roof displacement, x₁.

$$M\left\{\phi \right\}\ddot{x_1}+C\left\{\phi \right\}\dot{x_1}+Q=-M\left\{1\right\}\ddot{x_g}$$

(5)

The single degree of freedom situation can be defined via Equation (6).

$$x^{*}=\frac{{\left\{\phi \right\}}^T\left[M\right]\left\{\phi \right\}}{{\left\{\phi \right\}}^T\left[M\right]\left\{1\right\}}{x}_t$$

(6)

The differential Equation (7) regards the equivalent single degree-of-freedom system and can be obtained by multiplying ${\left\{\phi \right\}}^T$ in Equation (5) and substituting $x_t$ from Equation (6).

$$M^{*}{\ddot{x}}^{*}+C^{*}{\dot{x}}^{*}+Q^{*}=-M^{*}\ddot{x_g}$$

(7)

Presuming that the shape vector is known, from the results of the nonlinear pushover analysis of MDOF, the force deformation characteristics of the ESDF can be determined. Figure 8 presents the base shear vs. roof displacement (a) and idealized bilinear of ESDF with effective stiffness K_e (b). The effective stiffness K_e = V_y/x_t,y, and the hardening stiffness K_s = αK_e.

Sensitivity studies have shown that accurate predictions can be attained when the structural response is dominated by fundamental mode and the modification factor is constant for small to moderate changes in {φ}. This is also recommended by the National Hazard Reduction Program, and the seismic rehabilitation of existing buildings [42] is encouraged here as well as in various guidelines [43]. Nonlinear static pushover analysis is carried out to calculate the structural strength capacities and the deformation demand. This procedure involves pushing the structure under a lateral load pattern to the level of deformation expected in an earthquake. The main goal of this analysis is the evaluation of the deformation demands in critical elements with undesirable characteristics such as strength, stiffness discontinuities, extra loads on brittle elements, overall structural stability, and regions facing large deformation demands that require special detailing [38].

A pushover analysis can consist of different load cases with different load distributions on the structure, including acceleration, a lateral force proportional to a specified mode shape, static load pattern, and any combination of acceleration, lateral force, and static load pattern. The distributed plasticity is determined by employing fiber section “P-M2-M3” with a finite-length hinge zone, and the columns are meshed at intermediate joints and intersecting frames to increase the capture of local P-delta effects. Subsequently, nonlinear static pushover analysis was performed to calculate the overstrength and ductility factor of each structure and continued until the maximum interstory drift in the frame met the design limit of 2.5%. These values are calculated based on pushover results, and the idealized lateral force–displacement is shown in Figure 9 and tabulated in

Table 4. Pushover analysis results—BRB-encased steel with concrete infill.

Story	Bracing	Span Length	Yield Strength Vy (kN)	Design Strength Vd (kN)	Overstrength Factor Ro	Maximum Displacement Δmax (mm)	Yield Displacement Δy (mm)	Ductility µ
4	SLB	6	7113	5918	1.20	72	21	3.44
		8	8278	6149	1.34	80	22	3.63
	CIVB	6	8314	5911	1.41	65	21	3.09
		8	9130	6139	1.48	6	20	3.48
	CVB	6	8315	5914	1.41	60	24	2.50
		8	9262	6139	1.51	74	22	3.37
	SXB	6	8267	5909	1.39	69	22	3.15
		8	8926	6136	1.45	72	20	3.61
8	SLB	6	8464	7085	1.9	149	49	3.04
		8	9551	7246	1.32	176	56	3.14
	CIVB	6	10,468	7877	1.33	138	46	3.01
		8	11,403	8240	1.38	149	46	3.24
	CVB	6	11,403	8240	1.38	156	57	2.73
		8	10,468	7877	1.33	165	53	3.11
	SXB	6	9498	7179	1.33	157	50	3.11
		8	10,033	7710	1.31	155	47	3.25
14	SLB	6	8983	8420	1.06	220	71	3.49
		8	10,935	8590	1.27	250	78	3.65
	CIVB	6	9208	8447	1.09	222	74	3.78
		8	11,209	9084	1.23	260	80	4.03
	CVB	6	9531	8493	1.12	230	78	3.67
		8	11,417	8768	1.31	270	84	3.88
	SXB	6	9459	8781	1.07	215	72	3.85
		8	11,332	9180	1.24	257	82	3.93

Note: Single-Leg Braces (SLB), Chevron Inverted V Braces (CIVB), Chevron V Braces (CVB) and Split X braces (SXB).

and

Table 5. Pushover analysis results—BRB-encased steel with TDA infill.

Story	Bracing	Span Length	Yield Strength Vy (kN)	Design Strength Vd (kN)	Overstrength Factor Ro	Maximum Displacement Δmax (mm)	Yield Displacement Δy (mm)	Ductility µ
4	SLB	6	7008	5222	1.34	85	31	2.68
		8	7723	5409	1.42	101	32	3.07
	CIVB	6	7402	5599	1.32	75	27	2.77
		8	8088	5904	1.36	90	27	3.33
	CVB	6	6785	5460	1.24	75	27	2.77
		8	7973	5990	1.33	88	28	3.14
	SXB	6	6618	5654	1.17	73	24	3.04
		8	7855	6122	1.28	84	26	3.23
8	SLB	6	8383	5976	1.41	205	62	3.47
		8	8806	5997	1.46	220	62	3.54
	CIVB	6	9315	6405	1.45	190	56	3.39
		8	10,167	6753	1.51	205	58	3.53
	CVB	6	8697	6171	1.41	186	59	3.28
		8	8806	5997	1.47	197	60	3.15
	SXB	6	8757	6312	1.38	185	56	3.30
		8	10,190	6673	1.52	199	58	3.43
14	SLB	6	8995	7708	1.16	295	84	3.49
		8	11,470	7819	1.46	370	101	3.65
	CIVB	6	8900	7913	1.12	299	78	3.78
		8	11,489	7981	1.43	360	89	4.03
	CVB	6	8887	7897	1.12	298	81	3.67
		8	11,422	7971	1.43	360	92	3.88
	SXB	6	8862	8011	1.11	299	77	3.85
		8	11,332	8125	1.39	350	89	3.93

.

Figure 10 depicts the overstrength factor for BRB-encased steel with TDA and concrete infills for all brace configurations, as determined by the idealized bilinear response of base shear versus displacement. The overstrength factor ranges from 1.10 to 1.52 for the BRB-encased steel with TDA and 1.06 to 1.51 for the BRB-encased steel with concrete. The NBCC 2015 specifies an overstrength factor of 1.2, and the ASCE 7-22 [12] prescribes 2.5. These conservative values account for several factors, including member size, structural redundancy, and infill walls [44]. In general, overstrength increases with a greater span length, which shows an average value of 1.42 for BRB-encased steel with TDA infill and 1.35 for BRB-encased steel with concrete infill.

Ductility factors for BRB-encased steel with TDA and concrete infills are determined using the Miranda and Bertero (1994) [35] approach and compared to results using the Newmark and Hall (1982) [36] method, as presented in Figure 11 and Figure 12. It is evident that longer span lengths and higher building heights directly lead to increased ductility. The average ductility factors for BRB-encased steel with TDA infill were increased by about 5% compared to concrete infill. The average ductility factor computed using the Newmark and Hall [36] approach is lower by an average of about 15% than that determined using the Miranda and Bertero method [35]. The effect of bracing configuration can be neglected, with a maximum variation of about 3% for fourteen- and eight-story buildings and 4% for four-story buildings.

The results of response modification factors of BRB-encased steel with TDA and concrete infills and different frame configurations, derived via the Miranda and Bertero (1994) [35] and Newmark and Hall (1982) [36] methods, are presented in Figure 13 and Figure 14. The Miranda and Bereto method [35] gave higher values than Newmark and Hall [36], with an average increase of 17% and 14% for BRB-encased steel with TDA and concrete infills, respectively. This increase is due to implementing additional components, such as soil condition, ductility, and the structure’s natural period. ASCE 7-22 [12] and NBCC 2015 [13] prescribe the response modification values of 8 and 4.8 for BRBFs. The results show the maximum value of the response modification factor is 6.91 for TDA infill and 4.95 for concrete infill based on Miranda and Bertero [35]; however, these results are reduced to 5.80 and 4.48 under the Newmark and Hall method [36]. For BRB encased with TDA and concrete infills, the mean values are 4.97 and 4.21, respectively. Because different bracing configurations range from 5% to 12%, their effects should be considered.

9. Inelastic Response History Analysis

The nonlinear dynamic procedure or nonlinear response history analysis of a building is the nonlinear load deformation of individual components of the structure, incorporated directly via a mathematical model and subjected to ground motion acceleration histories [45]. The nonlinear behavior of the members shall be considered the same as in the pushover analysis. The equation of motion is modified to Equation (8) to recognize the inelastic behavior of the building, where u is the vector to lateral force–displacement, m is a diagonal matrix, c is the damping matrix, $f_s\left(u\right)$ is the inelastic force deformation relation, ${\ddot{u}}_g\left(t\right)$ is the ground acceleration, and $\iota$ is the influence vector. In this analysis, the force deformation for each member is hysteretic and nonlinear. The unloading and reloading curves differ from the initial loading curve. In this method, the stiffness matrix changes at each time step and must be formulated based on their element tangent stiffness matrices and deformation and the path dependence [46].

$$m\ddot{u}+c\dot{u}+f_s\left(u\right)=-m\iota {\ddot{u}}_g\left(t\right)$$

(8)

P-Δ effects, structural modeling assumptions, and ground motion characteristics are among the most important factors affecting the results. The second-order, or P-Δ, effect refers to the gravity loads acting on the laterally deformed structure. These effects reduce the initial stiffness of the structure slightly when the structure is in the elastic phase. However, when the structure is in the inelastic phase, they cause a rapid increase in lateral force resistance with negative stiffness.

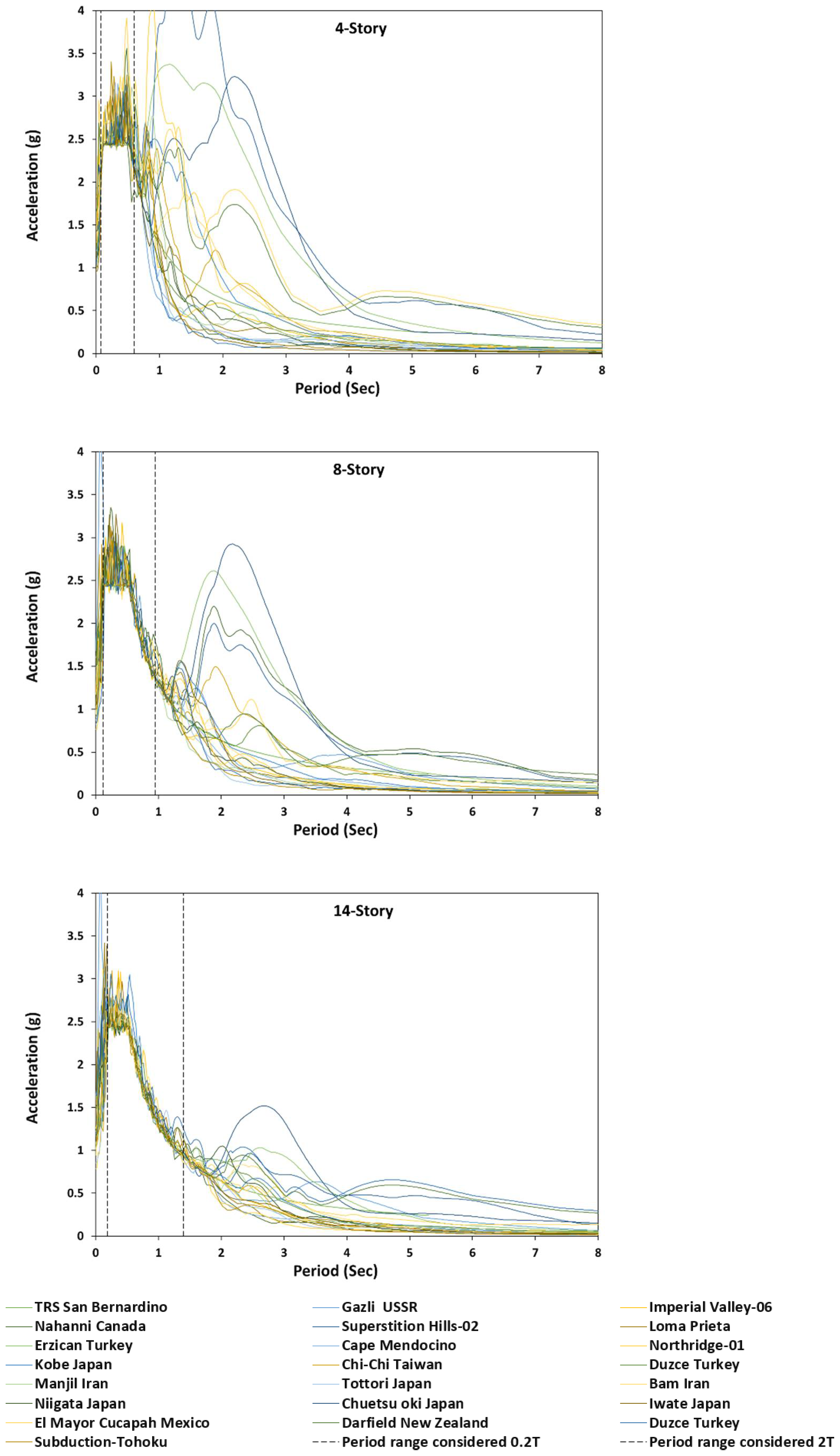
10. Ground Motion Selection

Earthquake ground motions resemble wave signals, and an accelerograph is used to record the ground motions. Ground motions have three major aspects: amplitude, frequency content, and duration [47]. The connections between the response of the structure and ground motion parameters have been explored through different strategies [48,49,50]. The earlier edition of ASCE 7-05/10 recommended three or seven ground motions for nonlinear response history analysis. When three sets of ground motions were used, the maximum values of the peak response of each were used to evaluate structural competence. If seven or more ground motions were used, the mean results were evaluated. These selections are insufficient to reach the required accuracy of the mean or the variability in the response. Therefore, the minimum number of ground motions was increased to eleven in the ASCE 7-16/22 standard. This larger number of ground motions is necessary to derive more reliable results in the mean structural response. In other words, it helps identify an unacceptable structural response in one or more ground motions, which indicates that the structure fails to meet the 10% target collapse reliability. The considered number of ground motion records and the attribution of the selected records are two important aspects when selecting ground motions. To identify the possible dispersion and mean of demand parameters, a large number of ground motion records are required due to the significant scatter of structural response to motions [51,52]. The first step of selection involves the consideration of important factors, including source mechanisms, magnitude, site soil conditions, usable frequency, period of sampling (between 0.001 s and 0.02 s), and the distance from the site to the source. Step two is selecting the final set of ground motions based on spectral shape, scale factor, and maximum motions from a single event.

In this study, the building is assumed to be located in Los Angeles, California, on stiff soil (Type D), with a latitude and longitude of 34.0522 and −118.2436. A single-target response spectrum with 5% damped and maximum considered earthquake (MCE_R) was developed by multiplying the design response spectrum by 1.5, as presented in Figure 15.

For the nonlinear response history analysis, 21 different ground motion records were selected based on the MCE_R target response spectrum from the Pacific Earthquake Engineering Research Center database [53], as presented in

Table 6. Summary of metadata of selected records.

ID	Scale Factor	Earthquake	Year	Magnitude	Arias Intensity (cm/s, OA)	Arias Intensity (cm/s, MA)	PGA (g)
1	1.0797	Gazli USSR	1976	6.8	5.28	13.19	0.702
2	1.3647	Imperial Valley-06	1979	6.53	3.98	14.91	0.598
3	1.3146	Nahanni Canada	1985	6.76	3.88	8.64	1.108
4	1.6071	Superstition Hills	1987	6.54	3.74	17.34	0.432
5	1.7282	Loma Prieta	1989	6.93	5.36	20.59	0.456
6	1.6220	Erzican Turkey	1992	6.69	1.53	10.62	0.386
7	0.9724	Cape Mendocino	1992	7.01	5.96	8.49	1.493
8	1.6892	Northridge-01	1994	6.69	3.08	17.91	0.443
9	1.2280	Kobe Japan	1995	6.90	8.39	16.09	0.834
10	1.1306	Chi-Chi Taiwan	1999	7.62	5.34	17.22	0.636
11	1.3235	Duzce Turkey	1999	7.14	3.72	12.12	0.739
12	1.4563	Manjil Iran	1990	7.37	4.64	31.79	0.514
13	1.7718	Tottori Japan	2000	6.61	5.29	18.07	0.733
14	1.1297	Bam Iran	2003	6.60	8.02	18.22	0.807
15	0.7919	Niigata Japan	2004	6.63	14.51	17.35	1.166
16	1.3327	Chuetsu-oki Japan	2007	6.80	2.81	16.73	0.482
17	1.0688	Iwate Japan	2008	6.90	11.82	19.25	1.343
18	1.5870	El Mayor Mexico	2010	7.20	6.01	29.53	0.537
19	1.0332	Darfield NZ	2010	7.00	4.49	10.71	0.764
20	1.6745	Duzce Turkey	1999	7.14	13.36	20.66	1.031
21	1.3840	Tohoku	1923	7.90	11.59	78.15	0.427

Note: Original accelerograms (OA), matched accelerograms (MA).

.

11. Ground Motion Scaling

Amplitude scaling and spectral matching are two approaches for adjusting time series to be consistent with the design response spectrum. Scaling includes multiplying the initial time series by a scaling factor, then the matched spectrum is made equal to or exceeds the design spectrum over a specified period range. Matching the time series frequency content to make it consistent with the design spectrum is known as spectral matching [48]. Since it is difficult to capture the tolerance over the entire spectrum, the idea is to focus on the period range of interest. The older version of ASCE 7-05/10 defined this range as between 0.2 T and 1.5 T, in which the lower and higher bounds were set to capture higher mode response and period elongation effects. In ASCE 7-16/22, nonlinear response history analysis is performed at MCE_R, which has a greater inelastic response than the design spectrum. Therefore, the higher bound has been increased to 2.0 T, where T is the maximum fundamental period of the building in both transitional directions as well as the fundamental torsional period. The lower bound period of 0.2 T should capture the periods required for 90% mass participation in both building directions. This additional requirement ensures that the ground motions can capture responses in higher modes for long-period structures. The accelerograms for each structure were scaled according to the maximum considered earthquake (MCE_R) with a period range of 0.2 T to 2.0 T using the applicable software [54], as shown in Figure 16.

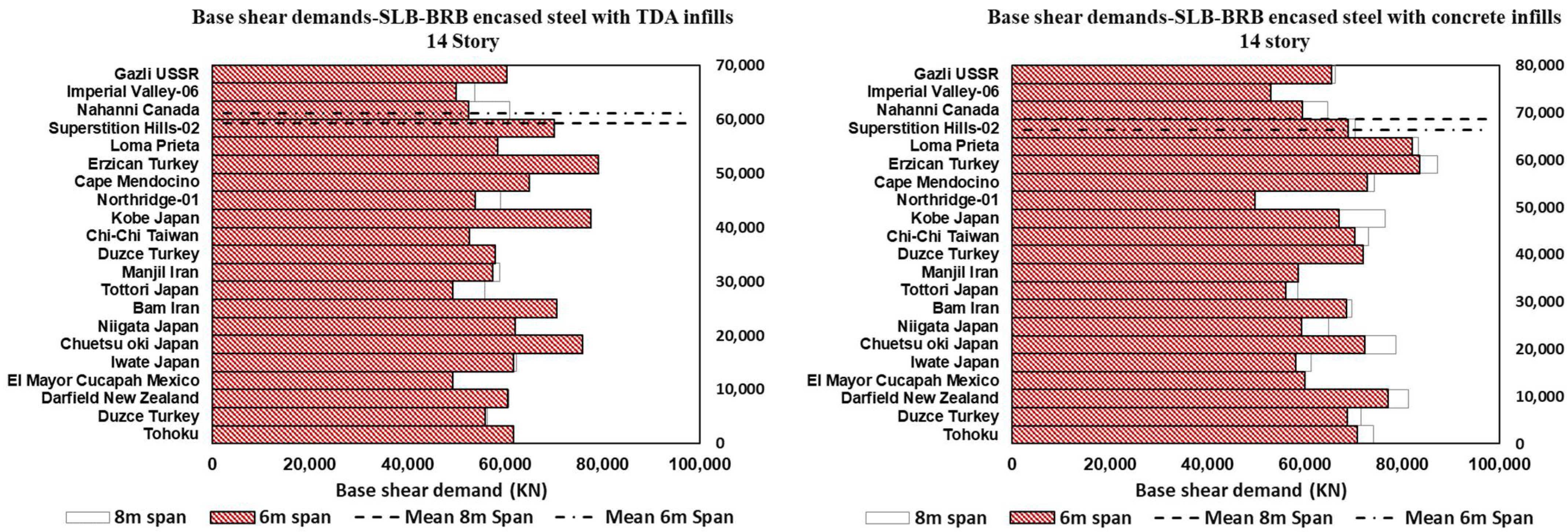
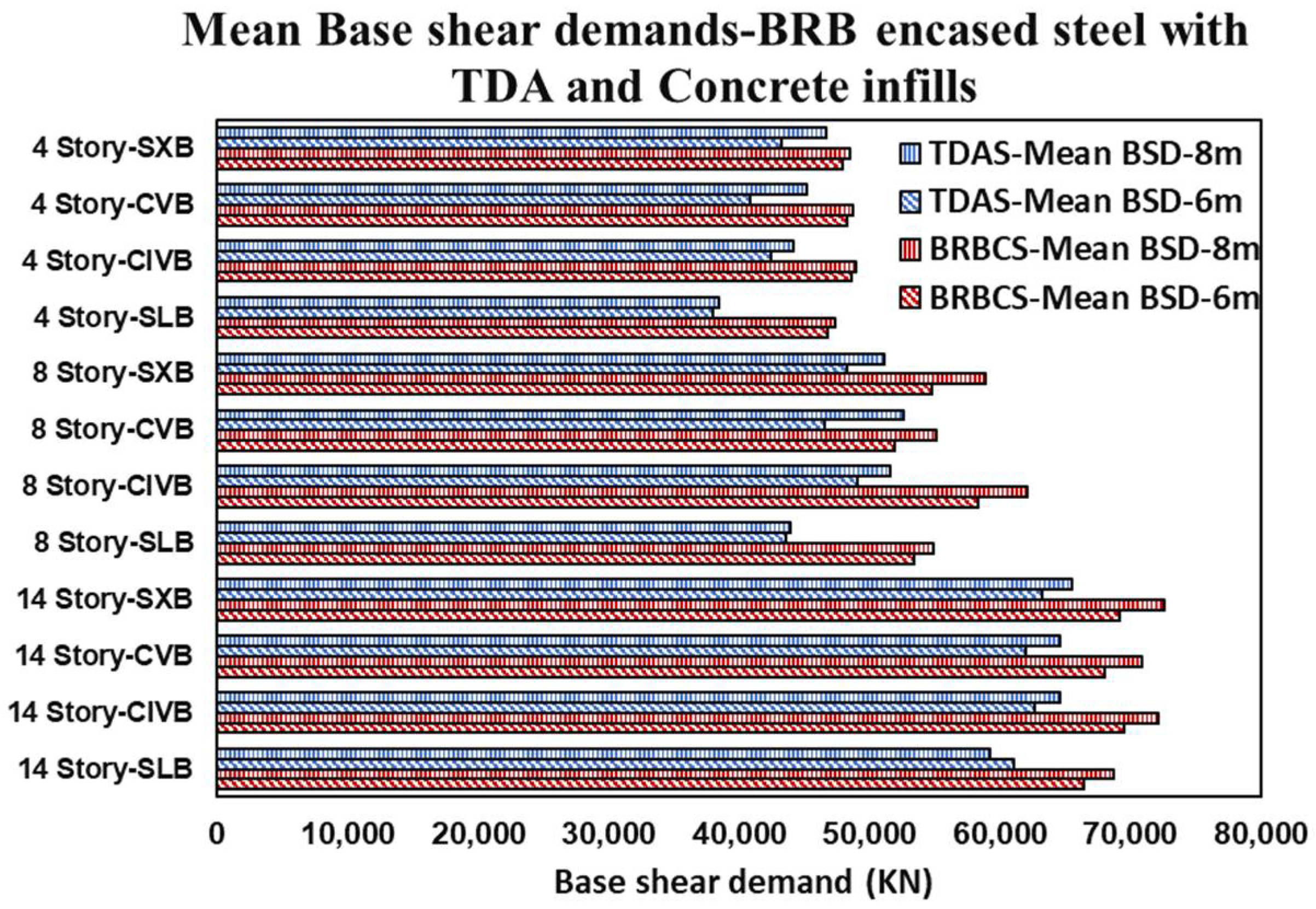
12. Roof, Inter-Story, and Base Shear Demand Results

The allowable drift for structures in ASCE 7 [12] is limited to 2%, which is implied at the design earthquake level. In this study, the allowable drift ratio is considered at the MCE_R level, which has a ratio of 1.5 to the design earthquake; therefore, the allowable drift becomes 3% (1.5 × 2%). However, in this research, the maximum allowable drift ratio of 2.5% is considered relevant to life safety performance. Based on the maximum mean value of the structural drift profiles, the allowable maximum drift ratio is less than 2% at the design earthquake intensity, and 2.5% at the maximum considered earthquake intensity, which is the deformation index used to judge the “failure” of the concrete frame structures.

Figure 17 presents the standard deviation plus the mean values of twenty-one ground motion records for different bracing configurations of BRB-encased steel with TDA and concrete infills at varying building heights and span lengths. The tenth level of a fourteen-story building with a BRB with encased steel with TDA infill has maximum mean peak values of 2.11% and 2.18%, which relate to the interstory demands for 6 m and 8 m spans of the SLB. However, the maximum mean interstory demand decreases to 2.23% and 2.32% at a similar level for the BRB with encased steel with concrete infill for 6 m and 8 m SLBs. The maximum mean interstory demands for the BRB-encased steel with TDA infill are 2.19% and 2.28% at the fourth level of an eight-story building for SLBs of 6 m and 8 m spans, respectively, while the maximum mean interstory demands for BRB-encased steel with concrete infill of SLB are 2% and 2.07% at the sixth level of an eight-story building. The third level of a four-story building with BRB with encased steel with TDA infill of the SLB has a maximum mean value of 2.12% and 2.34% for 6 m and 8 m span lengths, respectively, and the same level has maximum mean values of 1.94% and 2.17% for the BRB-encased steel with concrete infill for the same spans of SLB. The maximum mean values of the drift demand were observed at the third, fourth, and tenth levels for BRB-encased steel with TDA and concrete infills. In general, the drift demand has a higher value in relation to the BRB with encased steel with TDA compared to the BRB with encased steel with concrete.

The maximum base shear demands were calculated based on the nonlinear response history analysis results. In the interest of brevity, the results are only presented here for the base shear demand of BRB-encased steel with TDA and concrete with an SLB configuration, as shown in Figure 18, Figure 19 and Figure 20. It can be observed that the smaller span lengths have lower base shear demands compared with longer span lengths, and the base shear demand increases with the increase in building height and varies with different bracing configurations.

The mean base shear demands for BRB-encased steel with TDA and concrete infills with different span lengths, bracing configurations, and heights are presented in Figure 21. Overall, the base shear demands are reduced for the BRB-encased steel with TDA infill compared to the concrete infill and are higher in configurations with greater span lengths.

In addition, the base shear capacity over demand ratio is presented in Figure 22. This ratio is higher for 8 m-span configurations than for 6 m spans. The mean base shear demand values for BRB-encased with TDA infill are 1.49 and 1.38 for 8 m and 6 m spans, respectively, while these values increase to 1.63, and 1.45 for 8 m and 6 m spans of BRB encased in a concrete infill, respectively. Buildings equipped with BRB encased with TDA showed base shear demands that were reduced by an average of 7% compared to concrete infill.

13. Results and Discussions

It is critical to developing a system focused on sustainability in order to allow us to transition from simple curbside recycling to a broader perspective of employing different types of waste. Because aggregates account for a considerable amount of concrete mixtures, using waste aggregate materials such as tire-derived aggregates has a considerable influence on resource conservation. This study focuses on the effects of using tire-derived aggregate on a BRBF.

Furthermore, when the seismic design factors of a system are missing from the code, engineers/researchers work with the closest equivalent system with conservative values. This paper’s methodology is useful in evaluating and comparing these factors to the recommended factors set in the codes.

14. Conclusions

It is crucial to find different applications for utilizing scrap tires, which cause considerable environmental damage on a large scale [24]. This research introduced another application to reuse TDA in buckling restrained braces, which contributes to sustainability. They can be used in the retrofitting of new as well as existing structures, where the primary concern is the damping of the system. The seismic design factors for novel buckling restrained braces employing tire-derived lightweight aggregate concrete as a filling material were explored in this study. Four, eight, and fourteen-story special concrete moment frames were designed based on the ASCE 7-22 [12] and ACI 318 [37]. The effects of different bracing configurations, including Chevron (Inverted V and V), Split X, and Single-Leg BRBs with different span lengths of 6 m and 8 m, were discussed. The overstrength, ductility, and response modification factors of forty-eight frames were evaluated and discussed. Furthermore, nonlinear response history analysis was used to evaluate the performances of these buildings, utilizing twenty-one distinct ground motion recordings. The interpretation of inter-story and roof drifts, as well as their capacity over demand ratios, have been presented.

The following conclusions should be highlighted:

• The average fundamental periods of BRB-encased steel with concrete with different span lengths and bracing configurations are 0.47(s), 0.86(s), and 1.32(s) for four-, eight-, and fourteen-story SCMFs. These values are increased to 0.55(s), 1.01(s), and 1.47(s) for four-, eight-, and fourteen-story SCMFs of BRB-encased steel with TDA. In general, the fundamental period of the structures, when calculated by an empirical equation, is more conservative than the result when using eigenvalue analysis of the structures for BRB-encased steel with concrete infill. It underestimates the period of the structure in higher buildings equipped with BRB encased steel with TDA. The fundamental period of BRB-encased steel with TDA infill is about 15% higher than BRB-encased steel with concrete infill. Furthermore, while computing the natural period of the structures, the effect of bracing configuration can be ignored;
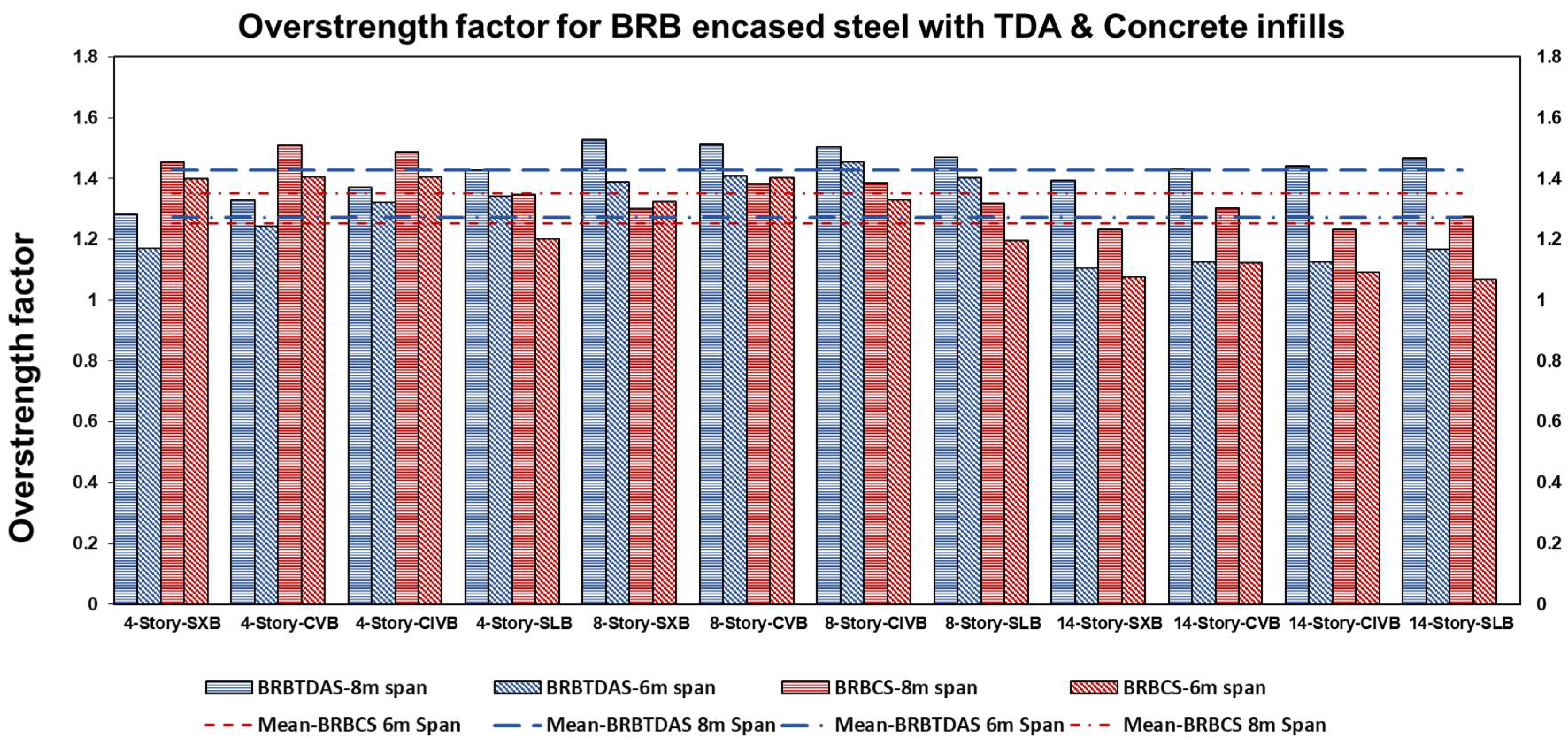
• The overstrength factor ranges from 1.10 to 1.52 and 1.06 to 1.51 for the BRB-encased steel with TDA and concrete infills. The prescribed overstrength factors in ASCE 7-22 and NBCC 2015 [13] are 2.5 and 1.2. ASCE 7-22 [12] gives a conservative value that accounts for several factors, including member size, effects of structural redundancy, and infill walls [44]. Moreover, span length directly affects the overstrength factor, and longer span lengths result in a greater overstrength factor;
• The ductility factors have been calculated and compared using the Miranda and Bertero (1994) [35] and Newmark and Hall (1982) [36] methods. We found that a longer span length and a higher building height increase the ductility factor. The BRB-encased steel with TDA infill increased the average ductility factors by 5% compared to the BRB-encased steel with concrete infill. The average ductility factor calculated using the Newmark and Hall (1982) [36] method is approximately 15% lower than that derived using the Miranda and Bertero (1994) [35] method. Additionally, because the variance in bracing configuration impact is less than 4%, their effect can be ignored;
• The calculated mean value of RMF based on the Miranda and Bertero (1994) [35] method for BRB encased with TDA infill is 4.97, and it is 4.21 for concrete infill, while the computed mean value of RMF based on the Newmark and Hall (1982) [36] approach is 4.25, and it is 3.68 for BRB encased with TDA and concrete infills. The Miranda and Bertero (1994) [35] method achieves a better result than the Newmark and Hall (1982) [36] method because it considers more parameters, such as soil condition, ductility, and the natural period of the structure. The response modification factor increases as the building height and span length increase. The response modification factor for BRB encased with TDA and concrete infills was in the range of 3.13 to 3.61, with a mean value minus standard deviation of about 4 in both cases. Accordingly, ASCE 7-22 [12] and NBCC 2015 [13] specify response modification values of 8 and 4.8 for BRBFs, which are conservative. As a result, for structures with a height equal to or less than 50 m, a response modification factor of 4 is recommended, which covers about 95% of the cases. It is evident that different bracing configurations range from 5% to 12%, hence their effect should be addressed;
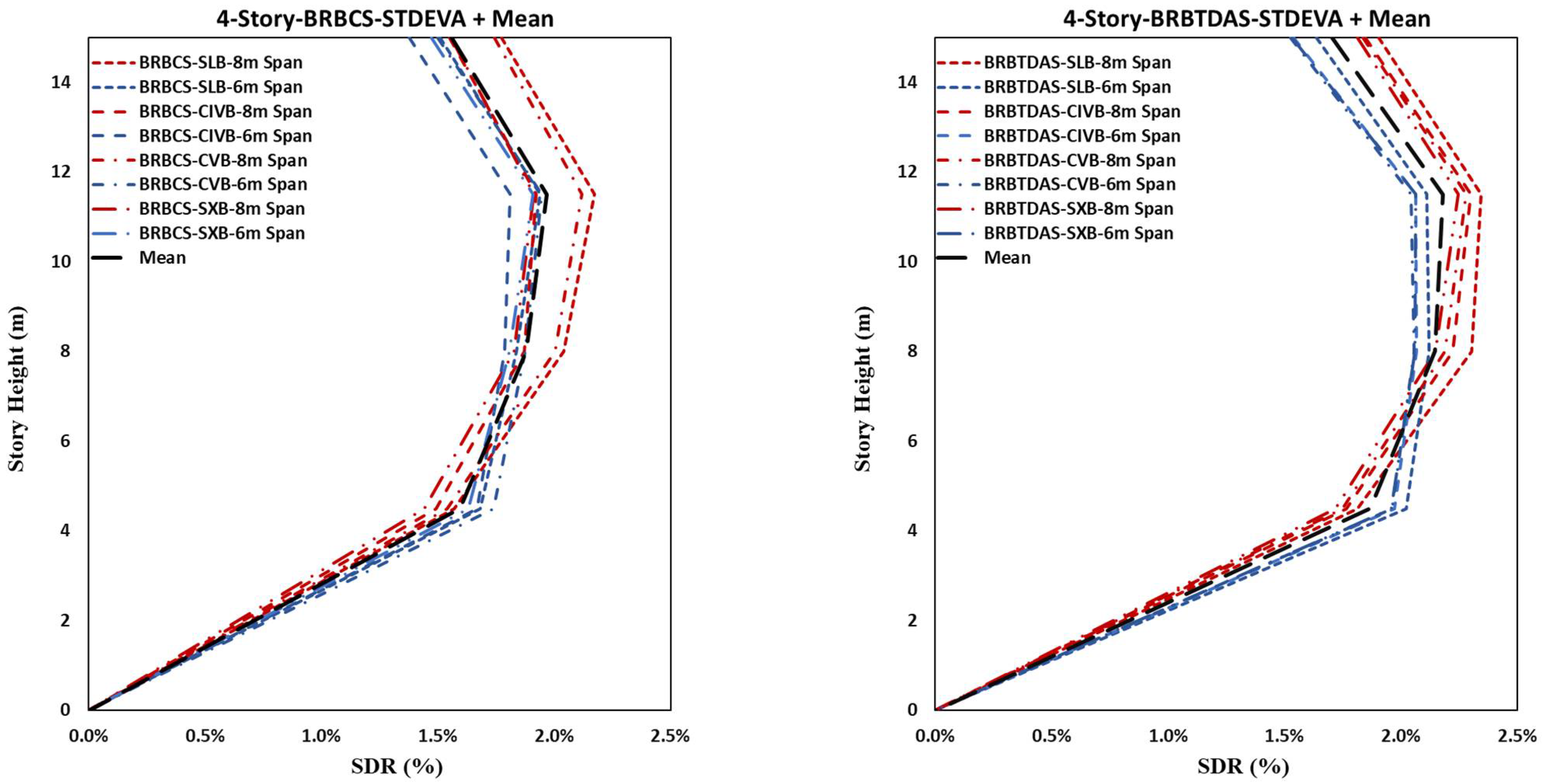
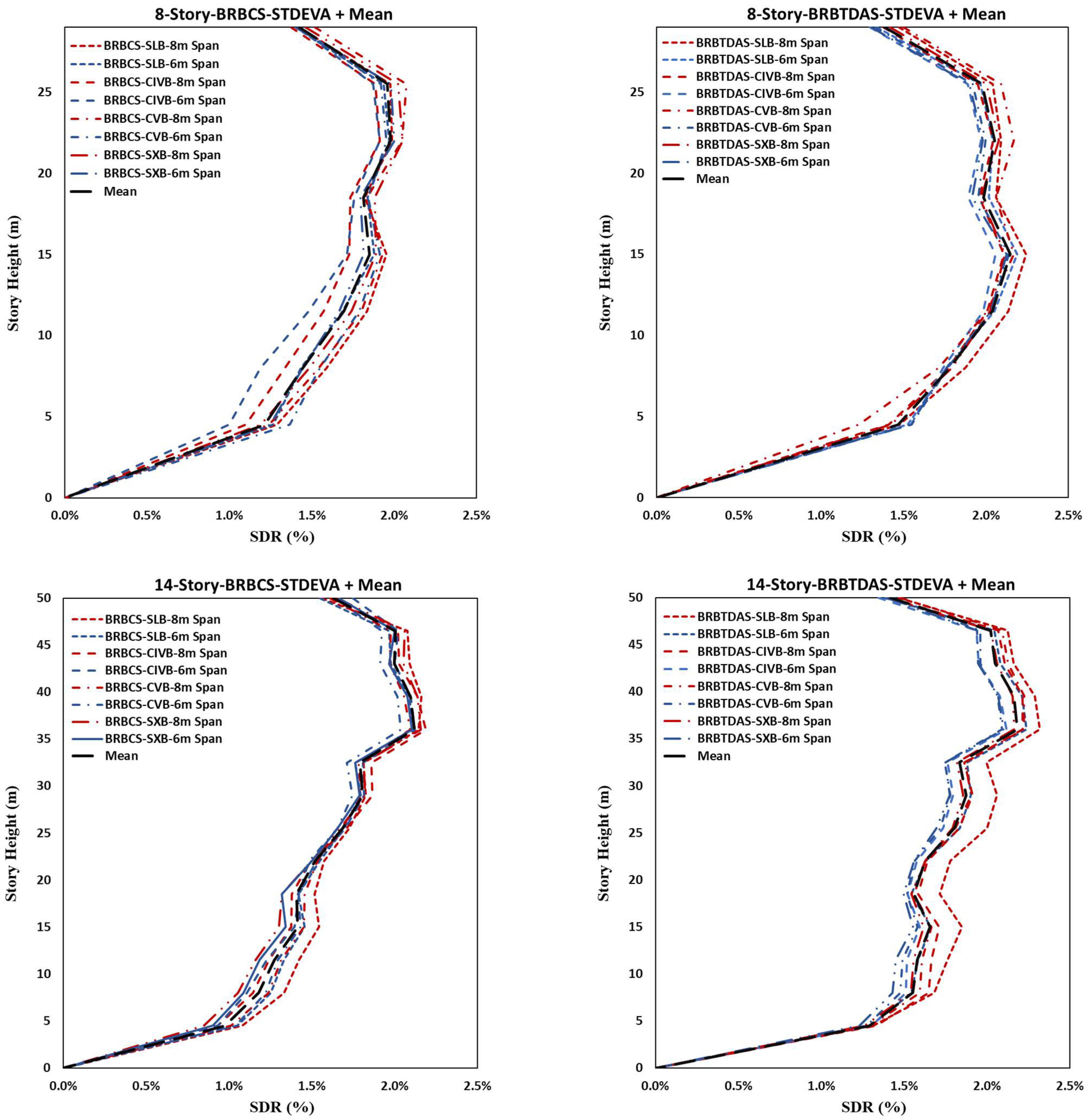
• The maximum drift demand of nonlinear response history analysis increases with height. For four-story BRBFs, the maximum mean value of interstory demand was found at the third level, while it shifted to the fourth and tenth levels for eight- and fourteen-story structures. We found that with greater heights of the structure, the maximum interstory drifts move to higher levels, and longer span lengths increase the story drift ratios. The interstory demands are higher for BRB-encased steel with TDA infill than BRB-encased steel with concrete infill;
• Base shear demands increase with greater span lengths and heights and vary with different framing configurations. Furthermore, compared to concrete infill, the base shear demands for BRB-encased steel with TDA infill are reduced in shorter span lengths, and are greater in longer span lengths.

This study is limited to the seismic design factors and overall performance of the system; further numerical and experimental studies are required to evaluate the effects of BRBFs with TDA filling in CMRF using different mechanical properties of tire-derived lightweight aggregate concrete (TDLWAC) to evaluate their seismic parameters, dissipation capacity, and performance under actual excitation conditions.