Research on Urban Distribution Routes Considering the Impact of Vehicle Speed on Carbon Emissions

Abstract

To solve the low-carbon vehicle routing problem (VRP) with sustainable development background, the VRP considering the impact of vehicle speed on carbon emissions is studied. A vehicle routing optimization model aims to minimize the total cost of distribution, penalty cost and carbon emission cost. In the model, the driving time and carbon emissions are calculated on the basis of the varying vehicle speed matching the real road network. Moreover, the improved genetic algorithm is applied to optimize vehicle routing in this paper. Using the Solomon standard datasets, the experimental results validate the carbon emission cost and the total cost from the dynamic road network are lower than those from the static network; furthermore, the carbon emission cost and the total cost from the improved GE algorithm are much lower than those from the general GE algorithm in the dynamic road network. Obviously, the built model and the improved algorithm are more feasible and effective.

1. Introduction

An increasing number of factors are considered in research on vehicle routing optimization, such as customer satisfaction expressed by the time window [1,2,3]. Its goal is to optimize the delivery route with time window constraints. Recently, as the low-carbon environment has attracted increasing attention, carbon emissions have gradually become one of the key factors in vehicle routing optimization [4,5,6,7,8]. Tang [9] proposed a multi-objective model to minimize travel time and carbon emissions that treated the travel speed as a critical variable. Additionally, a multi-objective particle swarm optimization algorithm was designed to solve the problem. Mustafa Cimen [10] proposed that the minimization of the carbon emission cost was more environmentally friendly than the minimization of distribution cost in the VRP, and the relevant models were established and calculated through a heuristic algorithm, which verified the correctness of the conclusion. Zhou Lin et al. [11] researched the low-carbon delivery and discrete scheduling problem considering timing dependence as a key factor, and a hybrid evolutionary algorithm combining a genetic algorithm and local search was designed to solve the problem. Ma Li et al. [12] researched the cold chain road distribution considering carbon emission cost and real road conditions, and the improved particle swarm optimization algorithm was designed to verify the model. An Lu et al. [13] found that more carbon dioxide would be generated in the process of cold chain distribution than in general distribution. To solve this problem, they established a carbon emission cold chain distribution model using the carbon tax mechanism and solved the model with the improved quantum ant colony algorithm. Finally, they verified the effectiveness of the model and the algorithm with simulations. To reduce carbon emissions and achieve the goal of a low carbon economy, most of the above studies consider the optimization of carbon emission costs.

In the distribution, the vehicle speed changes due to the vehicle jam and the speed limit of different road types, and some scholars considered the varied speed when solving the vehicle routing problem. CAI [14] built the minimizing the total cost model considering the varied speed as a key factor, and the adaptive ant colony algorithm was used to solve the problem. Li Shunyong et al. [15] designed a simulated annealing algorithm to solve the multipath low-carbon distribution path problem in a time-varying environment. Lin Yi et al. [16] established a UAV-vehicle routing problem model with a time window under a time-varying network and proposed a two-stage heuristic algorithm to solve the model. Considering both openness and time variability when constructing the VRP model, Fu Zhaohui et al. [17] and Liu Changshi et al. [18] applied the improved genetic algorithm and the improved ant colony algorithm, respectively, to solve the model.

According to the current research, there are relatively few studies that consider both “carbon dioxide emissions” and “the change of vehicle speed”, especially the impact of the varied speed on carbon dioxide emissions. To compensate for the defect of recent research, both the varying vehicle speed and carbon dioxide emissions are considered in the paper. Standing at the angle of enterprises, customers and social responsibility, an urban distribution path model was constructed to “minimize the vehicle number”, ”maximize customer satisfaction” and ”minimize carbon dioxide emissions” as the total goal, and an improved genetic algorithm was designed to solve the problem.

2. Description of the Problem and Setting of Relevant Variable

There are several light trucks of the same type in the distribution center. These vehicles start from the distribution center to distribute to each customer point and return to the distribution center after completion. In this paper, the change in vehicle speed, carbon dioxide emissions, load limits and customers’ requirements on distribution time and service quality are considered to realize the vehicle routing problem.

To solve the above problems, some restrictions on the distribution process are made as follows:

• S1: The number of vehicles in the distribution center is limited but meets the distribution needs.
• S2: The storage capacity of the distribution center can meet the needs of all customers.
• S3: The demand of each customer is fixed.
• S4: Normal traffic congestion is considered without any unexpected accidents.
• S5: The speed of the vehicle is time varying.
• S6: The distribution vehicle must return to the distribution center after completing the distribution from the starting point.
• S7: The demand of each customer is less than the prescribed carrying weight of the vehicle.
• S8: Each customer must be served in the specified time window.
• S9: Each customer can only be served by one vehicle and can only be served once.
• S10: In the process of distribution, the vehicle can pass through at most two types of roads to complete the distribution requirements.

2.1. Setting of Relevant Variables

2.1.1. The Change of Vehicle Speed under Multiple Road Types in Different Time Periods

The change of vehicle speed is always described by the time-varying road network, which means that the vehicle speed changes at different time points. Some researchers prefer to divide the time-varying road network into the early peak period, the flat peak period and the late peak period [19,20,21]. The division segments above are fewer, so the results may differ greatly from the actual situation. In this paper, the whole day is first divided into the morning peak, evening peak, afternoon peak and flat peak periods, and then each period is further subdivided into different time intervals of 20 min each to ensure that the vehicle speed is constant within the same time interval.

In real life, vehicle speed varies while driving on multiple roads. In this paper, the urban roads are classified into four types according to the traffic flow and the average speed: the main road, the secondary road, the express road and the branch road.

The vehicle speed under multiple road types in different time periods is expressed by Formula (1), where a, b, c and d represent the four road types and $1,2,\dots m$ corresponds to the divided time range.

$$V=\left|\begin{array}{ccccc}{v}_{a1}& v_{a2}& v_{a3}& \cdots & v_{am}\\ v_{b1}& v_{b2}& v_{b3}& \cdots & v_{bm}\\ v_{c1}& v_{c2}& v_{c3}& \cdots & v_{cm}\\ v_{d1}& v_{d2}& v_{d3}& \cdots & v_{dm}\end{array}\right|$$

(1)

2.1.2. Calculating the Delivery Time under Varying Vehicle Speed

The delivery vehicle may pass through multiple types of roads in different time periods between the two customers, so the change of speed should be considered when calculating the delivery time between the two customers. As the distribution sites$i$, $j$ as an example, suppose the vehicle finishes the delivery of customer $i$ and is ready to leave at time $t_s$,$t_s\in m=\left[t_a,t_b\right]$, where$m$ is a time segment and the speed corresponding to this time segment is $v_m$. Therefore, the distance travelled in the remaining time of this segment is$d_1=\left(t_b-t_s\right)·v_m$. According to the analysis above, the delivery time between customers $i$ and j can be calculated as follows. When $d_1\ge d_{ij}$, the vehicle speed between customers $i$ and $j$ is a constant as$v_m$, and (2) is designed to calculate the delivery time from customers $i$ to$j$. Otherwise, if $d_1<d_{ij}$, which denotes that the vehicle speed varies from $v_m$ to $v_{m+1}$ in different time periods, (3) is designed to calculate the delivery time from customers $i$ to $\mathrm{j}$.

$$t_{ij}=\frac{d_{ij}}{v_m} if d_1\ge d_{ij}$$

(2)

$$t_{ij}=\left[\frac{\left(d_{ij}-d_1\right)}{v_{m+1}}\right]+t_b-t_s if d_1<d_{ij}$$

(3)

2.1.3. Calculating Carbon Emissions Considering Vehicle Speed

Many scholars think there is a certain proportional relationship between fuel consumption and carbon emissions; others use the combination of the fuel consumption calculation model and the carbon dioxide emission coefficient to calculate the carbon tax of carbon dioxide and then convert it into cost. Because current fuel consumption models cannot accurately calculate fuel consumption, the carbon dioxide emission coefficient of fuel cannot be very accurate either; the model combining them may further amplify the errors, and the accuracy of the results obtained cannot be guaranteed [22,23].

In this paper, the carbon emissions are calculated by Formula (4) from the European Commission, which fits the data of a large number of different types of vehicles and different speeds in real life [24].

$$E=\left(110+0.000375v^3+\frac{8702}{v}\right)\times GC\times LC$$

(4)

$$LC=0.27\omega +1+0.0614\delta \omega -0.0011{\delta }^3\omega -0.00235v\omega -\left(\frac{1.33}{v}\right)\omega$$

(5)

$$GC=\exp \left(\left(0.0059v^2-0.0775v+11.936\right)\delta \right)$$

(6)

Formula (4) denotes the carbon emissions per unit distance of vehicles, $v$ represents the speed, $GC$ is the road slope correction coefficient, $LC$ is the vehicle load correction coefficient, $\delta$ is the road slope (percentage), and $\omega$ is the ratio of vehicle load to vehicle capacity, which is between [0, 1].

Per the above formula, vehicle speed is the most direct factor affecting carbon dioxide emissions, while vehicle speed varies in distribution. The change in vehicle speed must be considered in the calculation of carbon emissions.

Similar to the analysis of the delivery time between customers$i$ and $j$, if the speed is constant in the delivery as $v_m$, the carbon emissions can be denoted as follows:

$$E_{ij}=\left(110+0.000375v_m^3+\frac{8702}{v_m}\right)\times GC\times LC\times d_{ij}$$

(7)

If the delivery speed is varied between customers$i$ and $j$, the carbon emissions can be calculated as follows:

$$\begin{gathered} E_{ij}=\left(110+0.000375v_m^3+\frac{8702}{v_m}\right)\times GC\times LC\times d_1+ \\ \left(110+0.000375v_{m+1}^3+\frac{8702}{v_{m+1}}\right)\times GC\times LC\times d_2, \left(d_2=d_{ij}-d_1\right) \end{gathered}$$

(8)

2.2. The Proposed Model Considering the Impact of Varying Speeds on Carbon Emissions

2.2.1. Symbol Definition

• $D$: Set of customers’ nodes,$i,j\in D$;
• $k$: Set of vehicles, $k=k_1,k_2,k_3\dots k_n$;
• $N$: Set of paths between customers;
• $SC$: Subset of customer nodes, where $SC\in D$,$\left|SC\right|$ is the number of customers in the SC;
• $q_i$: Demand of customer$i$;
• $Q_k$: Capacity of vehicle $k$;
• $\left[0,T\right]$: Distribution center is open from 0 and closed at T;
• $\left[E_i,L_i\right]$: The earliest and latest time range expected by the customer;
• $\left[E{E}_i,L{L}_i\right]$: The time range within which delivery can be accepted beyond the customer’s desired time window, and $E{E}_i<E_i,L{L}_i>L_i$;
• $se{t}_i$: The stay time of the delivery vehicle at customer $i$;
• $d_{ij}$: Distance between customers$i$ and $j$;
• $c_{pn}$: The cost of service quality;

Variable and Decision Variable

$$x_{ij}^k=\left\{\begin{array}{c}1 if the vehicle k travels from customer i to j\\ 0 otherwise\end{array}\right.$$

$$y_{i\left(j\right)}^k=\left\{\begin{array}{c}1 if the vehicle k works at customer i\left(j\right)\\ 0 otherwise\end{array}\right.$$

• $t_{ij}$: Travel time between customers $i$ and $j$;
• $t_{re}^k$: The time that vehicle k returns to the distributor center;
• $E_{ij}^k$: The carbon emissions from vehicle k on path $\left(i,j\right)$;
• $N$: The total number of distribution points;
• ${\phi }_i$: Satisfaction at distribution $i$;
• $F$: The total carbon emissions during the distribution;
• ${\tau }_i$: Penalty cost at the distribution point $i$.

2.2.2. Formula

• Minimizing the number of delivery vehicles

In a distribution company, each delivery vehicle has many fixed costs, such as vehicle depreciation, driver salaries and insurance. We set this part of the fixed cost to $dp$, so the object “minimize the number of delivery vehicles” can be transformed into “minimize the enterprise delivery cost”.

$$min\left({\sum }_{k\in K}^{}{\sum }_{j\in D}^{}{x}_{0j}^k\right)dp$$

(9)

2.

Maximize customer satisfaction

In this paper, customer satisfaction is measured by the punctuality of delivery and service quality. First, the soft time window is used to denote the punctuality of delivery, and the time penalty cost function is designed to capitalize the punctuality of delivery as (10). Among (10), ${\mu }_1,{\mu }_2$ denotes the unit coefficient penalty coefficient, and S is set to a very large number, which means that if the delivery exceeds the time allowed by the customer, the penalty cost is very large.

$${\tau }_i=\left\{\begin{array}{c}S, t_i<E{E}_i\\ {\mu }_1\left(E_i-t_i\right), E{E}_i\le t_i<E_i\\ 0, E_i\le t_i\le L_i\\ {\mu }_2\left(t_i-L_i\right), L_i<t_i\le L{L}_i\\ S, L{L}_i<t_i\end{array}\right.$$

(10)

Second, the distribution service quality is collected from questionnaires that set the service quality into 5 levels. A total of 550 questionnaires were distributed, and 523 were actually recovered with a recovery rate of 95.09%. The results showed that 4.3% were very satisfied, 21.4% were satisfied, 54.2% were generally satisfied, 16.6% were unsatisfied, and 3.5% were extremely unsatisfied. In this paper, the above proportion is used as a probability to randomly assign to these 100 customer points so that each customer point has its own delivery service quality.

Similar to the punctuality of delivery, the service quality is also capitalized as one of the penalty costs to evaluate customer satisfaction; that is, the service quality penalty cost. There are three service quality penalty costs: $c_{p1}$ denotes the penalty cost aimed at the general service, $c_{p2}$ denotes the penalty cost aimed at the unsatisfactory service and $c_{p3}$ denotes the penalty cost aimed at the very unsatisfactory service. If the service quality is very satisfied or satisfied, the penalty cost is set to 0.

$$U={\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{\left(i,j\right)\in N}{x}_{ij}^k{c}_{pn}$$

(11)

Because the penalty cost designed above can describe customer satisfaction, the objective “maximizing the customer satisfaction” can be transformed into “minimizing the penalty cost”, which is represented by (12).

$$\min \left({\displaystyle \sum }_{i\in D}{\tau }_i+{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{\left(i,j\right)\in N}{x}_{ij}^k{c}_{pn}\right)$$

(12)

3.

Minimizing carbon emissions

According to the carbon emission analysis above, the objective “minimize carbon emissions” can be transformed to “minimize the cost of carbon emissions” by multiplying the carbon emissions by the marginal abatement cost of carbon emissions.

$$min{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{\left(i,j\right)\in N}p·E_{ij}^k$$

(13)

According to the above analysis, the overall optimization objective is as follows:

$$Z=min\left[\left({\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{j\in D}{x}_{0j}^k\right)·dp+{\displaystyle \sum }_{i\in D}{\tau }_i+{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{\left(i,j\right)\in N}{x}_{ij}^k{c}_{pn}+{\displaystyle \sum }_{k\in K}{\displaystyle \sum }_{\left(i,j\right)\in N}p·E_{ij}^k\right]$$

(14)

Constraint conditions:

$${\displaystyle \sum }_{j=1}^n{x}_{ij}^k={\displaystyle \sum }_{j=1}^n{x}_{ji}^k,i=0,k=1,2\cdots K$$

(15)

$$q_i\le Q_k,k=1,2\cdots K$$

(16)

$${\displaystyle \sum }_{i\in D}\left(y_i^k·q_i\right)\le Q_k,k=1,2\cdots K$$

(17)

$$t_{re}^k\le T$$

(18)

$${\displaystyle \sum }_{j\in D}{x}_{ij}^k=1,k=1,2,\cdots K$$

(19)

$${\displaystyle \sum }_{i,j\in D}{\displaystyle \sum }_{k=1}^{k_n}{x}_{ij}^k=1$$

(20)

$${\displaystyle \sum }_{i,j\in SC}{\displaystyle \sum }_{k=1}^{k_n}{x}_{ij}^k\le \left|SC\right|-1$$

(21)

$$E{E}_i\le t_i+se{t}_i+t_{ij}\le L{L}_j$$

(22)

$$k\le K$$

(23)

Equation (15) indicates that the vehicle starts from the distribution center and finally returns to the distribution center to realize the closed-loop distribution. Formula (16) shows that the vehicle can meet the demand of each customer, and (17) denotes that the vehicles of the distribution center can meet the demand of all customers. Formula (18) indicates that the vehicles must return before the end of the business. Formula (19) denotes that each customer must be serviced and only served once. Formula (20) means that after a customer is accessed, it cannot be accessed again. Formula (21) expresses that the distribution center must be included in the closed loop distribution path. Formula (22) means that customer $j$ must be serviced in the acceptable service time after the customer$i$ is serviced. Formula (23) denotes that the vehicles available are all the vehicles in the distribution center.

2.3. Solution Approach

The genetic algorithm has been successfully used for its advantages of a wide search range, parallel computing ability and high solving efficiency, although it easily falls into local optimal solutions. When solving the above model, to strengthen the local search ability of the genetic algorithm, the algorithm is improved, and evolution reversal is added as follows.

The specific distribution path optimization process is as follows:

• The chromosomal code

The natural number is used to code the vehicles and the customers. For example, the natural number between 1-Y is used to represent each customer, and the natural number between 1-X is used to represent each vehicle.

2.

Generation of the initial population

The initial distribution path, namely the initial population, is generated by a random method.

3.

Fitness calculation

Fitness is the inverse of the objective function in the path routing model.

4.

Selection operation

The roulette selection is used in the selection operation. First, the individual selection probability is calculated as $p_i=f\left(x_i\right)/{{\displaystyle \sum }}_{i=1}^{n}f\left(x_i\right)$. Then, the accumulative selection probability of the individual is calculated as $S_t={{\displaystyle \sum }}_{j=1}^{1}f\left(x_i\right)$. Finally, a random number is generated between [0,1). If $S_i<p_s<S_{i+1}$, then the selection $x_i$ will enter the next generation population.

5.

Cross operation

Two-point crossing is used to realize the crossover operation. First, two crossover positions are generated randomly in the parent chromosome, and then the two selected gene segments are crossed and placed in the chromosome head to form a new parent chromosome. Meanwhile, the same gene is removed to form the offspring chromosome.

6.

Mutation operation

The reversal mutation is used in the mutation operation. First, a chromosome is selected, and then two gene segments of this chromosome are selected randomly. Finally, the coding positions of the two segments are interchanged.

7.

Evolution reversal operation

First, a chromosome is selected, and then two gene segments of the chromosome are truncated; finally, reverse insertion is implemented.

8.

Algorithm termination

When the specified number of iterations is reached, the algorithm is finished, and the result is output.

3. Experimental Results

3.1. Experimental Background and Parameter Setting

In this paper, the Solomon RC102 standard dataset was researched as experimental data for simulation, and the location of the distribution center and each customer point are shown in Figure 1.

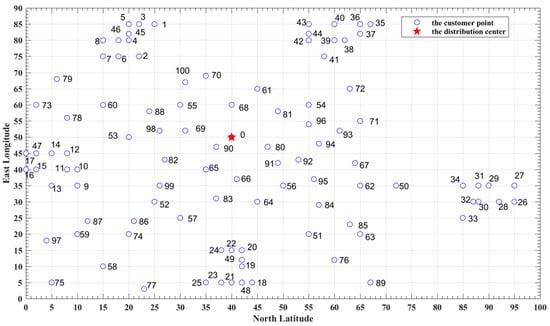
Figure 1. Coordinates of the distribution center and the customer point.

In addition to the above data, the GitHub dataset was researched and improved by the actual data of varied vehicle speeds under multiple road types in different time periods, which is consistent with the actual traffic network. The dataset divides the 24 h of one day into 72 time segments (each time segment is 20 min long) and shows the speed of the four road types in different time segments, as shown in Appendix A.

According to the model and the improved algorithm, the relevant parameters are set in Table 1 and Table 2.

Table 1. Parameters of the improved algorithm.

Parameter	Population Size	Iterations	Crossover Probability	Mutation Probability
Value	500	2000	0.9	0.2

Table 2. Parameters of the model.

Parameter	Value	Unit
$\delta$ Rode slope(percentage)	6	PCT
$\omega$ The ratio of vehicle load to vehicle capacity	0.5	--
$dp$ Fixed cost	150	RMB/car × time
$P$ Marginal abatement cost	0.002	RMB/kilogram
$Q_k$ The load weight of vehicle K	200	Kilogram
${\mu }_1$ Unit coefficient penalty function	20	RMB/time
${\mu }_2$ Unit coefficient penalty function	30	RMB/time
$c_{p1}$ General penalty costs	5	RMB/time
$c_{p2}$ The penalty cost of dissatisfaction	10	RMB/time
$c_{p3}$ The penalty cost of extreme unsatisfaction	15	RMB/time

3.2. Simulation Results and Analysis

3.2.1. Distribution Path under a Static Road Network

Under the static road network, the vehicle speed remains constant in the period of distribution. In this paper, the vehicle speed is the average speed of each road type in the static road network. The distribution path and the distribution cost under a static road network are shown respectively in Table 3 and Table 4.

Table 3. Distribution path under a static road network.

Distribution Path	Distribution Time	Total Path	Total Time
No.1: 0 → 81 → 39 → 41 → 54 → 12 → 15 → 16 → 9 → 52 → 99 → 65 → 0	0–3.6–93.3–94.7–98.1–153.7–155.8–156.4–159.4–163.4–164.6–167.4–170.5 min	28.34 km	170.5 min
No.2: 0 → 90 → 82 → 86 → 59 → 97 → 13 → 10 → 91 → 42 → 43 → 44 → 0	0–1.2–88.9–94.9–98–99.6–125.1–143.9–154.5–177.5–178.7–179.5–188.4 min	32.99 km	188.4 min
No.3: 0 → 96 → 84 → 63 → 76 → 89 → 18 → 21 → 48 → 24 → 0	0–3.9–139.5–142.7–145.3–148–154.2–155.4–155.9–158.3–167.7 min	24.47 km	167.7 min
No.4: 0 → 69 → 60 → 6 → 4 → 34 → 32 → 30 → 33 → 62 → 0	0–2.3–46.3–159.2–160.3–184–185.4–185.6–187.2–193.3–201.4 min	31.76 km	201.4 min
No.5: 0 → 64 → 85 → 29 → 27 → 26 → 28 → 31 → 50 → 56 → 0	0–5.2–58.8–95–96.4–97.5–115.8–117.7–122–128.5–134.9 min	24.15 km	134.9 min
No.6: 0 → 98 → 17 → 47 → 14 → 11 → 75 → 77 → 0	0–4.2–53.3–149.6–150.5–152.2–162.8–167.3–182.3 min	25.85 km	182.3 min
No.7: 0 → 78 → 73 → 79 → 1 → 3 → 5 → 45 → 68 → 0	0–8.8–91.9–93.9–100.4–145.7–146.3–147.2–155.2–157.9 min	20.32 km	157.9 min
No.8: 0 → 20 → 49 → 22 → 57 → 74 → 87 → 53 → 7 → 8 → 46 → 2 → 0	0–9.5–122.8–123.8–128–130.8–143.3–150.6–157.5–159–159.9–161.5–170.7 min	28.97 km	170.7 min
No.9: 0 → 67 → 95 → 51 → 19 → 23 → 25 → 58 → 83 → 66 → 80 → 0	0–6.4–72.8–77.9–86.6–88.3–88.9–160.2–167.8–169.4–172.9–194.3 min	25.85 km	194.3 min
No.10: 0 → 40 → 37 → 35 → 36 → 38 → 72 → 71 → 93 → 94 → 92 → 0	0–11–86.3–124.9–139.5–140.8–144.5–146.8–148.1–179.5–181.3–185.7 min	19.11 km	185.7 min
No.11: 0 → 61 → 70 → 100 → 88 → 55 → 0	0–4.3–69.2–181.3–184.2–185.9–190.1 min	10.49 km	190.1 min

Table 4. The distribution cost under the static road network (RMB).

Fixed Cost	Penalty Cost	Carbon Emission Cost	Total Cost
1650	170	714.9	2534.9

The distribution path optimization roadmap is shown in Figure 2.

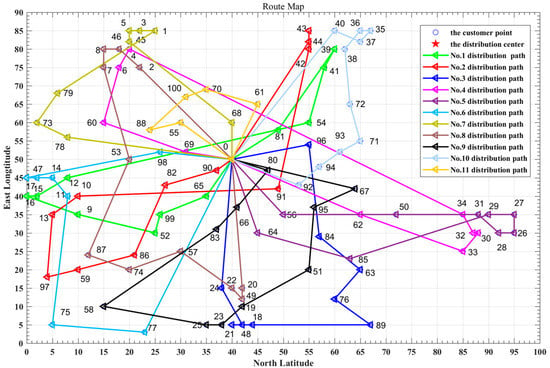
Figure 2. Route optimization roadmap under the static road network.

3.2.2. Distribution Path under a Dynamic Road Network

The vehicle speed changes at different time segment because of the uncertainty of the traffic condition. Experiments were implemented according to the time-varying speed, and the optimization results are shown in Table 5. The distribution cost under the dynamic road network is shown in Table 6.

Table 5. Distribution path under a dynamic road network.

Distribution Path	Distribution Time	Total Path	Total Time
No.1: 0 → 78 → 73 → 7 → 6 → 60 → 9 → 87 → 77 → 21 → 24 → 57 → 0	0–8.5–91.8–97.7–98.4–102.5–161.1–163.9–171.6–178–181.1–185.3–194.2 min	34.22 km	194.2 min
No.2: 0 → 69 → 88 → 82 → 86 → 74 → 11 → 10 → 0	0–3.1–43.6–70.7–76.6–87.9–149.1–149.7–159 min	19.12 km	159.0 min
No.3: 0 → 59 → 58 → 75 → 25 → 23 → 19 → 49 → 20 → 64 → 66 → 0	0–11.1–45.3–154.8–160.8–161.4–162.9–163.7–164.7–170.3–171.9–176.1 min	24.26 km	176.1 min
No.4: 0 → 81 → 96 → 54 → 68 → 100 → 4 → 5 → 45 → 8 → 55 → 0	0–3.6–88.2–133.2–144.2–147–184.1–185.1–186.2–188–197.2–201.5 min	20.20 km	201.5 min
No.5: 0 → 61 → 94 → 93 → 67 → 29 → 26 → 51 → 99 → 14 → 17 → 47 → 53 → 0	0–4.4–72.1–96.7–180.7–189.8–192.2–205.5–214.4–220–221.3–221.8–226.3–231.2 min	38.26 km	231.2 min
No.6: 0 → 65 → 83 → 22 → 97 → 16 → 13 → 52 → 56 → 91 → 80 → 0	0–2.9–14–39.6–100.3–126.1–127.9–146.2–154–155.8–168.1–194.8 min	28.07 km	194.8 min
No.7: 0 → 46 → 2 → 95 → 85 → 63 → 76 → 89 → 48 → 18 → 0	0–11.1–114.5–129.4–133.5–134.4–136.9–139.3–152.7–153.3–163.4 min	34.23 km	163.4 min
No.8: 0 → 31 → 27 → 28 → 34 → 37 → 40 → 43 → 44 → 1 → 70 → 90 → 0	0–14–63–64.5–66.9–125.5–126.6–128.2–129–138.3–149.9–188.2–189.2 min	35.33 km	189.2 min
No.9: 0 → 39 → 36 → 35 → 38 → 3 → 79 → 15 → 12 → 98 → 0	0–12.1–39.1–43.6–140.8–154.9–162.2–172.7–175.3–180–185.3 min	30.90 km	185.3 min
No.10: 0 → 42 → 41 → 72 → 71 → 50 → 30 → 32 → 33 → 62 → 84 → 92 → 0	0–10–34.6–94.3–96.4–100.7–120.7–120.9–132.4–138–140.4–144.7–149.8 min	27.80 km	149.8 min

Table 6. The distribution cost under the dynamic road network (RMB).

Fixed Cost	Penalty Cost	Carbon Emission Cost	Total Cost
1500	160	683	2343

The distribution path optimization roadmap is shown in Figure 3.

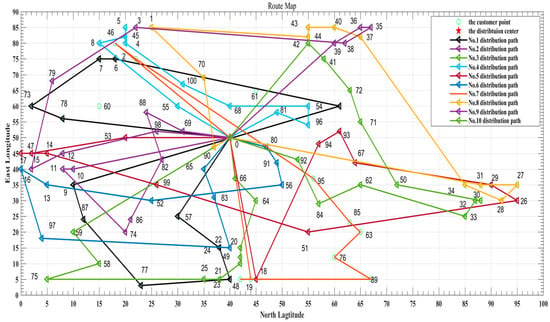
Figure 3. Route optimization roadmap under the dynamic road network.

3.2.3. Comparison and Analysis

1.

Optimization comparison between a static road network and a dynamic road network

Due to the different vehicle speeds between the static road network and the dynamic road network, the distribution paths are different. Therefore, it is difficult to make a direct comparison from the route optimization result. Thus, the cost comparison between the two road networks is shown in Table 7 below.

Table 7. The cost comparison between a static road network and a dynamic network.

	Static Road Network	Dynamic Network
Vehicle number	11	10
Fixed cost (RMB)	1650	1500
Penalty cost (RMB)	170	160
Carbon emissions cost (RMB)	714.9	683
Total cost (RMB)	2534.9	2343

According to Table 7, the cost of the dynamic road network is lower than that of the static road network.

2.

Optimization comparison of different algorithms

To study whether the improved genetic algorithm is effective, route optimization was carried out with the general genetic algorithm and the improved genetic algorithm using the same test data. The results are shown in Figure 4.

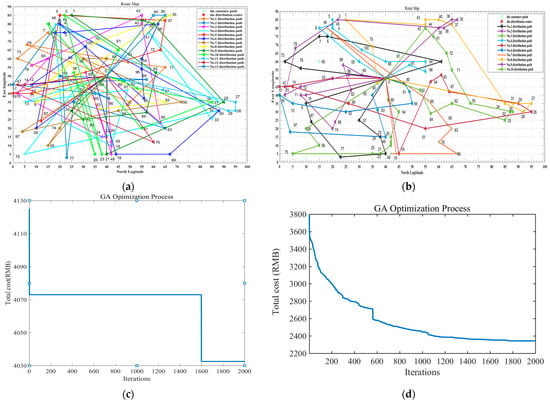
Figure 4. Optimization comparison with different algorithms. (a) Route optimization with a genetic algorithm; (b) Route optimization with an improved algorithm; (c) Optimization process of the genetic algorithm; (d) Optimization process of the improved algorithm.

As shown in Figure 4, the left route map shows that the distribution path is chaotic, and it easily falls into the local optimal solution in the algorithm iteration process. The right route map is more concise and clearer, and the target value is gradually optimized without falling into the local optimal solution.

As seen in Table 8, the vehicle number, fixed cost, penalty cost, carbon emission cost and total cost obtained from the improved algorithm are lower than the results of the general genetic algorithm, which indicates that the improved algorithm is effective and superior.

Table 8. Distribution cost comparison between the genetic algorithm and the improved algorithm.

	Before Improved	After Improved
Time (second)	3473.6	1844.5
Vehicle number	13	10
Fixed cost (RMB)	1950	1500
Penalty cost (RMB)	285	160
Carbon emission cost (RMB)	1797.5	683
Total cost (RMB)	4032.5	2343

4. Conclusions

To advocate for low-carbon and environmental protection, a vehicle routing optimization model considering the impact of varied vehicle speeds on carbon emissions was proposed in this paper. In the model, the objective function consisted of the distribution cost, penalty cost and carbon emission cost. In the calculation of the distribution time and carbon emissions, the varied vehicle speed reflecting the actual road condition was considered. To avoid falling into a local optimum, the general genetic algorithm was improved by evolutionary reversal. The experiment was designed using the standard Solomon dataset, and the varied vehicle speed was similar to the actual dynamic road network, which demonstrates that the model and the improved algorithm are feasible and efficacious.

The research results of this paper can provide a reference for logistics transportation companies to reduce carbon emissions in the process of transportation and can provide a reference for the government to reasonably formulate policies to manage transportation to achieve the goal of carbon neutralization and carbon peak. Of course, if real-time vehicle speed can be applied in our research, the results will be more scientific and usable. In the future we will apply real-time vehicle speed with help of GPS to the following research.