Economic Enhancement of Wind–Thermal–Hydro System Considering Imbalance Cost in Deregulated Power Market
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Wind Speed Data
2.2. Estimation of Wind Power, Generation, and Cost Studies
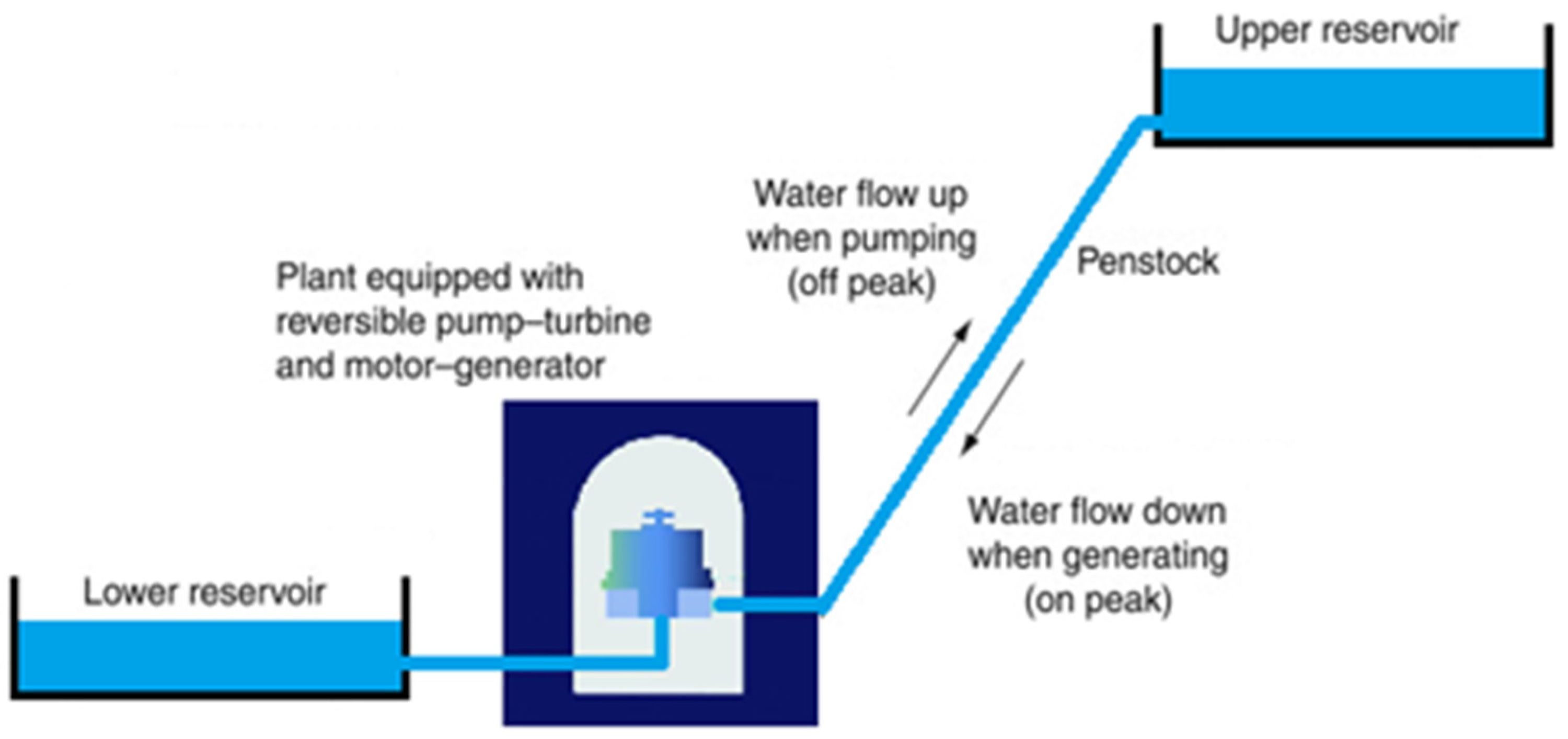
2.3. Pumped Hydroelectric Storage (PHES) System
2.3.1. Generating Mode
2.3.2. Pumping Mode
2.4. Locational Marginal Pricing (LMP)
2.5. Power Pool
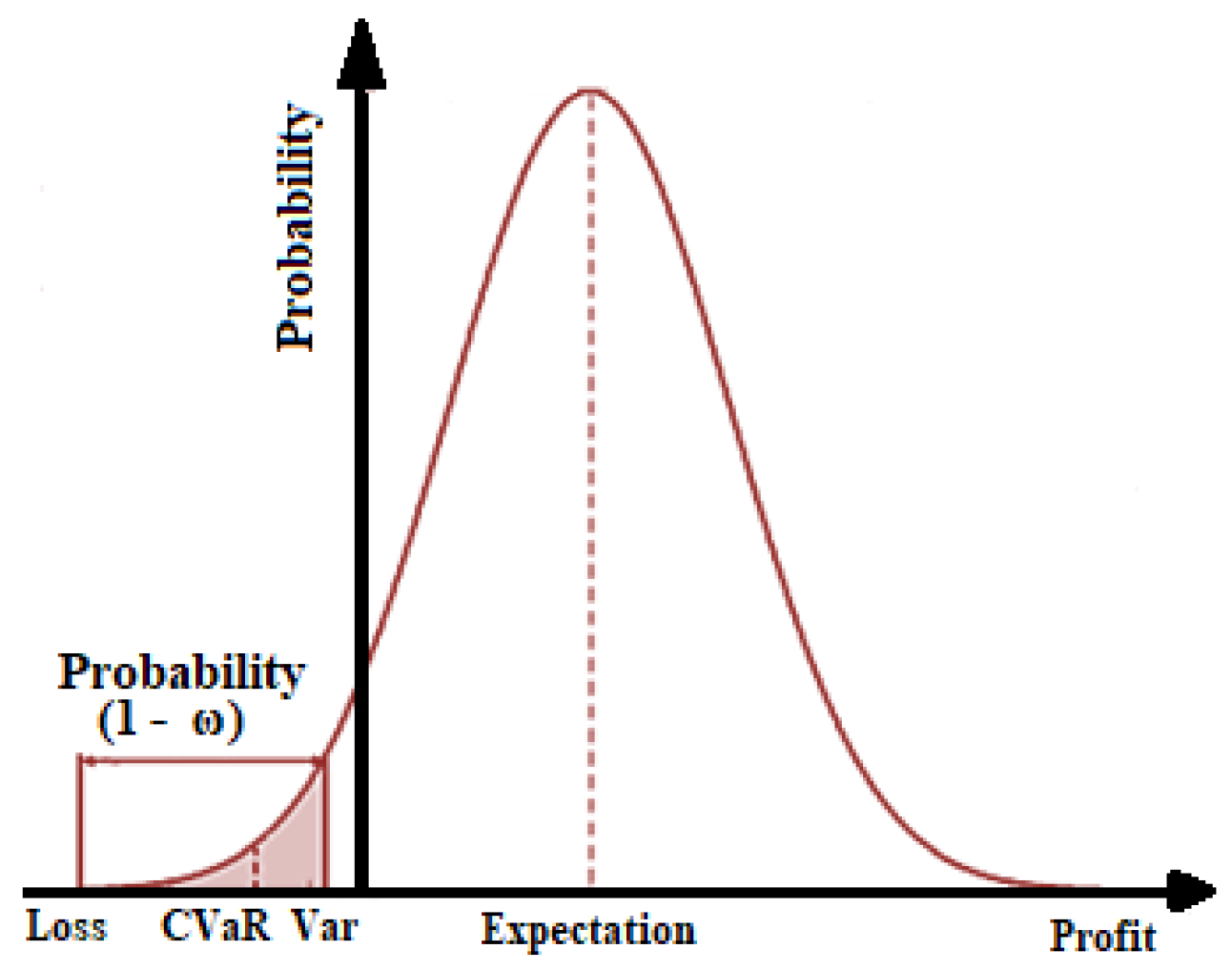
2.6. Value at Risk (VaR) and Conditional Value at Risk (CVaR)
3. Objective Function
- First Part of Objective Function:
- Second Part of Objective Function:
- Constraints for thermal power plant:
- Constraints for operation of PHES Plant:
4. Proposed Methodology
5. Results and Discussion
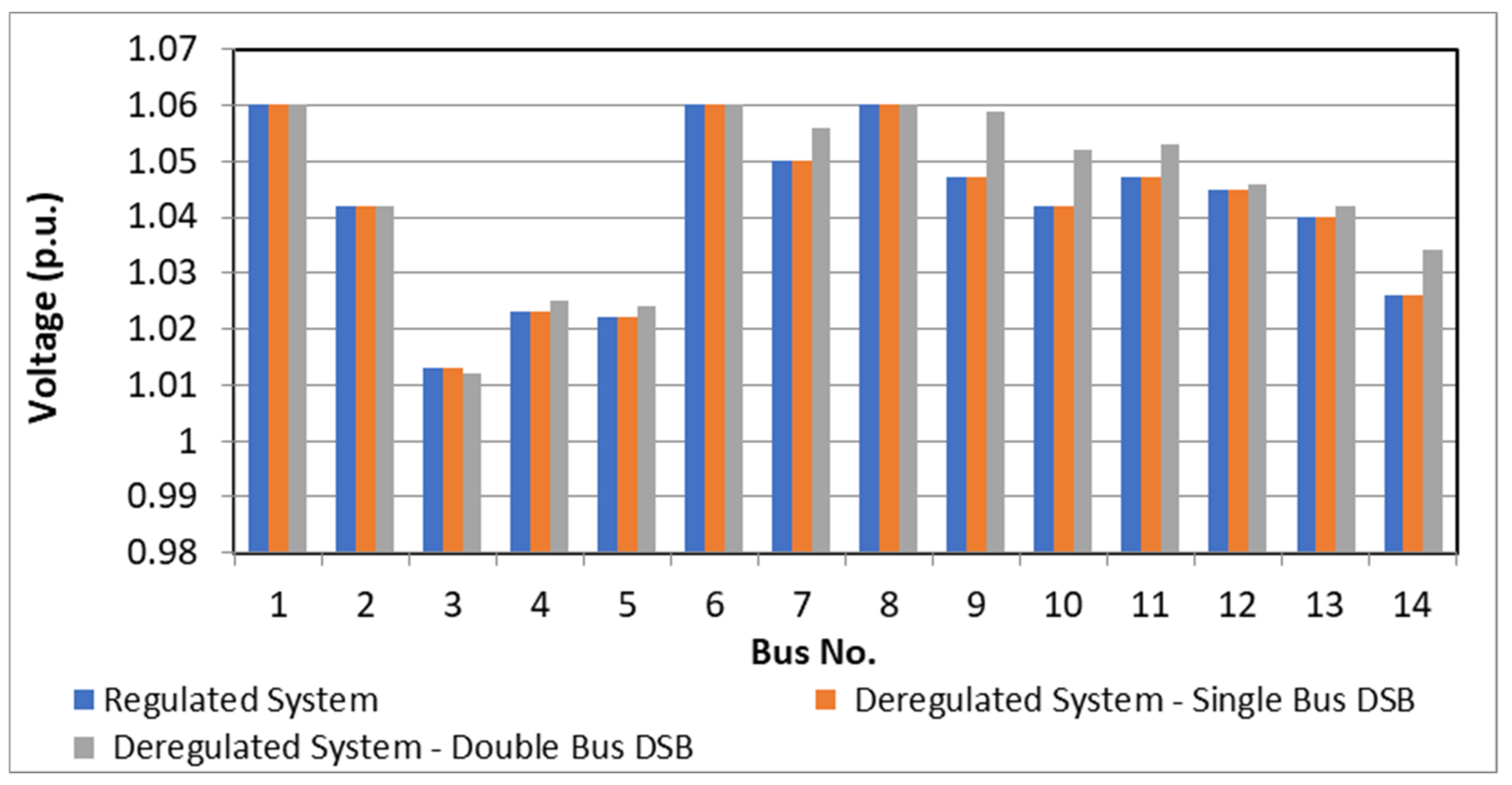
- A regulated system;
- A deregulated system with single-bus demand-side bidding;
- A deregulated system with double-bus demand-side bidding.
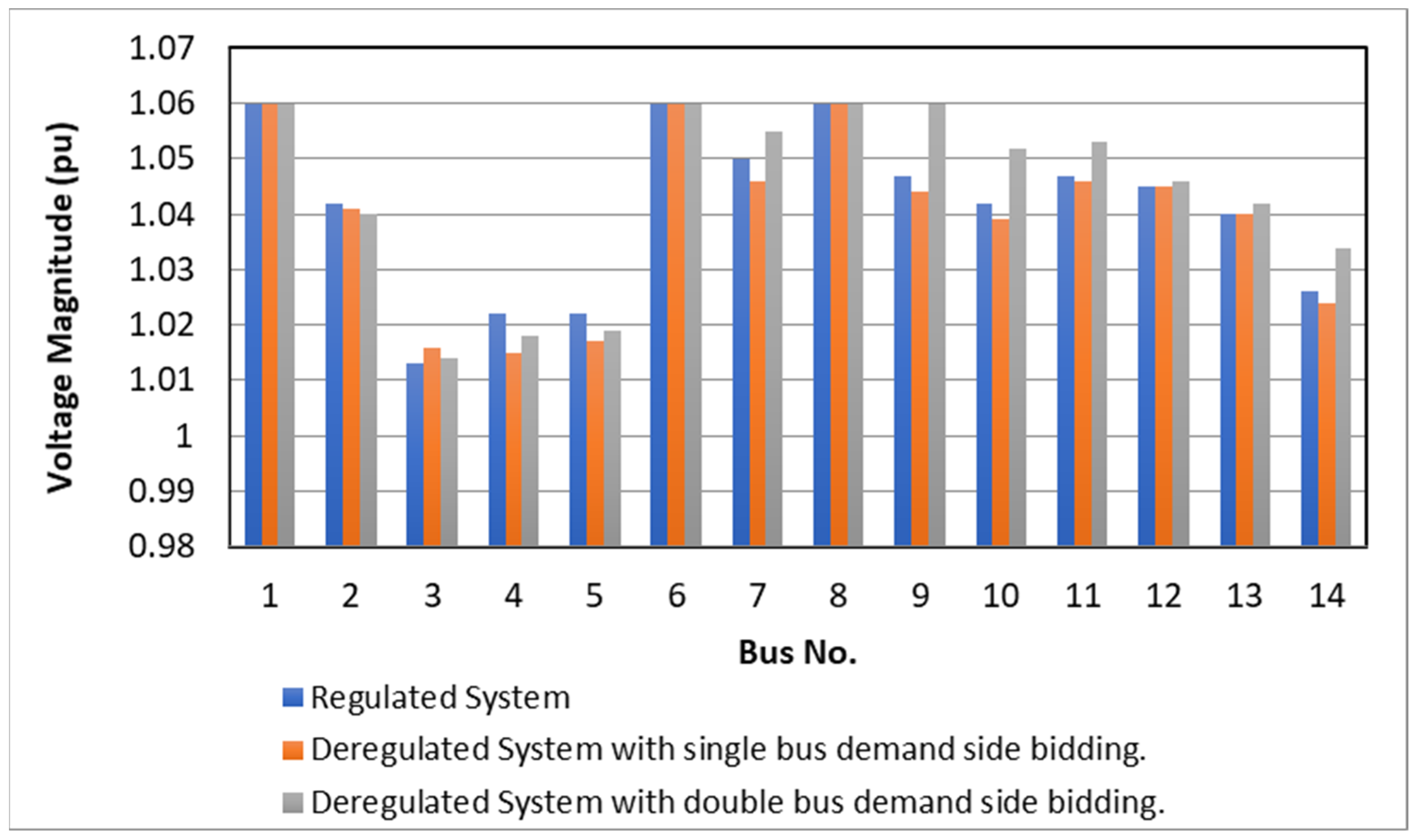
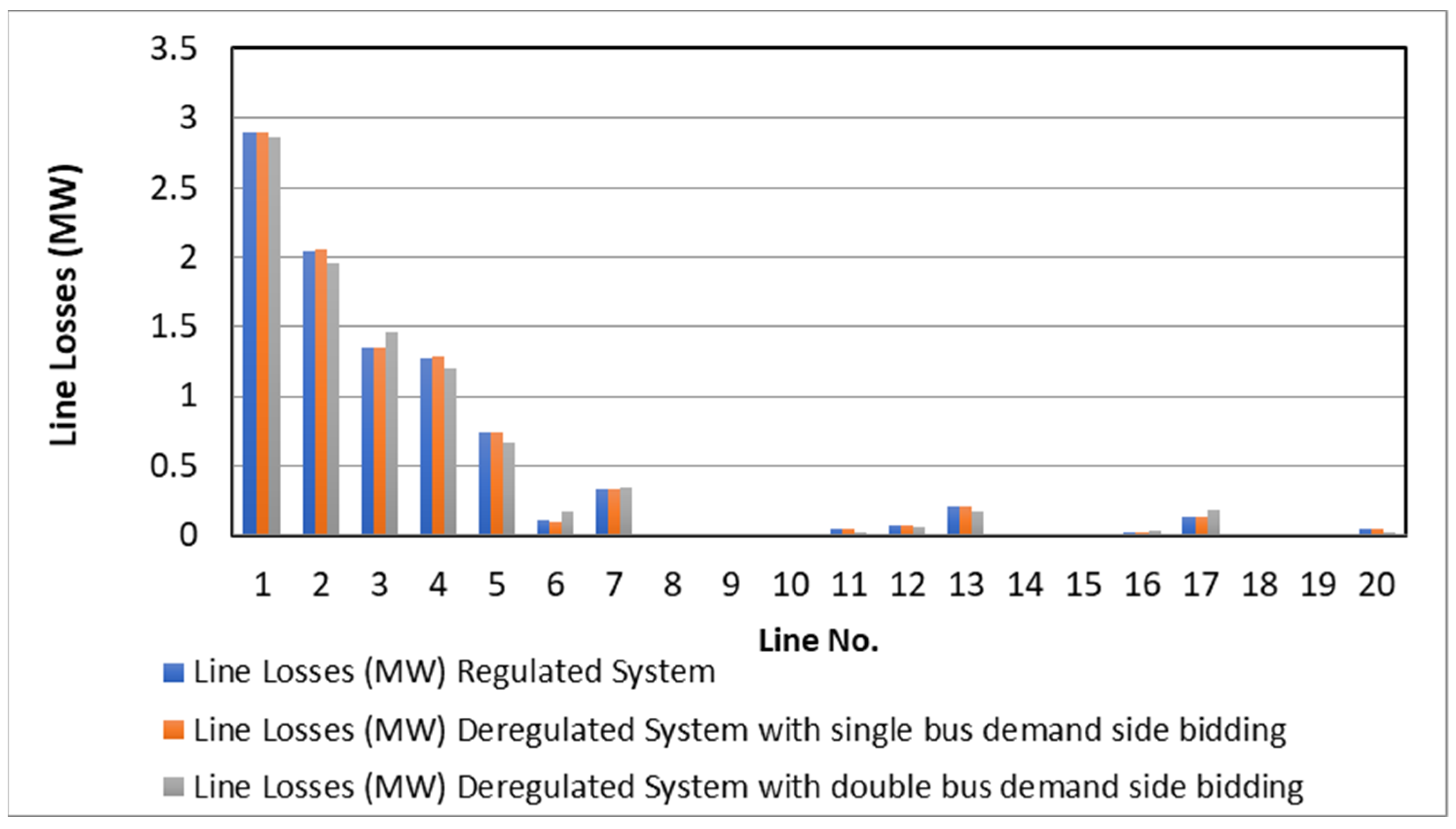
5.1. System Performance without Wind Placement
5.2. System Performance with Wind Placement without Considering Imbalance Cost
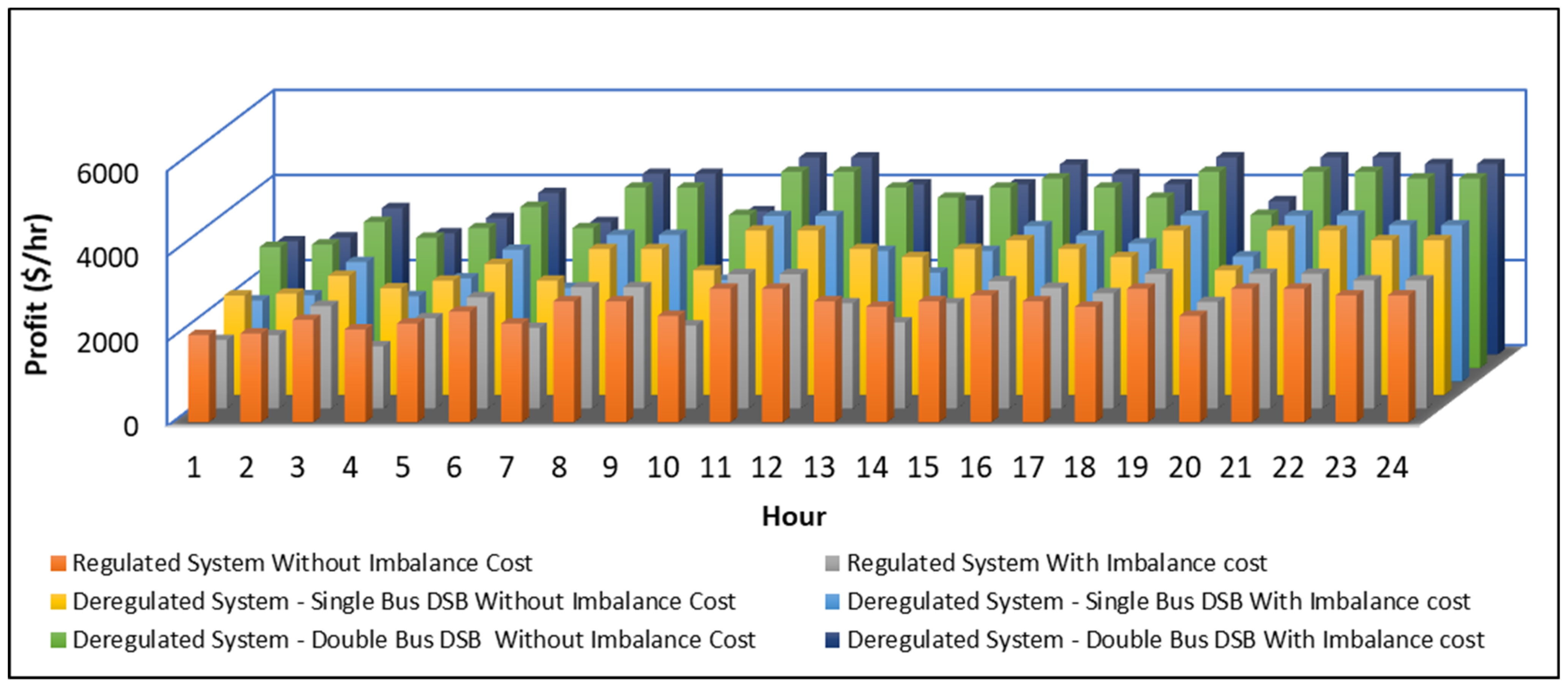
5.3. System Performance with Wind Placement Considering Imbalance Cost
- Calculation of individual generation and LMP for all generator buses;
- Calculation of imbalance cost;
- Calculation of overall system profit.
5.3.1. Calculation of Individual Generation and LMP for All Generator Buses
5.3.2. Calculation of Imbalance Cost
5.3.3. Calculation of Overall System Profit
5.3.4. Profit Comparison after Installing Wind Turbine Considering AWS and FWS
5.4. System Performance with Placement of Wind Farm and PHES System
5.5. System Risk Analysis with Placement of wind Farm and PHES System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Singh, S.; Chauhan, P.; Aftab, M.A.; Ali, I.; Hussain, S.M.S.; Ustun, T.S. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies 2020, 13, 1295. [Google Scholar] [CrossRef]
- Ustun, T.S.; Hashimoto, J.; Otani, K. Impact of Smart Inverters on Feeder Hosting Capacity of Distribution Networks. IEEE Access 2019, 7, 163526–163536. [Google Scholar] [CrossRef]
- Nadeem, F.; Aftab, M.A.; Hussain, S.M.S.; Ali, I.; Tiwari, P.K.; Goswami, A.K.; Ustun, T.S. Virtual Power Plant Management in Smart Grids with XMPP Based IEC 61850 Communication. Energies 2019, 12, 2398. [Google Scholar] [CrossRef]
- Basu, J.B.; Dawn, S.; Saha, P.K.; Chakraborty, M.R.; Ustun, T.S. A Comparative Study on System Profit Maximization of a Renewable Combined Deregulated Power System. Electronics 2022, 11, 2857. [Google Scholar] [CrossRef]
- Woo, C.; King, M.; Tishler, A.; Chow, L. Costs of electricity deregulation. Energy 2006, 31, 747–768. [Google Scholar] [CrossRef]
- McGovern, T.; Hicks, C. Deregulation and restructuring of the global electricity supply industry and its impact upon power plant suppliers. Int. J. Prod. Econ. 2004, 89, 321–337. [Google Scholar] [CrossRef]
- Talati, S.; Bednarz, J. Deregulation and opportunities for industrial customers. IEEE Trans. Ind. Appl. 1998, 34, 1378–1386. [Google Scholar] [CrossRef]
- Jaiswal, K.K.; Chowdhury, C.R.; Yadav, D.; Verma, R.; Dutta, S.; Jaiswal, K.S.; SelvaKumar, K.K. Renewable and sustainable clean energy development and impact on social, economic, and environmental health. Energy Nexus 2022, 7, 100118. [Google Scholar] [CrossRef]
- Deshmukh, K.G.; Sameeroddin, M.; Abdul, D.; Sattar, M.A. Renewable energy in the 21st century: A review. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Nieh, R.; Lai, L.L.; Rajkumar, N.; Lu, Y.; Tang, G. Renewable Energy in Deregulated Power Market. IFAC Proc. Vol. 2003, 36, 1173–1178. [Google Scholar] [CrossRef]
- Graf, C.; Marcantonini, C. Renewable energy and its impact on thermal generation. Energy Econ. 2017, 66, 421–430. [Google Scholar] [CrossRef]
- Kiunke, T.; Gemignani, N.; Malheiro, P.; Brudermann, T. Key factors influencing onshore wind energy development: A case study from the German North Sea region. Energy Policy 2022, 165, 112962. [Google Scholar] [CrossRef]
- Chompoo-Inwai, C.; Lee, W.-J.; Fuangfoo, P.; Williams, M.; Liao, J. System Impact Study for the Interconnection of Wind Generation and Utility System. IEEE Trans. Ind. Appl. 2005, 41, 163–168. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mahariq, I.; Murshid, N.; Wongwises, S.; Mahian, O.; Nazari, M.A. Applying wind energy as a clean source for reverse osmosis desalination: A comprehensive review. Alex. Eng. J. 2022, 61, 12977–12989. [Google Scholar] [CrossRef]
- Chinmoy, L.; Iniyan, S.; Goic, R. Modeling wind power investments, policies and social benefits for deregulated electricity market—A review. Appl. Energy 2019, 242, 364–377. [Google Scholar] [CrossRef]
- Liu, M.; Quilumba, F.L.; Lee, W.-J. Dispatch Scheduling for a Wind Farm with Hybrid Energy Storage Based on Wind and LMP Forecasting. IEEE Trans. Ind. Appl. 2014, 51, 1970–1977. [Google Scholar] [CrossRef]
- Abdmouleh, Z.; Gastli, A.; Ben-Brahim, L.; Haouari, M.; Al-Emadi, N.A. Review of optimization techniques applied for the integration of distributed generation from renewable energy sources. Renew. Energy 2017, 113, 266–280. [Google Scholar] [CrossRef]
- Patil, G.S.; Mulla, A.; Ustun, T.S. Impact of Wind Farm Integration on LMP in Deregulated Energy Markets. Sustainability 2022, 14, 4354. [Google Scholar] [CrossRef]
- Yu, Z.; Lusan, D. Optimal placement of FACTs devices in deregulated systems considering line losses. Int. J. Electr. Power Energy Syst. 2004, 26, 813–819. [Google Scholar] [CrossRef]
- Nabavi, S.M.H.; Hosseinipoor, N.A.; Hajforoosh, S. Social Welfare Maximization by Optimal Locating and Sizing of TCSC for Congestion Management in Deregulated Power Markets. Int. J. Comput. Appl. 2010, 6, 16–20. [Google Scholar] [CrossRef]
- Sharma, A.; Jain, S.K. Gravitational search assisted algorithm for TCSC placement for congestion control in deregulated power system. Electr. Power Syst. Res. 2019, 174, 105874. [Google Scholar] [CrossRef]
- Balamurugan, K.; Muthukumar, K. Differential Evolution algorithm for contingency analysis-based optimal location of FACTS controllers in deregulated electricity market. Soft Comput. 2018, 23, 163–179. [Google Scholar] [CrossRef]
- Besharat, H.; Taher, S.A. Congestion management by determining optimal location of TCSC in deregulated power systems. Int. J. Electr. Power Energy Syst. 2008, 30, 563–568. [Google Scholar] [CrossRef]
- Mithulananthan, N.; Acharya, N. A proposal for investment recovery of FACTS devices in deregulated electricity markets. Electr. Power Syst. Res. 2007, 77, 695–703. [Google Scholar] [CrossRef]
- Das, C.K.; Bass, O.; Kothapalli, G.; Mahmoud, T.S.; Habibi, D. Overview of energy storage systems in distribution networks: Placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 2018, 91, 1205–1230. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Chazarra, M.; García-González, J.; Cavazzini, G.; Stoppato, A. Trends and challenges in the operation of pumped-storage hydropower plants. Renew. Sustain. Energy Rev. 2015, 44, 767–784. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Finn, P.; Mathiesen, B.; Leahy, M. Practical operation strategies for pumped hydroelectric energy storage (PHES) utilising electricity price arbitrage. Energy Policy 2011, 39, 4189–4196. [Google Scholar] [CrossRef]
- Parastegari, M.; Hooshmand, R.-A.; Khodabakhshian, A.; Forghani, Z. Joint operation of wind farms and pump-storage units in the electricity markets: Modeling, simulation and evaluation. Simul. Model. Pract. Theory 2013, 37, 56–69. [Google Scholar] [CrossRef]
- Dawn, S.; Gope, S.; Das, S.S.; Ustun, T.S. Social Welfare Maximization of Competitive Congested Power Market Considering Wind Farm and Pumped Hydroelectric Storage System. Electronics 2021, 10, 2611. [Google Scholar] [CrossRef]
- Murage, M.W.; Anderson, C. Contribution of pumped hydro storage to integration of wind power in Kenya: An optimal control approach. Renew. Energy 2014, 63, 698–707. [Google Scholar] [CrossRef]
- Singh, N.K.; Koley, C.; Gope, S.; Dawn, S.; Ustun, T.S. An Economic Risk Analysis in Wind and Pumped Hydro Energy Storage Integrated Power System Using Meta-Heuristic Algorithm. Sustainability 2021, 13, 13542. [Google Scholar] [CrossRef]
- Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Strategy for System Risk Mitigation Using FACTS Devices in a Wind Incorporated Competitive Power System. Sustainability 2022, 14, 8069. [Google Scholar] [CrossRef]
- Dhillon, J.; Kumar, A.; Singal, S. Optimization methods applied for Wind–PSP operation and scheduling under deregulated market: A review. Renew. Sustain. Energy Rev. 2014, 30, 682–700. [Google Scholar] [CrossRef]
- Karhinen, S.; Huuki, H. Private and social benefits of a pumped hydro energy storage with increasing amount of wind power. Energy Econ. 2019, 81, 942–959. [Google Scholar] [CrossRef]
- Das, S.S.; Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Joint Scheduling Strategy for Wind and Solar Photovoltaic Systems to Grasp Imbalance Cost in Competitive Market. Sustainability 2022, 14, 5005. [Google Scholar] [CrossRef]
- Database: World Temperatures-Weather around the World. Available online: www.timeanddate.com/weather/ (accessed on 12 July 2022).
- Bataineh, K.M.; Dalalah, D. Assessment of wind energy potential for selected areas in Jordan. Renew. Energy 2013, 59, 75–81. [Google Scholar] [CrossRef]
- Boyle, G. (Ed.) Renewable Energy: Power for a Sustainable Future, 3rd ed.; Oxford University Press and Open University: Oxford, UK, 2012. [Google Scholar]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Pumped storage-based standalone photovoltaic power generation system: Modeling and techno-economic optimization. Appl. Energy 2015, 137, 649–659. [Google Scholar] [CrossRef]
- Orfanogianni, T.; Gross, G. A General Formulation for LMP Evaluation. IEEE Trans. Power Syst. 2007, 22, 1163–1173. [Google Scholar] [CrossRef]
- Tiwari, P.K.; Sood, Y.R. An Efficient Approach for Optimal Allocation and Parameters Determination of TCSC With Investment Cost Recovery Under Competitive Power Market. IEEE Trans. Power Syst. 2013, 28, 2475–2484. [Google Scholar] [CrossRef]
- Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Risk Curtailment Strategy for Solar PV-Battery Integrated Competitive Power System. Electronics 2022, 11, 1251. [Google Scholar] [CrossRef]
- MATPOWER—A MATLAB Power System Simulation Package, Version 5.1. Available online: https://matpower.org/download/ (accessed on 16 July 2022).













| Hour | Siliguri | Kolkata | Mumbai | Delhi | ||||
|---|---|---|---|---|---|---|---|---|
| FWS | AWS | FWS | AWS | FWS | AWS | FWS | AWS | |
| 1 | 2.50 | 2.78 | 3.33 | 2.22 | 5.56 | 5.00 | 1.94 | 1.94 |
| 2 | 2.50 | 2.22 | 3.33 | 2.50 | 5.28 | 6.67 | 2.50 | 1.94 |
| 3 | 2.22 | 1.94 | 3.33 | 3.89 | 5.00 | 5.00 | 2.78 | 2.50 |
| 4 | 1.94 | 1.94 | 3.89 | 3.06 | 4.72 | 6.11 | 2.50 | 3.33 |
| 5 | 1.94 | 1.94 | 3.89 | 3.61 | 4.17 | 6.11 | 2.50 | 3.89 |
| 6 | 2.22 | 2.22 | 3.89 | 4.44 | 3.61 | 6.11 | 2.50 | 2.78 |
| 7 | 2.22 | 1.94 | 4.17 | 3.61 | 3.61 | 4.61 | 2.78 | 3.06 |
| 8 | 1.94 | 1.67 | 4.72 | 5.00 | 3.61 | 6.11 | 2.78 | 1.94 |
| 9 | 2.50 | 1.94 | 4.72 | 5.00 | 3.89 | 5.56 | 2.78 | 2.50 |
| 10 | 2.50 | 1.94 | 4.72 | 4.17 | 4.17 | 6.67 | 2.50 | 3.61 |
| 11 | 2.22 | 2.50 | 4.72 | 5.56 | 5.00 | 6.67 | 2.50 | 3.61 |
| 12 | 2.50 | 2.50 | 4.72 | 5.56 | 5.83 | 6.11 | 2.78 | 2.78 |
| 13 | 1.94 | 2.50 | 5.28 | 5.00 | 6.11 | 5.00 | 3.06 | 2.50 |
| 14 | 1.94 | 2.22 | 5.28 | 4.72 | 5.00 | 5.00 | 3.61 | 4.17 |
| 15 | 1.94 | 1.94 | 5.28 | 5.00 | 5.00 | 6.67 | 3.33 | 3.33 |
| 16 | 1.94 | 1.94 | 5.00 | 5.28 | 5.00 | 5.56 | 2.78 | 3.61 |
| 17 | 2.22 | 1.94 | 5.00 | 5.00 | 4.72 | 5.56 | 2.50 | 3.33 |
| 18 | 2.22 | 1.94 | 4.72 | 4.72 | 4.72 | 4.72 | 2.50 | 4.72 |
| 19 | 1.94 | 1.94 | 4.17 | 5.56 | 4.44 | 5.00 | 2.78 | 5.28 |
| 20 | 1.94 | 2.22 | 3.89 | 4.17 | 4.17 | 4.72 | 3.06 | 4.17 |
| 21 | 2.78 | 1.94 | 3.61 | 5.56 | 4.17 | 5.56 | 3.06 | 2.50 |
| 22 | 2.78 | 2.22 | 3.61 | 5.56 | 4.17 | 5.00 | 3.06 | 1.94 |
| 23 | 2.50 | 2.78 | 3.61 | 5.28 | 4.44 | 4.17 | 3.06 | 2.50 |
| 24 | 2.22 | 2.78 | 3.61 | 5.28 | 4.72 | 6.67 | 3.06 | 2.78 |
| Hour | Siliguri | Kolkata | Mumbai | Delhi | ||||
|---|---|---|---|---|---|---|---|---|
| FWS | AWS | FWS | AWS | FWS | AWS | FWS | AWS | |
| 1 | 3.57 | 3.96 | 4.75 | 3.17 | 7.92 | 7.13 | 2.77 | 2.77 |
| 2 | 3.57 | 3.17 | 4.75 | 3.57 | 7.53 | 9.51 | 3.57 | 2.77 |
| 3 | 3.17 | 2.77 | 4.75 | 5.55 | 7.13 | 7.13 | 3.96 | 3.57 |
| 4 | 2.77 | 2.77 | 5.55 | 4.36 | 6.73 | 8.72 | 3.57 | 4.75 |
| 5 | 2.77 | 2.77 | 5.55 | 5.15 | 5.94 | 8.72 | 3.57 | 5.55 |
| 6 | 3.17 | 3.17 | 5.55 | 6.34 | 5.15 | 8.72 | 3.57 | 3.96 |
| 7 | 3.17 | 2.77 | 5.94 | 5.15 | 5.15 | 6.58 | 3.96 | 4.36 |
| 8 | 2.77 | 2.38 | 6.73 | 7.13 | 5.15 | 8.72 | 3.96 | 2.77 |
| 9 | 3.57 | 2.77 | 6.73 | 7.13 | 5.55 | 7.92 | 3.96 | 3.57 |
| 10 | 3.57 | 2.77 | 6.73 | 5.94 | 5.94 | 9.51 | 3.57 | 5.15 |
| 11 | 3.17 | 3.57 | 6.73 | 7.92 | 7.13 | 9.51 | 3.57 | 5.15 |
| 12 | 3.57 | 3.57 | 6.73 | 7.92 | 8.32 | 8.72 | 3.96 | 3.96 |
| 13 | 2.77 | 3.57 | 7.53 | 7.13 | 8.72 | 7.13 | 4.36 | 3.57 |
| 14 | 2.77 | 3.17 | 7.53 | 6.73 | 7.13 | 7.13 | 5.15 | 5.94 |
| 15 | 2.77 | 2.77 | 7.53 | 7.13 | 7.13 | 9.51 | 4.75 | 4.75 |
| 16 | 2.77 | 2.77 | 7.13 | 7.53 | 7.13 | 7.92 | 3.96 | 5.15 |
| 17 | 3.17 | 2.77 | 7.13 | 7.13 | 6.73 | 7.92 | 3.57 | 4.75 |
| 18 | 3.17 | 2.77 | 6.73 | 6.73 | 6.73 | 6.73 | 3.57 | 6.73 |
| 19 | 2.77 | 2.77 | 5.94 | 7.92 | 6.34 | 7.13 | 3.96 | 7.53 |
| 20 | 2.77 | 3.17 | 5.55 | 5.94 | 5.94 | 6.73 | 4.36 | 5.94 |
| 21 | 3.96 | 2.77 | 5.15 | 7.92 | 5.94 | 7.92 | 4.36 | 3.57 |
| 22 | 3.96 | 3.17 | 5.15 | 7.92 | 5.94 | 7.13 | 4.36 | 2.77 |
| 23 | 3.57 | 3.96 | 5.15 | 7.53 | 6.34 | 5.94 | 4.36 | 3.57 |
| 24 | 3.17 | 3.96 | 5.15 | 7.53 | 6.73 | 9.51 | 4.36 | 3.96 |
| Wind Speed at 10 m Height (m/s) | Wind Speed at 120 m Height (m/s) | Wind Power with 50 Turbines (MW) | Wind Gen Cost with 50 Turbines ($/h) |
|---|---|---|---|
| 1.67 | 2.38 | 1.01 | 3.799 |
| 1.94 | 2.77 | 1.61 | 6.032 |
| 2.22 | 3.17 | 2.40 | 9.004 |
| 2.50 | 3.57 | 3.42 | 12.820 |
| 2.78 | 3.96 | 4.69 | 17.586 |
| 3.06 | 4.36 | 6.24 | 23.407 |
| 3.33 | 4.75 | 8.10 | 30.389 |
| 3.61 | 5.15 | 10.30 | 38.637 |
| 3.89 | 5.55 | 12.87 | 48.257 |
| 4.17 | 5.94 | 15.83 | 59.353 |
| 4.44 | 6.34 | 19.21 | 72.033 |
| 4.72 | 6.73 | 23.04 | 86.401 |
| 5.00 | 7.13 | 27.35 | 102.563 |
| 5.28 | 7.53 | 32.17 | 120.624 |
| 5.56 | 7.92 | 37.52 | 140.690 |
| 5.83 | 8.32 | 43.43 | 162.866 |
| 6.11 | 8.72 | 49.94 | 187.258 |
| 6.67 | 9.51 | 64.83 | 243.112 |
| System Details | Parameter | Generator 1 (Bus No. 1) | Generator 2 (Bus No. 2) | Generator 3 (Bus No. 3) | Generator 4 (Bus No. 6) | Generator 5 (Bus No. 8) |
|---|---|---|---|---|---|---|
| Regulated system | Generation (MW) | 194.33 | 36.72 | 28.74 | 0 | 8.49 |
| LMP ($/MWh) | 36.724 | 38.36 | 40.575 | 39.734 | 40.17 | |
| Generation cost ($/h) | 8081.530 | |||||
| Revenue cost ($/h) | 10,052.323 | |||||
| Profit ($/h) | 1970.793 | |||||
| Deregulated system with single-bus demand-side bidding | Generation (MW) | 194.33 | 36.72 | 28.75 | 0 | 8.49 |
| LMP ($/MWh) | 36.724 | 38.36 | 40.575 | 39.734 | 40.17 | |
| Generation cost ($/h) | 7777.780 | |||||
| Revenue cost ($/h) | 10,051.925 | |||||
| Profit ($/h) | 2274.145 | |||||
| Deregulated system with double-bus demand-side bidding | Generation (MW) | 192.03 | 36.29 | 22.53 | 0 | 0.02 |
| LMP ($/MWh) | 36.526 | 38.144 | 40.451 | 39.504 | 39.794 | |
| Generation cost ($/h) | 6597.930 | |||||
| Revenue cost ($/h) | 9310.490 | |||||
| Profit ($/h) | 2712.560 | |||||
| Sl. No. | Wind Speed (m/s) | Generator 1 (Bus No. 1) | Generator 2 (Bus No. 2) | Generator 3 (Bus No. 3) | Generator 4 (Bus No. 6) | Generator 5 (Bus No. 8) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Generation (MW) | LMP ($/MWh) | Generation (MW) | LMP ($/MWh) | Generation (MW) | LMP ($/MWh) | Generation (MW) | LMP ($/MWh) | Generation (MW) | LMP ($/MWh) | ||
| 1 | 1.67 | 191.92 | 36.516 | 36.27 | 38.133 | 22.23 | 40.445 | 0.00 | 39.485 | 0.00 | 39.781 |
| 2 | 1.94 | 191.85 | 36.511 | 36.25 | 38.127 | 22.05 | 40.441 | 0.00 | 39.473 | 0.00 | 39.773 |
| 3 | 2.22 | 191.76 | 36.503 | 36.24 | 38.119 | 21.81 | 40.436 | 0.00 | 39.458 | 0.00 | 39.763 |
| 4 | 2.50 | 191.65 | 36.493 | 36.22 | 38.108 | 21.50 | 40.430 | 0.00 | 39.439 | 0.00 | 39.750 |
| 5 | 2.78 | 191.51 | 36.481 | 36.19 | 38.095 | 21.12 | 40.422 | 0.00 | 39.415 | 0.00 | 39.733 |
| 6 | 3.06 | 191.34 | 36.466 | 36.16 | 38.079 | 20.65 | 40.413 | 0.00 | 39.386 | 0.00 | 39.713 |
| 7 | 3.33 | 191.13 | 36.448 | 36.12 | 38.059 | 20.10 | 40.402 | 0.00 | 39.351 | 0.00 | 39.689 |
| 8 | 3.61 | 190.89 | 36.427 | 36.07 | 38.036 | 19.43 | 40.389 | 0.00 | 39.309 | 0.00 | 39.660 |
| 9 | 3.89 | 190.6 | 36.403 | 36.02 | 38.009 | 18.66 | 40.373 | 0.00 | 39.261 | 0.00 | 39.627 |
| 10 | 4.17 | 190.27 | 36.374 | 35.96 | 37.978 | 17.77 | 40.355 | 0.00 | 39.206 | 0.00 | 39.589 |
| 11 | 4.44 | 189.9 | 36.342 | 35.89 | 37.943 | 16.76 | 40.335 | 0.00 | 39.142 | 0.00 | 39.545 |
| 12 | 4.72 | 189.47 | 36.306 | 35.81 | 37.903 | 15.61 | 40.312 | 0.00 | 39.071 | 0.00 | 39.496 |
| 13 | 5.00 | 188.99 | 36.264 | 35.72 | 37.858 | 14.32 | 40.286 | 0.00 | 38.990 | 0.00 | 39.440 |
| 14 | 5.28 | 188.15 | 36.192 | 35.56 | 37.78 | 12.07 | 40.241 | 0.00 | 38.871 | 0.00 | 39.332 |
| 15 | 5.56 | 186.76 | 36.072 | 35.30 | 37.65 | 8.36 | 40.167 | 0.00 | 38.696 | 0.00 | 39.142 |
| 16 | 5.83 | 185.22 | 35.940 | 35.01 | 37.506 | 4.26 | 40.085 | 0.00 | 38.503 | 0.00 | 38.933 |
| 17 | 6.11 | 183.28 | 35.773 | 34.65 | 37.325 | 0.03 | 39.962 | 0.00 | 38.266 | 0.00 | 38.677 |
| 18 | 6.67 | 169.99 | 34.629 | 32.06 | 36.028 | 0.00 | 38.484 | 0.00 | 36.807 | 0.00 | 37.145 |
| Hour | Siliguri | Kolkata | Mumbai | Delhi | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regulated System | Deregulated-System Single-Bus DSB | Deregulated-System Double-Bus DSB | Regulated System | Deregulated-System Single-Bus DSB | Deregulated-System Double-Bus DSB | Regulated System | Deregulated-System Single-Bus DSB | Deregulated-System Double-Bus DSB | Regulated System | Deregulated-System Single-Bus DSB | Deregulated-System Double-Bus DSB | |
| 1 | 4.350 | 4.325 | 2.106 | −435.565 | −434.861 | −183.762 | −760.981 | −760.982 | −640.060 | 0.000 | 0.000 | 0.000 |
| 2 | −77.993 | −77.294 | −32.894 | −357.474 | −357.477 | −150.839 | 61.451 | 61.474 | 61.582 | −138.618 | −138.683 | −58.308 |
| 3 | −60.610 | −61.373 | −25.409 | 7.711 | 7.502 | 7.307 | 0.000 | 0.000 | 0.000 | −96.958 | −96.197 | −41.070 |
| 4 | 0.000 | 0.000 | 0.000 | −714.471 | −504.751 | −214.202 | 28.821 | 28.850 | 24.774 | 10.363 | 10.336 | 7.207 |
| 5 | 0.000 | 0.000 | 0.000 | −194.940 | −263.848 | −82.774 | 35.606 | 35.634 | 27.742 | 13.408 | 13.244 | 13.169 |
| 6 | 0.000 | 0.000 | 0.000 | 17.638 | 17.806 | 9.197 | 38.650 | 38.997 | 29.987 | 4.350 | 4.325 | 2.106 |
| 7 | −60.610 | −61.373 | −25.409 | −419.666 | −488.577 | −178.247 | 26.948 | 27.557 | 15.990 | 5.005 | 5.018 | 2.549 |
| 8 | −45.478 | −44.715 | −20.138 | 13.331 | 13.348 | 6.444 | 38.650 | 38.997 | 29.987 | −235.621 | −234.923 | −99.392 |
| 9 | −138.618 | −138.683 | −58.308 | 13.331 | 13.348 | 6.444 | 32.800 | 32.857 | 24.207 | −96.958 | −96.197 | −41.070 |
| 10 | −138.618 | −138.683 | −58.308 | −543.402 | −544.945 | −231.729 | 72.568 | 72.609 | 67.223 | 11.721 | 11.233 | 10.140 |
| 11 | 3.661 | 3.623 | 1.695 | 24.018 | 24.052 | 19.716 | 64.845 | 64.867 | 63.853 | 11.721 | 11.233 | 10.140 |
| 12 | 0.000 | 0.000 | 0.000 | 24.018 | 24.052 | 19.716 | 8.264 | 8.260 | 8.112 | 0.000 | 0.000 | 0.000 |
| 13 | 6.021 | 6.001 | 2.957 | −361.487 | −361.487 | −241.609 | −1.686 | −1.687 | −1.564 | −215.100 | −215.102 | −91.133 |
| 14 | 2.937 | 2.966 | 1.316 | −686.405 | −686.329 | −380.198 | 0.000 | 0.000 | 0.000 | 11.686 | 12.752 | 8.259 |
| 15 | 0.000 | 0.000 | 0.000 | −361.487 | −361.487 | −241.609 | 64.845 | 64.867 | 63.853 | 0.000 | 0.000 | 0.000 |
| 16 | 0.000 | 0.000 | 0.000 | 13.687 | 13.687 | 10.045 | 19.514 | 19.514 | 17.559 | 10.195 | 9.606 | 8.474 |
| 17 | −60.610 | −61.373 | −25.409 | 0.000 | 0.000 | 0.000 | 24.018 | 24.052 | 19.716 | 10.363 | 10.336 | 7.207 |
| 18 | −60.610 | −61.373 | −25.409 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 31.191 | 31.197 | 21.771 |
| 19 | 0.000 | 0.000 | 0.000 | 30.795 | 30.826 | 22.959 | 21.325 | 21.315 | 11.082 | 35.390 | 35.421 | 25.930 |
| 20 | 2.937 | 2.966 | 1.316 | 8.216 | 8.337 | 4.681 | 20.629 | 20.655 | 10.163 | 16.249 | 16.249 | 13.206 |
| 21 | −235.621 | −234.923 | −99.392 | 33.763 | 34.104 | 25.268 | 30.795 | 30.826 | 22.959 | −215.100 | −215.102 | −91.133 |
| 22 | −174.978 | −173.515 | −73.972 | 33.763 | 34.104 | 25.268 | 26.731 | 26.770 | 14.502 | −353.817 | −353.882 | −149.472 |
| 23 | 4.350 | 4.325 | 2.106 | 33.295 | 33.672 | 22.936 | −253.389 | −255.623 | −108.063 | −215.100 | −215.102 | −91.133 |
| 24 | 7.074 | 7.017 | 3.715 | 33.295 | 33.672 | 22.936 | 67.775 | 67.818 | 65.128 | −118.106 | −118.866 | −50.052 |
| Average Hourly Profit ($/h) | |||||
|---|---|---|---|---|---|
| Optimization Technique | Conditions | Siliguri | Delhi | ||
| Regulated System | Deregulated-System Double-Bus DSB | Regulated System | Deregulated-System Double-Bus DSB | ||
| SQP | With WF | 2008.910 | 2827.310 | 2183.927 | 3151.654 |
| With WF and PHES | 2010.68 | 2830.38 | 2185.27 | 3154.68 | |
| ABC | With WF | 2009.510 | 2827.967 | 2184.657 | 3152.428 |
| With WF and PHES | 2011.687 | 2831.234 | 2186.821 | 3155.921 | |
| MFO | With WF | 2009.715 | 2828.184 | 2184.835 | 3152.709 |
| With WF and PHES | 2011.834 | 2831.368 | 2186.934 | 3155.825 | |
| Sl. No. | Wind Power | VaR | CVaR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| With Wind Farm Using SQP | With Wind Farm–PHES System Using SQP | With Wind Farm–PHES System Using ABC | With Wind Farm–PHES System Using MFO | With Wind Farm Using SQP | With Wind Farm–PHES System Using SQP | With Wind Farm–PHES System Using ABC | With Wind Farm–PHES System Using MFO | ||
| 1 | 10.3 MW | −0.3617 | −0.3515 | −0.3425 | −0.3319 | −0.5619 | −0.5426 | −0.5316 | −0.5216 |
| 2 | 8.1 MW | −0.3646 | −0.3534 | −0.3448 | −0.3339 | −0.5663 | −0.5486 | −0.5374 | −0.5257 |
| 3 | 3.42 MW | −0.365 | −0.3547 | −0.3459 | −0.3342 | −0.567 | −0.5491 | −0.5365 | −0.5268 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basu, J.B.; Dawn, S.; Saha, P.K.; Chakraborty, M.R.; Ustun, T.S. Economic Enhancement of Wind–Thermal–Hydro System Considering Imbalance Cost in Deregulated Power Market. Sustainability 2022, 14, 15604. https://doi.org/10.3390/su142315604
Basu JB, Dawn S, Saha PK, Chakraborty MR, Ustun TS. Economic Enhancement of Wind–Thermal–Hydro System Considering Imbalance Cost in Deregulated Power Market. Sustainability. 2022; 14(23):15604. https://doi.org/10.3390/su142315604
Chicago/Turabian StyleBasu, Jayanta Bhusan, Subhojit Dawn, Pradip Kumar Saha, Mitul Ranjan Chakraborty, and Taha Selim Ustun. 2022. "Economic Enhancement of Wind–Thermal–Hydro System Considering Imbalance Cost in Deregulated Power Market" Sustainability 14, no. 23: 15604. https://doi.org/10.3390/su142315604
APA StyleBasu, J. B., Dawn, S., Saha, P. K., Chakraborty, M. R., & Ustun, T. S. (2022). Economic Enhancement of Wind–Thermal–Hydro System Considering Imbalance Cost in Deregulated Power Market. Sustainability, 14(23), 15604. https://doi.org/10.3390/su142315604








