Seamless Power Management for a Distributed DC Microgrid with Minimum Communication Links under Transmission Time Delays
Abstract
1. Introduction
- (i)
- A system communication topology for a distributed DCMG with minimum DCLs is proposed to achieve an optimal system cost. Because the proposed scheme relies on a limited exchange data size in a packet, general digital I/O port pins are sufficient to exchange the data between neighboring agents of a distributed DCMG system, which significantly simplifies the hardware architecture of the power agent.
- (ii)
- Seamless power management can be maintained even under transmission time delays, such as the grid fault detection delay and grid recovery detection delay conditions. In these situations, the DCMG system smoothly switches the operation to the decentralized scheme based on the droop control method to avoid miscoordination of each power unit, which may result in a system imbalance. When other power agents clearly detect the utility grid information precisely after a transmission time delay, the DCMG system changes the operation from decentralized control to distributed control to maintain the DCV at a nominal value.
- (iii)
- To enhance the scalability of the DCMG system, the proposed scheme presents a DCL topology with minimum communication data even when an AESS agent is present in an existing distributed DCMG system. The proposed scheme only requires two additional DCLs for AESS involvement, which enables power units to participate in or leave the distributed DCMG system easily.
2. System Configuration of a Distributed DCMG
2.1. Configuration of DCMG
2.2. System Communication Topology
3. Power Management and Control Strategy of Local Agents under Transmission Time Delays
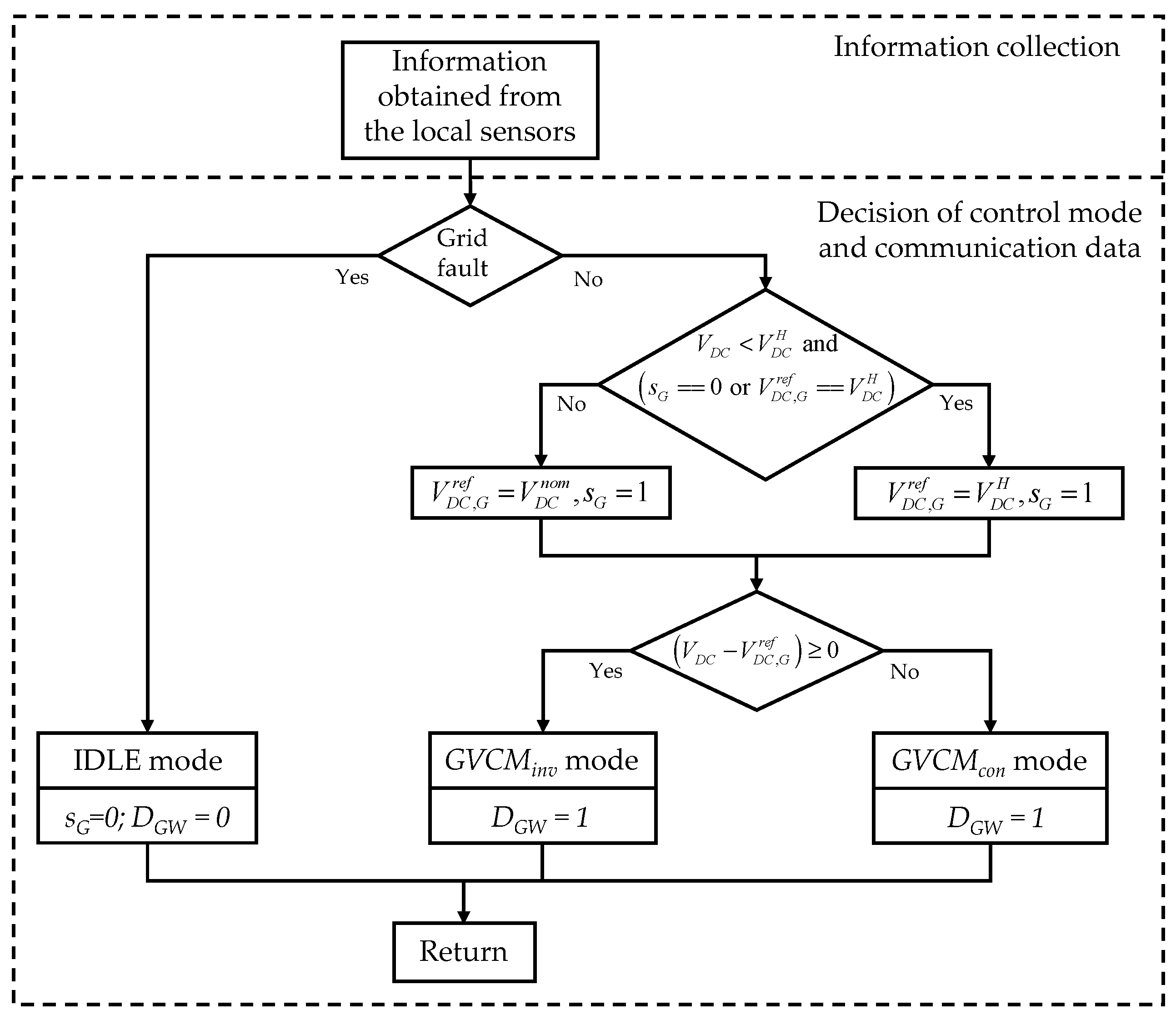
3.1. Control Strategy of the Utility Grid Agent
3.2. Control Strategy of the Wind Turbine Agent
- Distributed scheme in grid-connected or islanded mode—when = 1;
- Decentralized scheme in islanded mode—when = 2;
- Decentralized scheme in grid-connected mode—when = 3.
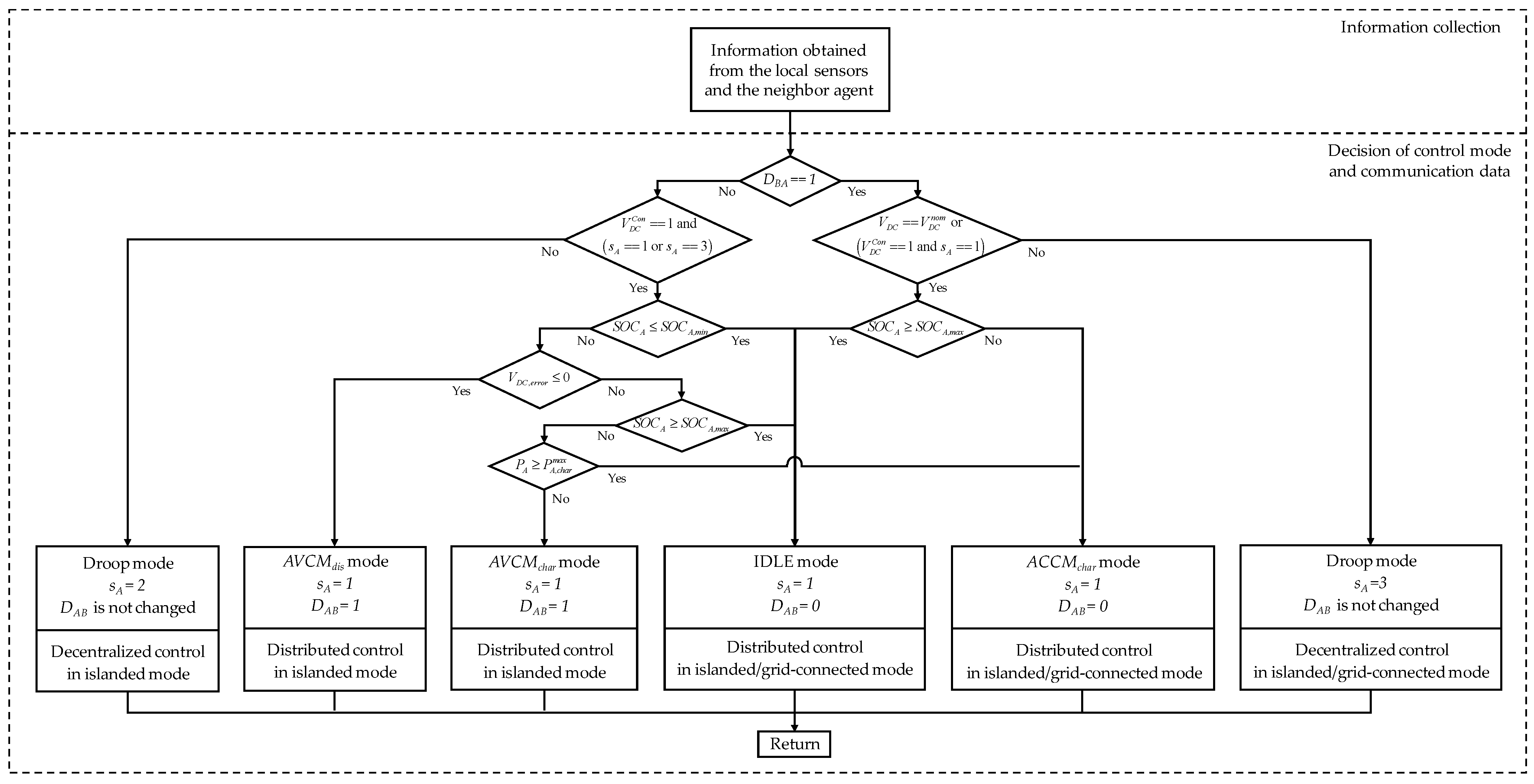
3.3. Control Strategy of the Battery Agent
- Distributed scheme in grid-connected or islanded mode—when = 1;
- Decentralized scheme in islanded mode—when = 2, = 0;
- Decentralized scheme in grid-connected or islanded mode—when = 3, = 1.
3.4. Load Agent
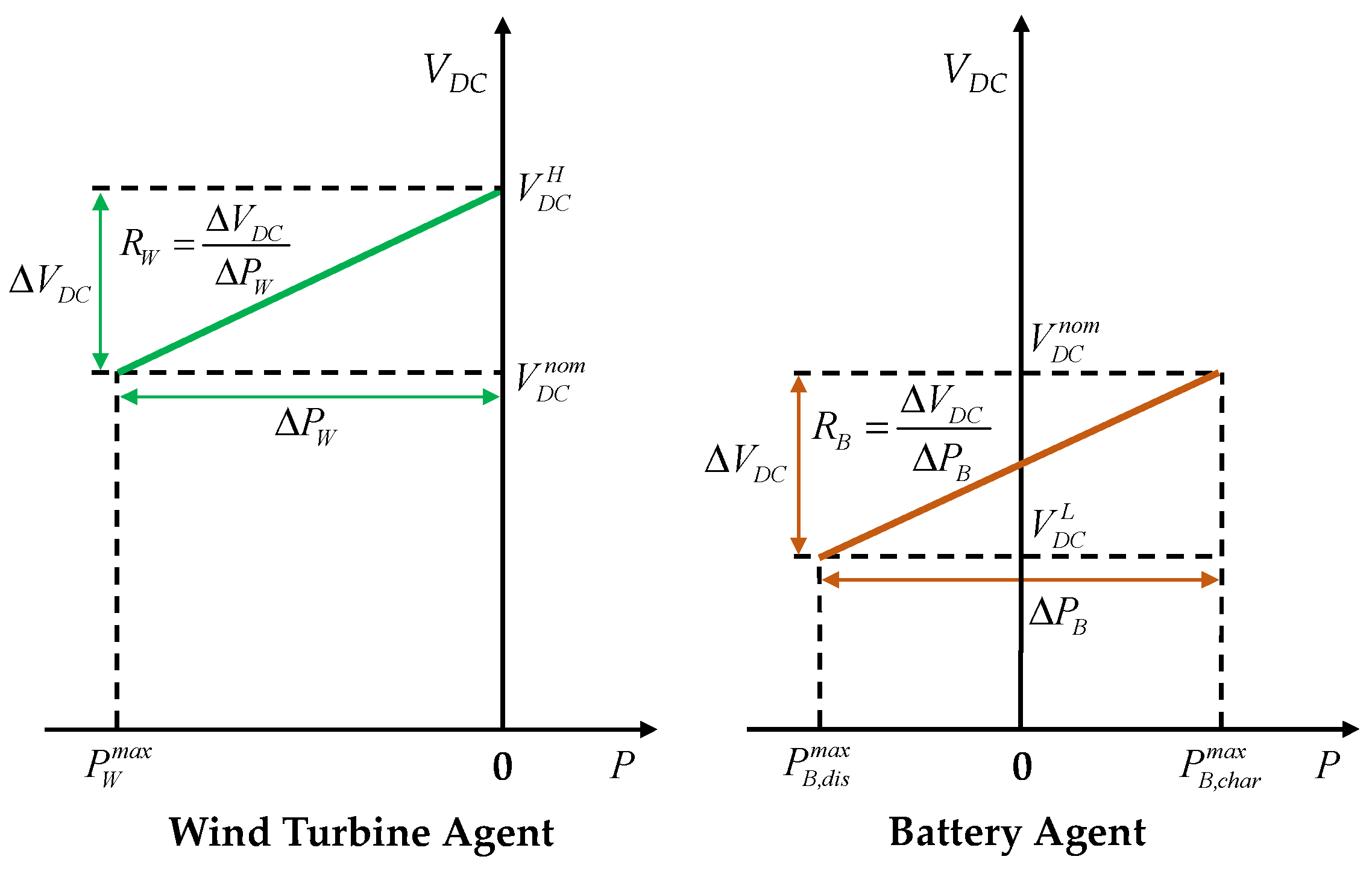
3.5. Droop Control for Wind Turbine and Battery Agents under Transmission Time Delays
- For : During this voltage interval, the wind turbine agent regulates the DCV via the voltage droop control mode (VDCM). In the V-P droop control scheme shown in Figure 7, can be obtained via and . In this case, the battery agent operates in the BCCMchar mode for maximum charging.
- For : During this voltage interval, the battery agent regulates the DCV via the voltage droop control mode (BVDM). With and , can be obtained as shown in Figure 7. The wind turbine agent operates in the MPPT mode to supply the maximum level of power.
4. Scalability of the Proposed Distributed DCMG System
4.1. Control Strategy of the Battery Agent in the Event of AESS Agent Involvement
4.2. Control Strategy of an AESS Agent
- For : As mentioned earlier, the wind turbine agent regulates the DCV via VDCM with droop characteristic . In this case, the battery and AESS agents operate in the and modes for maximum charging.
- For : During this voltage interval, the battery agent regulates the DCV by BVDM with droop characteristic . With and , can be obtained, as shown in Figure 10. The wind turbine agent operates in the MPPT mode and the AESS operates in the mode.
- For : During this voltage interval, the AESS agent regulates the DCV via the voltage droop control mode (AVDM) with droop characteristic , which can be obtained as in Figure 10 with = and = . The battery and wind turbine agents operate in the and MPPT mode, respectively, to supply the maximum level of power.
5. Simulation Results
5.1. Transition from Grid-Connected to Islanded Mode without Grid Fault Detection Delay
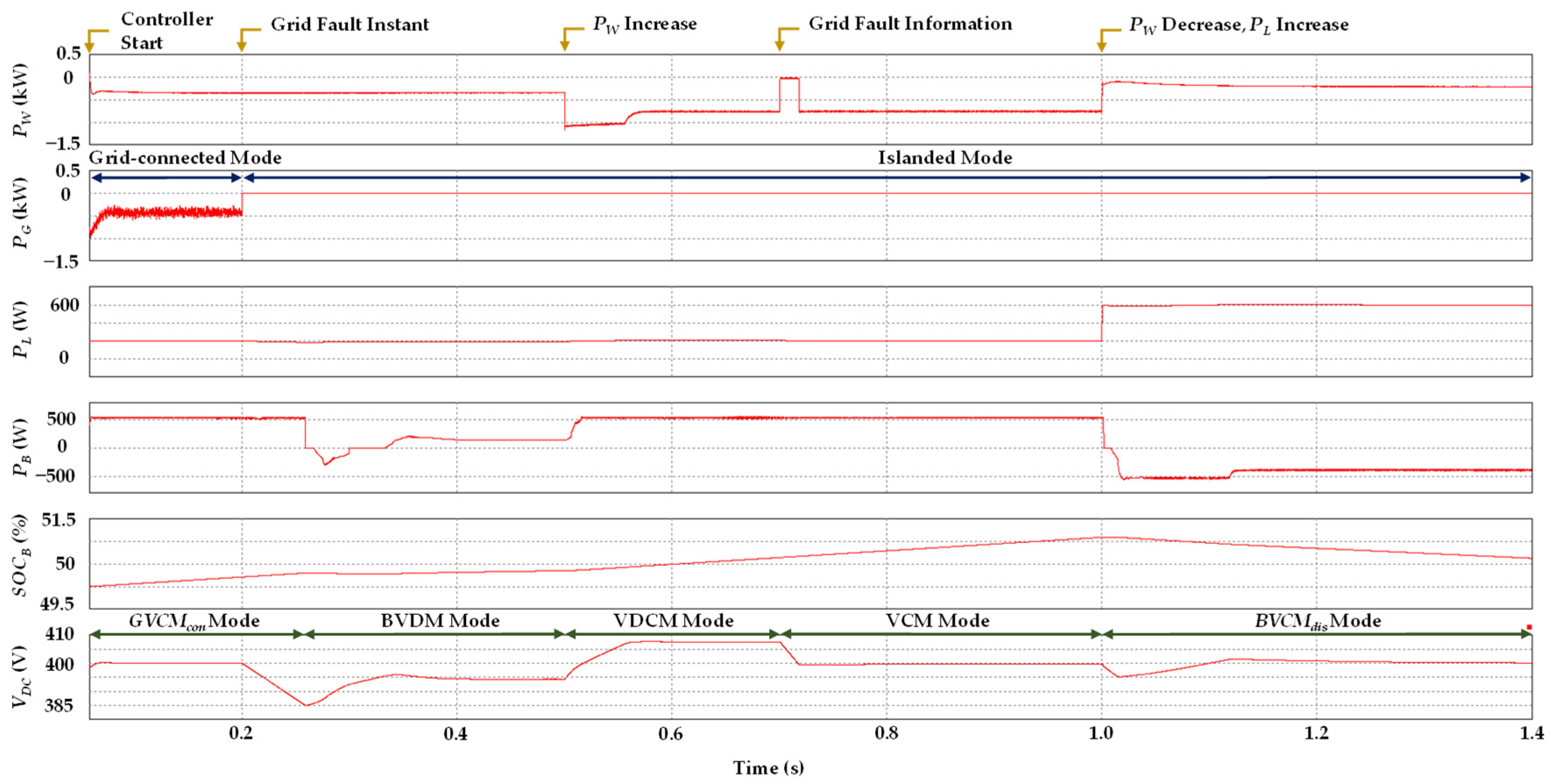
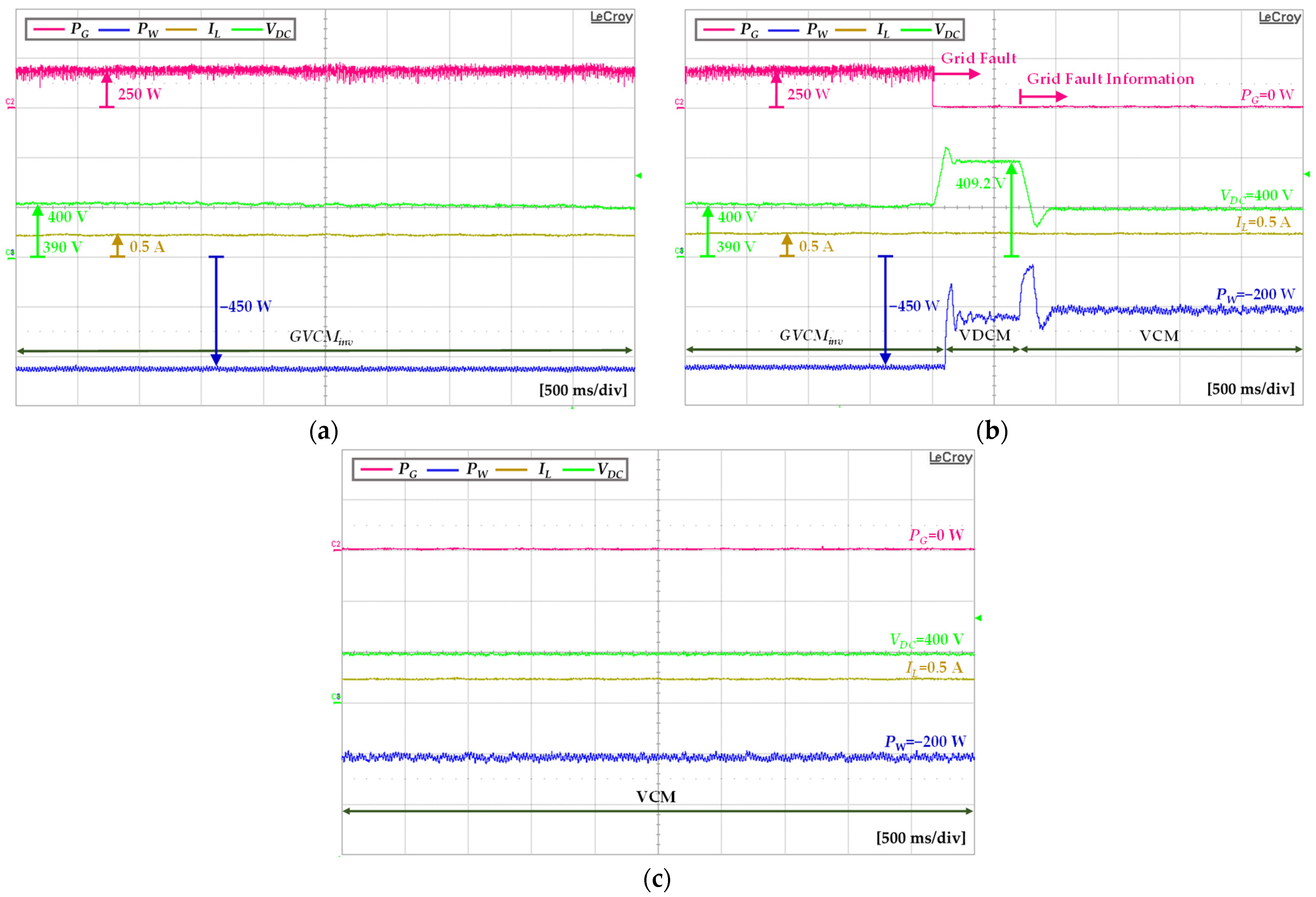
5.2. Case of Grid Fault Detection Delay
5.3. Case of Grid Recovery Detection Delay
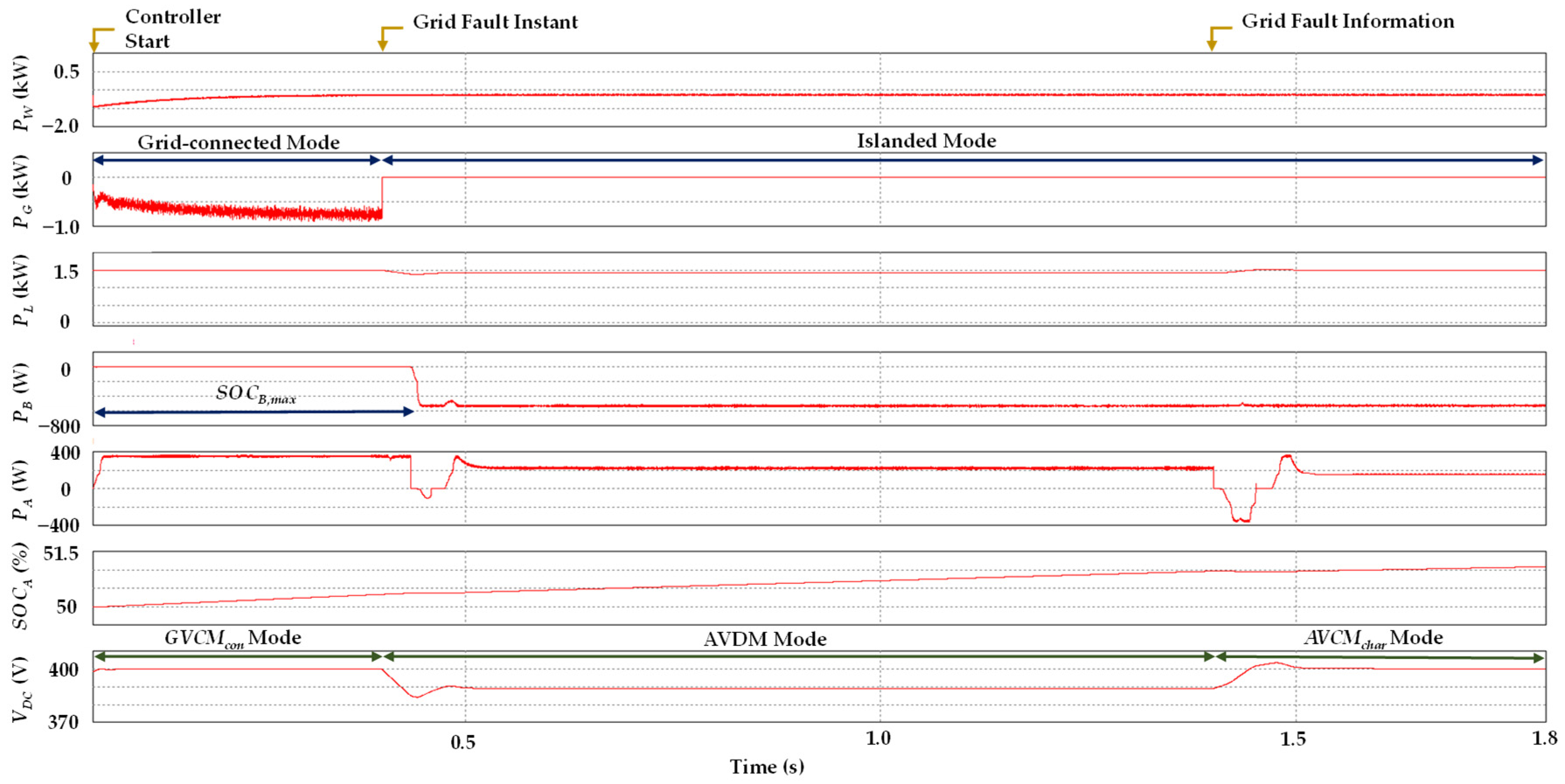
5.4. Case of AESS Agent Involvement
6. Experimental Results
6.1. Case of Load Shedding Process
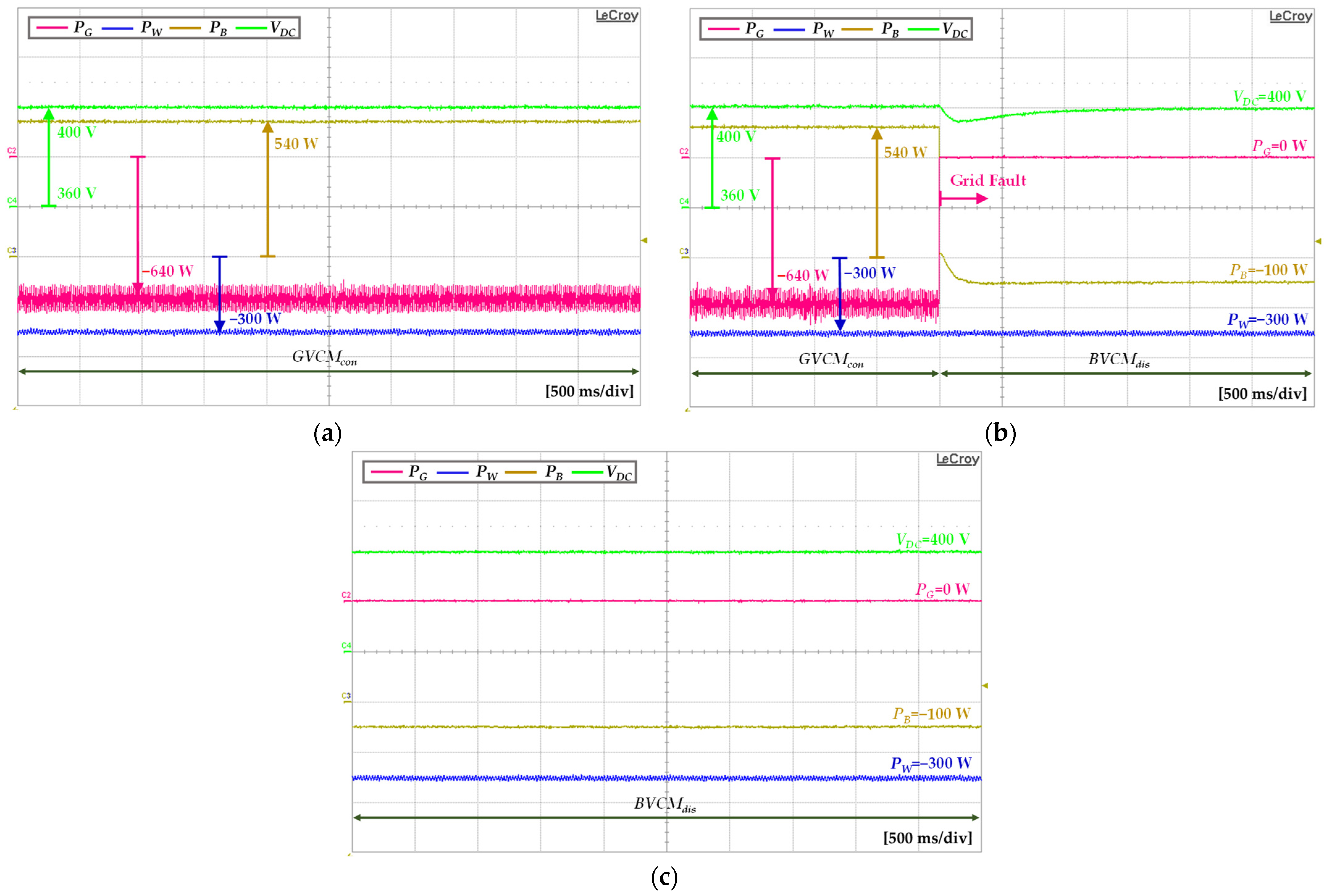
6.2. Transition from Grid-Connected to Islanded Mode without Grid Fault Detection Delay
6.3. Case of Grid Fault Detection Delay
6.4. Case of AESS Agent Involvement
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| AESS | Additional ESS agent |
| AVDM | Voltage droop control mode by AESS agent |
| BVDM | Voltage droop control mode by battery agent |
| DC | Direct current |
| DCMG | DC microgrid |
| DCV | DC-link voltage |
| DCLs | Digital communication links |
| DSP | Digital signal processor |
| ESS | Energy storage system |
| IDLE | Idle mode by the battery or the utility grid agent |
| MPPT | Maximum power point tracking |
| PI | Proportional integral |
| PMSG | Permanent magnet synchronous generator |
| PV | Photovoltaic |
| RES | Renewable energy source |
| SOC | State of charge |
| VCM | DCV control by the wind turbine agent |
| VDCM | Voltage droop control mode by wind turbine agent |
| Constant current control by AESS charging | |
| DCV control by AESS charging | |
| DCV control by AESS discharging | |
| Constant current control by battery charging | |
| Constant current control by battery discharging | |
| DCV control by battery charging | |
| DCV control by battery discharging | |
| Capacitance of DC-link | |
| Cf | Filter capacitance of LCL filter |
| Data information from the AESS agent to the battery agent | |
| Data information from the battery agent to the AESS agent | |
| Data information from the battery agent to the wind turbine agent | |
| Data information from the utility grid agent to the wind turbine agent | |
| Data information from the wind turbine agent to the battery agent | |
| Data information from the wind turbine agent to the load agent | |
| Grid frequency | |
| DCV control by inverter mode of the utility grid agent | |
| DCV control by converter mode of the utility grid agent | |
| Number of operating loads | |
| J | PMSG inertia |
| LA | Converter filter inductance of AESS agent |
| LB | Converter filter inductance of battery agent |
| Ldq | PMSG dq-axis inductance |
| LW | Converter filter inductance of wind turbine agent |
| L1 | Inverter-side inductance of LCL filter |
| L2 | Grid-side inductance of LCL filter |
| Number of loads in a DCMG | |
| Maximum AESS charging power | |
| Maximum AESS discharging power | |
| Maximum battery charging power | |
| Maximum battery discharging power | |
| Maximum power of the wind turbine agent | |
| PA | Exchange power between DC-link and AESS agent |
| PB | Exchange power between DC-link and battery agent |
| PG | Exchange power between DC-link and utility grid agent |
| PL | Power absorbed by load agent |
| PL1 | Power of load 1 |
| PL2 | Power of load 2 |
| PW | Generation power by wind turbine agent |
| Droop characteristic of AESS agent | |
| Droop characteristic of battery agent | |
| Droop characteristic of wind turbine agent | |
| PMSG stator resistance | |
| R1 | Parasitic resistance in |
| R2 | Parasitic resistance in |
| Maximum AESS state of charge | |
| Minimum AESS state of charge | |
| AESS state of charge | |
| Maximum battery state of charge | |
| Maximum battery state of charge | |
| Battery state of charge | |
| State of the AESS agent | |
| State of the battery agent | |
| State of the utility grid agent | |
| State of the wind turbine agent | |
| Maximum AESS voltage | |
| Maximum battery voltage | |
| Grid voltage | |
| Low DCV level of battery agent | |
| DC-link reference voltage of the utility grid agent | |
| Error of and | |
| Maximum voltage error between and | |
| Measured DCV | |
| DCV state | |
| Highest DCV level | |
| Lowest DCV level | |
| Limited DCV level | |
| Nominal DCV | |
| DCV in the previous time step | |
| VA | AESS voltage |
| VB | Battery voltage |
| PMSG flux linkage |
References
- Saeed, M.H.; Fangzong, W.; Kalwar, B.A.; Iqbal, S. A review on microgrids’ challenges & perspectives. IEEE Access 2021, 9, 166502–166517. [Google Scholar]
- Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cárdenas-Dobson, R.; Martínez-Gómez, M.; Sáez, D. Distributed control strategies for microgrids: An overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
- Lee, J.; Guo, J.; Choi, J.K.; Zukerman, M. Distributed energy trading in microgrids: A game-theoretic model and its equilibrium analysis. IEEE Trans. Ind. Electron. 2015, 62, 3524–3533. [Google Scholar] [CrossRef]
- Dou, C.; Yue, D.; Zhang, Z.; Ma, K. MAS-based distributed cooperative control for DC microgrid through switching topology communication network with time-varying delays. IEEE Trans. Syst. J. 2019, 13, 615–624. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W. Overview of power management strategies of hybrid AC/DC microgrid. IEEE Trans. Power Electron. 2015, 30, 7072–7089. [Google Scholar] [CrossRef]
- Yu, C.; Zhou, H.; Lu, X.; Lai, J.; Liu, G.-P. Distributed optimal synchronization rate control for AC microgrids under event-triggered mechanism. IEEE Trans. Power Syst. 2021, 36, 1780–1793. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Wu, L. Optimal operation for community-based multi-party microgrid in grid-connected and islanded modes. IEEE Trans. Smart Grid 2018, 9, 756–765. [Google Scholar] [CrossRef]
- Liu, Y.; Yuen, C.; Ul Hassan, N.; Huang, S.; Yu, R.; Xie, S. Electricity cost minimization for a microgrid with distributed energy resource under different information availability. IEEE Trans. Ind. Electron. 2015, 62, 2571–2583. [Google Scholar] [CrossRef]
- Habibullah, A.F.; Padhilah, F.A.; Kim, K.-H. Decentralized control of DC microgrid based on droop and voltage controls with electricity price consideration. Sustainability 2021, 13, 11398. [Google Scholar] [CrossRef]
- Xia, Y.; Wei, W.; Peng, Y.; Yang, P.; Yu, M. Decentralized coordination control for parallel bidirectional power converters in a grid-connected DC microgrid. IEEE Trans. Smart Grid 2018, 9, 6850–6861. [Google Scholar] [CrossRef]
- Li, X.; Jiang, W.; Wang, J.; Wang, P.; Wu, X. An autonomous control scheme of global smooth transitions for bidirectional DC-DC converter in DC microgrid. IEEE Trans. Energy Convers. 2021, 36, 950–960. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Roldan-Perez, J.; Vasquez, J.C.; Guerrero, J.M. Modeling and sensitivity study of consensus algorithm-based distributed herarchical control for DC microgrids. IEEE Trans. Smart Grid 2016, 7, 1504–1515. [Google Scholar] [CrossRef]
- Lee, S.-J.; Choi, J.-Y.; Lee, H.-J.; Won, D.-J. Distributed coordination control strategy for a multi-microgrid based on a consensus algorithm. Energies 2017, 10, 1017. [Google Scholar] [CrossRef]
- Dehkordi, N.M.; Sadati, N.; Hamzeh, M. Distributed robust finite-time secondary voltage and frequency control of islanded microgrids. IEEE Trans. Power Syst. 2017, 32, 3648–3659. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, B.; Peng, J.; Liu, W. Operation loss minimization targeted distributed optimal control of DC microgrids. IEEE Syst. J. 2021, 15, 5186–5196. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Q.; Wen, C.; Wang, L.; Wang, P. Distributed secondary control for power allocation and voltage restoration in islanded DC microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1857–1869. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Chen, J.; Wang, C.; Guo, L. Operation optimization of standalone microgrids considering lifetime characteristics of battery energy storage system. IEEE Trans. Sustain. Energy 2013, 4, 934–943. [Google Scholar] [CrossRef]
- Al-Hanahi, B.; Ahmad, I.; Habibi, D.; Masoum, M.A.S. Charging infrastructure for commercial electric vehicles: Challenges and future works. IEEE Access 2021, 9, 121476–121492. [Google Scholar] [CrossRef]
- Padhilah, F.A.; Kim, K.-H. A power flow control strategy for hybrid control architecture of DC microgrid under unreliable grid connection considering electricity price constraint. Sustainability 2020, 12, 7628. [Google Scholar] [CrossRef]
- Tian, G.; Zheng, Y.; Liu, G.; Zhang, J. SOC balancing and coordinated control based on adaptive droop coefficient algorithm for energy storage units in DC microgrid. Energies 2022, 15, 2943. [Google Scholar] [CrossRef]
- Hoang, K.D.; Lee, H.-H. Accurate power sharing with balanced battery state of charge in distributed DC microgrid. IEEE Trans. Ind. Electron. 2019, 66, 1883–1893. [Google Scholar] [CrossRef]
- Morstyn, T.; Savkin, A.V.; Hredzak, B.; Agelidis, V.G. Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a DC microgrid. IEEE Trans. Smart Grid 2018, 9, 4735–4743. [Google Scholar] [CrossRef]
- Chen, X.; Shi, M.; Sun, H.; Li, Y.; He, H. Distributed cooperative control and stability analysis of multiple DC electric springs in a DC microgrid. IEEE Trans. Ind. Electron. 2018, 65, 5611–5622. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, W.; Wang, J.; Li, Q.; Mu, D.; Xu, X. Distributed cooperative secondary control for islanded microgrid with Markov time-varying delays. IEEE Trans. Energy Convers. 2019, 34, 2235–2247. [Google Scholar] [CrossRef]
- Zhang, R.; Hredzak, B. Distributed finite-time multiagent control for DC microgrids with time delays. IEEE Trans. Smart Grid 2018, 10, 2692–2701. [Google Scholar] [CrossRef]
- Huang, B.; Liu, L.; Li, Y.; Zhang, H. Distributed optimal energy management for microgrids in the presence of time-varying communication delays. IEEE Access 2019, 7, 83702–83712. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Majumder, R.; Pal, B.C. Wide-area measurement-based stabilizing control of power system considering signal transmission delay. IEEE Trans. Power Syst. 2004, 19, 1971–1979. [Google Scholar] [CrossRef]
- Yan, H.; Zhou, X.; Zhang, H.; Yang, F.; Wu, Z.-G. A novel sliding mode estimation for microgrid control with communication time delays. IEEE Trans. Smart Grid 2019, 10, 1509–1520. [Google Scholar] [CrossRef]
- Xing, L.; Guo, F.; Liu, X.; Wen, C.; Mishra, Y.; Tian, Y.-C. Voltage restoration and adjustable current sharing for DC microgrid with time delay via distributed secondary control. IEEE Trans. Sustain. Energy 2021, 12, 1068–1077. [Google Scholar] [CrossRef]
- Dong, M.; Li, L.; Nie, Y.; Song, D.; Yang, J. Stability analysis of a novel distributed secondary control considering communication delay in DC microgrids. IEEE Trans. Smart Grid 2019, 10, 6690–6700. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Kim, K.-H. An improved power management strategy for MAS-based distributed control of DC microgrid under communication network problems. Sustainability 2020, 12, 122. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Kim, K.-H. Power flow control strategy and reliable DC-Link voltage restoration for DC Microgrid under grid fault conditions. Sustainability 2019, 11, 3781. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Communication delay robustness for multi agent state of charge balancing between distributed AC microgrid storage systems. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015. [Google Scholar]
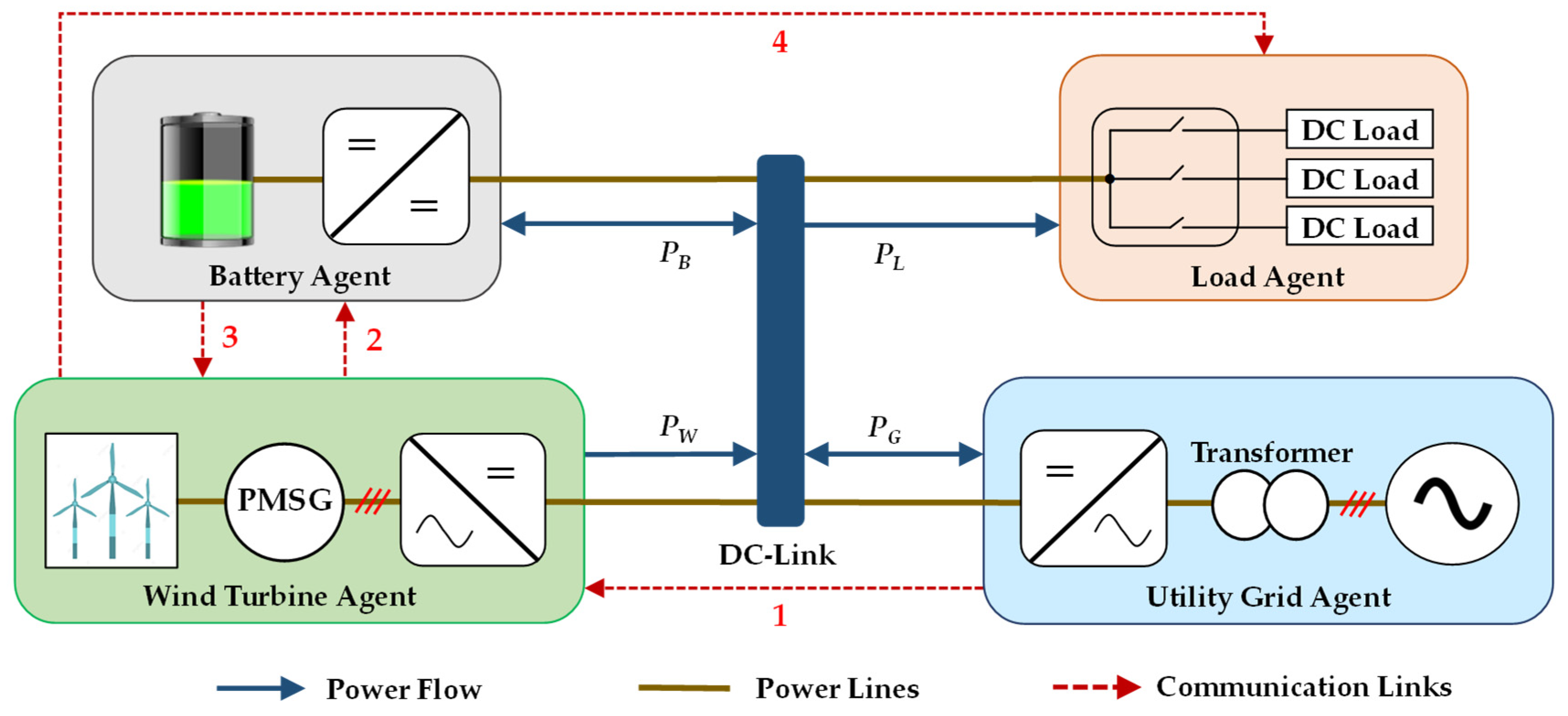
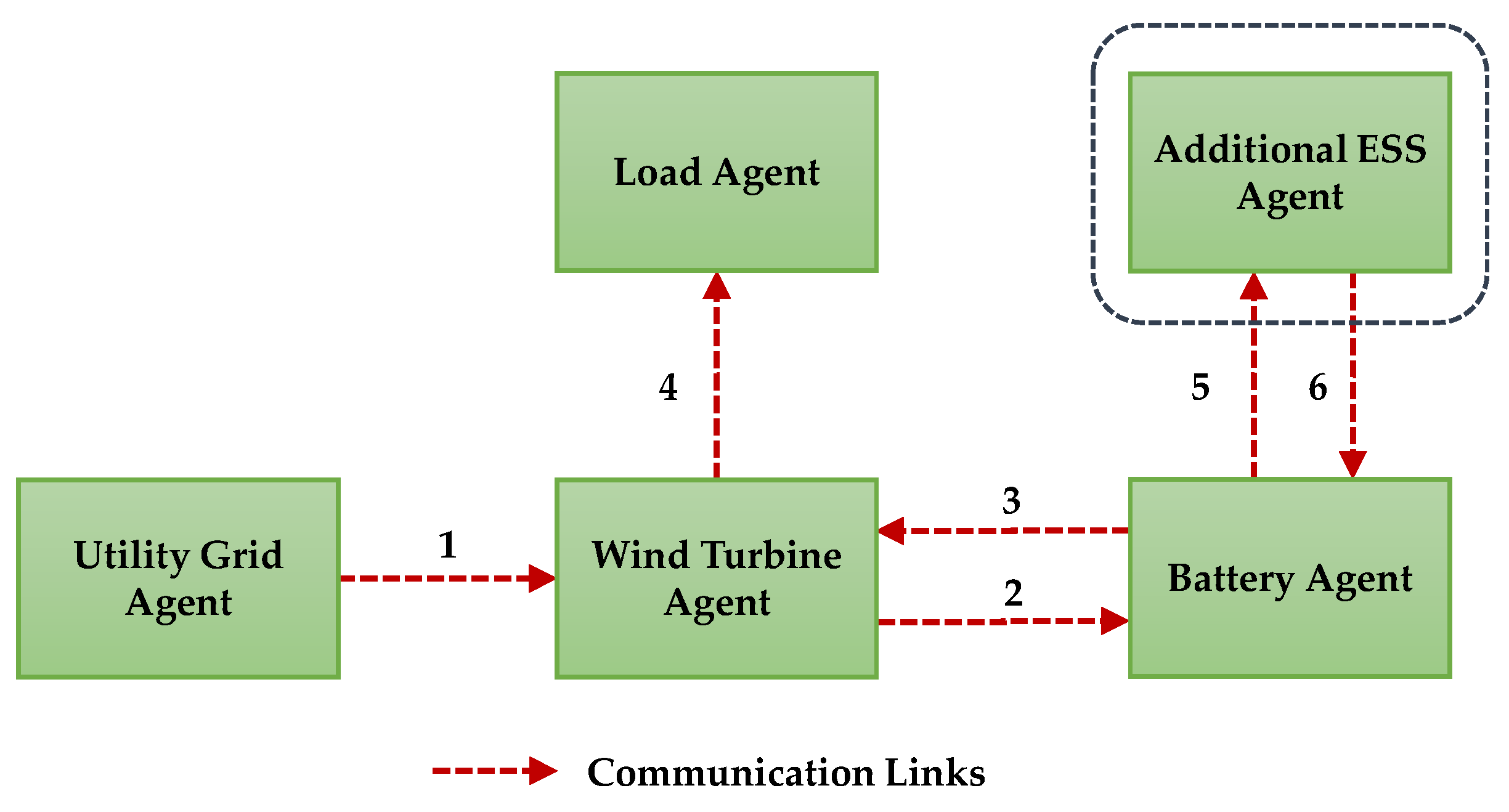












| Communication Link | Exchange Data | Data Type | Data Information |
|---|---|---|---|
| 1 | Binary | 0: Utility grid agent does not regulate DCV. | |
| 1: Utility grid agent regulates DCV. | |||
| 2 | Binary | 0: Wind turbine and utility grid agents do not regulate DCV. | |
| 1: Wind turbine/utility grid agent regulates DCV. | |||
| 3 | Binary | 0: Battery agent does not regulate DCV. | |
| 1: Battery agent regulates DCV. | |||
| 4 | Binary | 0: Load agent operates in the normal/load reconnecting mode. | |
| 1: Load agent operates in the normal/load-shedding mode. | |||
| 5 | Binary | 0: Wind turbines, utility grids, and battery agents do not regulate DCV. | |
| 1: Wind turbine/utility grid/battery agent regulates DCV. | |||
| 6 | Binary | 0: AESS agent does not regulate DCV. | |
| 1: AESS agent regulates DCV. |
| Power Agents | Parameters | Symbol | Value |
|---|---|---|---|
| Utility grid agent | Grid voltage | 220 V | |
| Grid frequency | 60 Hz | ||
| Transformer | T | 380/220 V | |
| Inverter-side inductance of LCL filter | 1.7 mH | ||
| Parasitic resistance in | 0.5 Ω | ||
| Grid-side inductance of LCL filter | 1.7 mH | ||
| Parasitic resistance in | 0.5 Ω | ||
| Filter capacitance of LCL filter | 4.5 μF | ||
| Grid fault detection delay time | - | 0.5–1.0 s | |
| Grid recovery detection delay time | - | 0.5–1.0 s | |
| Wind turbine agent | PMSG stator resistance | 0.64 Ω | |
| PMSG dq-axis inductance | 0.82 mH | ||
| PMSG number of poles | 6 | ||
| PMSG inertia | 0.111 kgm2 | ||
| PMSG flux linkage | 0.18 Wb | ||
| Converter filter inductance | 7 mH | ||
| Maximum power of the wind turbine agent | −3000 W | ||
| Battery agent | Maximum SOC | 90% | |
| Minimum SOC | 20% | ||
| Rated capacity | C | 30 Ah | |
| Maximum charging power | 540 W | ||
| Maximum discharging power | −540 W | ||
| Maximum voltage | 180 V | ||
| Converter filter inductance L | 7 mH | ||
| AESS agent | Maximum SOC | 90% | |
| Minimum SOC | 20% | ||
| Rated capacity | C | 30 Ah | |
| Maximum charging power | 360 W | ||
| Maximum discharging power | −360 W | ||
| Maximum voltage | 180 V | ||
| Converter filter inductance L | 7 mH | ||
| Load agent | Power of load 1 | 200 W | |
| Power of load 2 | 200 W | ||
| Priority level: load 1 > load 2 | - | - | |
| DC-link | Nominal DCV | 400 V | |
| Highest DCV level | 410 V | ||
| Low DCV level of battery agent | 390 V | ||
| Lowest DCV level | 385 V | ||
| Limited DCV level | 380 V | ||
| Capacitance | 4 mF |
| Simulation | Experiment | |
|---|---|---|
| Load shedding process | 0.175% | 1.050% |
| Transition from grid-connected mode to islanded mode without transmission time delay | 0.200% | 1.000% |
| Grid fault detection delay when the wind turbine agent regulates DCV | 0.125% | 1.050% |
| Grid fault detection delay when the battery agent regulates DCV | 0.025% | 0.625% |
| AESS involvement regulates DCV | 0.450% | 0.925% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, D.T.; Habibullah, A.F.; Kim, K.-H. Seamless Power Management for a Distributed DC Microgrid with Minimum Communication Links under Transmission Time Delays. Sustainability 2022, 14, 14739. https://doi.org/10.3390/su142214739
Tran DT, Habibullah AF, Kim K-H. Seamless Power Management for a Distributed DC Microgrid with Minimum Communication Links under Transmission Time Delays. Sustainability. 2022; 14(22):14739. https://doi.org/10.3390/su142214739
Chicago/Turabian StyleTran, Dat Thanh, Al Faris Habibullah, and Kyeong-Hwa Kim. 2022. "Seamless Power Management for a Distributed DC Microgrid with Minimum Communication Links under Transmission Time Delays" Sustainability 14, no. 22: 14739. https://doi.org/10.3390/su142214739
APA StyleTran, D. T., Habibullah, A. F., & Kim, K.-H. (2022). Seamless Power Management for a Distributed DC Microgrid with Minimum Communication Links under Transmission Time Delays. Sustainability, 14(22), 14739. https://doi.org/10.3390/su142214739







