1. Introduction
The accessibility of a site is one of the main factors influencing its ability to attract residential, commercial, and industrial settlements. In the literature, it is possible to find numerous works that confirm this assumption. Good accessibility makes a place easy to reach (passive accessibility) and allows those who live or work there to easily reach other places (active accessibility), making it more attractive to live in or establish a commercial or industrial activity.
From the tourism point of view, the accessibility of a site or a city can influence the choice of users when planning a trip, thus indirectly affecting the destination attractiveness; in fact, tourists tend to prefer an easily accessible destination over another that is more difficult to reach.
The accessibility of a place, in general, and even more so in tourism, is strongly influenced by the available public transport services. In this context, high-speed rail transport systems play an important role in the tourist development of a location, increasing its tourist accessibility as well as its general accessibility.
The purpose of this paper is to study the impact that high-speed rail (HSR) systems may have on tourism. To achieve this, two linear regression models were calibrated and specified to estimate tourist flows as a function of several accessibility variables, including the number of runs of high-speed rail services, as well as variables of cultural and tourist assets consistency. The models were calibrated with data from 111 provincial capitals in Italy, with reference to the year 2018, which is not affected by the impact of the COVID-19 pandemic. Although similar models could be calibrated for other Western countries, the Italian case study is significant because high-speed services are not widespread: of 111 provincial capitals, 49 are not served by high-speed rail at all, and 41 are served with no more than 10 rides per day.
In this study, we consider high-speed services not only those which exceed a maximum speed of 300 km/h (such as Trenitalia Frecciarossa services) but also those which reach a maximum speed of 250 km/h (Trenitalia Frecciargento services) and 200 km/h (Trenitalia Frecciabianca services), according to the UIC definition: “
High-speed rail combines many different elements which constitute a ‘whole, integrated system’: an infrastructure for new lines designed for speeds of 250 km/h and above; upgraded existing lines for speeds of up to 200 or even 220 km/h, including interconnecting lines between high-speed sections” [
1].
The limitations of the proposed models lie in their applicability only to the Italian case, but similar models can be specified and calibrated in other territories with the same approach proposed in the paper; from a temporal point of view, the models can be re-calibrated with reference to years different from the one under study, just as they can be applied after the construction of new high-speed railway lines to check whether the predictions remain valid. This work can contribute to the evaluation of investments in high-speed rail transport systems at the regional and national levels.
The goals of this study are basically twofold: (i) to verify whether and to what extent the presence of high-speed services has a real impact on tourist attractiveness; (ii) to carry out this verification through quantitative methods (mathematical models, in our case) that also provide a numerical estimate of the corresponding impact.
The paper is articulated as follows:
Section 2 examines the background of the problem;
Section 3 describes the data; multiple linear regression models are specified and calibrated in
Section 4; an application to the city of Benevento is described in
Section 5; conclusions and research perspectives are summarised in
Section 6.
3. Data
Various data sources were used in this study. The main tourism data are taken from ISTAT (Italian Institute of Statistics) and quantify monthly arrivals and presences, classified by the origin and category of accommodation (hotel and non-hotel). These data were available at the regional, provincial, and municipal levels. Here, ‘arrivals’ correspond to the registration of customers in the accommodation facility, while ‘presences’ correspond to the total number of nights spent in a facility; therefore, in this study, the term ‘presence’ is equivalent to the term ‘overnight stay’; in the following, we use the term ‘presence’ to be congruent with the ISTAT terminology. In the development of this work, the data on tourist movements refer to 2018, so that they are not affected by the COVID-19 pandemic event.
Overall, in Italy, there were 128.1 million arrivals and 428.8 million presences, with an average stay of 3.35 nights. The regional data on arrivals and presences are reported in
Table 1, while
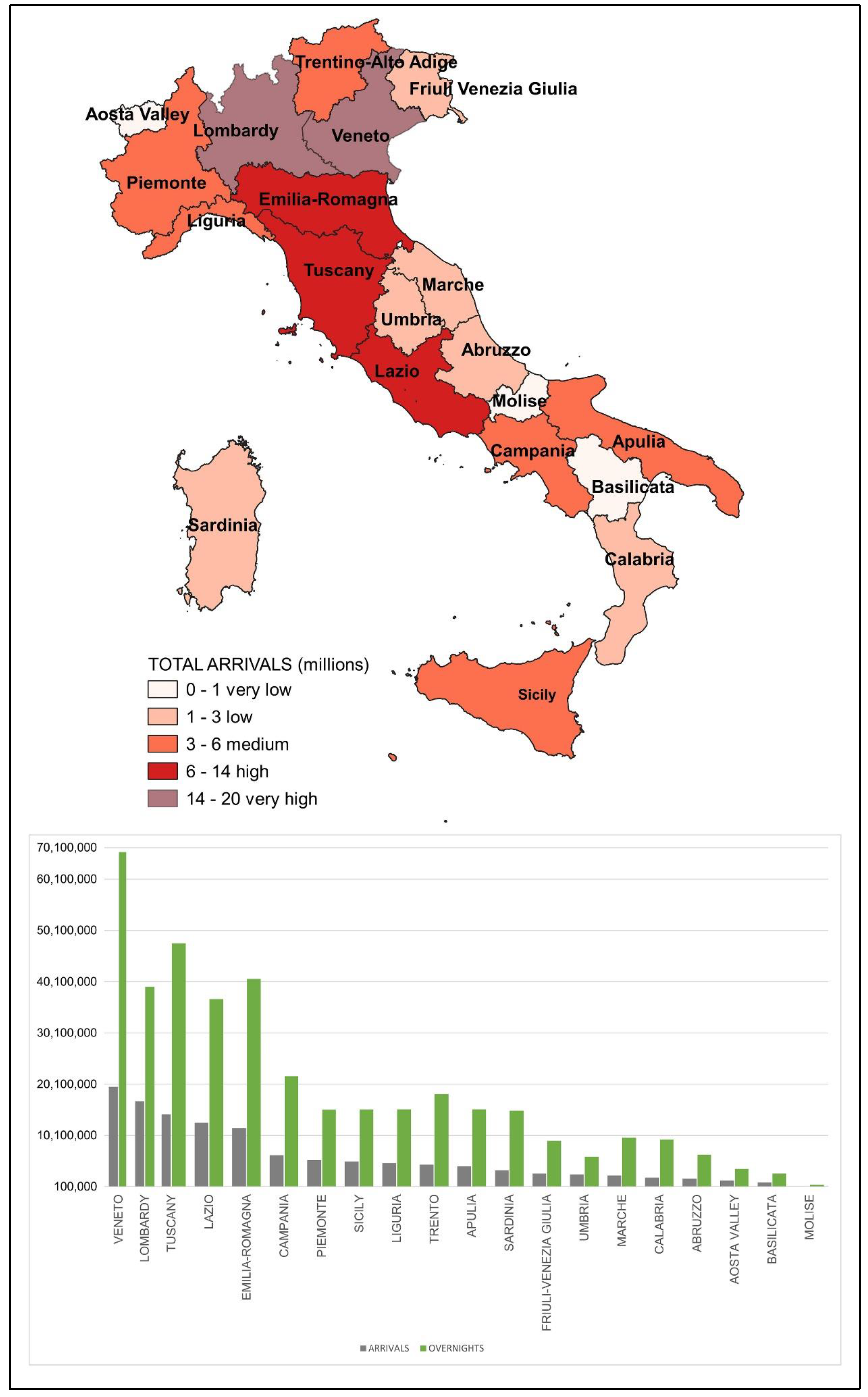
Table 2 shows the same data with reference to the provinces of the regional capitals. It can be seen that Veneto, Lombardy, Tuscany, and Lazio are the regions with the most arrivals, while the provinces with the most arrivals are Rome, Venice, Milan, and Florence, with an obvious correlation with the attractiveness of the capital cities.
On the other hand, the most attractive regions in terms of presence are Veneto, Trentino-Alto Adige, Tuscany, and Emilia-Romagna and the provinces Venice, Rome, Trento, and Milan. The difference between regional arrivals and presences, clearly linked to the average length of stay, is related to the type of holiday, often weekly, in Trentino-Alto Adige (mainly in winter periods) and Emilia-Romagna (mainly in summer periods).
Table 3 reports the data on arrivals and presences for the 111 Italian provincial capitals, on which the models have been specified and calibrated. The cities of Rome, Milan, and Venice have over 5 million arrivals and the same cities, with the addition of Florence, have over 10 million presences per year.
We underline that the data used does not allow, at this territorial scale, to distinguish tourist trips from those for other reasons (work, business, study, etc.) and does not include stays in holiday homes or those trips that do not include a stay in an accommodation facility (one-day tourist visits, stays with relatives or friends, etc.); despite all these limitations, we believe that these data are the best available for the analyses we wish to conduct.
On the supply side, the accommodation establishments (see
Table 4 and
Table 5) show the clear prevalence of Veneto and the Province of Venice, decidedly higher also than Lazio and the Province of Rome.
Data on supply have not been used as possible explanatory variables in our models, since there is a direct relationship between supply and demand (supply increases where there is more demand) that could invalidate the modelling analysis aimed at identifying the other variables that can influence tourist flows.
Once the dependent variables had been identified and the corresponding data collected, the possible explanatory (or independent) variables were examined; these variables are the factors that could influence the choice of a touristic destination. Five categories of variables have been identified:
- (a)
Variables related to the supply of historical/cultural assets:
- 1.
Number of state cultural sites [
55];
- 2.
Number of cultural heritage items [
56];
- 3.
Employees in libraries, archives, museums, and other cultural activities [
57];
- 4.
Consistency of historic urban fabric (elaboration on data) [
58].
- (b)
Variables related to the supply of entertainment/amusement activities:
- 1.
Employees in creative, artistic, and entertainment activities [
57];
- 2.
Employees in leisure and entertainment activities [
57].
- (c)
Variables related to the supply of commercial activities:
- 1.
Employees in retail trade (excluding motor vehicles and motorbikes) [
57].
- (d)
Accessibility variables:
- 1.
Number of direct runs on high-speed rail services (based on 2018 data);
- 2.
Distance from Leonardo da Vinci airport in Rome (main Italian hub);
- 3.
Distance from the nearest international airport;
- 4.
Population-weighted road accessibility;
- 5.
Total road travel time to all other possible destinations;
- 6.
Total road travel distance to all other possible destinations.
- (e)
Importance variables:
- 1.
Dummy variable (0/1) indicating the regional capital.
Not all variables refer to the same year. The most recent data on employees date back to the last census, which is carried out every ten years, but there are no better or more reliable statistical sources. On the other hand, the data on State places of culture and the stock of cultural assets, although referring to different years and before 2018, can be considered valid because the variation of these numbers over the years is negligible.
The following subsections describe the sources of the data and how they were obtained or derived.
3.1. Variables Related to the Supply of Historical/Cultural Assets
The number of cultural sites is a figure taken from [
55] and refers to fortified architecture, archaeological areas, historical monuments, monuments of industrial archaeology, funerary monuments, archives and libraries, churches and places of worship, villas and palaces, archaeological parks, museums and galleries, parks and gardens. Only those under state jurisdiction and management are considered, and therefore, this variable does not include all possible cultural goods. This variable is indicated as
scsi, where
i indicates the city.
The same source, but with reference to 2017 [
56], provides the total number of cultural assets, understood as architectural assets, archaeological assets, parks, and gardens. This variable is indicated with
tchi.
The data on employees in libraries, archives, museums, and other cultural activities are taken from the ISTAT census [
57]; clearly, the number of employees in this sector is assumed to be a proxy for the supply of the same type of activity to tourists. This variable is indicated with
musi.
The size of the historical urban fabric was estimated from ISTAT data [
58] by calculating the percentage of houses built before 1919. This variable is indicated with
huci.
The values of these variables for the provincial capitals are shown in
Table A1 in
Appendix A.
3.2. Variables Related to the Supply of Entertainment/Amusement Activities
The data on employees in creative, artistic, and entertainment activities and employees in recreational and leisure activities are taken from the ISTAT census [
57]. In addition, in this case, it is assumed that these data represent a proxy for the supply of this type of activity on the territory. The values for the provincial capitals are reported in
Table A2 in
Appendix A, and the variables are indicated, respectively, by
acei and
reei.
3.3. Variables Related to the Supply of Commercial Activities
The data on retail trade employees (excluding motor vehicles and motorbikes) are taken from the ISTAT census [
57] and are assumed to be a proxy for the commercial offer in the territory. The values for the Provincial capitals are reported in
Table A3 in
Appendix A. This variable is indicated with
reti.
3.4. Accessibility Variables
The tourist accessibility of a place, particularly a city, is determined by several factors depending on the infrastructures and transport services available. The data source or calculation methods for these variables are described below.
3.4.1. Number of Direct Runs on High-Speed Rail Services
This variable indicates the number of runs of Italian high-speed lines. The data refer to the number of runs of this type of service arriving/departing from the station of the municipality; for some municipalities, this value is zero, if not served by this type of service. This variable is indicated with hsri.
3.4.2. Distance from Rome’s Leonardo da Vinci Airport (Italy’s Main Hub)
The calculation of this variable, as well as all the following variables based on times or distances, required the construction of a graph of the national road network. This graph was implemented starting from the ‘OpenStreetMap’ database, correcting some connection errors and considering only the roads of the main network: all motorways; all primary roads with separated carriageways and their ramps; all main trunk roads (typically state roads and regional roads); some secondary roads necessary to ensure the full connection of the network.
Overall, this model represents 202,628 km of roads;
Table 6 reports the extension of the network, while
Figure 3 shows the overall graph. In addition to the length of the different road sections, which is necessary to calculate the distance between municipalities, it is also necessary to attribute a speed to each link, to calculate the corresponding travel time. In this work, we consider the use of the free-flow speeds sufficient, i.e., uncongested conditions, assuming the values reported in
Table 7.
With this model, the matrix of times and the matrix of distances between all the municipalities were generated; these matrices have a dimension of 8091 × 8091, being 8091 the Italian municipalities according to the 2011 ISTAT surveys. This matrix was simplified into a 111 × 8091 matrix, considering that the indicators were calculated only for the provincial capitals.
From this matrix, the variables in question were calculated as:
where:
3.4.3. Distance from the Nearest International Airport
This variable was calculated as:
where:
The international airports considered, those with the most traffic in each region, are listed in
Table 8.
3.4.4. Population-Weighted Road Accessibility Function Variable
For the calculation of this variable, the ‘gravity-based measures’ model proposed by Hansen [
59] was adopted. The general formulation of the model is as follows:
where:
Ai is the indicator measuring the accessibility of zone i;
Wjβ is a measure of the importance of zone j, based on activities, services, population, and so on;
β is a coefficient of the model;
f(ci,j, α) is an impedance function, based on generalised cost, distance, etc., between zone i and zone j.
We have calculated the accessibility indicator as:
where:
inhj is the number of inhabitants in the municipality j;
ti,j is the travel time in hours between municipality i and municipality j.
3.4.5. Total Travel Time by Road with All Other Possible Destinations
For each provincial capital,
i, we calculated the total travel time (h × 10
−3) from all other Italian municipalities and calculated the variable as the reciprocal, with the following formula:
3.4.6. Total Road Distance to All Other Possible Destinations
For each provincial capital,
i, we calculated the total travel distance (km × 10
−5) from all other Italian municipalities, based on the implemented graph, and calculated the variable as the reciprocal, with the following formula:
where
di,j is the distance between capital city
i and municipality
j.
3.5. Importance Variables
We consider a dummy variable indicating whether the city is a regional capital (1) or not (0). The values of these variables, indicated with
capi, are reported in
Table A5 in
Appendix A.
4. Regression Models
The impact and significance of the explanatory variables on the tourism phenomenon are assessed with multiple linear regression models. These models relate the dependent variables (in our case, presences and arrivals) to the explanatory variables (independent) that may affect them.
Linear regression models take the following general form:
where:
Y is the expected value of the dependent variable;
β0 is a coefficient of the model, which does not depend on the independent variables (intercept of the regression line);
βk are the coefficients of the model, which together with β0, have to be calibrated;
Xk are the independent variables.
Any model must be specified and calibrated. The specification phase consists of defining which of the independent variables can be included in the model; the calibration phase consists of finding the coefficient values that can best reproduce the observed values of the independent variables for that specification.
The observed data of the independent variables are denoted by
yi and ordered in a vector
y; the vector
y has as many elements as the number of municipalities on which we are going to calibrate the model (in our case, 111 municipalities). The values that the independent variables assume for each observation are also called ‘predictors’ and indicated with
xi,k, where
i represents the provincial capital and
k the independent variable; these values can be ordered in a matrix,
x, which has as many rows as the number of cities and as many columns as the number of independent variables plus one (coefficient
β0: the elements of the first column of the matrix are equal to 1). The coefficients
βk can be ordered in a vector
β that has as many elements as the number of coefficients. Finally, we need to add the vector of statistical errors,
ε, which has as many elements ε
i as the number of cities. With these notations, it is possible to write:
or, in matrix form:
This formula represents, in short, the relationship between the observed data, y, and the independent variables, x. The calibration of the model consists in searching for the vector of coefficients, β, that minimises the vector of statistical errors, ε; in the theoretical case in which all statistical errors are equal to 0, the model would perfectly reproduce all the observed data.
If we denote by
xi the
i-th row of the matrix
x, we can write:
whence:
The optimal values of the coefficients can be obtained using the generalised least squares method, which minimises the sum of squares of the statistical errors; the corresponding optimisation model can be written as follows:
The ability of a model to reproduce observed data, and thus its goodness, is measured by several indicators; one of them is the coefficient of determination,
R2, which is calculated as:
where
y^ is the average of the
yi values; this indicator measures the ability of the
yi variables to explain the model, and the closer its value to 1 (statistical errors equal to 0 and perfect reproducibility of the observed phenomenon), the greater the goodness of the model.
The coefficient of determination always increases (or at least does not decrease) as the number of explanatory variables increases. To avoid this problem, it is possible to use the adjusted coefficient of determination,
R2adj, which penalises the inclusion of variables that are not necessary to explain the phenomenon; this indicator is calculated as:
where
n is the number of observations and
p is the number of degrees of freedom (
df) in the model. Clearly, as the number of explanatory variables, i.e., degrees of freedom, increases, the value of
R2adj decreases with respect to the value of
R2, the more so as there are few observations. In our case, with 111 observed data, we do not expect a great difference between the two values, which, in any case, will be calculated to verify the goodness of the model.
The coefficient of determination cannot, however, be the unique indicator to evaluate the goodness of a model. Indeed, it does not always decrease (it usually increases) with the number of variables
k, even if some of them are not useful to explain the phenomenon. The other indicators that must be used to evaluate the model are the hypothesis tests that are able to measure whether the parameters adopted in the model are indeed significant to reproduce the phenomenon. In this study, we use the
F-test, obtained from the analysis of variance, and the
t-test, concerning the significance of each independent variable. We will assume that a model is acceptable if the significance
F is close to 0 (at least < 0.05) and if the
t-test of each coefficient
βk is higher [lower] than
t95 [−
t95] for positive [negative]
βk, where
t95 is the value of the
t-student distribution corresponding to the degrees of freedom (
df) of the model with 95% confidence. The degree of freedom of a model is equal to the number of independent variables
xk of the model. The values of
t95 for the different degrees of freedom (1 to 10) are reported in
Table 9.
The specification and calibration procedure used in this study is based on a trial-and-error approach, based on the values of the Pearson correlation coefficients between the dependent variable and one of the independent variables. The correlation coefficient is calculated as the ratio of the covariance between two variables,
σxy, and the product of the standard deviations,
σx and
σy:
This coefficient can assume values between −1 and 1; the higher the absolute value of the index, the more the two variables are correlated with each other, either positively or negatively, depending on the sign. The value of the correlation index indicates the possibility that the independent variable has a significant influence, within the model, on the dependent variable; therefore, in the trial-and-error procedure, variables with a higher absolute correlation index will be tested first, verifying if the sign is physically admissible. After a variable has been introduced, the model will be calibrated, and it will be checked whether the inserted variable is significant. If it is, the variable is kept in the model and another one is added; if it is not, another variable is tried. To be valid, a model must have all the independent variables significant, i.e., they must respect the minimum values of the indicator t-test, and a sign of the corresponding coefficient that has a physical meaning; among all the calibrated models that respect these conditions, those with the greatest coefficient of determination are preferable. This first phase leads to a model with all significant variables and with a coefficient of determination greater than all the other models tested; from this model, we try to introduce other variables and, then, to eliminate a variable and replace it with another, to test other possible combinations.
In
Table 10, we report the correlation coefficients of each explanatory variable with the independent variables in decreasing order of value.
All specified and calibrated models are summarised in
Table 11, for arrivals, and in
Table 12, for presences, where, for each model, the considered variables, the
R2 and
R2adj indicators, the significance
F, the model coefficients and, for each variable, the
t-test value, whose limit value is also reported, and the validity or not of the model are indicated.
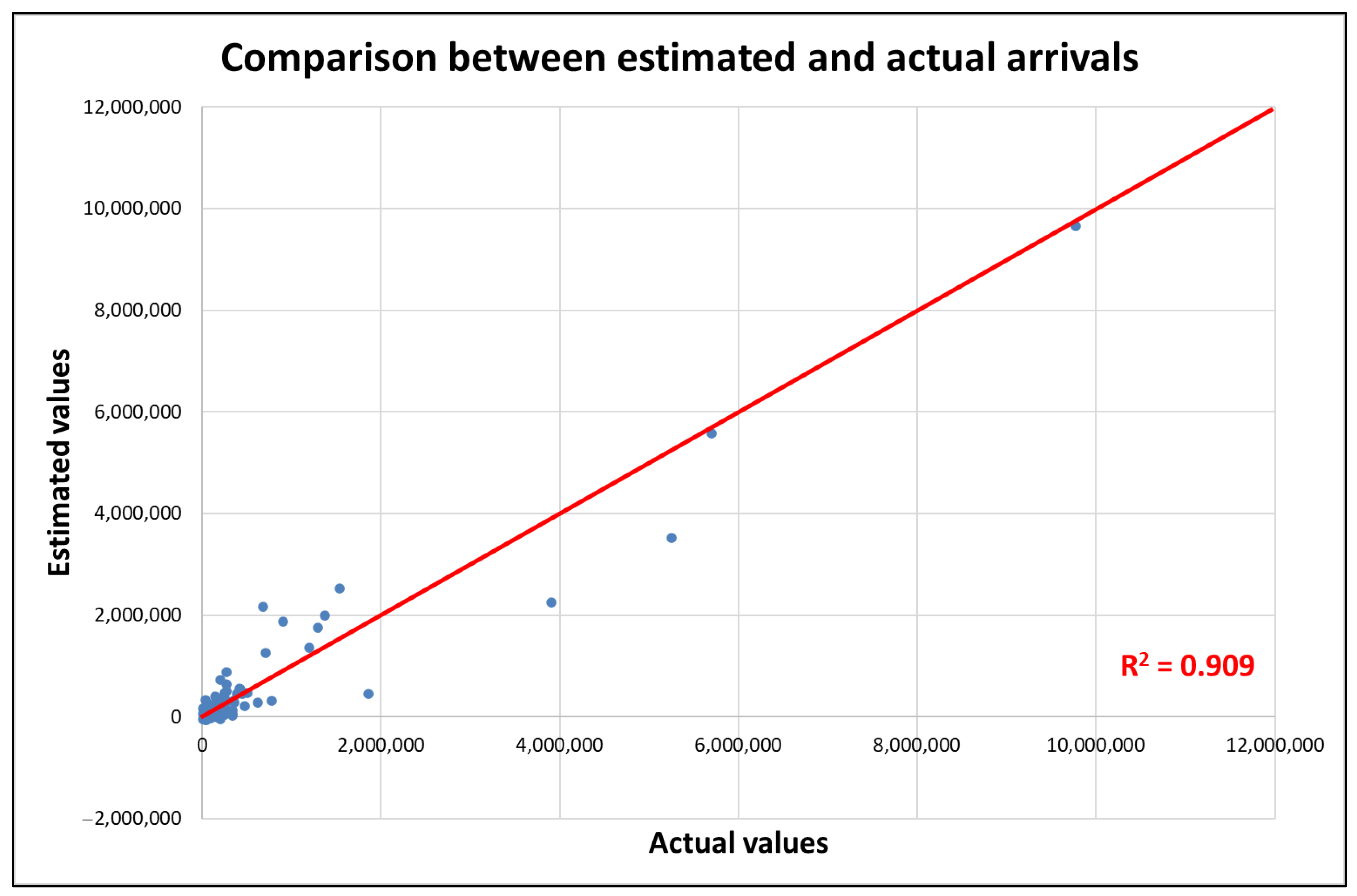
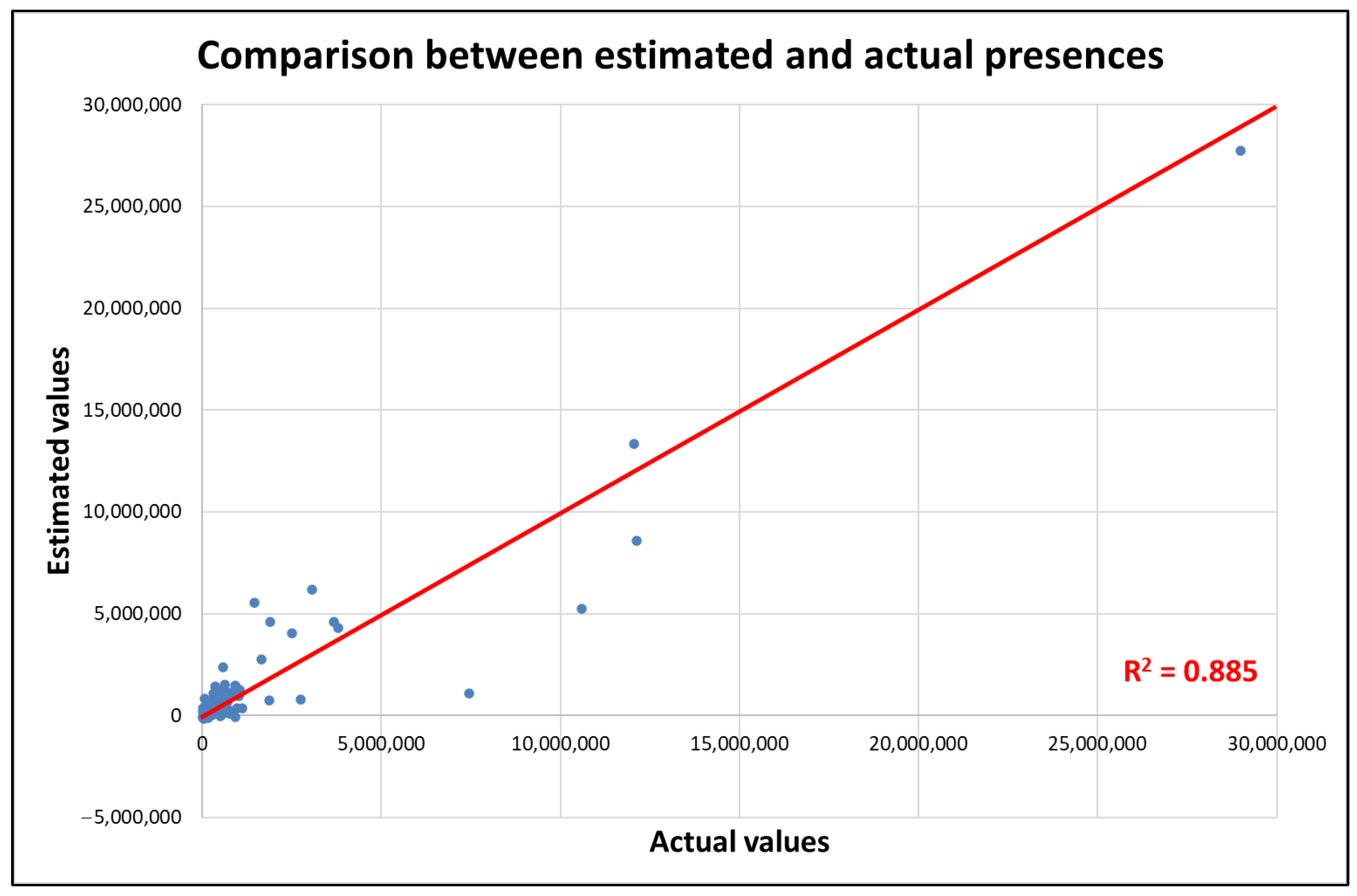
Overall, 18 models for estimating arrivals and 19 models for estimating presences were calibrated; of these models, five models for estimating arrivals and five models for estimating presences were valid in terms of significance and sign of the coefficients. At the end of the procedure, model no. 16 for estimating arrivals and model no. 18 for estimating presences were identified as the best. These models have the maximum values of R2 and R2adj, and comply with all the significance tests. The values of the coefficients of determination are sufficiently high in both cases (0.909 for arrivals and 0.885 for presences). It is important to note that in both models, the only accessibility variable found to be significant is the one related to high-speed rail services, hsri. The other accessibility variables were not statistically significant.
Figure 4 and
Figure 5 show the scatter diagrams comparing the actual and estimated values.
The best models are formulated as follows:
The analysis of these models highlights the following aspects:
- (a)
The intercept assumes a negative value. This property permits the models to be used only for overall evaluations of the entire set of municipalities (remember that, having used the generalised least squares method, the sum of the values estimated by the model for all the municipalities is equal to the sum of the true values). The application to a specific municipality could give implausible values, and for municipalities with less tourist importance, negative values.
- (b)
The variables linked to creative, artistic, and entertainment activities, total cultural assets, the presence of libraries, museums and other cultural activities, and direct rides on high-speed services always appear in both models. In the arrivals model, the variable related to commercial activities is also significant, while it is not statistically significant for presences. This indicates that commercial activities have a greater influence on shorter-duration trips than longer ones. In all cases, the variables closely linked to the tourist offer of the place of destination are significant.
- (c)
Among the accessibility variables, only the one representing high-speed rail services is statistically significant in estimating arrivals and presences. The other accessibility variables, at least for the provincial capitals, are not influential.
To evaluate the importance of high-speed services with respect to the other factors, a sensitivity analysis was carried out, increasing the overall values of each variable by 10% and evaluating the percentage increase in the number of arrivals and presences. The results are summarised in
Table 13 and
Table 14.
The analysis of these results leads to the following considerations:
High-speed rail services have an important impact on the flow of arrivals and presences in accommodation facilities. The elasticity is greater for arrivals, where an increase of +10% in supply can be estimated as a +3.27% increase in arrivals, while this value is reduced to +2.65% for presences. In both cases, the values are significant: for arrivals, the elasticity is second only to that linked to total cultural assets, while for presences, it is third, being also preceded by creative, artistic, and entertainment activities.
A comparison of the model’s elasticities between arrivals and presences shows that there is practically the same elasticity for the variable on total cultural heritage (+3.42% arrivals and +3.49% presences), highlighting how this explanatory variable has more or less the same effect on all stays, regardless of their duration. On the other hand, creative, artistic, and entertainment activities have a greater elasticity on arrivals than on presences, showing a tendency to influence shorter stays more.
Museums, libraries, and other cultural activities have practically the same elasticity, as total cultural heritage, on both arrivals and presences (+1.69% arrivals and +1.80% presences).
Commercial activities, as already mentioned, show an influence only on arrivals and, therefore, a greater influence on shorter stays.
From the calibration of these models and analyses, it can be concluded that the impact of high-speed rail services on tourism flows, as measured by arrivals and presences in accommodation establishments, is significant. For arrivals, the elasticity of the variable is high, of the same order of magnitude as for the total number of cultural assets. For presences, it is lower, but still very significant. Another fact to note is that, of all the accessibility variables considered, high-speed services are the only statistically significant.
5. An Application to a Case Study
The calibrated models were applied to a specific case study, the city of Benevento. Benevento is a small-medium-sized provincial capital with about 60,000 inhabitants (only 36 out of 111 provincial capitals have fewer residents than Benevento), but it has several important historical/archaeological sites, including the monumental complex of Santa Sofia, a UNESCO World Heritage Site, the Arch of Trajan, the Roman Theatre and the Rocca dei Rettori, as well as several museums and churches of great value. The accessibility of the city, however, is not as good as the artistic and historical heritage: the railway connections with the regional capital (Naples) are not efficient and have a modest frequency, while Trenitalia’s Frecce services connect the city on the Rome-Bari route, for a total of only 28 runs, as the sum of those arriving and departing.
Currently (2018 data, pre-COVID), annual arrivals in accommodation amount to 36,252 (on average, 99 per day), while presences stand at 80,144 (on average, 220 per day), with an accommodation supply of 57 establishments for a total of 1039 beds; therefore, there are about 35 arrivals and 77 presences per bed; for comparison, the city of Naples has about 87 arrivals and 232 presences per bed.
A new HS railway line is currently under construction, which will serve a Naples-Benevento-Bari route, with a maximum line speed of 250 km/h. As it is under construction, the frequency of services has not yet been established, but it can be assumed that the service will be organised on 12 pairs of daily runs, increasing the service to a total of 40 daily runs, as the sum of arriving and departing runs.
Assuming the same elasticity as estimated in
Section 4, the new services would increase the current services by 42.8% and, therefore, could lead to an increase, other factors unchanged, of 15.8% in arrivals (+5728) and 11.3% in presences (+9056), increasing the overall annual occupancy rate from 21.1% to 23.5%.
These results further underline how high-speed railway lines can have a significant impact on tourist attractiveness.