Soft Computing Approach for Predicting the Effects of Waste Rubber–Bitumen Interaction Phenomena on the Viscosity of Rubberized Bitumen
Abstract
1. Introduction
2. Principle of Genetic Programming
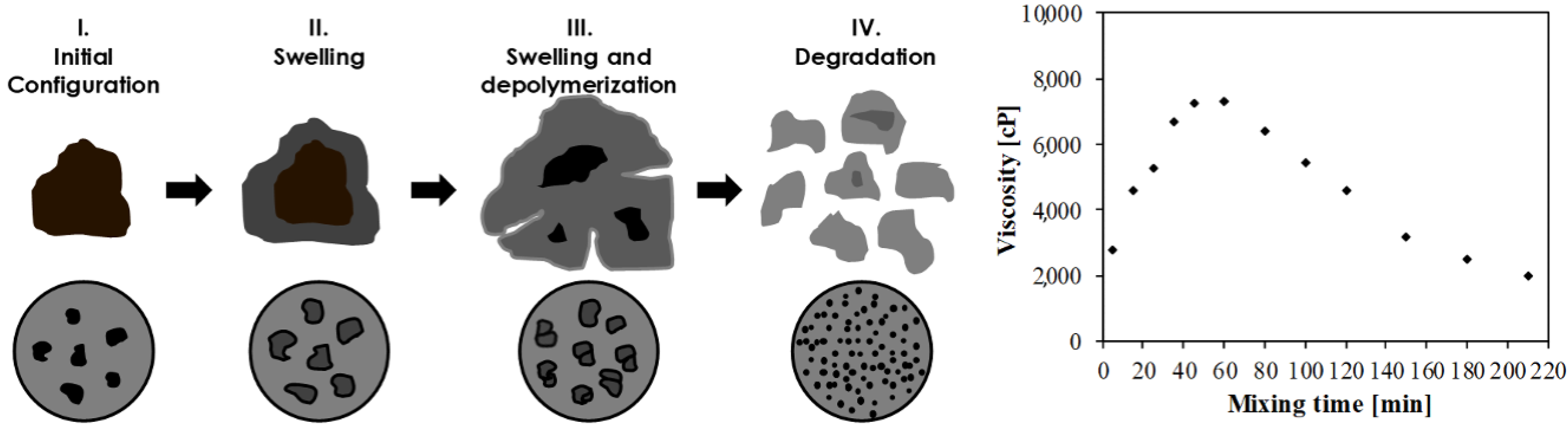
3. Materials and Methods
4. Development of the Predictive Model
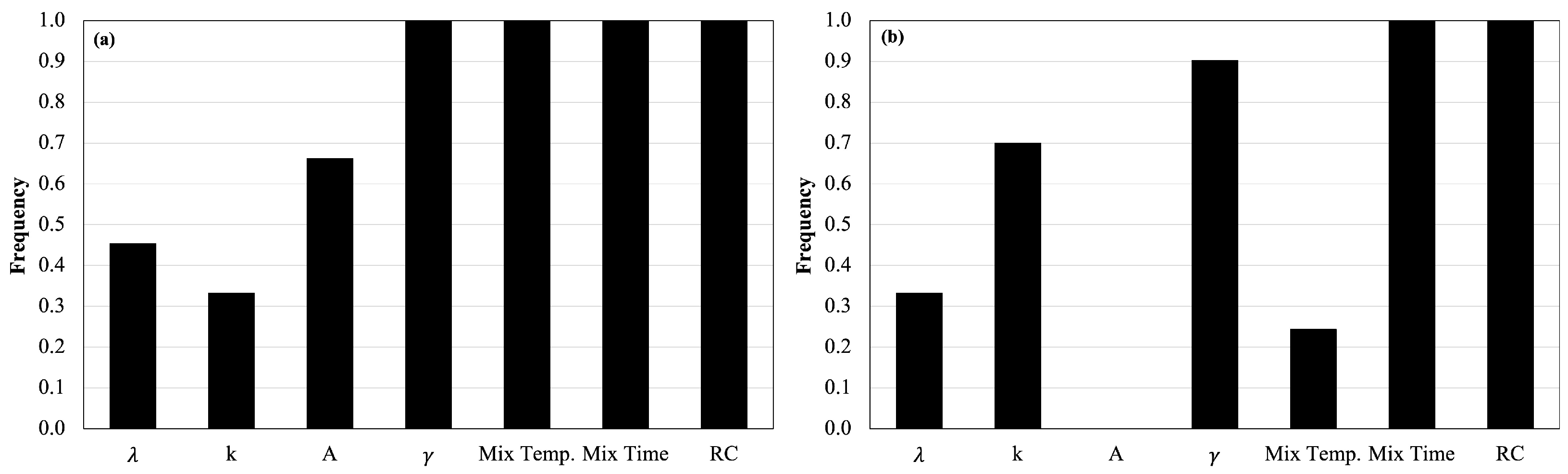
4.1. Phase I: Preliminary Analyses with MGGP and MLSR Approaches
- Set 1: Weibull parameter , density (, g/cm), mixing temperature (T, C), mixing time (t, min), and rubber content (RC, %),
- Set 2: Weibull parameter k, density, mixing temperature, mixing time, and rubber content,
- Set 3: Surface area (SA, mm), density, mixing temperature, mixing time, and rubber content,
- Set 4: Weibull parameter k, mixing temperature, mixing time, and rubber content.
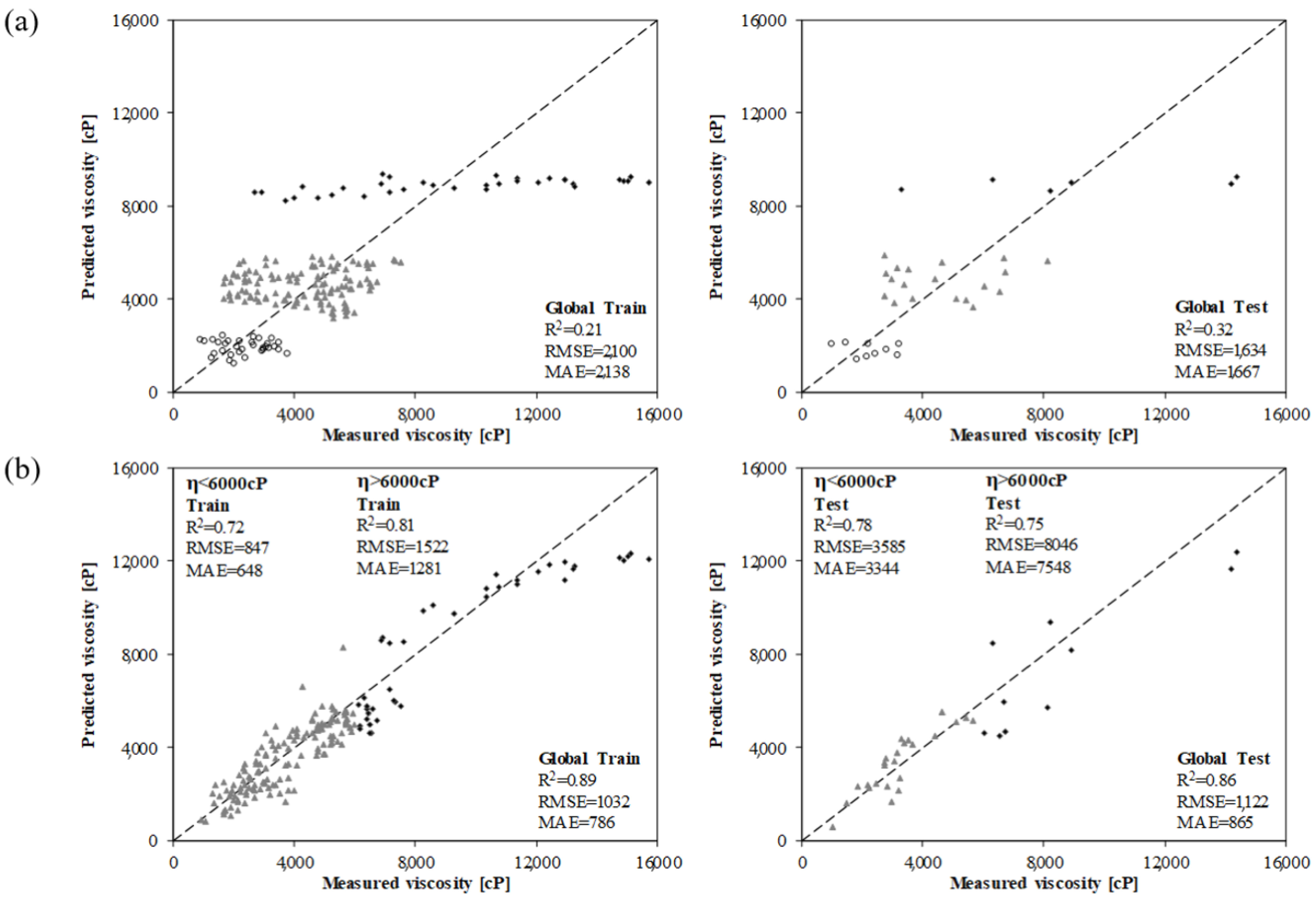
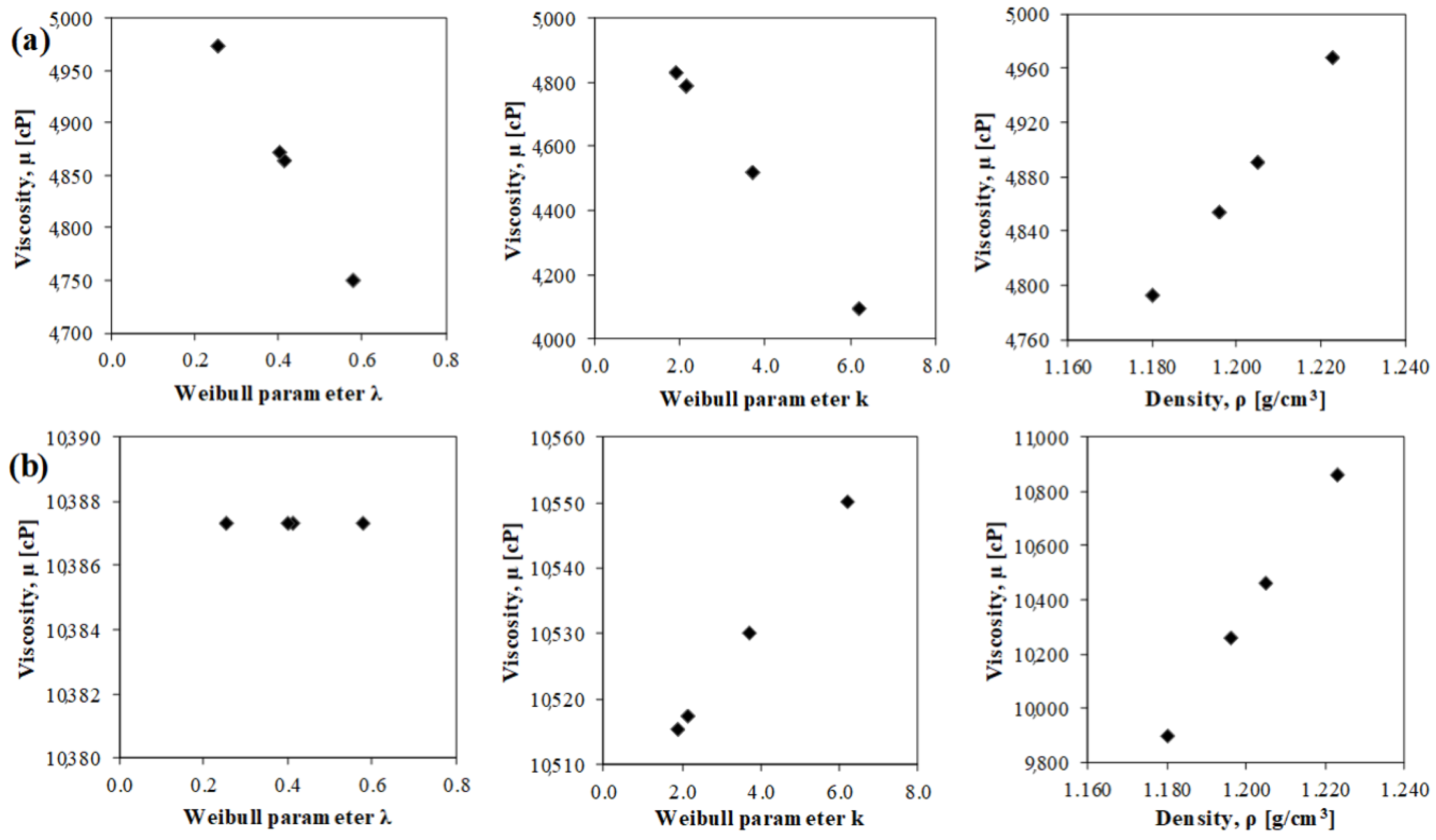
4.2. Phase II: Refined MGGP Model
4.3. Predictive Models and Performance Analysis
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiang, L.; Cheng, J.; Que, G. Microstructure and performance of crumb rubber modified asphalt. Constr. Build. Mater. 2009, 23, 3586–3590. [Google Scholar] [CrossRef]
- Lee, S.J.; Akisetty, C.K.; Amirkhanian, S.N. The effect of crumb rubber modifier (CRM) on the performance properties of rubberized binders in HMA pavements. Constr. Build. Mater. 2008, 22, 1368–1376. [Google Scholar] [CrossRef]
- Lee, S.J.; Akisetty, C.K.; Amirkhanian, S.N. Recycling of laboratory-prepared long-term aged binders containing crumb rubber modifier. Constr. Build. Mater. 2008, 22, 1906–1913. [Google Scholar] [CrossRef]
- Chiu, C.T.; Lu, L.C. A laboratory study on stone matrix asphalt using ground tire rubber. Constr. Build. Mater. 2007, 21, 1027–1033. [Google Scholar] [CrossRef]
- Navarro, F.J.; Partal, P.; Martínez-Boza, F.; Gallegos, C. Thermo-rheological behaviour and storage stability of ground tire rubber-modified bitumens. Fuel 2004, 83, 2041–2049. [Google Scholar] [CrossRef]
- Shatnawi, S. Performance of Asphalt Rubber Mixes in California. Int. J. Pavement Eng. 2001, 2, 1–16. [Google Scholar] [CrossRef]
- Bahia, H.; Davies, R. Effect of Crumb Rubber Modifiers (CRM) in Performance-Related Properties of Asphalt Binders. Asph. Paving Technol. 1994, 63, 414–438. [Google Scholar]
- Yang, X.; Yiu, Z.; Perram, D.; Hand, D.; Zeyad, H.; Wei, W.; Luo, S. Emission analysis of recycled tire rubber modified asphalt in hot and warm mix conditions. J. Hazard. Mater. 2019, 365. [Google Scholar] [CrossRef]
- Farina, A.; Zanetti, M.C.; Santagata, E.; Blengini, G.A. Life cycle assessment applied to bituminous mixtures containing recycled materials: Crumb rubber and reclaimed asphalt pavement. Resour. Conserv. Recycl. 2017, 117, 204–212. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Carpenter, S. Mechanism of interaction of asphalt cement with crumb rubber modifier. Transp. Res. Rec. J. Transp. Res. Board 1999, 1661, 106–113. [Google Scholar] [CrossRef]
- Peralta, J.; Silva, H.M.R.D.; Hilliou, L.; MacHado, A.V.; Pais, J.; Christopher Williams, R. Mutual changes in bitumen and rubber related to the production of asphalt rubber binders. Constr. Build. Mater. 2012, 36, 557–565. [Google Scholar] [CrossRef]
- Artamendi, I.; Khalid, H.A. Diffusion Kinetics of Bitumen into Waste Tyre Rubber (with Discussion). J. Assoc. Asph. Paving Technol. 2006, 75, 133–164. [Google Scholar]
- Lo Presti, D.; Airey, G.D.; Partal, P. Manufacturing Terminal and Field Bitumen-Tyre Rubber Blends: The Importance of Processing Conditions. Procedia—Soc. Behav. Sci. 2012, 53, 485–494. [Google Scholar] [CrossRef]
- Lanotte, M.A. Evaluation of the Interaction between Bitumen and Crumb Rubber from ELTs in Modified Binders Produced by “Wet” Technology. Doctoral Dissertation, Politecnico di Torino, Torino, Italy, 2014. (In Italian). [Google Scholar]
- Santagata, E.; Dalmazzo, D.; Lanotte, M.; Zanetti, M.C.; Ruffino, B. Relationship between Crumb Rubber Morphology and Asphalt Rubber Viscosity. In Proceedings of the 5th Asphalt Rubber International Conference, Munich, Germany, 23–26 October 2012; pp. 513–532. [Google Scholar]
- Shen, J.; Amirkhanian, S.; Xiao, F.; Tang, B. Surface area of crumb rubber modifier and its influence on high-temperature viscosity of CRM binders. Int. J. Pavement Eng. 2009, 10, 375–381. [Google Scholar] [CrossRef]
- Cook, D. IBISWorld Industry Report OD5022—Tire & Rubber Recycling in the US; Technical Report September 2018; IBISWorld Publisher: Melburne, Australia, 2018. [Google Scholar]
- Ecopneus Scpa. Sustainability Report 2017; Technical Report; Ecopneus Scpa: Milano, Italy, 2017. [Google Scholar]
- Xiao, F.; Putman, B.; Amirkhanian, S. Viscosity prediction of CRM binders using artificial neural network approach. Int. J. Pavement Eng. 2011, 12, 485–495. [Google Scholar] [CrossRef]
- Specht, L.P.; Khatchatourian, O.; Brito, L.; Ceratti, J. Modeling of Asphalt-rubber Rotational Viscosity by Statistical Analysis and Neural Networks. Mater. Res. 2007, 10, 69–74. [Google Scholar] [CrossRef]
- Thodesen, C.; Xiao, F.; Amirkhanian, S.N. Modeling viscosity behavior of crumb rubber modified binders. Constr. Build. Mater. 2009, 23, 3053–3062. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Liu, Q.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to non-linear system modeling. Part II: Geotechnical and earthquake engineering problems. Neural Comput. Appl. 2012, 21, 189–201. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to nonlinear system modeling. Part I: Materials and structural engineering problems. Neural Comput. Appl. 2012, 21, 171–187. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; p. 819. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Searson, D.P.; Leahy, D.E.; Willis, M.J. GPTIPS: An Open Source Genetic Programming Toolbox for Multigene Symbolic Regression. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010; Volume I, pp. 77–80. [Google Scholar]
- Smith, G.N. Probability and Statistics in Civil Engineering. Collins Prof. Tech. Books 1986, 244, 10007808566. [Google Scholar]

| Parameter | Settings |
|---|---|
| Function set | |
| Population size | 600 |
| Number of generations | 100 |
| Maximum number of genes allowed in an individual | 8 |
| Maximum tree depth | 8 |
| Tournament size | 25 |
| Elitism | 0.01% of population |
| Crossover events | 0.85 |
| High-level crossover | 0.2 |
| Low-level crossover | 0.8 |
| Mutation events | 0.1 |
| Sub-tree mutation | 0.9 |
| Replacing input terminal with another random terminal | 0.05 |
| Gaussian perturbation of randomly selected constant | 0.05 |
| Direct reproduction | 0.05 |
| Ephemeral random constants | [−10 10] |
| Parameter | k | SA | T | t | RC | |||
|---|---|---|---|---|---|---|---|---|
| [mm] | [g/cm] | [C] | [min] | [%] | [cP] | |||
| Mean | 0.409 | 3.46 | 225 | 1.201 | 177.2 | 86.1 | 18.5 | 4883 |
| Median | 0.402 | 2.17 | 221 | 1.196 | 190.0 | 70.0 | 18.5 | 4295 |
| Maximum | 0.580 | 6.21 | 386 | 1.223 | 190.0 | 210.0 | 22.0 | 15,715 |
| Minimum | 0.254 | 1.91 | 113 | 1.180 | 150.0 | 5.0 | 15.0 | 945 |
| Std.Dev. | 0.114 | 1.69 | 102 | 0.016 | 16.21 | 65.8 | 2.13 | 3057 |
| Skewness | 0.156 | 0.72 | 0.67 | 0.084 | −0.744 | 0.524 | 0.004 | 1.619 |
| Kurtosis | 2.054 | 1.97 | 1.97 | 1.808 | 1.928 | 1.984 | 2.707 | 5.632 |
| Sum | 90.7 | 767 | 49,951 | 266.7 | 39,340 | 19,110 | 4100 | 1.1 |
| Sq.Dev. | 2.894 | 627 | 2.30 | 0.055 | 58,068 | 9.5 | 1004 | 2.1 |
| Observations | 222 | 222 | 222 | 222 | 222 | 222 | 222 | 222 |
| Parameter | k | SA | T | t | RC | |||
|---|---|---|---|---|---|---|---|---|
| [mm] | [g/cm] | [C] | [min] | [%] | [cP] | |||
| Mean | 0.413 | 3.430 | 219.0 | 1.202 | 173.9 | 92.3 | 17.8 | 3544 |
| Median | 0.413 | 3.726 | 171.0 | 1.205 | 190.0 | 80.0 | 18.5 | 3300 |
| Maximum | 0.580 | 6.213 | 386.0 | 1.223 | 190.0 | 210.0 | 22.0 | 5975 |
| Minimum | 0.254 | 1.908 | 113.0 | 1.180 | 150.0 | 5.0 | 15.0 | 945 |
| Std.Dev. | 0.107 | 1.613 | 95.5 | 0.017 | 17.63 | 70.4 | 1.88 | 1372 |
| Skewness | 0.156 | 0.778 | 0.839 | 0.032 | −0.392 | 0.37 | −0.13 | 0.123 |
| Kurtosis | 2.359 | 2.165 | 2.387 | 1.628 | 1.408 | 1.68 | 2.84 | 1.825 |
| Sum | 68.82 | 524.2 | 33,502 | 183.8 | 26,610 | 14,120 | 2715 | 5.4 |
| Sq.Dev. | 1.730 | 395.3 | 1.4 | 0.042 | 4.7 | 7.5 | 537.5 | 2.9 |
| Observations | 153 | 153 | 153 | 153 | 153 | 153 | 153 | 153 |
| Parameter | k | SA | T | t | RC | |||
|---|---|---|---|---|---|---|---|---|
| [mm] | [g/cm] | [C] | [min] | [%] | [cP] | |||
| Mean | 0.393 | 3.230 | 232.5 | 1.200 | 186.9 | 65.3 | 20.9 | 9549 |
| Median | 0.402 | 2.167 | 221.0 | 1.196 | 190.0 | 60.0 | 22.0 | 8245 |
| Maximum | 0.580 | 6.213 | 386.0 | 1.223 | 190.0 | 150.0 | 22.0 | 15,715 |
| Minimum | 0.254 | 1.908 | 113.0 | 1.180 | 170.0 | 5.0 | 18.5 | 6025 |
| Std.Dev. | 0.108 | 1.580 | 100.5 | 0.016 | 7.331 | 41.8 | 1.64 | 3219 |
| Skewness | 0.250 | 0.988 | 0.612 | 0.184 | −1.90 | 0.34 | −0.82 | 0.533 |
| Kurtosis | 2.357 | 2.558 | 1.932 | 1.711 | 4.613 | 2.19 | 1.67 | 1.792 |
| Sum | 17.87 | 145.5 | 10,461 | 54.01 | 8410 | 2940 | 941 | 4.2 |
| Sq.Dev. | 1.730 | 395.3 | 1.4 | 0.042 | 4.7 | 7.5 | 537.5 | 2.9 |
| Observations | 45 | 45 | 45 | 45 | 45 | 45 | 45 | 45 |
| Set 1: , , T, t, RC | ||||
|---|---|---|---|---|
| RMSE | MAE | |||
| > 6000 cP | Train | 0.89 | 443 | 359 |
| Test | 0.88 | 543 | 475 | |
| < 6000 cP | Train | 0.95 | 641 | 531 |
| Test | 0.88 | 1071 | 903 | |
| Set 2: SA, , T, t, RC | ||||
| RMSE | MAE | |||
| > 6000 cP | Train | 0.89 | 437 | 353 |
| Test | 0.88 | 534 | 458 | |
| < 6000 cP | Not found | |||
| Set 3: k, , T, t, RC | ||||
| RMSE | MAE | |||
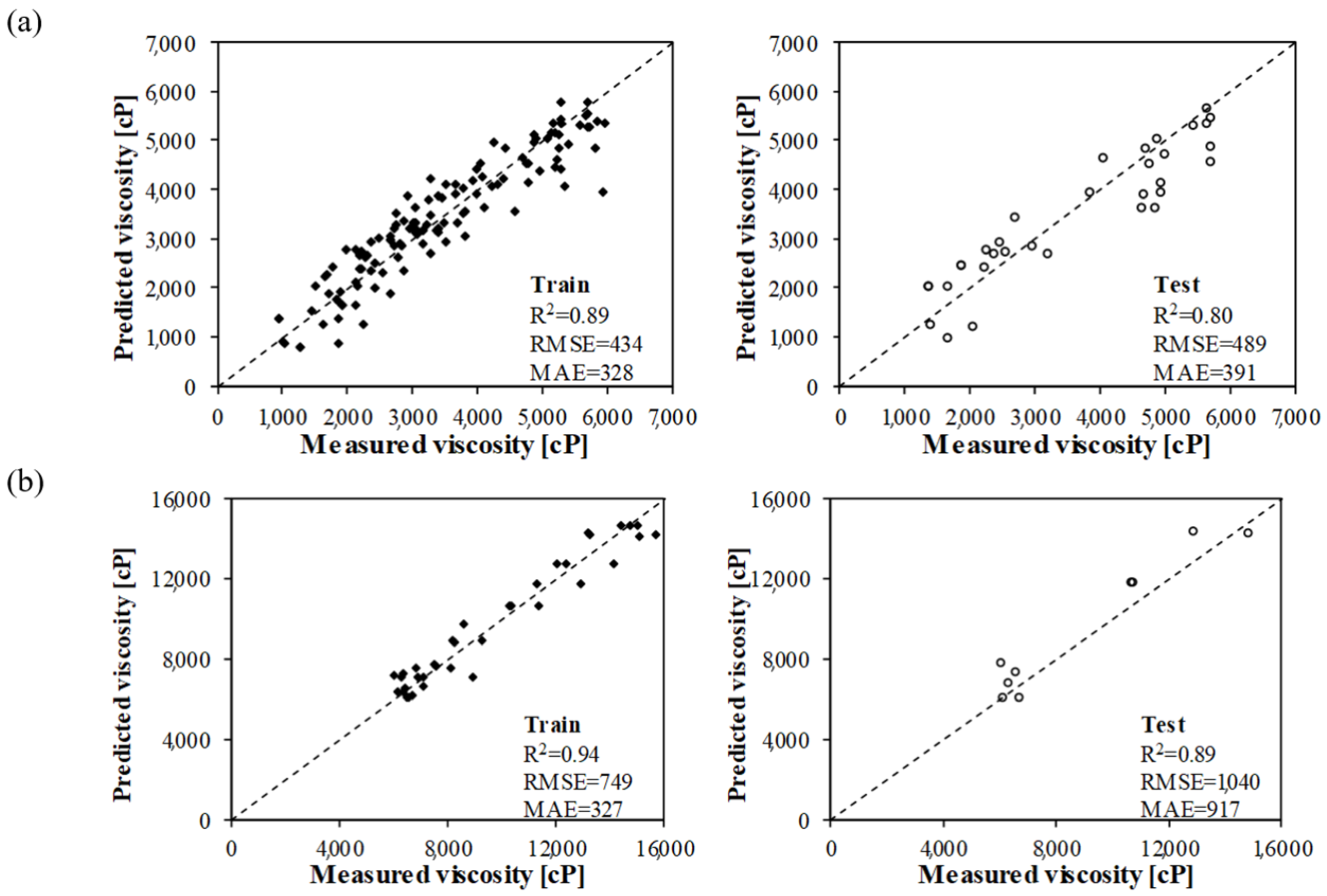
| > 6000 cP | Train | 0.89 | 434 | 328 |
| Test | 0.88 | 486 | 391 | |
| < 6000 cP | Train | 0.95 | 678 | 582 |
| Test | 0.88 | 1118 | 990 | |
| Set 4: k, T, t, RC | ||||
| RMSE | MAE | |||
| > 6000 cP | Train | 0.86 | 490 | 386 |
| Test | 0.85 | 604 | 518 | |
| < 6000 cP | Train | 0.94 | 749 | 327 |
| Test | 0.89 | 1040 | 917 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lanotte, M. Soft Computing Approach for Predicting the Effects of Waste Rubber–Bitumen Interaction Phenomena on the Viscosity of Rubberized Bitumen. Sustainability 2022, 14, 13798. https://doi.org/10.3390/su142113798
Lanotte M. Soft Computing Approach for Predicting the Effects of Waste Rubber–Bitumen Interaction Phenomena on the Viscosity of Rubberized Bitumen. Sustainability. 2022; 14(21):13798. https://doi.org/10.3390/su142113798
Chicago/Turabian StyleLanotte, Michele. 2022. "Soft Computing Approach for Predicting the Effects of Waste Rubber–Bitumen Interaction Phenomena on the Viscosity of Rubberized Bitumen" Sustainability 14, no. 21: 13798. https://doi.org/10.3390/su142113798
APA StyleLanotte, M. (2022). Soft Computing Approach for Predicting the Effects of Waste Rubber–Bitumen Interaction Phenomena on the Viscosity of Rubberized Bitumen. Sustainability, 14(21), 13798. https://doi.org/10.3390/su142113798





