Optimal Power Dispatch of DGs in Radial and Mesh AC Grids: A Hybrid Solution Methodology between the Salps Swarm Algorithm and Successive Approximation Power Flow Method
Abstract
1. Introduction
1.1. General Context
1.2. State of the Art
1.3. Scope and Main Contributions
- A new solution methodology for solving the AC OPF problem based on a master–slave strategy by considering the reduction of power loss as objective function and all sets of constraints that make up the operation of a AC grid under a distributed generation environmental.
- An OPF solution approach that solves different distribution network topologies (radial and meshed) and improves recent literature reports based on combinatorial optimization algorithms such as continuous genetic algorithm, Multi-Verse Optimizer, black hole optimization, particle swarm optimization, and ant lion optimization.
- The implementation of a global parameter-tuning optimization algorithm to guarantee the same conditions for each technique being employed in terms of solution quality, repeatability, and processing times.
1.4. Structure of the Paper
2. Mathematical Formulation
2.1. Objective Function
2.2. Set of Constraints
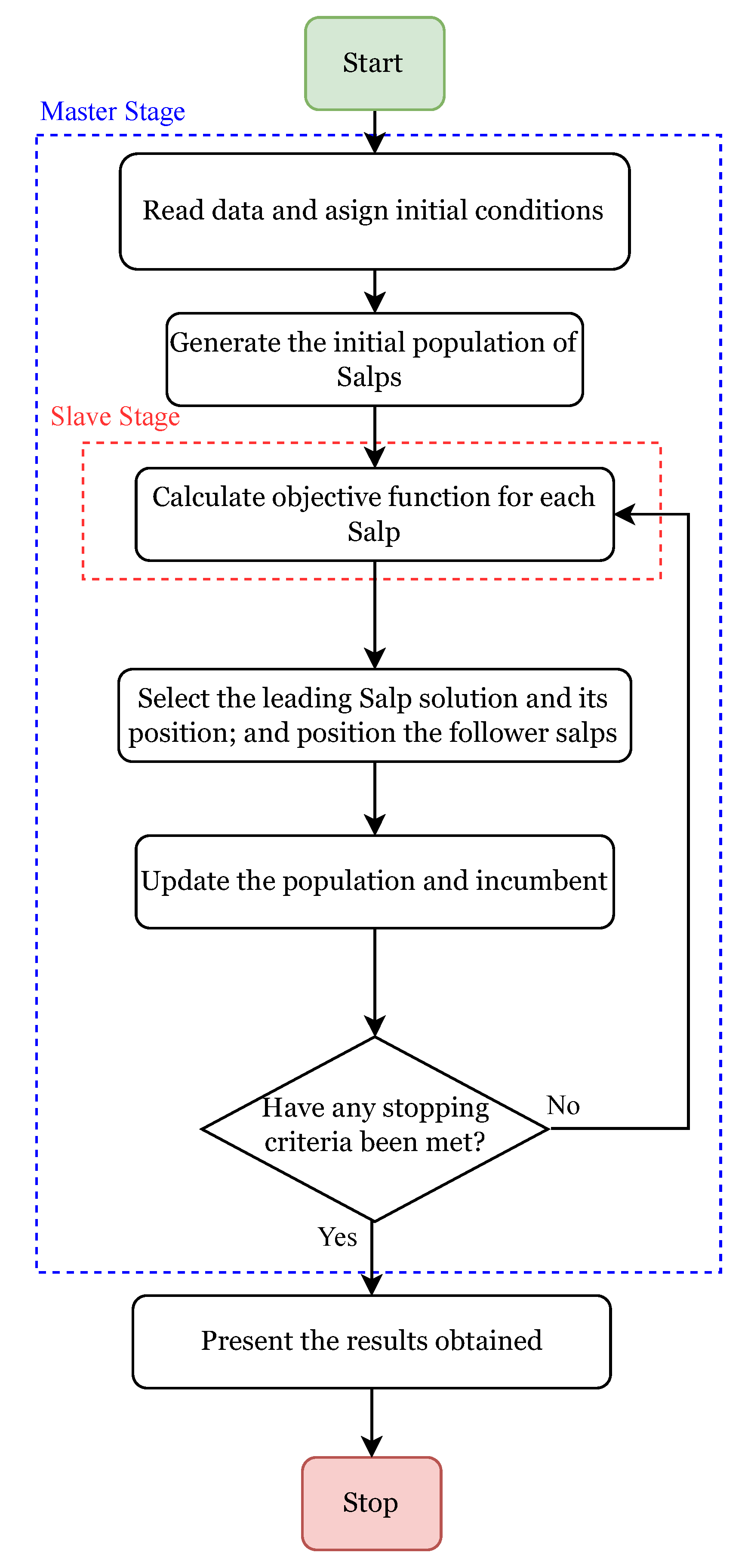
3. Proposed Solution Methodology
3.1. Master Stage: Salp Swarm Algorithm (SSA)
Generating the Initial Population
3.2. Slave Stage
4. Optimization Algorithms Employed for Comparison and Parameters
5. Test Scenarios and Considerations
5.1. Radial Test Systems
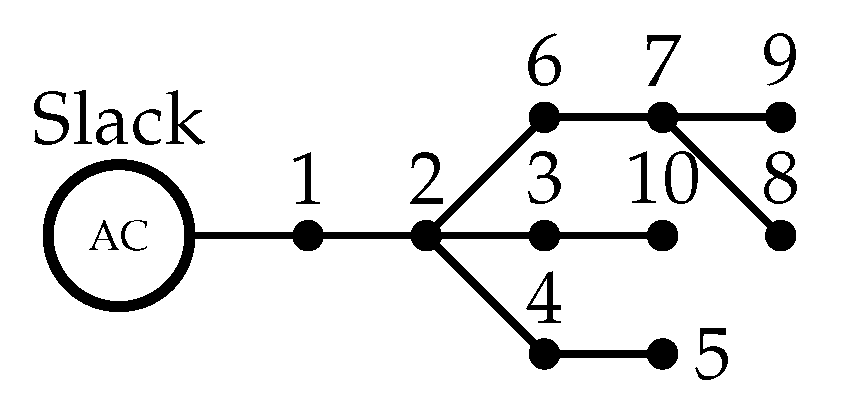
5.1.1. 10-Node Radial Test System
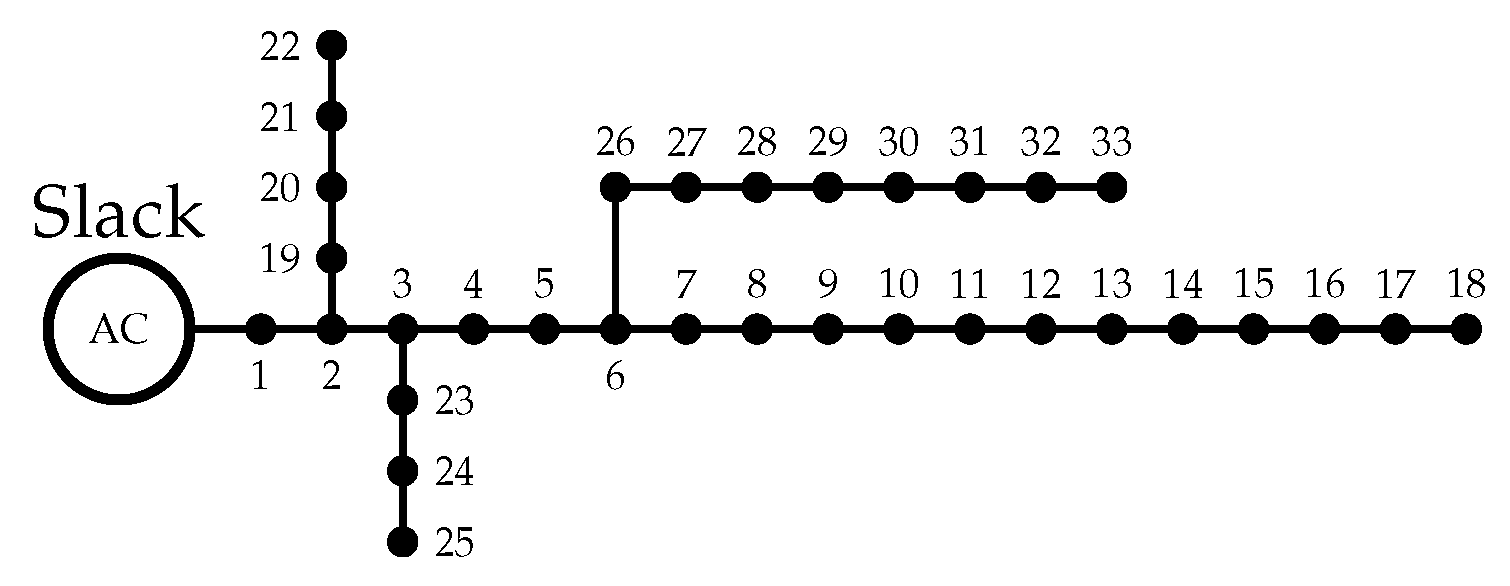
5.1.2. 33-Node Radial Test System
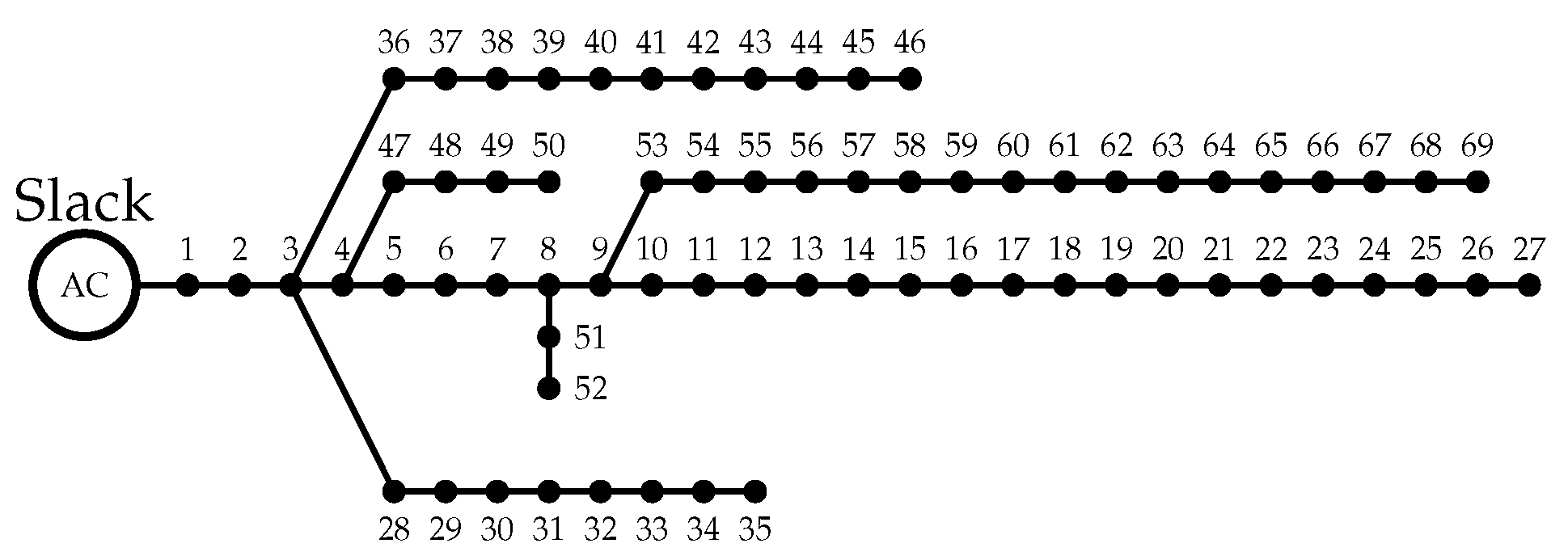
5.1.3. 69-Node Radial Test System
5.2. Mesh Test System
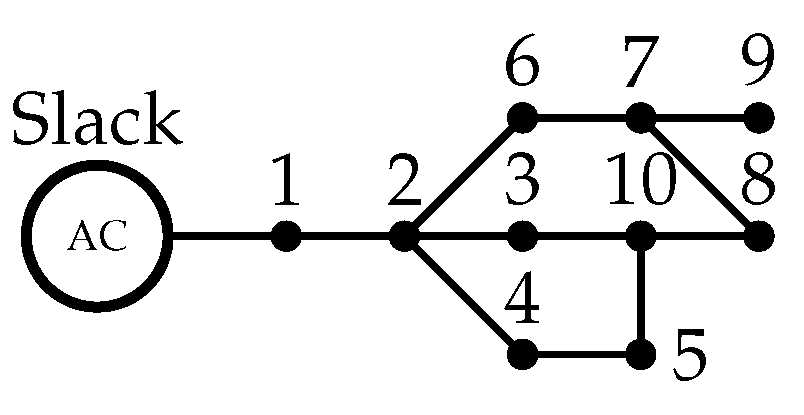
10-Node Mesh Test System
6. Simulations and Results
6.1. Radial Test Systems
6.1.1. 10-Node Radial Test System
6.1.2. 33-Node Radial Test System
6.1.3. 69-Node Radial Test System
6.2. Mesh Test Systems
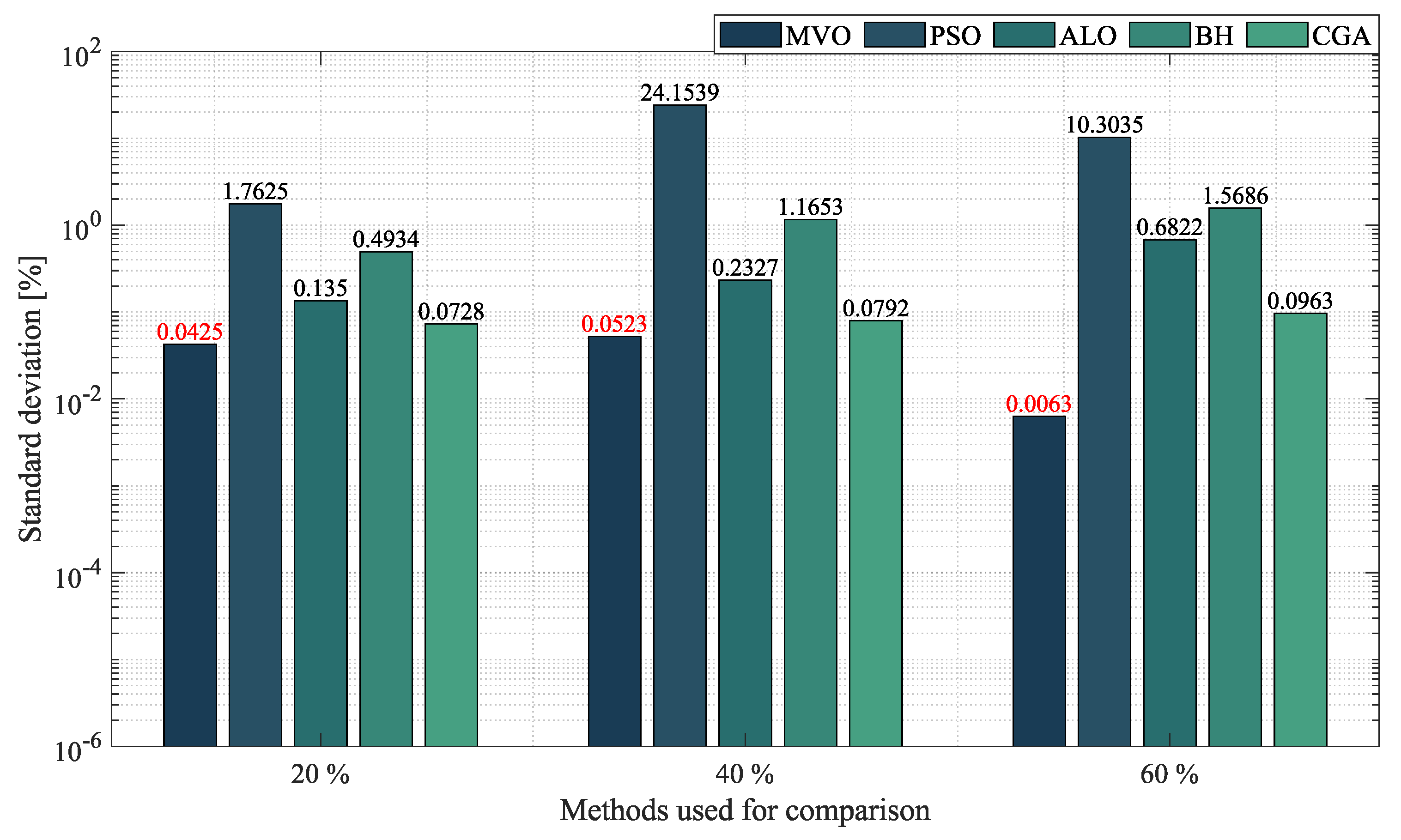
10-Node Mesh Test System
7. Conclusions
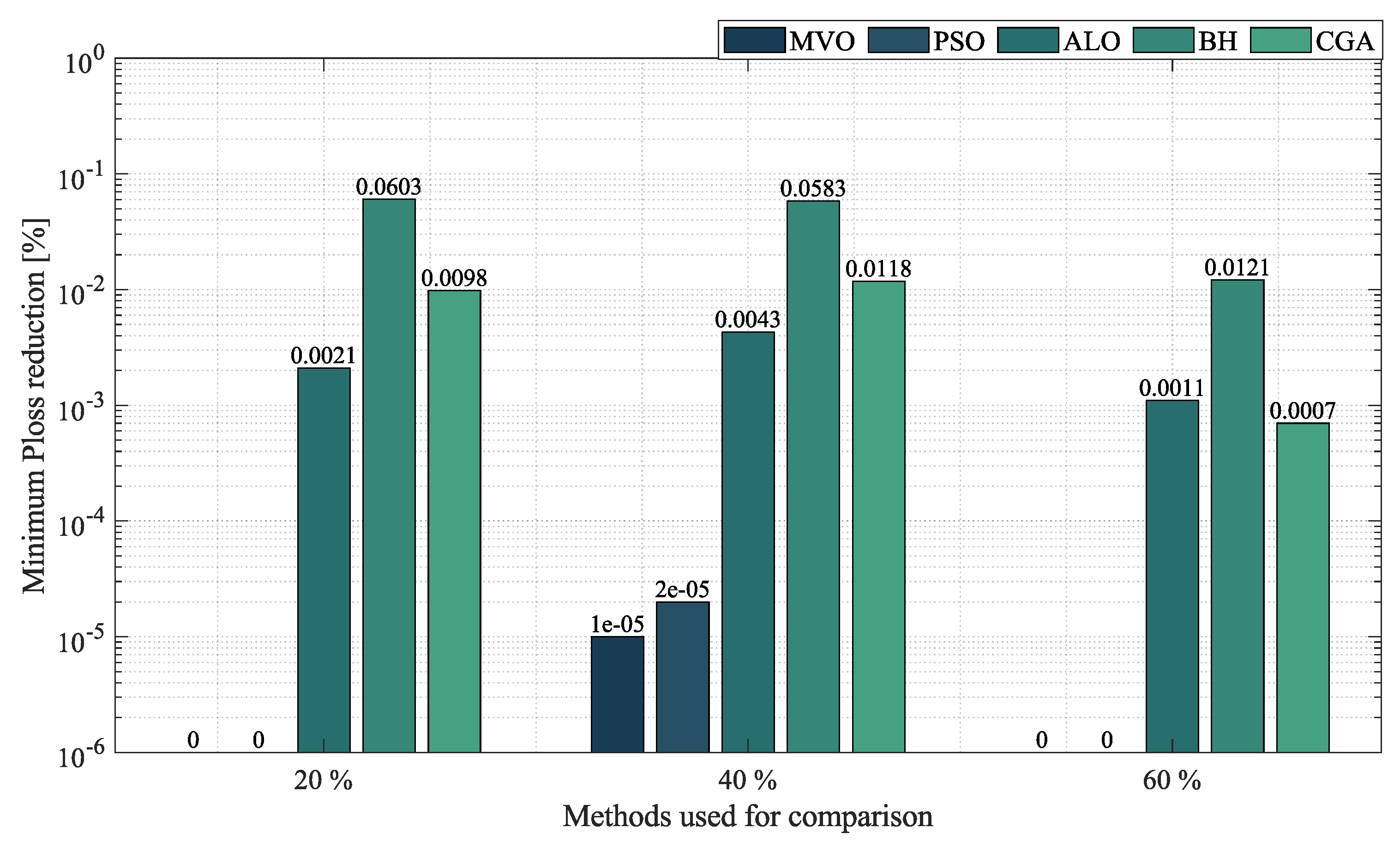
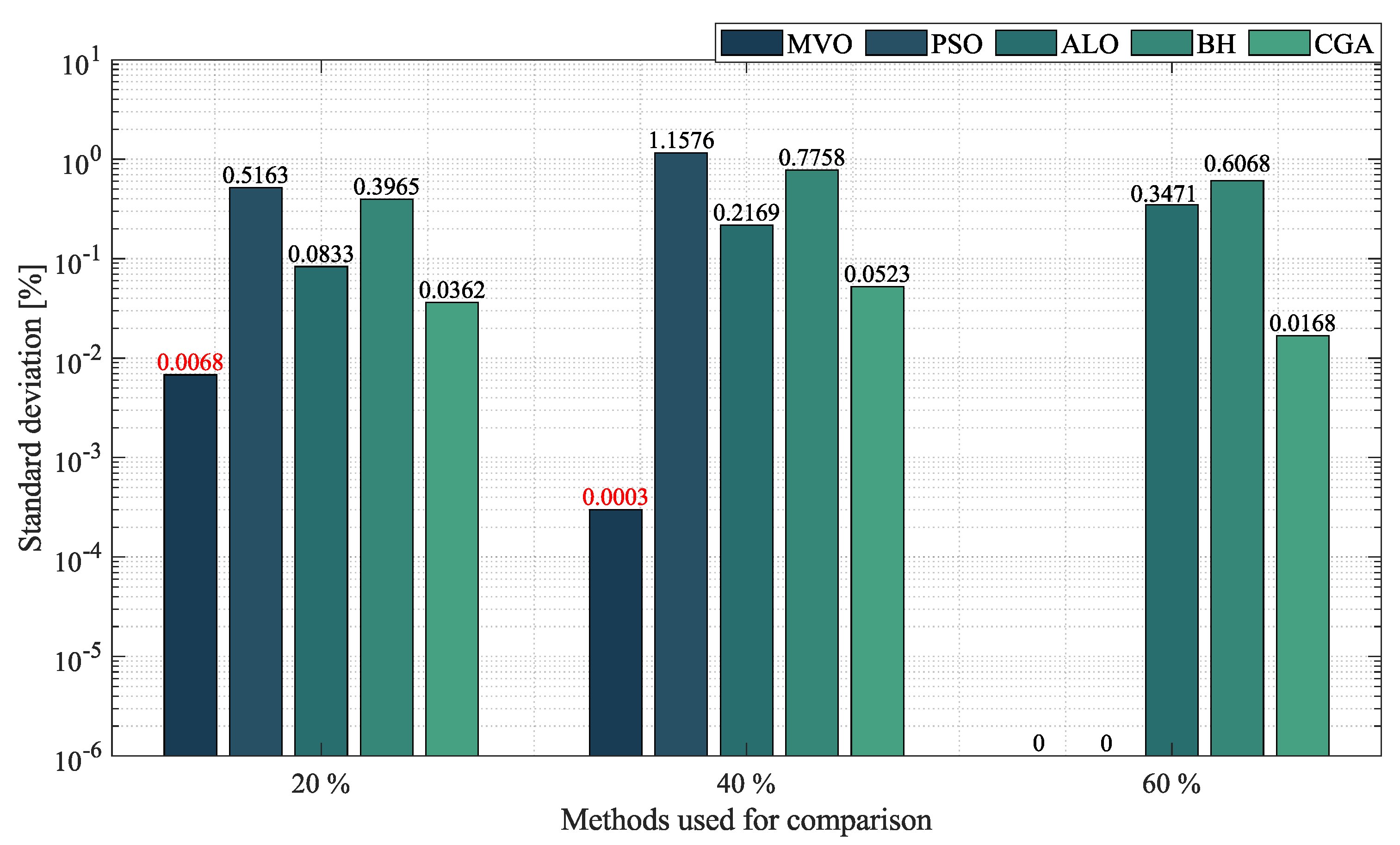
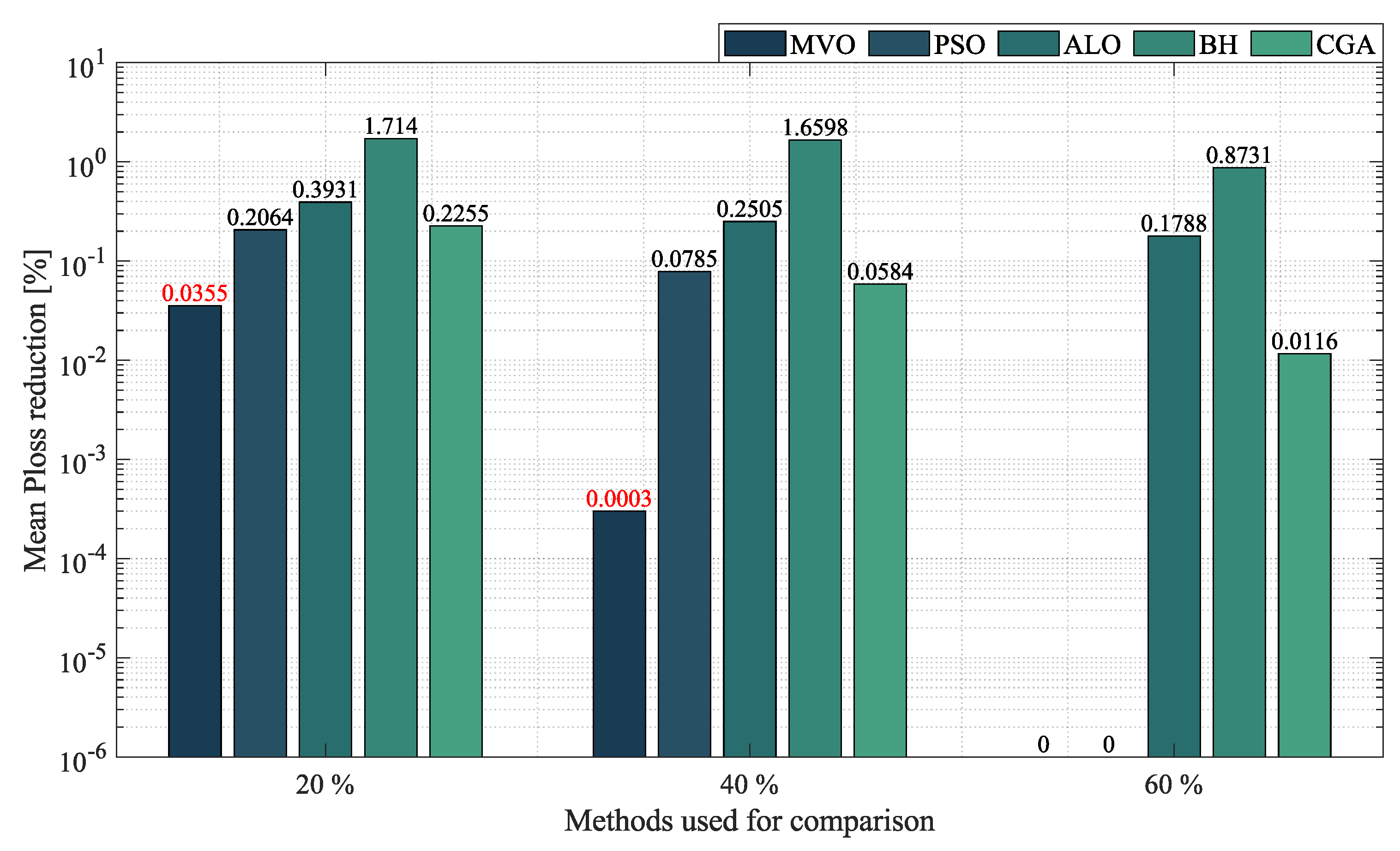
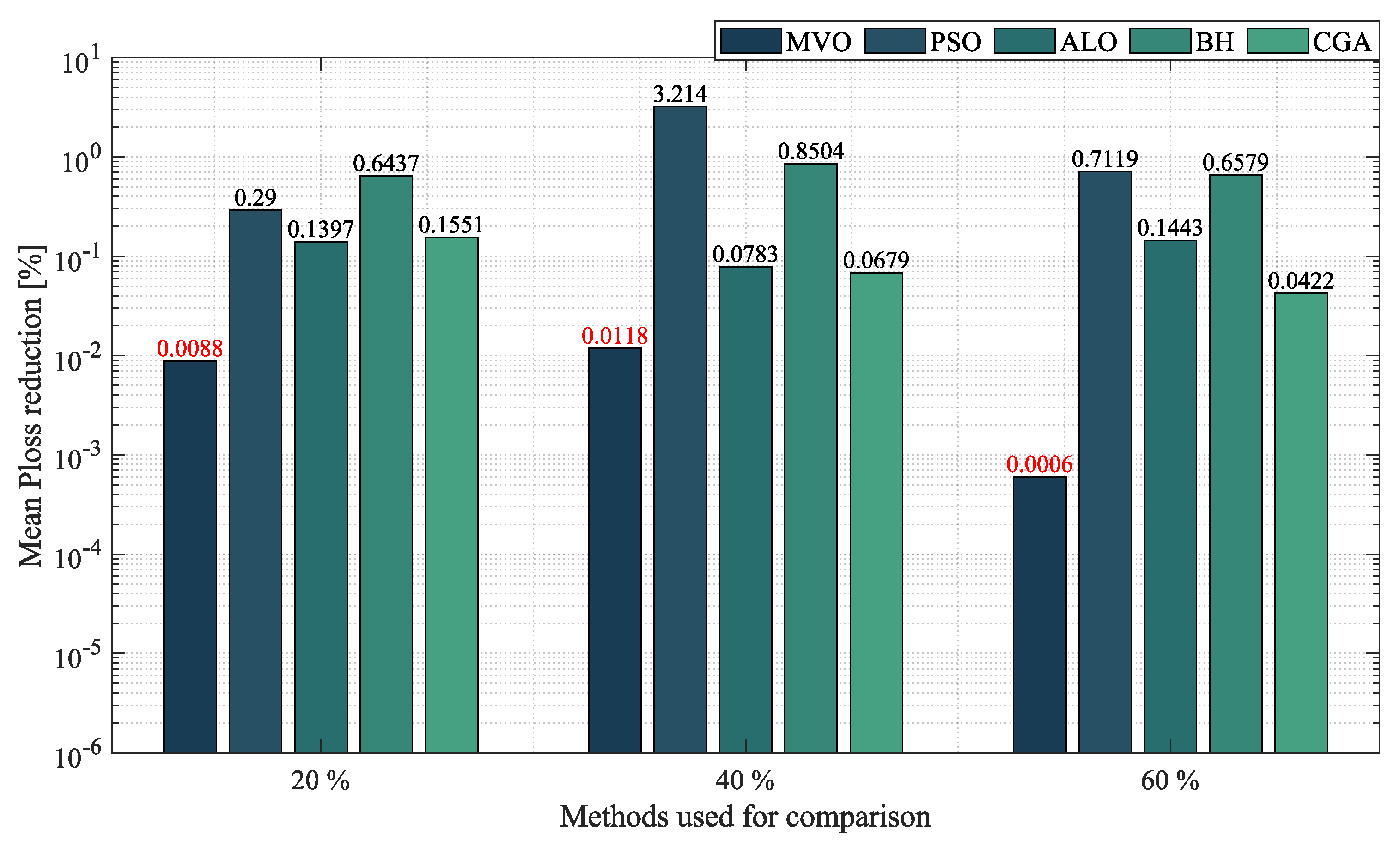
- In the case of radial networks, the SSA proved to be superior in terms of minimum reduction, as it outperformed the other optimization algorithms by an average percentage of , , and in the 10-, 33- and 69-node radial test systems, respectively. It produced such good results in short processing times and with low standard deviations: an average processing time of s, s, and s in the 10-, 33- and 69-node radial test systems, respectively, and an average STD of at the three penetration levels of distributed generation (, and ). This demonstrates the superiority and convergence capacity of the SSA, which is why we may conclude that it is the most suitable optimization algorithm to solve the OPF problem in radial networks of any size.
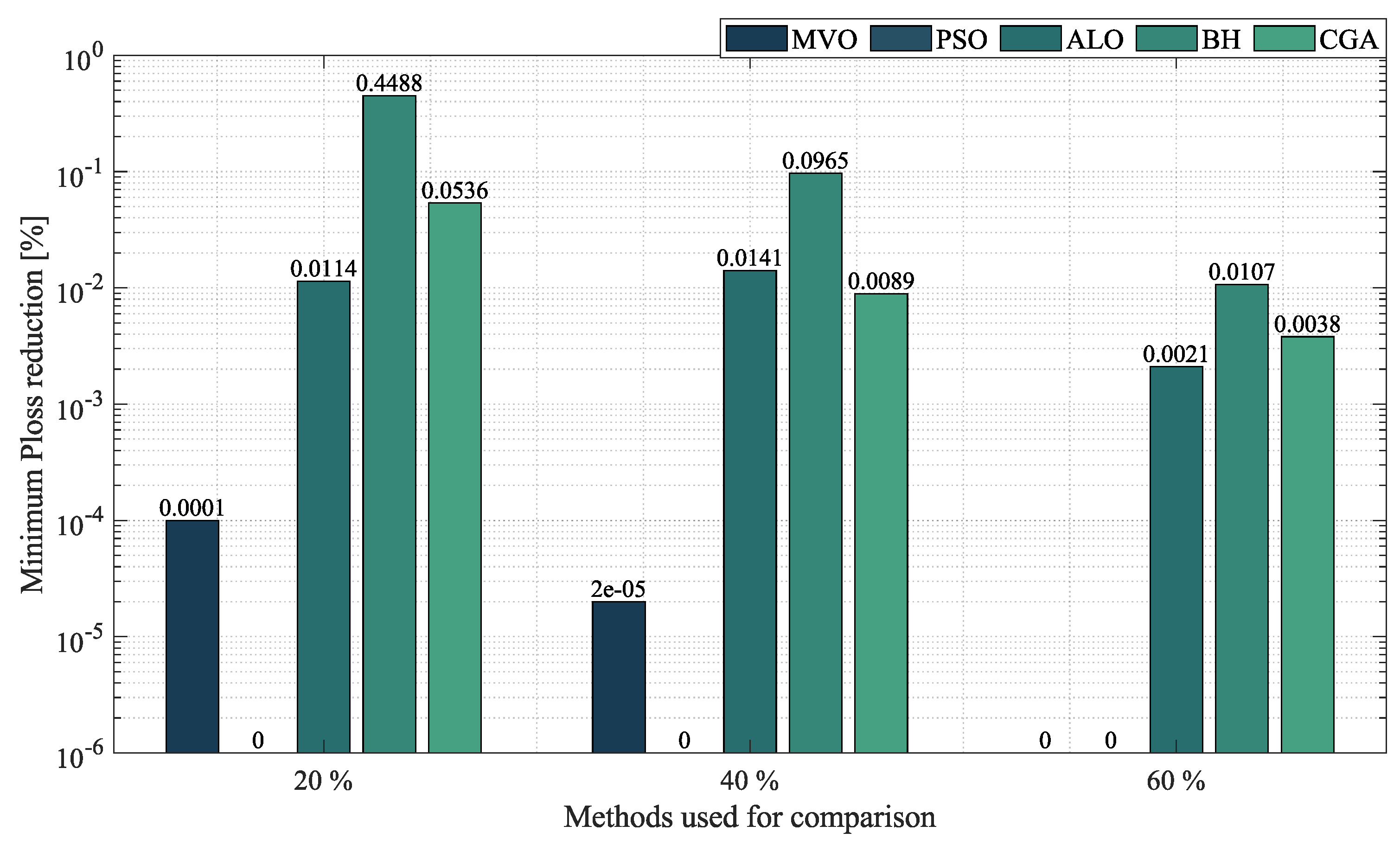
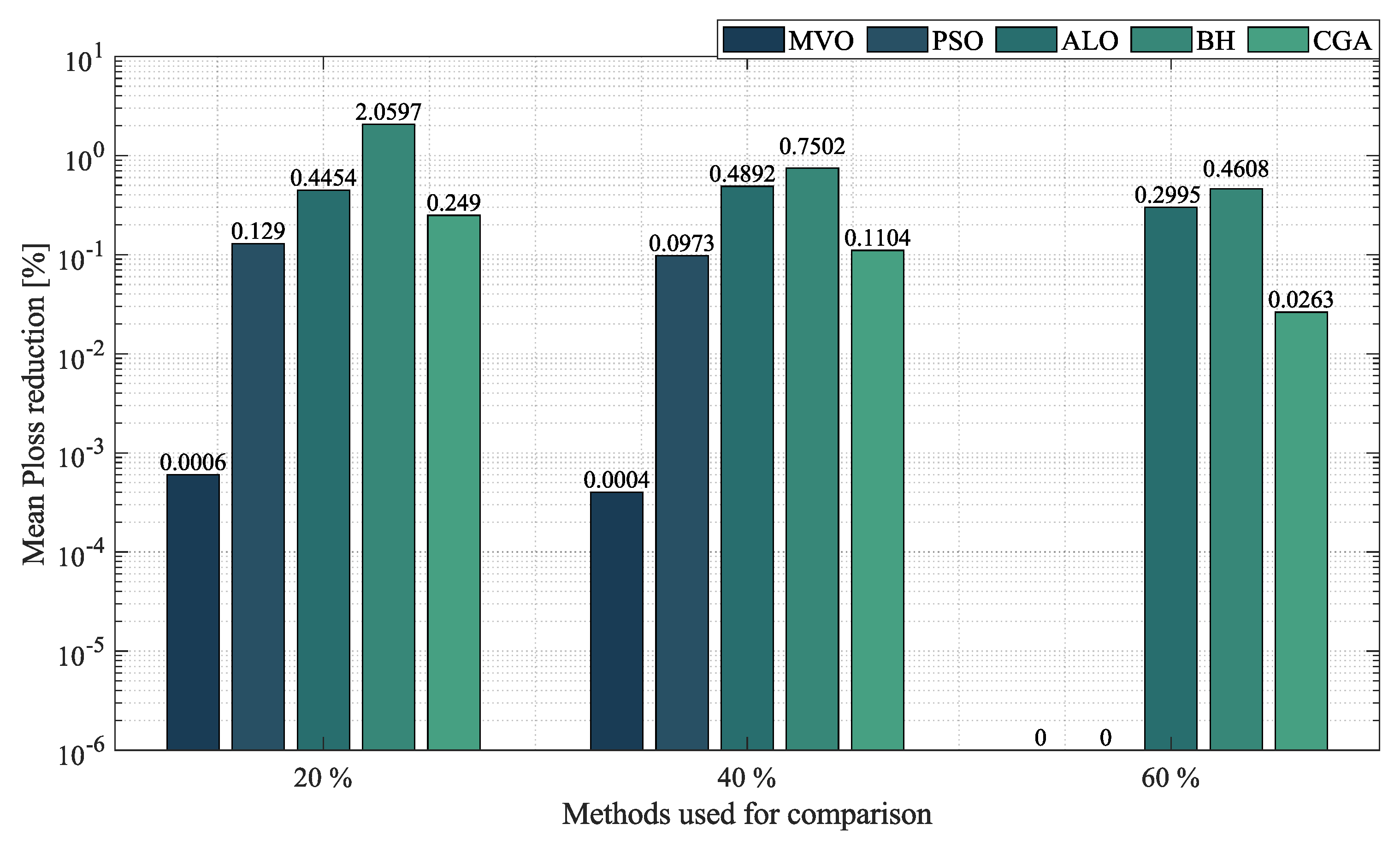
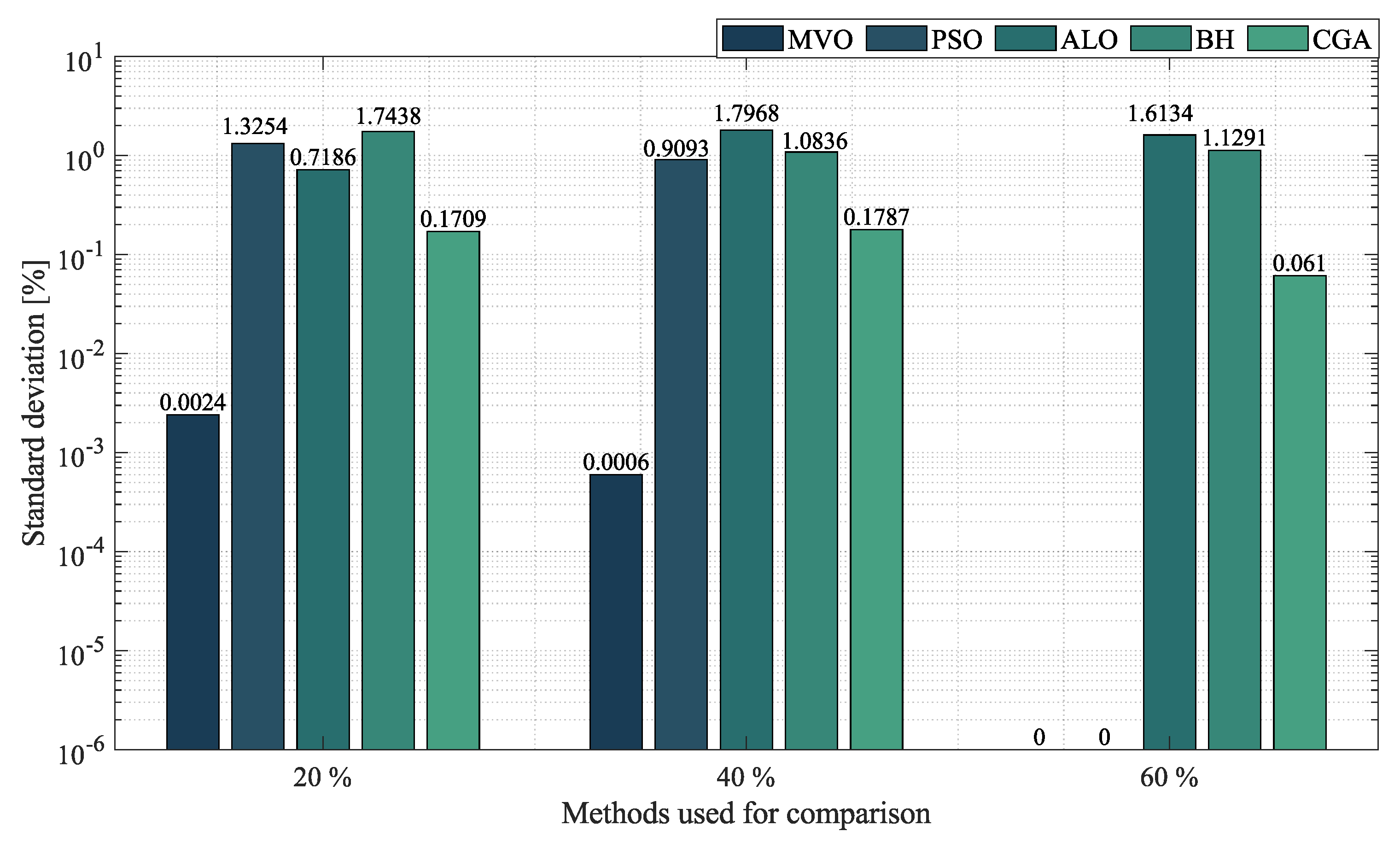
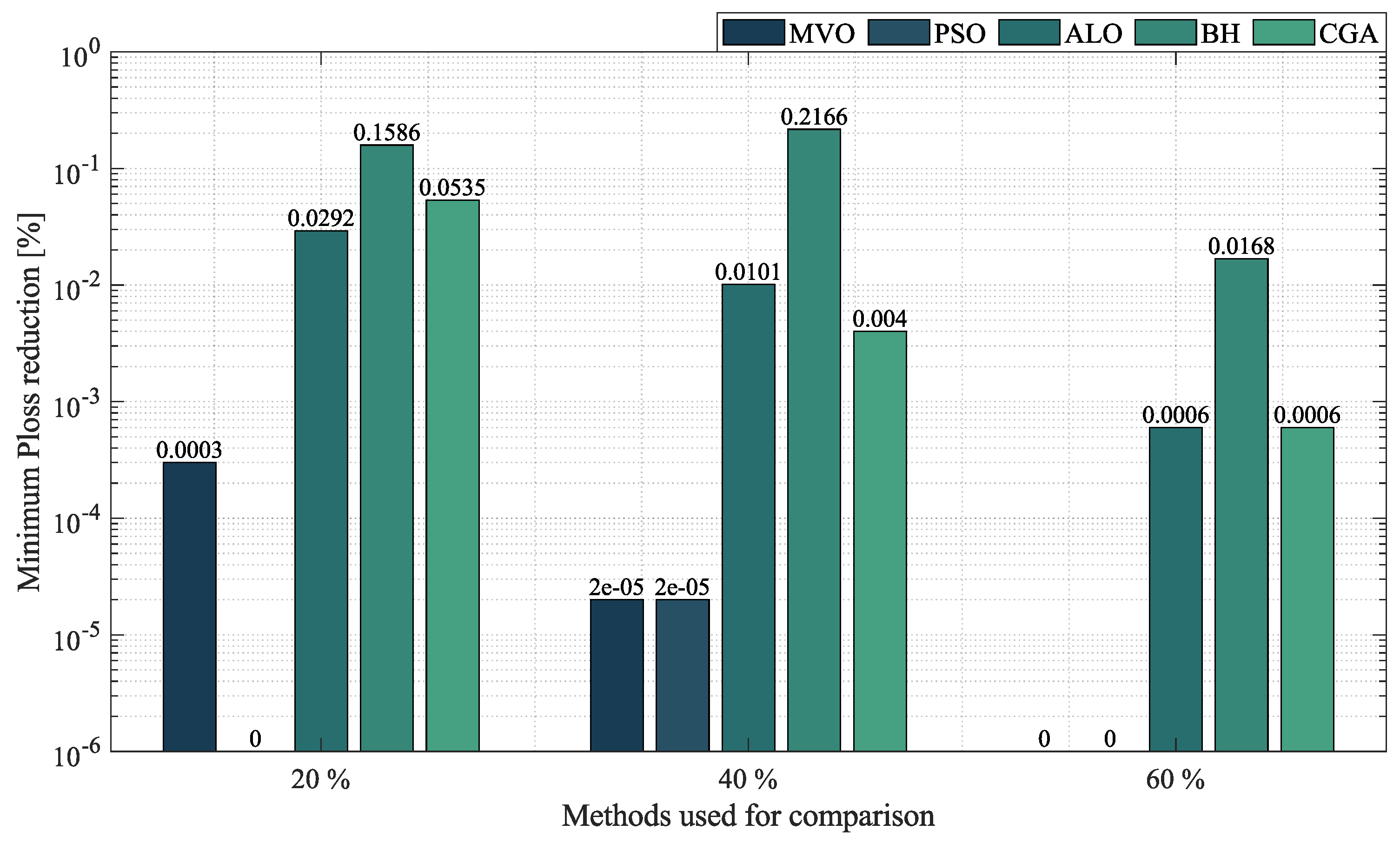
- In the case of mesh networks, the SSA also proved its superiority, as it provided the best solution in terms of minimum reduction in every test scenario, with an average reduction of , outperforming the other algorithms by an average percentage of . It produced such results in processing times of around s and with an average STD of . This demonstrates the superiority of the SSA in providing the best solution in terms of minimum reduction in very short processing times. Thus, we may conclude that it is the most suitable optimization algorithm to solve the OPF problem in mesh networks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ban, K.M. Sustainable Development Goals. Ecol. Indic. 2016, 60, 565–573. [Google Scholar]
- SDG, U. Sustainable development goals. In The Energy Progress Report. Tracking SDG; IEA: Paris, France, 2019; Volume 7. [Google Scholar]
- Swain, R.B.; Karimu, A. Renewable electricity and sustainable development goals in the EU. World Dev. 2020, 125, 104693. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Karabulut, Y.; Mukul, E. A novel renewable energy selection model for United Nations’ sustainable development goals. Energy 2018, 165, 290–302. [Google Scholar] [CrossRef]
- Revesz, R.L.; Unel, B. Managing the future of the electricity grid: Energy storage and greenhouse gas emissions. Harv. Environ. Law Rev. 2018, 42, 139. [Google Scholar]
- Ensini, L.; Sandrolini, L.; Thomas, D.; Sumner, M.; Rose, C. Conducted emissions on dc power grids. In Proceedings of the 2018 International Symposium on Electromagnetic Compatibility (EMC EUROPE), Amsterdam, The Netherlands, 27–30 August 2018; pp. 214–219. [Google Scholar]
- Hyvärinen, M. Electrical Networks and Economies of Load Density; Teknillinen Korkeakoulu: Espoo, Finland, 2008. [Google Scholar]
- Grisales-Noreña, L.F.; Montoya, O.D.; Hincapié-Isaza, R.A.; Granada Echeverri, M.; Perea-Moreno, A.J. Optimal location and sizing of DGs in DC networks using a hybrid methodology based on the PPBIL algorithm and the VSA. Mathematics 2021, 9, 1913. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Kumar, J.; Agarwal, A.; Agarwal, V. A review on overall control of DC microgrids. J. Energy Storage 2019, 21, 113–138. [Google Scholar] [CrossRef]
- Martins, A.S.C.; de Araujo, L.R.; Penido, D.R.R. Sensibility Analysis with Genetic Algorithm to Allocate Distributed Generation and Capacitor Banks in Unbalanced Distribution Systems. Electr. Power Syst. Res. 2022, 209, 107962. [Google Scholar] [CrossRef]
- Erdinc, O.; Tascikaraoglu, A.; Paterakis, N.G.; Dursun, I.; Sinim, M.C.; Catalão, J.P. Optimal sizing and siting of distributed generation and EV charging stations in distribution systems. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Erdinç, O.; Taşcıkaraoǧlu, A.; Paterakis, N.G.; Dursun, I.; Sinim, M.C.; Catalao, J.P. Comprehensive optimization model for sizing and siting of DG units, EV charging stations, and energy storage systems. IEEE Trans. Smart Grid 2017, 9, 3871–3882. [Google Scholar] [CrossRef]
- Rosales Muñoz, A.A.; Grisales-Noreña, L.F.; Montano, J.; Montoya, O.D.; Perea-Moreno, A.J. Application of the Multiverse Optimization Method to Solve the Optimal Power Flow Problem in Alternating Current Networks. Electronics 2022, 11, 1287. [Google Scholar] [CrossRef]
- Montoya, O.D.; Giral-Ramírez, D.A.; Grisales-Noreña, L.F. Black hole optimizer for the optimal power injection in distribution networks using DG. J. Phys. Conf. Ser. 2021, 2135, 012010. [Google Scholar] [CrossRef]
- Rosales-Muñoz, A.A.; Grisales-Noreña, L.F.; Montano, J.; Montoya, O.D.; Perea-Moreno, A.J. Application of the Multiverse Optimization Method to Solve the Optimal Power Flow Problem in Direct Current Electrical Networks. Sustainability 2021, 13, 8703. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Gonzalez Montoya, D.; Ramos-Paja, C.A. Optimal sizing and location of distributed generators based on PBIL and PSO techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Garzón Rivera, O.D.; Ocampo Toro, J.A.; Ramos-Paja, C.A.; Rodriguez Cabal, M.A. Metaheuristic optimization methods for optimal power flow analysis in DC distribution networks. Trans. Energy Syst. Eng. Appl. 2020, 1, 13–31. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.; González-Montoya, D.; Ramos-Paja, C.; Garces, A. Linear power flow formulation for low-voltage DC power grids. Electr. Power Syst. Res. 2018, 163, 375–381. [Google Scholar] [CrossRef]
- Gallego, R.; Escobar, A.; Toro, E.; Romero, R. Técnicas heurísticas y metaheurísticas de optimización; Editorial Universidad Tecnológica de Pereira: Pereira, Colombia, 2015; ISBN 9789587222074. [Google Scholar]
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust design optimization and emerging technologies for electrical machines: Challenges and open problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]
- Montano, J.; Mejia, A.F.T.; Rosales Muñoz, A.A.; Andrade, F.; Garzon Rivera, O.D.; Palomeque, J.M. Salp Swarm Optimization Algorithm for Estimating the Parameters of Photovoltaic Panels Based on the Three-Diode Model. Electronics 2021, 10, 3123. [Google Scholar] [CrossRef]
- Rosales Muñoz, A.A.; Grisales-Noreña, L.F.; Montano, J.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Power Dispatch of Distributed Generators in Direct Current Networks Using a Master–Slave Methodology That Combines the Salp Swarm Algorithm and the Successive Approximation Method. Electronics 2021, 10, 2837. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Ramos-Paja, C.A.; Gonzalez-Montoya, D.; Alcalá, G.; Hernandez-Escobedo, Q. Energy management in PV based microgrids designed for the Universidad Nacional de Colombia. Sustainability 2020, 12, 1219. [Google Scholar] [CrossRef]
- Ara, A.L.; Kazemi, A.; Gahramani, S.; Behshad, M. Optimal reactive power flow using multi-objective mathematical programming. Sci. Iran. 2012, 19, 1829–1836. [Google Scholar]
- Moreno, E.A.; Hinojosa, V.H. Flujo Optimo de Potencia utilizando algoritmos evolutivos programación en Digsilent. Rev. Técnica” Energía” 2009, 5, 20–30. [Google Scholar] [CrossRef]
- Bernal-Romero, D.L.; Montoya, O.D.; Arias-Londoño, A. Solution of the optimal reactive power flow problem using a discrete-continuous CBGA implemented in the DigSILENT programming language. Computers 2021, 10, 151. [Google Scholar] [CrossRef]
- Ayan, K.; Kılıç, U. Artificial bee colony algorithm solution for optimal reactive power flow. Appl. Soft Comput. 2012, 12, 1477–1482. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Solution of optimal reactive power flow using biogeography-based optimization. Int. J. Electr. Electron. Eng 2010, 4, 568–576. [Google Scholar]
- Gutiérrez, D.; Villa, W.M.; López-Lezama, J.M. Flujo óptimo reactivo mediante optimización por enjambre de partículas. Inf. Tecnol. 2017, 28, 215–224. [Google Scholar] [CrossRef][Green Version]
- Montoya, O.; Gil-González, W.; Grisales-Noreña, L. Optimal Power Dispatch of DGS in DC Power Grids: A Hybrid Gauss-Seidel-Genetic-Algorithm Methodology for Solving the OPF Problem. 2018. Available online: https://www.semanticscholar.org/paper/Optimal-Power-Dispatch-of-DGs-in-DC-Power-Grids%3A-a-Montoya-Gil-Gonz%C3%A1lez/9c6f54dcda06b39af91cb8b7e61a2beb6f13eda3 (accessed on 1 September 2022).
- Wang, P.; Wang, W.; Xu, D. Optimal sizing of distributed generations in DC microgrids with comprehensive consideration of system operation modes and operation targets. IEEE Access 2018, 6, 31129–31140. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. A novel hybrid antlion optimization algorithm for multi-objective task scheduling problems in cloud computing environments. Clust. Comput. 2021, 24, 205–223. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Salp swarm optimizer to solve optimal power flow comprising voltage stability analysis. Neural Comput. Appl. 2020, 32, 5267–5283. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.; Anjum, W.; Ayub, S. Salp swarm optimization algorithm-based controller for dynamic response and power quality enhancement of an islanded microgrid. Processes 2019, 7, 840. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garrido, V.M.; Gil-González, W.; Grisales-Noreña, L.F. Power flow analysis in DC grids: Two alternative numerical methods. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1865–1869. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. On the numerical analysis based on successive approximations for power flow problems in AC distribution systems. Electr. Power Syst. Res. 2020, 187, 106454. [Google Scholar] [CrossRef]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Tamilselvan, V.; Jayabarathi, T.; Raghunathan, T.; Yang, X.S. Optimal capacitor placement in radial distribution systems using flower pollination algorithm. Alex. Eng. J. 2018, 57, 2775–2786. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Optimal location and sizing of Distribution Static Synchronous Series Compensator using Particle Swarm Optimization. Int. J. Electr. Power Energy Syst. 2014, 62, 646–653. [Google Scholar] [CrossRef]
- Penaloza, J.; Yumbla, J.; Lopez, J.; Padilha-Feltrin, A. Optimal Distribution Network Reconfiguration with Distributed Generation using a Genetic Algorithm. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Gramado City, Brazil, 15–18 September 2019. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp swarm algorithm: A comprehensive survey. Neural Comput. Appl. 2020, 32, 11195–11215. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Sahoo, N.; Prasad, K. A fuzzy genetic approach for network reconfiguration to enhance voltage stability in radial distribution systems. Energy Convers. Manag. 2006, 47, 3288–3306. [Google Scholar] [CrossRef]
- Ocampo-Toro, J.; Garzon-Rivera, O.; Grisales-Noreña, L.; Montoya-Giraldo, O.; Gil-González, W. Optimal Power Dispatch in Direct Current Networks to Reduce Energy Production Costs and CO2 Emissions Using the Antlion Optimization Algorithm. Arab. J. Sci. Eng. 2021, 46, 9995–10006. [Google Scholar] [CrossRef]
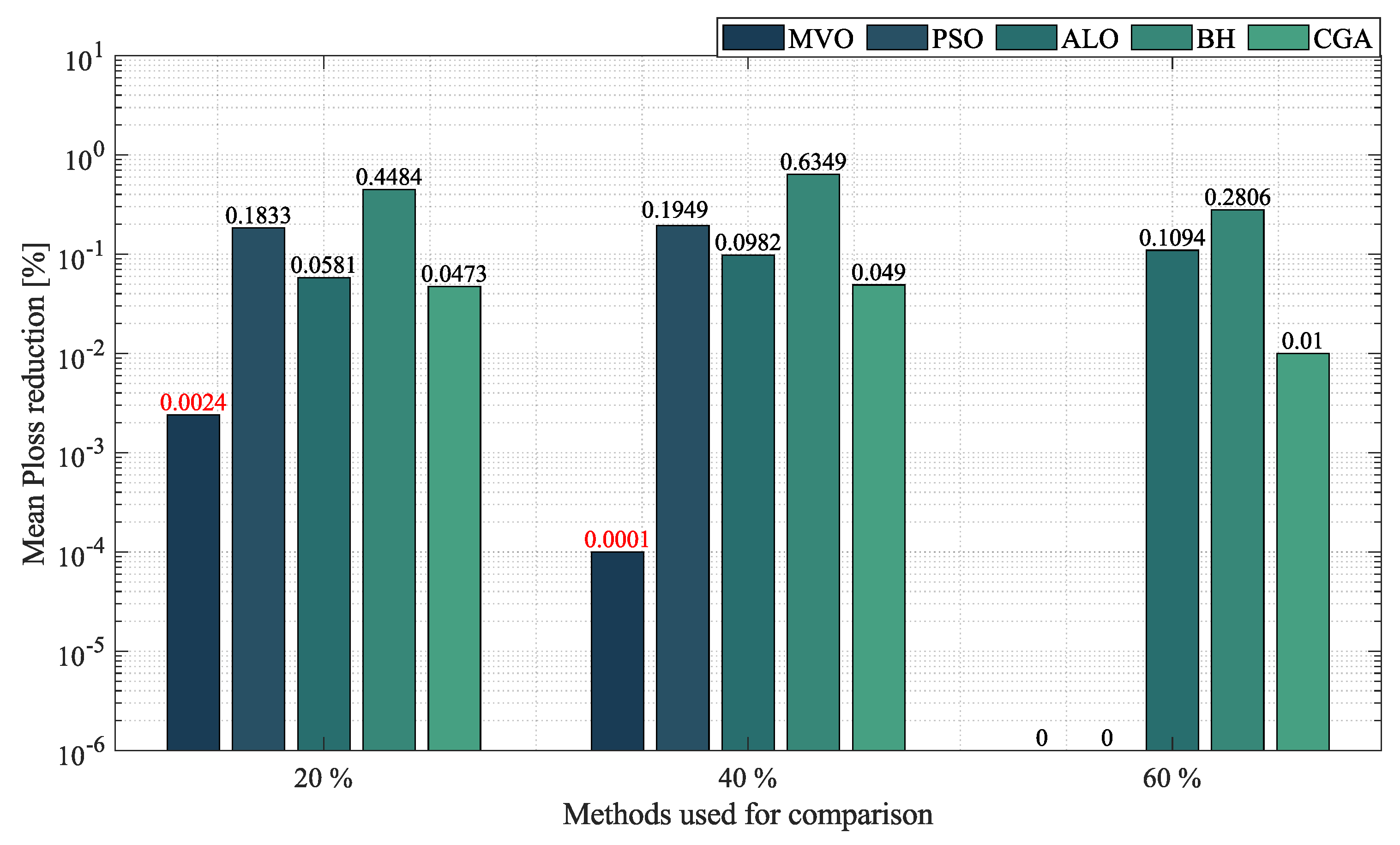
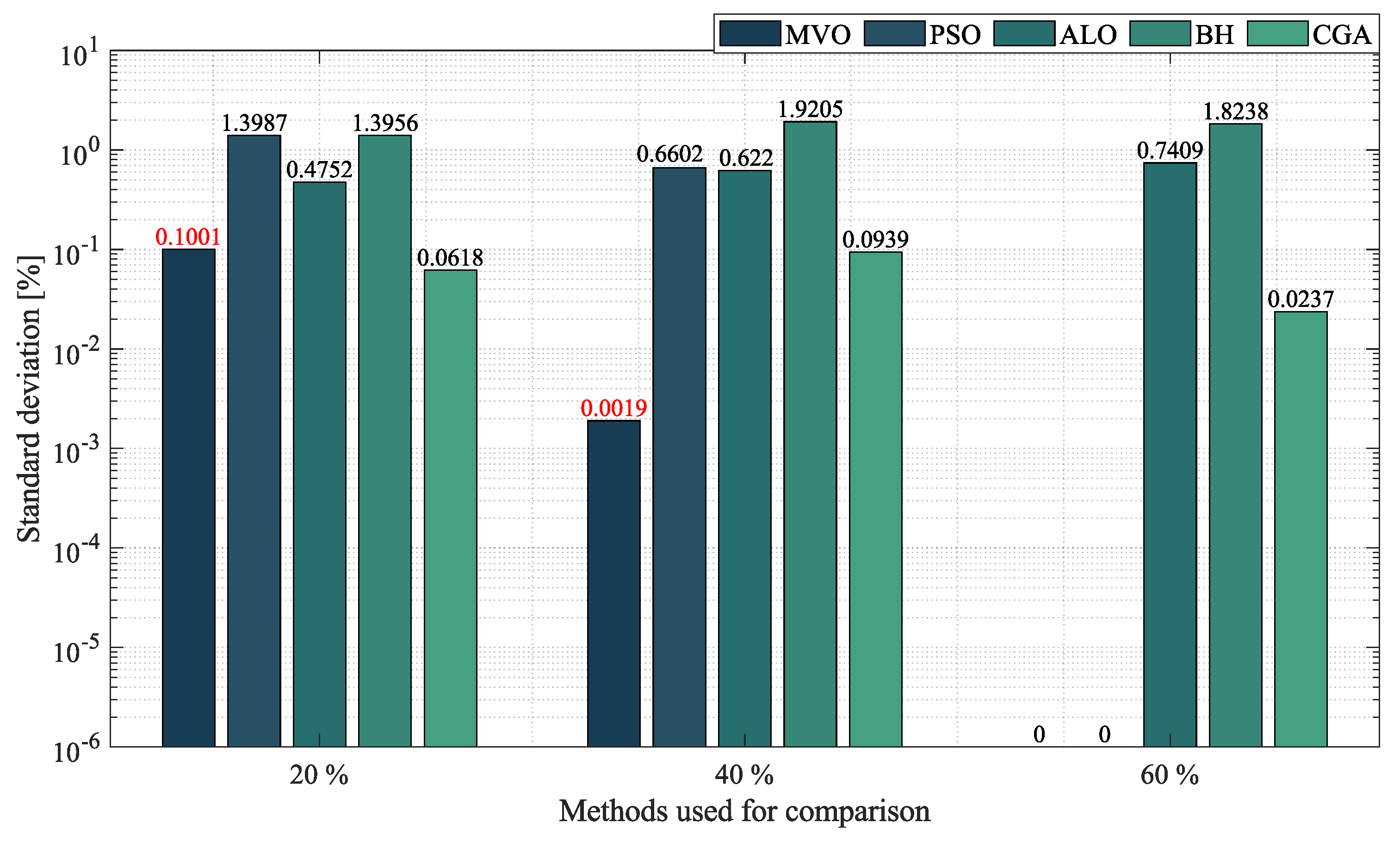
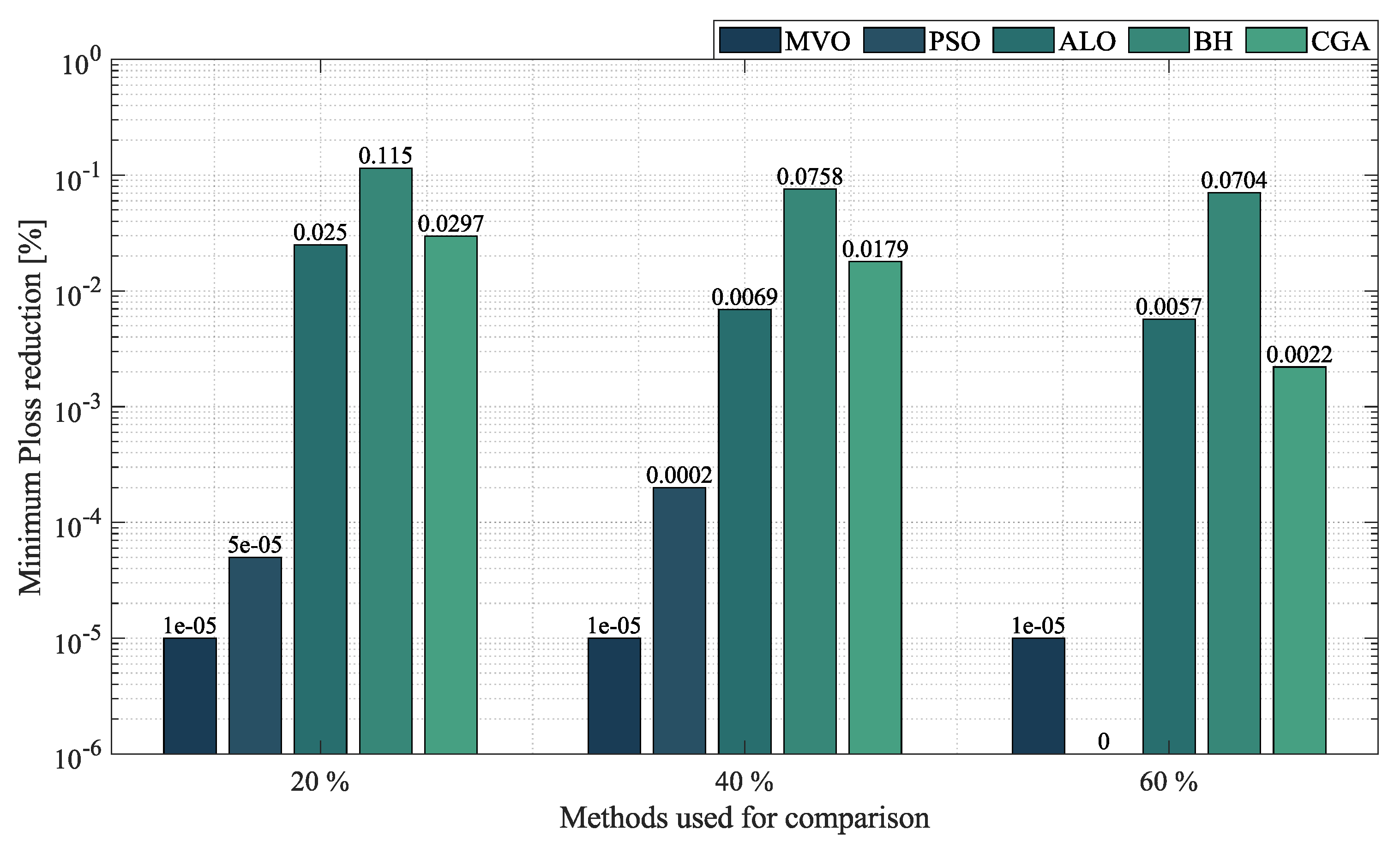
| Commercial Software | ||
|---|---|---|
| Method | Year | Reference |
| Particle Swarm Optimization- DigSILENT | 2009 | [26] |
| GAMS-DICOPT | 2012 | [25] |
| Genetic Algorithm- DigSILENT | 2021 | [27] |
| Sequential Programming | ||
| Method | Year | Reference |
| Bio-geography Optimization Algorithm | 2010 | [29] |
| Artificial Bee Swarm Optimization Algorithm | 2012 | [28] |
| Turbulent Crazy Particle Swarm Optimization | 2017 | [30] |
| Continuous Genetic Algorithm | 2018 | [31] |
| Particle Swarm Optimization | 2018 | [32] |
| Ant Lion Optimizer | 2021 | [33] |
| Black Hole | 2021 | [15] |
| Multi-Verse Optimizer | 2022 | [14] |
| Parameters | |||
|---|---|---|---|
| Method |
Number of Particles |
Maximum Iterations |
Non-Improvement Iterations |
| SSA | 78 | 433 | 154 |
| MVO | 80 | 432 | 300 |
| PSO | 58 | 723 | 252 |
| ALO | 62 | 992 | 725 |
| BH | 83 | 667 | 340 |
| CGA | 57 | 551 | 551 |
| Node i | Node j | [] | [] | P [kW] | Q [kVAr] |
|---|---|---|---|---|---|
| 1 | 2 | 0.1233 | 0.4127 | 1840 | 460 |
| 2 | 3 | 0.2467 | 0.6051 | 980 | 340 |
| 2 | 4 | 0.7469 | 1.2050 | 1790 | 446 |
| 4 | 5 | 0.6984 | 0.6084 | 1598 | 1840 |
| 2 | 6 | 1.9837 | 1.7276 | 1610 | 600 |
| 6 | 7 | 0.9057 | 0.7886 | 780 | 110 |
| 7 | 8 | 2.0552 | 1.1640 | 1150 | 60 |
| 7 | 9 | 4.7953 | 2.7160 | 980 | 130 |
| 3 | 10 | 5.3434 | 3.0264 | 1640 | 200 |
| 5 | 10 | 0.1426 | 0.4522 | - | - |
| 8 | 10 | 0.2018 | 0.5214 | - | - |
| 10-Node Radial Test System | |||||||
|---|---|---|---|---|---|---|---|
| Method |
Node/ Power [kW] | Power Losses |
Vworst [pu]/ Node | Imax [A] | |||
|
Minimum [kW]/ Reduction [%] |
Average [kW]/ Reduction [%] | Time [s] | STD [%] | ||||
| Without DGs | - | 223.4181 | - | - | - | 0.9–1.1 | 590 |
| 20% penetration | |||||||
| SSA | 5/0.05 | 116.9218/47.6668 | 116.9237/47.6660 | 3.49 | 0.0025 | 0.9723/8 | 433.3321 |
| 9/1589.82 | |||||||
| 10/928.41 | |||||||
| MVO | 5/0.05 | 116.9220/47.6667 | 116.9250/47.6654 | 3.75 | 0.0049 | 0.9723/8 | 433.3324 |
| 9/1589.82 | |||||||
| 10/928.41 | |||||||
| PSO | 5/0 | 116.9218/47.6668 | 117.2119/47.5370 | 4.50 | 1.3279 | 0.9723/8 | 433.3321 |
| 9/1589.55 | |||||||
| 10/928.73 | |||||||
| ALO | 5/0.51 | 116.9473/47.6554 | 117.9188/47.2206 | 6.66 | 0.7210 | 0.9723/8 | 433.3827 |
| 9/1586.68 | |||||||
| 10/929.96 | |||||||
| BH | 5/96.28 | 117.9244/47.2181 | 121.5254/45.6063 | 3.35 | 1.7463 | 0.9729/8 | 433.5938 |
| 9/1696.06 | |||||||
| 10/720.92 | |||||||
| CGA | 5/18.86 | 117.0415/47.6132 | 117.4801/47.4169 | 3.29 | 0.1733 | 0.9725/8 | 433.4102 |
| 9/1619.67 | |||||||
| 10/878.08 | |||||||
| 40% penetration | |||||||
| SSA | 5/1620.63 | 80.7608/63.8522 | 80.7610/63.8521 | 3.47 | 0.0003 | 0.9751/8 | 322.2693 |
| 9/1970.64 | |||||||
| 10/1445.29 | |||||||
| MVO | 5/1619.69 | 80.7608/63.8522 | 80.7619/63.8517 | 3.68 | 0.0009 | 0.9752/8 | 322.2694 |
| 9/1971.25 | |||||||
| 10/1445.62 | |||||||
| PSO | 5/1620.68 | 80.7608/63.8522 | 80.9785/63.7547 | 4.25 | 0.9097 | 0.9751/8 | 322.2693 |
| 9/1970.20 | |||||||
| 10/1445.69 | |||||||
| ALO | 5/1570.43 | 80.7922/63.8381 | 81.8538/63.3629 | 6.61 | 1.7971 | 0.9752/8 | 322.2936 |
| 9/1979.08 | |||||||
| 10/1486.52 | |||||||
| BH | 5/1606.93 | 80.9765/63.7556 | 82.4371/63.1019 | 3.29 | 1.0840 | 0.9751/8 | 323.3491 |
| 9/1969.06 | |||||||
| 10/1435.96 | |||||||
| CGA | 5/1642.03 | 80.7807/63.8433 | 81.0075/63.7417 | 3.30 | 0.1791 | 0.9751/8 | 322.3464 |
| 9/1959.77 | |||||||
| 10/1433.01 | |||||||
| 60% penetration | |||||||
| SSA | 5/2992.59 | 72.1260/67.7170 | 72.1260/67.7170 | 3.51 | 4.23 | 0.9771/8 | 235.1409 |
| 9/2235.17 | |||||||
| 10/1804.13 | |||||||
| MVO | 5/2992.61 | 72.1260/67.7170 | 72.1260/67.7170 | 3.88 | 9.38 | 0.9771/8 | 235.1382 |
| 9/2235.19 | |||||||
| 10/1804.14 | |||||||
| PSO | 5/2992.59 | 72.1260/67.7170 | 72.1260/67.7170 | 2.39 | 1.22 | 0.9771/8 | 235.1409 |
| 9/2235.17 | |||||||
| 10/1804.13 | |||||||
| ALO | 5/2993.04 | 72.1308/67.7149 | 72.7952/67.4175 | 6.70 | 1.6134 | 0.9770/8 | 236.2086 |
| 9/2219.08 | |||||||
| 10/1795.22 | |||||||
| BH | 5/2941.39 | 72.1498/67.7064 | 73.1556/67.2562 | 3.78 | 1.1291 | 0.9773/8 | 236.3767 |
| 9/2267.73 | |||||||
| 10/1794.37 | |||||||
| CGA | 5/3020.79 | 72.1345/67.7132 | 72.1848/67.6907 | 3.46 | 0.0610 | 0.9772/8 | 234.3459 |
| 9/2245.92 | |||||||
| 10/1783.47 | |||||||
| 33-Node Radial Test System | |||||||
|---|---|---|---|---|---|---|---|
| Method |
Node/ Power [kW] | Power Losses |
Vworst [p.u.]/ Node | Imax [A] | |||
|
Minimum [kW]/ Reduction [%] |
Average [kW]/ Reduction [%] | Time [s] | STD [%] | ||||
| Without DGs | - | 210.9785 | - | - | - | 0.9–1.1 | 385 |
| 20% penetration | |||||||
| SSA | 12/48.44 | 127.4984/39.5680 | 127.5044/39.5652 | 10.17 | 0.0077 | 0.9377/33 | 241.4931 |
| 15/396.14 | |||||||
| 31/340.61 | |||||||
| MVO | 12/44.88 | 127.4984/39.5680 | 127.4994/39.5676 | 11.18 | 0.0009 | 0.9377/33 | 241.4931 |
| 15/398.94 | |||||||
| 31/341.37 | |||||||
| PSO | 12/45.68 | 127.4984/39.5680 | 127.8911/39.3819 | 11.97 | 0.5240 | 0.9377/33 | 241.4931 |
| 15/398.71 | |||||||
| 31/340.81 | |||||||
| ALO | 12/55.13 | 127.5029/39.5659 | 127.6270/39.5071 | 17.44 | 0.0910 | 0.9376/33 | 241.4970 |
| 15/391.34 | |||||||
| 31/338.68 | |||||||
| BH | 12/88.70 | 127.6257/39.5077 | 128.4504/39.1168 | 9.19 | 0.4042 | 0.9358/18 | 241.5142 |
| 15/333.88 | |||||||
| 31/362.48 | |||||||
| CGA | 12/76.31 | 127.5192/39.5582 | 127.6041/39.5180 | 9.27 | 0.0439 | 0.9376/33 | 241.4996 |
| 15/370.19 | |||||||
| 31/338.64 | |||||||
| 40% penetration | |||||||
| SSA | 12/409.59 | 90.3771/57.1629 | 90.3779/57.1625 | 9.68 | 0.0012 | 0.9594/33 | 176.5392 |
| 15/397.41 | |||||||
| 31/763.40 | |||||||
| MVO | 12/409.59 | 90.3771/57.1629 | 90.3777/57.1626 | 10.73 | 0.0008 | 0.9594/33 | 176.5392 |
| 15/397.41 | |||||||
| 31/763.40 | |||||||
| PSO | 12/410.02 | 90.3771/57.1629 | 90.7890/56.9677 | 11.47 | 1.1588 | 0.9594/33 | 176.5392 |
| 15/397.60 | |||||||
| 31/762.78 | |||||||
| ALO | 12/429.24 | 90.3861/57.1586 | 90.5850/57.0644 | 17.30 | 0.2181 | 0.9591/33 | 176.5422 |
| 15/388.74 | |||||||
| 31/752.38 | |||||||
| BH | 12/348.19 | 90.5000/57.1047 | 91.7172/56.5277 | 9.04 | 0.7770 | 0.9594/33 | 176.7536 |
| 15/455.18 | |||||||
| 31/764.43 | |||||||
| CGA | 12/432.88 | 90.4019/57.1511 | 90.4811/57.1136 | 9.48 | 0.0535 | 0.9591/33 | 176.5933 |
| 15/384.37 | |||||||
| 31/752.48 | |||||||
| 60% penetration | |||||||
| SSA | 12/596.31 | 85.7789/59.3423 | 85.7789/59.3423 | 9.97 | 8.65 | 0.9700/33 | 114.2656 |
| 15/397.74 | |||||||
| 31/980.32 | |||||||
| MVO | 12/596.31 | 85.7789/59.3423 | 85.7789/59.3423 | 10.68 | 6.11 | 0.9700/33 | 144.2656 |
| 15/397.76 | |||||||
| 31/980.31 | |||||||
| PSO | 12/596.32 | 85.7789/59.3423 | 85.7789/59.3423 | 6.63 | 8.00 | 0.9700/33 | 144.2657 |
| 15/397.74 | |||||||
| 31/980.32 | |||||||
| ALO | 12/604.99 | 85.7813/59.3412 | 86.0098/59.2329 | 18.03 | 0.3471 | 0.9699/33 | 144.6453 |
| 15/388.35 | |||||||
| 31/976.24 | |||||||
| BH | 12/598.86 | 85.8045/59.3302 | 86.3709/59.0618 | 9.80 | 0.6068 | 0.9694/33 | 146.3655 |
| 15/380.11 | |||||||
| 31/968.85 | |||||||
| CGA | 12/594.56 | 85.7803/59.3417 | 85.7999/59.3324 | 10.07 | 0.0168 | 0.9699/33 | 144.7778 |
| 15/395.17 | |||||||
| 31/978.16 | |||||||
| 69-Node Radial Test System | |||||||
|---|---|---|---|---|---|---|---|
| Method | Node/ Power [kW] | Power Losses | Vworst [pu]/ Node | Imax [A] | |||
| Minimum [kW]/ Reduction [%] | Average [kW]/ Reduction [%] | Time [s] | STD [%] | ||||
| Without DGs | - | 242.1523 | - | - | - | 0.9–1.1 | 400 |
| 20% penetration | |||||||
| SSA | 26/0 | 133.5626/44.8435 | 133.6548/44.8055 | 44.62 | 0.1034 | 0.9397/64 | 252.6391 |
| 61/580.52 | |||||||
| 66/246.05 | |||||||
| MVO | 26/0.01 | 133.5632/44.8433 | 133.5687/44.8410 | 44.84 | 0.0033 | 0.9385/69 | 252.5817 |
| 61/583.13 | |||||||
| 66/243.43 | |||||||
| PSO | 26/0 | 133.5626/44.8435 | 134.1547/44.5990 | 57.16 | 1.5020 | 0.9385/69 | 252.5817 |
| 61/580.16 | |||||||
| 66/246.41 | |||||||
| ALO | 26/0 | 133.6333/44.8143 | 134.6068/44.4123 | 76.89 | 0.5786 | 0.9390/69 | 252.6323 |
| 61/546.38 | |||||||
| 66/279.62 | |||||||
| BH | 26/9.55 | 133.9468/44.6849 | 137.8053/43.0915 | 38.64 | 1.4990 | 0.9378/69 | 252.6825 |
| 61/595.61 | |||||||
| 66/220.52 | |||||||
| CGA | 26/4.08 | 133.6923/44.7900 | 134.2007/44.5800 | 43.18 | 0.1652 | 0.9381/69 | 252.5921 |
| 61/595.66 | |||||||
| 66/226.83 | |||||||
| 40% penetration | |||||||
| SSA | 26/152.93 | 86.4573/64.2963 | 86.4593/64.2955 | 42.06 | 0.0036 | 0.9634/69 | 183.5728 |
| 61/1254.04 | |||||||
| 66/246.17 | |||||||
| MVO | 26/152.51 | 86.4574/64.2963 | 86.4585/64.2958 | 45.11 | 0.0017 | 0.9638/69 | 183.5712 |
| 61/1253.71 | |||||||
| 66/246.91 | |||||||
| PSO | 26/152.72 | 86.4574/64.2963 | 86.6493/64.2170 | 56.62 | 0.6638 | 0.9638/69 | 183.5711 |
| 61/1252.84 | |||||||
| 66/247.57 | |||||||
| ALO | 26/152.77 | 86.4817/64.2862 | 87.0658/64.0450 | 81.02 | 0.6258 | 0.9639/69 | 183.6309 |
| 61/1243.67 | |||||||
| 66/255.96 | |||||||
| BH | 26/208.65 | 86.9818/64.0797 | 90.4786/62.6357 | 45.23 | 1.9240 | 0.9632/69 | 183.9434 |
| 61/1110.03 | |||||||
| 66/330.27 | |||||||
| CGA | 26/144.73 | 86.4671/64.2923 | 86.6006/64.2371 | 37.99 | 0.0974 | 0.9638/69 | 183.5754 |
| 61/1274.50 | |||||||
| 66/233.87 | |||||||
| 60% penetration | |||||||
| SSA | 26/382.16 | 76.9578/68.2193 | 76.9578/68.2193 | 43.89 | 5.42 | 0.9784/69 | 134.0925 |
| 61/1641.63 | |||||||
| 66/246.24 | |||||||
| MVO | 26/382.16 | 76.9578/68.2193 | 76.9578/68.2193 | 44.49 | 1.31 | 0.9784/69 | 134.0951 |
| 61/1641.63 | |||||||
| 66/246.21 | |||||||
| PSO | 26/382.17 | 76.9578/68.2193 | 76.9578/68.2193 | 55.59 | 1.46 | 0.9784/69 | 134.0926 |
| 61/1641.64 | |||||||
| 66/246.23 | |||||||
| ALO | 26/386.59 | 76.9593/68.2186 | 77.3907/68.0405 | 86.72 | 0.7409 | 0.9785/69 | 133.6689 |
| 61/1637.61 | |||||||
| 66/251.20 | |||||||
| BH | 26/358.03 | 76.9986/68.2024 | 79.0719/67.3462 | 43.35 | 1.8238 | 0.9778/69 | 136.5195 |
| 61/1653.47 | |||||||
| 66/227.85 | |||||||
| CGA | 26/382.31 | 76.9593/68.2186 | 76.9859/68.2077 | 38.06 | 0.0237 | 0.9784/69 | 134.4437 |
| 61/1629.83 | |||||||
| 66/253.45 | |||||||
| 10-Node Mesh Test System | |||||||
|---|---|---|---|---|---|---|---|
| Method |
Node/ Power [kW] | Power Losses |
Vworst [pu]/ Node | Imax [A] | |||
|
Minimum [kW]/ Reduction [%] |
Average [kW]/ Reduction [%] | Time [s] | STD [%] | ||||
| Without DGs | - | 190.3237 | - | - | - | 0.9–1.1 | 590 |
| 20% penetration | |||||||
| SSA | 5/0 | 104.7510/44.9617 | 104.7707/44.9513 | 4.16 | 0.0446 | 0.9793/8 | 433.0907 |
| 9/1039.33 | |||||||
| 10/1472.33 | |||||||
| MVO | 5/0 | 104.75110/44.9616 | 104.7540/44.9601 | 4.09 | 0.0021 | 0.9793/8 | 433.0907 |
| 9/1039.96 | |||||||
| 10/1471.71 | |||||||
| PSO | 5/0.02 | 104.7511/44.9616 | 105.3226/44.6613 | 4.72 | 1.8071 | 0.9793/8 | 433.0907 |
| 9/1038.24 | |||||||
| 10/1473.40 | |||||||
| ALO | 5/32.05 | 104.7986/44.9367 | 105.0366/44.8116 | 6.53 | 0.1796 | 0.9793/8 | 433.1153 |
| 9/1012.16 | |||||||
| 10/1466.94 | |||||||
| BH | 5/1.87 | 104.9699/44.8467 | 105.9958/44.3076 | 3.48 | 0.5380 | 0.9793/8 | 433.4899 |
| 9/1037.61 | |||||||
| 10/1463.23 | |||||||
| CGA | 5/18.12 | 104.8075/44.9320 | 105.0660/44.7962 | 3.40 | 0.1174 | 0.9793/8 | 433.1163 |
| 9/1087.18 | |||||||
| 10/1405.83 | |||||||
| 40% penetration | |||||||
| SSA | 5/587.06 | 58.4855/69.2705 | 58.5107/69.2573 | 3.94 | 0.0580 | 0.9838/7 | 321.8763 |
| 9/1222.72 | |||||||
| 10/3213.55 | |||||||
| MVO | 5/586.03 | 58.4855/69.2705 | 58.4882/69.2691 | 3.81 | 0.0058 | 0.9838/7 | 321.8764 |
| 9/1224.24 | |||||||
| 10/3213.06 | |||||||
| PSO | 5/611.96 | 58.4859/69.2703 | 64.6277/66.0433 | 4.38 | 24.2119 | 0.9838/7 | 321.8764 |
| 9/1227.34 | |||||||
| 10/3184.03 | |||||||
| ALO | 5/526.13 | 58.4985/69.2637 | 58.6598/69.1789 | 6.37 | 0.2907 | 0.9838/7 | 321.9142 |
| 9/1215.08 | |||||||
| 10/3281.26 | |||||||
| BH | 5/1253.67 | 58.6297/69.1947 | 60.1293/68.4068 | 3.45 | 1.2234 | 0.9838/7 | 321.8891 |
| 9/1241.74 | |||||||
| 10/2527.77 | |||||||
| CGA | 5/813.33 | 58.5195/69.2526 | 58.6400/69.1894 | 3.44 | 0.1372 | 0.9838/7 | 321.8762 |
| 9/1215.85 | |||||||
| 10/2994.17 | |||||||
| 60% penetration | |||||||
| SSA | 5/2447.21 | 39.3867/79.3054 | 39.3886/79.3044 | 3.91 | 0.0081 | 0.9874/6 | 211.8432 |
| 9/1395.92 | |||||||
| 10/3691.86 | |||||||
| MVO | 5/2440.87 | 39.3867/79.3054 | 39.3874/79.3050 | 3.88 | 0.0018 | 0.9874/6 | 211.8432 |
| 9/1396.49 | |||||||
| 10/3697.63 | |||||||
| PSO | 5/2448.40 | 39.3867/79.3054 | 40.7435/78.5925 | 4.31 | 10.3116 | 0.9874/6 | 211.8432 |
| 9/1396.09 | |||||||
| 10/3690.50 | |||||||
| ALO | 5/2445.34 | 39.3976/79.2997 | 39.6632/79.1601 | 6.56 | 0.6903 | 0.9874/6 | 212.0355 |
| 9/1399.98 | |||||||
| 10/3685.25 | |||||||
| BH | 5/3065.27 | 39.5207/79.2350 | 40.6407/78.6465 | 3.40 | 1.5767 | 0.9873/6 | 212.0846 |
| 9/1368.25 | |||||||
| 10/3096.05 | |||||||
| CGA | 5/2378.87 | 39.3908/79.3033 | 39.4689/79.2622 | 3.56 | 0.1044 | 0.9874/6 | 211.8915 |
| 9/1399.13 | |||||||
| 10/3755.89 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosales-Muñoz, A.A.; Montano, J.; Grisales-Noreña, L.F.; Montoya, O.D.; Andrade, F. Optimal Power Dispatch of DGs in Radial and Mesh AC Grids: A Hybrid Solution Methodology between the Salps Swarm Algorithm and Successive Approximation Power Flow Method. Sustainability 2022, 14, 13408. https://doi.org/10.3390/su142013408
Rosales-Muñoz AA, Montano J, Grisales-Noreña LF, Montoya OD, Andrade F. Optimal Power Dispatch of DGs in Radial and Mesh AC Grids: A Hybrid Solution Methodology between the Salps Swarm Algorithm and Successive Approximation Power Flow Method. Sustainability. 2022; 14(20):13408. https://doi.org/10.3390/su142013408
Chicago/Turabian StyleRosales-Muñoz, Andrés Alfonso, Jhon Montano, Luis Fernando Grisales-Noreña, Oscar Danilo Montoya, and Fabio Andrade. 2022. "Optimal Power Dispatch of DGs in Radial and Mesh AC Grids: A Hybrid Solution Methodology between the Salps Swarm Algorithm and Successive Approximation Power Flow Method" Sustainability 14, no. 20: 13408. https://doi.org/10.3390/su142013408
APA StyleRosales-Muñoz, A. A., Montano, J., Grisales-Noreña, L. F., Montoya, O. D., & Andrade, F. (2022). Optimal Power Dispatch of DGs in Radial and Mesh AC Grids: A Hybrid Solution Methodology between the Salps Swarm Algorithm and Successive Approximation Power Flow Method. Sustainability, 14(20), 13408. https://doi.org/10.3390/su142013408










