Actuarial Credibility Approach in Adjusting Initial Cost Estimates of Transport Infrastructure Projects
Abstract
1. Introduction
2. Literature Review
3. Methodology and Data
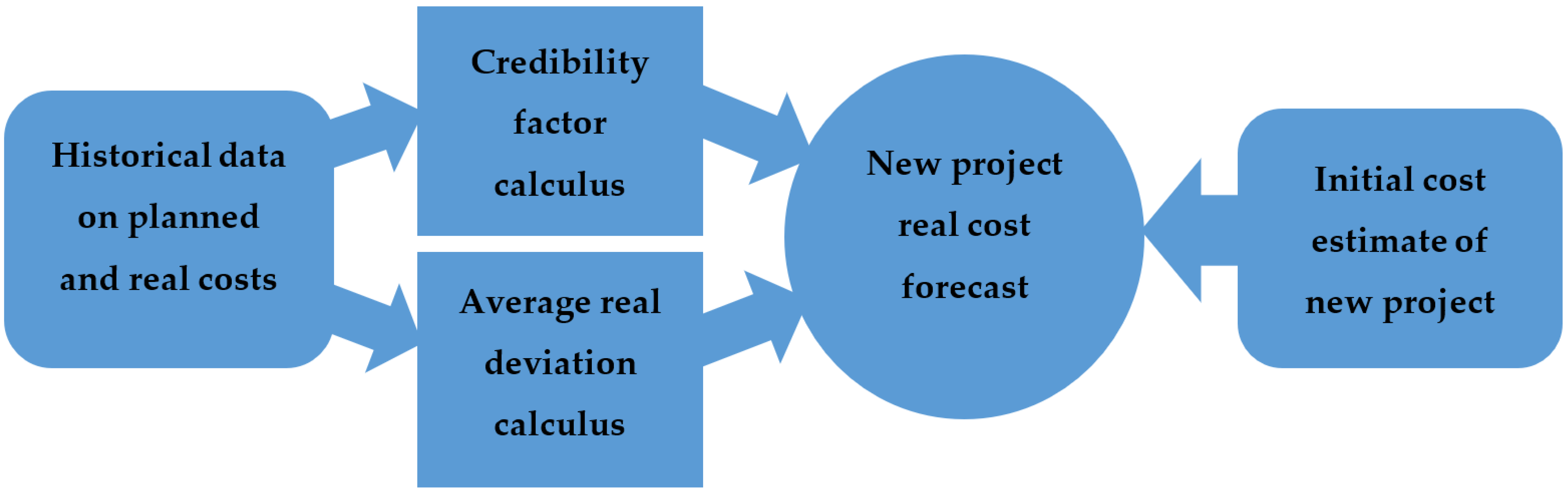
3.1. Methodology
3.2. Data
4. Empirical Results
Credibility Calculus Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Global Infrastructure Hub. Global Infrastructure Outlook. 2017. Available online: https://outlook.gihub.org/ (accessed on 22 January 2020).
- Cantarelli, C.; Flyvbjerg, B.; Molin, E.; van Wee, B. Cost Overruns in Large-Scale Transportation Infrastructure Projects: Explanations and Their Theoretical Embeddedness. Eur. J. Transp. Infrastruct. Res. 2010, 10, 5–18. [Google Scholar]
- Flyvbjerg, B.; Skamris Holm, M.; Buhl, S. Underestimating Costs in Public Works Projects: Error or Lie? J. Am. Plan. Assoc. 2002, 68, 279–295. [Google Scholar] [CrossRef]
- De Jong, M.; Annema, J.A.; Van Wee, G.P. How to Build Major Transport Infrastructure Projects within Budget, in Time and with the Expected Output: A Literature Review. Transp. Rev. 2013, 33, 195–218. [Google Scholar] [CrossRef]
- Cantarelli, C.; Flyvbjerg, B. Decision-Making and Major Transport Infrastructure Projects: The Role of Project Ownership. In Handbook on Transport and Development; Hickman, R., Bonilla, D., Givoni, M., Banister, D., Eds.; Edward Elgar: Cheltenham, UK, 2015. [Google Scholar]
- Flyvbjerg, B. Policy and Planning for Large-Infrastructure Projects: Problems, Causes, Cures. Environ. Plan. B Plan. Des. 2007, 34, 578–597. [Google Scholar] [CrossRef]
- Berechman, J.; Chen, L. Incorporating Risk of Cost Overruns into Transportation Capital Projects Decision Making. J. Transp. Econ. Policy 2011, 45, 83–104. [Google Scholar]
- Sayadi, A.R.; Hamidi, J.K.; Monjezi, M.; Najafzadeh, M. A Preliminary Cost Estimation for Short Tunnels Construction Using Parametric Method. In Engineering Geology for Society and Territory, Volume 1: Climate Change and Engineering Geology; Lollino, G., Manconi, A., Clague, J., Shan, W., Chiarle, M., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 461–465. [Google Scholar]
- Petroutsatou, K.; Lambropoulos, S. Road tunnels construction cost estimation: A structural equation model development and comparison. Oper. Res. 2009, 10, 163–173. [Google Scholar] [CrossRef]
- Barakchi, M.; Torp, O.; Belay, A.M. Cost Estimation Methods for Transport Infrastructure: A Systematic Literature Review. Procedia Eng. 2017, 196, 270–277. [Google Scholar] [CrossRef]
- Love, P.E.; Sing, C.P.; Ika, L.A.; Newton, S. The cost performance of transportation projects: The fallacy of the Planning Fallacy account. Transp. Res. Part A Policy Pract. 2019, 122, 1–20. [Google Scholar] [CrossRef]
- Välilä, T. An overview of economic theory and evidence of public-private partnerships in the procurement of (transport) infrastructure. Util. Policy 2020, 62, 1–11. [Google Scholar] [CrossRef]
- Lewis, G.; Bajari, P. Procurement contracting with time incentives: Theory and evidence. Q. J. Econ. 2011, 126, 1173–1211. [Google Scholar] [CrossRef]
- Love, P.E.D.; Smith, J.; Simpson, I.; Regan, M.; Olatunji, O. Understanding the Landscape of Overruns in Transport Infrastructure Projects. Environ. Plan. B Plan. Des. 2015, 42, 490–509. [Google Scholar] [CrossRef]
- Love, P.; Ahiaga-Dagbui, D. Debunking fake news in a post-truth era: The plausible untruths of cost underestimation in transport infrastructure projects. Transp. Res. Part A Policy Pract. 2018, 113, 357–368. [Google Scholar] [CrossRef]
- Samset, K.; Volden, G.; Olson, N.; Kvalheim, E. Governance Schemes for Major Investment Projects. A Comparative Study of Principles and Practices in Six Countries; Concept Report No. 47; Ex Ante Academic Publisher: Trondheim, Norway, 2016. [Google Scholar]
- Klakegg, O.; Torp OAusteng, K. Good and simple—A dilemma in analytical processes? Int. J. Manag. Proj. Bus. 2010, 3, 402–421. [Google Scholar] [CrossRef]
- Themsen, T.N. The processes of public megaproject cost estimation: The inaccuracy of reference class forecasting. Financial Account. Manag. 2019, 35, 337–352. [Google Scholar] [CrossRef]
- Lee, J.-K. Cost Overrun and Cause in Korean Social Overhead Capital Projects: Roads, Rails, Airports, and Ports. J. Urban Plan. Dev. 2008, 134, 59–62. [Google Scholar] [CrossRef]
- Makovšek, D. Systematic construction risk, cost estimation mechanism and unit price movements. Transp. Policy 2014, 35, 135–145. [Google Scholar] [CrossRef]
- Membah, J.; Asa, E. Estimating cost for transportation tunnel projects: A systematic literature review. Int. J. Constr. Manag. 2015, 15, 196–218. [Google Scholar] [CrossRef]
- Kim, B.S. The approximate cost estimating model for railway bridge project in the planning phase using CBR method. KSCE J. Civ. Eng. 2011, 15, 1149–1159. [Google Scholar] [CrossRef]
- Kim, G.-H.; An, S.-H.; Kang, K.-I. Comparison of construction cost estimating models based on regression analysis, neural networks, and case-based reasoning. Build. Environ. 2004, 39, 1235–1242. [Google Scholar] [CrossRef]
- Sodikov, J. Road Cost Models for Prefeasibility Studies in Developing Countries. J. Infrastruct. Syst. 2009, 15, 278–289. [Google Scholar] [CrossRef]
- Tijanić, K.; Car-Pušić, D.; Šperac, M. Cost estimation in road construction using artificial neural network. Neural Comput. Appl. 2019, 32, 9343–9355. [Google Scholar] [CrossRef]
- Hashemi, S.T.; Ebadati, O.M.; Kaur, H. Cost estimation and prediction in construction projects: A systematic review on machine learning techniques. SN Appl. Sci. 2020, 2, 1703. [Google Scholar] [CrossRef]
- Kim, S.; Choi, C.-Y.; Shahandashti, M.; Ryu, K.R. Improving Accuracy in Predicting City-Level Construction Cost Indices by Combining Linear ARIMA and Nonlinear ANNs. J. Manag. Eng. 2022, 38, 04021093. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Nejati, H.R.; Mohammadi, M. Optimized machine learning modelling for predicting the construction cost and duration of tunnelling projects. Autom. Constr. 2022, 139, 104305. [Google Scholar] [CrossRef]
- Zachares, P.; Hovhannisyan, V.; Ledezma, C.; Gante, J.; Mosca, A. On Forecasting Project Activity Durations with Neural Networks. In Proceedings of the EANN 2022, Crete, Greece, 17–20 June 2022; Communications in Computer and Information Science 1600. Iliadis, L., Jayne, C., Tefas, A., Pimenidis, E., Eds.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Kim, S. Hybrid Forecasting System Based on Case-Based Reasoning and Analytic Hierarchy Process for Cost Estimation. J. Civ. Eng. Manag. 2013, 19, 86–96. [Google Scholar] [CrossRef]
- Natarajan, A. Reference Class Forecasting and Machine Learning for Improved Offshore Oil and Gas Megaproject Planning: Methods and Application. Proj. Manag. J. 2022, 53, 456–484. [Google Scholar] [CrossRef]
- Longley-Cook, L. An Introduction to Credibility Theory; Casualty Actuarial Society: New York, NY, USA, 1962. [Google Scholar]
- Ostaszewski, K.; Karwowski, W. An Analysis of Possible Applications of Fuzzy Set Theory to the Actuarial Credibility Theory; NASA, Johnson Space Center, North American Fuzzy Logic Processing Society: Houston, TX, USA, 1992.
- Liu, B. A survey of credibility theory. Fuzzy Optim. Decis. Mak. 2006, 5, 387–408. [Google Scholar] [CrossRef]
- Norberg, R. Credibility Theory. Wiley StatsRef: Statistics Reference Online. 2015, pp. 1–15. Available online: http://onlinelibrary.wiley.com/doi/10.1002/9781118445112.stat04723.pub2/full (accessed on 22 January 2020).
- Mahler, H.; Dean, C. Credibility. In Foundations of Casualty Actuarial Science; Casualty Actuarial Society: New York, NY, USA, 2001. [Google Scholar]
- Mowbray, A. How extensive a payroll exposure is necessary to give a dependable pure premium. In Proceedings of the Casualty Actuarial Society; Casualty Actuarial Society: Arlington County, VA, USA, 1914; Volume 1, pp. 24–30. [Google Scholar]
- Bühlmann, H. Experience Rating and Credibility. ASTIN Bull. 1967, 4, 199–207. [Google Scholar] [CrossRef]
- Bühlmann, H. Experience rating and credibility. ASTIN Bull. 1968, 5, 157–165. [Google Scholar] [CrossRef]
- Hachemeister, C. Credibility for regression models with application to trend. In Credibility: Theory and Applications; Kahn, P., Ed.; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Jewell, W.S. The use of collateral data in credibility theory: A hierarchical model. G. Dell Ist. Degli Attuari Italiani. 1975, 38, 1–16. [Google Scholar]
- Wei, Y.; Watada, J. Building a type-2 fuzzy regression model based on credibility theory and its application on arbitrage pricing theory. IEEJ Trans. Electr. Electron. Eng. 2016, 11, 720–729. [Google Scholar] [CrossRef]
- Sordo, M.; Zeng, Q. On Sample Size and Classification Accuracy: A Performance Comparison. In Biological and Medical Data Analysis, Proceedings of the ISBMDA 2005, Wroclaw, Poland, 8–10 September 2005; Oliveira, J.L., Maojo, V., Martín-Sánchez, F., Pereira, A.S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 193–201. [Google Scholar] [CrossRef]
| Roads | Railways | |||
|---|---|---|---|---|
| Statistics | planned costs | real costs | planned costs | real costs |
| mean | 1,074,104 | 1,031,646 | 797,417 | 638,497 |
| max | 6,110,346 | 5,859,780 | 5,924,274 | 5,976,094 |
| min | 112,368 | 91,123 | 94,575 | 105,451 |
| observations | 95 | 50 | ||
| Roads | Railways | |||
|---|---|---|---|---|
| Statistics | planned costs | real costs | planned costs | real costs |
| mean | 877,815 | 842,701 | 616,661 | 507,633 |
| max | 6,110,346 | 5,859,780 | 5,924,274 | 5,976,094 |
| min | 21,944 | 15,144 | 22,989 | 23,194 |
| observations | 118 | 87 | ||
| Environment | Public places | |||
| Statistics | planned costs | real costs | planned costs | real costs |
| mean | 246,985 | 203,640 | 80,725 | 83,328 |
| max | 2,213,304 | 1,813,718 | 819,000 | 819,000 |
| min | 4664 | 4626 | 4807 | 4342 |
| observations | 76 | 96 | ||
| Forecasting Method | Roads | Railways | ||
|---|---|---|---|---|
| MAPE | WAPE | MAPE | WAPE | |
| Actuarial credibility | 7.10 | 4.35 | 33.09 | 25.79 |
| OLS | 10.15 | 7.32 | 31.38 | 32.38 |
| LASSO | 8.37 | 4.79 | 33.45 | 33.56 |
| Forecasting Method | Roads | Railways | Environment | Public Services | ||||
|---|---|---|---|---|---|---|---|---|
| MAPE | WAPE | MAPE | WAPE | MAPE | WAPE | MAPE | WAPE | |
| Actuarial credibility | 8.04 | 4.45 | 26.02 | 23.45 | 30.17 | 21.83 | 13.21 | 10.82 |
| OLS | 9.02 | 4.81 | 23.78 | 26.68 | 29.65 | 22.63 | 13.68 | 12.92 |
| LASSO | 9.02 | 4.79 | 23.57 | 26.39 | 29.50 | 22.56 | 13.68 | 12.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rokicki, B.; Ostaszewski, K. Actuarial Credibility Approach in Adjusting Initial Cost Estimates of Transport Infrastructure Projects. Sustainability 2022, 14, 13371. https://doi.org/10.3390/su142013371
Rokicki B, Ostaszewski K. Actuarial Credibility Approach in Adjusting Initial Cost Estimates of Transport Infrastructure Projects. Sustainability. 2022; 14(20):13371. https://doi.org/10.3390/su142013371
Chicago/Turabian StyleRokicki, Bartlomiej, and Krzysztof Ostaszewski. 2022. "Actuarial Credibility Approach in Adjusting Initial Cost Estimates of Transport Infrastructure Projects" Sustainability 14, no. 20: 13371. https://doi.org/10.3390/su142013371
APA StyleRokicki, B., & Ostaszewski, K. (2022). Actuarial Credibility Approach in Adjusting Initial Cost Estimates of Transport Infrastructure Projects. Sustainability, 14(20), 13371. https://doi.org/10.3390/su142013371








