A Numerical Parametric Study of a Double-Pipe LHTES Unit with PCM Encapsulated in the Annular Space
Abstract
1. Introduction
2. Materials and Methods
2.1. LHTES System Design
2.2. Numerical Model
3. Results and Discussion
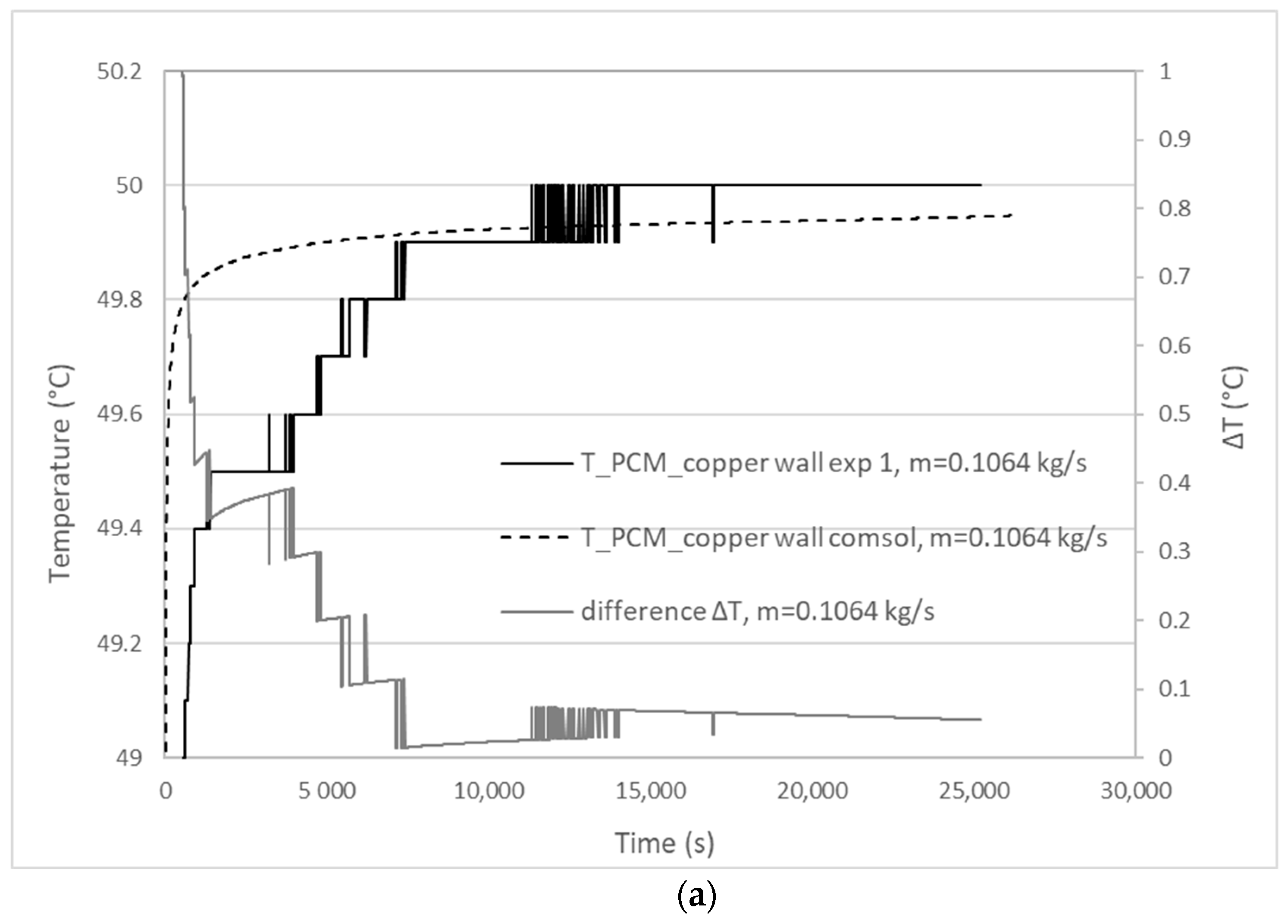
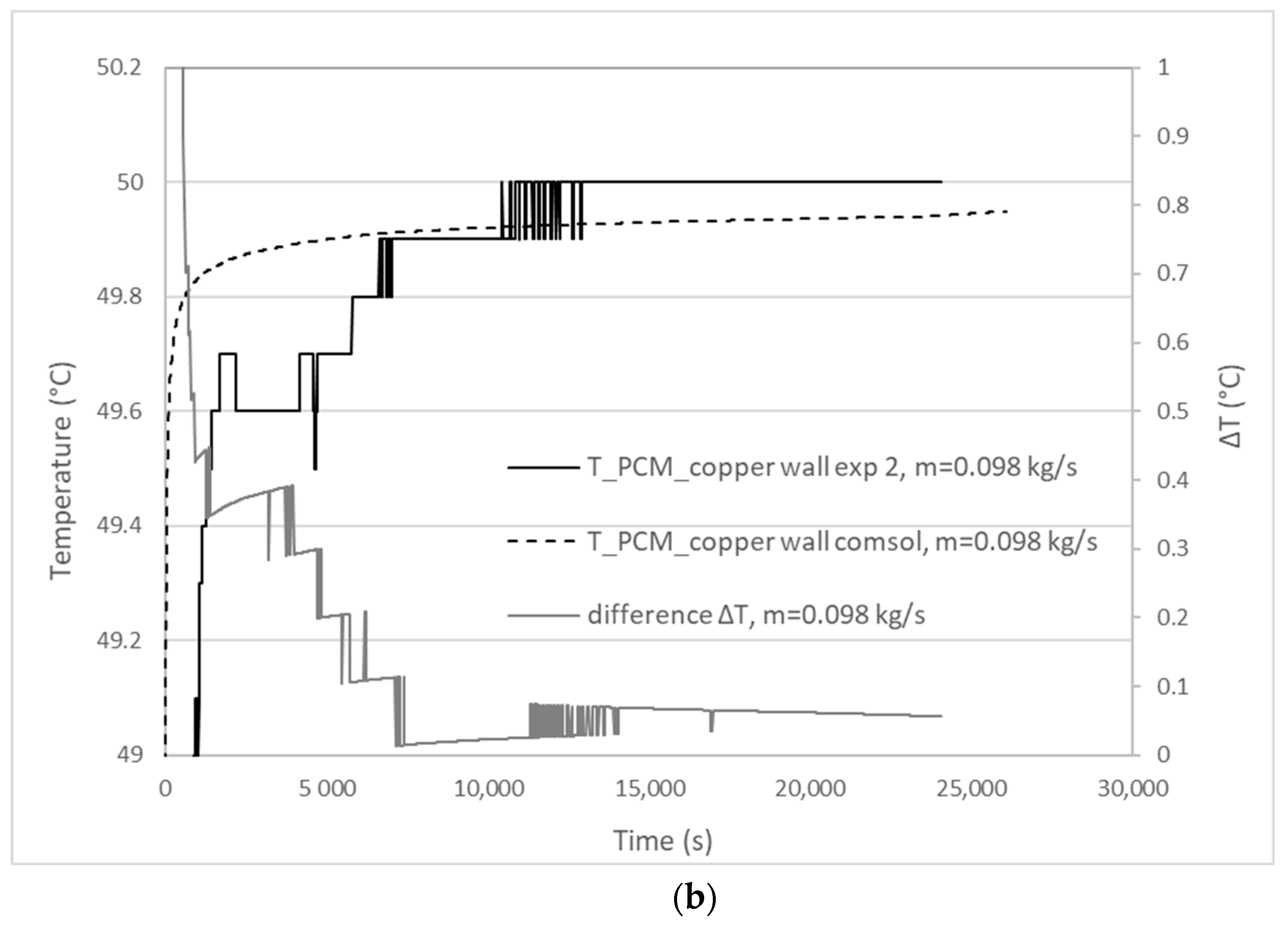
3.1. Validation Model Analysis
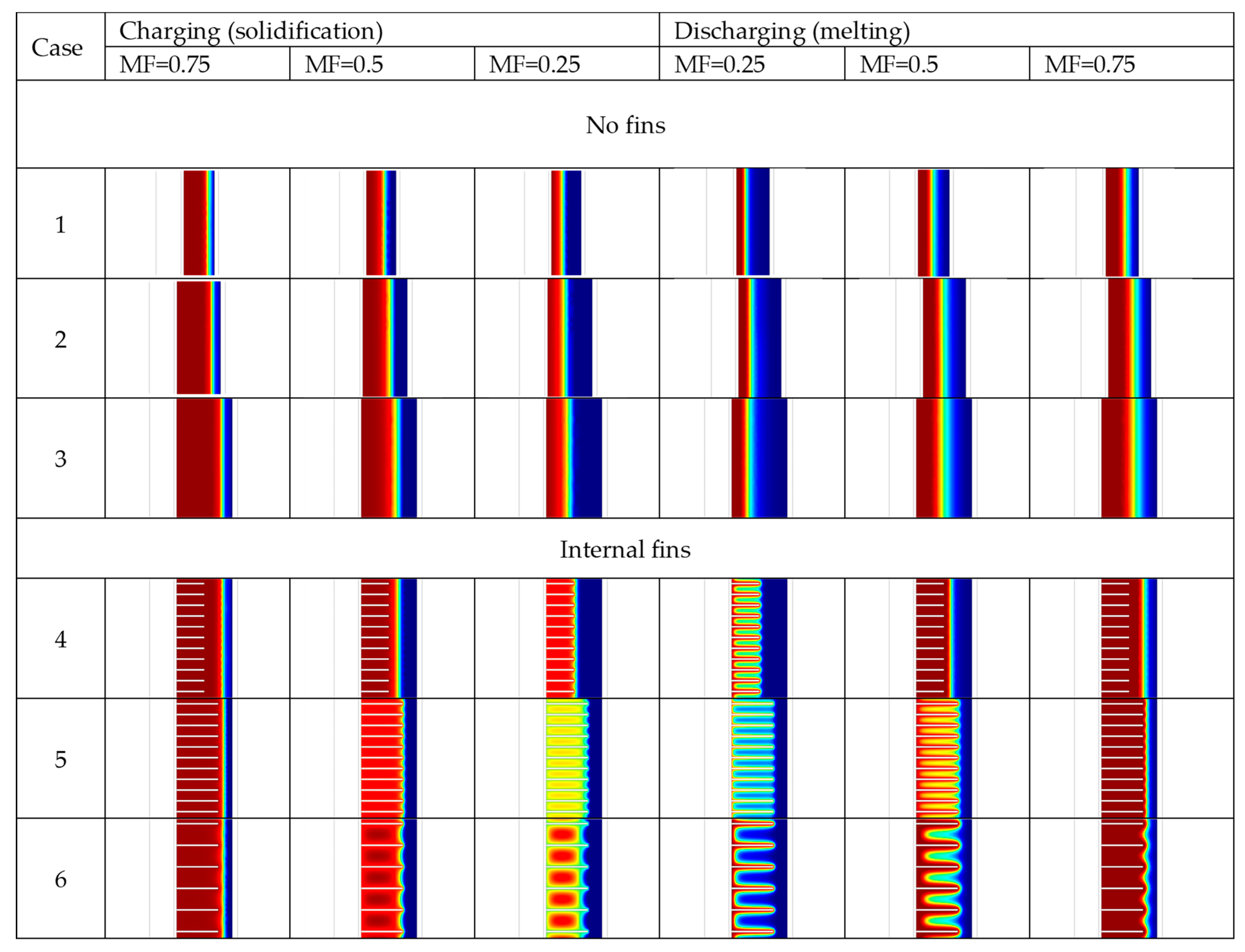
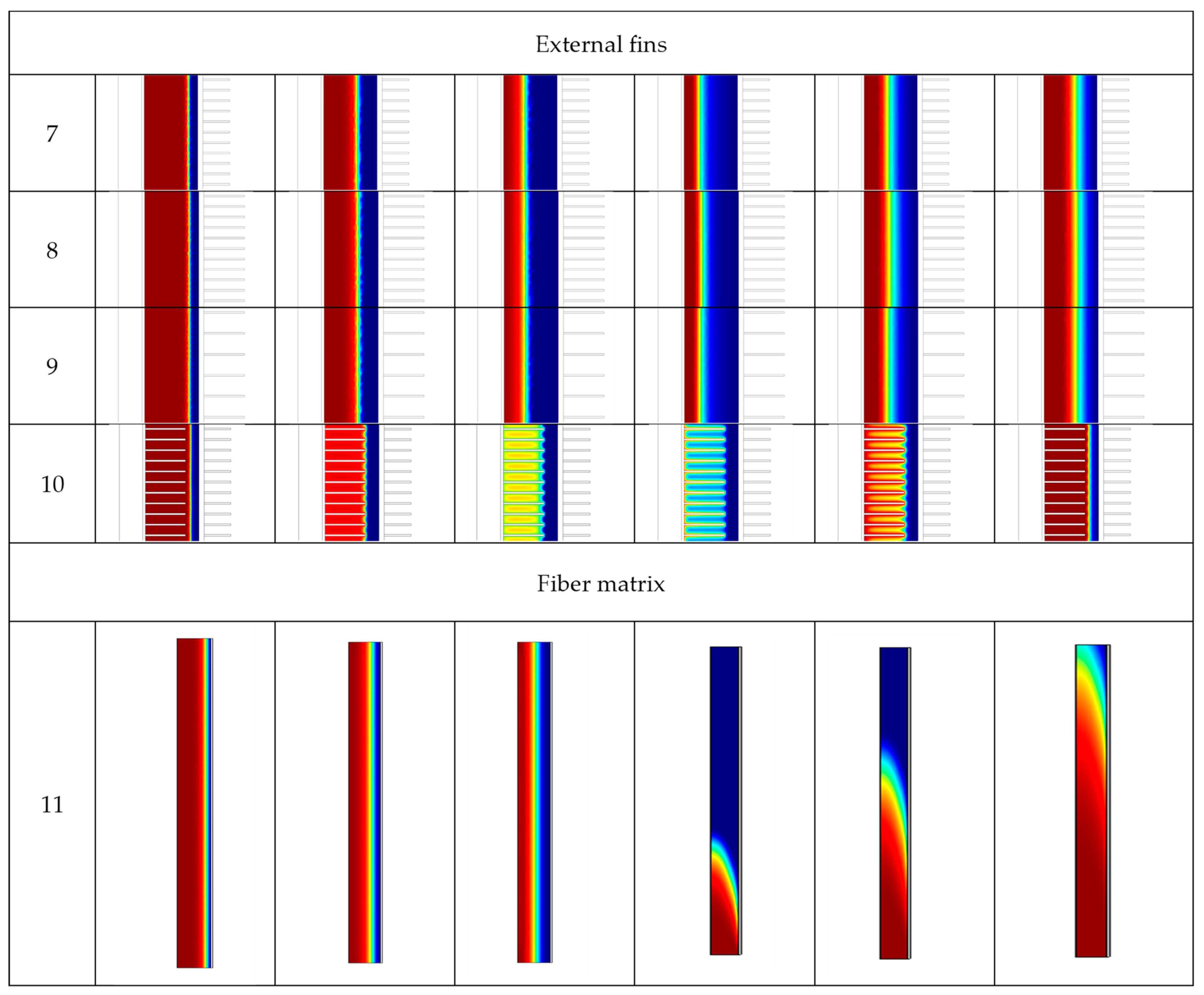
3.2. Charging and Discharging Thermal Cycles
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameter | Description | Unit |
| ρ | Density | kg/m3 |
| P | Pressure | Pa |
| u | Velocity | m/s |
| θ | Fraction/Indicator of phase transition | - |
| Specific heat | J/kgK | |
| am | Mass fraction | - |
| k | Thermal conductivity | W/mK |
| HTF | Heat Transfer Fluid | - |
| LHTES | Latent Heat Thermal Energy Storage | - |
| PCM | Phase Change Material | - |
References
- Souayfane, F.; Fardoun, F.; Biwole, H.P. Phase change materials (PCM) for cooling applications in buildings: A review. Energy Build 2016, 129, 396–431. [Google Scholar] [CrossRef]
- Osterman, E.; Tyagi, V.V.; Butala, V.; Rahim, N.A.; Stritih, U. Review of PCM based cooling technologies for buildings. Energy Build. 2012, 49, 37–49. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Bin Mat, S.; Sopian, K.; Sulaiman, M.Y.; Lim, C.H. The Review of thermal energy storage for air conditioning systems. Renew. Sustain. Energy Rev. 2012, 16, 5802–5819. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Wang, X.L.; Wang, T.; Wang, R.Z. A review on phase change cold storage in air-conditioning system: Materials and applications. Renew. Sustain. Energy Rev. 2013, 22, 108–120. [Google Scholar] [CrossRef]
- Lin, Y.; Jia, Y.; Alva, G.; Fang, G. Review on thermal conductivity enhancement, thermal properties and applications of phase change materials in thermal energy storage. Renew. Sustain. Energy Rev. 2018, 82, 2730–2742. [Google Scholar] [CrossRef]
- Rathod, M.K.; Banerjee, J. Thermal stability of phase change materials used in latent heat energy storage systems: A review. Renew. Sustain. Energy Rev. 2013, 18, 246–258. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Paroutoglou, E.; Afshari, A.; Bergsøe, N.C.; Fojan, P.; Hultmark, G. A PCM based cooling system for office buildings: A state of the art review. E3S Web Conf. 2019, 111, 01026. [Google Scholar] [CrossRef]
- Zhang, H.L.; Baeyens, J.; Degrève, J.; Cáceres, G.; Segal, R.; Pitié, F. Latent heat storage with tubular-encapsulated phase change materials (PCMs). Energy 2014, 76, 66–72. [Google Scholar] [CrossRef]
- Zhao, W.; France, D.M.; Yu, W.; Kim, T.; Singh, D. Phase change material with graphite foam for applications in high-temperature latent heat storage systems of concentrated solar power plants. Renew. Energy 2014, 69, 134–146. [Google Scholar] [CrossRef]
- Aadmi, M.; Karkri, M.; El Hammouti, M. Heat transfer characteristics of thermal energy storage for PCM (phasechange material) melting in horizontal tube: Numerical andexperimental investigations. Energy 2015, 85, 339–352. [Google Scholar] [CrossRef]
- Parrado, C.; Cáceres, G.; Bize, F.; Bubnovich, V.; Baeyens, J.; Degrève, J.; Zhang, H.L. Thermo-mechanical analysis of copper-encapsulated NaNO3-KNO3. Chem. Eng. Res. Des. 2015, 93, 224–231. [Google Scholar] [CrossRef]
- Arena, S.; Casti, E.; Gasia, J.; Cabeza, L.F.; Cau, G. Numerical simulation of a finned-tube LHTES system: Influence of the mushy zone constant on the phase change behaviour. Energy Procedia 2017, 126, 517–524. [Google Scholar] [CrossRef]
- Moulahi, C.; Trigui, A.; Boudaya, C.; Karkri, M. Smart macroencapsulated resin/wax composite for energy conservation in the built environment. J. Thermoplast. Compos. Mater. 2017, 30, 887–914. [Google Scholar] [CrossRef]
- Herbinger, F.; Bhouri, M.; Groulx, D. Investigation of heat transfer inside a PCM-air heat exchanger: A numerical parametric study. Heat Mass Transf. Stoffuebertragung 2018, 54, 2433–2442. [Google Scholar] [CrossRef]
- Arena, S.; Casti, E.; Gasia, J.; Cabeza, L.F.; Cau, G. Numerical analysis of a latent heat thermal energy storage system under partial load operating conditions. Renew. Energy 2018, 128, 350–361. [Google Scholar] [CrossRef]
- Purohit, B.K.; Sistla, V.S. Studies on solution crystallization of Na2SO4·10H2O embedded in porous polyurethane foam for thermal energy storage application. Thermochim. Acta 2018, 668, 9–18. [Google Scholar] [CrossRef]
- Afsharpanah, F.; Izadi, M.; Hamedani, F.A.; Mousavi Ajarostaghi, S.S.; Yaïci, W. Solidification of nano-enhanced PCM-porous composites in a cylindrical cold thermal energy storage enclosure. Case Stud. Therm. Eng. 2022, 39, 1DUMMY. [Google Scholar] [CrossRef]
- Afsharpanah, F.; Mousavi Ajarostaghi, S.S.; Arıcı, M. Parametric study of phase change time reduction in a shell-and-tube ice storage system with anchor-type fin design. Int. Commun. Heat Mass Transf. 2022, 137, 106281. [Google Scholar] [CrossRef]
- Afsharpanah, F.; Pakzad, K.; Mousavi Ajarostaghi, S.S.; Arıcı, M. Assessment of the charging performance in a cold thermal energy storage container with two rows of serpentine tubes and extended surfaces. J. Energy Storage 2022, 51, 104464. [Google Scholar] [CrossRef]
- Shahsavar, A.; Goodarzi, A.; Mohammed, H.I.; Shirneshan, A.; Talebizadehsardari, P. Thermal performance evaluation of non-uniform fin array in a finned double-pipe latent heat storage system. Energy 2020, 193, 116800. [Google Scholar] [CrossRef]
- Shahsavar, A.; Goodarzi, A.; Talebizadehsardari, P.; Arıcı, M. Numerical investigation of a double-pipe latent heat thermal energy storage with sinusoidal wavy fins during melting and solidification. Int. J. Energy Res. 2021, 45, 20934–20948. [Google Scholar] [CrossRef]
- Boulaktout, N.; Mezaache, E.H.; Teggar, M.; Arici, M.; Ismail, K.A.R.; Yildiz, Ç. Effect of Fin Orientation on Melting Process in Horizontal Double Pipe Thermal Energy Storage Systems. J. Energy Resour. Technol. Trans. ASME 2021, 143, 1–14. [Google Scholar] [CrossRef]
- Nicholls, R.A.; Moghimi, M.A.; Griffiths, A.L. Impact of fin type and orientation on performance of phase change material-based double pipe thermal energy storage. J. Energy Storage 2022, 50, 104671. [Google Scholar] [CrossRef]
- Paroutoglou, E.; Fojan, P.; Gurevich, L.; Hultmark, G.; Afshari, A. Thermal Analysis of Organic and Nanoencapsulated Electrospun Phase Change Materials. Energies 2021, 14, 995. [Google Scholar] [CrossRef]
- Paroutoglou, E.; Afshari, A.; Fojan, P.; Hultmark, G. Investigation of Thermal Behavior of Paraffins, Fatty Acids, Salt Hydrates and Renewable Based Oils as PCM. In Proceedings of the International Renewable Energy Storage Conference 2020 (IRES 2020), Düsseldorf, Germany, 10–12 March 2020; Volume 6, pp. 34–40. [Google Scholar] [CrossRef]
- Paroutoglou, E.; Fojan, P.; Gurevich, L. Thermal Properties of Novel Phase-Change Materials Based on Tamanu and Coconut Oil Encapsulated in Electrospun Fiber Matrices. Sustainability 2022, 14, 7432. [Google Scholar] [CrossRef]
- Medrano, M.; Yilmaz, M.O.; Nogués, M.; Martorell, I.; Roca, J.; Cabeza, L.F. Experimental evaluation of commercial heat exchangers for use as PCM thermal storage systems. Appl. Energy 2009, 86, 2047–2055. [Google Scholar] [CrossRef]



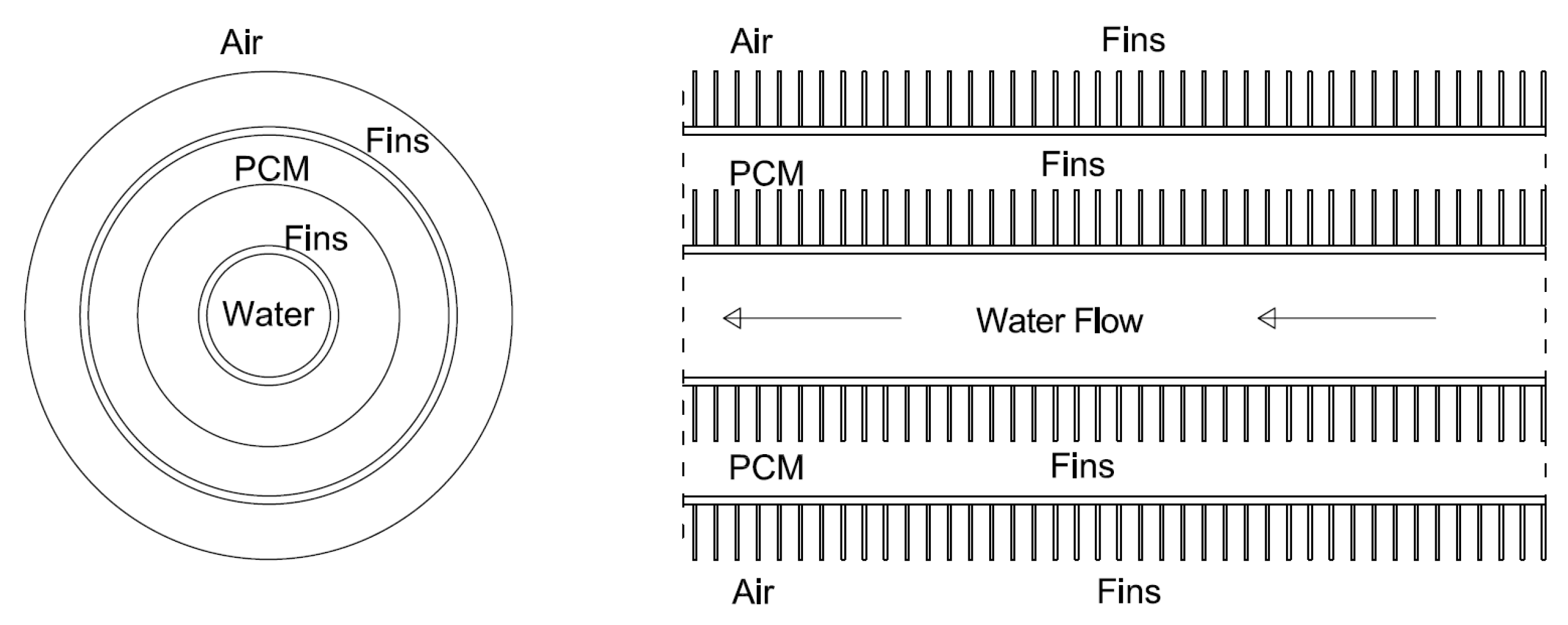
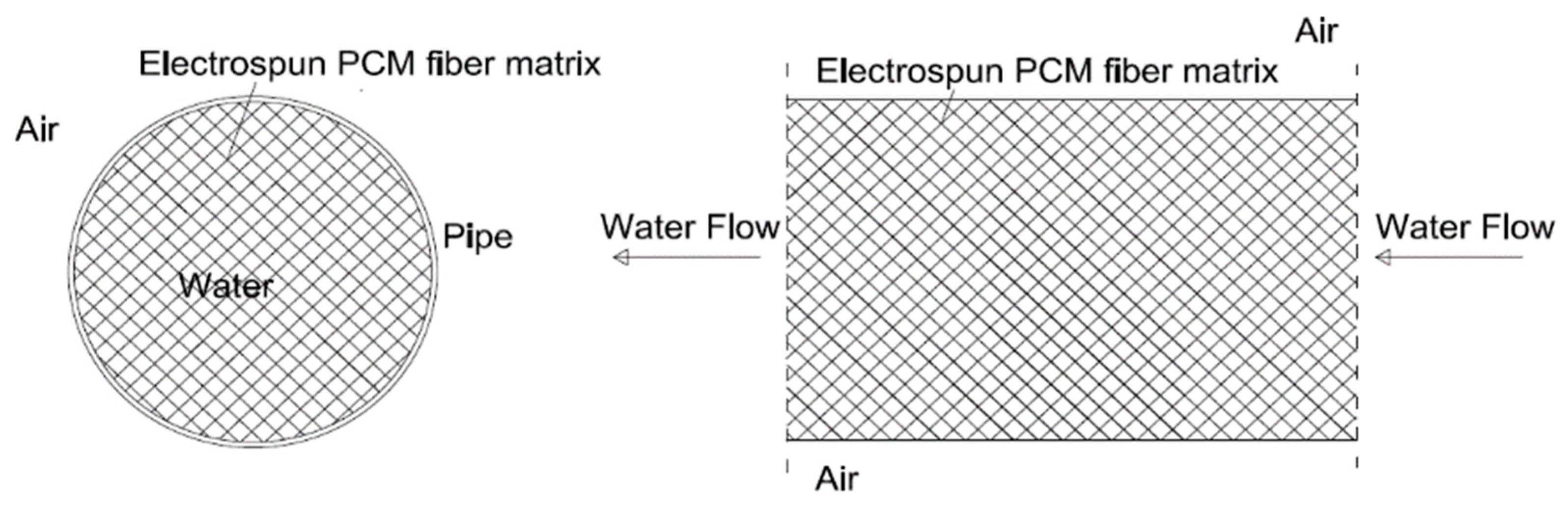


| Case | Copper PCM Pipe Inner Diameter (m) | Thickness of PCM Pipe (m) | PCM Mass (kg) | Internal Fins | External Fins | Fins Width (m) | Fins Height (m) | Distance between Fins (m) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.026797 m | 0.000889 m | 0.158 | - | - | - | |||
| 2 | 0.0327914 m | 0.0010668 m | 0.257 | - | - | - | |||
| 3 | 0.0387858 m | 0.0012446 m | 0.376 | - | - | - | |||
| 4 | 0.0387858 m | 0.0012446 m | 0.362 | x | 0.0065 m | 0.0004 m | 0.0021 m | ||
| 5 | 0.0387858 m | 0.0012446 m | 0.352 | x | 0.00975 m | 0.0004 m | 0.0021 m | ||
| 6 | 0.0387858 m | 0.0012446 m | 0.364 | x | 0.00975 m | 0.0004 m | 0.0046 m | ||
| 7 | 0.0387858 m | 0.0012446 m | 0.376 | x | 0.0065 m | 0.0004 m | 0.0021 m | ||
| 8 | 0.0387858 m | 0.0012446 m | 0.376 | x | 0.00975 m | 0.0004 m | 0.0021 m | ||
| 9 | 0.0387858 m | 0.0012446 m | 0.376 | x | 0.00975 m | 0.0004 m | 0.0046 m | ||
| 10 | 0.0387858 m | 0.0012446 m | 0.352 | x | x | Int. fins | Ext. fins | 0.0004 m | 0.0021 m |
| 0.00975 m | 0.0065 m | ||||||||
| 11 | 0.0387858 m | 0.0012446 m | 0.198 | - | - | - | |||
| Theoretical Properties | |
| Density (Solid) | 0.88 kg/L |
| Density (Liquid) | 0.77 kg/L |
| Heat Capacity (Solid) | 2 kJ/kg·K |
| Heat Capacity (Liquid) | 2 kJ/kg·K |
| Latent Heat of Fusion | 260 kJ/kg |
| Thermal Conductivity | 0.2 W/m·K |
| Melting Point | 18 °C |
| Experimental Properties (Pure RT18) | |
| Melting temperature | 17.5 °C |
| Solidification temperature | 15.4 °C |
| Latent heat of melting | 137.8 kJ/kg |
| Latent heat of solidification | 139.3 kJ/kg |
| Experimental Properties (RT18 Electrospun Fiber Matrix) | |
| Melting temperature | 17.3 °C |
| Solidification temperature | 15.2 °C |
| Latent heat of melting | 102.1 kJ/kg |
| Latent heat of solidification | 82.2 kJ/kg |
| Porosity of fiber matrix | 0.474 |
| Experiment | Process | Temperature Conditions | Turbulent Flow | PCM Properties | Air Temperature (°C) | ||
|---|---|---|---|---|---|---|---|
| Water Inlet (°C) | PCM at Start (°C) | Volumetric Flow Rate (m3/h) | Latent Heat (J/g) | Phase Change Temp. (°C) | |||
| 1 | Charge (Melting) | 50 | 24 | 0.38 | 157 | 35 | 22–24 |
| 2 | Charge (Melting) | 50 | 24 | 0.35 | 157 | 35 | 22–24 |
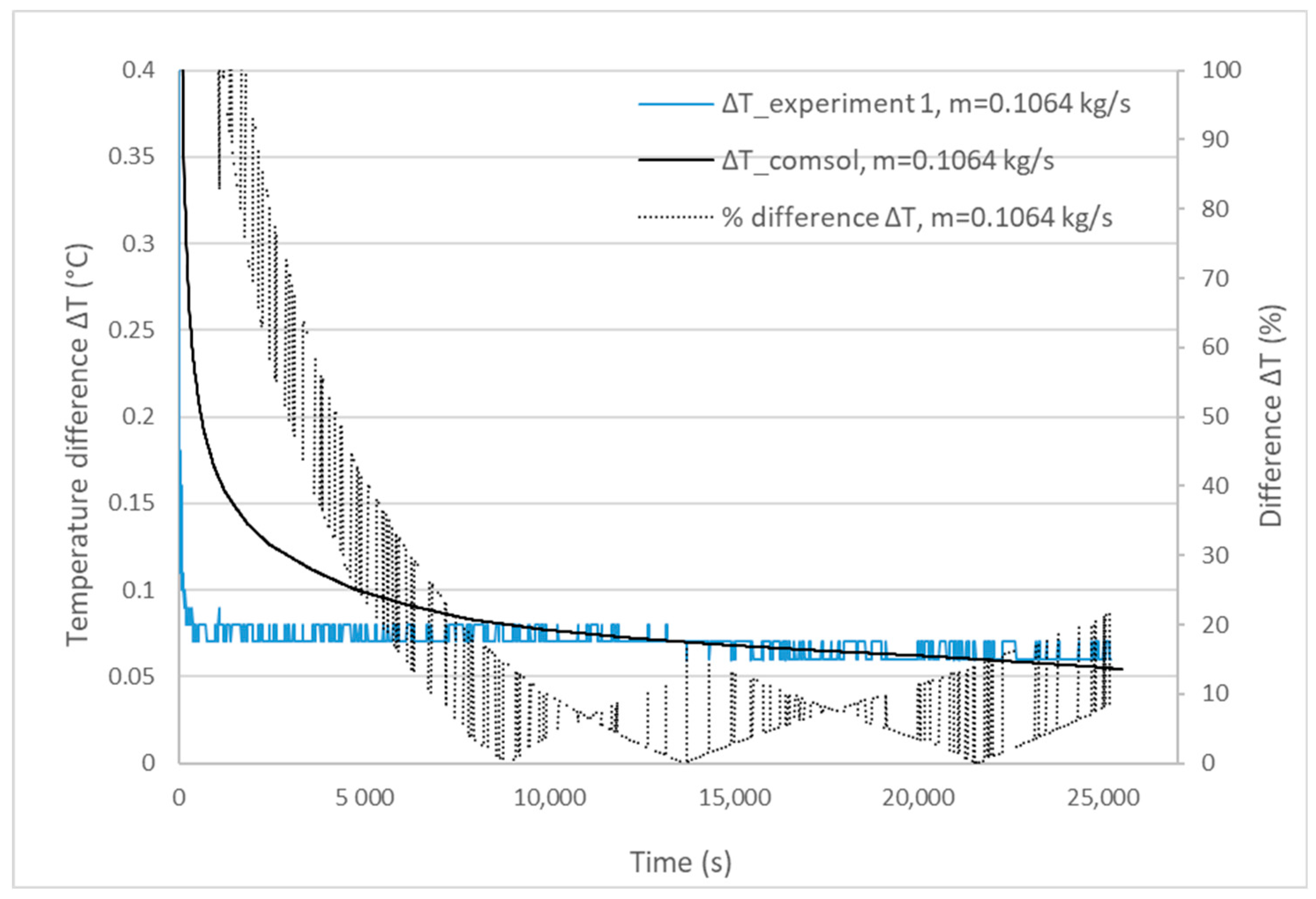
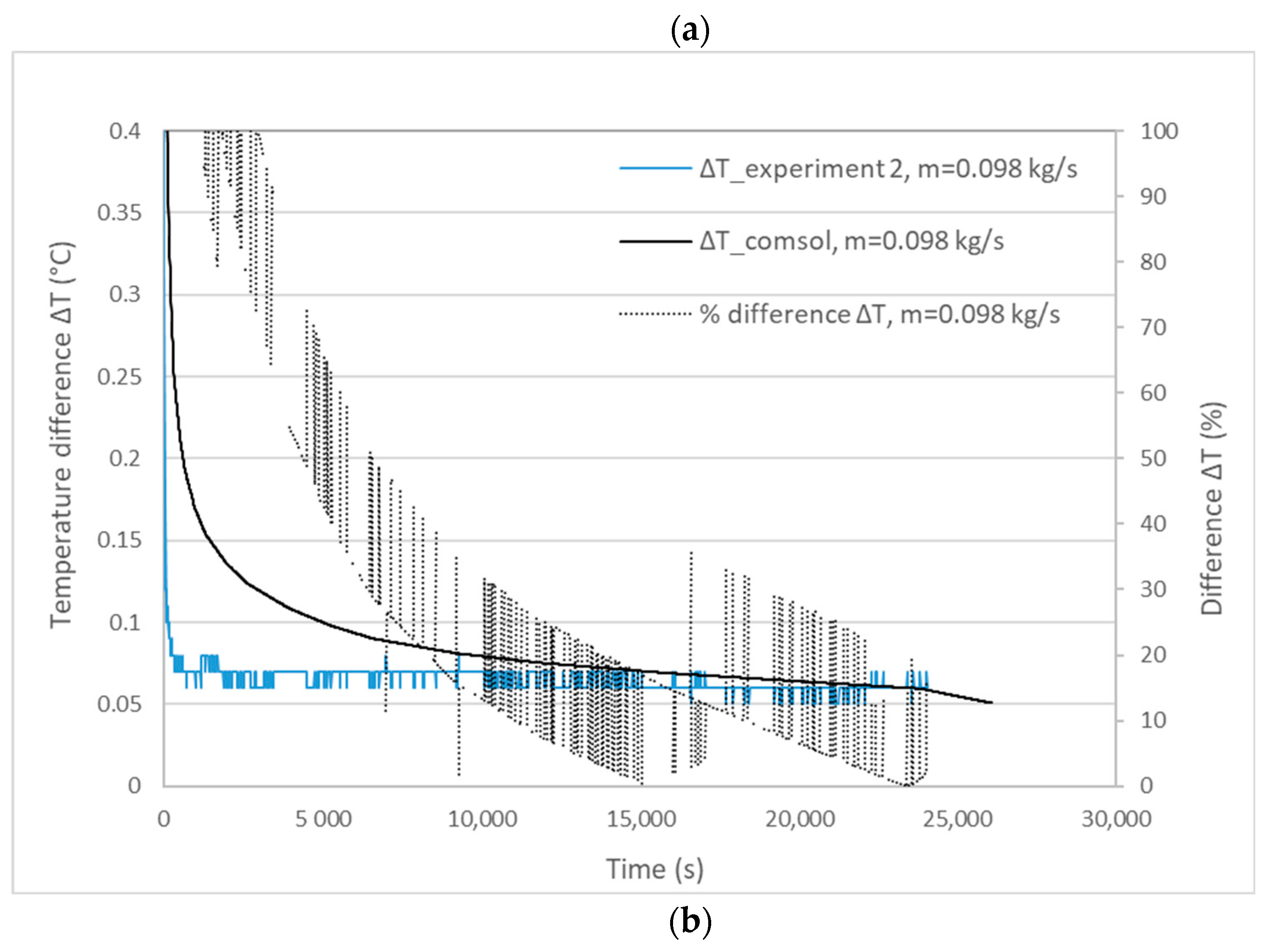
| Experiment | Mass Flow Rate (kg/s) | Experimental Melting Time | Calculated Melting Time | Percentage Difference |
|---|---|---|---|---|
| 1 | 0.1064 | 25,200 s | 26,470 s | 5% < 10% |
| 2 | 0.0980 | 24,060 s | 26,060 s | 8.3% < 10% |
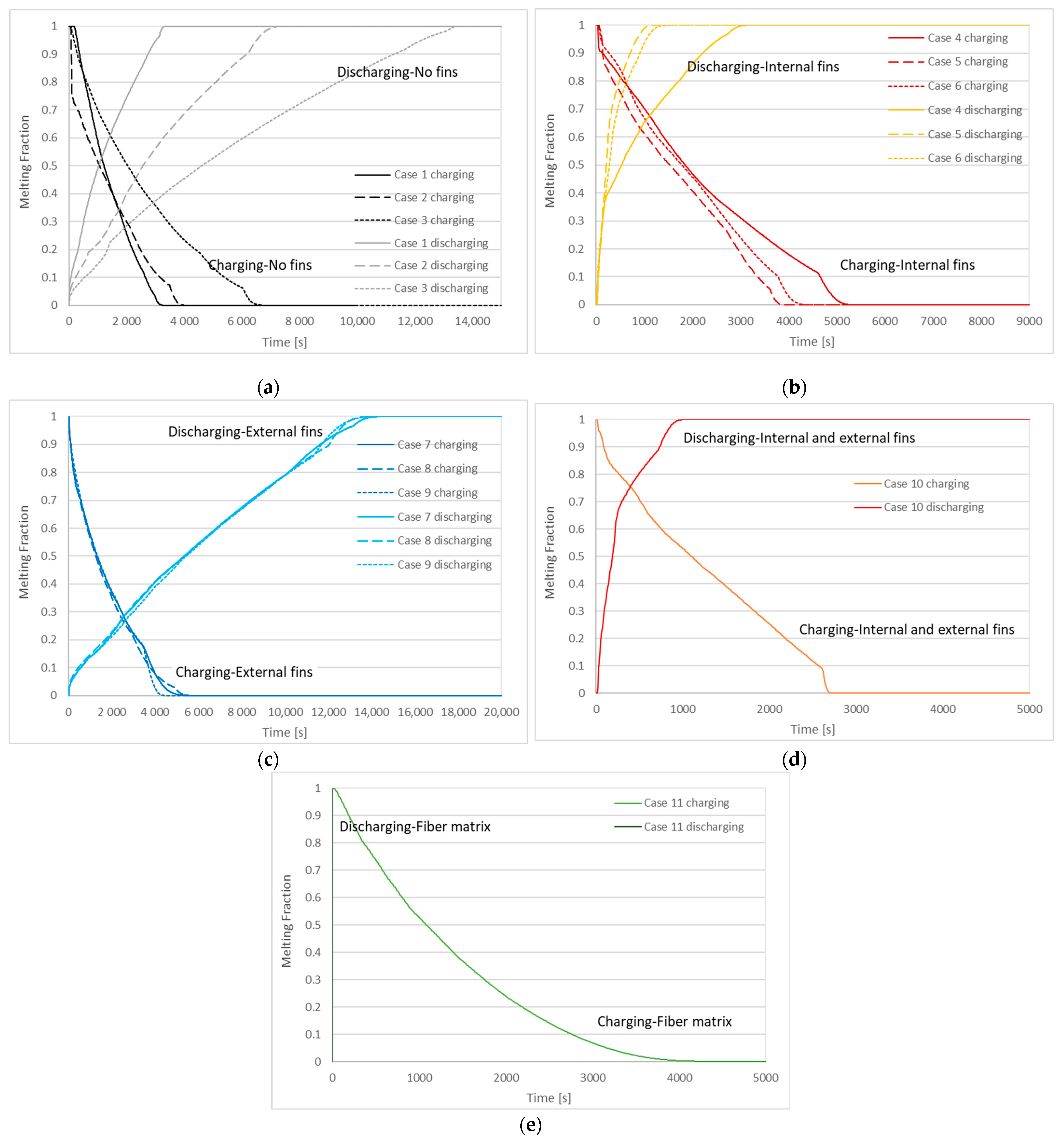
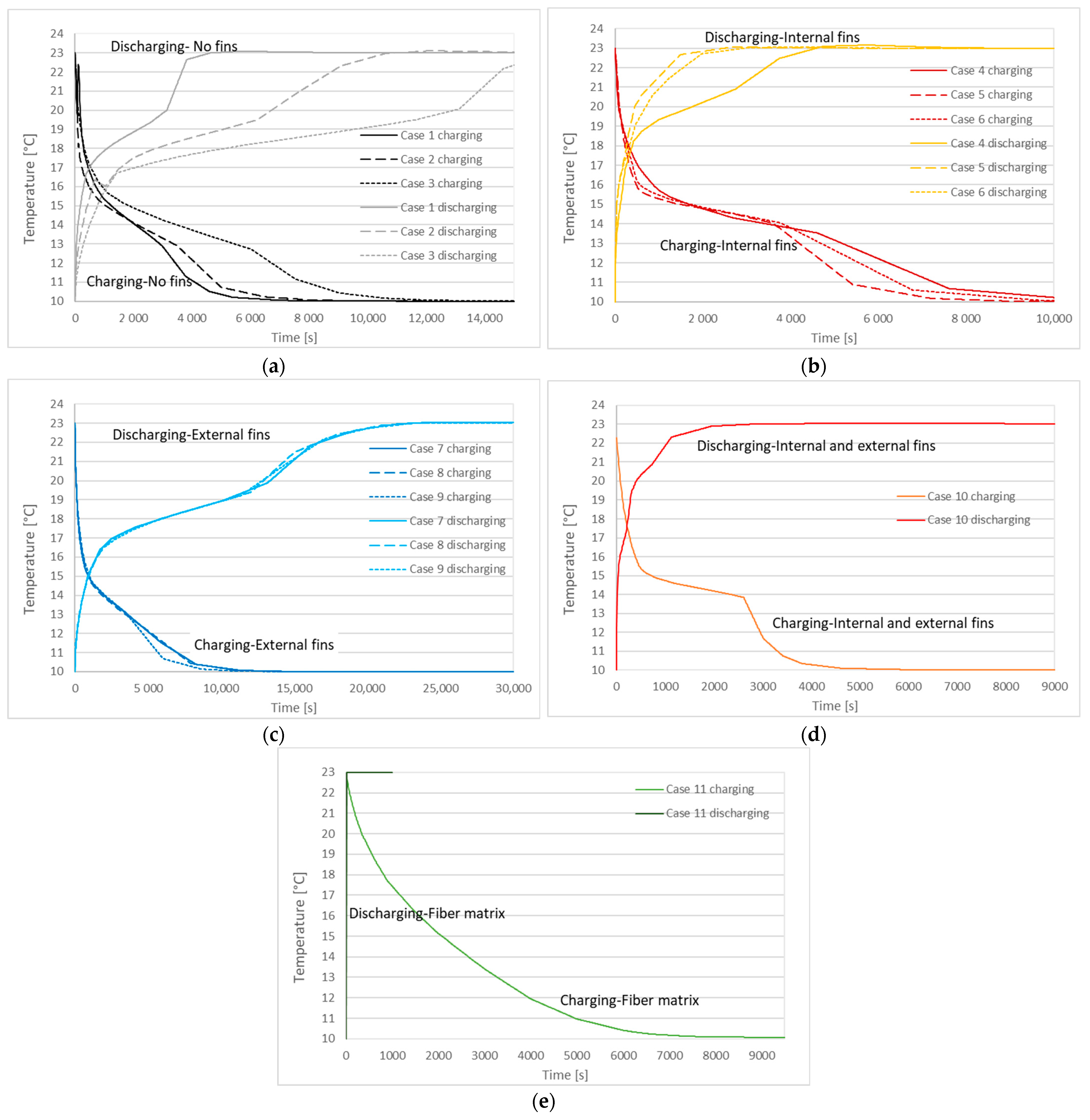
| Case | Charging (Solidification) Time | Discharging (Melting) Time |
|---|---|---|
| 1 | 3310 s | 3420 s |
| 2 | 4090 s | 7070 s |
| 3 | 6940 s | 13,620 s |
| 4 | 5500 s | 3220 s |
| 5 | 4060 s | 1230 s |
| 6 | 4500 s | 1530 s |
| 7 | 5830 s | 14,590 s |
| 8 | 5710 s | 14,070 s |
| 9 | 4520 s | 14,510 s |
| 10 | 3040 s | 1040 s |
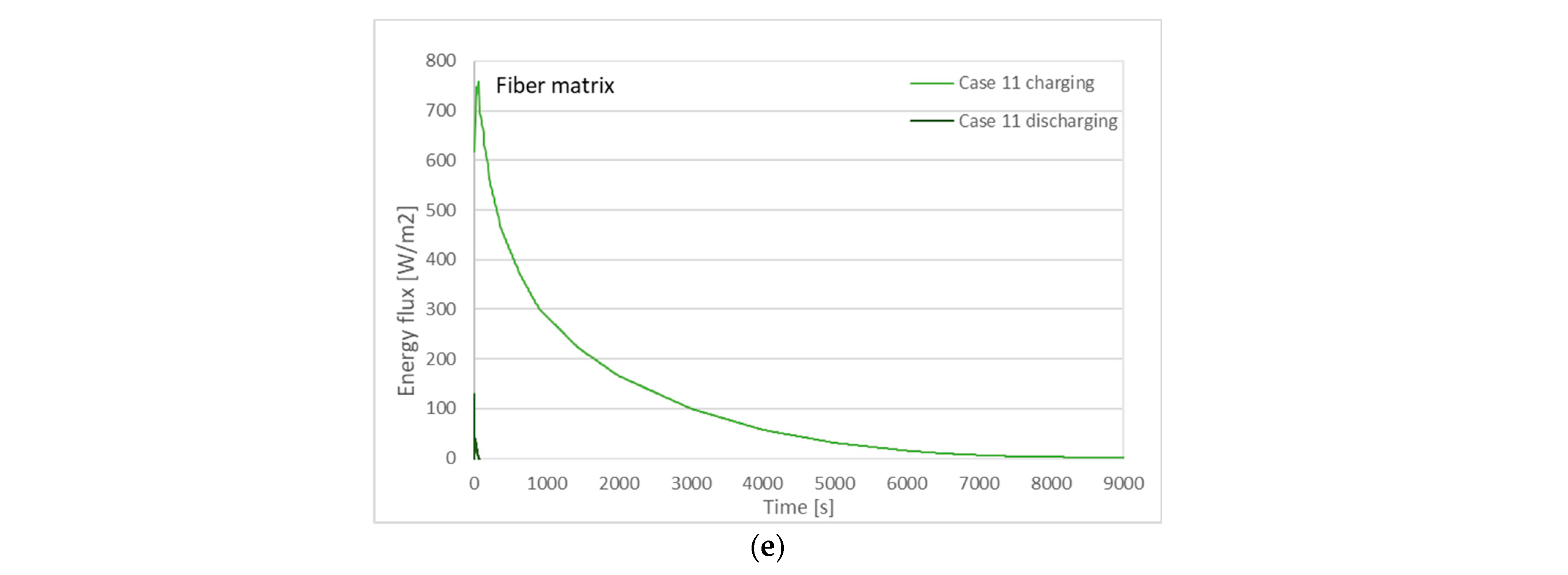
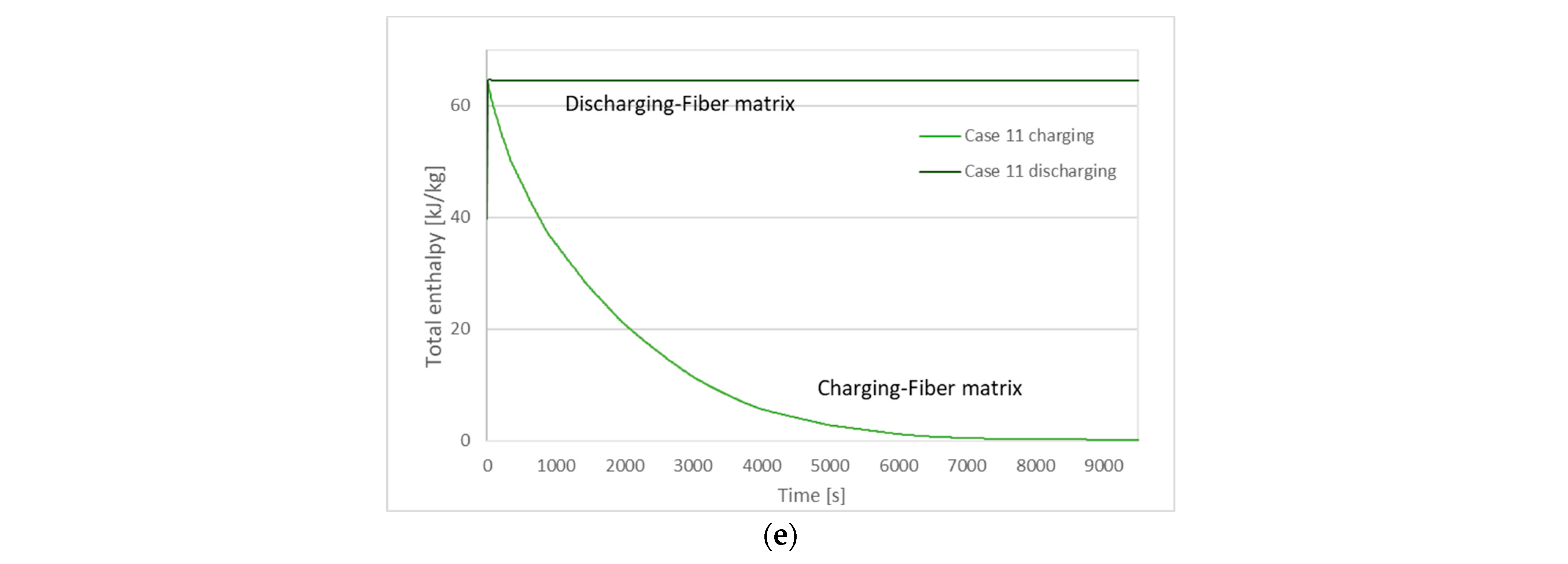
| 11 | 4780 s | 4 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paroutoglou, E.; Fojan, P.; Gurevich, L.; Furbo, S.; Fan, J.; Medrano, M.; Afshari, A. A Numerical Parametric Study of a Double-Pipe LHTES Unit with PCM Encapsulated in the Annular Space. Sustainability 2022, 14, 13317. https://doi.org/10.3390/su142013317
Paroutoglou E, Fojan P, Gurevich L, Furbo S, Fan J, Medrano M, Afshari A. A Numerical Parametric Study of a Double-Pipe LHTES Unit with PCM Encapsulated in the Annular Space. Sustainability. 2022; 14(20):13317. https://doi.org/10.3390/su142013317
Chicago/Turabian StyleParoutoglou, Evdoxia, Peter Fojan, Leonid Gurevich, Simon Furbo, Jianhua Fan, Marc Medrano, and Alireza Afshari. 2022. "A Numerical Parametric Study of a Double-Pipe LHTES Unit with PCM Encapsulated in the Annular Space" Sustainability 14, no. 20: 13317. https://doi.org/10.3390/su142013317
APA StyleParoutoglou, E., Fojan, P., Gurevich, L., Furbo, S., Fan, J., Medrano, M., & Afshari, A. (2022). A Numerical Parametric Study of a Double-Pipe LHTES Unit with PCM Encapsulated in the Annular Space. Sustainability, 14(20), 13317. https://doi.org/10.3390/su142013317








